Spatial Frequency Response of Epoxy-Based Volume Holographic Recording Material
Abstract
1. Introduction
2. Results and Discussion
2.1. Spectral Width of the Material Response
2.2. The Optimum Spatial Frequency Response
2.3. The Maximum Spatial Frequency Response
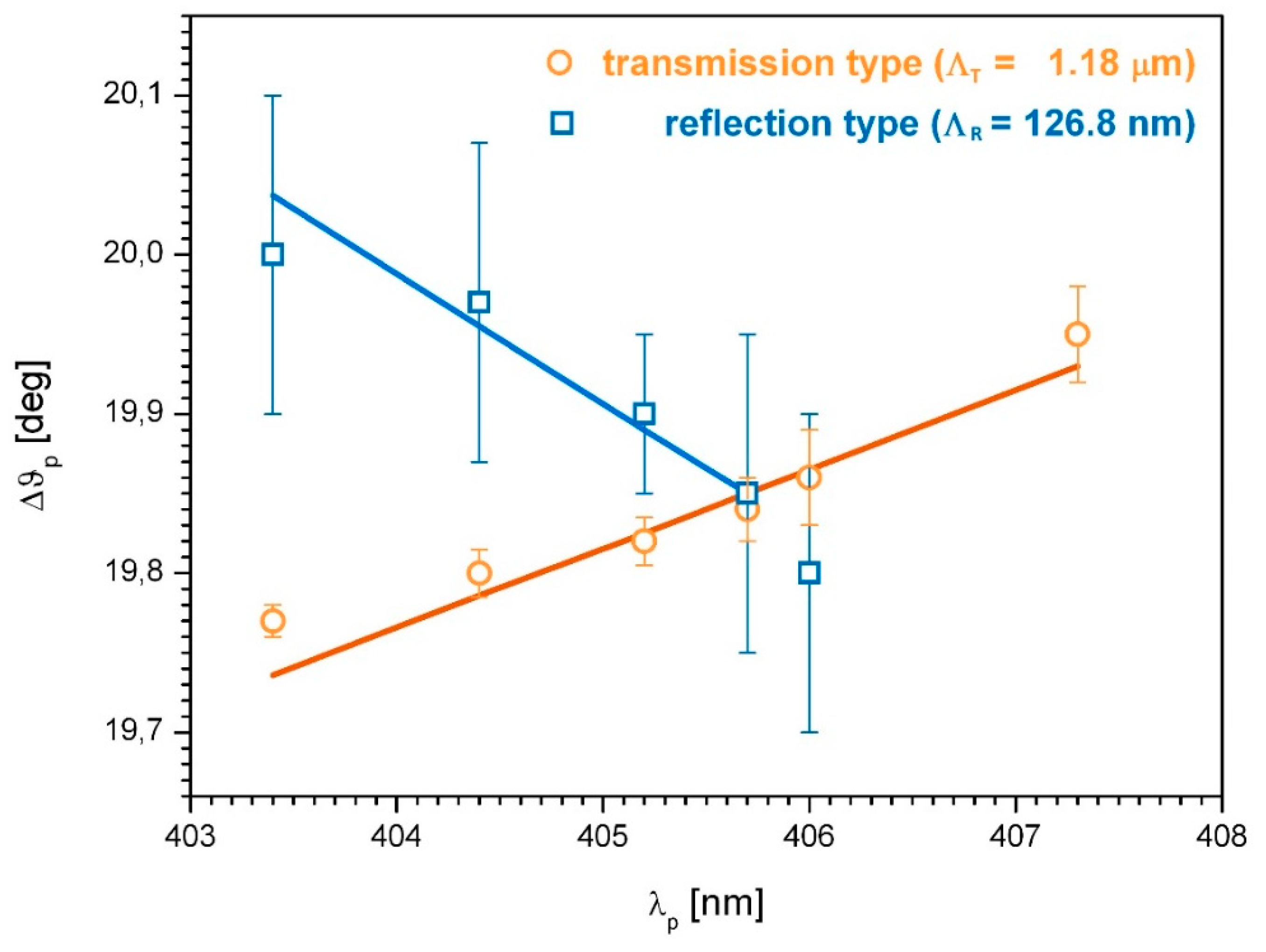
2.4. Separation of High Spatial Frequency Gratings
3. Materials and Methods
3.1. Sample Preparation
3.2. Holographic Exposure
3.3. Hologram Characterization
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Roy, D.; Cambre, J.N.; Sumerlin, B.S. Future perspectives and recent advances in stimuli-responsive materials. Prog. Polym. Sci. 2010, 35, 278–301. [Google Scholar] [CrossRef]
- Colburn, W.S.; Haines, K.A. Volume Hologram Formation in Photopolymer Materials. Appl. Opt. 1971, 10, 1636–1641. [Google Scholar] [CrossRef]
- Malallah, R.; Li, H.; Kelly, D.P.; Healy, J.J.; Sheridan, J.T. A Review of Hologram Storage and Self-Written Waveguides Formation in Photopolymer Media. Polymers 2017, 9, 337. [Google Scholar] [CrossRef]
- Sabel, T.; Lensen, M.C. Volume Holography: Novel Materials, Methods and Applications. In Holographic Materials and Optical Systems; InTech: Rijeka, Croatia, 2017. [Google Scholar]
- Naydenova, I.; Akbari, H.; Dalton, C.; Mohamed, M.Y.; Wei, C.P.T.; Toal, V.; Martin, S. Photopolymer Holographic Optical Elements for Application in Solar Energy Concentrators. In Holography—Basic Principles and Contemporary Applications; Mihaylova, E., Ed.; InTech: Rijeka, Croatia, 2013; pp. 129–145. [Google Scholar]
- Sabel, T.; Lensen, M.C. Function and structure—Combined optical functionality and specific bio- interaction for multifunctional biomedical materials. J. Med. Mater. Technol. 2017, 1, 10–12. [Google Scholar]
- Sabel, T. Volume hologram formation in SU-8 photoresist. Polymers 2017, 9, 198. [Google Scholar] [CrossRef]
- Sabel, T.; de Vicente Lucas, G.; Lensen, M.C. Simultaneous formation of holographic surface relief gratings and volume phase gratings in photosensitive polymer. Mater. Res. Lett. 2019. submitted. [Google Scholar]
- Fukuda, Y.; Tomita, Y. Spatial Frequency Responses of Anisotropic Refractive Index Gratings Formed in Holographic Polymer Dispersed Liquid Crystals. Materials 2016, 9, 188. [Google Scholar] [CrossRef] [PubMed]
- Gallego, S.; Neipp, C.; Estepa, L.A.; Ortuño, M.; Márquez, A.; Francés, J.; Pascual, I.; Beléndez, A. Volume Holograms in Photopolymers: Comparison between Analytical and Rigorous Theories. Materials 2012, 5, 1373–1388. [Google Scholar] [CrossRef]
- Trout, T.J.; Schmieg, J.J.; Gambogi, W.J.; Weber, A.M. Optical Photopolymers: Design and Applications. Adv. Mater. 1998, 10, 1219–1224. [Google Scholar] [CrossRef]
- Martin, S.; Feely, C.A.; Toal, V. Holographic recording characteristics of an acrylamide-based photopolymer. Appl. Opt. 1997, 36, 5757–5768. [Google Scholar] [CrossRef] [PubMed]
- Sabel, T.; Orlic, S.; Pfeiffer, K.; Ostrzinski, U.; Grützner, G. Free-surface photopolymerizable recording material for volume holography. Opt. Mater. Express 2013, 3, 329–338. [Google Scholar] [CrossRef]
- Andreeva, O.V.; Korzinin, Y.L.; Manukhin, B.G. Volume Transmission Hologram Gratings—Basic Properties, Energy Channelizing, Effect of Ambient Temperature and Humidity. In Holography—Basic Principles and Contemporary Applications; Mihaylova, E., Ed.; InTech: Rijeka, Croatia, 2013; pp. 37–60. [Google Scholar]
- Sabel, T.; Zschocher, M. Dynamic Bragg Angle Shift in the Course of Volume Hologram Formation. Mater. Res. Lett. 2014, 2, 76–81. [Google Scholar] [CrossRef]
- Moothanchery, M.; Naydenova, I.; Toal, V. Study of the shrinkage caused by holographic grating formation in acrylamide based photopolymer film. Opt. Express 2011, 19, 13395–13404. [Google Scholar] [CrossRef]
- Sheridan, J.T.; Lawrence, J.R. Nonlocal-response diffusion model of holographic recording in photopolymer. J. Opt. Soc. Am. A 2000, 17, 1108–1114. [Google Scholar] [CrossRef]
- Fernandez, E.; Fuentes, R.; Ortuño, M.; Beléndez, A.; Pascual, I. Diffraction efficiency improvement in high spatial frequency holographic gratings stored in PVA/AA photopolymers: Several ACPA concentrations. J. Opt. 2014, 17, 15401. [Google Scholar] [CrossRef]
- Juodkazis, S.; Mizeikis, V.; Seet, K.K.; Miwa, M.; Misawa, H. Two-photon lithography of nanorods in SU-8 photoresist. Nanotechnology 2005, 16, 846. [Google Scholar] [CrossRef]
- Sabel, T.; Zschocher, M. Transition of refractive index contrast in course of grating growth. Sci. Rep. 2013, 3, 1–7. [Google Scholar] [CrossRef]
- Gleeson, M.R.; Guo, J.; Sheridan, J.T. Optimisation of photopolymers for holographic applications using the Non- local Photopolymerization Driven Diffusion model Optimisation of photopolymers for holographic applications using the Non-local Photo- polymerization Driven Diffusion model. Opt. Express 2011, 19, 22423–22436. [Google Scholar] [CrossRef]
- Sheridan, J.T.; Downey, M.; Neill, F.O. Diffusion-based model of holographic grating formation in photopolymers: Generalized non-local material responses. J. Opt. A Pure Appl. Opt. 2001, 3, 477–488. [Google Scholar] [CrossRef]
- Guo, J.; Gleeson, M.R.; Liu, S.; Sheridan, J.T. Non-local spatial frequency response of photopolymer materials containing chain transfer agents: I. Theoretical modelling. J. Opt. 2011, 13, 095601. [Google Scholar] [CrossRef]
- Suzuki, N.; Tomita, Y. Highly transparent ZrO2 nanoparticle-dispersed acrylate photopolymers for volume holographic recording. Opt. Express 2006, 14, 2125–2129. [Google Scholar] [CrossRef]
- Booth, B.L. Photopolymer Material for Holography. Appl. Opt. 1975, 14, 593–601. [Google Scholar] [CrossRef]
- Akbari, H.; Naydenova, I.; Martin, S. Using Acrylamide Based Photopolymers for Fabrication of Holographic Optical Elements in Solar Energy Applications. Appl. Opt. 2014, 53, 1343–1353. [Google Scholar] [CrossRef]
- Jallapuram, R.; Naydenova, I.; Toal, V.; Martin, S.; Howard, R. Spatial Frequency Response of Acrylamide Based Holographic Photopolymer. In Proceedings of the International Conference on Laser Applications and Optical Metrology; Shakher, C., Mehta, D.S., Eds.; Anamaya Publishers: New Delhi, India, 2003; pp. 275–279. [Google Scholar]
- Trentler, T.J.; Boyd, J.E.; Colvin, V.L. Epoxy Resin—Photopolymer Composites for Volume Holography. Chem. Mater. 2000, 12, 1431–1438. [Google Scholar] [CrossRef]
- Jeong, Y.-C.; Lee, S.; Park, J.-K. Holographic diffraction gratings with enhanced sensitivity based on epoxy-resin photopolymers. Opt. Express 2007, 15, 1497–1504. [Google Scholar] [CrossRef]
- Guo-Dong, L.; Qing-Sheng, H.; Shou-Jun, L.; Min-Xian, W.; Guo-Fan, J.; Meng-Quan, S.; Fei-Peng, W. Epoxy Resin-Photopolymer Composite with None-Shrinkage for Volume Holography. Chin. Phys. Lett. 2003, 20, 1733–1735. [Google Scholar] [CrossRef]
- Sabel, T.; Zschocher, M. Imaging of Volume Phase Gratings in a Photosensitive Polymer, Recorded in Transmission and Reflection Geometry. Appl. Sci. 2014, 4, 19–27. [Google Scholar] [CrossRef]
- Sabel, T. Spatially resolved analysis of Bragg selectivity. Appl. Sci. 2015, 5, 1064–1075. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are not available from the authors. |



© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabel, T. Spatial Frequency Response of Epoxy-Based Volume Holographic Recording Material. Molecules 2019, 24, 1018. https://doi.org/10.3390/molecules24061018
Sabel T. Spatial Frequency Response of Epoxy-Based Volume Holographic Recording Material. Molecules. 2019; 24(6):1018. https://doi.org/10.3390/molecules24061018
Chicago/Turabian StyleSabel, Tina. 2019. "Spatial Frequency Response of Epoxy-Based Volume Holographic Recording Material" Molecules 24, no. 6: 1018. https://doi.org/10.3390/molecules24061018
APA StyleSabel, T. (2019). Spatial Frequency Response of Epoxy-Based Volume Holographic Recording Material. Molecules, 24(6), 1018. https://doi.org/10.3390/molecules24061018





