Pressure-Dependent Structural and Luminescence Properties of 1-(Pyren-1-yl)but-2-yn-1-one
Abstract
:1. Introduction
2. Results and Discussion
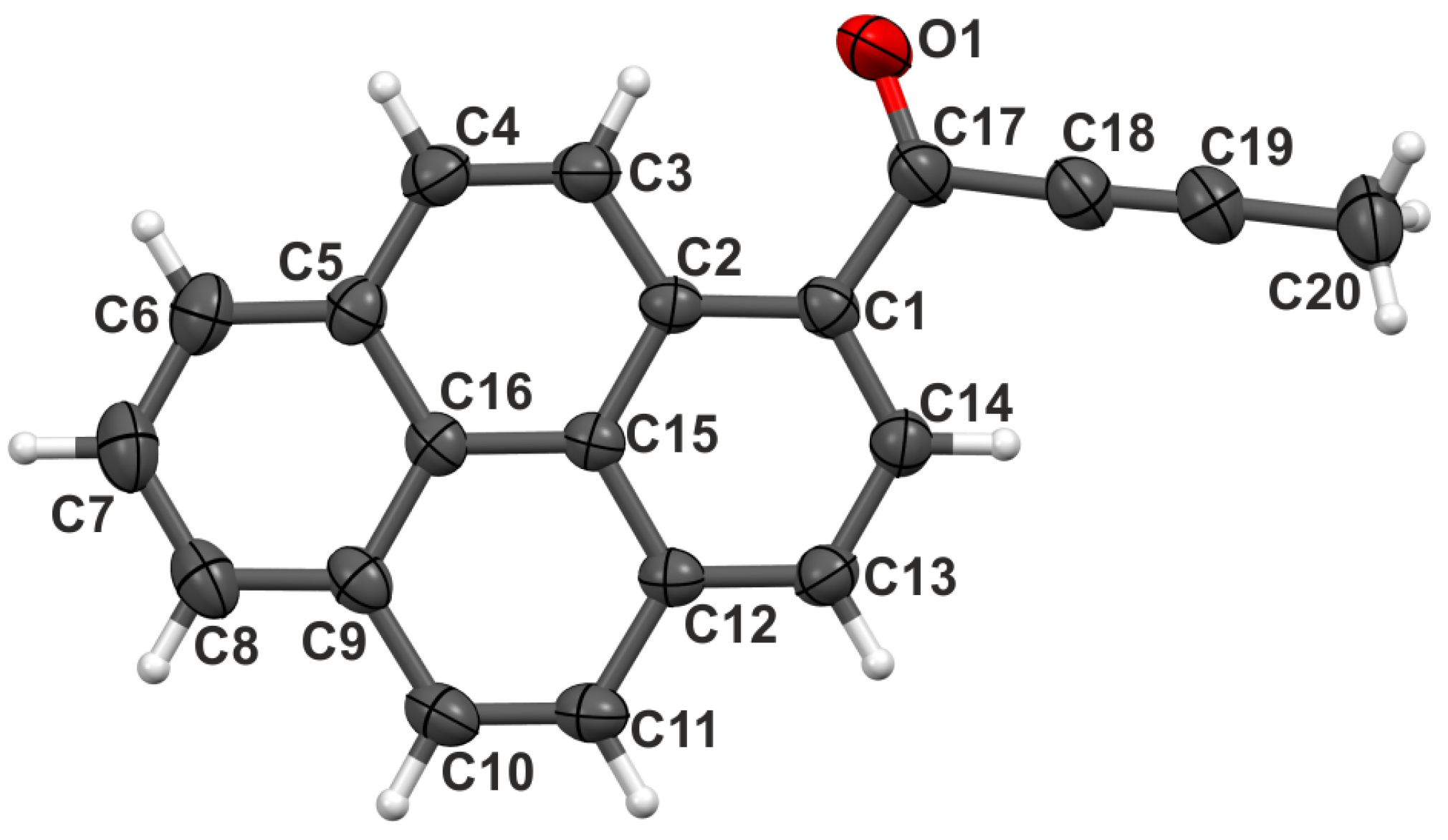
2.1. Structure at Ambient Pressure
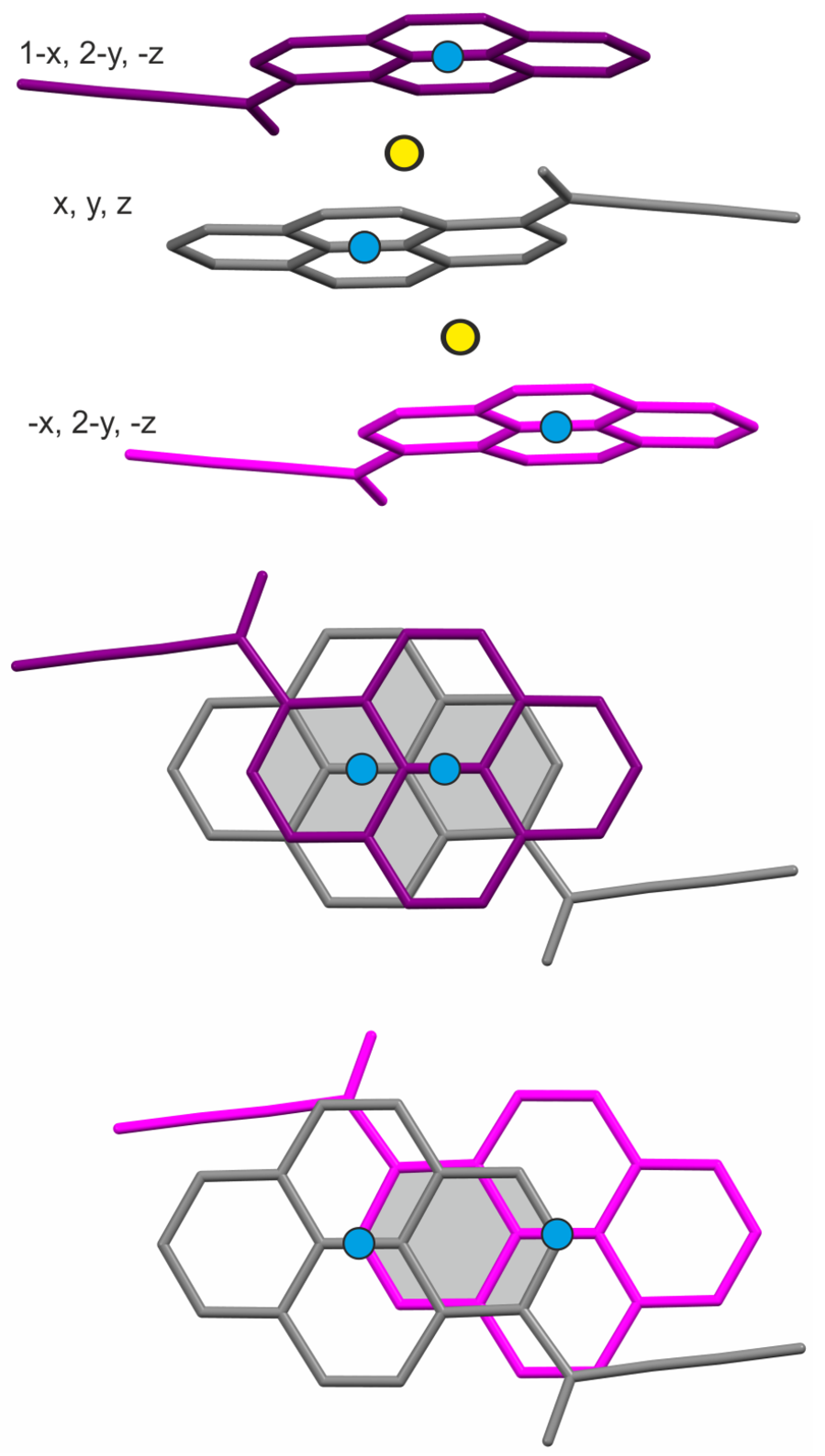
2.2. Energy Frameworks
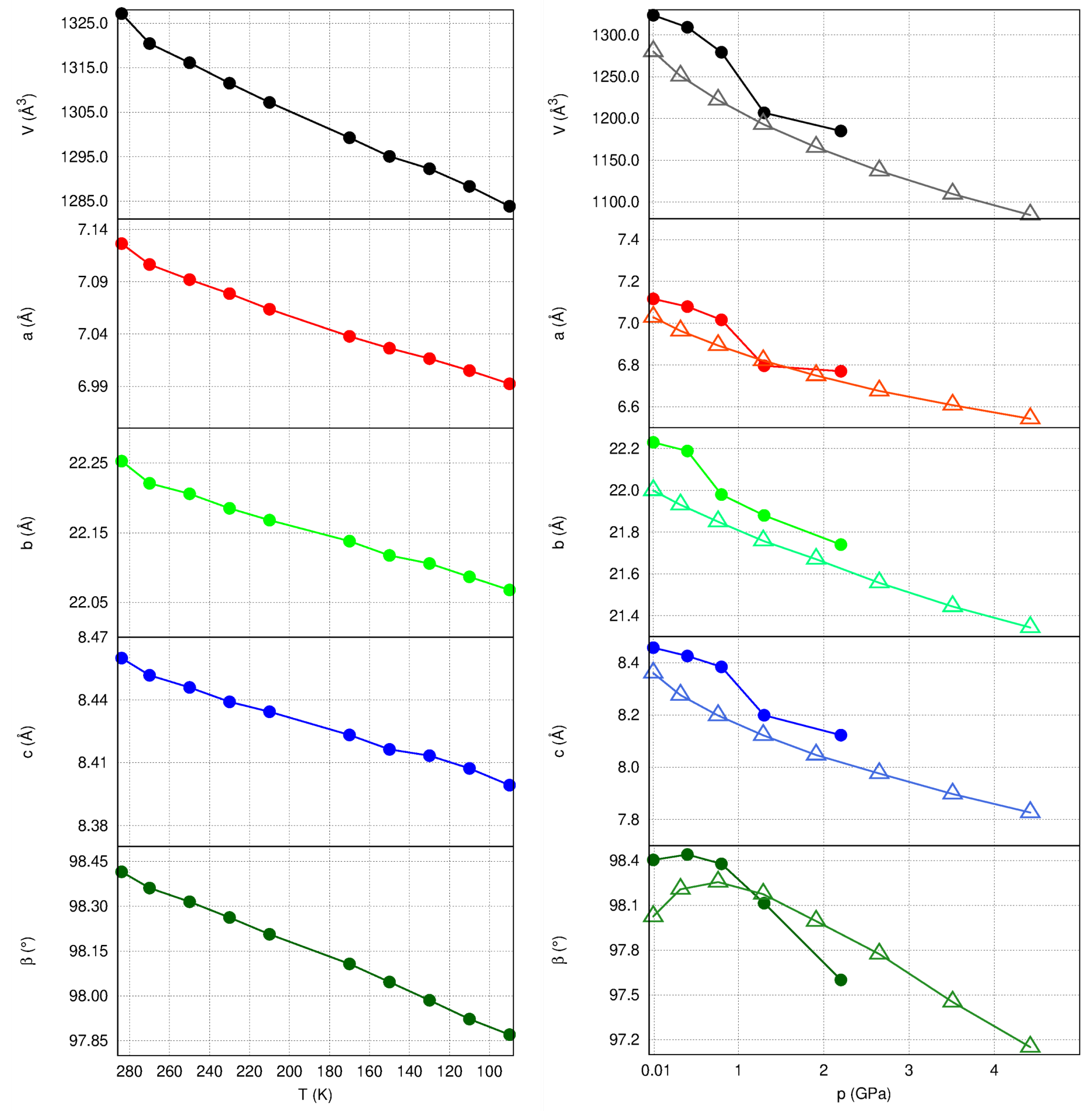
2.3. Unit Cell Changes and Strain Analysis at Non-Ambient Conditions
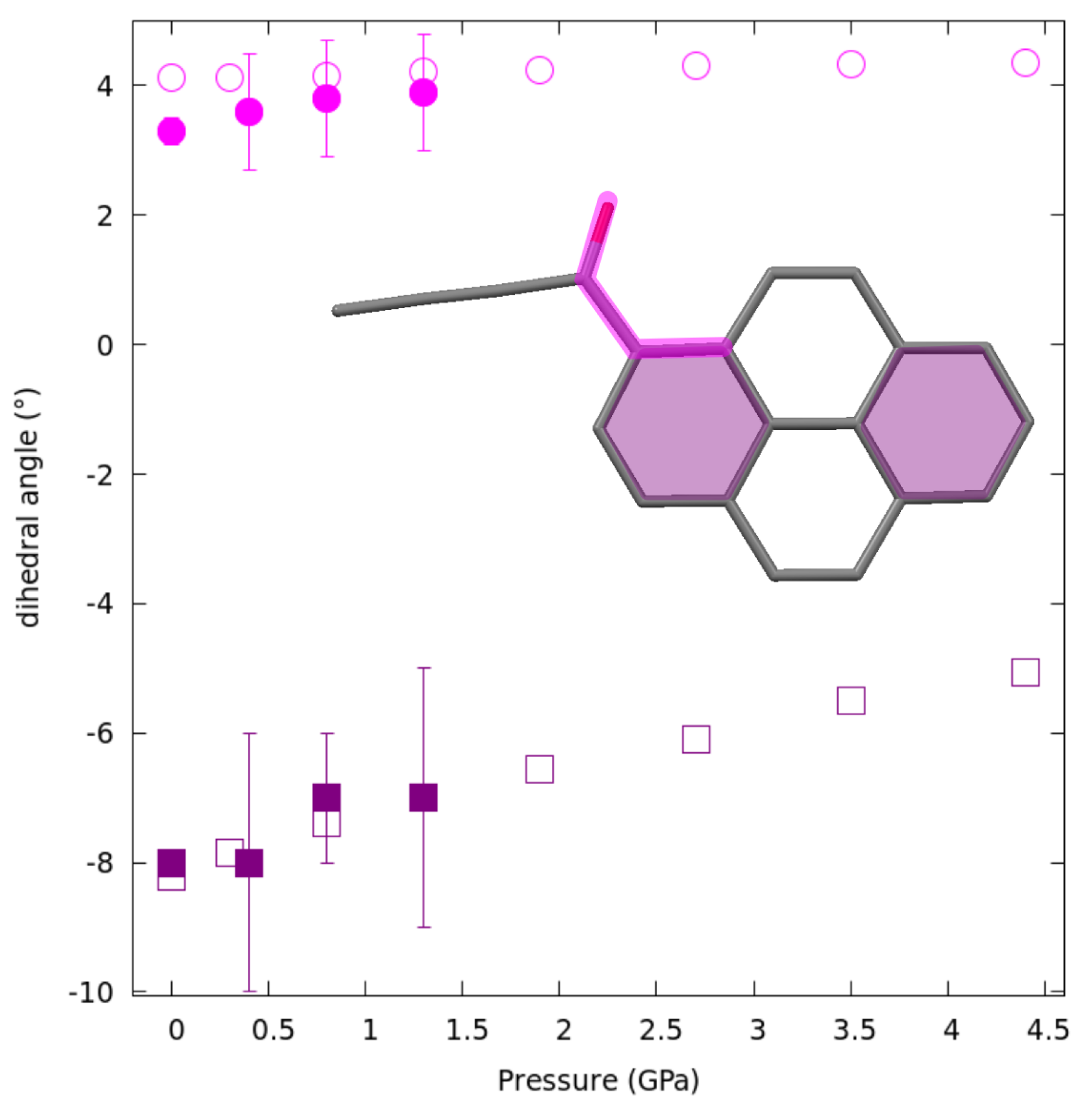
2.4. Structural Changes at Non-Ambient Conditions: Experiment and Theory
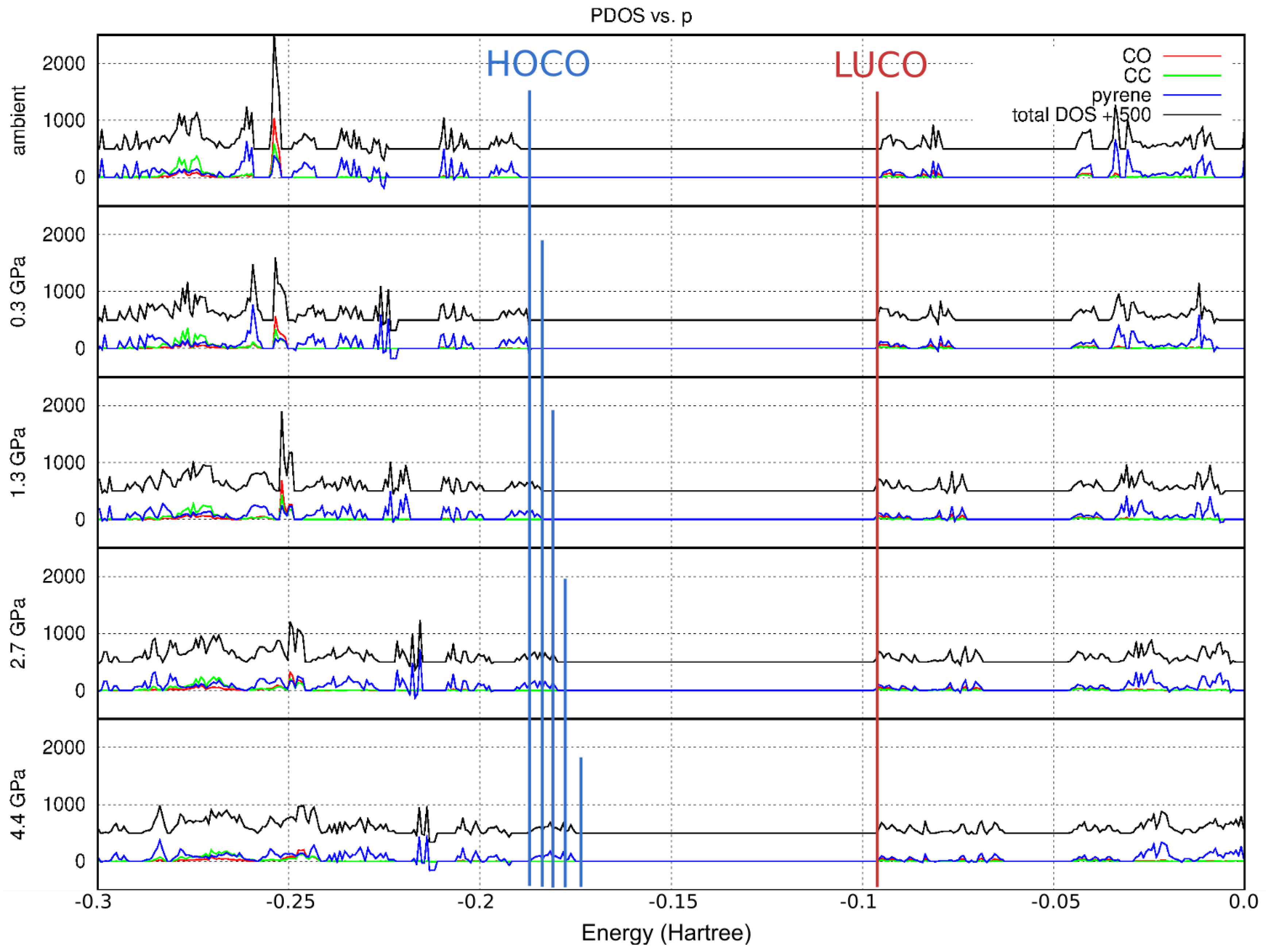
2.5. Theoretical Calculations
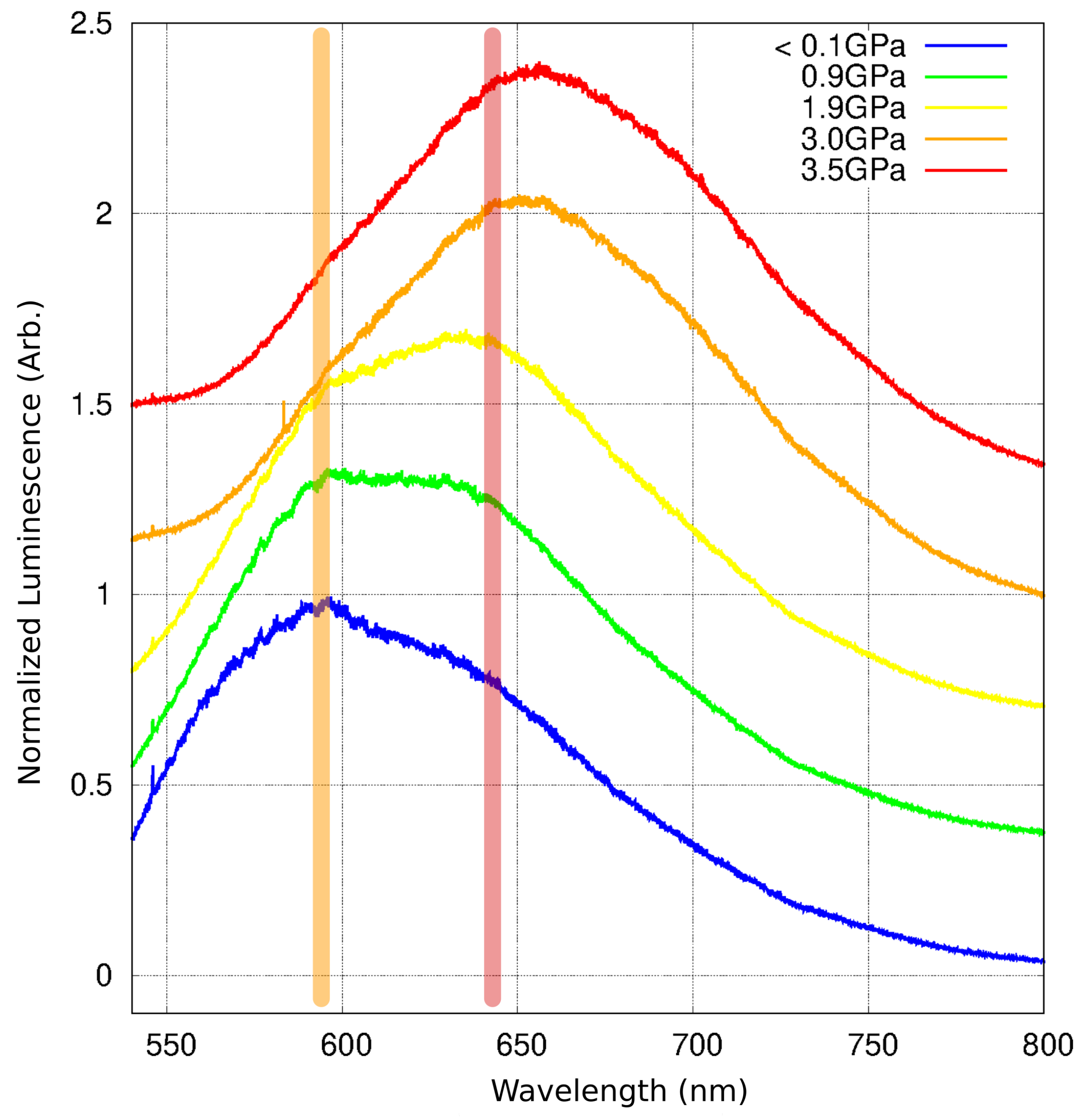
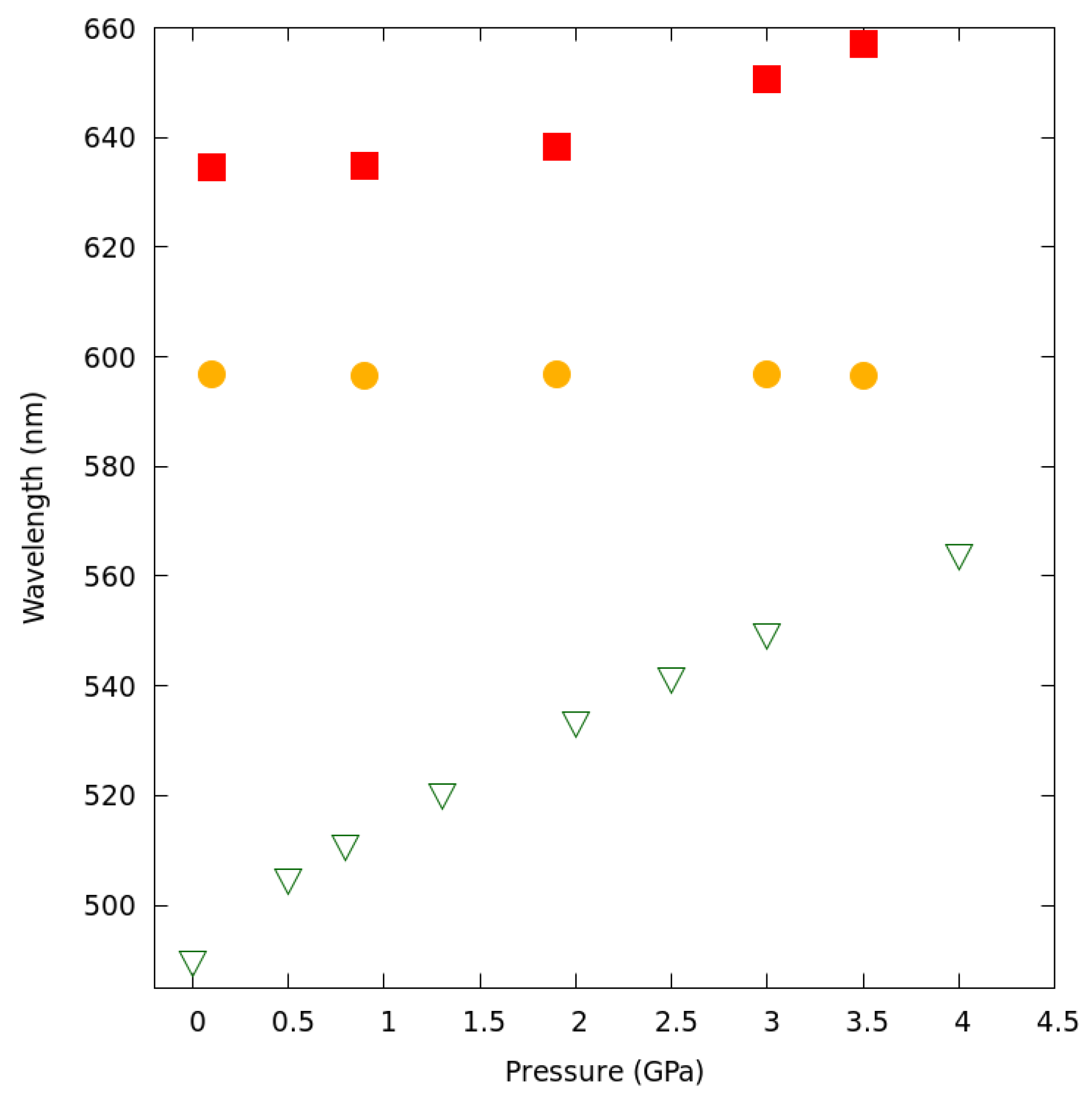
2.6. Luminescence Changes
3. Materials and Methods
3.1. Crystallization
3.2. Sample Preparation for High Pressure Experiments
3.3. Ambient Pressure X-Ray Data Collection and Refinement
Multi-Temperature X-Ray Data Collection
3.4. High-Pressure X-Ray Data Collection and Refinement
3.5. Spectroscopic Measurements
3.6. Theoretical Calculations
- (a)
- geometry optimization using B3LYP-D*, where B3LYP was augmented with an empirical dispersion term as proposed by Grimme [51] and modified for molecular crystals by Civalleri et al. [52]. A full relaxation of both lattice parameters and atomic coordinates by means of analytical energy gradients was applied,
- (b)
- Equations Of State (EOS) calculations were performed for the pressure range from atmospheric up to 4.5 GPa (8 points in total), with full relaxation of both lattice parameters and atomic coordinates by means of analytical energy gradients. The bulk modulus of the solid has been estimated using a third order Birch–Murnaghan-type equation of state [32],
- (c)
- crystal cohesive energy and intermolecular interaction energies were estimated, using the procedure described in the Supporting Information,
- (d)
- Crystalline band structure and partial electronic density of states were calculated with CRYSTAL14 in order to estimate the band gap changes and atomic contributions to frontier orbitals.
3.7. Energy Frameworks
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PAH | Poly-Aromatic Hydrocarbon |
| DAC | Diamond Anvil Cell |
| ADP | Atomic Displacement Parameter |
References
- Anthony, J. The larger acenes: Versatile organic semiconductors. Angew. Chem. Int. Ed. 2008, 47, 452–483. [Google Scholar] [CrossRef] [PubMed]
- Figueira-Duarte, T.M.; Müllen, K. Pyrene-based materials for organic electronics. Chem. Rev. 2011, 111, 7260–7314. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.Q.; Liu, C.L.; Zheng, C.J.; Wang, W.Z.; Xu, C.; Zhu, M.; Ji, B.M.; Li, F.; Zhang, X.H. Efficient violet non-doped organic light-emitting device based on a pyrene derivative with novel molecular structure. Org. Electron. 2015, 23, 179–185. [Google Scholar] [CrossRef]
- Ivanov, M.V.; Thakur, K.; Boddeda, A.; Wang, D.; Rathore, R. Nodal arrangement of HOMO controls the turning on/off the electronic coupling in isomeric polypyrene wires. J. Phys. Chem. C 2017, 121, 9202–9208. [Google Scholar] [CrossRef]
- Faggi, E.; Serra-Vinardell, J.; Pandey, M.D.; Casas, J.; Fabriàs, G.; Luis, S.V.; Alfonso, I. Pseudopeptidic fluorescent on-off pH sensor based on pyrene excimer emission: Imaging of acidic cellular organelles. Sens. Actuators B Chem. 2016, 234, 633–640. [Google Scholar] [CrossRef] [Green Version]
- Aparin, I.O.; Proskurin, G.V.; Golovin, A.V.; Ustinov, A.V.; Formanovsky, A.A.; Zatsepin, T.S.; Korshun, V.A. Fine tuning of pyrene excimer fluorescence in molecular beacons by alteration of the monomer structure. J. Org. Chem. 2017, 82, 10015–10024. [Google Scholar] [CrossRef] [PubMed]
- Kumar, C.V.; Chattopadhyay, S.K.; Das, P.K. A laser flash photolysis study of pyrene-1-aldehyde. Intersystem crossing efficiency, photoreactivity and triplet state properties in various solvents. Photochem. Photobiol. 1983, 38, 141–152. [Google Scholar] [CrossRef]
- Petaccia, M.; Giansanti, L.; Leonelli, F.; Bella, A.L.; Villalva, D.G.; Mancini, G. Synthesis, characterization and inclusion into liposomes of a new cationic pyrenyl amphiphile. Chem. Phys. Lipids 2016, 200, 83–93. [Google Scholar] [CrossRef] [PubMed]
- Niko, Y.; Hiroshige, Y.; Kawauchi, S.; Konishi, G.I. Fundamental photoluminescence properties of pyrene carbonyl compounds through absolute fluorescence quantum yield measurement and density functional theory. Tetrahedron 2012, 68, 6177–6185. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Gavezzotti, A. Crystal structures of polynuclear aromatic hydrocarbons. Classification, rationalization and prediction from molecular structure. Acta Crystallogr. Sec. B Struct. Sci. 1989, 45, 473–482. [Google Scholar] [CrossRef] [Green Version]
- Hinoue, T.; Shigenoi, Y.; Sugino, M.; Mizobe, Y.; Hisaki, I.; Miyata, M.; Tohnai, N. Regulation of π-stacked anthracene arrangement for fluorescence modulation of organic solid from monomer to excited oligomer emission. Chem. A Eur. J. 2012, 18, 4634–4643. [Google Scholar] [CrossRef] [PubMed]
- Varghese, S.; Das, S. Role of molecular packing in determining solid-state optical properties of π-conjugated materials. J. Phys. Chem. Lett. 2011, 2, 863–873. [Google Scholar] [CrossRef]
- Kumar, N.S.S.; Varghese, S.; Suresh, C.H.; Rath, N.P.; Das, S. Correlation between solid-state photophysical properties and molecular packing in a series of indane-1,3-dione containing butadiene derivatives. J. Phys. Chem. C 2009, 113, 11927–11935. [Google Scholar] [CrossRef]
- Ghosh, S.; Li, X.Q.; Stepanenko, V.; Würthner, F. Control of H- and J-type π stacking by peripheral alkyl chains and self-sorting phenomena in perylene bisimide homo- and heteroaggregates. Chem. A Eur. J. 2008, 14, 11343–11357. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Peng, J.; Zhao, K.; Usman, R.; Khan, A.; Wang, M. Efficient luminescent microtubes of charge-transfer organic cocrystals involving 1,2,4,5-tetracyanobenzene, carbazole derivatives, and pyrene derivatives. Cryst. Growth Des. 2017, 17, 6684–6691. [Google Scholar] [CrossRef]
- Flamholc, R.; Plazuk, D.; Zakrzewski, J.; Metivier, R.; Nakatani, K.; Makal, A.; Wozniak, K. A new class of pyrenyl solid-state emitters: 1-pyrenyl ynones. Synthesis via the Friedel-Crafts route, molecular and electronic structure and photophysical properties. RSC Adv. 2014, 4, 31594–31601. [Google Scholar] [CrossRef]
- Eikeland, E.; Thomsen, M.K.; Overgaard, J.; Spackman, M.A.; Iversen, B.B. Intermolecular interaction energies in hydroquinone clathrates at high pressure. Cryst. Growth Des. 2017, 17, 3834–3846. [Google Scholar] [CrossRef]
- Fanetti, S.; Citroni, M.; Dziubek, K.; Nobrega, M.M.; Bini, R. The role of H-bond in the high-pressure chemistry of model molecules. J. Phys. Condens. Matter 2018, 30, 094001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moggach, S.; Parsons, S. Molecular solids at extreme pressure. CrystEngComm 2010, 12, 2515. [Google Scholar] [CrossRef]
- Zakharov, B.A.; Boldyreva, E.V. High pressure: A complementary tool for probing solid-state processes. CrystEngComm 2019. [Google Scholar] [CrossRef]
- Fabbiani, F.P.A.; Allan, D.R.; David, W.I.F.; Moggach, S.A.; Parsons, S.; Pulham, C.R. High-pressure recrystallisation—A route to new polymorphs and solvates. CrystEngComm 2004, 6, 505–511. [Google Scholar] [CrossRef]
- Fabbiani, F.P.A.; Allan, D.R.; Parsons, S.; Pulham, C.R. Exploration of the high-pressure behaviour of polycyclic aromatic hydrocarbons: Naphthalene, phenanthrene and pyrene. Acta Crystallogr. Sect. B Struct. Sci. 2006, 62, 826–842. [Google Scholar] [CrossRef] [PubMed]
- Capitani, F.; Höppner, M.; Malavasi, L.; Marini, C.; Artioli, G.A.; Hanfland, M.; Dore, P.; Boeri, L.; Postorino, P. Structural evolution of solid phenanthrene at high pressures. J. Phys. Chem. C 2016, 120, 14310–14316. [Google Scholar] [CrossRef]
- Chanyshev, A.D.; Litasov, K.D.; Rashchenko, S.V.; Sano-Furukawa, A.; Kagi, H.; Hattori, T.; Shatskiy, A.F.; Dymshits, A.M.; Sharygin, I.S.; Higo, Y. High-pressure-high-temperature study of benzene: Refined crystal structure and new phase diagram up to 8 GPa and 923 K. Cryst. Growth Des. 2018, 18, 3016–3026. [Google Scholar] [CrossRef]
- Contag, B. Die polymorphic von benzo[a]pyren. Naturwissenschaften 1978, 65, 108–109. [Google Scholar] [CrossRef]
- Bergantin, S.; Moret, M.; Buth, G.; Fabbiani, F.P.A. Pressure-induced conformational change in organic semiconductors: Triggering a reversible phase Transition in Rubrene. J. Phys. Chem. C 2014, 118, 13476–13483. [Google Scholar] [CrossRef]
- McKinnon, J.J.; Jayatilaka, D.; Spackman, M.A. Towards quantitative analysis of intermolecular interactions with Hirshfeld surfaces. Chem. Commun. 2007, 0, 3814–3816. [Google Scholar] [CrossRef]
- Mackenzie, C.F.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer model energies and energy frame-works: extension to metal coordination compounds, organic salts, solvates and open-shell systems. IUCrJ 2017, 4, 575–587. [Google Scholar] [CrossRef]
- Cliffe, M.J.; Goodwin, A.L. PASCal: A principal axis strain calculator for thermal expansion and compressibility determination. J. Appl. Crystallogr. 2012, 45, 1321–1329. [Google Scholar] [CrossRef]
- Goodwin, A.L.; Calleja, M.; Conterio, M.J.; Dove, M.T.; Evans, J.S.O.; Keen, D.A.; Peters, L.; Tucker, M.G. Colossal positive and negative thermal expansion in the framework material Ag3[Co(CN)6]. Science 2008, 319, 794–797. [Google Scholar] [CrossRef]
- Marciniak, J.; Katrusiak, A. Direct and inverse relations between temperature and pressure effects in crystals: A case study on o-Xylene. J. Phys. Chem. C 2017, 121, 22303–22309. [Google Scholar] [CrossRef]
- Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sec. A 2008, 64, 112–122. [Google Scholar] [CrossRef]
- Allen, F.H.; Kennard, O.; Watson, D.G.; Brammer, L.; Orpen, A.G.; Taylor, R. Tables of bond lengths determined by X-ray and neutron diffraction. Part 1. Bond lengths in organic compounds. J. Chem. Soc. Perkin Trans. 2 1987, 12, S1–S19. [Google Scholar] [CrossRef]
- Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-mechanical condensed matter simulations with CRYSTAL. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar] [CrossRef]
- Merrill, L.; Bassett, W.A. Miniature diamond anvil pressure cell for single crystal x-ray diffraction studies. Rev. Sci. Instrum. 1974, 45, 290–294. [Google Scholar] [CrossRef]
- Piermarini, G.J.; Block, S.; Barnett, J.D.; Forman, R.A. Calibration of the pressure dependence of the R 1 ruby fluorescence line to 195 kbar. J. Appl. Phys. 1975, 46, 2774–2780. [Google Scholar] [CrossRef]
- Ragan, D.D.; Gustavsen, R.; Schiferl, D. Calibration of the ruby R1 and R2 fluorescence shifts as a function of temperature from 0 to 600 K. J. Appl. Phys. 1992, 72, 5539–5544. [Google Scholar] [CrossRef]
- Bruker AXS Inc. APEXII V1.0; Bruker AXS Inc.: Madison, WI, USA, 2012. [Google Scholar]
- Bruker AXS Inc. SAINT V8.34A; Bruker AXS Inc.: Madison, WI, USA, 2013. [Google Scholar]
- Bruker AXS Inc. SADABS 2012/1 Bruker Area Detector Scaling and Absorption Correction; Bruker AXS Inc.: Madison, WI, USA, 2012. [Google Scholar]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sec. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Macrae, C.F.; Bruno, I.J.; Chisholm, J.A.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Rodriguez-Monge, L.; Taylor, R.; van der Streek, J.; Wood, P.A. Mercury CSD 2.0—New features for the visualization and investigation of crystal structures. J. Appl. Crystallogr. 2008, 41, 466–470. [Google Scholar] [CrossRef]
- Jmol. Jmol: An Open-Source Java Viewer for Chemical Structures in 3D. 2016. Available online: http://www.jmol.org/ (accessed on November 2018).
- CrysAlis. CrysAlisPro 1.171.38.46; Rigaku Oxford Diffraction: Yarnton, UK, 2015. [Google Scholar]
- Angel, R.J. Absorption corrections for diamond-anvil pressure cells implemented in the software package Absorb6.0. J. Appl. Crystallogr. 2004, 37, 486–492. [Google Scholar] [CrossRef]
- Burnham, C.W. Computation of absorption corrections, and the significance of end effect. Am. Mineral. 1966, 51, 159–167. [Google Scholar]
- Thorn, A.; Dittrich, B.; Sheldrick, G.M. Enhanced rigid-bond restraints. Acta Crystallogr. Sec. A 2012, 68, 448–451. [Google Scholar] [CrossRef] [Green Version]
- Dovesi, R.; Orlando, R.; Civalleri, B.; Roetti, C.; Saunders, V.R.; Zicovich-Wilson, C.M. CRYSTAL: A computational tool for the ab initio study of the electronic properties of crystals. Z. Kristallogr. Cryst. Mater. 2009, 220, 571–573. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Civalleri, B.M.; Zicovich-Wilson, C.; Valenzano, L.; Ugliengo, P. B3LYP augmented with an empirical dispersion term (B3LYP-D*) as applied to molecular crystals. CrystEngComm 2008, 10, 405–410. [Google Scholar] [CrossRef]
- Turner, M.J.; Thomas, S.P.; Shi, M.W.; Jayatilaka, D.; Spackman, M.A. Energy frameworks: insights into interaction anisotropy and the mechanical properties of molecular crystals. Chem. Commun. 2015, 51, 3735–3738. [Google Scholar] [CrossRef]
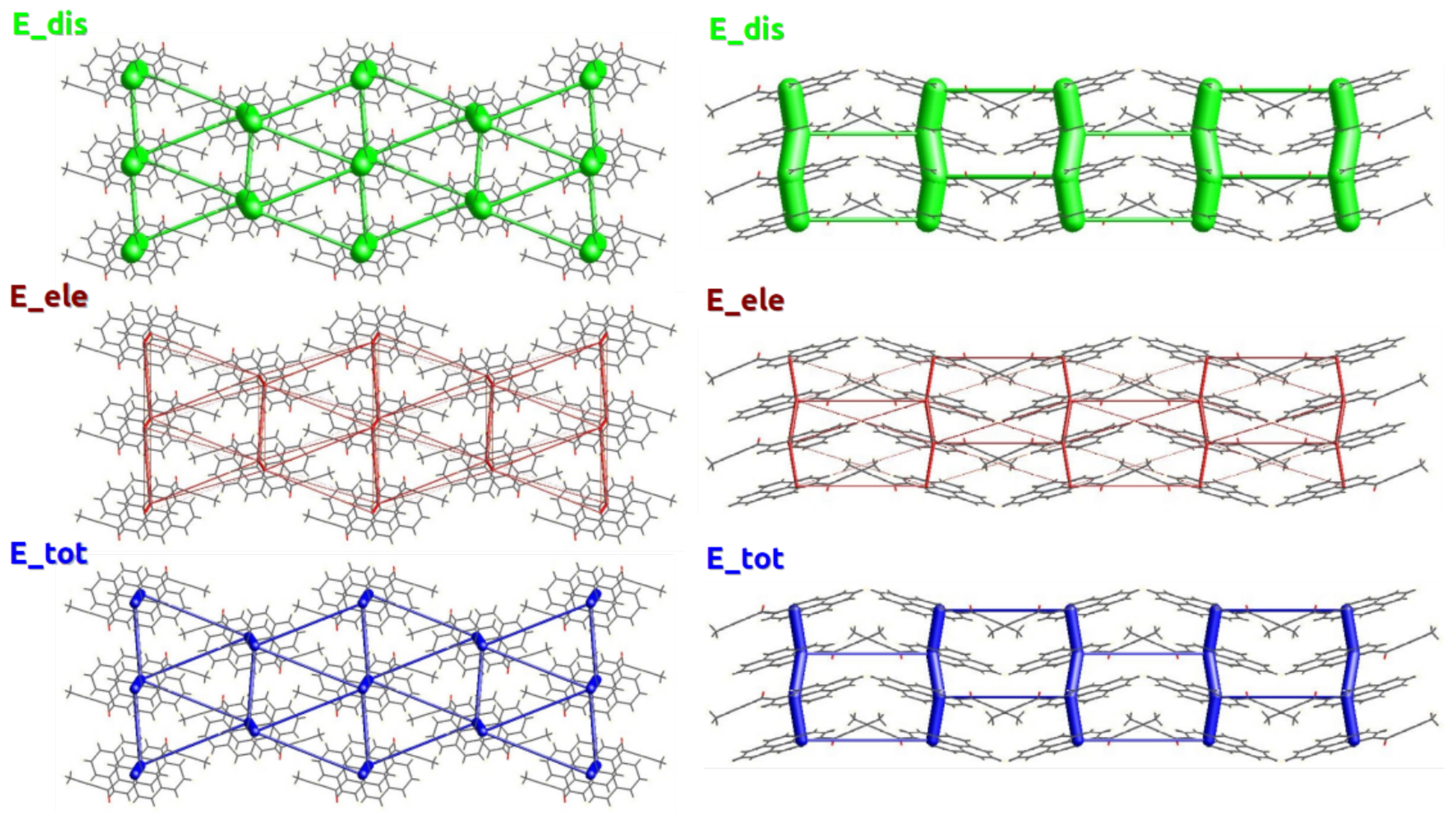


| Symmetry Operation (Translation) | E | E | E | E | E |
|---|---|---|---|---|---|
| −x, −y, −z (0, 0, 0) | −13.4 | −3 | −101.2 | 68 | −61.4 |
| −x, y+1/2, −z+1/2 (0, −1, −1) | 0.5 | −0.5 | −6.5 | 5.1 | −2.3 |
| −x, −y, −z (0, 2, −1) | 1.4 | −0.2 | −4.7 | 0.6 | −2.3 |
| x, −y+1/2, z+1/2 (0, 1, −1) | −6.5 | −2.6 | −17.4 | 13.3 | −15.6 |
| −x, y+1/2, −z+1/2 (0, −1, 0) | −2.7 | −0.6 | −8.6 | 4.7 | −7.8 |
| −x, −y, −z (1, 0, 0) | −13.5 | −3.8 | −107.7 | 74.3 | −63.8 |
| x, y, z (0, 0, 1) | −3.2 | −0.9 | −14.3 | 9.1 | −10.7 |
| −x, −y, −z (1, 2, 1) | −18 | −5.8 | −24.5 | 27.6 | −27.8 |
| −x, y+1/2, −z+1/2 (−1, −1, 0) | −4.4 | −1.2 | −10.1 | 4.3 | −11.5 |
| x, −y+1/2, z+1/2 (0, 2, 0) | −0.8 | −0.5 | −10.6 | 8.1 | −5.3 |
| (A) | ||||
| Component along the Crystallographic Axis | ||||
| Principal axis, i | a | b | c | |
| 3 | 100(3) | −0.9498 | 0 | 0.3130 |
| 2 | 40(1) | 0 | 1 | 0 |
| 1 | 22(1) | −0.5189 | 0 | −0.8548 |
| (B) | ||||
| Component along the Crystallographic Axis | ||||
| Principal axis, i | a | b | c | |
| 1 | 26(18) | 0.9996 | 0 | 0.0268 |
| 2 | 17(10) | 0 | −1 | 0 |
| 3 | 11(4) | 0.1353 | 0 | 0.9908 |
| (C) | ||||
| Component along the Crystallographic Axis | ||||
| Principal axis, i | a | b | c | |
| 1 | 14.4(0.6) | 0.9994 | 0 | −0.0349 |
| 2 | 12.2(1.9) | −0.2095 | 0 | −0.9778 |
| 3 | 6.2(2.6) | 0 | −1 | 0 |
| p | E | E |
|---|---|---|
| GPa | kJ/mol | |
| 0.0001 | −130.06 | −63.97 (−63.80) |
| 0.3 | −128.62 | −61.70 |
| 0.8 | −124.72 | −56.23 |
| 1.3 | −119.58 | −49.82 |
| 1.9 | −111.97 | −41.38 |
| 2.7 | −101.45 | −30.47 |
| 3.5 | −87.84 | −17.50 |
| 4.4 | −72.40 | −3.58 |
| Ambient | 0.8 GPa | 1.0 GPa | 1.3 GPa | 2.2 GPa | 2.6 GPa | |
|---|---|---|---|---|---|---|
| Empirical formula | C20 H12 O | C20 H12 O | C20 H12 O | C20 H12 O | C20 H12 O | C20 H12 O |
| Formula weight/g | 268.3 | 268.3 | 268.3 | 268.3 | 268.3 | 268.3 |
| Crystal system | monoclinic | monoclinic | monoclinic | monoclinic | monoclinic | monoclinic |
| Space group | P21/c | P21/c | P21/c | P21/c | P21/c | P21/c |
| a (Å) | 7.1164 (2) | 7.0094 (6) | 7.080 (4) | 6.8019 (9) | 6.664 (4) | 6.63 (3) |
| b (Å) | 22.2299 (7) | 21.98 (2) | 22.37 (16) | 21.80 (4) | 21.9 (2) | 21.16 (9) |
| c (Å) | 8.4575 (3) | 8.3822 (5) | 8.438 (4) | 8.2116 (9) | 8.114 (7) | 8.03 (3) |
| () | 90 | 90 | 90 | 90 | 90 | 88.3 (6) |
| () | 98.4040 (10) | 98.391 (6) | 98.33 (5) | 98.044 (11) | 97.50 (6) | 97.7 (3) |
| () | 90 | 90 | 90 | 90 | 90 | 87.2 (7) |
| Volume (Å) | 1323.58 (7) | 1277.7 (13) | 1322 (9) | 1206 (2) | 1173 (14) | 1115 (8) |
| Z | 4 | 4 | 4 | 4 | 4 | 4 |
| (mg/mm) | 1.346 | 1.395 | 1.348 | 1.478 | 1.520 | 1.599 |
| F (000) | 560 | 560 | 560 | 560 | 560 | 560 |
| (/mm) | 0.082 | 0.055 | 0.053 | 0.058 | 0.060 | 0.063 |
| Max. transmission | 1 | 1 | 1 | 1 | - | - |
| Min. transmission | 0.9396 | 0.739 | 0.387 | 0.389 | - | - |
| Abs.correction type | Gaussian | Gaussian | Gaussian | multi-scan | - | - |
| Crystal color | yellow | yellow | yellow | orange | orange | orange |
| Crystal size (mm) | 0.22 | 0.339 | 0.339 | 0.339 | 0.339 | 0.339 |
| 0.18 | 0.275 | 0.275 | 0.275 | 0.275 | 0.275 | |
| 0.07 | 0.144 | 0.144 | 0.144 | 0.144 | 0.144 | |
| Data completeness (%) | 0.997 | 0.311 | 0.3226 | 0.3 | 0.3169 | 0.2344 |
| R | 0.0408 | 0.08 | 0.0875 | 0.1022 | 0.3725 | 0.7271 |
| R | 0.0214 | 0.0342 | 0.0479 | 0.0561 | 0.5098 | 2.321 |
| Index ranges h k l | −12:12 | −9:9 | −8:8 | −9:9 | −7:7 | −7:7 |
| −39:38 | −6:6 | −6:7 | −6:6 | −6:6 | −9:9 | |
| −14:14 | −11:11 | −10:10 | −10:10 | −9:9 | −9:10 | |
| Reflections collected | 68,366 | 14,847 | 8821 | 11,618 | 6191 | 10,501 |
| 2 range for data collection | 1.832:38.661 | 2.071:21.958 | 2.055:20.52 | 2.386:22.074 | 1.998:19.264 | 2.955:18.475 |
| Temperature (K) | 301 (2) | 295.0 (8) | 263 (40) | 294.5 (3) | 294.9 (2) | 294.8 (2) |
| X-ray wavelength (Å) | 0.71073 | 0.56087 | 0.56087 | 0.56087 | 0.56087 | 0.56087 |
| Independent reflections I | 7499 | 910 | 826 | 822 | - | - |
| Independent reflections I > 2 (I) | 4569 | 496 | 413 | 492 | - | - |
| Largest diff. peak/hole/e (Å) | 0.471 | 0.074 | 0.095 | 0.097 | - | - |
| −0.284 | −0.084 | −0.148 | −0.094 | - | - | |
| Goof | 1.018 | 1.002 | 1.035 | 1.091 | - | - |
| Parameters | 191 | 191 | 191 | 191 | - | - |
| Data | 7499 | 910 | 826 | 822 | - | - |
| Restraints | 0 | 177 | 303 | 177 | - | - |
| R1 all data | 0.0963 | 0.0932 | 0.1173 | 0.1045 | - | - |
| R1 [I >= 2 (I)] | 0.0596 | 0.0348 | 0.0533 | 0.0496 | - | - |
| wR2 [I >= 2 (I)] | 0.1721 | 0.0727 | 0.1277 | 0.1055 | - | - |
| wR2 all data | 0.2065 | 0.0944 | 0.1657 | 0.1268 | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makal, A.; Krzeszczakowska, J.; Gajda, R. Pressure-Dependent Structural and Luminescence Properties of 1-(Pyren-1-yl)but-2-yn-1-one. Molecules 2019, 24, 1107. https://doi.org/10.3390/molecules24061107
Makal A, Krzeszczakowska J, Gajda R. Pressure-Dependent Structural and Luminescence Properties of 1-(Pyren-1-yl)but-2-yn-1-one. Molecules. 2019; 24(6):1107. https://doi.org/10.3390/molecules24061107
Chicago/Turabian StyleMakal, Anna, Joanna Krzeszczakowska, and Roman Gajda. 2019. "Pressure-Dependent Structural and Luminescence Properties of 1-(Pyren-1-yl)but-2-yn-1-one" Molecules 24, no. 6: 1107. https://doi.org/10.3390/molecules24061107
APA StyleMakal, A., Krzeszczakowska, J., & Gajda, R. (2019). Pressure-Dependent Structural and Luminescence Properties of 1-(Pyren-1-yl)but-2-yn-1-one. Molecules, 24(6), 1107. https://doi.org/10.3390/molecules24061107






