Crystallization of Polytetrafluoroethylene in a Wide Range of Cooling Rates: Nucleation and Diffusion in the Presence of Nanosilica Clusters
Abstract
:1. Introduction
2. Results and Discussion
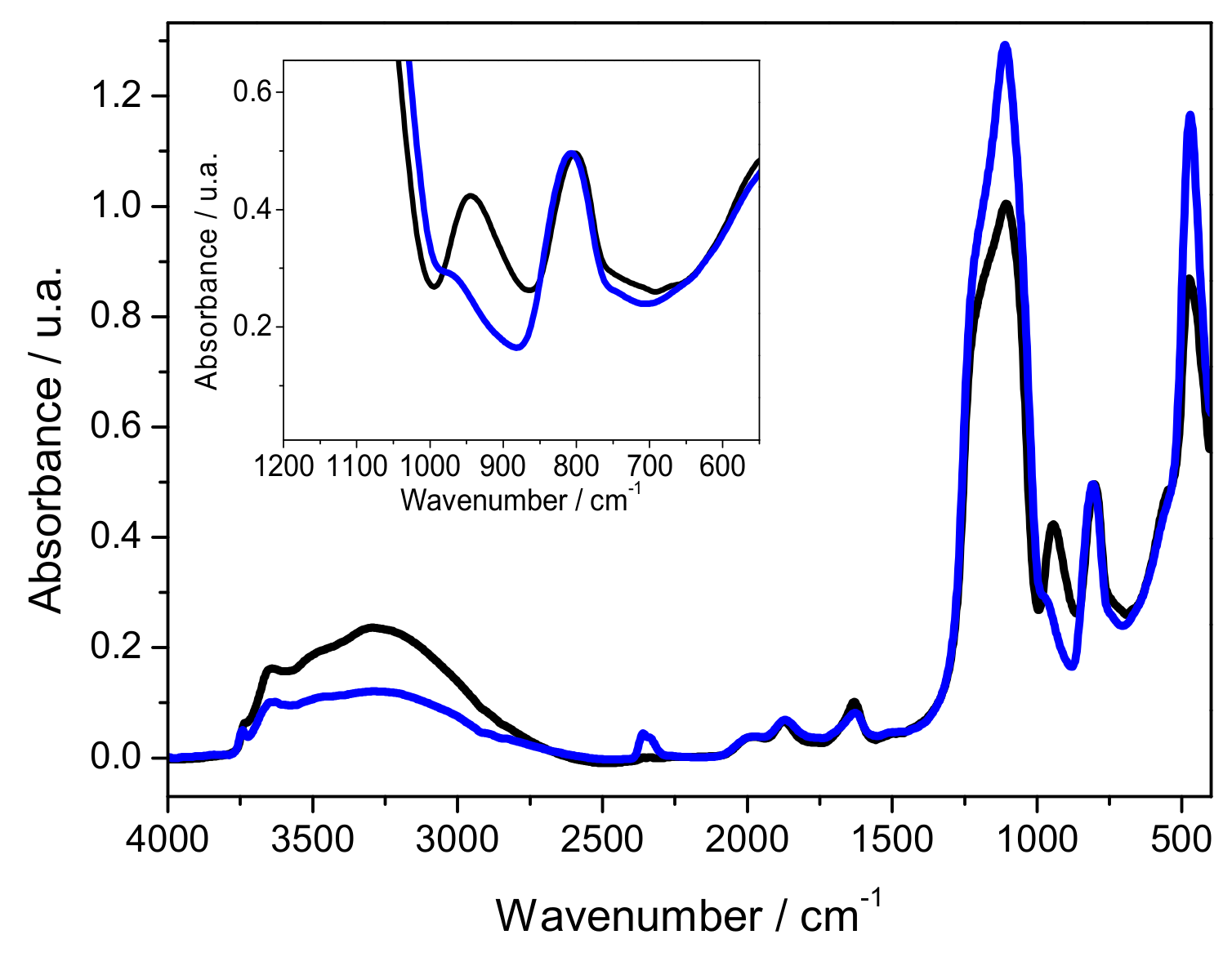
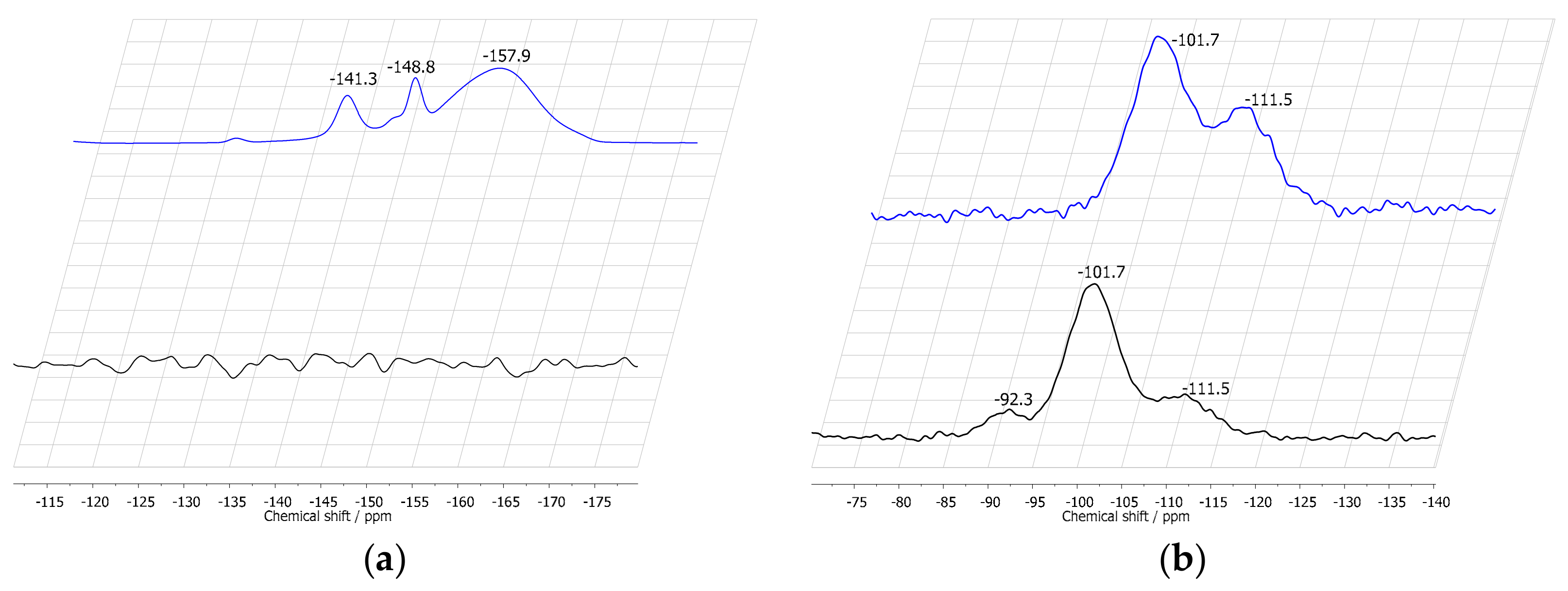
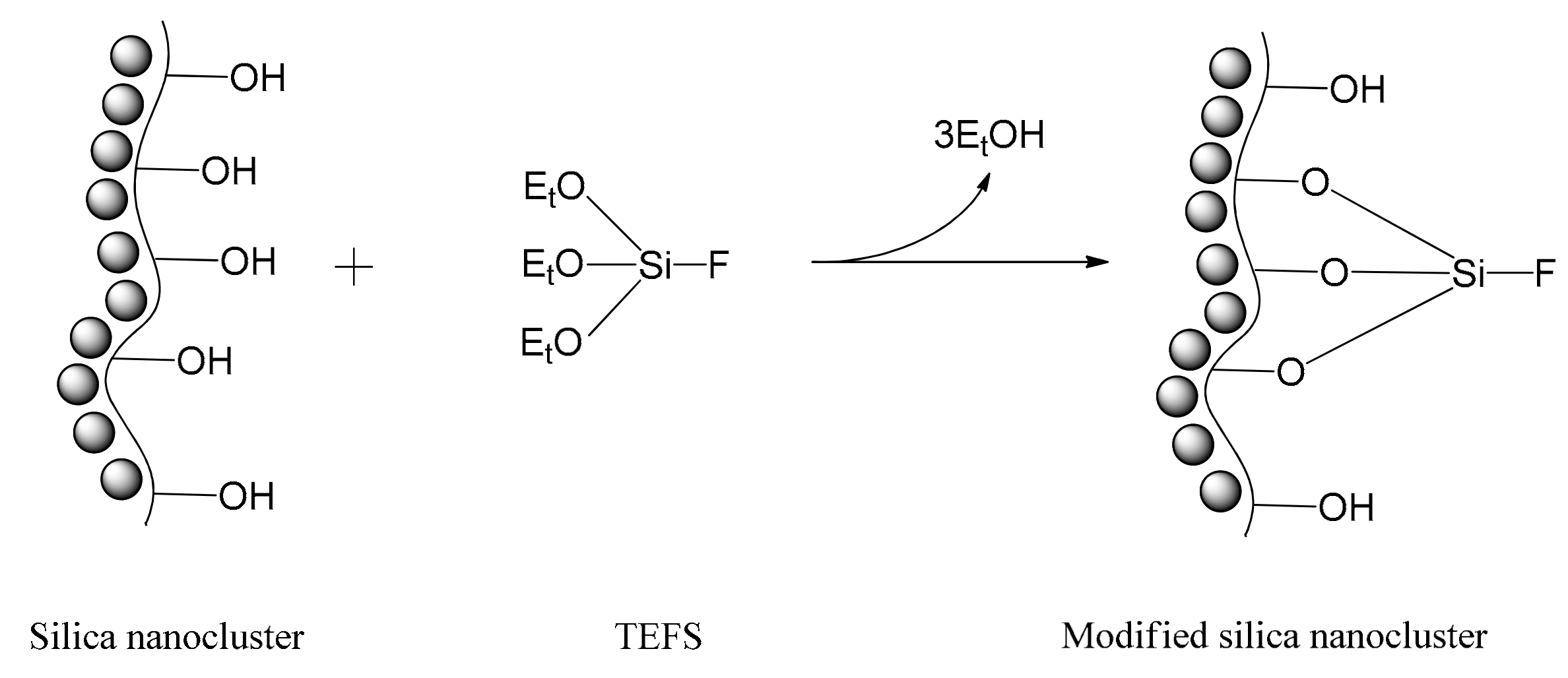
2.1. Characterization of Silica Surface Modification
2.2. Morphology of PTFE/SiO2(c)F Nanocomposite
2.3. Crystallization Kinetics of Neat PTFE and PTFE/SiO2(c)F
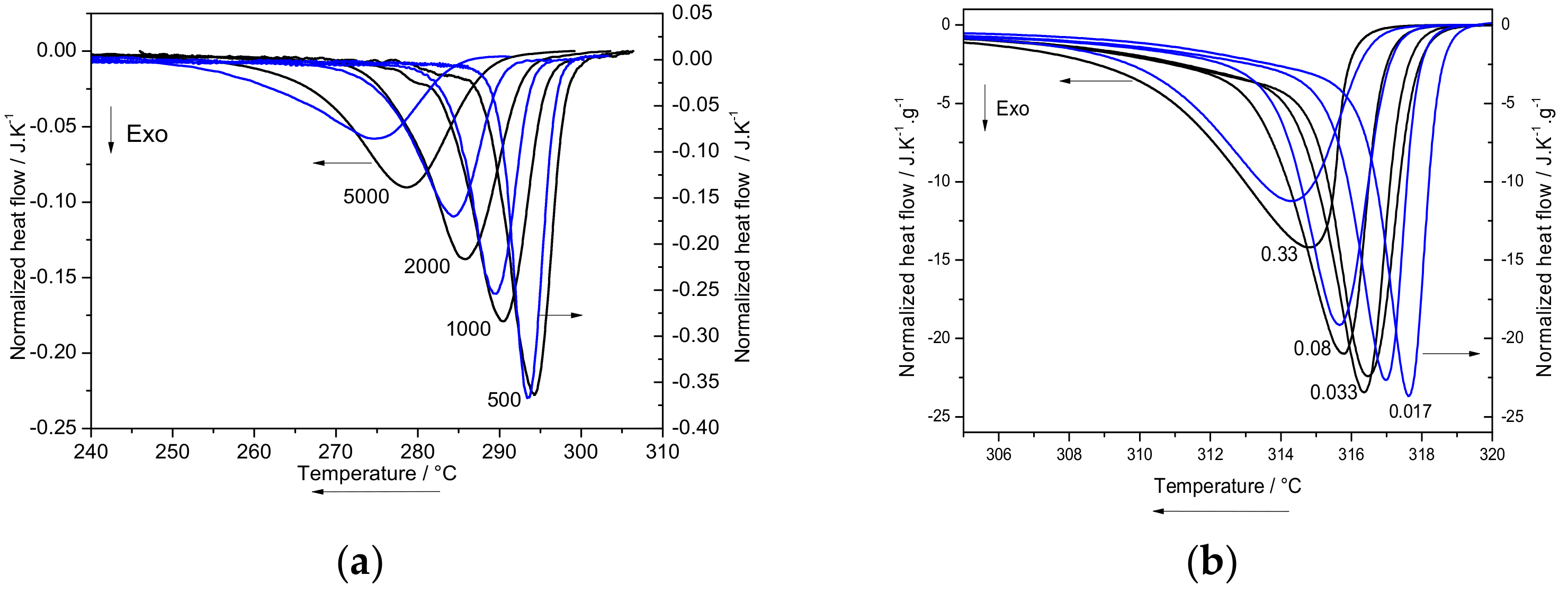
2.3.1. Melt Crystallization
2.3.2. Crystal Morphology of PTFE/SiO2(c)F
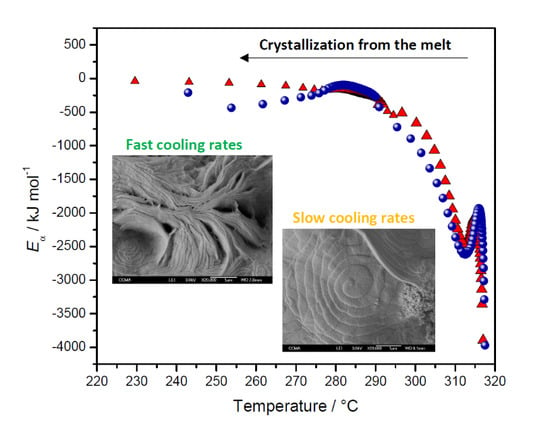
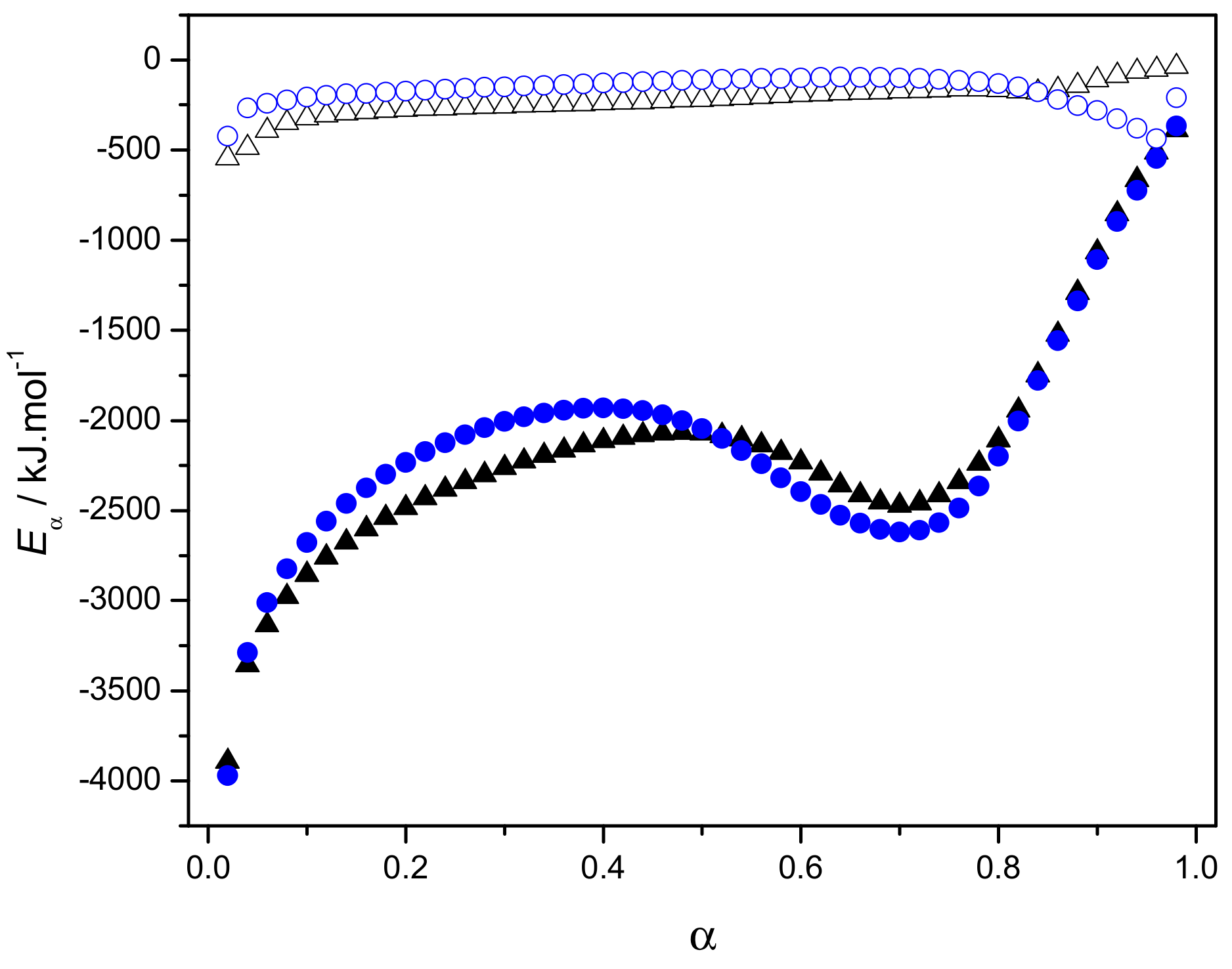
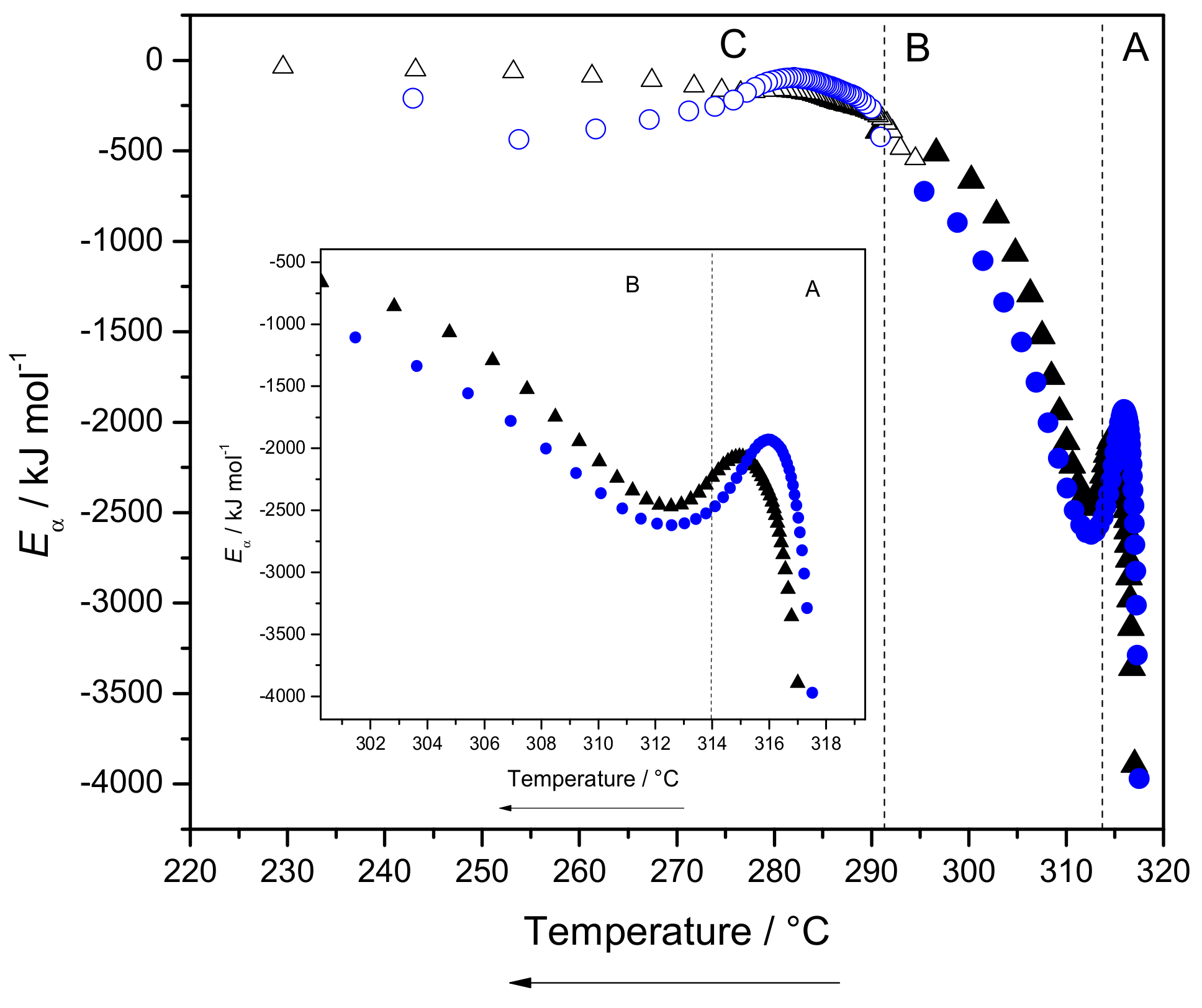
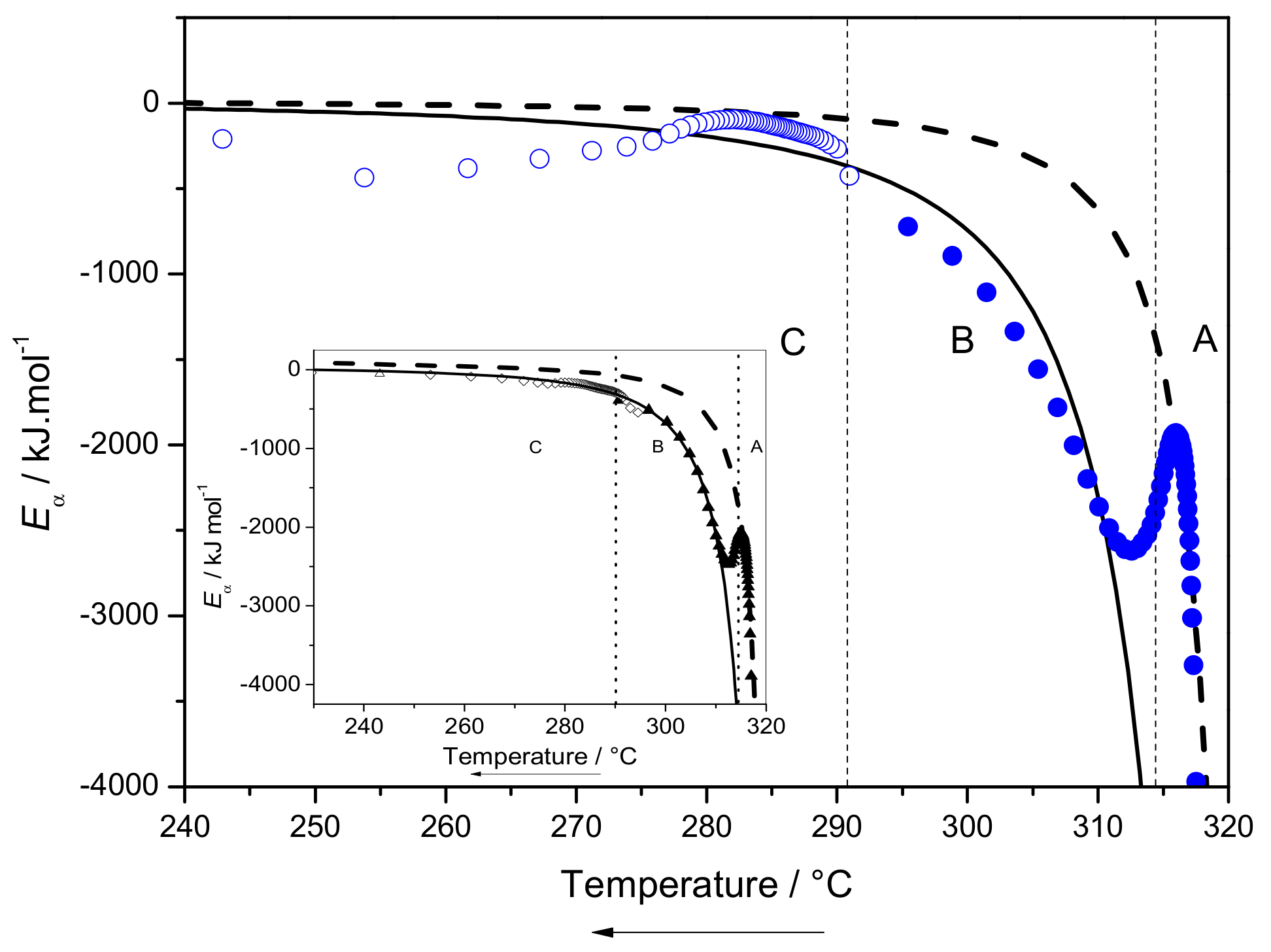
2.3.3. Eα Dependences and Evaluation of Hoffman-Lauritzen Parameters
3. Materials and Methods
3.1. Materials
3.2. Nanosilica Clusters Synthesis
3.3. Surface Modification of Nanosilica Clusters
3.4. Elaboration of PTFE/SiO2(c)F Nanocomposite
3.5. Experimental Techniques
3.6. Theoretical Approaches
3.6.1. Kinetics
3.6.2. Advanced Isoconversional Kinetic Analysis
3.6.3. Hoffman-Lauritzen Theory of Crystallization
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Blanchet, T.A. Polytetrafluoroethylene. Plast. Eng. 1997, 41, 981–1000. [Google Scholar]
- André, T.; Valensi, F.; Teulet, P.; Cressault, Y.; Zink, T.; Caussé, R. Arc Tracking Energy Balance for Copper and Aluminum Aeronautic Cables. J. Phys. 2017, 825, 012001. [Google Scholar] [CrossRef]
- Huang, X.L.; Martinez-Vega, J.; Malec, D. Morphological evolution of polytetrafluoroethylene in extreme temperature conditions for aerospace applications. J. Appl. Polym. Sci. 2014, 131. [Google Scholar] [CrossRef]
- Halbur, J.C.; Padbury, R.P.; Jur, J.S. Induced wetting of polytetrafluoroethylene by atomic layer deposition for application of aqueous-based nanoparticle inks. Mater. Lett. 2013, 101, 25–28. [Google Scholar] [CrossRef]
- Dhanumalayan, E.; Joshi, G.M. Performance properties and applications of polytetrafluoroethylene (PTFE)—A review. Adv. Compos. Hybrid Mater. 2018, 1, 247–268. [Google Scholar] [CrossRef]
- Biswas, S.K.; Vijayan, K. Friction and wear of PTFE—A review. Wear 1992, 158, 193–211. [Google Scholar] [CrossRef]
- Sattari, M.; Molazemhosseini, A.; Naimi-Jamal, M.; Khavandi, A. Nonisothermal crystallization behavior and mechanical properties of PEEK/SCF/nano-SiO2 composites. Mater. Chem. Phys. 2014, 147, 942–953. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, J. Non-isothermal crystallization kinetics of high density polyethylene/titanium dioxide composites via melt blending. J. Therm. Anal. Calorim. 2014, 115, 63–71. [Google Scholar] [CrossRef]
- Bosq, N.; Guigo, N.; Zhuravlev, E.; Sbirrazzuoli, N. Nonisothermal Crystallization of Polytetrafluoroethylene in a Wide Range of Cooling Rates. J. Phys. Chem. B 2013, 117, 3407–3415. [Google Scholar] [CrossRef]
- Wang, X.Q.; Chen, D.R.; Han, J.C.; Du, S.Y. Crystallization behavior of polytetrafluoroethylene (PTFE). J. Appl. Polym. Sci. 2002, 83, 990–996. [Google Scholar] [CrossRef]
- Kolesov, I.; Mileva, D.; Androsch, R.; Schick, C. Structure formation of polyamide 6 from the glassy state by fast scanning chip calorimetry. Polymer 2011, 52, 5156–5165. [Google Scholar] [CrossRef]
- Zhuravlev, E.; Schmelzer, J.W.P.; Wunderlich, B.; Schick, C. Kinetics of nucleation and crystallization in poly(ɛ-caprolactone) (PCL). Polymer 2011, 52, 1983–1997. [Google Scholar] [CrossRef]
- Wurm, A.; Zhuravlev, E.; Eckstein, K.; Jehnichen, D.; Pospiech, D.; Androsch, R.; Wunderlich, B.; Schick, C. Crystallization and homogeneous nucleation kinetics of poly (ε-caprolactone)(PCL) with different molar masses. Macromolecules 2012, 45, 3816–3828. [Google Scholar] [CrossRef]
- Silvestre, C.; Cimmino, S.; Duraccio, D.; Schick, C. Isothermal Crystallization of Isotactic Poly(propylene) Studied by Superfast Calorimetry. Macromol. Rapid Commun. 2007, 28, 875–881. [Google Scholar] [CrossRef]
- Mileva, D.; Androsch, R. Effect of co-unit type in random propylene copolymers on the kinetics of mesophase formation and crystallization. Colloid Polym. Sci. 2012, 290, 465–471. [Google Scholar] [CrossRef]
- Arthur, D.J.; Swei, G.S. Electrical Substrate Material. U.S. Patent 5,149,590, 22 September 1992. [Google Scholar]
- Arthur, D.J.; Mosko, J.C.; Jackson, C.S.; Traut, G.R. Electrical Substrate Material. U.S. Patent 4,849,284, 18 July 1989. [Google Scholar]
- Arthur, D.J.; Horn, A.F. Ceramic Filled Fluoropolymeric Composite Material. U.S. Patent 5,061,548, 29 October 1991. [Google Scholar]
- Kostov, G.; Charadjiev, P.; Popov, A. Microscopic and thermophysical studies of polymerization-filled polytetrafluoroethylene. Eur. Polym. J. 1993, 29, 1025–1029. [Google Scholar] [CrossRef]
- Wang, Z.C.; Kou, K.C.; Chao, M.; Bi, H.; Yan, L.K. Nonisothermal crystallization kinetics of polytetrafluoroethylene/solid glass microsphere composites. J. Appl. Polym. Sci. 2010, 117, 1218–1226. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Lin, H.-C.; Lee, Y.-D. The effects of phenyltrimethoxysilane coupling agents on the properties of PTFE/silica composites. J. Polym. Res. 2004, 11, 1–7. [Google Scholar] [CrossRef]
- Martins, S.; Borges, L.; D’Almeida, J.R. Effects of Accelerated Ageing in a PTFE Matrix Polymer Composite. Macromol. Syst. 2011, 299–300, 92–98. [Google Scholar] [CrossRef]
- Martins, S.A.; Dias, F.W.; Nunes, L.S.; Borges, L.A.; D’Almeida, J.R. Mechanical Characterization of Silica Reinforced-PTFE Matrix Composites. Procedia Eng. 2011, 10, 2651–2656. [Google Scholar] [CrossRef] [Green Version]
- Madani, M.; MacQueen, R.; Granata, R. Positron annihilation lifetime study of PTFE/silica composites. J. Polym. Sci. Pol. Phys. 1996, 34, 2767–2770. [Google Scholar] [CrossRef]
- Beckford, S.; Wang, Y.; Zou, M. Wear-resistant PTFE/SiO2 nanoparticle composite films. Tribol. Trans. 2011, 54, 849–858. [Google Scholar] [CrossRef]
- Huang, S.-I.; Chen, T.-H.; Chen, H. Study on the composites of two sized silica filled in PTFE. J. Reinf. Plast. Compos. 2006, 25, 1053–1058. [Google Scholar] [CrossRef]
- Arthur, D.J.; Swei, G.S.; Horn, A.F.; Kilhenny, B., III. Low Volume Fraction Ceramic Filled Fluoropolymeric Composite Material. U.S. Patent 5,281,466, 25 January 1994. [Google Scholar]
- Arthur, D.J.; Swei, G.S.; Horn, A.F., III. Ceramic filled fluoropolymeric composite material. U.S. Patent 5,194,326, 16 March 1993. [Google Scholar]
- Chen, Y.-C.; Lin, H.-C.; Lee, Y.-D. The Effects of Filler Content and Size on the Properties of PTFE/SiO2 Composites. J. Polym. Res. 2003, 10, 247–258. [Google Scholar] [CrossRef]
- Dong-na, Z.; Kai-chang, K.; Pan, G.; Mei, H.; Min, C. Preparation and characterization of PTFE-g-GMA modified PTFE/SiO2 organic–inorganic hybrids. J. Polym. Res. 2012, 19, 9873. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Weeks, J.J. Melting process and the equilibrium melting temperature of polychlorotrifluoroethylene. J. Res. Natl. Bur. Stand. A 1962, 66, 13–28. [Google Scholar] [CrossRef]
- Hoffman, J.; Davis, G.T.; Lauritzen, J.I. Treatise on Solid State Chemistry; Plenum Press: New York, NY, USA, 1976. [Google Scholar]
- Bosq, N.; Guigo, N.; Vincent, L.; Sbirrazzuoli, N. Thermomechanical behavior of a novel biobased poly(furfurylalcohol)/silica nanocomposite elaborated by smart functionalization of silica nanoparticles. Polym. Degrad. Stabil. 2015, 118, 137–146. [Google Scholar] [CrossRef]
- Ogura, K.; Nakaoka, K.; Nakayama, M.; Kobayashi, M.; Fujii, A. Thermogravimetry/mass spectrometry of urease-immobilized sol–gel silica and the application of such a urease-modified electrode to the potentiometric determination of urea. Anal. Chim. Acta 1999, 384, 219–225. [Google Scholar] [CrossRef]
- Hayakawa, S.; Hench, L.L. AM1 study on infra-red spectra of silica clusters modified by fluorine. J. Non-Cryst. Solids 2000, 262, 264–270. [Google Scholar] [CrossRef]
- Lataste, E.; Legein, C.; Body, M.; Buzaré, J.-Y.; Tressaud, A.; Demourgues, A. Highly Fluorinated Silica Obtained by Direct F2-Gas Fluorination: Stability and Unprecedented Fluorosilicate Species Revealed by Solid State NMR Investigations. J. Phys. Chem. C 2009, 113, 18652–18660. [Google Scholar] [CrossRef]
- Bosq, N.; Guigo, N.; Persello, J.; Sbirrazzuoli, N. Melt and glass crystallization of PDMS and PDMS silica nanocomposites. Phys. Chem. Chem. Phys. 2014, 16, 7830–7840. [Google Scholar] [CrossRef] [PubMed]
- Ozawa, T. Nonisothermal crystallization of poly (tetrafluoroethylene). Bull. Chem. Soc. Jpn. 1984, 57, 952–955. [Google Scholar] [CrossRef]
- Seo, Y. Nonisothermal crystallization kinetics of polytetrafluoroethylene. Polym. Eng. Sci. 2000, 40, 1293–1297. [Google Scholar] [CrossRef]
- Treviño-Quintanilla, C.D.; Krishnamoorti, R.; Bonilla-Ríos, J. Flash DSC crystallization study for blown film grade bimodal HDPE resins. I. Isothermal kinetics and its application of the blown film modeling. J. Polym. Sci. Pol. Phys. 2016, 54, 2425–2431. [Google Scholar] [CrossRef]
- Smith, L.; Vasanthan, N. Effect of clay on melt crystallization, crystallization kinetics and spherulitic morphology of poly(trimethylene terephthalate) nanocomposites. Thermochim. Acta 2015, 617, 152–162. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Sbirrazzuoli, N. Isoconversional Kinetic Analysis of Thermally Stimulated Processes in Polymers. Macromol. Rapid Commun. 2006, 27, 1515–1532. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Sbirrazzuoli, N. Isoconversional Analysis of Calorimetric Data on Nonisothermal Crystallization of a Polymer Melt. J. Phys. Chem. B 2003, 107, 882–888. [Google Scholar] [CrossRef]
- Papageorgiou, G.Z.; Achilias, D.S.; Bikiaris, D.N. Crystallization Kinetics of Biodegradable Poly(butylene succinate) under Isothermal and Non-Isothermal Conditions. Macromol. Chem. Phys. 2007, 208, 1250–1264. [Google Scholar] [CrossRef]
- Ma, W.; Wang, X.; Zhang, J. Crystallization kinetics of poly(vinylidene fluoride)/MMT, SiO2, CaCO3, or PTFE nanocomposite by differential scanning calorimeter. J. Therm. Anal. Calorim. 2010, 103, 319–327. [Google Scholar] [CrossRef]
- Guigo, N.; Van Berkel, J.; De Jong, E.; Sbirrazzuoli, N. Modelling the non-isothermal crystallization of polymers: Application to poly (ethylene 2, 5-furandicarboxylate). Thermochim. Acta 2017, 650, 66–75. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Sbirrazzuoli, N. Isoconversional approach to evaluating the Hoffman–Lauritzen parameters (U* and Kg) from the overall rates of nonisothermal crystallization. Macromol. Rapid Commun. 2004, 25, 733–738. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Dranca, I. Isoconversional Analysis of Combined Melt and Glass Crystallization Data. Macromol. Chem. Phys. 2006, 207, 20–25. [Google Scholar] [CrossRef]
- Roitman, D.B.; Marand, H.; Miller, R.L.; Hoffman, J.D. Kinetics of crystallization and morphology of poly (pivalolactone): Regime II. fwdarw. III transition and nucleation constants. J. Phys. Chem. 1989, 93, 6919–6926. [Google Scholar] [CrossRef]
- Cheng, S.Z.; Janimak, J.J.; Zhang, A.; Cheng, H. Regime transitions in fractions of isotactic polypropylene. Macromolecules 1990, 23, 298–303. [Google Scholar] [CrossRef]
- Gan, Z.; Abe, H.; Doi, Y. Biodegradable Poly(ethylene succinate) (PES). 1. Crystal Growth Kinetics and Morphology. Biomacromolecules 2000, 1, 704–712. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, J.D.; Miller, R.L. Response to criticism of nucleation theory as applied to crystallization of lamellar polymers. Macromolecules 1989, 22, 3502–3505. [Google Scholar] [CrossRef]
- Guigo, N.; Sbirrazzuoli, N.; Vyazovkin, S. Atypical gelation in gelatin solutions probed by ultra-fast calorimetry. Soft Matter 2012, 8, 7116–7121. [Google Scholar] [CrossRef]
- Iler, R.K. The Chemistry of Silica: Solubility, Polymerization, Colloid and Surface Properties and Biochemistry of Silica; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Parneix, C.; Persello, J.; Schweins, R.; Cabane, B. How Do Colloidal Aggregates Yield to Compressive Stress? Langmuir 2009, 25, 4692–4707. [Google Scholar] [CrossRef] [PubMed]
- Hartmeyer, G.; Marichal, C.; Lebeau, B.; Caullet, P.; Hernandez, J. Fluorination of Silica Nanoparticles by Aqueous NH4F Solutions. J. Phys. Chem. C 2007, 111, 6634–6644. [Google Scholar] [CrossRef]
- Barabash, R.M.; Zaitsev, V.N.; Kovalchuk, T.V.; Sfihi, H.; Fraissard, J. Low-Temperature Fluorination of Silica by a Nonaqueous Solution of NH4F. J. Phys. Chem. A 2003, 107, 4497–4505. [Google Scholar] [CrossRef]
- Schaefer, J.; Stejskal, E.O. Carbon-13 nuclear magnetic resonance of polymers spinning at the magic angle. J. Am. Chem. Soc. 1976, 98, 1031–1032. [Google Scholar] [CrossRef]
- Peersen, O.B.; Wu, X.L.; Kustanovich, I.; Smith, S.O. Variable-Amplitude Cross-Polarization MAS NMR. J. Magn. Reson. Ser. A 1993, 104, 334–339. [Google Scholar] [CrossRef]
- Cook, R.L.; Langford, C.H.; Yamdagni, R.; Preston, C.M. A Modified Cross-Polarization Magic Angle Spinning 13C NMR Procedure for the Study of Humic Materials. Anal. Chem. 1996, 68, 3979–3986. [Google Scholar] [CrossRef]
- Gerbaud, G.; Ziarelli, F.; Caldarelli, S. Increasing the robustness of heteronuclear decoupling in magic-angle sample spinning solid-state NMR. Chem. Phys. Lett. 2003, 377, 1–5. [Google Scholar] [CrossRef]
- Mathot, V.; Pyda, M.; Pijpers, T.; Vanden Poel, G.; van de Kerkhof, E.; van Herwaarden, S.; van Herwaarden, F.; Leenaers, A. The Flash DSC 1, a power compensation twin-type, chip-based fast scanning calorimeter (FSC): First findings on polymers. Thermochim. Acta 2011, 522, 36–45. [Google Scholar] [CrossRef]
- van Herwaarden, S.; Iervolino, E.; van Herwaarden, F.; Wijffels, T.; Leenaers, A.; Mathot, V. Design, performance and analysis of thermal lag of the UFS1 twin-calorimeter chip for fast scanning calorimetry using the Mettler-Toledo Flash DSC 1. Thermochim. Acta 2011, 522, 46–52. [Google Scholar] [CrossRef]
- Zhuravlev, E.; Schick, C. Fast scanning power compensated differential scanning nano-calorimeter: 1. The device. Thermochim. Acta 2010, 505, 1–13. [Google Scholar] [CrossRef]
- Zhuravlev, E.; Schick, C. Fast scanning power compensated differential scanning nano-calorimeter: 2. Heat capacity analysis. Thermochim. Acta 2010, 505, 14–21. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Vyazovkin, S. Evaluation of activation energy of thermally stimulated solid-state reactions under arbitrary variation of temperature. J. Comput. Chem. 1997, 18, 393–402. [Google Scholar] [CrossRef]
- Sbirrazzuoli, N.; Girault, Y.; Elégant, L. Simulations for evaluation of kinetic methods in differential scanning calorimetry. Part 3—Peak maximum evolution methods and isoconversional methods. Thermochim. Acta 1997, 293, 25–37. [Google Scholar] [CrossRef]
- Vyazovkin, S. The Handbook of Thermal Analysis & Calorimetry; Brown, M.E., Gallagher, P.K., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; Volume 5. [Google Scholar]
- Vyazovkin, S. Modification of the integral isoconversional method to account for variation in the activation energy. J. Comput. Chem. 2001, 22, 178–183. [Google Scholar] [CrossRef]
- Sbirrazzuoli, N.; Vincent, L.; Vyazovkin, S. Comparison of several computational procedures for evaluating the kinetics of thermally stimulated condensed phase reactions. Chemom. Intell. Lab. Syst. 2000, 54, 53–60. [Google Scholar] [CrossRef]
- Sbirrazzuoli, N. Is the Friedman method applicable to transformations with temperature dependent reaction heat? Macromol. Chem. Phys. 2007, 208, 1592–1597. [Google Scholar] [CrossRef]
- Sbirrazzuoli, N. Determination of pre-exponential factors and of the mathematical functions f(α) or G(α) that describe the reaction mechanism in a model-free way. Thermochim. Acta 2013, 564, 59–69. [Google Scholar] [CrossRef]
- Sbirrazzuoli, N.; Brunel, D.; Elegant, L. Different kinetic equations analysis. J. Therm. Anal. Calorim. 1992, 38, 1509–1524. [Google Scholar] [CrossRef]



| Region | U*/J·mol−1 | PTFE | PTFE/SiO2(c)F | ||||
|---|---|---|---|---|---|---|---|
| 104 Kg/K2 | Ic (Kg)/% | r2 | 104 Kg/K2 | Ic (Kg)/% | r2 | ||
| AC | 6270 | 3.4 | ~1 | 0.983 | 2.7 | 1.7 | 0.981 |
| BC | 6270 | 9.0 | ~1 | 0.994 | 8.6 | 2.6 | 0.983 |
| U*/J·mol−1 | Ic (U*)/% | 104 Kg/K2 | Ic (Kg)/% | r2 | |
|---|---|---|---|---|---|
| PTFE | 5870 | ~37 | 8.7 | ~0.8 | 0.995 |
| PTFE/SiO2(c)F | 90334 | ~3.9 | 11.3 | ~1 | 0.997 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bosq, N.; Guigo, N.; Persello, J.; Sbirrazzuoli, N. Crystallization of Polytetrafluoroethylene in a Wide Range of Cooling Rates: Nucleation and Diffusion in the Presence of Nanosilica Clusters. Molecules 2019, 24, 1797. https://doi.org/10.3390/molecules24091797
Bosq N, Guigo N, Persello J, Sbirrazzuoli N. Crystallization of Polytetrafluoroethylene in a Wide Range of Cooling Rates: Nucleation and Diffusion in the Presence of Nanosilica Clusters. Molecules. 2019; 24(9):1797. https://doi.org/10.3390/molecules24091797
Chicago/Turabian StyleBosq, Nicolas, Nathanaël Guigo, Jacques Persello, and Nicolas Sbirrazzuoli. 2019. "Crystallization of Polytetrafluoroethylene in a Wide Range of Cooling Rates: Nucleation and Diffusion in the Presence of Nanosilica Clusters" Molecules 24, no. 9: 1797. https://doi.org/10.3390/molecules24091797
APA StyleBosq, N., Guigo, N., Persello, J., & Sbirrazzuoli, N. (2019). Crystallization of Polytetrafluoroethylene in a Wide Range of Cooling Rates: Nucleation and Diffusion in the Presence of Nanosilica Clusters. Molecules, 24(9), 1797. https://doi.org/10.3390/molecules24091797