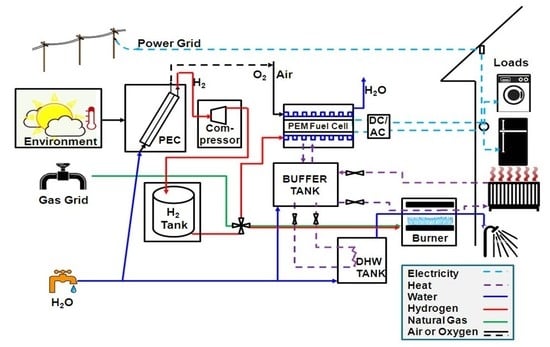
The overall system model is composed of individual device models for each unit in the system. Established models and parameter values were taken from the literature or mass and energy balances were derived when existing models were not available. Environmental parameters, such as solar radiation and ambient temperature, as well as load profiles were used as time-varying inputs with hourly resolution.
2.2.1. Photo-Electrochemical Model
Three different photo-electrochemical models were considered: (1) Ross–Hsiao model, (2) Modified Ross–Hsiao model, and (3) the so-called ‘constant efficiency’ model.
The Ross–Hsiao model [
16,
22,
23] is a thermodynamic efficiency model for photo-electrochemical systems where the model shows the thermodynamic limits for solar conversion to chemical energy. The power for such a solar converter system is equal to the quantity of photoproduct multiplied by the free-energy difference between the initial state of the material and the product state. This model assumes that there are three states in the system: a ground state (initial state); an excited state, which is only radiatively coupled to the ground state and a product state, which is kinetically coupled to the excited state by a chemical reaction path. According to the model, the maximum power can be obtained when the rate of light emission is equal to the rate of light absorption between electronic states. The rate of conversion of solar radiation to chemical energy is given by Equation (1),
where
P (W m
−2) is the total power converted to chemical energy,
JS (number of photons m
−2 s
−1) is the flux of absorbed photons,
μ (J (number of photons)
−1) is the chemical potential generated in the system. In the last term,
Φloss is the quantum yield that is lost via radiative mechanism from the excited state, but without leading to a photoproduct. The 1-
Φloss term thus represents the fraction of the absorbed photons which turn to photoproduct. In the Ross–Hsiao model, it was assumed that there is no non-radiative loss such as electron–hole recombination in the bulk or in surface states. This means the internal conversion, i.e., incident-photon-to-current efficiency (
ηIPCE) or briefly quantum efficiency, was assumed to be 100%.
The thermodynamic efficiency is given by Equation (2), where the denominator describes the total solar energy over all wavelengths which entered the PEC system.
In
Figure 2, thermodynamic efficiency profiles can be seen according to the Ross–Hsiao model for different PEC cell temperatures.
The hydrogen generation rate can be calculated by using the heat of combustion of hydrogen,
(Wh kg
−1), (Equation (3)).
APEC (m
2) is the area of the cell and
G (W m
−2) is the solar radiation intensity.
The solar-to-hydrogen efficiency (in Equation (3)) represents an ideal limit in the conversion; however, there are loss factors which need to be taken into consideration to obtain a more realistic model; this will be presented as the ‘modified Ross–Hsiao model’ in the present paper. The loss factors are now described.
Since the Ross–Hsiao model does not describe the PEC unit as a device, the first loss comes from the optical loss which is mainly due to reflectance of light from the optical window and the electrode surface. Solar collectors have data measured for this kind of light fraction loss, represented as the optical efficiency (
η0) [
24]. This approximation will be used in the modified Ross–Hsiao model.
Inside the photo-electrode, if there is non-radiative loss, such as electron–hole recombination, then in contrast to the Ross–Hsiao model the incident-photon-to-current efficiency (IPCE or also
η IPCE) is not 100%. The IPCE varies depending on the chemistry and material processing, and is a function of wavelength. To be considered in Equation (1),
JS is defined according to Equation (4),
where the new
JS (number of photons m
−2 s
−1) is the flux of absorbed photons corrected by the quantum efficiency,
Ns (number of photons m
−2 s
−1 nm
−1) is the incident solar photon flux and
λg (nm) is the band-gap wavelength of the semiconductor.
ηIPCE can be based on measured data or on calculations. For calculated data, a theoretical approximation can be used, such as the model presented by Ghosh and Maruska [
23]. In the modified Ross–Hsiao model for non-radiative loss, the Ghosh and Maruska model is used according to Equation (5) [
25,
26].
where
ηQE is the quantum conversion efficiency,
k (cm
−1) is the absorption coefficient,
lb (cm) is the width of space charge region,
β (cm
−1) is the inverse of the particles’ diffusion length and
h (cm) is the semiconductor layer thickness. The first term in the main bracket (1-
exp(-
klb)) is the fraction of the generated carriers within the barrier region and the second term in the main bracket (the rest) is the fraction of carriers generated in the bulk region. Parameters change according to the preparation method and can be obtained from measured data with regression analysis.
IPCE curves can be seen in
Figure 3, based on the Ross–Hsiao model and the Ghosh–Maruska model, together with measured data for the case of a GaAs semiconductor.
Figure 3 shows that with the Ross–Hsiao model the IPCE was uniform and 100% due to the lack of non-radiative loss. A real IPCE curve can be seen for GaAs [
27]. For most semiconductors, high-energy photons have low or near-zero quantum efficiencies. The Ghosh–Maruska model is not able to describe that part of the IPCE spectrum (shaded part on the graph). This is a systematic deficiency of the model where the extent of it changes from material to material.
The last loss which has been considered relates to the kinetic loss of the charge transfer (
ηchem) at surface reactions. For this loss term, the model used was from Bolton [
23]. This model assumes that 0.8 eV must be lost in each photochemical step. The model equation can be seen in Equation (6).
where Δ
G is the free-energy change in the overall reaction (Δ
G = 237 kJ mol
−1 at the water-splitting reaction),
n is the number of electrons transferred (
n = 2 for water splitting),
e (C) is the elementary charge and
N0 (mol
−1) is Avogadro’s constant.
The overall efficiency for the modified Ross–Hsiao model is the same as the solar-to-hydrogen efficiency (STH) for the PEC cell. The applied STH efficiency used here is given by Equation (7).
The overall efficiency in Equation (7) can be extended with additional terms to get a more accurate model. Such terms could come from geometry aspects of the cell design, optical aspects caused by bubble formation of generated gases and age effects of photo-electrodes caused by photo- and electrochemical corrosions. These terms are not considered in this work because of the lack of intensive research and available PEC cell unit.
The third model is the ‘constant efficiency’ model. This considers the efficiency to be a constant number, which comes from the yearly average of the PEC thermodynamic efficiency. This constant efficiency does not change with cell temperature and is not affected by the changes in the solar spectrum, which arise from weather/environmental effects. In
Figure 2, we can see that the temperature has a higher effect on higher band-gap wavelength materials, thus the ‘constant efficiency’ model can show the extent of this at different band-gap wavelength materials. The photo-electrochemical cell operated at ambient temperature without any heat accumulation.
2.2.3. PEM Fuel Cell Model
For the PEM fuel cell, a lumped model was chosen with constant operation temperature (Tcell = 80 °C) and atmospheric pressure. Inlet gas composition was assumed to be 90% hydrogen and 10% water vapour in the anode side and 21% oxygen and 79% nitrogen in the cathode side.
The model generates a polarisation curve by adopting equations and the parameters reported in Spiegel [
28]. The main formulas are shown in Equations (8)–(12).
And
where the cell voltage (
Vcell [V]) based on the difference between the Nernstian potential (
ENernst [V]) and the various overpotentials, such as activation overpotential (
ηact [V]), ohmic overpotential (
ηohmic [V]) and the concentration overpotential (
ηconc [V]). The further parameters are the Regnault constant (gas constant,
R [J mol
−1 K
−1]), cell operation temperature (
Tcell [°C]), the number of electrons involved in the anode and cathode reaction (
zi={
za,
zc}), the transfer coefficient for the reaction of interest (αi), the Faraday constant (
F [C mol
−1]), the current density (
i [A cm
−2]), the exchange current density (
i0,i [A cm
−2]) for both the hydrogen oxidation reaction (HOR) and oxygen reduction reaction (ORR), the internal resistance (
Rin [Ω cm
−2]), the limiting current density (
iL [A cm
−2]) and the partial pressure for the components (
pi [Pa]).
The characteristic polarisation curve of the cell provides the specific power (
Pcell [W cm
−2]) from Equation (13).
The next step is to determine the fuel cell electrode area for the demand/hydrogen supplied. It can be calculated from the cell specific power and the maximum power (
Pmax [W]) of the fuel cell, which is the highest output that can support electricity demand.
Pmax depends on the electricity demand of the family. Since any electrochemical cell produces DC current and voltage, this current must be converted to AC to be used in a household for equipment which is normally powered from the grid. An inverter does this with high conversion efficiency,
ηinv. Equation (14) tells us the total area (
Atot [cm
2]) which needs for the calculation of hydrogen quantity to cover the actual electricity demand.
Whether the total area is concentrated into one single cell or in a stack with many smaller area individual cells linked together in series is irrelevant in terms of energy calculation in the lumped model.
In Equation (14), the specific power (Pcell) can be different in time according to the operation mode of the fuel cell. However, it does not mean that the total area of the fuel cell changes during the yearly simulation since the cell is a fixed geometrical unit. The fuel cell can operate with constant output voltage and so the specific power is fixed during operation or the voltage can be changed, thus the output specific power will change as well. At constant voltage mode, an optimal voltage value is selected which is also referred to as the nominal voltage or operation voltage (Vop [V]). The fuel cell model continuously checks the hydrogen level in the tank and if it is insufficient to deliver the power required, the grid is used to make up the shortfall. During simulations, these two operation modes are also called full and partial power modes.
Calculating the amount of hydrogen (see Equation (15)) from the required power, the current is determined by the fuel cell power density-current density curve. From the current, the required hydrogen quantity can be determined using Faraday’s law (see Equation (15)) assuming 100% utilization factor.
During the operation of the fuel cell, heat is generated which can be used to meet thermal demands by utilizing it in the CHP system. Equations (16) and (17) give the generated heat flow (
Qcell [W]) [
20] at full power and partial power mode, respectively. For the partial power mode, the generated heat is proportional to the actual power (
Pactual) for which the hydrogen is just enough to cover and not the maximum power.
2.2.4. CHP Operation with Thermal Units
Thermal units include a buffer tank and a hot water tank, as shown in
Figure 1. The operation of the CHP system is such that the heat from the fuel cell is accumulated in the buffer tank as a central collector unit. The heat from the buffer tank can be used for space heating or hot water supply, in which case the heat is transferred to a hot water tank via an internal heat exchanger such that the liquid medium in the closed buffer tank system is not mixed with the water in the hot water tank. This kind of integrated buffer tank system has a positive effect on the cogeneration system performance, as reported by Beyer and Kelly [
29].
The water inlet temperature to the system from the mains supply is taken to be 10 °C (
TMAIN) and assumed to be independent of seasonal effects. The hot water outlet temperature was chosen to be 60 °C at the consumer side. This value is enough for setting the required temperature for given applications which typically vary between 35 °C and 60 °C. A value of 60 °C also mitigates against legionella bacteria [
30].
The thermal system model is based on heat balance that incorporates heat accumulation in the two thermal storage units (see Equations (24) and (25)). The driving force is the temperature difference between units. Heat transfer between units was modelled by using simplified counter-flow heat exchange with uniform wall temperature (see Equations (18), (20) and (22)). The total heat transfer is proportional to the inlet and outlet temperature differences in the heat exchanger pipes (see Equations (19), (21) and (23)). The only heat source in the CHP storage system is the fuel cell heat, which exits at 80 °C.
Buffer tank-Radiators heat transfer:
Buffer tank-Hot Water tank heat transfer:
Fuel cell-Buffer tank heat transfer:
Heat balance for the buffer tank (Buff) and for the hot water tank (HW):
where
TSET (°C) is the required room temperature. When there is no hourly load or the temperature in the buffer tank is less than TSET, then the flowrate (
ṁSH) is zero in the buffer tank and radiators loop. A single total radiator area (
Arad) is considered.
Urad (W m
−2 K
−1) is the overall heat transfer coefficient of the radiators and UHE is the overall heat transfer coefficient of the heat exchangers in the tanks.
VHW (m
3) is the volume of the hot water tank and
VBuff the buffer tank.
(m
3 s
−1) is the flow rate of hot water in a given hour,
ρ (kg m
−3) is the density of water,
cp,H2O (J kg
−1 K
−1) is the specific heat capacity of water and
t (s) is time.
The multi-fuel burner provides additional heat and is taken to have an efficiency of 90%. The boiler model checks the hydrogen content in the gas tank and switches to natural gas when the hydrogen is consumed. The quantity of fuel required is calculated using Equation (26), where
Qdeficit (J) is the deficit energy that is needed for the remaining load after reducing the energy from the buffer tank or the hot water tank. For the hot water tank, the deficit is the temperature difference between the actual temperature in the tank and 60 °C, as the final temperature requirement.
HHVH2/NG (J kg
−1) is the higher heating value of the given fuel gas and
ηboiler is the boiler efficiency. It was assumed that the flue gas temperature is the same as the fuel temperature, i.e., a condensing boiler was used.