Laser-Inscribed Diamond Waveguide Resonantly Coupled to Diamond Microsphere
Abstract
1. Introduction
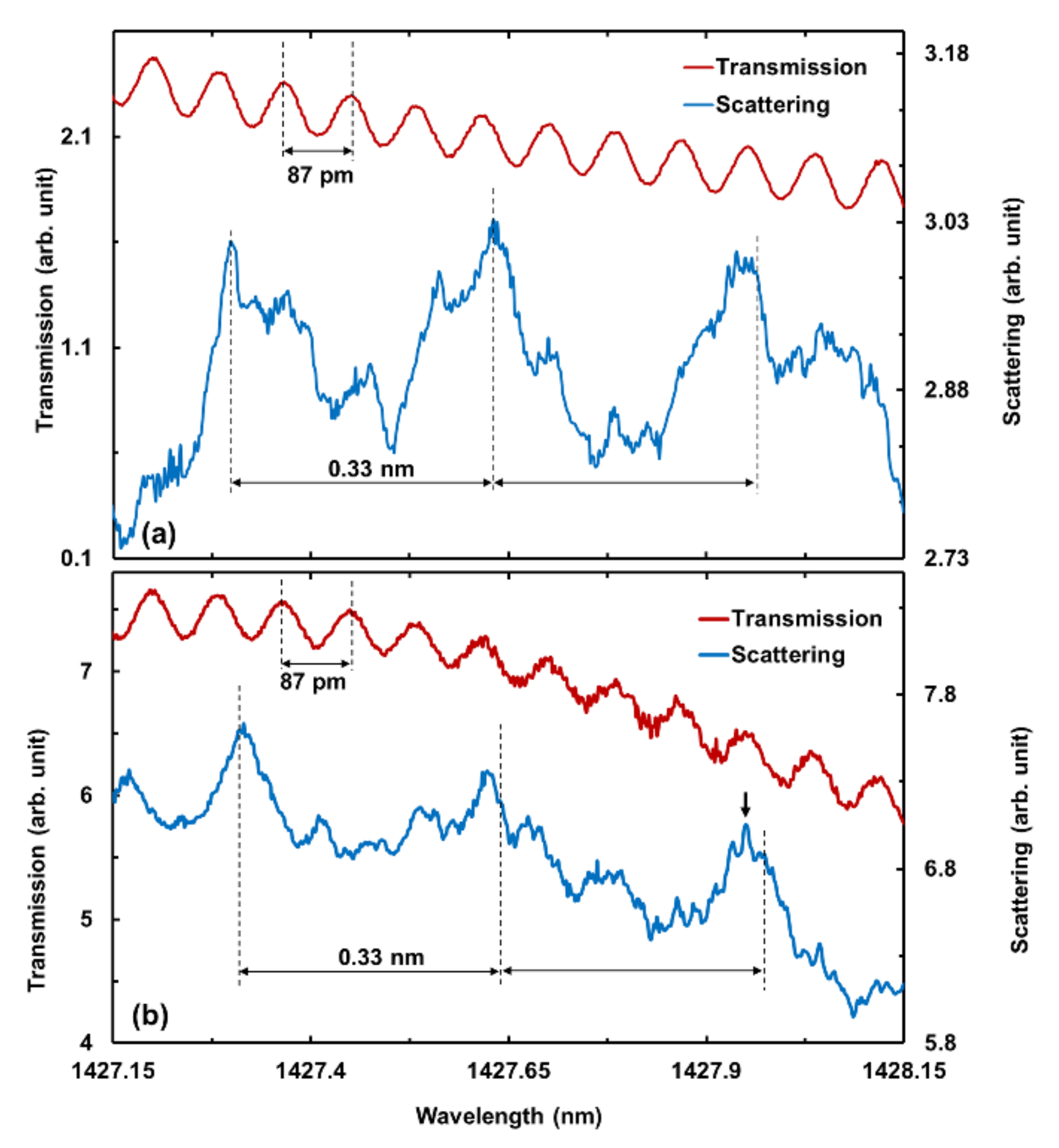
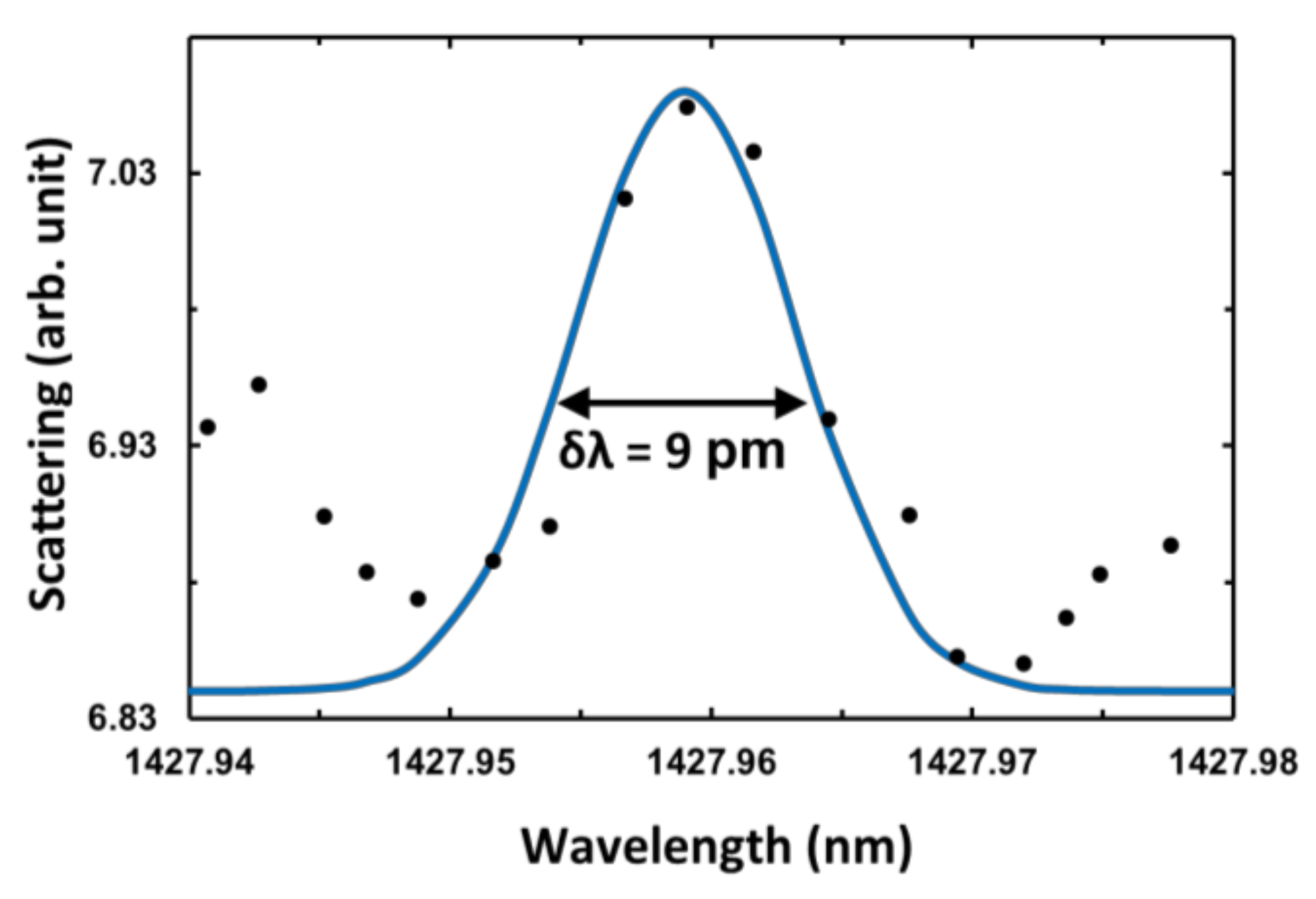
2. Results and Discussions
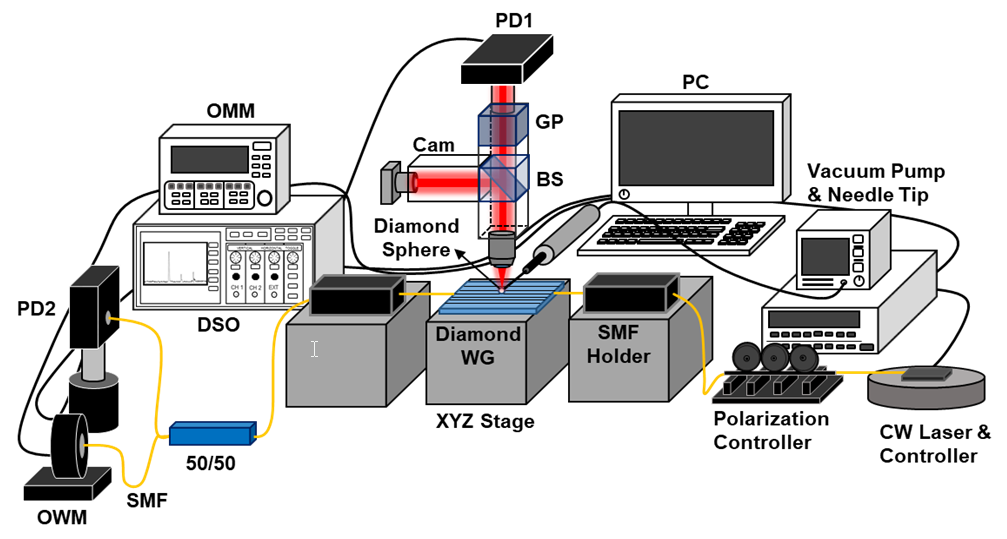
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jalali, B.; Paniccia, M.; Reed, G. Silicon photonics. IEEE Microw. Mag. 2006, 7, 58–68. [Google Scholar] [CrossRef]
- Aharonovich, I.; Greentree, A.D.; Prawer, S. Diamond photonics. Nat. Photon. 2011, 5, 397–405. [Google Scholar] [CrossRef]
- Himpsel, F.J.; Knapp, J.A.; VanVechten, J.A.; Eastman, D.E. Quantum photoyield of diamond(111)—A stable negative-affinity emitter. Phys. Rev. B 1979, 20, 624–627. [Google Scholar] [CrossRef]
- Ilchenko, V.S.; Bennett, A.M.; Santini, P.; Savchenkov, A.A.; Matsko, A.; Maleki, L. Whispering gallery mode diamond resonator. Opt. Lett. 2013, 38, 4320. [Google Scholar] [CrossRef] [PubMed]
- Philipp, H.R.; Taft, E.A. Optical Properties of Diamond in the Vacuum Ultraviolet. Phys. Rev. 1962, 127, 159–161. [Google Scholar] [CrossRef]
- Chiasera, A.; Dumeige, Y.; Féron, P.; Ferrari, M.; Jestin, Y.; Conti, G.N.; Pelli, S.; Soria, S.; Righini, G.C. Spherical whispering-gallery-mode microresonators. Laser Photon. Rev. 2010, 4, 457–482. [Google Scholar] [CrossRef]
- Gökay, U.S.; Zakwan, M.; Demir, A.; Serpenguzel, A. Optical Fiber Excitation of Fano Resonances in a Silicon Microsphere. Fiber Integr. Opt. 2016, 35, 38–46. [Google Scholar] [CrossRef]
- Cai, M.; Painter, O.; Vahala, K. Observation of Critical Coupling in a Fiber Taper to a Silica-Microsphere Whispering-Gallery Mode System. Phys. Rev. Lett. 2000, 85, 74–77. [Google Scholar] [CrossRef] [PubMed]
- Prabhu, A.; Tsay, A.; Han, Z.; Van, V. Ultracompact SOI Microring Add–Drop Filter With Wide Bandwidth and Wide FSR. IEEE Photon. Technol. Lett. 2009, 21, 651–653. [Google Scholar] [CrossRef]
- Bilici, T.; Işçi, S.; Kurt, A.; Serpengüzel, A. Microsphere-Based Channel Dropping Filter with an Integrated Photodetector. IEEE Photon. Technol. Lett. 2004, 16, 476–478. [Google Scholar] [CrossRef]
- Sandoghdar, V.; Treussart, F.; Hare, J.; Lefèvre-Seguin, V.; Raimond, J.-M.; Haroche, S. Very low threshold whispering-gallery-mode microsphere laser. Phys. Rev. A 1996, 54, R1777–R1780. [Google Scholar] [CrossRef] [PubMed]
- Vollmer, F.; Arnold, S. Whispering-gallery-mode biosensing: Label-free detection down to single molecules. Nat. Methods 2008, 5, 591–596. [Google Scholar] [CrossRef] [PubMed]
- Steglich, P.; Hülsemann, M.; Dietzel, B.; Mai, A. Optical Biosensors Based on Silicon-On-Insulator Ring Resonators: A Review. Molecules 2019, 24, 519. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Jiang, M.-Y.; Shi, J.; Zheng, M.-M.; Huang, F. Preparation of Immobilized Lipase Based on Hollow Mesoporous Silica Spheres and Its Application in Ester Synthesis. Molecules 2019, 24, 395. [Google Scholar] [CrossRef] [PubMed]
- Jun, B.-H.; Kang, H.; Lee, J.-Y.; Jeong, D.H. Fluorescence-Based Multiplex Protein Detection Using Optically Encoded Microbeads. Molecules 2012, 17, 2474–2490. [Google Scholar] [CrossRef] [PubMed]
- Braginsky, V.; Gorodetsky, M.L.; Ilchenko, V. Quality-factor and nonlinear properties of optical whispering-gallery modes. Phys. Lett. A 1989, 137, 393–397. [Google Scholar] [CrossRef]
- Serpengüzel, A.; Griffel, G.; Arnold, S. Excitation of resonances of microspheres on an optical fiber. Opt. Lett. 1995, 20, 654. [Google Scholar] [CrossRef] [PubMed]
- Çirkinoğlu, H.O.; Bayer, M.M.; Gokay, U.S.; Serpenguzel, A.; Sotillo, B.; Bharadwaj, V.; Ramponi, R.; Eaton, S.M. Silicon microsphere whispering gallery modes excited by femtosecond-laser-inscribed glass waveguides. Appl. Opt. 2018, 57, 3687–3692. [Google Scholar] [CrossRef] [PubMed]
- Choy, J.; Hausmann, B.; Burek, M.; Babinec, T.; Loncar, M. Nanofabrication of photonic devices from single-crystal diamond for quantum information processing (QIP). In Quantum Information Processing with Diamond; Elsevier: Amsterdam, The Netherlands, 2014; Volume 63, pp. 98–123. [Google Scholar]
- Del’Haye, P.; Schliesser, A.; Arcizet, O.; Wilken, T.; Holzwarth, R.; Kippenberg, T.J. Optical frequency comb generation from a monolithic microresonator. Nature 2007, 450, 1214–1217. [Google Scholar] [CrossRef] [PubMed]
- Kippenberg, T.J.; Holzwarth, R.; Diddams, S.A. Microresonator-Based Optical Frequency Combs. Science 2011, 332, 555–559. [Google Scholar] [CrossRef] [PubMed]
- Feve, J.-P.M.; Shortoff, K.E.; Bohn, M.J.; Brasseur, J.K. High average power diamond Raman laser. Opt. Express 2011, 19, 913–922. [Google Scholar] [CrossRef] [PubMed]
- Hadden, J.P.; Bharadwaj, V.; Sotillo, B.; Rampini, S.; Osellame, R.; Witmer, J.D.; Jayakumar, H.; Fernandez, T.T.; Chiappini, A.; Armellini, C.; et al. Integrated waveguides and deterministically positioned nitrogen vacancy centers in diamond created by femtosecond laser writing. Opt. Lett. 2018, 43, 3586–3589. [Google Scholar] [CrossRef] [PubMed]
- Sotillo, B.; Chiappini, A.; Bharadwaj, V.; Hadden, J.P.; Bosia, F.; Olivero, P.; Ferrari, M.; Ramponi, R.; Barclay, P.E.; Eaton, S.M. Polarized micro-Raman studies of femtosecond laser written stress-induced optical waveguides in diamond. Appl. Phys. Lett. 2018, 112, 031109. [Google Scholar] [CrossRef]
- Çirkinoğlu, H.O.; Bayer, M.M.; Serpenguzel, A.; Rampini, S.; Sotillo, B.; Bharadwaj, V.; Ramponi, R.; Eaton, S.M. Femtosecond laser written diamond waveguide excitation of the whispering gallery modes in a silicon microsphere. Opt. Mater. 2019, 92, 418–424. [Google Scholar] [CrossRef]
- Bayer, M.M.; Çirkinoğlu, H.O.; Serpenguzel, A. Observation of Whispering-Gallery Modes in a Diamond Microsphere. IEEE Photon. Technol. Lett. 2017, 30, 3–6. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: New York, NY, USA, 1998; p. 100. [Google Scholar]
- Chýlek, P. Partial-wave resonances and the ripple structure in the Mie normalized extinction cross section. J. Opt. Soc. Am. 1976, 66, 285. [Google Scholar] [CrossRef]
- Hood, C.J.; Kimble, H.J.; Ye, J. Characterization of high-finesse mirrors: Loss, phase shifts, and mode structure in an optical cavity. Phys. Rev. A 2001, 64, 033804. [Google Scholar] [CrossRef]
- Gorodetsky, M.L.; Savchenkov, A.A.; Ilchenko, V.S. Ultimate Q of optical microsphere resonators. Opt. Lett. 1996, 21, 453. [Google Scholar] [CrossRef] [PubMed]
- Ilchenko, V.; Gorodetsky, M.L.; Vyatchanin, S. Coupling and tunability of optical whispering-gallery modes: A basis for coordinate meter. Opt. Commun. 1994, 107, 41–48. [Google Scholar] [CrossRef]
- Liang, Q.; Yan, C.-S.; Meng, Y.; Lai, J.; Krasnicki, S.; Mao, H.-K.; Hemley, R.J. Recent advances in high-growth rate single-crystal CVD diamond. Diam. Relat. Mater. 2009, 18, 698–703. [Google Scholar] [CrossRef]
- Griffel, G.; Arnold, S.; Taskent, D.; Serpengüzel, A.; Connolly, J.; Morris, N. Morphology-dependent resonances of a microsphere-optical fiber system. Opt. Lett. 1996, 21, 695. [Google Scholar] [CrossRef] [PubMed]
- Serpengüzel, A.; Arnold, S.; Griffel, G.; Lock, J.A. Enhanced coupling to microsphere resonances with optical fibers. J. Opt. Soc. Am. B 1997, 14, 790. [Google Scholar] [CrossRef]
Sample Availability: Diamond microsphere available from the manufacturer and waveguide sample available from the authors. |


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yavuz, N.; Bayer, M.M.; Ҫirkinoğlu, H.O.; Serpengüzel, A.; Le Phu, T.; Giakoumaki, A.; Bharadwaj, V.; Ramponi, R.; Eaton, S.M. Laser-Inscribed Diamond Waveguide Resonantly Coupled to Diamond Microsphere. Molecules 2020, 25, 2698. https://doi.org/10.3390/molecules25112698
Yavuz N, Bayer MM, Ҫirkinoğlu HO, Serpengüzel A, Le Phu T, Giakoumaki A, Bharadwaj V, Ramponi R, Eaton SM. Laser-Inscribed Diamond Waveguide Resonantly Coupled to Diamond Microsphere. Molecules. 2020; 25(11):2698. https://doi.org/10.3390/molecules25112698
Chicago/Turabian StyleYavuz, Nurperi, Mustafa Mert Bayer, Hüseyin Ozan Ҫirkinoğlu, Ali Serpengüzel, Thien Le Phu, Argyro Giakoumaki, Vibhav Bharadwaj, Roberta Ramponi, and Shane M. Eaton. 2020. "Laser-Inscribed Diamond Waveguide Resonantly Coupled to Diamond Microsphere" Molecules 25, no. 11: 2698. https://doi.org/10.3390/molecules25112698
APA StyleYavuz, N., Bayer, M. M., Ҫirkinoğlu, H. O., Serpengüzel, A., Le Phu, T., Giakoumaki, A., Bharadwaj, V., Ramponi, R., & Eaton, S. M. (2020). Laser-Inscribed Diamond Waveguide Resonantly Coupled to Diamond Microsphere. Molecules, 25(11), 2698. https://doi.org/10.3390/molecules25112698






