The Structure of the “Vibration Hole” around an Isotopic Substitution—Implications for the Calculation of Nuclear Magnetic Resonance (NMR) Isotopic Shifts
Abstract
:1. Introduction
2. Theory
2.1. Standard Versus Difference-Dedicated Second-Order Perturbation Theory
- 1
- Determine the and the for A and B. Complement each set of by three modes for rigid translations along the principal axes of inertia of and 3 (or 2) modes for rigid rotations around the principle axes of inertia. The scaling of these additional modes is arbitrary.
- 2
- Find the coefficient matrix for the expansion(the J stands for Jacobian). Here, the indices v, r, and t stand for vibrational, rotational, and translational modes, respectively.
- 3
- Construct the matrix according towhere is 1 if k refers to a vibration mode and 0 otherwise.
- 4
- Diagonalize the matrix , denote the eigenvalues as , which are ordered such that the decrease monotonously. Collect the eigenvectors as column vectors in the matrix
- 5
- Calculate the difference-dedicated vibration modes according to
2.2. Local Second-Order Vibrational Perturbation Theory (Loc-Vpt2)
2.3. Geometry Parameters
3. Results
3.1. Cyclic and Polycyclic Molecules
3.2. Large Systems: Halonium Complexes of Bis(Phenylethynyl)Benzene Derivatives
3.3. Molecules with Intramolecular Hydrogen Bonds: Salicyl Aldehyde Derivatives
4. Implementation, Computational Details
5. Conclusions
- 1
- For a H/D substitution on a C-bonded H atom (thus not involved in a hydrogen bond), the vibration hole is distinctly localized at the C–H bond, with respect to both bond lengths and mean-square amplitudes as well as amplitude covariances. Regarding the bond-length contractions, this localization is seen more clearly in the than in the values. The values for the C–H bonds are typically around , those for the C–C’ bonds around −150 to the remaining ones generally between 0 and . In particular, the values for the C–H’ bonds are very small, between and . The isotope effect on the mean-square amplitude for the C–H bonds is around , to for the C–C’ bonds, between 0 and for the C’–C” bonds, and between 0 and for the remaining bonds. For the amplitude covariances with , the corresponding values are to (C–C’ bond), to (C–H’ bond), to (C’–C” bond) and to otherwise. One sees that the localization is (expectedly) stronger for the mean-square amplitudes than for the amplitude covariances.
- 2
- The isotope effects are quite uniform across the different compounds for the C–H, C–C’, and C–H’ bonds. For vicinal bonds in aliphatic molecules, the isotope effects distinctly depend on the conformation relative to the C–H bond.
- 3
- Both for the cyclic and polycyclic systems from Section 3.1 and the bpeb-derivative complexes from Section 3.2, the parameters describing the correlation hole decay from the substitution site up to a topological distance of 3 to 4. Beyond that value, no consistent decay of the values is found (see in particular Figure 6). However, the geometry and amplitude changes beyond this topological distance are rather small (absolute values up to or , respectively) so that they are expected to make only minor contributions to the NMR isotopic shifts.We note though that the large molecules studied in this work all are aromatic with a contiguous set of orbitals over the whole molecule. The vibration hole may behave differently in an aliphatic molecule of comparable size.
- 4
- The loc-VPT2 description of the vibration hole at the C–H bond follows the corresponding DD-VT2 description relatively closely. Generally, loc-VPT2 predicts slightly larger isotope effects on geometry parameters than DD-VPT2.
- 5
- As a consequence of 4, the loc-VPT2 values for the NMR isotopic shifts are relatively close to their DD-VPT2 counterparts, and there are no systematic trends in the deviations between DD-VPT2 and loc-VPT2 values.Still, we recommend to use the DD-VPT2 approach since it predicts NMR isotopic shifts at a cost comparable to loc-VPT2 but without a priori assumptions on the vibration hole. Furthermore, the correlation between calculated and measured values tends to be slightly higher for DD-VPT2 than for loc-VPT2, which indicates that DD-VPT2 reflects relevant features of the vibration hole that are missing in loc-VPT2.
- 6
- The LMZL approach by Yang and Hudson [60] systematically underestimates the isotope effect on and, in extension, the NMR isotopic shifts. This is due not to the a priori local approach but to the missing anharmonic coupling between bond-stretching and bond-bending as well as out-of-plane bending vibrations. With the help of a relatively simple centrifugal correction (see Appendix B), this shortcoming can be remedied effectively.
- 7
- For a substitution in benzene (i.e., the substitution site is involved in more than one bond), loc-VPT2 can in principle not provide a correct description of the vibration hole. Still, the isotope effects on the bond lengths are relatively close to their DD-VPT2 counterparts, and the deviations between the DD-VPT2 and loc-VPT2 NMR isotopic shifts are moderate. To some extent, the changes in the vibrational amplitudes “cover up” for the lacking flexibility of the loc-VPT2 approach.
- 8
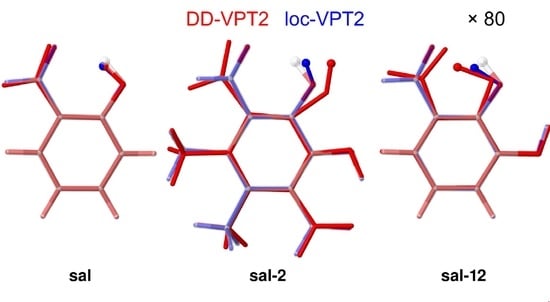
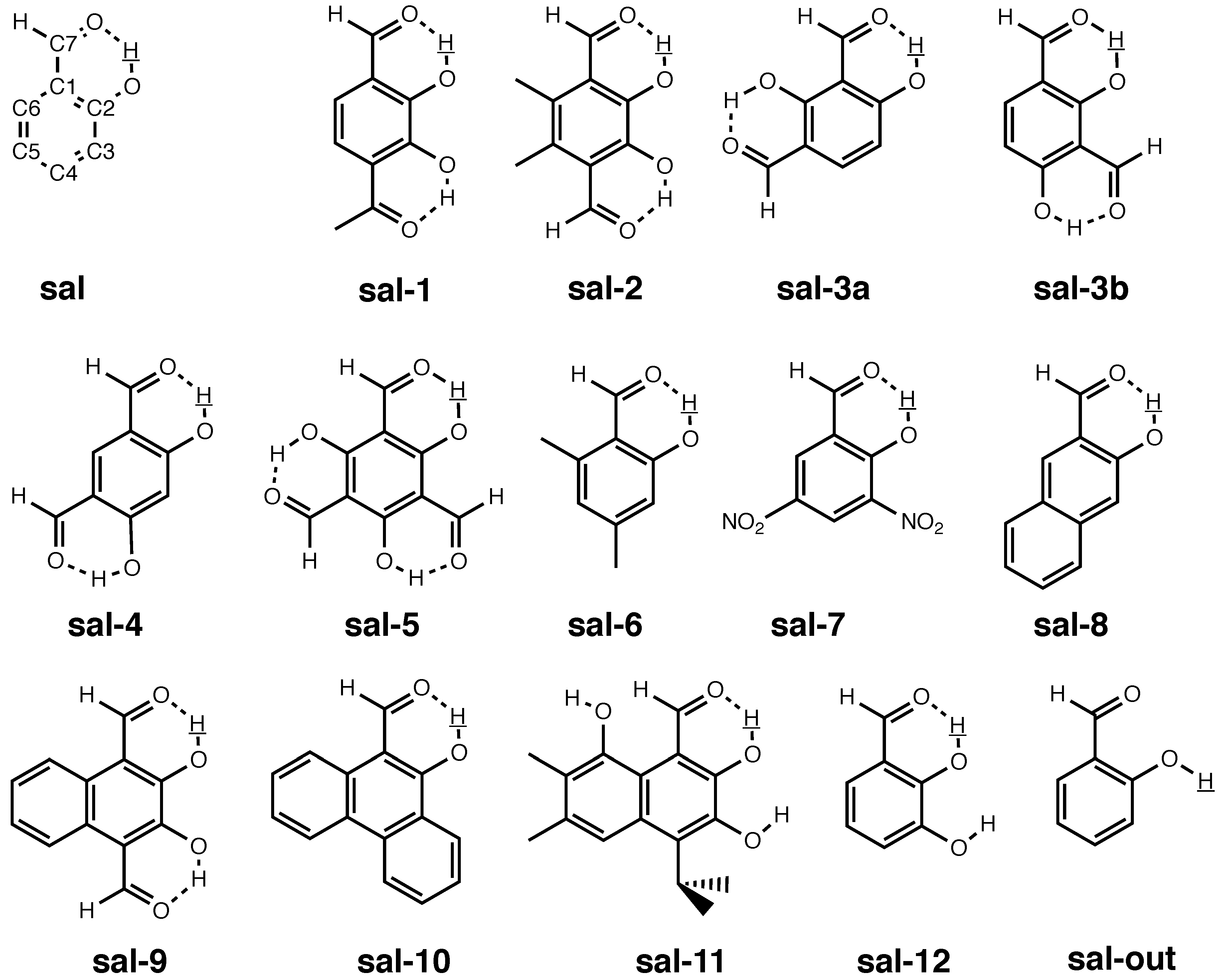
- If the H atom at the substitution site is involved in an intra-molecular hydrogen bond the picture changes thoroughly. In this case, the vibration hole is delocalized all over the hydrogen-bond moiety; in the case of the sal derivatives studied in Section 3.3, over the whole HC=O···OH moiety. As a consequence, loc-VPT2 calculations cannot provide a proper description of the vibration hole and not either correctly predict NMR isotopic shifts. However, loc-VPT2 calculations can be used, in conjunction with DD-VPT2 calculations, to elucidate the mechanism behind the NMR isotopic shifts.
- 9
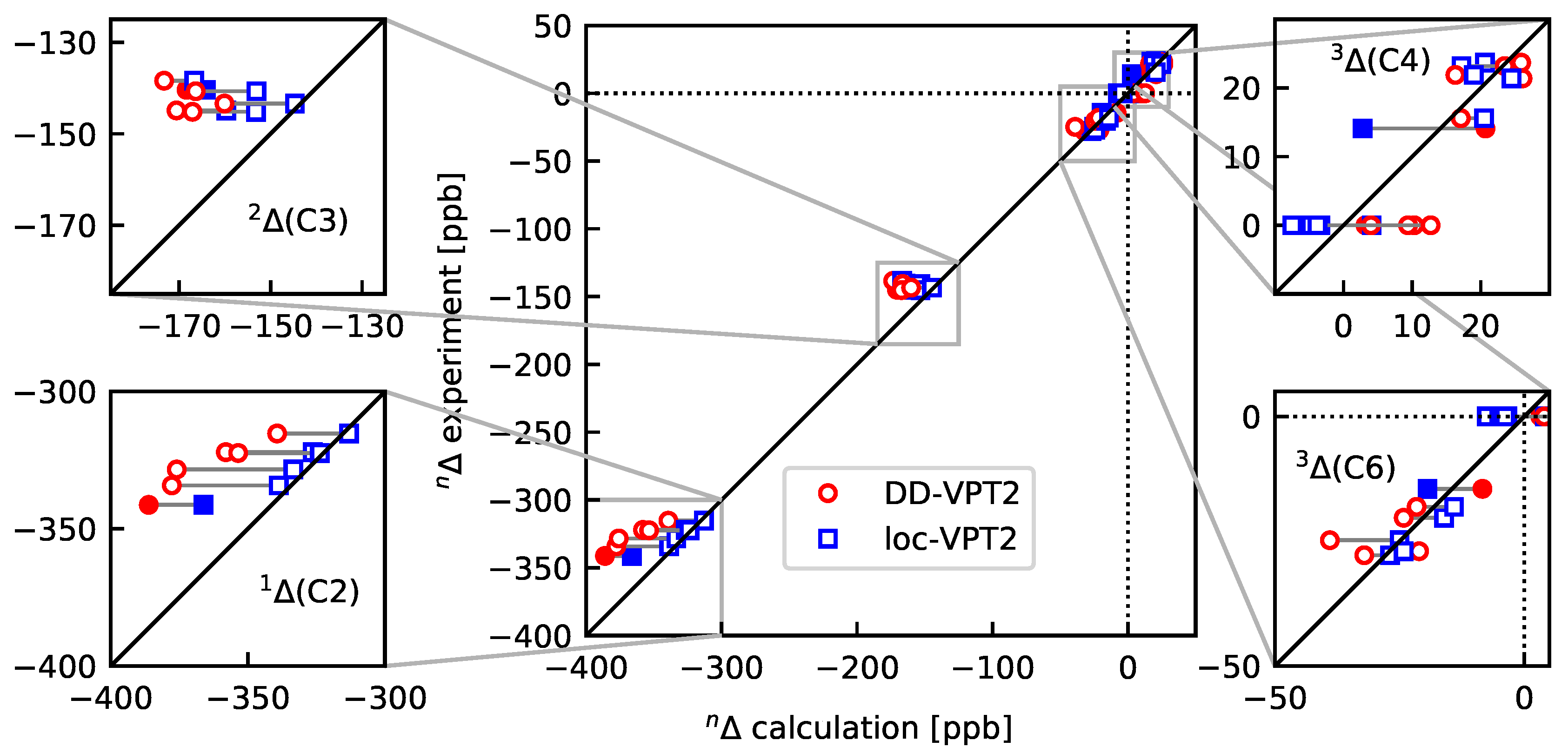
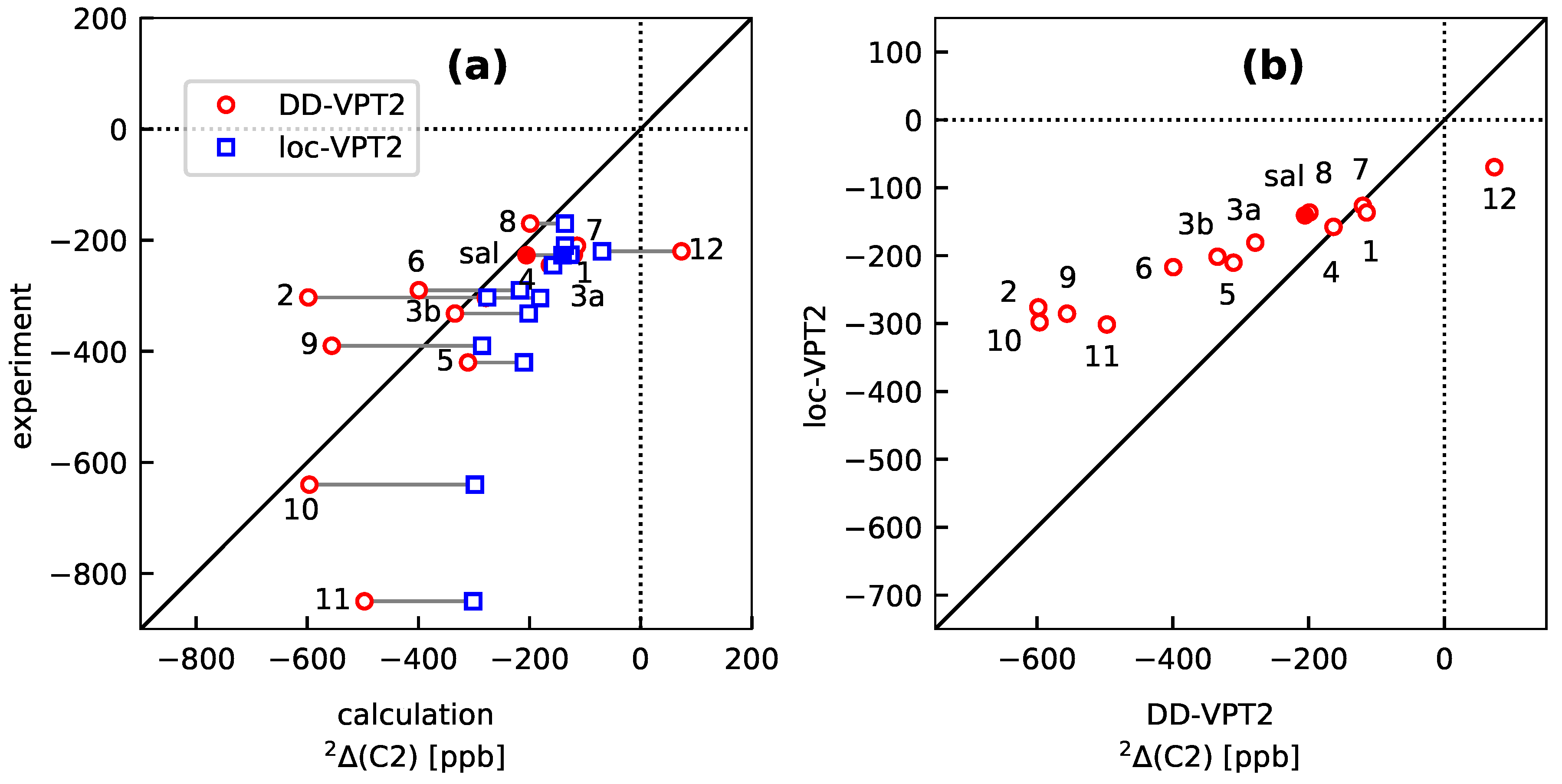
- For the sal derivatives studied in Section 3.3, the substituent effects on stretch over a range of several 100 ppb. loc-VPT2 calculations predict values with too low a variance, since loc-VPT2 misses important features of the vibration hole. The variance of the DD-VPT2 values is approximately correct; however, neither with regard to the RMS deviation or the correlation between calculated and experimental values is DD-VPT2 clearly superior to loc-VPT2. There is a clear correlation between loc-VPT2 and DD-VPT2 values.
- 10
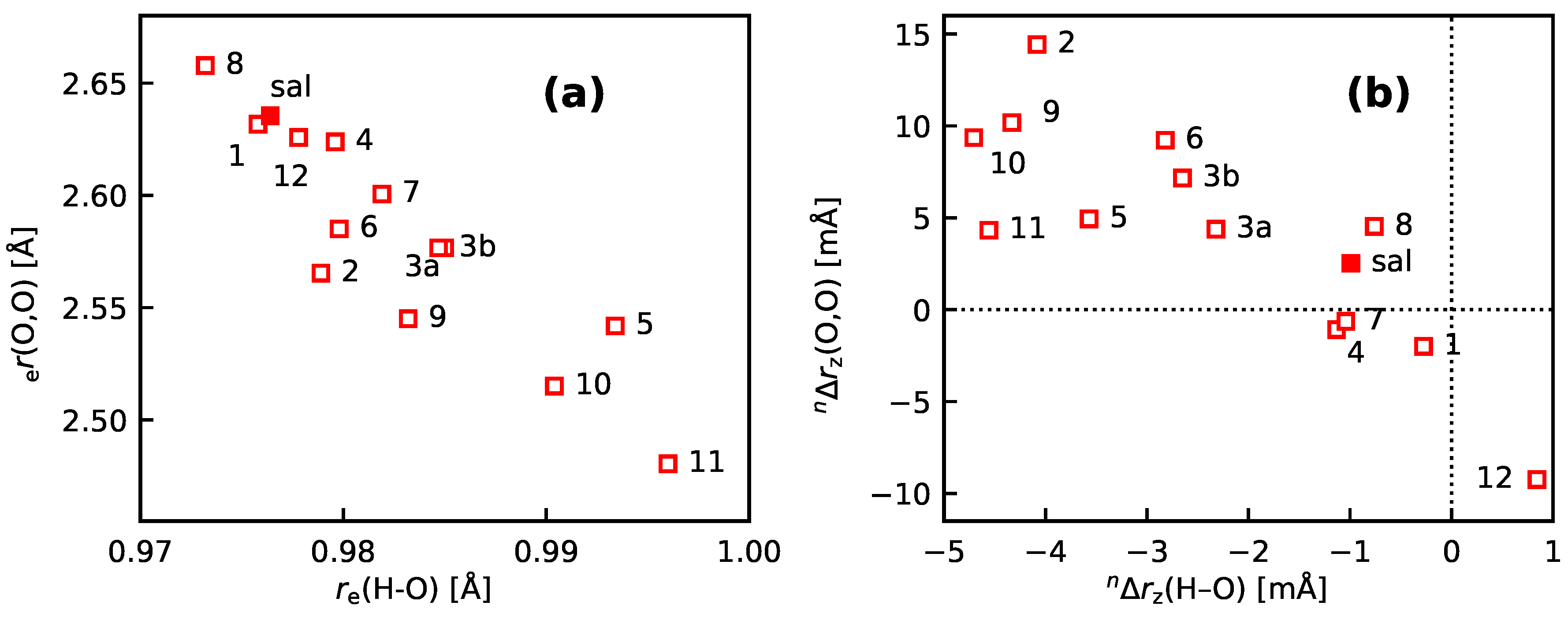
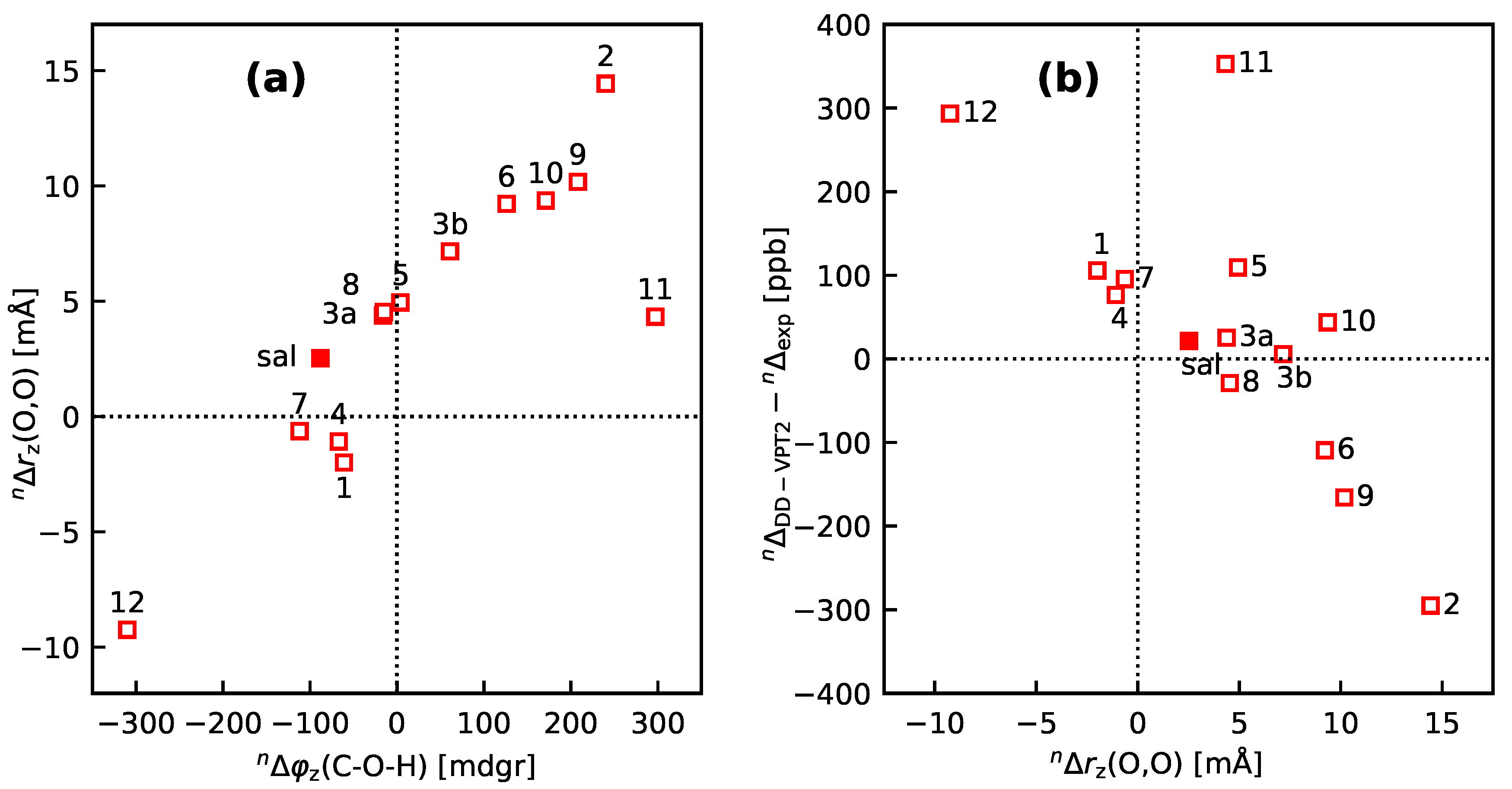
- An analysis of the vibration holes for the sal derivatives calculated with DD-VPT2 and loc-VPT2 reveals that the two descriptions agree relatively well at the O–H bond. This gives at hand that these changes are mainly a direct response to the anharmonic molecular potential of at the H site, whereas the geometry change in the HC=O moiety is a response to the displacement of the H atom. This is corroborated by the (albeit not perfect) correlations between and on the one hand and on the other hand.
- 11
- Point 10 gives at hand that a part of is caused directly by the change of the geometry at the O–H bond (this part is covered by loc-VPT2), while the geometric response of the HC=O moiety (only covered in DD-VPT2) “leverages” and amplifies this effect. This explains the correlation between loc-VPT2 and DD-VPT2 values and offers an explanation for the limited accuracy of the former—the potential around the H site is supposed to be strongly anharmonic, and VPT2 may not be sufficient for a proper description. The errors in this description are then “leveraged” by the HC=O moiety, which causes the relatively large errors in the DD-VPT2 values.
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Geometry Parameters for VPT2 And DD-VPT2
Appendix B. The Centrifugal Potential for the Corrected LMZL Approach
References
- Wolfsberg, M.; Van Hook, W.A.; Paneth, P. Isotope Effects on Dipole Moments, Polarizability, NMR Shielding, and Molar Volume. In Isotope Effects: In the Chemical, Geological, and Bio Sciences; Springer: Dordrecht, The Netherlands, 2009; pp. 389–412. [Google Scholar] [CrossRef]
- Muenter, J.S.; Laurie, V.W. Deuterium isotope effects on molecular dipole moments by microwave spectroscopy. J. Chem. Phys. 1966, 45, 855–858. [Google Scholar] [CrossRef]
- Assafrao, D.; Mohallem, J.R. The isotopic dipole moment of HDO. J. Phys. B 2007, 40, F85–F91. [Google Scholar] [CrossRef]
- Bridge, N.J.; Buckingham, A.D. Polarization of laser light scattered by gases. J. Chem. Phys. 1964, 40, 2733–2734. [Google Scholar] [CrossRef]
- Arapiraca, A.F.C.; Jonsson, D.; Mohallem, J.R. Vibrationally averaged post Born-Oppenheimer isotopic dipole moment calculations approaching spectroscopic accuracy. J. Chem. Phys. 2011, 135, 244313. [Google Scholar] [CrossRef] [PubMed]
- Carrington, A.; Longueth, H.; Moss, R.; Todd, P. Isotope effects in electron spin resonance: The negative ion of cyclo-octatetraene-1-d. Mol. Phys. 1965, 9, 187–190. [Google Scholar] [CrossRef]
- Stößer, R.; Herrmann, W. Isotope Effects in ESR Spectroscopy. Molecules 2013, 18, 6679–6722. [Google Scholar] [CrossRef]
- Muenter, J.S.; Klemperer, W. Hyperfine structure constants of HF and DF. J. Chem. Phys. 1970, 52, 6033–6037. [Google Scholar] [CrossRef]
- Coriani, S.; Jaszunski, M.; Rizzo, A.; Ruud, K. MCSCF nuclear magnetic shieldings and spin-rotation constants of 16O in 16O–17O–16O and 17O–16O–16O. Chem. Phys. Lett. 1998, 287, 677–681. [Google Scholar] [CrossRef]
- Batiz-Hernandez, H.; Bernheim, R.A. The Isotope Shift. In Progress in Nuclear Resonance Spectroscopy; Emsley, J., Feeney, J., Sutcliffe, L., Eds.; Pergamon Press: Oxford, UK, 1967; Volume 3, p. 63. [Google Scholar]
- Hansen, P.E. Isotope effects in nuclear shielding. Progr. Nucl. Magn. Res. Sp. 1988, 20, 207–255. [Google Scholar] [CrossRef]
- Hansen, P.E. Isotope effects on chemical shifts of proteins and peptides. Magn. Res. Chem. 2000, 38, 1–10. [Google Scholar] [CrossRef]
- Jameson, C.J. Isotope Effects on Chemical Shifts and Coupling Constants. In eMagRes; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Hansen, P.E.; Spanget-Larsen, J. NMR and IR Investigations of Strong Intramolecular Hydrogen Bonds. Molecules 2017, 22, 552. [Google Scholar] [CrossRef] [Green Version]
- Hansen, P.E. Isotope Effects on Chemical Shifts in the Study of Intramolecular Hydrogen Bonds. Molecules 2015, 20, 2405–2424. [Google Scholar] [CrossRef] [Green Version]
- Gunnarsson, G.; Wennerström, H.; Egan, W.; Forsén, S. Proton and deuterium NMR of hydrogen-bonds— Relationship between isotope-effects and hydrogen-bond potential. Chem. Phys. Lett. 1976, 38, 96–99. [Google Scholar] [CrossRef]
- Smirnov, S.N.; Golubev, N.S.; Denisov, G.S.; Benedict, H.; SchahMohammedi, P.; Limbach, H.H. Hydrogen deuterium isotope effects on the NMR chemical shifts and geometries of intermolecular low-barrier hydrogen-bonded complexes. J. Am. Chem. Soc. 1996, 118, 4094–4101. [Google Scholar] [CrossRef]
- Tolstoy, P.M.; Koeppe, B.; Denisov, G.S.; Limbach, H.H. Combined NMR and UV/Vis Spectroscopy in the Solution State: Study of the Geometries of Strong OHO Hydrogen Bonds of Phenols with Carboxylic Acids. Angew. Chem. Int. Ed. 2009, 48, 5745–5747. [Google Scholar] [CrossRef]
- Ip, B.C.K.; Shenderovich, I.G.; Tolstoy, P.M.; Frydel, J.; Denisov, G.S.; Buntkowsky, G.; Limbach, H.H. NMR Studies of Solid Pentachlorophenol-4-Methylpyridine Complexes Exhibiting Strong OHN Hydrogen Bonds: Geometric H/D Isotope Effects and Hydrogen Bond Coupling Cause Isotopic Polymorphism. J. Phys. Chem. A 2012, 116, 11370–11387. [Google Scholar] [CrossRef] [PubMed]
- Hansen, P.E.; Kamounah, F.S.; Saeed, B.A.; MacLachlan, M.J.; Spanget-Larsen, J. Intramolecular Hydrogen Bonds in Normal and Sterically Compressed O-Hydroxy Aromat. Aldehydes. Isotope Effects on Chemical Shifts and Hydrogen Bond Strength. Molecules 2019, 24, 4533. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ullah, S.; Ishimoto, T.; Williamson, M.P.; Hansen, P.E. Ab Initio Calculations of Deuterium Isotope Effects on Chemical Shifts of Salt-Bridged Lysines. J. Phys. Chem. B 2011, 115, 3208–3215. [Google Scholar] [CrossRef] [PubMed]
- Williamson, M.P.; Hounslow, A.M.; Ford, J.; Fowler, K.; Hebditch, M.; Hansen, P.E. Detection of salt bridges to lysines in solution in barnase. Chem. Commun. 2013, 49, 9824–9826. [Google Scholar] [CrossRef] [PubMed]
- Ottiger, M.; Bax, A. An empirical correlation between amide deuterium isotope effects on 13Cα chemical shifts and protein backbone conformation. J. Am. Chem. Soc. 1997, 119, 8070–8075. [Google Scholar] [CrossRef]
- Sun, H.; Tugarinov, V. Precision Measurements of Deuterium Isotope Effects on the Chemical Shifts of Backbone Nuclei in Proteins: Correlations with Secondary Structure. J. Phys. Chem. B 2012, 116, 7436–7448. [Google Scholar] [CrossRef]
- Maltsev, A.S.; Ying, J.; Bax, A. Deuterium isotope shifts for backbone 1H, 15N and 13C nuclei in intrinsically disordered protein alpha-synuclein. J. Biomol. NMR 2012, 54, 181–191. [Google Scholar] [CrossRef]
- Newmark, R.A.; Hill, J.R. Use of 13C isotope shifts to assign carbon atoms α and carbon atoms β (and para) to a hydroxy group in alkyl substituted phenols and alcohols. Org. Magn. Reson. 1980, 13, 40–44. [Google Scholar] [CrossRef]
- Aydin, R.; Wesener, J.R.; Günther, H.; Santillan, R.L.; Garibay, M.E.; Joseph-Nathan, P. On the stereospecifity of intrinsic 2H–1H NMR isotope effects on carbon-13 chemical-shifts in cyclohexanes. J. Org. Chem. 1984, 49, 3845–3847. [Google Scholar] [CrossRef]
- Böhm, K.H.; Banert, K.; Auer, A.A. Identifying Stereoisomers by ab-initio Calculation of Secondary Isotope Shifts on NMR Chemical Shieldings. Molecules 2014, 19, 5301–5312. [Google Scholar] [CrossRef] [PubMed]
- Koch, K.R.; Engelbrecht, L. Intrinsic 37/35Cl and 18/16O isotope shifts in 195Pt and 103Rh NMR of purely inorganic Pt and Rh complexes as unique spectroscopic fingerprints for unambiguous assignment of structure. Dalton Trans. 2017, 46, 9303–9315. [Google Scholar] [CrossRef] [PubMed]
- Gräfenstein, J. Efficient calculation of NMR isotopic shifts: Difference-dedicated vibrational perturbation theory. J. Chem. Phys. 2019, 151, 244120. [Google Scholar] [CrossRef]
- Bigeleisen, J.; Mayer, M.G. Calculation of equilibrium constants for isotopic exchange reactions. J. Chem. Phys. 1947, 15, 261–267. [Google Scholar] [CrossRef]
- Perrin, C.L. Symmetries of hydrogen-bonds in solution. Science 1994, 266, 1665–1668. [Google Scholar] [CrossRef]
- Perrin, C.L.; Lau, J.S.; Kim, Y.J.; Karri, P.; Moore, C.; Rheingold, A.L. Asymmetry of the “Strongest” OHO Hydrogen Bond, in the Monoanion of (±)-α,α′-Di-tert-butylsuccinate. J. Am. Chem. Soc. 2009, 131, 13548–13554. [Google Scholar] [CrossRef]
- Perrin, C.L.; Wu, Y. Symmetry of Hydrogen Bonds in Two Enols in Solution. J. Am. Chem. Soc. 2019, 141, 4103–4107. [Google Scholar] [CrossRef]
- Ohta, B.K. The structure of halonium ions in superacidic solutions. Pure Appl. Chem. 2013, 85, 1959–1965. [Google Scholar] [CrossRef]
- Carlsson, A.C.C.; Gräfenstein, J.; Laurila, J.L.; Bergquist, J.; Erdélyi, M. Symmetry of [N–X–N]+ halogen bonds in solution. Chem. Commun. 2012, 48, 1458–1460. [Google Scholar] [CrossRef] [Green Version]
- Carlsson, A.C.C.; Gräfenstein, J.; Budnjo, A.; Laurila, J.L.; Bergquist, J.; Karim, A.; Kleinmaier, R.; Brath, U.; Erdélyi, M. Symmetric Halogen Bonding Is Preferred in Solution. J. Am. Chem. Soc. 2012, 134, 5706–5715. [Google Scholar] [CrossRef]
- Carlsson, A.C.C.; Uhrbom, M.; Karim, A.; Brath, U.; Gräfenstein, J.; Erdélyi, M. Solvent effects on halogen bond symmetry. CrystEngComm 2013, 15, 3087–3092. [Google Scholar] [CrossRef]
- Bedin, M.; Karim, A.; Reitti, M.; Carlsson, A.C.C.; Topic, F.; Cetina, M.; Pan, F.; Havel, V.; Al-Ameri, F.; Sindelar, V.; et al. Counterion influence on the N–I–N halogen bond. Chem. Sci. 2015, 6, 3746–3756. [Google Scholar] [CrossRef] [Green Version]
- Hakkert, S.B.; Erdélyi, M. Halogen bond symmetry: The N–X–N bond. J. Phys. Org. Chem. 2015, 28, 226–233. [Google Scholar] [CrossRef]
- Carlsson, A.C.C.; Mehmeti, K.; Uhrbom, M.; Karim, A.; Bedin, M.; Puttreddy, R.; Kleinmaier, R.; Neverov, A.A.; Nekoueishahraki, B.; Gräfenstein, J.; et al. Substituent Effects on the [N–I–N]+ Halogen Bond. J. Am. Chem. Soc. 2016, 138, 9853–9863. [Google Scholar] [CrossRef] [Green Version]
- Karim, A.; Schulz, N.; Andersson, H.; Nekoueishahraki, B.; Carlsson, A.C.C.; Sarabi, D.; Valkonen, A.; Rissanen, K.; Gräfenstein, J.; Keller, S.; et al. Carbon’s Three-Center, Four-Electron Tetrel Bond, Treated Experimentally. J. Am. Chem. Soc. 2018, 140, 17571–17579. [Google Scholar] [CrossRef]
- Tachikawa, M.; Mori, K.; Nakai, H.; Iguchi, K. An extension of ab initio molecular orbital theory to nuclear motion. Chem. Phys. Lett. 1998, 290, 437–442. [Google Scholar] [CrossRef]
- Udagawa, T.; Ishimoto, T.; Tachikawa, M. Theoretical Study of H/D Isotope Effects on Nuclear Magnetic Shieldings Using an ab initio Multi-Component Molecular Orbital Method. Molecules 2013, 18, 5209–5220. [Google Scholar] [CrossRef] [Green Version]
- Dračínský, M.; Hodgkinson, P. Effects of Quantum Nuclear Delocalisation on NMR Parameters from Path Integral Molecular Dynamics. Chem. Eur. J. 2014, 20, 2201–2207. [Google Scholar] [CrossRef] [Green Version]
- Dračínský, M.; Bouř, P.; Hodgkinson, P. Temperature dependence of NMR parameters calculated from Path Integral Molecular Dynamics simulations. J. Chem. Theory Comput. 2016, 12, 968–973. [Google Scholar] [CrossRef] [Green Version]
- Pohl, R.; Socha, O.; Slavíček, P.; Šála, M.; Hodgkinson, P.; Dračínský, M. Proton transfer in guanine-cytosine base pair analogues studied by NMR spectroscopy and PIMD simulations. Faraday Discuss. 2018, 212, 331–344. [Google Scholar] [CrossRef] [Green Version]
- Born, M.; Oppenheimer, J. Zur Quantentheorie der Molekeln. Ann. Der Phys. (Leipzig) 1927, 84, 457–484. [Google Scholar] [CrossRef]
- Kern, C.W.; Matcha, R.L. Nuclear corrections to electronic expectation values—Zero-point vibrational effects in water molecule. J. Chem. Phys. 1968, 49, 2081–2091. [Google Scholar] [CrossRef]
- Åstrand, P.O.; Ruud, K.; Taylor, P.R. Calculation of the vibrational wave function of polyatomic Molecules. J. Chem. Phys. 2000, 112, 2655–2667. [Google Scholar] [CrossRef] [Green Version]
- Ruud, K.; Åstrand, P.O.; Taylor, P.R. An efficient approach for calculating vibrational wave functions and zero-point vibrational corrections to molecular properties of polyatomic molecules. J. Chem. Phys. 2000, 112, 2668–2683. [Google Scholar] [CrossRef]
- Jameson, C.J. Isotope shift in NMR. J. Chem. Phys. 1977, 66, 4983–4988. [Google Scholar] [CrossRef]
- Raynes, W.T.; Fowler, P.W.; Lazzeretti, P.; Zanasi, R.; Grayson, M. The effects of rotation and vibration on the 13C shielding, magnetizabilities and geometrical parameters of some methane isotopomers. Mol. Phys. 1988, 64, 143–162. [Google Scholar] [CrossRef]
- Dransfeld, A. Isotope effects on nuclear magnetic shieldings calculated by including zero-point vibration corrections: The VMF approach. Chem. Phys. 2004, 298, 47–53. [Google Scholar] [CrossRef]
- Auer, A.A. High-level ab-initio calculation of gas-phase NMR chemical shifts and secondary isotope effects of methanol. Chem. Phys. Lett. 2009, 467, 230–232. [Google Scholar] [CrossRef]
- Dračínský, M.; Kaminský, J.; Bouř, P. Relative importance of first and second derivatives of nuclear magnetic resonance chemical shifts and spin-spin coupling constants for vibrational averaging. J. Chem. Phys. 2009, 130, 094106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jameson, C.J. The dynamic and electronic factors in isotope effects on NMR parameters. In Isotopes in the Physical and Biomedical Science; Buncel, E., Jones, J.R., Eds.; Elsevier: Amsterdam, The Netherlands, 1991; Volume 2, p. 1. [Google Scholar]
- Hansen, P.E. Intrinsic deuterium isotope effects on NMR chemical shifts of hydrogen bonded systems. Nukleonika 2002, 47, S37–S42. [Google Scholar] [CrossRef]
- Golubev, N.S.; Detering, C.; Smirnov, S.N.; Shenderovich, I.G.; Denisov, G.S.; Limbach, H.H.; Tolstoy, P.M. H/D isotope effects on NMR chemical shifts of nuclei involved in a hydrogen bridge of hydrogen isocyanide complexes with fluoride anion. Phys. Chem. Chem. Phys. 2009, 11, 5154–5159. [Google Scholar] [CrossRef]
- Yang, K.S.; Hudson, B. Computation of deuterium isotope perturbation of 13C NMR chemical shifts of alkanes: A Local Mode Zero-Point Level approach. J. Phys. Chem. A 2010, 114, 12283–12290. [Google Scholar] [CrossRef]
- Mills, I.M. Vibration–Rotation Structure in Asymmetric- and Symmetric-Top Molecules. In Molecular Spectroscopy: Modern Research; Rao, K.N., Mathews, C.W., Eds.; Academic Press: Cambridge, MA, USA, 1972; Chapter 3.2; p. 115. [Google Scholar] [CrossRef]
- Kuchitsu, K. The potential energy surface and the meaning of internuclear distances. In Accurate Molecular Structures: Their Determination and Importance; Domenicano, A., Hargittai, I., Eds.; Oxford University Press: Oxford, UK, 1992; p. 14. [Google Scholar]
- Berger, S.; Diehl, B.W.K. Correlation between deuterium-isotope effects and 13C-NMR chemical-shifts in substituted benzenes. Tetrahedron Lett. 1987, 28, 1243–1246. [Google Scholar] [CrossRef]
- Tiainen, M.; Maaheimo, H.; Soininen, P.; Laatikainen, R. 13C isotope effects on 1H chemical shifts: NMR spectral analysis of 13C-labelled D-glucose and some 13C-labelled amino acids. Magn. Res. Chem. 2010, 48, 117–122. [Google Scholar] [CrossRef]
- O’Leary, D.J.; Allis, D.G.; Hudson, B.S.; James, S.; Morgera, K.B.; Baldwin, J.E. Vicinal deuterium perturbations on hydrogen NMR chemical shifts in cyclohexanes. J. Am. Chem. Soc. 2008, 130, 13659–13663. [Google Scholar] [CrossRef]
- Aydin, R.; Frankmölle, W.; Schmalz, D.; Günther, H. Deuterium-Induced NMR Isotope Shifts for 13C Resonance Frequencies of Norbornane—Quantitative Data for the Dihedral Angle Dependence of Vicinal Shifts. Magn. Res. Chem. 1988, 26, 408–411. [Google Scholar] [CrossRef]
- Mlinarić-Majerski, K.; Vinković, V.; Meić, Z.; Gassman, P.G.; Chyall, L.J. Long-Range Deuterium-Isotope Effects In 13C NMR-Spectra of Adamantane And 2-Adamantanone. J. Mol. Struct. 1992, 267, 389–394. [Google Scholar] [CrossRef]
- Schaftenaar, G.; Noordik, J.H. Molden: A pre- and post-processing program for molecular and electronic structures. J. Comput. Aided Mol. Des. 2000, 14, 123–134. [Google Scholar] [CrossRef]
- Turunen, L.; Warzok, U.; Puttreddy, R.; Beyeh, N.K.; Schalley, C.A.; Rissanen, K. [NI+N] Halogen-Bonded Dimeric Capsules from Tetrakis(3-pyridyl)ethylene Cavitands. Angew. Chem. Int. Ed. 2016, 55, 14033–14036. [Google Scholar] [CrossRef] [PubMed]
- Turunen, L.; Warzok, U.; Schalley, C.A.; Rissanen, K. Nano-sized I12L6 Molecular Capsules Based on the [N ⋯ I+⋯ N] Halogen Bond. Chem 2017, 3, 861–869. [Google Scholar] [CrossRef]
- Barluenga, J. Recent advances in selective organic synthesis mediated by transition metal complexes. Pure Appl. Chem. 1999, 71, 1385–1391. [Google Scholar] [CrossRef]
- Hansen, P.E. Deuterium-isotope effects on the 13C nuclear shielding of intramolecularly hydrogen-bonded systems. Magn. Res. Chem. 1986, 24, 903–910. [Google Scholar] [CrossRef]
- Hansen, P.E. Substituent effects on deuterium-isotope effects on nuclear shielding of intramolecularly hydrogen-bonded aromatic ketones, aldehydes and esters. Magn. Res. Chem. 1993, 31, 23–37. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-functional thermochemistry. 3. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic-behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.T.; Yang, W.T.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron-density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate Spin-Dependent Electron Liquid Correlation Energies For Local Spin-Density Calculations—A Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef] [Green Version]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab-initio calculation of vibrational absorption and circular-dichroism spectra using density-functional force-fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Jensen, F. Polarization consistent basis sets: Principles. J. Chem. Phys. 2001, 115, 9113–9125. [Google Scholar] [CrossRef]
- Jensen, F. Basis set convergence of nuclear magnetic shielding constants calculated by density functional methods. J. Chem. Theory Comput. 2008, 4, 719–727. [Google Scholar] [CrossRef] [PubMed]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef]
- Jensen, F. Polarization consistent basis sets. II. Estimating the Kohn-Sham basis set limit. J. Chem. Phys. 2002, 116, 7372–7379. [Google Scholar] [CrossRef] [Green Version]
- Curtiss, L.A.; McGrath, M.P.; Blaudeau, J.P.; Davis, N.E.; Binning, R.C.; Radom, L. Extension of Gaussian-2 theory to Molecules containing third-row atoms Ga-Kr. J. Chem. Phys. 1995, 103, 6104–6113. [Google Scholar] [CrossRef]
- Glukhovtsev, M.N.; Pross, A.; McGrath, M.P.; Radom, L. Extension of Gaussian-2 (G2) theory to bromine- and iodine-containing Molecules: Use of effective core potentials. J. Chem. Phys. 1995, 103, 1878–1885. [Google Scholar] [CrossRef]
- Feller, D. The role of databases in support of computational chemistry calculations. J. Comput. Chem. 1996, 17, 1571–1586. [Google Scholar] [CrossRef]
- Schuchardt, K.L.; Didier, B.T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T.L. Basis Set Exchange: A Community Database for Computational Sciences. J. Chem. Inf. Model. 2007, 47, 1045–1052. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jmol: An Open-Source Java Viewer for Chemical Structures in 3D, Version 14.29.46. Available online: http://www.jmol.org/ (accessed on 5 June 2019).
- Christiansen, O. Vibrational structure theory: New vibrational wave function methods for calculation of anharmonic vibrational energies and vibrational contributions to molecular properties. Phys. Chem. Chem. Phys. 2007, 9, 2942–2953. [Google Scholar] [CrossRef] [PubMed]
- Christiansen, O. Selected new developments in vibrational structure theory: Potential construction and vibrational wave function calculations. Phys. Chem. Chem. Phys. 2012, 14, 6672–6687. [Google Scholar] [CrossRef]
- König, C.; Christiansen, O. Linear-scaling generation of potential energy surfaces using a double incremental expansion. J. Chem. Phys. 2016, 145, 064105. [Google Scholar] [CrossRef] [Green Version]
- Madsen, D.; Christiansen, O.; König, C. Anharmonic vibrational spectra from double incremental potential energy and dipole surfaces. Phys. Chem. Chem. Phys. 2018, 20, 3445–3456. [Google Scholar] [CrossRef]






| Method/ | 25 °C | 0 K | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Condition | C2 | C3 | C4 | C5 | C6 | MSgD | RMS | MSgD | RMS | |
| DD-VPT2 | B97X-D | −381.5 | −168.1 | 5.8 | 24.4 | −4.5 | −11.9 | 25.8 | 1.4 | 13.0 |
| B3LYP | −416.1 | −172.2 | 4.2 | 25.0 | −3.8 | −21.3 | 41.6 | −7.9 | 27.1 | |
| loc-VPT2 | B97X-D | −362.2 | −165.1 | 4.9 | 7.6 | −15.6 | −13.3 | 16.7 | 0.0 | 10.1 |
| B3LYP | −399.0 | −169.4 | 3.3 | 8.0 | −15.2 | −23.4 | 32.6 | −10.1 | 18.8 | |
| LMZL | B97X-D | −310.4 | -−137.1 | 8.1 | 7.2 | −20.1 | 5.4 | 15.9 | 18.7 | 33.1 |
| B3LYP | −339.1 | −138.6 | 6.6 | 7.9 | −20.4 | −2.0 | 4.2 | 11.3 | 21.5 | |
| LMZL+cent | B97X-D | −351.1 | −138.8 | 6.8 | 7.7 | −19.5 | −4.9 | 6.4 | 8.4 | 18.3 |
| B3LYP | −387.6 | −140.8 | 5.3 | 8.3 | −19.6 | −14.4 | 23.6 | −1.1 | 18.5 | |
| experiment | ||||||||||
| 25 °C | [36] | −341.0 | −140.0 | 14.0 | −15.0 | |||||
| 0 K (extrapolated) | [30] | −367.1 | −166.4 | 24.2 | −26.0 | |||||
| MSgD | RMS | ||||
|---|---|---|---|---|---|
| Norbornane | DD-VPT2 | −16.8 | 26.9 | 0.9993 | |
| loc-VPT2 | −9.9 | 20.4 | 0.9960 | ||
| Adamantane | DD-VPT2 | −19.9 | 34.5 | 0.9994 | |
| loc-VPT2 | −18.3 | 37.2 | 0.9984 | ||
| bpeb derivatives | 25 °C | DD-VPT2 | −13.9 | 23.8 | 0.9977 |
| loc-VPT2 | 12.4 | 20.6 | 0.9960 | ||
| 0 K | DD-VPT2 | 2.0 | 12.9 | 0.9932 | |
| loc-VPT2 | −6.2 | 10.7 | 0.9916 |
| Geometry | Amplitude (Mean Square) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| All-H | IE | All-H | IE | All-H | IE | ||||
| Pyridine | DD-VPT2 | −989 | −5437 | 5703 | −1525 | 39.0 | −9.8 | 84.0 | −12.9 |
| loc-VPT2 | −1367 | −5719 | 5468 | −1600 | 35.5 | −10.4 | 54.6 | −16.0 | |
| LMZL | −4427 | 5467 | −1593 | 35.7 | −10.4 | 54.6 | −15.9 | ||
| LMZL+cent | −5407 | 5440 | −1580 | 35.7 | −10.4 | 54.6 | −15.9 | ||
| Benzene (H/D) | DD-VPT2 | −769 | −5369 | 5655 | −1512 | 41.1 | −10.3 | 85.2 | −13.6 |
| loc-VPT2 | −1132 | −5652 | 5425 | −1588 | 37.7 | −11.0 | 56.1 | −16.4 | |
| LMZL | −4319 | 5410 | −1577 | 38.1 | −11.1 | 57.4 | −16.7 | ||
| LMZL+cent | −5252 | 5385 | −1564 | 38.1 | −11.1 | 57.4 | −16.7 | ||
| Cyclohexane (axial) | DD-VPT2 | −1740 | −5987 | 5957 | −1584 | 41.3 | −10.5 | 56.8 | −11.5 |
| loc-VPT2 | −2542 | −6320 | 5695 | −1667 | 37.7 | −11.0 | 39.7 | −11.6 | |
| LMZL | −4997 | 5691 | −1659 | 38.2 | −11.1 | 39.7 | −11.6 | ||
| Ref. [60] | −4700 | −1900 | −11.0 | −11.6 | |||||
| LMZL+cent | −6111 | 5653 | −1641 | 38.2 | −11.1 | 39.7 | −11.6 | ||
| Cyclohexane (equatorial) | DD-VPT2 | −1563 | −5851 | 5885 | −1567 | 42.0 | −10.7 | 58.0 | −11.5 |
| loc-VPT2 | −2341 | −6169 | 5632 | −1648 | 38.5 | −11.3 | 40.2 | −11.8 | |
| LMZL | −4768 | 5601 | −1633 | 38.9 | −11.3 | 40.6 | −11.8 | ||
| Ref. [60] | −4700 | −1900 | −11.2 | −11.6 | |||||
| LMZL+cent | −5854 | 5589 | −1623 | 38.9 | −11.3 | 40.6 | −11.8 | ||
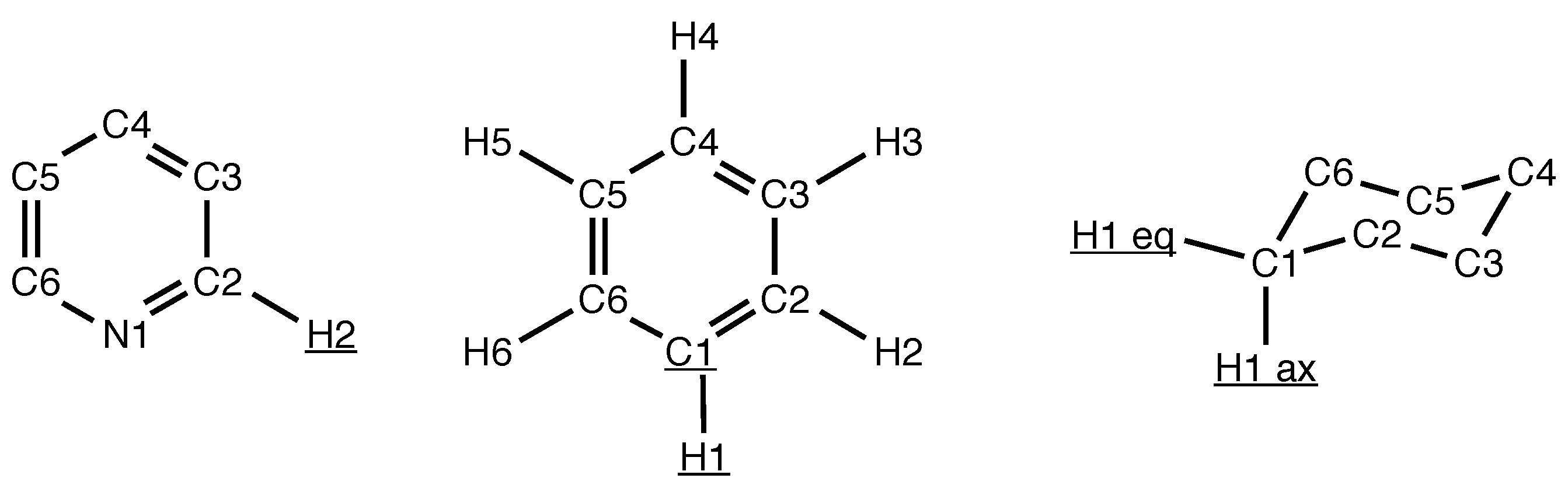
| Method | H1 | H2 | H3 | H4 | MSgD | RMS | |
|---|---|---|---|---|---|---|---|
| DD-VPT2 | B97X-D | −2.46 | −0.97 | 0.07 | 0.20 | −0.14 | 0.23 |
| B3LYP | −2.39 | −0.99 | 0.04 | 0.21 | −0.13 | 0.20 | |
| loc-VPT2 | B97X-D | −1.79 | −0.76 | 0.17 | 0.05 | 0.07 | 0.17 |
| B3LYP | −1.74 | −0.81 | 0.15 | 0.07 | 0.07 | 0.18 | |
| experiment [64] | −2.04 | −0.81 | 0.02 | 0.22 |
| Geometry | Amplitude (Mean Square) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All-H | IE | All-H | IE | All-H | IE | All-H | IE | |||||
| DD-VPT2 | −42 | −67 | −63 | −119 | 5655 | −16.4 | 2010 | −38.5 | 41.1 | −0.18 | 85.2 | −1.18 |
| loc-VPT2 | 17 | −50 | −8 | −60 | 1088 | −42.8 | 1137 | −44.7 | 6.3 | −0.25 | 46.0 | −1.81 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gräfenstein, J. The Structure of the “Vibration Hole” around an Isotopic Substitution—Implications for the Calculation of Nuclear Magnetic Resonance (NMR) Isotopic Shifts. Molecules 2020, 25, 2915. https://doi.org/10.3390/molecules25122915
Gräfenstein J. The Structure of the “Vibration Hole” around an Isotopic Substitution—Implications for the Calculation of Nuclear Magnetic Resonance (NMR) Isotopic Shifts. Molecules. 2020; 25(12):2915. https://doi.org/10.3390/molecules25122915
Chicago/Turabian StyleGräfenstein, Jürgen. 2020. "The Structure of the “Vibration Hole” around an Isotopic Substitution—Implications for the Calculation of Nuclear Magnetic Resonance (NMR) Isotopic Shifts" Molecules 25, no. 12: 2915. https://doi.org/10.3390/molecules25122915
APA StyleGräfenstein, J. (2020). The Structure of the “Vibration Hole” around an Isotopic Substitution—Implications for the Calculation of Nuclear Magnetic Resonance (NMR) Isotopic Shifts. Molecules, 25(12), 2915. https://doi.org/10.3390/molecules25122915