Sound Velocities of Lennard-Jones Systems Near the Liquid-Solid Phase Transition
Abstract
:1. Introduction
2. Approach
2.1. Formulation
2.2. Inverse-Power-Law Model
3. Results
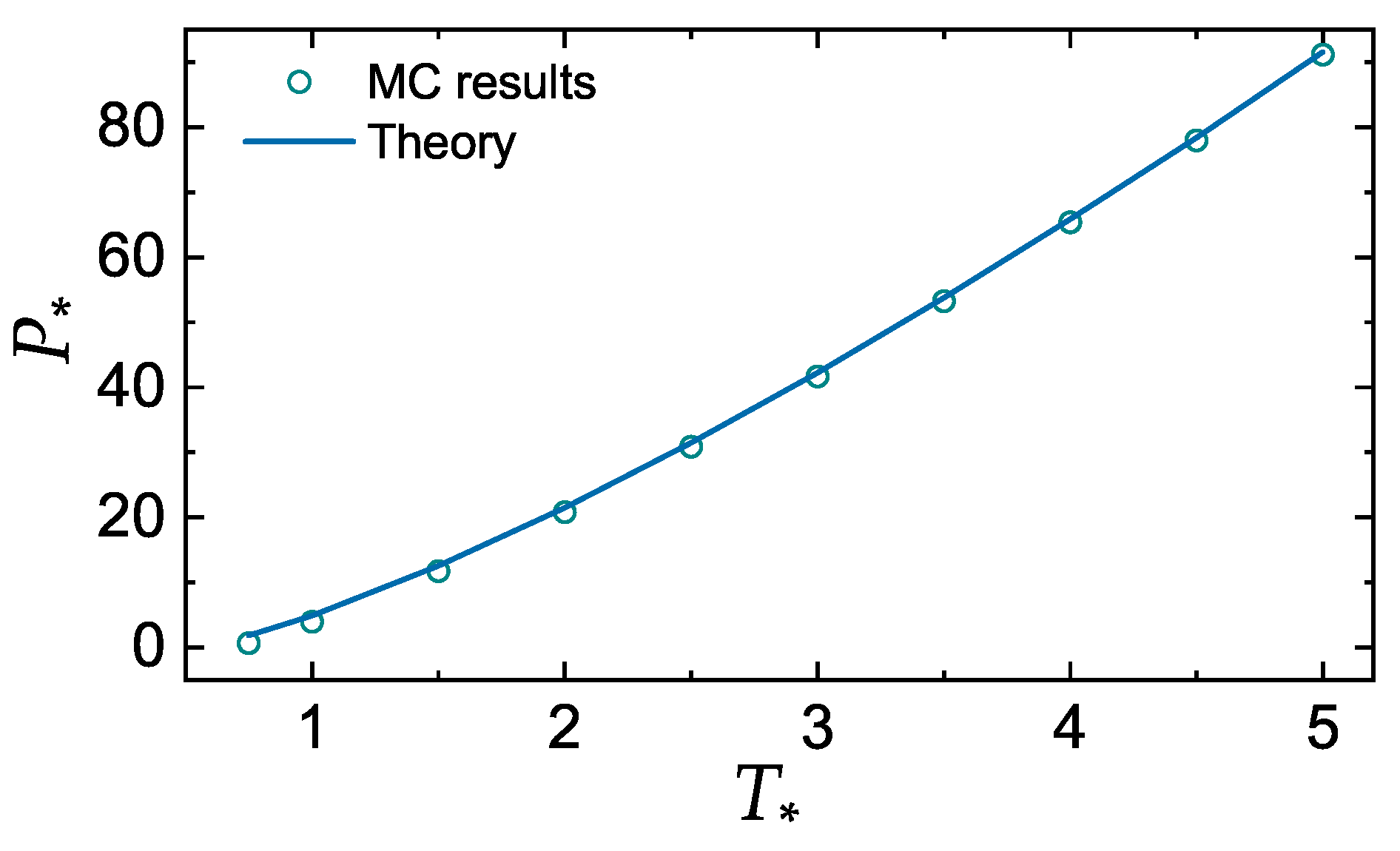
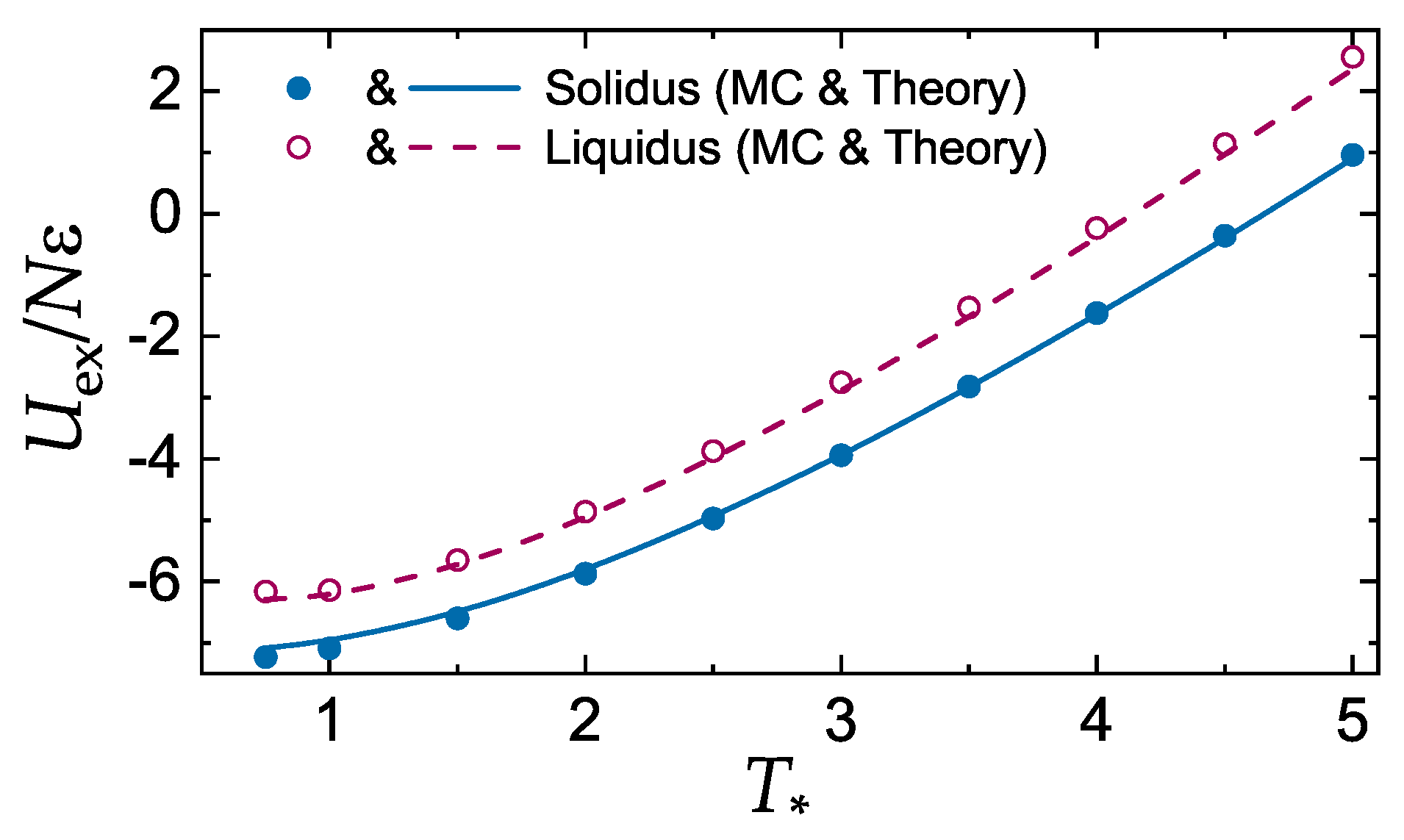
3.1. Additivity of Melting Curves
3.2. Sound Velocities of the LJ System
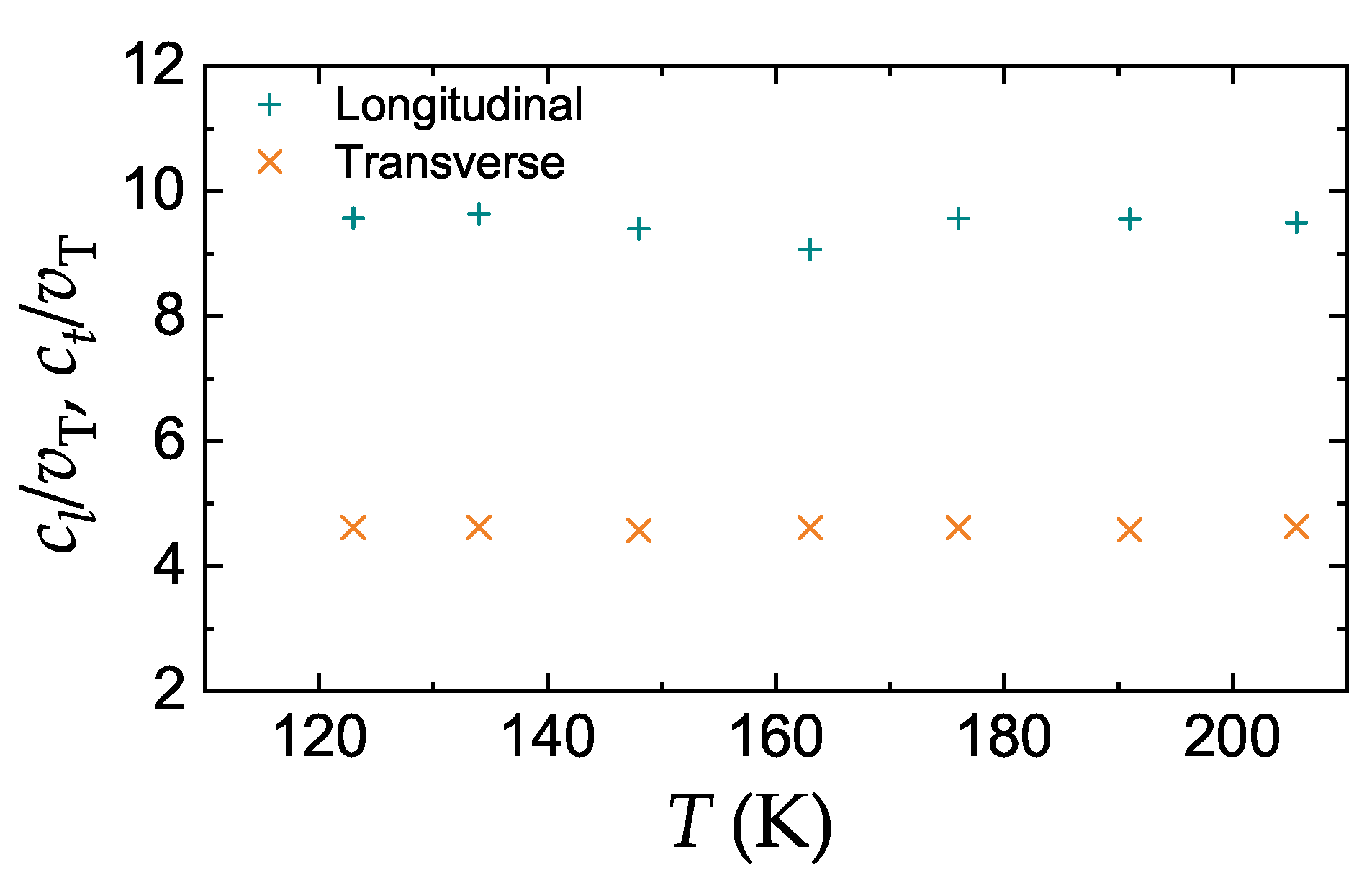
3.3. Comparison with Experiment
4. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Trachenko, K.; Brazhkin, V.V. Collective modes and thermodynamics of the liquid state. Rep. Progr. Phys. 2015, 79, 016502. [Google Scholar] [CrossRef] [PubMed]
- Khrapak, S. Elastic properties of dense hard-sphere fluids. Phys. Rev. E 2019, 100, 032138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zwanzig, R. On the relation between self-diffusion and viscosity of liquids. J. Chem. Phys. 1983, 79, 4507–4508. [Google Scholar] [CrossRef]
- Khrapak, S. Stokes–Einstein relation in simple fluids revisited. Mol. Phys. 2019, 118, e1643045. [Google Scholar] [CrossRef]
- Buchenau, U.; Zorn, R.; Ramos, M.A. Probing cooperative liquid dynamics with the mean square displacement. Phys. Rev. E 2014, 90, 042312. [Google Scholar] [CrossRef] [Green Version]
- Khrapak, S.A. Lindemann melting criterion in two dimensions. Phys. Rev. Res. 2020, 2, 012040. [Google Scholar] [CrossRef] [Green Version]
- Bilgram, J. Dynamics at the solid-liquid transition: Experiments at the freezing point. Phys. Rep. 1987, 153, 1–89. [Google Scholar] [CrossRef]
- Dyre, J.C.; Olsen, N.B. Landscape equivalent of the shoving model. Phys. Rev. E 2004, 69, 042501. [Google Scholar] [CrossRef] [Green Version]
- Dyre, J.C.; Wang, W.H. The instantaneous shear modulus in the shoving model. J. Chem. Phys. 2012, 136, 224108. [Google Scholar] [CrossRef] [Green Version]
- Iida, T.; Guthrie, R. The Physical Properties of Liquid Metals; Oxford University Press: Oxford, UK, 1988. [Google Scholar]
- Blairs, S. Sound velocity of liquid metals and metalloids at the melting temperature. Phys. Chem. Liq. 2007, 45, 399–407. [Google Scholar] [CrossRef]
- Rosenfeld, Y. Sound velocity in liquid metals and the hard-sphere model. J. Phys. Condens. Matter 1999, 11, L71–L74. [Google Scholar] [CrossRef]
- Ishizaki, K.; Spain, I.L.; Bolsaitis, P. Measurements of longitudinal and transverse ultrasonic wave velocities in compressed solidified argon and their relationship to melting theory. J. Chem. Phys. 1975, 63, 1401–1410. [Google Scholar] [CrossRef]
- Liebenberg, D.H.; Mills, R.L.; Bronson, J.C. Measurement ofP, V, T, and sound velocity across the melting curve ofn-H2andn-D2to 19 kbar. Phys. Rev. B 1978, 18, 4526–4532. [Google Scholar] [CrossRef]
- Khrapak, S.A. Note: Sound velocity of a soft sphere model near the fluid–solid phase transition. J. Chem. Phys. 2016, 144, 126101. [Google Scholar] [CrossRef] [Green Version]
- Khrapak, S. Note: Melting criterion for soft particle systems in two dimensions. J. Chem. Phys. 2018, 148, 146101. [Google Scholar] [CrossRef] [Green Version]
- Rosenfeld, Y. Additivity of melting curves. Chem. Phys. Lett. 1976, 38, 591–593. [Google Scholar] [CrossRef]
- Rosenfeld, Y. Universality of melting and freezing indicators and additivity of melting curves. Mol. Phys. 1976, 32, 963–977. [Google Scholar] [CrossRef]
- Schofield, P. Wavelength-dependent fluctuations in classical fluids: I. The long wavelength limit. Proc. Phys. Soc. 1966, 88, 149–170. [Google Scholar] [CrossRef]
- Balucani, U.; Balucani, U.; Zoppi, M.; Balucani, Z. Dynamics of the Liquid State; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Takeno, S.; Gôda, M. A Theory of Phonons in Amorphous Solids and Its Implications to Collective Motion in Simple Liquids. Progress Theor. Phys. 1971, 45, 331–352. [Google Scholar] [CrossRef] [Green Version]
- Zwanzig, R.; Mountain, R.D. High-Frequency Elastic Moduli of Simple Fluids. J. Chem. Phys. 1965, 43, 4464–4471. [Google Scholar] [CrossRef]
- Hubbard, J.; Beeby, J. Collective motion in liquids. J. Phys. C 1969, 2, 556–571. [Google Scholar] [CrossRef]
- Rosenberg, M.; Kalman, G. Dust acoustic waves in strongly coupled dusty plasmas. Phys. Rev. E 1997, 56, 7166–7173. [Google Scholar] [CrossRef]
- Golden, K.I.; Kalman, G.J. Quasilocalized charge approximation in strongly coupled plasma physics. Phys. Plasmas 2000, 7, 14–32. [Google Scholar] [CrossRef]
- Kalman, G.; Rosenberg, M.; DeWitt, H.E. Collective Modes in Strongly Correlated Yukawa Liquids: Waves in Dusty Plasmas. Phys. Rev. Lett. 2000, 84, 6030–6033. [Google Scholar] [CrossRef] [PubMed]
- Donko, Z.; Kalman, G.J.; Hartmann, P. Dynamical correlations and collective excitations of Yukawa liquids. J. Phys. Condens. Matter 2008, 20, 413101. [Google Scholar] [CrossRef]
- Khrapak, S.A.; Klumov, B.; Couedel, L.; Thomas, H.M. On the long-waves dispersion in Yukawa systems. Phys. Plasmas 2016, 23, 023702. [Google Scholar] [CrossRef] [Green Version]
- Dubin, D.H.E.; Dewitt, H. Polymorphic phase transition for inverse-power-potential crystals keeping the first-order anharmonic correction to the free energy. Phys. Rev. B 1994, 49, 3043–3048. [Google Scholar] [CrossRef]
- Agrawal, R.; Kofke, D.A. Thermodynamic and structural properties of model systems at solid-fluid coexistence. Mol. Phys. 1995, 85, 23–42. [Google Scholar] [CrossRef]
- Miller, B.N. Elastic Moduli of a Fluid of Rigid Spheres. J. Chem. Phys. 1969, 50, 2733–2740. [Google Scholar] [CrossRef]
- Bryk, T.; Huerta, A.; Hordiichuk, V.; Trokhymchuk, A.D. Non-hydrodynamic transverse collective excitations in hard-sphere fluids. J. Chem. Phys. 2017, 147, 064509. [Google Scholar] [CrossRef]
- Khrapak, S.; Klumov, B.; Couedel, L. Collective modes in simple melts: Transition from soft spheres to the hard sphere limit. Sci. Rep. 2017, 7, 7985. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hansen, J.P.; Schiff, D. Influence of interatomic repulsion on the structure of liquids at melting. Mol. Phys. 1973, 25, 1281–1290. [Google Scholar] [CrossRef]
- Schroder, T.B.; Dyre, J.C. Simplicity of condensed matter at its core: Generic definition of a Roskilde-simple system. J. Chem. Phys. 2014, 141, 204502. [Google Scholar] [CrossRef] [Green Version]
- Dyre, J.C. Hidden Scale Invariance in Condensed Matter. J. Phys. Chem. B 2014, 118, 10007–10024. [Google Scholar] [CrossRef] [PubMed]
- Gnan, N.; Schrøder, T.B.; Pedersen, U.R.; Bailey, N.P.; Dyre, J.C. Pressure-energy correlations in liquids. IV. “Isomorphs” in liquid phase diagrams. J. Chem. Phys. 2009, 131, 234504. [Google Scholar] [CrossRef] [PubMed]
- Costigliola, L.; Schrøder, T.B.; Dyre, J.C. Freezing and melting line invariants of the Lennard-Jones system. Phys. Chem. Chem. Phys. 2016, 18, 14678–14690. [Google Scholar] [CrossRef] [Green Version]
- Pedersen, U.R.; Costigliola, L.; Bailey, N.P.; Schrøder, T.B.; Dyre, J.C. Thermodynamics of freezing and melting. Nat. Commun. 2016, 7, 12386. [Google Scholar] [CrossRef] [Green Version]
- Heyes, D.M.; Brańka, A.C. The Lennard-Jones melting line and isomorphism. J. Chem. Phys. 2015, 143, 234504. [Google Scholar] [CrossRef]
- Heyes, D.M.; Dini, D.; Brańka, A.C. Scaling of Lennard-Jones liquid elastic moduli, viscoelasticity and other properties along fluid–solid coexistence. Phys. Stat. Solidi (b) 2015, 252, 1514–1525. [Google Scholar] [CrossRef] [Green Version]
- Tan, T.B.; Schultz, A.J.; Kofke, D.A. Virial coefficients, equation of state, and solid–fluid coexistence for the soft sphere model. Mol. Phys. 2011, 109, 123–132. [Google Scholar] [CrossRef]
- Sousa, J.M.G.; Ferreira, A.L.; Barroso, M.A. Determination of the solid-fluid coexistence of the n - 6 Lennard-Jones system from free energy calculations. J. Chem. Phys. 2012, 136, 174502. [Google Scholar] [CrossRef] [PubMed]
- Khrapak, S.A.; Morfill, G.E. Accurate freezing and melting equations for the Lennard-Jones system. J. Chem. Phys. 2011, 134, 094108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khrapak, S.A.; Ning, N. Freezing and melting equations for the n-6 Lennard-Jones systems. AIP Adv. 2016, 6, 055215. [Google Scholar] [CrossRef] [Green Version]
- Costigliola, L.; Heyes, D.M.; Schrøder, T.B.; Dyre, J.C. Revisiting the Stokes-Einstein relation without a hydrodynamic diameter. J. Chem. Phys. 2019, 150, 021101. [Google Scholar] [CrossRef] [Green Version]
- White, J.A. Lennard-Jones as a model for argon and test of extended renormalization group calculations. J. Chem. Phys. 1999, 111, 9352–9356. [Google Scholar] [CrossRef] [Green Version]
- Squire, D.; Holt, A.; Hoover, W. Isothermal elastic constants for argon. theory and Monte Carlo calculations. Physica 1969, 42, 388–397. [Google Scholar] [CrossRef]
- Preston, D.L.; Wallace, D.C. A model of the shear modulus. Solid State Commun. 1992, 81, 277–281. [Google Scholar] [CrossRef]
- Burakovsky, L.; Greeff, C.W.; Preston, D.L. Analytic model of the shear modulus at all temperatures and densities. Phys. Rev. B 2003, 67, 094107. [Google Scholar] [CrossRef] [Green Version]
- Ogata, S.; Ichimaru, S. First-principles calculations of shear moduli for Monte Carlo–simulated Coulomb solids. Phys. Rev. A 1990, 42, 4867–4870. [Google Scholar] [CrossRef]
- Khrapak, S.A.; Chaudhuri, M.; Morfill, G.E. Communication: Universality of the melting curves for a wide range of interaction potentials. J. Chem. Phys. 2011, 134, 241101. [Google Scholar] [CrossRef] [Green Version]
- Rosenberg, M. Waves in a 1D electrorheological dusty plasma lattice. J. Plasma Phys. 2015, 81, 905810407. [Google Scholar] [CrossRef]
- Schwabe, M.; Khrapak, S.; Zhdanov, S.; Pustylnik, M.; Räth, C.; Fink, M.; Kretschmer, M.; Lipaev, A.; Molotkov, V.; Schmitz, A.; et al. Slowing of acoustic waves in electrorheological and string-fluid complex plasmas. New J. Phys. 2020, in press. [Google Scholar] [CrossRef]


| = | ||||
|---|---|---|---|---|
| 2 | 8 | |||
| 2 | 4 |
| n | |||||
|---|---|---|---|---|---|
| 23.74 | 1.211 | 1.167 | 4.325 | 5.214 | |
| 105.0 | 2.358 | 2.330 | 7.829 | 8.106 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khrapak, S.A. Sound Velocities of Lennard-Jones Systems Near the Liquid-Solid Phase Transition. Molecules 2020, 25, 3498. https://doi.org/10.3390/molecules25153498
Khrapak SA. Sound Velocities of Lennard-Jones Systems Near the Liquid-Solid Phase Transition. Molecules. 2020; 25(15):3498. https://doi.org/10.3390/molecules25153498
Chicago/Turabian StyleKhrapak, Sergey A. 2020. "Sound Velocities of Lennard-Jones Systems Near the Liquid-Solid Phase Transition" Molecules 25, no. 15: 3498. https://doi.org/10.3390/molecules25153498
APA StyleKhrapak, S. A. (2020). Sound Velocities of Lennard-Jones Systems Near the Liquid-Solid Phase Transition. Molecules, 25(15), 3498. https://doi.org/10.3390/molecules25153498






