Spin Density Topology
Abstract
:1. Introduction
1.1. Introductory Remarks and Scope
1.2. Literature Context
2. Theoretical Details
2.1. Topology of the Electron Spin Density
2.1.1. Electron Spin Density Critical Points
2.1.2. Critical Points of the Electron Spin Density and the Poincaré–Hopf Relationship [11,14,15,16]
2.1.3. Spin Maxima and Spin Minima Joining Paths
2.1.4. Spin Density Basins
3. Results and Discussion
3.1. Spin Density Topology of the Water Molecule in the 3B1 State
3.1.1. Critical Points of the 3B1 Water Spin Density
3.1.2. Critical Points of the 3B1 Water Spin Density and Poincaré–Hopf Relationships
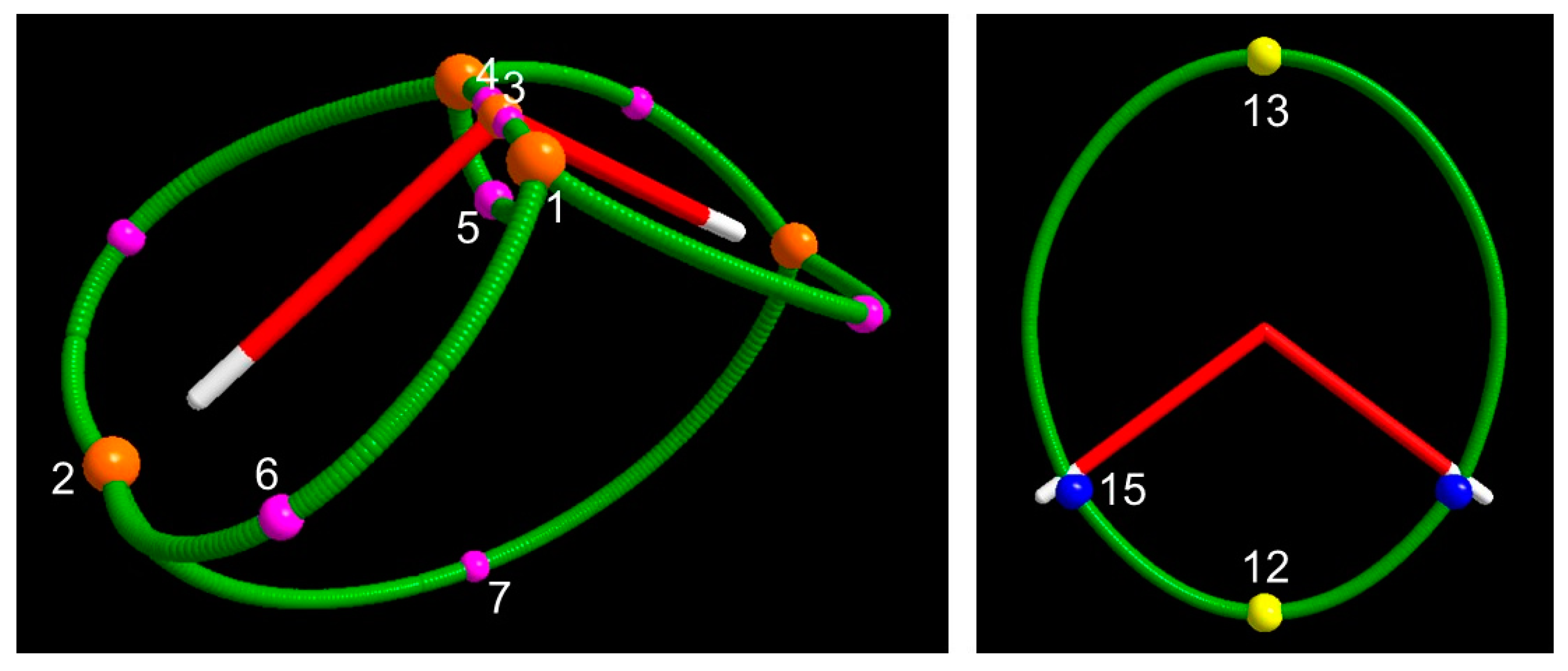
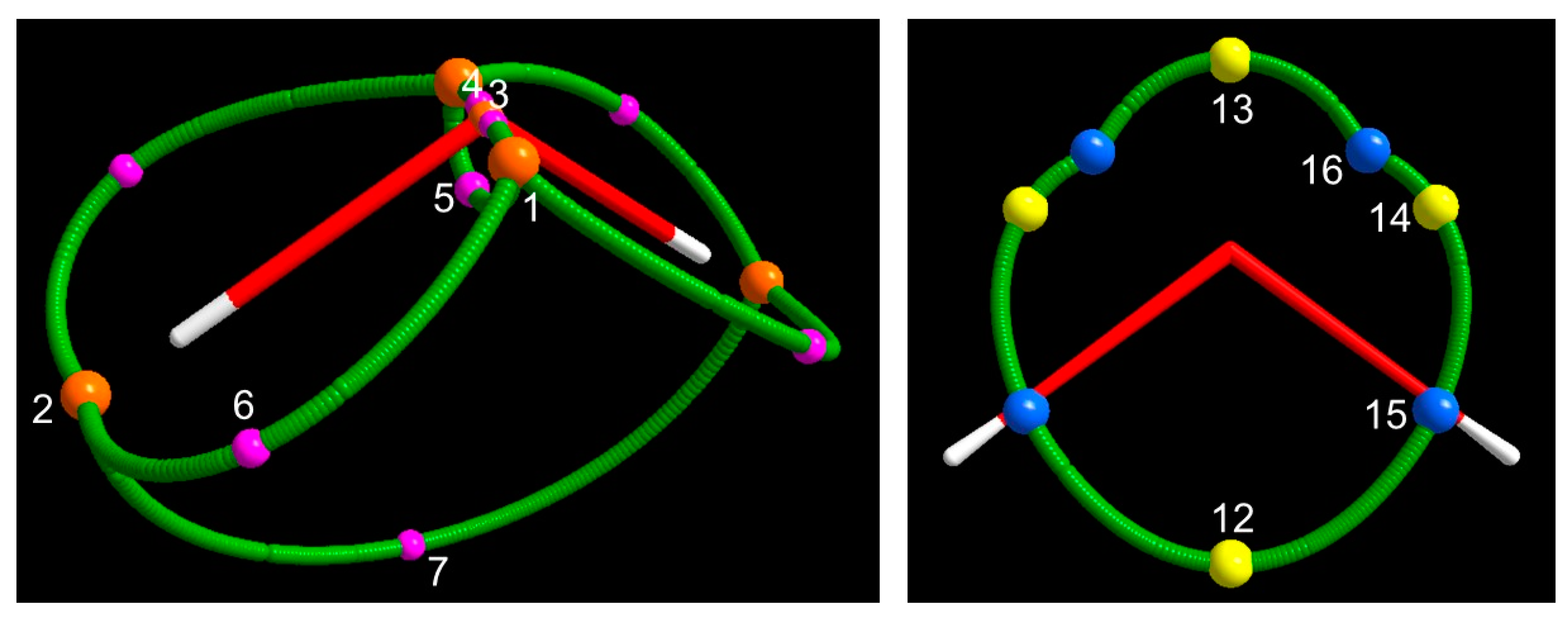
3.1.3. Spin Maxima and Spin Minima Joining Paths and Molecular Spin Graphs of the 3B1 Water Molecule
3.1.4. Spin Density Basins of the Water Molecule in the 3B1 State
3.1.5. Source Function Reconstructions
4. Materials and Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Parr, R.G.; Yang, W. Density–Functional Theory of Atoms and Molecules. In International Series of Monographs on Chemistry; Oxford University Press: Oxford, UK, 1989; Volume 16. [Google Scholar]
- Getzlaff, M. Fundamentals of Magnetism, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef] [Green Version]
- Miller, J.S.; Drillon, M. (Eds.) Magnetism: Molecules to Materials I–V; VCH: New York, NY, USA, 2001. [Google Scholar]
- Ruiz, E.; Cirera, J.; Alvarez, S. Spin density distribution in transition metal complexes. Coord. Chem. Rev. 2005, 249, 2649–2660. [Google Scholar] [CrossRef]
- Novoa, J.J.; Lafuente, P.; Deumal, M. Theoretical Study of the Electronic Structure and Magnetic Interactions in Purely Organic Nitronyl Nitroxide Crystals. In Magnetism: Molecules to Materials IV; Miller, J.S., Drillon, M., Eds.; VCH: New York, NY, USA, 2002; Volume IV, pp. 65–117. [Google Scholar] [CrossRef]
- Gillon, B. Spin Distributions in Molecular Systems with Interacting Transition Metal Ions. In Magnetism: Molecules to Materials I; Miller, J.S., Drillon, M., Eds.; VCH: New York, NY, USA, 2001; Volume I, pp. 357–378. [Google Scholar] [CrossRef]
- Campo, J.; Luzon, J.; Palacio, F.; Rawson, J. Spin Density Distribution and Interaction Mechanisms in Thiazyl–based Magnets. In Carbon Based Magnetism; Makarova, T., Palacio, F., Eds.; Elsevier: Oxford, UK, 2006; pp. 159–188. [Google Scholar] [CrossRef] [Green Version]
- Dos Santos, L.H.R.; Lanza, A.; Barton, A.M.; Brambleby, J.; Blackmore, W.J.A.; Goddard, P.A.; Xiao, F.; Williams, R.C.; Lancaster, T.; Pratt, F.L.; et al. Experimental and Theoretical Electron Density Analysis of Copper Pyrazine Nitrate Quasi–Low–Dimensional Quantum Magnets. J. Am. Chem. Soc. 2016, 138, 2280–2291. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chauvin, R.; Lepetit, C.; Silvi, B.; Alikhani, E. Applications of Topological Methods in Molecular Chemistry; In Challenges and Advances in Computational Chemistry and Physics book series; Springer International Publishing: Cham, Switzerland, 2016; Volume 22. [Google Scholar]
- Popelier, P.L.A. On Quantum Chemical Topology. In Applications of Topological Methods in Molecular Chemistry, 1st ed.; Chauvin, R., Lepetit, C., Silvi, B., Alikhani, E., Eds.; Challenges and Advances in Computational Chemistry and Physics; Springer International Publishing: Cham, Switzerland, 2016; Volume 22, pp. 23–52. [Google Scholar]
- Gatti, C. Chemical bonding in crystals: New directions. Z. Kristallogr. 2005, 220, 399–457. [Google Scholar] [CrossRef]
- Gatti, C.; Macchi, P. A guided tour through Modern Charge Density Analysis. In Modern Charge Density Analysis, 1st ed.; Gatti, C., Macchi, P., Eds.; Springer: New York, NY, USA, 2012; pp. 1–78. [Google Scholar]
- Bader, R.F.W. Atoms in molecules: A quantum theory. In International Series of Monographs on Chemistry; Oxford University Press: Oxford, UK, 1990; Volume 22. [Google Scholar]
- Hopf, H. Vektorfelder in n–dimensionalen Mannigfaltigkeiten. Math. Ann. 1926, 96, 225–249. [Google Scholar] [CrossRef]
- Collard, K.; Hall, G.G. Orthogonal trajectories of the electron density. Int. J. Q. Chem. 1977, 12, 623–637. [Google Scholar] [CrossRef]
- Jones, W.; March, N.H. Theoretical Solid State Physics Appendix A1.6; Dover: New York, NY, USA, 1985; Volume 1, Appendix A1.6. [Google Scholar]
- Bader, R.F.W.; Gatti, C. A Green’s function for the density. Chem. Phys. Lett. 1998, 287, 233–238. [Google Scholar] [CrossRef]
- Gatti, C. The Source Function Descriptor as a Tool to Extract Chemical Information from Theoretical and Experimental Electron Densities. Stru. Bond. 2012, 147, 193–286. [Google Scholar] [CrossRef]
- Gatti, C.; Orlando, A.M.; Lo Presti, L. Insights on spin polarization through the spin density source function. Chem. Sci. 2015, 6, 3845–3852. [Google Scholar] [CrossRef] [Green Version]
- Lobayan, R.M.; Bochicchio, R.C.; Lain, L.; Torre, A. Electron–density topology in molecular systems: Paired and unpaired densities. J. Chem. Phys. 2005, 123, 144116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lobayan, R.M.; Alcoba, D.R.; Bochicchio, R.C.; Torre, A.; Lain, L. Topology of the Electron Density in Open–Shell Systems. J. Phys. Chem. A 2010, 114, 1200–1206. [Google Scholar] [CrossRef] [PubMed]
- Jones, T.E.; Eberhart, M.E.; Clougherty, D.P. Topology of the Spin–Polarized Charge Density in bcc and fcc Iron. Phys. Rev. Lett. 2008, 100, 017208. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deutsch, M.; Claiser, N.; Pillet, S.; Chumakov, Y.; Becker, P.; Gillet, J.-M.; Gillon, B.; Lecomte, C.; Souhassou, M. Experimental determination of spin-dependent electron density by joint refinement of X-ray and polarized neutron diffraction data. Acta Cryst. A 2012, 68, 675–686. [Google Scholar] [CrossRef] [PubMed]
- Deutsch, M.; Gillon, B.; Claiser, N.; Gillet, J.-M.; Lecomte, C.; Souhassou, M. First spin–resolved electron distributions in crystals from combined polarized neutron and X–ray diffraction experiments. IUCrJ 2014, 1, 194–199. [Google Scholar] [CrossRef] [PubMed]
- Hansen, N.K.; Coppens, P. Testing aspherical atom refinements on small–molecule data sets. Acta Cryst. A 1978, 34, 909–921. [Google Scholar] [CrossRef]
- Conradie, J.; Ghosh, A. DFT Calculations on the Spin–Crossover Complex Fe(salen)(NO): A Quest for the Best Functional. J. Phys. Ch. B 2007, 111, 12621–12624. [Google Scholar] [CrossRef] [PubMed]
- Boguslawski, K.; Jacob, C.R.; Reiher, M. Can DFT Accurately Predict Spin Densities? Analysis of Discrepancies in Iron Nitrosyl Complexes. J. Chem. Theory Comput. 2011, 7, 2740–2752. [Google Scholar] [CrossRef]
- Boguslawski, K.; Marti, K.H.; Legeza, O.; Reiher, M. Accurate ab Initio Spin Densities. J. Chem. Theory Comput. 2012, 8, 1970–1982. [Google Scholar] [CrossRef] [Green Version]
- Gatti, C.; Macetti, G.; Lo Presti, L. Insights on spin delocalization and spin polarization mechanisms in crystals of azido copper(II) dinuclear complexes through the electron spin density Source Function. Acta Cryst. 2017, B73, 565–583. [Google Scholar] [CrossRef]
- Macetti, G.; Lo Presti, L.; Gatti, C. Spin density accuracy and distribution in azido Cu(II) complexes: A source function analysis. J. Comput. Chem. 2018, 10, 587–603. [Google Scholar] [CrossRef] [Green Version]
- Gatti, C.; Orlando, A.M.; Monza, E.; Lo Presti, L. Applications of Topological Methods in Molecular Chemistry. In Applications of Topological Methods in Molecular Chemistry, 1st ed.; Chauvin, R., Lepetit, C., Silvi, B., Alikhani, E., Eds.; Challenges and Advances in Computational Chemistry and Physics; Springer International Publishing: Cham, Switzerland, 2016; Volume 22, pp. 101–129. [Google Scholar] [CrossRef]
- Abraham, R.H.; Shaw, C.D. Dynamics: The Geometry of Behavior; Addison Wesley: Redwood City, CA, USA, 1992. [Google Scholar]
- Abraham, R.H.; Marsden, J.E. Foundations of Mechanics, 2nd ed.; Addison Wesley: Redwood City, CA, USA, 1987. [Google Scholar]
- Silvi, B.; Gillespie, R.J.; Gatti, C. Electron Density Analysis. In Comprehensive Inorganic Chemistry II; Reedijk, J., Poeppelmeier, K., Eds.; Elsevier: Oxford, UK, 2013; Volume 9, pp. 187–226. [Google Scholar] [CrossRef]
- Leboeuf, M.; Köster, A.M.; Jug, K.; Salahub, D.R. Topological analysis of the molecular electrostatic potential. J. Chem. Phys. 1999, 111, 4893–4905. [Google Scholar] [CrossRef]
- Gadre, S.R.; Pathak, R.K. Topography of molecular scalar fields. I. Algorithm and Poincaré–Hopf relation. J. Chem. Phys. 2003, 119, 5037–5043. [Google Scholar] [CrossRef]
- Popelier, P.L.A. On the full topology of the Laplacian of the electron density. Coord. Chem. Rev. 2000, 197, 169–189. [Google Scholar] [CrossRef]
- Cremer, D.; Kraka, E. A Description of the Chemical Bond in Terms of Local Properties of Electron Density and Energy. Croat. Chem. Acta 1984, 57, 1259–1281. [Google Scholar]
- Putz, H.; Brandenburg, K. (1997–2012). Diamond – Crystal and Molecular Structure Visualization. Crystal Impact, GbR, Kreuzherrenstrasse 102, 53227 Bonn, Germany. Available online: http://www.crystalimpact.com/diamond (accessed on 31 July 2020).
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera – a visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gatti, C.; Cargnoni, F.; Bertini, L. Chemical information from the source function. J. Comput. Chem. 2003, 24, 422–436. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, A.; Nakatsuji, H.; et al. Gaussian 09; Revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Biegler-König, F.W.; Bader, R.F.W.; Tang, T.-H. Calculation of the average properties of atoms in molecules. II. J. Comput. Chem. 1982, 3, 317–328. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyser. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three–dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]



| CP(r,s) | −∇2s | Type | −∇2ρα | −∇2ρβ | Constraint |
|---|---|---|---|---|---|
| (3, −3), max | > 0 | 1 | > 0 | > 0 | −∇2ρα > −∇2ρβ |
| > 0 | 2 | > 0 | < 0 | None | |
| > 0 | 3 | < 0 | < 0 | |−∇2ρα| < |−∇2ρβ| | |
| (3, −1), 1st order SP | > 0 | 1 | > 0 | > 0 | −∇2ρα > −∇2ρβ |
| > 0 | 2 | > 0 | < 0 | None | |
| > 0 | 3 | < 0 | < 0 | |−∇2ρα| < |−∇2ρβ| | |
| < 0 | 4 | > 0 | > 0 | −∇2ρα < −∇2ρβ | |
| < 0 | 5 | < 0 | > 0 | None | |
| < 0 | 6 | < 0 | < 0 | |−∇2ρα| > |−∇2ρβ| | |
| (3, +1), 2nd order SP | Same as for (3, −1) | ||||
| (3, +3), min | < 0 | 1 | > 0 | > 0 | −∇2ρα < −∇2ρβ |
| < 0 | 2 | < 0 | > 0 | None | |
| < 0 | 3 | < 0 | < 0 | |−∇2ρα| > |−∇2ρβ| |
| WFN | Type | s | smag | ρ | ∇ρα ≡ ∇ρβ | ∇2s | ∇2ρα | ∇2ρβ | SPI(rc) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Maxima (3, −3) | |||||||||||
| 1 | 2 | ROHF | 3 | 0.603 | 0.603 | 1.938 | 8.715 | −26.978 | 81.209 | 108.186 | 1.269 |
| 2 | UHF | 3 | 0.613 | 0.607 | 1.816 | 7.714 | −25.944 | 71.334 | 97.278 | 1.346 | |
| 2 | CAS | 3 | 0.617 | 0.615 | 1.820 | 7.681 | −25.670 | 71.105 | 96.775 | 1.351 | |
| 2 | 2 | ROHF | 1 | 0.018 | 0.018 | 0.263 | 0.341 | −0.697 | −5.517 | −4.821 | 0.765 |
| 2 | UHF | 2 | 0.015 | 0.016 | 0.090 | 0.123 | −0.119 | −0.091 | 0.028 | 0.923 | |
| 2 | CAS | 3 | 0.012 | 0.014 | 0.072 | 0.096 | −0.082 | 0.003 | 0.086 | 0.936 | |
| 3 | 1 | ROHF | 1 | 0.683 | 0.683 | 295.534 | 557.768 | −5.6 × 103 | −1.2 × 106 | −1.2 × 106 | 0.670 |
| 1 | UHF | 1 | 0.840 | 0.706 | 295.432 | 587.366 | −6.7 × 103 | −1.2 × 106 | −1.2 × 106 | 0.670 | |
| 1 | CAS | 1 | 1.262 | 0.725 | 295.814 | 408.328 | −10.1 × 103 | −1.2 × 106 | −1.2 × 106 | 0.672 | |
| Saddles (3, −1) | |||||||||||
| 4 | 2 | ROHF | 1 | 0.367 | 0.367 | 82.250 | 648.694 | −45.534 | −4.85 × 103 | −4.80 × 103 | 0.673 |
| 2 | UHF | 1 | 0.415 | 0.380 | 64.569 | 503.389 | −47.064 | −1.91 × 103 | −1.86 × 103 | 0.675 | |
| 2 | CAS | 1 | 0.474 | 0.417 | 41.885 | 323.092 | −45.172 | −66.122 | −20.950 | 0.682 | |
| 5 | 1 | ROHF | 6 | 0.094 | 0.094 | 1.265 | 1.691 | 2.051 | 8.785 | 6.734 | 0.773 |
| 1 | UHF | 6 | 0.130 | 0.100 | 1.308 | 1.921 | 1.206 | 11.013 | 9.807 | 0.813 | |
| 1 | CAS | 6 | 0.147 | 0.102 | 1.327 | 2.032 | 0.850 | 11.728 | 10.877 | 0.833 | |
| 6 | 4 | ROHF | 6 | 0.006 | 0.006 | 0.085 | 0.098 | 0.023 | 0.099 | 0.077 | 0.744 |
| 4 | UHF | 6 | 0.005 | 0.006 | 0.048 | 0.057 | 0.013 | 0.086 | 0.073 | 0.819 | |
| 4 | CAS | 6 | 0.004 | 0.005 | 0.039 | 0.047 | 0.010 | 0.076 | 0.066 | 0.826 | |
| 7 | 1 | ROHF | 3 | 0.003 | 0.003 | 0.006 | 0.003 | −0.002 | 0.003 | 0.006 | 2.455 |
| 1 | UHF | 3 | 0.003 | 0.004 | 0.006 | 0.003 | −0.003 | 0.003 | 0.005 | 2.575 | |
| 1 | CAS | 3 | 0.003 | 0.003 | 0.006 | 0.003 | −0.003 | 0.002 | 0.005 | 2.581 | |
| N | M | WFN | Type | s | smag | ρ | ∇ρα ≡ ∇ρβ | ∇2s | ∇2ρα | ∇2ρβ | SPI(rc) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 2 | ROHF | 6 | 0.003 | 0.003 | 0.009 | 0.007 | 0.004 | 0.018 | 0.014 | 1.252 |
| 2 | UHF | 6 | 0.003 | 0.003 | 0.008 | 0.006 | 0.003 | 0.015 | 0.012 | 1.315 | |
| 2 | CAS | 6 | 0.002 | 0.003 | 0.007 | 0.006 | 0.003 | 0.014 | 0.011 | 1.350 | |
| 9 | 2 | ROHF | 6 | 0.001 | 0.001 | 0.039 | 0.055 | 0.007 | 0.108 | 0.101 | 0.694 |
| 10 | 1 | UHF | 3 | 0.000 | 0.000 | 0.0051 | 0.0058 | −0.0003 | 0.0082 | 0.0085 | 0.754 |
| 1 | CAS | 3 | 0.000 | 0.000 | 0.0056 | 0.0061 | −0.0002 | 0.0083 | 0.0085 | 0.750 | |
| 11 | 1 | UHF | 6 | 0.011 | 0.000 | 25.929 | 195.627 | 52.020 | 637.129 | 585.109 | 0.667 |
| 1 | CAS | 6 | 0.030 | 0.001 | 20.991 | 156.382 | 49.062 | 692.826 | 643.765 | 0.669 | |
| 12 | 1 | UHF | 6 | −0.001 | 0.000 | 0.062 | 0.077 | 0.055 | 0.191 | 0.136 | 0.644 |
| 1 | CAS | 6 | −0.002 | 0.000 | 0.063 | 0.078 | 0.059 | 0.194 | 0.136 | 0.631 | |
| 13 | 1 | UHF | 6 | −0.001 | 0.001 | 0.297 | 0.409 | 0.176 | 0.321 | 0.145 | 0.661 |
| 1 | CAS | 6 | −0.000 | 0.001 | 0.068 | 0.095 | 0.021 | 0.159 | 0.138 | 0.667 | |
| 14 | 2 | UHF | 6 | −0.002 | 0.000 | 0.225 | 0.289 | 0.166 | 0.390 | 0.224 | 0.654 |
| 2 | CAS | 6 | 0.023 | 0.000 | 1.517 | 3.758 | 7.252 | 38.928 | 31.677 | 0.687 | |
| 15 | 2 | UHF | 1 | −0.007 | 0.000 | 0.295 | 0.063 | 0.261 | −0.577 | −0.837 | 0.638 |
| 2 | CAS | 1 | −0.008 | 0.001 | 0.289 | 0.053 | 0.260 | −0.696 | −0.956 | 0.631 | |
| 16 | 2 | UHF | 2 | −0.002 | 0.000 | 0.390 | 0.508 | 0.380 | 0.289 | −0.091 | 0.658 |
| 2 | CAS | 3 | 0.020 | 0.000 | 6.369 | 42.376 | 23.418 | 346.437 | 323.019 | 0.671 |
| Ω | M | WFN | NΩ | SPΩ | SPmag,Ω | SPIΩ | V1Ω | V2Ω | |
|---|---|---|---|---|---|---|---|---|---|
| ∇ρ ZFS boundaries | |||||||||
| O | 1 | ROHF | 8.867 | 1.409 | = | 0.919 | 180.6 | 127.4 | 0.008 |
| 1 | UHF | 8.856 | 1.417 | 1.409 | 0.921 | 179.2 | 126.8 | 0.008 | |
| 1 | CAS | 8.743 | 1.406 | 1.387 | 0.922 | 173.3 | 122.5 | 0.008 | |
| H | 2 | ROHF | 0.565 | 0.294 | = | 2.113 | 71.8 | 39.8 | 0.004 |
| 2 | UHF | 0.571 | 0.290 | 0.295 | 2.046 | 72.2 | 40.3 | 0.004 | |
| 2 | CAS | 0.628 | 0.296 | 0.306 | 1.856 | 76.9 | 42.6 | 0.004 | |
| ∇s ZFS boundaries | |||||||||
| Ω1 | 2 | ROHF | 3.469 | 0.587 | = | 0.938 | 53.9 | 42.0 | 0.011 |
| 2 | UHF | 3.740 | 0.597 | 0.591 | 0.920 | 52.1 | 40.9 | 0.011 | |
| 2 | CAS | 3.620 | 0.604 | 0.595 | 0.934 | 52.4 | 40.9 | 0.012 | |
| Ω2 | 2 | ROHF | 0.901 | 0.409 | = | 1.773 | 108.3 | 61.4 | 0.004 |
| 2 | UHF | 0.907 | 0.402 | 0.407 | 1.727 | 109.8 | 62.7 | 0.004 | |
| 2 | CAS | 0.913 | 0.394 | 0.403 | 1.676 | 111.2 | 63.0 | 0.004 | |
| Ω3 | 1 | ROHF | 1.231 | 0.006 | = | 0.673 | 0.04 | 0.04 | 0.174 |
| 1 | UHF | 0.699 | 0.003 | 0.002 | 0.672 | 0.01 | 0.01 | 0.196 | |
| 1 | CAS | 0.935 | 0.005 | 0.002 | 0.674 | 0.02 | 0.02 | 0.231 | |
| s = 0 isovalue surface boundaries | |||||||||
| Ω1 | 2 | UHF | 3.574 | 0.598 | 0.587 | 0.935 | 50.9 | 39.7 | 0.012 |
| 2 | CAS | 3.509 | 0.606 | 0.589 | 0.945 | 51.6 | 40.2 | 0.012 | |
| Ω2 | 2 | UHF | 0.836 | 0.403 | 0.409 | 1.906 | 109.4 | 62.3 | 0.004 |
| 2 | CAS | 0.821 | 0.395 | 0.407 | 1.901 | 110.6 | 62.3 | 0.004 | |
| Ω3 | 1 | UHF | 0.640 | 0.002 | 0.002 | 0.671 | 0.01 | 0.01 | 0.210 |
| 1 | CAS | 0.916 | 0.005 | 0.004 | 0.674 | 0.02 | 0.02 | 0.237 | |
| Ω15 | 2 | UHF | 0.173 | −0.002 | 0.002 | 0.653 | 1.02 | 1.02 | −0.002 |
| 2 | CAS | 0.212 | −0.003 | 0.003 | 0.650 | 1.45 | 1.45 | −0.002 | |
| Ω16 | 2 | UHF | 0.097 | −0.000 | 0.001 | 0.660 | 0.68 | 0.68 | −0.001 |
| Ω | SF%CP1 | SF%CP2 | SF%CP3 | SF%CP4 | SF%CP5 | SF%CP6 | SF%CP7 |
|---|---|---|---|---|---|---|---|
| ∇s ZFS boundaries | |||||||
| Ω1 | 94.53 | −0.12 | 8.23 | 61.82 | 50.40 | −0.08 | 1.30 |
| Ω1’ | 3.91 | −0.12 | 8.23 | 10.72 | 50.40 | 36.88 | 1.30 |
| Ω2 | 0.05 | 96.50 | 0.02 | 0.06 | 0.14 | 51.63 | 47.20 |
| Ω2’ | 0.05 | 2.72 | 0.02 | 0.06 | 0.14 | 7.81 | 47.20 |
| Ω3 | 1.46 | 1.02 | 83.49 | 27.35 | −1.08 | 3.77 | 3.00 |
| ∇ρ ZFS boundaries | |||||||
| O | 99.29 | −33.98 | 99.62 | 99.00 | 96.45 | −62.50 | −75.30 |
| H | 0.39 | 121.21 | 0.19 | 0.50 | 1.77 | 123.05 | 87.60 |
| H’ | 0.39 | 12.77 | 0.19 | 0.50 | 1.77 | 39.54 | 87.60 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruno, G.; Macetti, G.; Lo Presti, L.; Gatti, C. Spin Density Topology. Molecules 2020, 25, 3537. https://doi.org/10.3390/molecules25153537
Bruno G, Macetti G, Lo Presti L, Gatti C. Spin Density Topology. Molecules. 2020; 25(15):3537. https://doi.org/10.3390/molecules25153537
Chicago/Turabian StyleBruno, Giovanna, Giovanni Macetti, Leonardo Lo Presti, and Carlo Gatti. 2020. "Spin Density Topology" Molecules 25, no. 15: 3537. https://doi.org/10.3390/molecules25153537
APA StyleBruno, G., Macetti, G., Lo Presti, L., & Gatti, C. (2020). Spin Density Topology. Molecules, 25(15), 3537. https://doi.org/10.3390/molecules25153537









