A Hidden Coordination-Bond Torsional Deformation as a Sign of Possible Spin Transition in Nickel(II)-Bis(nitroxide) Compounds
Abstract
1. Introduction
2. Results
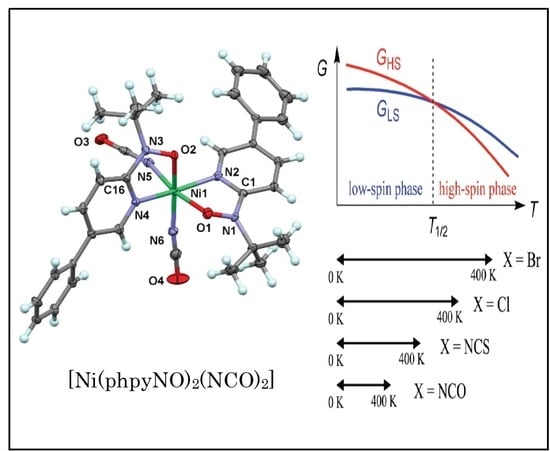
2.1. Structural Study
2.2. Magnetic Study
2.3. DFT Calculation Study
3. Discussion
4. Materials and Methods
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gütlich, P.; Goodwin, H.A. (Eds.) Spin Crossover in Transition Metal Compounds I, II, and III; Springer: Berlin, Germany, 2004. [Google Scholar]
- Halcrow, M.A. (Ed.) Spin-Crossover Materials: Properties and Applications; John Wiley & Sons, Inc.: Oxford, UK, 2013. [Google Scholar]
- Molnár, G.; Rat, S.; Salmon, L.; Nicolazzi, W.; Bousseksou, A. Spin Crossover Nanomaterials: From Fundamental Concepts to Devices. Adv. Mater. 2018, 30, 1703862. [Google Scholar] [CrossRef] [PubMed]
- Coronado, E. Molecular magnetism: From chemical design to spin control in molecules, materials and devices. Nat. Rev. Mater. 2020, 5, 87–104. [Google Scholar] [CrossRef]
- Kumar, K.S.; Ruben, M. Emerging trends in spin crossover (SCO) based functional materials and devices. Coord. Chem. Rev. 2017, 346, 176–205. [Google Scholar] [CrossRef]
- Sato, O.; Tao, J.; Zhang, Y.Z. Control of magnetic properties through external stimuli. Angew. Chem. Int. Ed. 2007, 46, 2152–2187. [Google Scholar] [CrossRef]
- Ratera, I.; Veciana, J. Playing with organic radicals as building blocks for functional molecular materials. Chem. Soc. Rev. 2012, 41, 303–349. [Google Scholar] [CrossRef]
- Iwamura, H. What role has organic chemistry played in the development of molecule-based magnets? Polyhedron 2013, 66, 3–14. [Google Scholar] [CrossRef]
- Aromí, G.; Real, J.A. Special Issue “Spin Crossover (SCO) Research”. Magnetochemistry 2016, 2, 28. [Google Scholar] [CrossRef]
- Takahashi, K. Special Issue “Spin-Crossover Complexes”. Inorganics 2018, 6, 32. [Google Scholar] [CrossRef]
- Kitazawa, T. Special Issue “Synthesis and Applications of New Spin Crossover Compounds”. Crystals 2019, 9, 382. [Google Scholar] [CrossRef]
- Hayami, S.; Holmes, S.M.; Halcrow, M.A. Themed Issue “Spin-State Switches in Molecular Materials Chemistry”. J. Mater. Chem. C 2015, 3, 7767. [Google Scholar] [CrossRef]
- Kimura, A.; Ishida, T. Spin-crossover temperature predictable from DFT calculation for iron(II) complexes with 4-substituted pybox and related heteroaromatic ligands. ACS Omega 2018, 3, 6737–6747. [Google Scholar] [CrossRef] [PubMed]
- Kashiro, A.; Kohno, W.; Ishida, T. Odd–Even Effect on the Spin-Crossover Temperature in Iron (II) Complex Series Involving an Alkylated or Acyloxylated Tripodal Ligand. Inorg. Chem. 2020, 59, 10163–10171. [Google Scholar] [CrossRef]
- Caneschi, A.; Gatteschi, D.; Sessoli, R.; Rey, P. Toward molecular magnets: The metal-radical approach. Acc. Chem. Res. 1989, 22, 392–398. [Google Scholar] [CrossRef]
- Meng, X.; Shi, W.; Cheng, P. Magnetism in one-dimensional metal–nitronyl nitroxide radical system. Coord. Chem. Rev. 2019, 378, 134–150. [Google Scholar] [CrossRef]
- Osanai, K.; Okazawa, A.; Nogami, T.; Ishida, T. Strong Ferromagnetic Exchange Couplings in Copper(II) and Nickel(II) Complexes with a Paramagnetic Tridentate Chelate Ligand, 2,2′-Bipyridin-6-yl tert-Butyl Nitroxide. J. Am. Chem. Soc. 2006, 128, 14008–14009. [Google Scholar] [CrossRef] [PubMed]
- Okazawa, A.; Nogami, T.; Ishida, T. tert-Butyl 2-Pyridyl Nitroxide Available as a Paramagnetic Chelate Ligand for Strongly Exchange-Coupled Metal−Radical Compounds. Chem. Mater. 2007, 19, 2733–2735. [Google Scholar] [CrossRef]
- Okazawa, A.; Nagaichi, Y.; Nogami, T.; Ishida, T. Magneto-structure relationship in copper(II) and nickel(II) complexes chelated with stable tert-butyl 5-phenyl-2-pyridyl nitroxide and related radicals. Inorg. Chem. 2008, 47, 8859–8868. [Google Scholar] [CrossRef] [PubMed]
- Okazawa, A.; Nogami, T.; Ishida, T. Strong intramolecular ferromagnetic couplings in nickel(II) and copper(II) complexes chelated with tert-butyl 5-methoxy-2-pyridyl nitroxide. Polyhedron 2009, 28, 1917–1921. [Google Scholar] [CrossRef]
- Kawakami, H.; Tonegawa, A.; Ishida, T. A designed room-temperature triplet ligand from pyridine-2,6-diyl bis(tert-butyl nitroxide). Dalton Trans. 2016, 45, 1306–1309. [Google Scholar] [CrossRef]
- Homma, Y.; Okazawa, A.; Ishida, T. Ground triplet pyrimidine-4,6-diyl bis(tert-butyl nitroxide) as a paramagnetic building block for metal-organic frameworks. Tetrahedron Lett. 2013, 54, 3120–3123. [Google Scholar] [CrossRef]
- Okazawa, A.; Terakado, Y.; Ishida, T.; Kojima, N. A triplet biradical with double bidentate sites based on tert-butyl pyridyl nitroxide as a candidate for strong ferromagnetic couplers. New J. Chem. 2018, 42, 17874–17878. [Google Scholar] [CrossRef]
- Ishida, T.; Murakami, R.; Kanetomo, T.; Nojiri, H. Magnetic study on radical-gadolinium(III) complexes. Relationship between the exchange coupling and coordination structure. Polyhedron 2013, 66, 183–187. [Google Scholar] [CrossRef]
- Kanetomo, T.; Ishida, T. Strongest exchange coupling in gadolinium(III) and nitroxide coordination compounds. Inorg. Chem. 2014, 53, 10794–10796. [Google Scholar] [CrossRef] [PubMed]
- Kanetomo, T.; Yoshitake, T.; Ishida, T. Strongest Ferromagnetic Coupling in Designed Gadolinium(III)–Nitroxide Coordination Compounds. Inorg. Chem. 2016, 55, 8140–8146. [Google Scholar] [CrossRef] [PubMed]
- Kanetomo, T.; Kihara, T.; Miyake, A.; Matsuo, A.; Tokunaga, M.; Kindo, K.; Nojiri, H.; Ishida, T. Giant Exchange Coupling Evidenced with a Magnetization Jump at 52 T for a Gadolinium-Nitroxide Chelate. Inorg. Chem. 2017, 56, 3310–3314. [Google Scholar] [CrossRef]
- Baker, M.L.; Tanaka, T.; Murakami, R.; Ohira-Kawamura, S.; Nakajima, K.; Ishida, T.; Nojiri, H. Relationship between torsion and anisotropic exchange coupling in a TbIII-radical-based single-molecule magnet. Inorg. Chem. 2015, 54, 5732–5738. [Google Scholar] [CrossRef]
- Kahn, O.; Prins, R.; Reedijk, J.; Thompson, J.S. Orbital symmetries and magnetic interaction between copper (II) ions and the o-semiquinone radical. Magnetic studies of (di-2-pyridylamine)(3,5-di-tert-butyl-o-semiquinonato)copper(II) perchlorate and bis(bis(3,5-di-tert-butyl-o-semiquinonato)copper(II)). Inorg. Chem. 1987, 26, 3557–3561. [Google Scholar] [CrossRef]
- Olguín, J. Unusual metal centres/coordination spheres in spin crossover compounds. Coord. Chem. Rev. 2020, 407, 213148. [Google Scholar] [CrossRef]
- Kyoden, Y.; Homma, Y.; Ishida, T. High-Spin and Incomplete Spin-Crossover Polymorphs in Doubly Chelated [Ni(L)2Br2] (L = tert-Butyl 5-Phenyl-2-pyridyl Nitroxide). Inorg. Chem. 2019, 58, 10743–10755. [Google Scholar] [CrossRef]
- Homma, Y.; Ishida, T. A new S = 0 ⇄ S = 2 “Spin-crossover” scenario found in a Nickel(II) Bis(nitroxide) system. Chem. Mater. 2018, 30, 1835–1838. [Google Scholar] [CrossRef]
- Kyoden, Y.; Ishida, T. An indication of spin-transition accompanied by an order-disorder structural transformation in [Ni(phpyNO)2(NCS)2] (phpyNO = tert-butyl 5-phenyl-2-pyridyl nitroxide). RSC Adv. 2020, 10, 16009–16015. [Google Scholar] [CrossRef]
- Guionneau, P.; Marchivie, M.; Bravic, G.; Letard, J.-F.; Chasseau, D. Structural Aspects of Spin Crossover. Example of the [FeIILn(NCS)2] Complexes. Top. Curr. Chem. 2004, 234, 97–128. [Google Scholar]
- Lluncll, M.; Casanova, D.; Circra, J.; Bofill, J.M.; Alcmany, P.; Alvarez, S.; Pinsky, M.; Avnir, D. SHAPE, v2.1; University of Barcelona: Barcelona, Spain, 2005. [Google Scholar]
- Okazawa, A. Magneto-Structural Relationship on Strong Exchange Interactions between Chelating Nitroxide Radical and Transition-Metal Spins. IOP Conf. Ser. Mater. Sci. Eng. 2017, 202, 012002. [Google Scholar] [CrossRef]
- Taibi, M.; Ammar, S.; Jouini, N.; Fiévet, F.; Molinié, P.; Drillon, M. Layered nickel hydroxide salts: Synthesis, characterization and magnetic behaviour in relation to the basal spacing. J. Mater. Chem. 2002, 12, 3238–3244. [Google Scholar] [CrossRef]
- Kurmoo, M.; Day, P.; Derory, A.; Estournes, C.; Poinsot, R.; Stead, M.J.; Kepert, C.J. 3D Long-Range Magnetic Ordering in Layered Metal–Hydroxide Triangular Lattices 25 Å Apart. J. Solid State Chem. 1999, 145, 452–459. [Google Scholar] [CrossRef]
- Hall, D.S.; Lockwood, D.J.; Bock, C.; MacDougall, B.R. Nickel hydroxides and related materials: A review of their structures, synthesis and properties. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20140792. [Google Scholar] [CrossRef]
- Kahn, O. Molecular Magnetism; VCH: New York, NY, USA, 1993; pp. 53–69. [Google Scholar]
- Boca, R. (Ed.) Theoretical Foundations of Molecular Magnetism: Current Methods in Inorganic Chemistry; Elsevier: Amsterdam, The Netherlands, 1999; Volume 1, pp. 541–563. [Google Scholar]
- Noodleman, L. Valence bond description of antiferromagnetic coupling in transition metal dimers. J. Chem. Phys. 1981, 74, 5737–5743. [Google Scholar] [CrossRef]
- Cramer, C.J.; Truhlar, D.G. Density functional theory for transition metals and transition metal chemistry. Phys. Chem. Chem. Phys. 2009, 11, 10757–10816. [Google Scholar] [CrossRef]
- Pantazis, D.A. Assessment of Double-Hybrid Density Functional Theory for Magnetic Exchange Coupling in Manganese Complexes. Inorganics 2019, 7, 57. [Google Scholar] [CrossRef]
- Ito, S.; Ishida, T. Practically Diamagnetic Macrocycle Consisting of Nickel-Biradical Heterospins with the Largest Out-of-Plane Torsion at Coordination Bonds. Chem. Lett. 2020, 49, 1062–1065. [Google Scholar] [CrossRef]
- Bondi, A. Van der Waals volumes and radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Ishida, T. Moving Molecules in Crystalline Solids: Gradual Structure Transition and Spin Transition/Crossover. IOP Conf. Ser. Mater. Sci. Eng. 2019, 515, 12001. [Google Scholar] [CrossRef]
- Adams, D.M.; Dei, A.; Rheingold, A.L.; Hendrickson, D.N. Bistability in the [CoII(semiquinonate)2] to [CoIII(catecholate)(semiquinonate)] valence-tautomeric conversion. J. Am. Chem. Soc. 1993, 115, 8221–8229. [Google Scholar] [CrossRef]
- Letard, J.-F.; Real, J.A.; Moliner, N.; Gaspar, A.B.; Capes, L.; Cador, O.; Kahn, O. Light Induced Excited Pair Spin State in an Iron(II) Binuclear Spin-Crossover Compound. J. Am. Chem. Soc. 1999, 121, 10630–10631. [Google Scholar] [CrossRef]
- Okazawa, A.; Ishida, T. Spin-Transition-Like Behavior on One Side in a Nitroxide-Copper(II)-Nitroxide Triad System. Inorg. Chem. 2010, 49, 10144–10147. [Google Scholar] [CrossRef] [PubMed]
- Okazawa, A.; Hashizume, D.; Ishida, T. Ferro- and Antiferromagnetic Coupling Switch Accompanied by Twist Deformation around the Copper(II) and Nitroxide Coordination Bond. J. Am. Chem. Soc. 2010, 132, 11516–11524. [Google Scholar] [CrossRef] [PubMed]
- Ovcharenko, V.; Fokin, S.; Chubakova, E.; Romanenko, G.; Bogomyakov, A.; Dobrokhotova, Z.; Lukzen, N.; Morozov, V.; Petrova, M.; Petrova, M.; et al. A Copper-Nitroxide Adduct Exhibiting Separate Single Crystal-to-Single Crystal Polymerization−Depolymerization and Spin Crossover Transitions. Inorg. Chem. 2016, 55, 5853–5861. [Google Scholar] [CrossRef]
- Fedin, M.V.; Verber, S.L.; Bagryanskaya, E.; Ovcharenko, V.I. Electron Paramagnetic Resonance of Switchable Copper-Nitroxide-Based Molecular Magnets: An Indispensable Tool for Intriguing Systems. Coord. Chem. Rev. 2015, 289, 341–356. [Google Scholar] [CrossRef]
- Lanfranc de Panthou, F.; Belorizky, E.; Calemczuk, R.; Luneau, D.; Marcenat, C.; Ressouche, E.; Turek, P.; Rey, P. A New Type of Thermally Induced Spin Transition Associated with an Equatorial ↔ Axial Conversion in a Copper(II)-Nitroxide Cluster. J. Am. Chem. Soc. 1995, 117, 11247–11253. [Google Scholar] [CrossRef]
- Lanfranc de Panthou, F.; Luneau, D.; Musin, R.; Öhrström, L.; Grand, A.; Turek, P.; Rey, P. Spin-Transition and Ferromagnetic Interactions in Copper(II) Complexes of a 3-Pyridyl-Substituted Imino Nitroxide. Dependence of the Magnetic Properties upon Crystal Packing. Inorg. Chem. 1996, 35, 3484–3491. [Google Scholar] [CrossRef]
- Crystal Structure; Version 4.2; Rigaku/MSC: The Woodlands, TX, USA, 2010–2015.
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Bain, G.A.; Berry, J.F. Diamagnetic Corrections and Pascal’s Constants. J. Chem. Educ. 2008, 85, 532–536. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2019. [Google Scholar]
Sample Availability: Not available. |







| Compound | [Ni(phpyNO)2(NCO)2] (4) | |
|---|---|---|
| T/K | 100 | 400 |
| Formula, formula weight | C32H34N6NiO4, 625.36 | |
| Crystal system | orthorhombic | |
| Space group | Pna21 | |
| a/Å | 19.489(4) | 19.727(9) |
| b/Å | 8.992(2) | 9.409(4) |
| c/Å | 17.316(4) | 17.217(7) |
| V/Å3 | 3034.5(11) | 3196(2) |
| Z | 4 | 4 |
| dcalcd/g·cm−3 | 1.369 | 1.300 |
| μ (MoKα)/mm−1 | 0.686 | 0.652 |
| No. of unique reflections | 6948 | 7227 |
| R(F) (I > 2σ(I)) a | 0.0525 | 0.0805 |
| wR(F2) (all reflections) b | 0.0989 | 0.1932 |
| Goodness-of-fit parameter | 1.054 | 1.155 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kyoden, Y.; Ishida, T. A Hidden Coordination-Bond Torsional Deformation as a Sign of Possible Spin Transition in Nickel(II)-Bis(nitroxide) Compounds. Molecules 2020, 25, 3790. https://doi.org/10.3390/molecules25173790
Kyoden Y, Ishida T. A Hidden Coordination-Bond Torsional Deformation as a Sign of Possible Spin Transition in Nickel(II)-Bis(nitroxide) Compounds. Molecules. 2020; 25(17):3790. https://doi.org/10.3390/molecules25173790
Chicago/Turabian StyleKyoden, Yukiya, and Takayuki Ishida. 2020. "A Hidden Coordination-Bond Torsional Deformation as a Sign of Possible Spin Transition in Nickel(II)-Bis(nitroxide) Compounds" Molecules 25, no. 17: 3790. https://doi.org/10.3390/molecules25173790
APA StyleKyoden, Y., & Ishida, T. (2020). A Hidden Coordination-Bond Torsional Deformation as a Sign of Possible Spin Transition in Nickel(II)-Bis(nitroxide) Compounds. Molecules, 25(17), 3790. https://doi.org/10.3390/molecules25173790