Surface Plasmon Resonances in Sierpinski-Like Photonic Crystal Fibers: Polarization Filters and Sensing Applications
Abstract
:1. Introduction
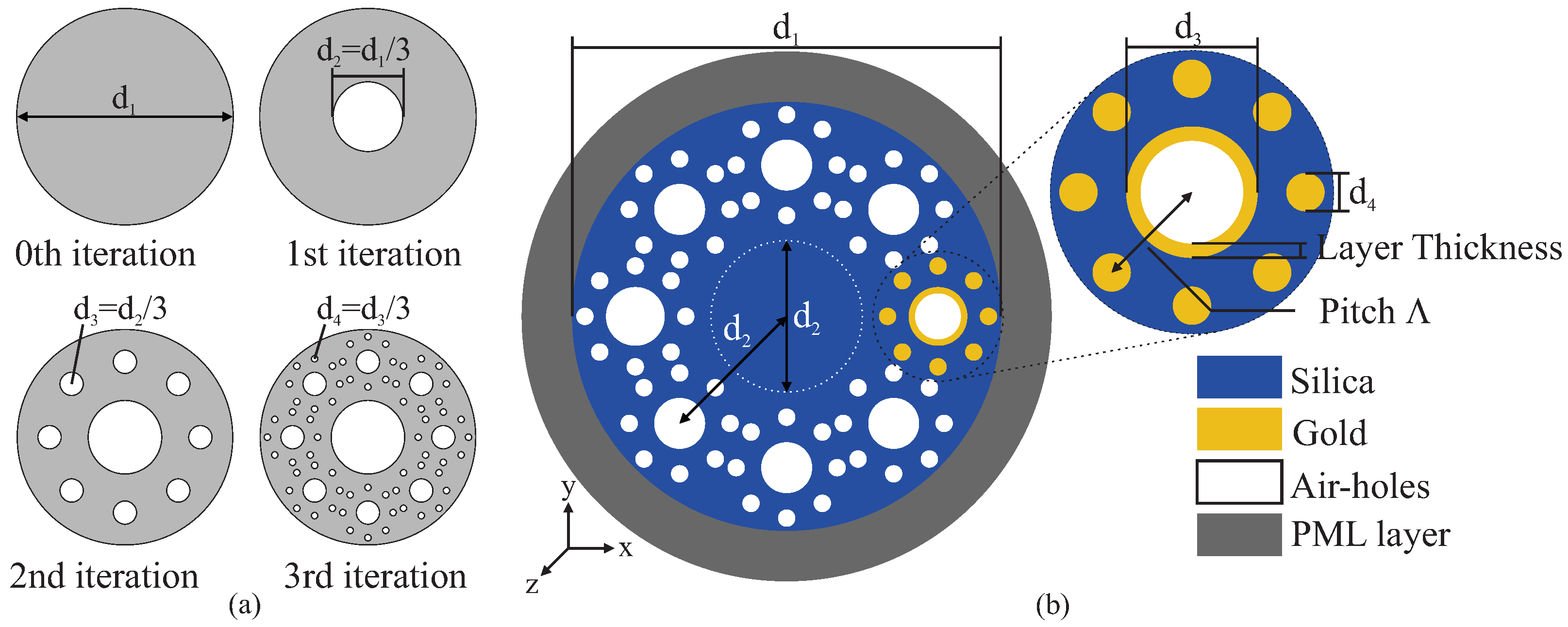
2. PCF Design and Modeling
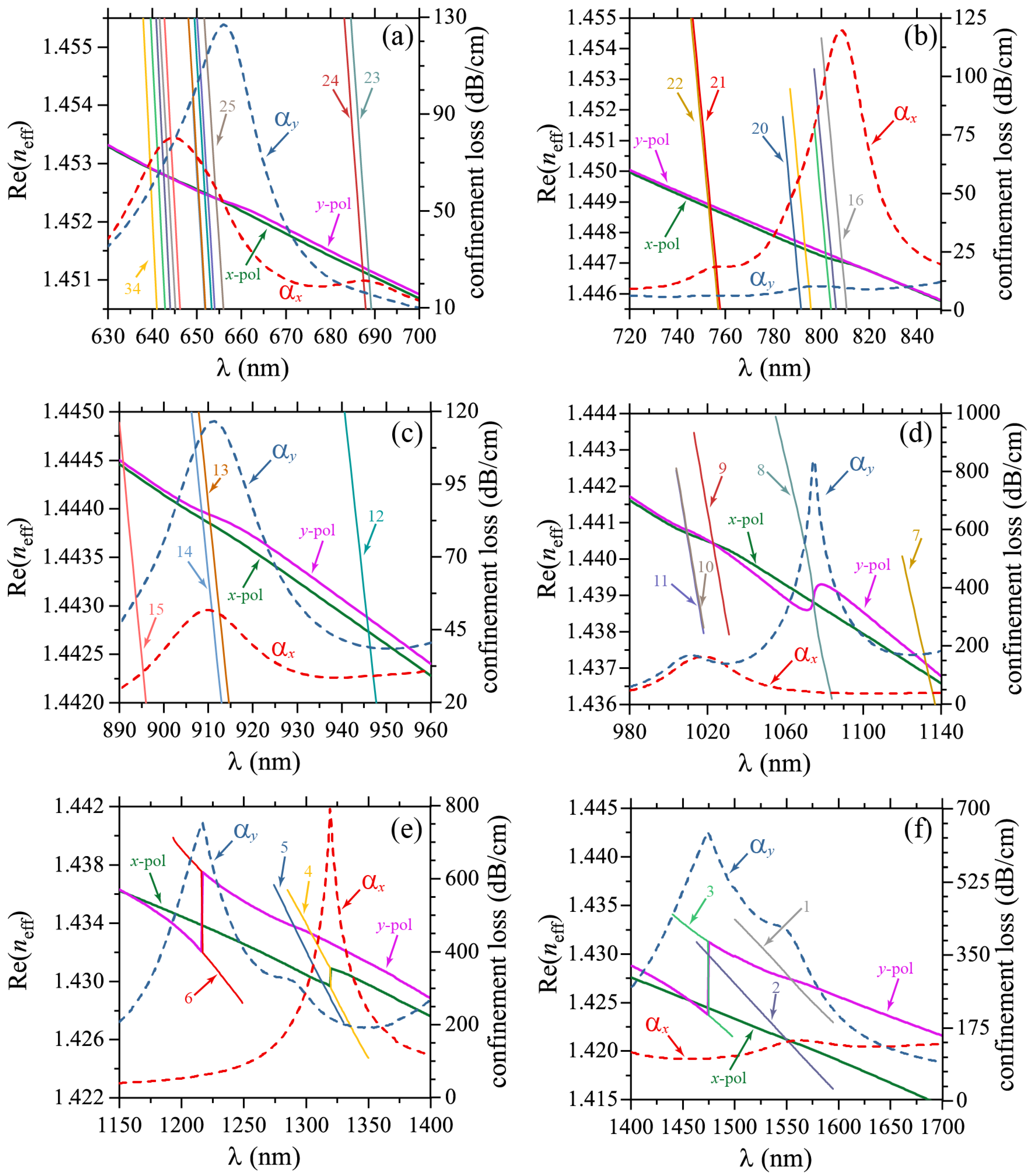
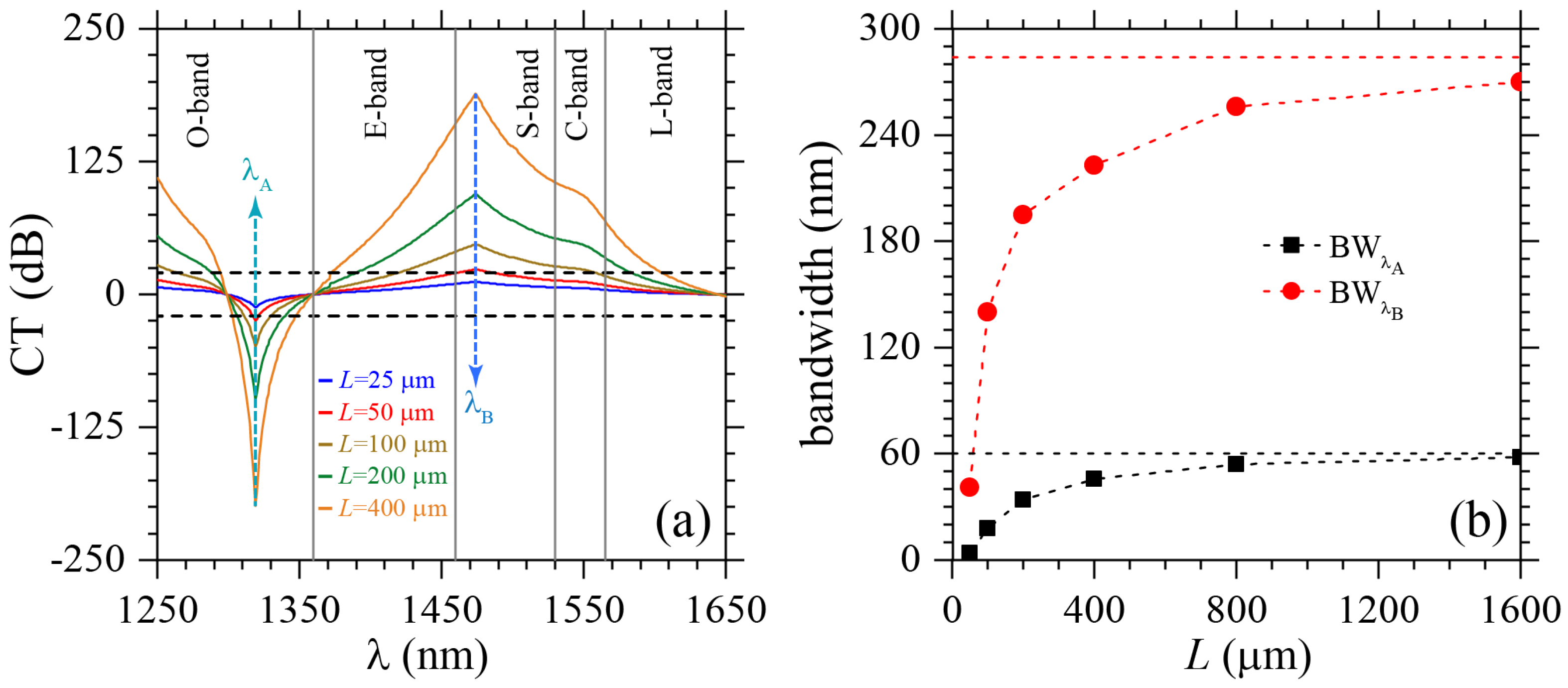
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Baumberg, J.J.; Aizpurua, J.; Mikkelsen, M.H.; Smith, D.R. Extreme nanophotonics from ultrathin metallic gaps. Nat. Mater. 2019, 18, 668–678. [Google Scholar] [CrossRef] [PubMed]
- Luan, N.; Yao, J. A hollow-core photonic crystal fiber-based SPR sensor with large detection range. IEEE Photonic J. 2017, 9, 1–7. [Google Scholar] [CrossRef]
- Chien, F.-C.; Lo, J.-L.; Zhang, X.; Cubukcu, E.; Luo, Y.-T.; Huang, K.-L.; Tang, X.; Chen, C.-S.; Chen, C.-C.; Lai, K.-Y. Nitride-based microarray biochips: A new route of plasmonic imaging. ACS Appl. Mater. Interfaces 2018, 10, 39898–39903. [Google Scholar] [CrossRef] [PubMed]
- Mejía-Salazar, J.R.; Oliveira, O.N., Jr. Plasmonic biosensing. Chem. Rev. 2018, 118, 10617–10625. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Rahman, B. Design of on-chip hybrid plasmonic mach-zehnder interferometer for temperature and concentration detection of chemical solution. Sens. Actuat. B-Chem. 2019, 279, 490–502. [Google Scholar] [CrossRef]
- Yang, P.-S.; Yin, Y.-T.; Lin, P.-C.; Chen, L.-Y.; Chen, M.-J. High chemical resistance and raman enhancement in Ag/Al2O3 core-shell plasmonic nanostructures tailored by atomic layer deposition. Mater. Chem. Phys. 2019, 223, 441–446. [Google Scholar] [CrossRef]
- Simoncelli, S.; Pensa, E.L.; Brick, T.; Gargiulo, J.; Lauri, A.; Cambiasso, J.; Li, Y.; Maier, S.A.; Cortés, E. Monitoring plasmonic hot-carrier chemical reactions at the single particle level. Faraday Discuss. 2019, 214, 73–87. [Google Scholar] [CrossRef]
- Borile, G.; Rossi, S.; Filippi, A.; Gazzola, E.; Capaldo, P.; Tregnago, C.; Pigazzi, M.; Romanato, F. Label-free, real-time on-chip sensing of living cells via grating-coupled surface plasmon resonance. Biophys. Chem. 2019, 254, 106262. [Google Scholar] [CrossRef]
- Paiva-Marques, W.A.; Gómez, F.R.; Oliveira, O.N., Jr.; Mejía-Salazar, J.R. Chiral plasmonics and their potential for point-of-care biosensing applications. Sensors 2020, 20, 944. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, W.O.F.; Mejía-Salazar, J.R. Plasmonics for telecommunications applications. Sensors 2020, 20, 2488. [Google Scholar] [CrossRef]
- Dhiman, M. Plasmonic nanocatalysis for solar energy harvesting and sustainable chemistry. J. Mater. Chem. A 2020, 8, 10074–10095. [Google Scholar] [CrossRef]
- Saeidifard, S.; Sohrabi, F.; Ghazimoradi, M.H.; Hamidi, S.M.; Farivar, S.; Ansari, M.A. Two-dimensional plasmonic biosensing platform: Cellular activity detection under laser stimulation. J. Appl. Phys. 2019, 126, 104701. [Google Scholar] [CrossRef]
- Jia, Y.; Li, Z.; Wang, H.; Saeed, M.; Cai, H. Sensitivity enhancement of a surface plasmon resonance sensor with platinum diselenide. Sensors 2019, 20, 131. [Google Scholar] [CrossRef] [Green Version]
- Xue, T.; Liang, W.; Li, Y.; Sun, Y.; Xiang, Y.; Zhang, Y.; Dai, Z.; Duo, Y.; Wu, L.; Qi, K.; et al. Ultrasensitive detection of mirna with an antimonene-based surface plasmon resonancesensor. Nat. Commun. 2019, 10, 28. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Xu, Z. Tunable temperature sensor based on an integrated plasmonic grating. Opt. Mater. Express 2019, 9, 435–440. [Google Scholar] [CrossRef]
- Fan, Z.; Li, S.; Liu, Q.; Li, J.; Xie, Y. Plasmonic polarization beam splitter based on dual-core photonic crystal fiber. Plasmonics 2015, 10, 1283–1289. [Google Scholar] [CrossRef]
- Chen, N.; Zhang, X.; Chang, M.; Lu, X.; Zhou, J. Broadband plasmonic polarization filter based on photonic crystal fiber with dual-ring gold layer. Micromachines 2020, 11, 470. [Google Scholar] [CrossRef] [PubMed]
- Yasli, A.; Ademgil, H. Geometrical comparison of photonic crystal fiber-based surface plasmon resonance sensors. Opt. Eng. 2018, 57, 1–10. [Google Scholar] [CrossRef]
- Mahfuz, M.A.; Mollah, M.A.; Momota, M.R.; Paul, A.K.; Masud, A.; Akter, S.; Hasan, M.R. Highly sensitive photonic crystal fiber plasmonic biosensor: Design and analysis. Opt. Mater. 2019, 90, 315–321. [Google Scholar] [CrossRef]
- Dou, C.; Jing, X.; Li, S.; Wu, J.; Wang, Q. A compact and low-loss polarization splitter based on dual-core photonic crystal fiber. Opt. Quant. Electron. 2018, 50, 255. [Google Scholar] [CrossRef]
- Dou, C.; Jing, X.; Li, S.; Liu, Q.; Bian, J. A photonic crystal fiber polarized filter at 1.55 μm based on surface plasmon resonance. Plasmonics 2016, 11, 1163–1168. [Google Scholar] [CrossRef]
- Li, H.; Li, S.; Chen, H.; Li, J.; An, G.; Zi, J. A polarization filter based on photonic crystal fiber with asymmetry around gold-coated holes. Plasmonics 2016, 11, 103–108. [Google Scholar] [CrossRef]
- Rifat, A.A.; Ahmed, R.; Yetisen, A.K.; Butt, H.; Sabouri, A.; Mahdiraji, G.A.; Yun, S.H.; Adikan, F.M. Photonic crystal fiber based plasmonic sensors. Sens. Actuat. B-Chem. 2017, 243, 311–325. [Google Scholar] [CrossRef]
- Lou, J.; Li, S.; Cheng, T.; Yan, X.; Zhang, X.; Shao, Y. Polarization filter based on plasmonic photonic crystal fiber with asymmetry around au-coated and liquid-filled air holes. Optik 2017, 149, 162–168. [Google Scholar] [CrossRef]
- Haider, F.; Aoni, R.A.; Ahmed, R.; Miroshnichenko, A.E. Highly amplitude-sensitive photonic-crystal-fiber-based plasmonic sensor. J. Soc. Am. B 2018, 35, 2816–2821. [Google Scholar] [CrossRef]
- Rifat, A.A.; Haider, F.; Ahmed, R.; Mahdiraji, G.A.; Adikan, F.R.M.; Miroshnichenko, A.E. Highly sensitive selectively coated photonic crystal fiber-based plasmonic sensor. Opt. Lett. 2018, 43, 891–894. [Google Scholar] [CrossRef]
- Hossen, M.N.; Ferdous, M.; Ahmed, K.; Khalek, M.A.; Chakma, S.; Paul, B.K. Single polarization photonic crystal fiber filter based on surface plasmon resonance. Front. Optoelectron. 2019, 12, 157–164. [Google Scholar] [CrossRef]
- Qu, Y.; Yuan, J.; Zhou, X.; Li, F.; Mei, C.; Yan, B.; Wu, Q.; Wang, K.; Sang, X.; Long, K.; et al. A v-shape photonic crystal fiber polarization filter based on surface plasmon resonance effect. Opt. Commun. 2019, 452, 1–6. [Google Scholar] [CrossRef]
- Liu, C.; Wang, L.; Yang, L.; Wang, F.; Xu, C.; Lv, J.; Fu, G.; Li, X.; Liu, Q.; Mu, H.; et al. The single-polarization filter composed of gold-coated photonic crystal fiber. Phys. Lett. A 2019, 383, 3200–3206. [Google Scholar] [CrossRef]
- Almewafy, B.H.; Areed, N.F.F.; Hameed, M.F.O.; Obayya, S.S.A. Multifunctional surface plasmon resonance photonic-crystal fiber polarization filter at telecommunication wavelengths. J. Nanophoton. 2019, 13, 1–9. [Google Scholar] [CrossRef]
- Liu, C.; Fu, G.; Wang, F.; Yi, Z.; Xu, C.; Yang, L.; Liu, Q.; Liu, W.; Li, X.; Mu, H.; et al. Ex-centric core photonic crystal fiber sensor with gold nanowires based on surface plasmon resonance. Optik 2019, 196, 163173. [Google Scholar] [CrossRef]
- Almewafy, B.H.; Areed, N.F.F.; Hameed, M.F.O.; Obayya, S.S.A. Modified D-shaped SPR PCF polarization filter at telecommunication wavelengths. Opt. Quant. Electron. 2019, 51, 193. [Google Scholar] [CrossRef]
- Rahman, M.M.; Khaleque, A.; Rahman, M.T.; Rabbi, F. Gold-coated photonic crystal fiber based polarization filter for dual communication windows. Opt. Commun. 2020, 461, 125293. [Google Scholar] [CrossRef]
- Werner, D.H.; Haupt, R.L.; Werner, P.L. Fractal antenna engineering: The theory and design of fractal antenna arrays. IEEE Antennas Propag. Mag. 1999, 41, 37–58. [Google Scholar] [CrossRef] [Green Version]
- Werner, D.H.; Ganguly, S. An overview of fractal antenna engineering research. IEEE Antennas Propag. Mag. 2003, 45, 38–57. [Google Scholar] [CrossRef] [Green Version]
- Romeu, J.; Soler, J. Generalized sierpinski fractal multiband antenna. IEEE Trans. Antennas Propag. 2001, 49, 1237–1239. [Google Scholar] [CrossRef]
- Mejía-Salazar, J.R.; Porras-Montenegro, N.; Reyes-Gómez, E.; Cavalcanti, S.B.; Oliveira, L.E. Plasmon polaritons in 1D cantor-like fractal photonic superlattices containing a left-handed material. Europhys. Lett. 2011, 95, 24004. [Google Scholar] [CrossRef]
- Bellido, E.P.; Bernasconi, G.D.; Rossouw, D.; Butet, J.; Martin, O.J.F.; Botton, G.A. Self-similarity of plasmon edge modes on koch fractal antennas. ACS Nano 2017, 11, 11240–11249. [Google Scholar] [CrossRef]
- Gómez, F.R.; Porras-Montenegro, N.; Oliveira, O.N., Jr.; Mejía-Salazar, J.R. Second harmonic generation in the plasmon-polariton gap of quasiperiodic metamaterial photonic superlattices. Phys. Rev. B 2018, 98, 075406. [Google Scholar] [CrossRef]
- Wallace, G.Q.; Lagugné-Labarthet, F. Advancements in fractal plasmonics: Structures, optical properties, and applications. Analyst 2019, 144, 13–30. [Google Scholar] [CrossRef]
- Bicket, I.C.; Bellido, E.P.; McRae, D.M.; Lagugné-Labarthet, F.; Botton, G.A. Hierarchical plasmon resonances in fractal structures. ACS Photonics 2020, 7, 1246–1254. [Google Scholar] [CrossRef]
- Jena, M.R.; Mangaraj, B.B.; Pathak, R. Design of a novel sierpinski fractal antenna arrays based on circular shapes with low side lobes for 3G applications. Am. J. Electric. Electron. Eng. 2014, 2, 137–140. [Google Scholar] [CrossRef] [Green Version]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen comparison of the refractive index of fused silica. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- Kim, K.-H.; No, Y.-S. Subwavelength core/shell cylindrical nanostructures for novel plasmonic and metamaterial devices. Nano Converg. 2017, 4, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Ito, T.; Sakoda, K. Photonic bands of metallic systems. II. features of surface plasmon polaritons. Phys. Rev. B 2001, 64, 045117. [Google Scholar] [CrossRef]
- Halas, N.J.; Lal, S.; Chang, W.-S.; Link, S.; Norlander, P. Plasmon in strongly coupled metallic nanostructures. Chem. Rev. 2011, 111, 3913–3961. [Google Scholar] [CrossRef]
- Prodan, E.; Radloff, C.; Halas, N.J.; Norlander, P. A hybridization model for the plasmon response of complex nanostructures. Science 2003, 302, 419–422. [Google Scholar] [CrossRef]
- Norlander, P.; Oubre, C.; Prodan, E.; Li, K.; Stockman, M.I. Plasmon Hybridization in Nanoparticle Dimers. Nano Lett. 2014, 4, 899–903. [Google Scholar] [CrossRef]
- Mejía-Salazar, J.R. Optical properties of two-dimensional metamaterial photonic crystals. J. Appl. Phys. 2013, 114, 223513. [Google Scholar] [CrossRef]
- Jabin, M.A.; Ahmed, K.; Rana, M.J.; Paul, B.K.; Luo, Y.; Vigneswaran, D. Titanium-coated dual-core D-shaped SPR-based PCF for hemoglobin sensing. Plasmonics 2019, 14, 1601–1610. [Google Scholar] [CrossRef]
- Sakib, M.N.; Hossain, M.B.; Al-tabatabaie, K.F.; Mehedi, I.M.; Hasan, M.T.; Hossain, M.A.; Amiri, I.S. High performance dual core D-shape PCF-SPR sensor modeling employing gold coat. Results Phys. 2019, 15, 102788. [Google Scholar] [CrossRef]
- Hossain, M.B.; Hossain, M.S.; Islam, S.M.R.; Sakib, M.N.; Islam, K.Z.; Hossain, M.A.; Hossain, M.S.; Hosen, A.S.M.S.; Cho, G.H. Numerical development of high performance quasi D-shape PCF-SPR biosensor: An external sensing approach employing gold. Results Phys. 2020, 18, 103281. [Google Scholar] [CrossRef]

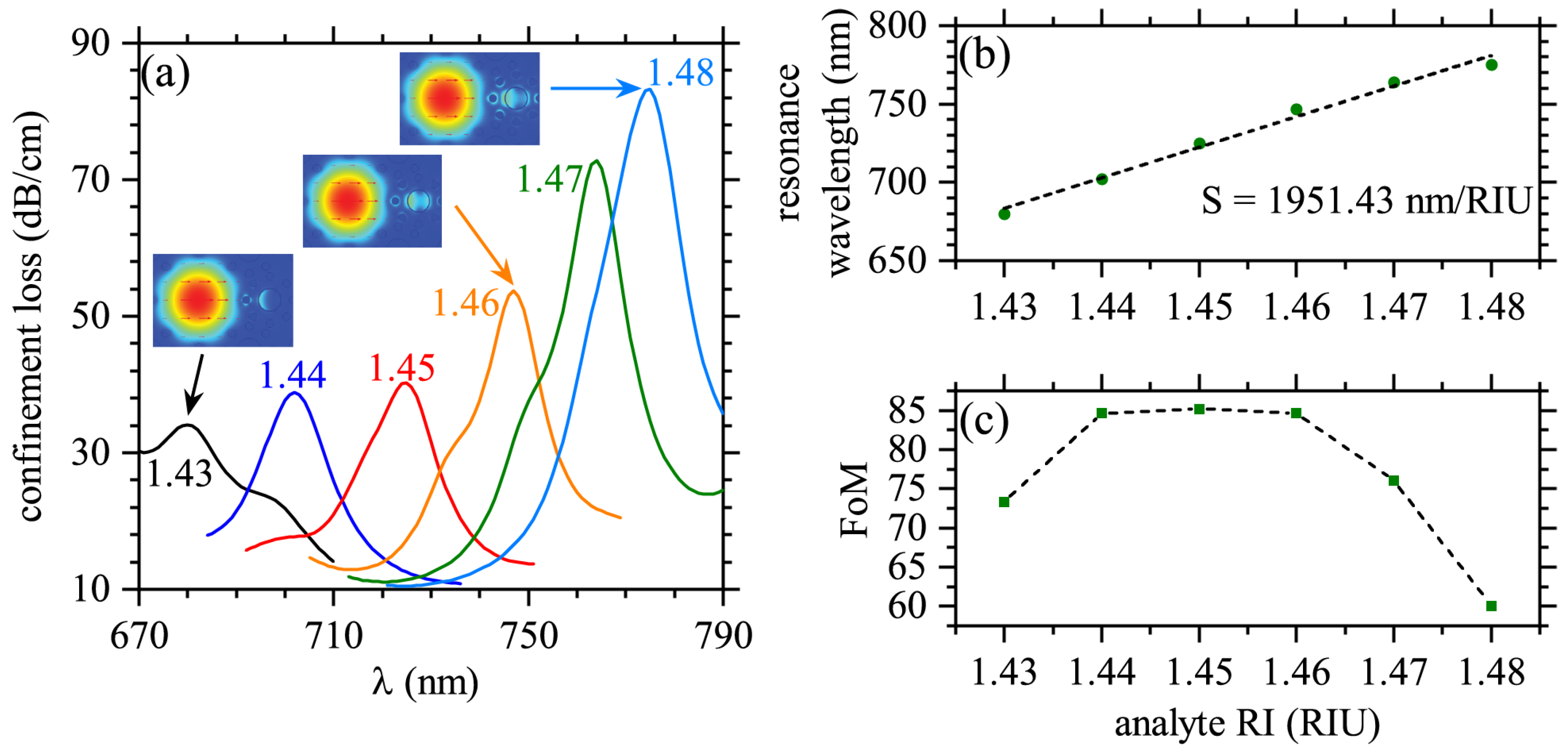
| Analyte RI | Res. Peak Wave. [nm] | Peak Loss [dB/cm] | Res. Peak Shifting [nm] | Wave. Sensitivity [nm/RIU] | Wave. Resolution [RIU] |
|---|---|---|---|---|---|
| 1.43 | 680 | 34.12 | – | – | – |
| 1.44 | 702 | 38.08 | 22 | 2200 | 4.5454 × 10 |
| 1.45 | 725 | 40.27 | 23 | 2300 | 4.3478 × 10 |
| 1.46 | 747 | 53.68 | 22 | 2200 | 4.5454 × 10 |
| 1.47 | 764 | 72.82 | 17 | 1700 | 5.8823 × 10 |
| 1.48 | 775 | 83.20 | 11 | 1100 | 9.0909 × 10 |
| Average | – | – | 95 | 1900 | 5.2631 × 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvalho, W.O.F.; Mejía-Salazar, J.R. Surface Plasmon Resonances in Sierpinski-Like Photonic Crystal Fibers: Polarization Filters and Sensing Applications. Molecules 2020, 25, 4654. https://doi.org/10.3390/molecules25204654
Carvalho WOF, Mejía-Salazar JR. Surface Plasmon Resonances in Sierpinski-Like Photonic Crystal Fibers: Polarization Filters and Sensing Applications. Molecules. 2020; 25(20):4654. https://doi.org/10.3390/molecules25204654
Chicago/Turabian StyleCarvalho, William O. F., and J. R. Mejía-Salazar. 2020. "Surface Plasmon Resonances in Sierpinski-Like Photonic Crystal Fibers: Polarization Filters and Sensing Applications" Molecules 25, no. 20: 4654. https://doi.org/10.3390/molecules25204654
APA StyleCarvalho, W. O. F., & Mejía-Salazar, J. R. (2020). Surface Plasmon Resonances in Sierpinski-Like Photonic Crystal Fibers: Polarization Filters and Sensing Applications. Molecules, 25(20), 4654. https://doi.org/10.3390/molecules25204654







