Memory Effect in the Spatial Series Based on Diamond and Graphite Crystals
Abstract
:1. Introduction
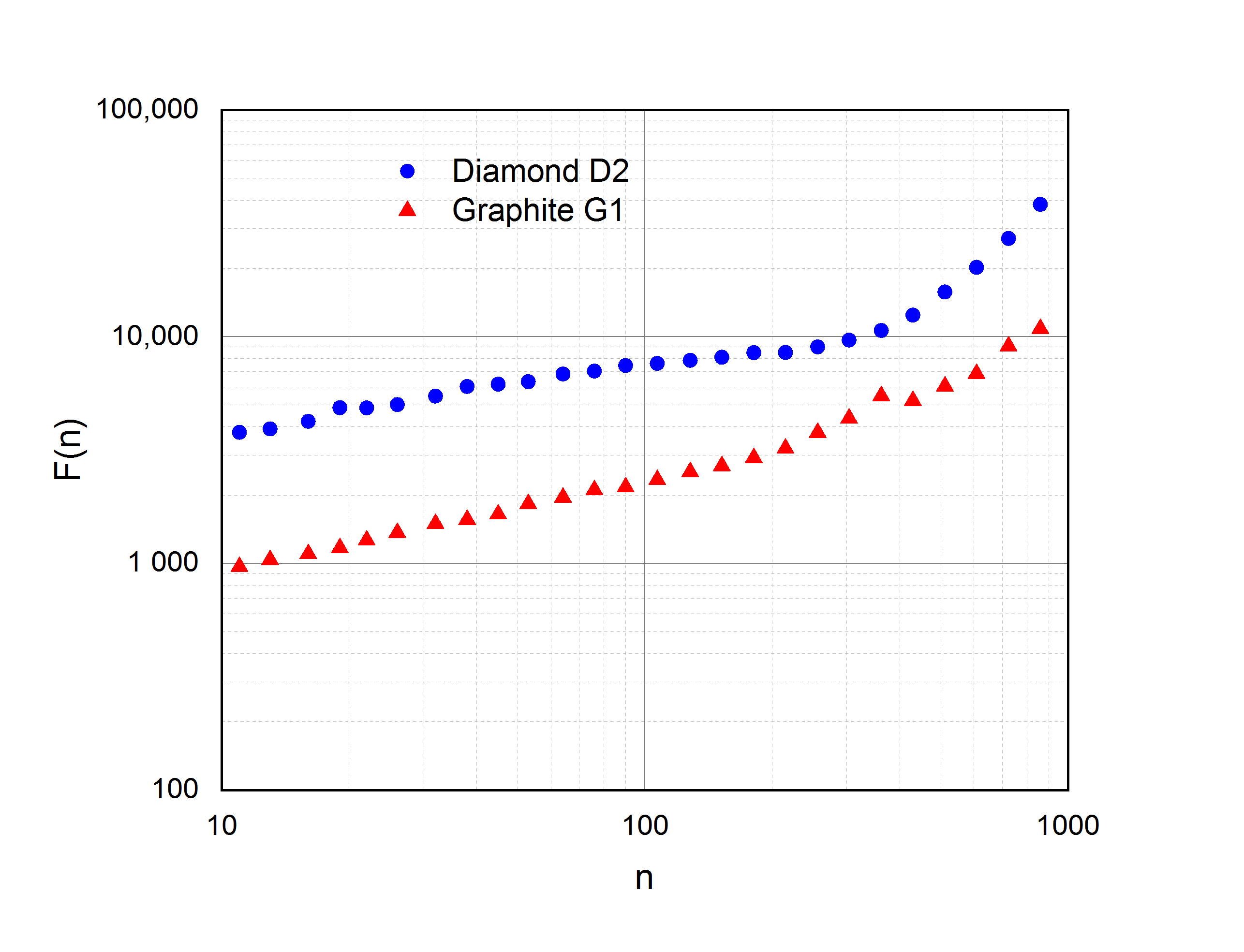
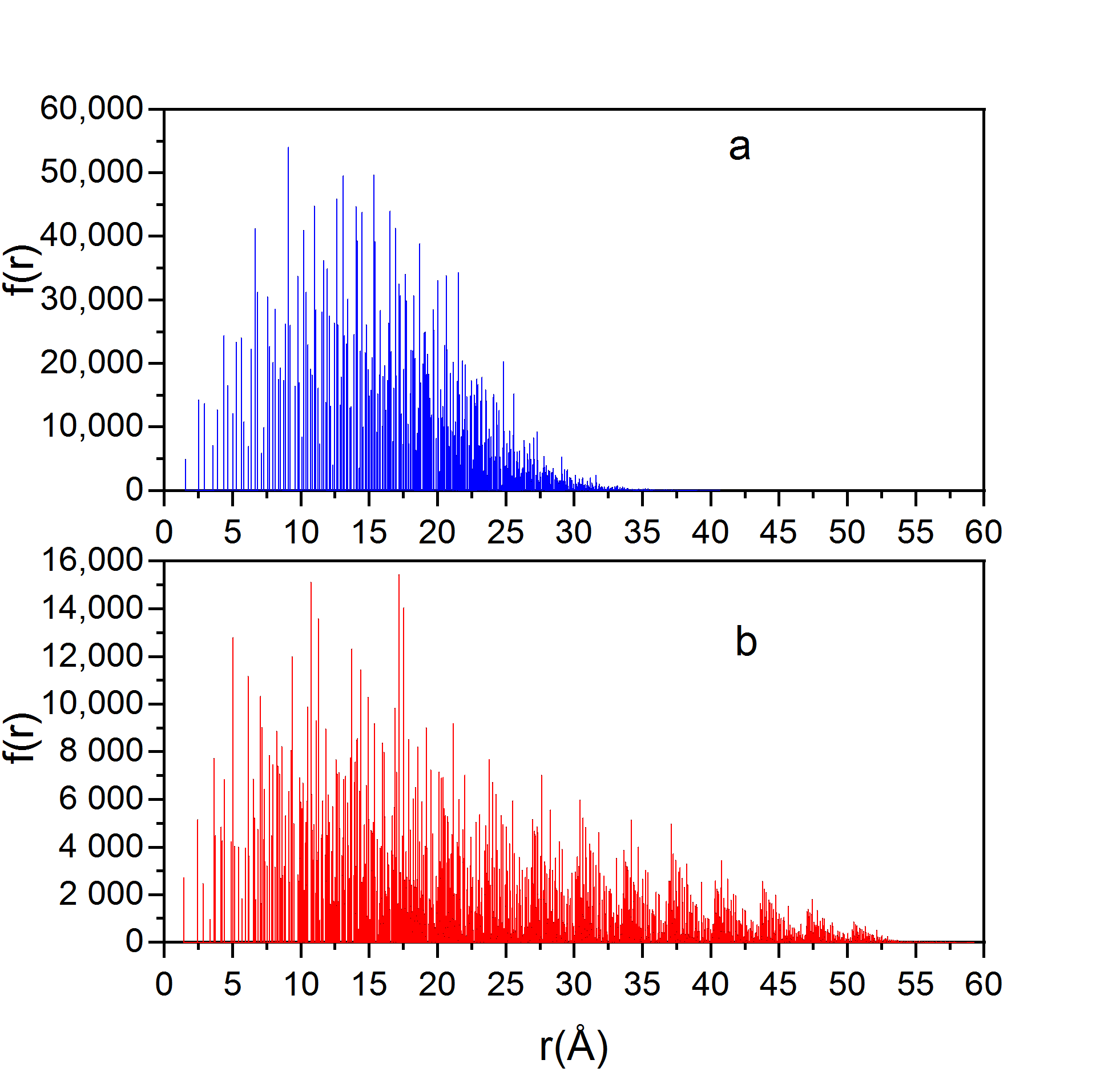
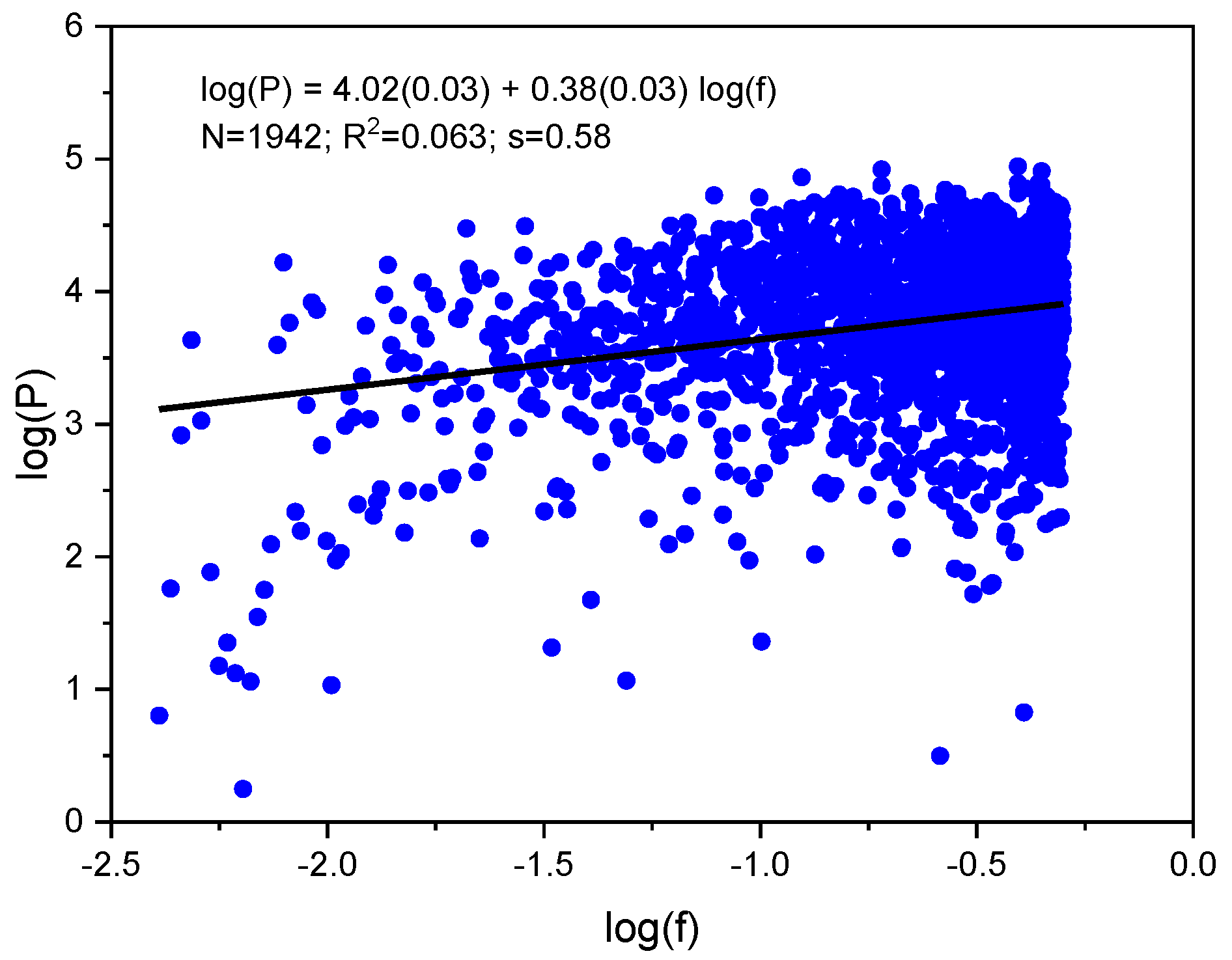
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gaite, J. The fractal geometry of the cosmic web and its formation. Adv. Astron. 2019, 6587138. [Google Scholar] [CrossRef]
- Grizzi, F.; Castello, A.; Qehajaj, D.; Russo, C.; Lopci, E. The complexity and fractal geometry of nuclear medicine images. Mol. Imaging Biol. 2019, 21, 401–409. [Google Scholar] [CrossRef] [PubMed]
- Quaranta, G.; Lacarbonara, W.; Masri, S.F. A review on computational intelligence for identification of nonlinear dynamical systems. Nonlinear Dyn. 2020, 99, 1709–1761. [Google Scholar] [CrossRef]
- Covas, E. Spatial-temporal forecasting the sunspot diagram. Astron. Astrophys. 2017, 605, A44. [Google Scholar] [CrossRef]
- Ma, K.; Guo, L.; Liu, W. Investigation of the spatial clustering properties of seismic time series: A comparative study from shallow to intermediate-depth earthquakes. Complexity 2018, 7169482. [Google Scholar] [CrossRef]
- Roca, J.L.; Rodríguez-Bermúdez, G.; Fernández-Martínez, M. Fractal-based techniques for physiological time series: An updated approach. Open Phys. 2018, 16, 741–750. [Google Scholar] [CrossRef] [Green Version]
- Krzyszczak, J.; Baranowski, P.; Zubik, M.; Kazandjiev, V.; Georgieva, V.; Sławiński, C.; Siwek, K.; Kozyra, J.; Nieróbca, A. Multifractal characterization and comparison of meteorological time series from two climatic zones. Theor. Appl. Climatol. 2019, 137, 1811–1824. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Z.-Q.; Xie, W.-J.; Zhou, W.-X.; Sornette, D. Multifractal analysis of financial markets: A review. Rep. Prog. Phys. 2019, 82, 125901. [Google Scholar] [CrossRef] [Green Version]
- Karain, W.I. Detecting transitions in protein dynamics using a recurrence quantification analysis based bootstrap method. BMC Bioinform. 2017, 18, 525. [Google Scholar] [CrossRef] [Green Version]
- Cramer, J.A.; Booksh, K.S. Chaos theory in chemistry and chemometrics: A review. J. Chemom. 2006, 20, 447–454. [Google Scholar] [CrossRef]
- Mandelbrot, B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eke, A.; Herman, P.; Kocsis, L.; Kozak, L.R. Fractal characterization of complexity in temporal physiological signals. Physiol. Meas. 2002, 23, R1–R38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kristoufek, L. How are rescaled range analyses affected by different memory and distributional properties? A Monte Carlo study. Physica A 2012, 391, 4252–4260. [Google Scholar] [CrossRef]
- Hurst, H. Long term storage capacity of reservoirs. Trans. Am. Soc. Civil. Eng. 1951, 116, 770–799. [Google Scholar]
- Peng, C.-K.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 1995, 5, 82–87. [Google Scholar] [CrossRef]
- Shiomi, K.; Sato, H.; Ohtake, M. Broad-band power-law spectra of well-log data in Japan. Geophys. J. Int. 1997, 130, 57–64. [Google Scholar] [CrossRef] [Green Version]
- Simonsen, I.; Hansen, A.; Nes, O.M. Determination of the Hurst exponent by use of wavelet transforms. Phys. Rev. E 1998, 58, 2779–2787. [Google Scholar] [CrossRef] [Green Version]
- Grigorev, V.; Raevskii, O. Fractal dimension of the interatomic distance histogram: New 3D descriptor of molecular structure. Russ. J. Gen. Chem. 2011, 81, 449–455. [Google Scholar] [CrossRef]
- Grigorev, V.Y.; Grigoreva, L.D. Long-term memory effect in spatial series of model peptides composed of glycine and alanine. Mosc. Univ. Chem. Bull. 2019, 74, 216–222. [Google Scholar] [CrossRef]
- Grigorev, V.Y.; Grigoreva, L.D. The study of molecular histograms of interatomic distances in organic homologs on the basis of R/S analysis. Mosc. Univ. Chem. Bull. 2017, 72, 144–148. [Google Scholar] [CrossRef]
- Falcao, E.H.L.; Wudl, F. Carbon allotropes: Beyond graphite and diamond. J. Chem. Technol. Biotechnol. 2007, 82, 524–531. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L. Self-affine time series: I. Generation and analyses. Adv. Geophys. 1999, 40, 1–90. [Google Scholar] [CrossRef]
- Lopez-Lambrano, A.A.; Fuentes, C.; Lopez-Ramos, A.A.; Mata-Ramirez, J.; Lopez-Lambrano, M. Spatial and temporal Hurst exponent variability of rainfall series based on the climatological distribution in a semiarid region in Mexico. Atmosfera 2018, 31, 199–219. [Google Scholar] [CrossRef]
- Muratov, E.N.; Bajorath, J.; Sheridan, R.P.; Tetko, I.V.; Filimonov, D.; Poroikov, V.; Oprea, T.I.; Baskin, I.I.; Varnek, A.; Roitberg, A.; et al. QSAR without borders. Chem. Soc. Rev. 2020, 49, 3525–3564. [Google Scholar] [CrossRef]
- HyperChem. Available online: http://www.hyper.com (accessed on 10 October 2020).
- CrystalMaker. Available online: http://www.crystalmaker.com/index.html (accessed on 10 October 2020).
- AMCSD. Available online: http://rruff.geo.arizona.edu/AMS/minerals (accessed on 10 October 2020).
- CCDC. Available online: https://www.ccdc.cam.ac.uk (accessed on 10 October 2020).
- arXiv. Available online: https://arxiv.org/abs/0804.0747 (accessed on 10 October 2020).
- IMSL. Available online: https://docs.roguewave.com/en/imsl-main (accessed on 10 October 2020).

| Crystal | α ± Δ | Hα ± Δ | Hαrand ± Δ | −β ± Δ | Hβ ± Δ | Hβrand ± Δ |
|---|---|---|---|---|---|---|
| D1 | 0.27 ± 0.01 | 0.27 ± 0.01 | 0.50 ± 0.02 | 0.37 ± 0.03 | 0.32 ± 0.02 | 0.51 ± 0.02 |
| D2 | 0.27 ± 0.01 | 0.27 ± 0.01 | 0.49 ± 0.02 | 0.38 ± 0.03 | 0.31 ± 0.02 | 0.50 ± 0.01 |
| G1 | 0.40 ± 0.01 | 0.40 ± 0.01 | 0.49 ± 0.02 | 0.26 ± 0.03 | 0.37 ± 0.01 | 0.50 ± 0.01 |
| G2 | 0.39 ± 0.01 | 0.39 ± 0.01 | 0.51 ± 0.02 | 0.17 ± 0.03 | 0.42 ± 0.01 | 0.51 ± 0.01 |
Sample Availability: Samples of the compounds D1, D2, G1 and G2 are not available from the authors. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grigoreva, L.; Razdolsky, A.; Kazachenko, V.; Strakhova, N.; Grigorev, V. Memory Effect in the Spatial Series Based on Diamond and Graphite Crystals. Molecules 2020, 25, 5387. https://doi.org/10.3390/molecules25225387
Grigoreva L, Razdolsky A, Kazachenko V, Strakhova N, Grigorev V. Memory Effect in the Spatial Series Based on Diamond and Graphite Crystals. Molecules. 2020; 25(22):5387. https://doi.org/10.3390/molecules25225387
Chicago/Turabian StyleGrigoreva, Ludmila, Alexander Razdolsky, Vladimir Kazachenko, Nadezhda Strakhova, and Veniamin Grigorev. 2020. "Memory Effect in the Spatial Series Based on Diamond and Graphite Crystals" Molecules 25, no. 22: 5387. https://doi.org/10.3390/molecules25225387






