Proton Dynamics in Palladium–Silver: An Inelastic Neutron Scattering Investigation
Abstract
:1. Introduction
2. Data Analysis and Results
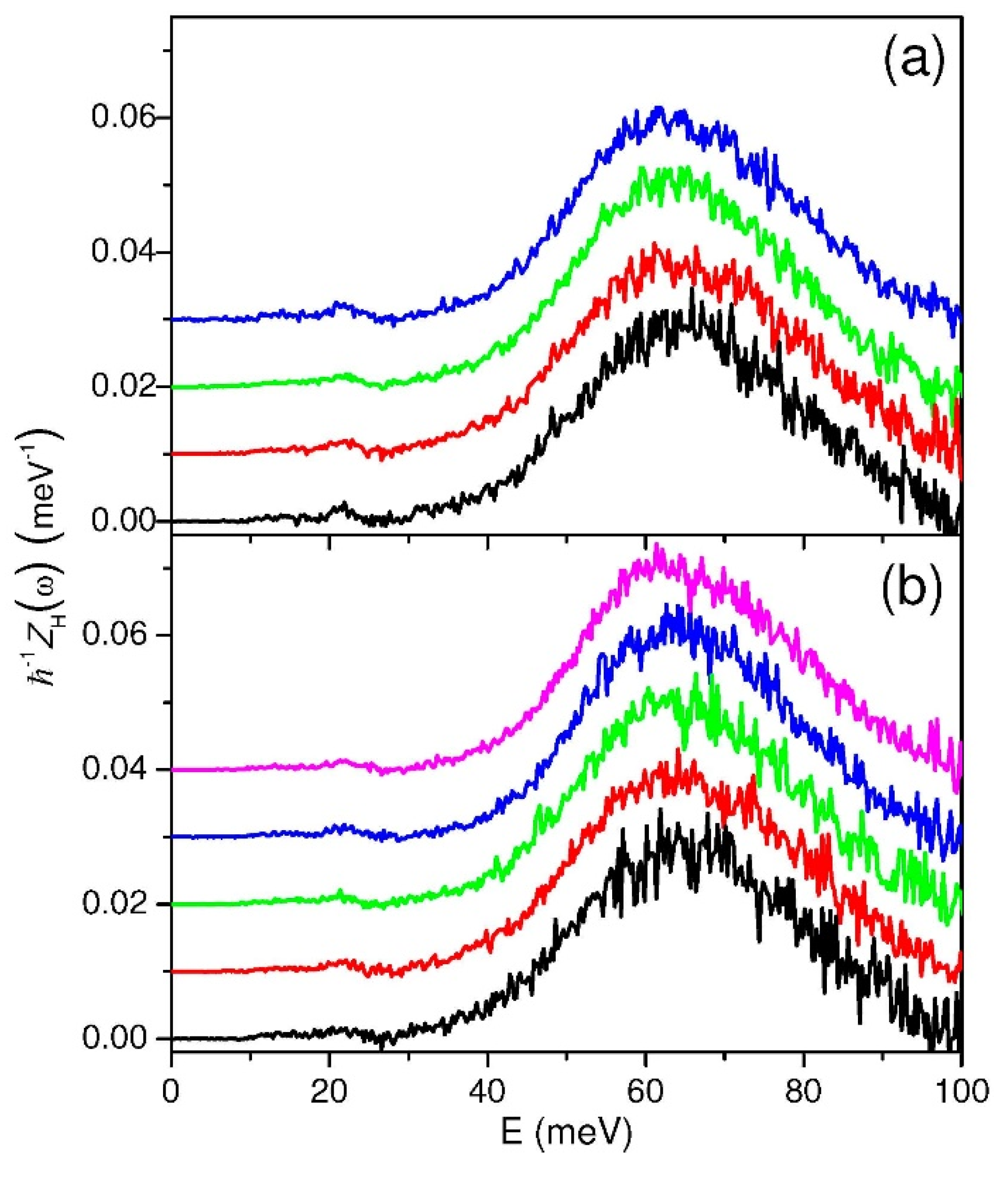
2.1. Incoherent Inelastic Neutron Scattering
- (i).
- fast neutron background evaluation and removal;
- (ii).
- container and Pd-Ag alloy scattering subtraction (after considering the neutron beam attenuation by H);
- (iii).
- sample self-shielding and multiple scattering evaluation and correction.
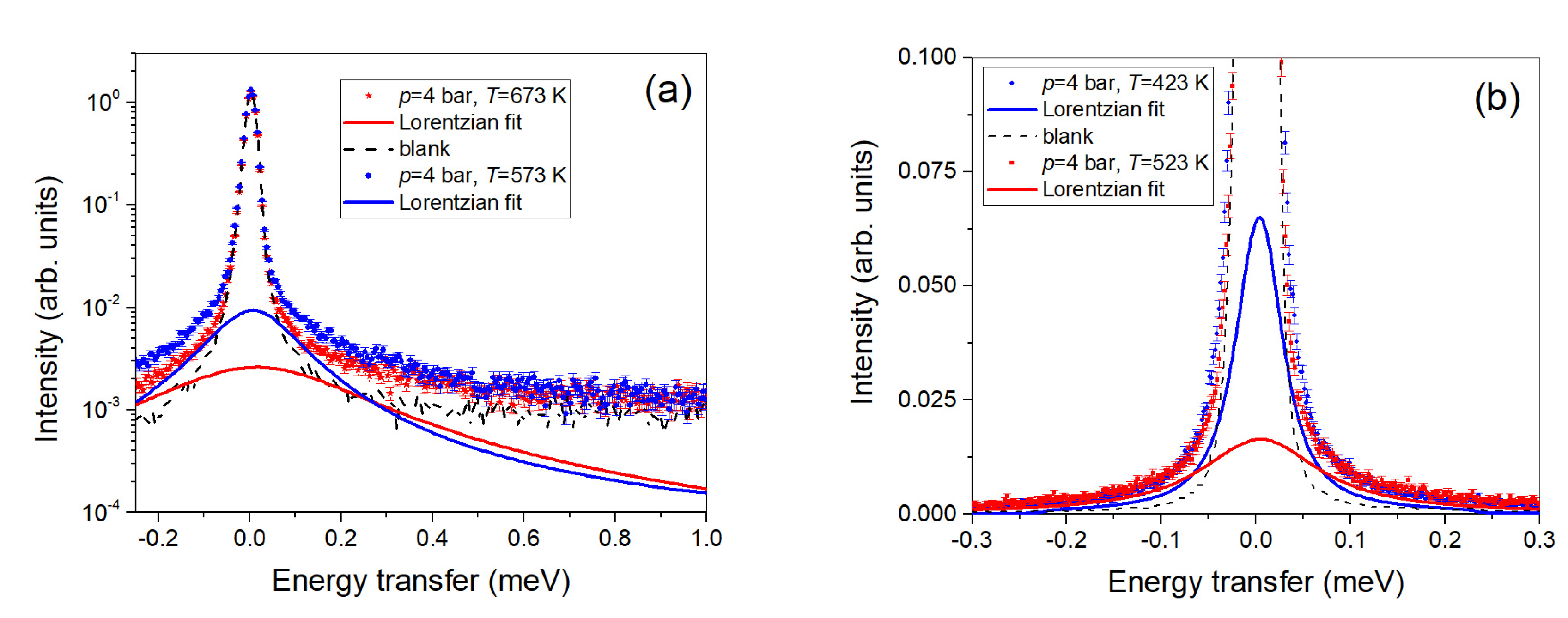
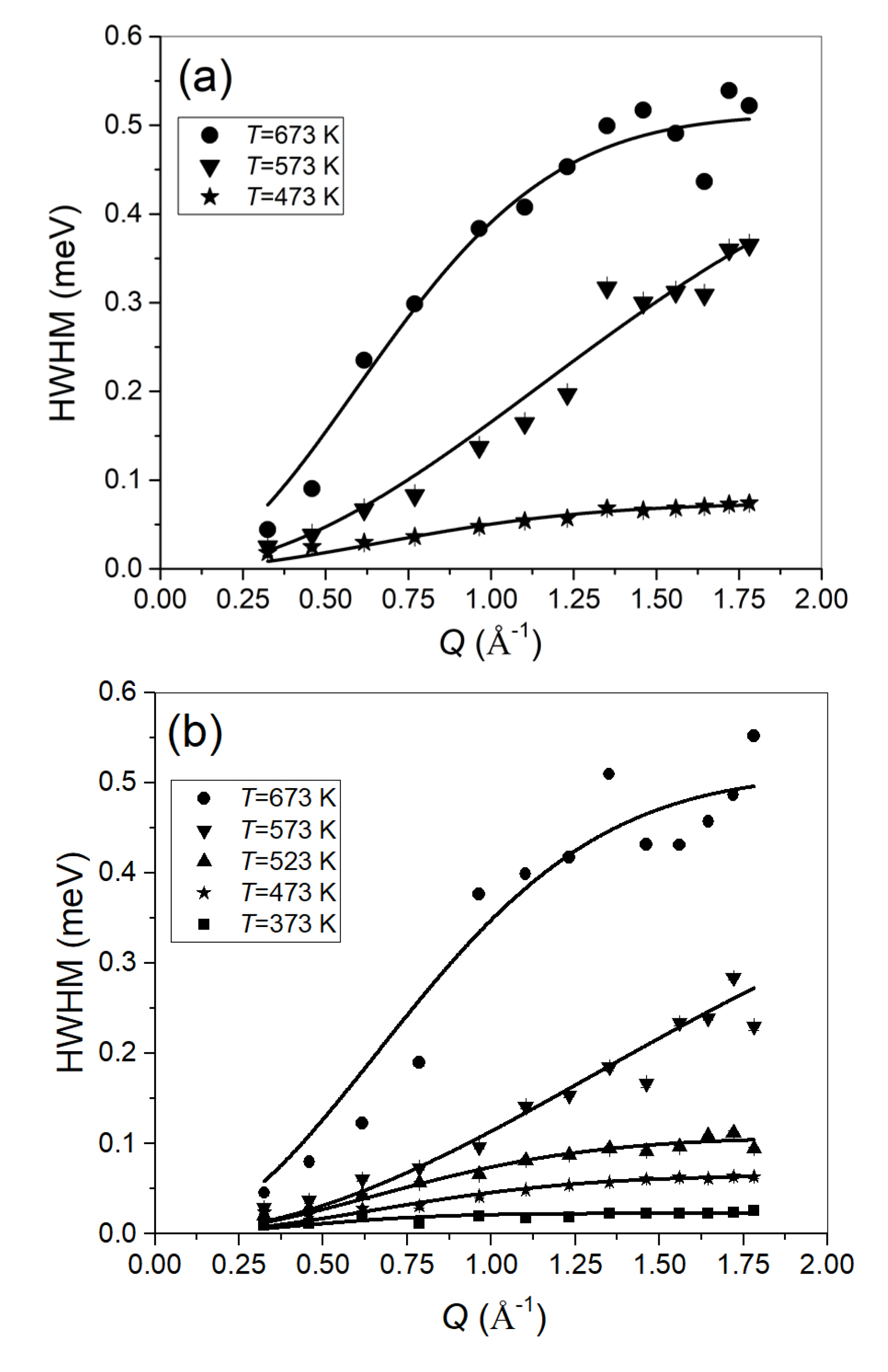
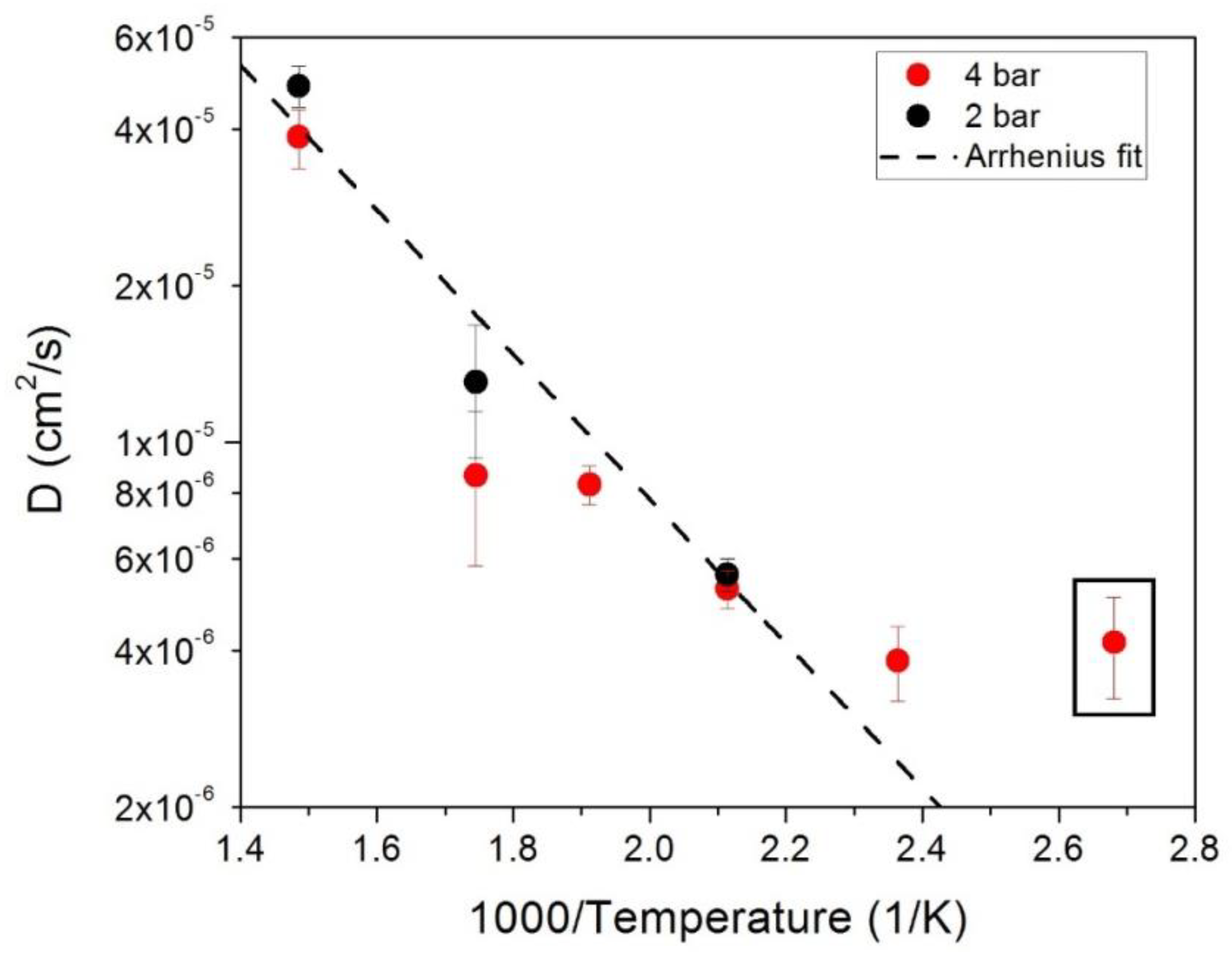
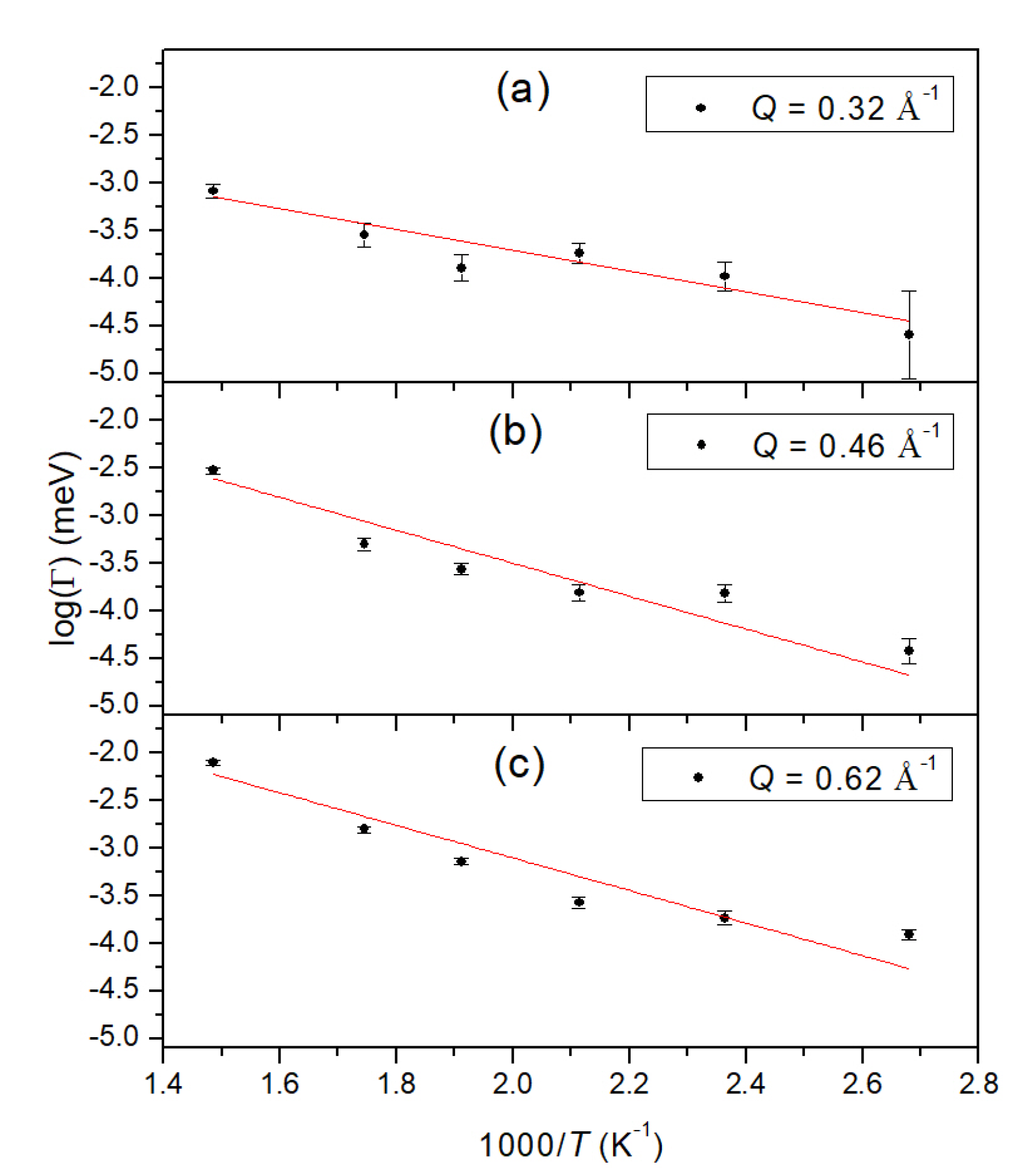
2.2. Quasi-Elastic Neutron Scattering
2.3. Deep Inelastic Neutron Scattering
2.4. Energy-Resolved Neutron Transmission
3. Experimental Procedure
- 1.
- Blank: sample cell containing unloaded Pd0.77Ag0.23 at the chosen temperature, T0;
- 2.
- Gas filling: keeping T0 constant, hydrogen gas (from CK Special Gases, 99.99% assay) is fed into the cell at the chosen pressure, p0;
- 3.
- Neutron measurements: along an isobaric line p0, data are recorded by decreasing the temperature, i.e., from the lowest to the highest H loading, in order to avoid hysteretic effects. Before starting the measurement at the chosen temperature, we wait for the system stabilization for about 1 h.
- 4.
- Hydrogen discharging: the sample is heated up to 600–700 K and H is pumped out under dynamic vacuum for about 1 h.
3.1. Incoherent Inelastic Neutron Scattering on MARI
Experimental Setup
3.2. Quasi-Elastic Neutron Scattering on OSIRIS
Experimental Setup
3.3. Deep Inelastic Neutron Scattering and Neutron Transmission on VESUVIO
Experimental Setup
4. Discussion
4.1. Incoherent Inelastic Neutron Scattering on MARI
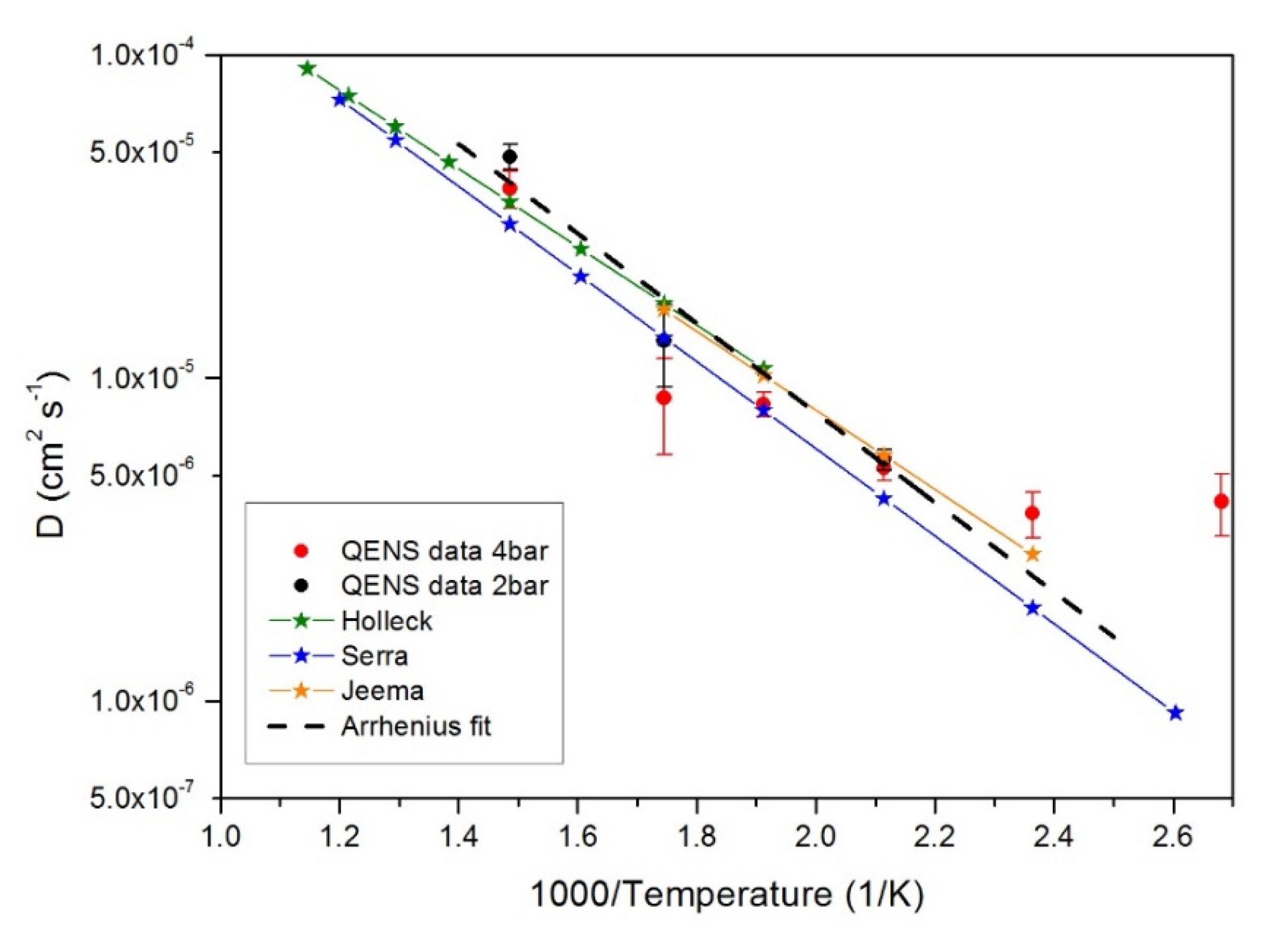
4.2. Quasi-Elastic Neutron Scattering on OSIRIS
4.3. Deep Inelastic Neutron Scattering and Neutron Transmission on VESUVIO
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- David, O.C.; Gorri, D.; Nijmeijer, K.; Ortiz, I.; Urtiaga, A. Hydrogen separation from multicomponent gas mixtures containing CO, N2 and CO2 using Matrimid® asymmetric hollow fiber membranes. J. Membr. Sci. 2012, 419–420, 49–56. [Google Scholar] [CrossRef]
- Lee, S.M.; Xu, N.; Kim, S.S.; Li, A.; Grace, J.R.; Lim, C.J.; Boyd, T.; Ryi, S.-K.; Susdorf, A.; Schaadt, A. Palladium/ruthenium composite membrane for hydrogen separation from the off-gas of solar cell production via chemical vapor deposition. J. Membr. Sci. 2017, 541, 1–8. [Google Scholar] [CrossRef]
- Acha, E.; Requies, J.M.; Barrio, V.; Cambra, J.F.; Güemez, M.; Arias, P.L.; Van Delft, Y. PdCu membrane applied to hydrogen production from methane. J. Membr. Sci. 2012, 415, 66–74. [Google Scholar] [CrossRef]
- Sołowski, G.; Shalaby, M.S.; Abdallah, H.; Shaban, A.M.; Cenian, A. Production of hydrogen from biomass and its separation using membrane technology. Renew. Sustain. Energy Rev. 2018, 82, 3152–3167. [Google Scholar]
- Zheng, H.; Zhu, L.; He, D.; Guo, T.; Li, X.; Chang, X.; Xueb, Q. Two-dimensional graphene oxide membrane for H2/CH4 separation: Insights from molecular dynamics simulations. Int. J. Hydrog. Energy 2017, 42, 30653–30660. [Google Scholar] [CrossRef]
- Zeng, G.; Goldbach, A.; Shi, L.; Xu, H. On alloying and low-temperature stability of thin, supported PdAg membranes. Int. J. Hydrogen Energy 2012, 37, 6012–6019. [Google Scholar] [CrossRef]
- Ribeiro, A.M.; Grande, C.A.; Lopes, F.V.; Loureiro, J.M.; Rodrigues, A.E. A parametric study of layered bed PSA for hydrogen purification. Chem. Eng. Sci. 2008, 63, 5258–5273. [Google Scholar] [CrossRef]
- Huang, Q.; Malekian, A.; Eić, M. Optimization of PSA process for producing enriched hydrogen from plasma reactor gas. Sep. Purif. Technol. 2008, 62, 22–31. [Google Scholar] [CrossRef]
- Atsonios, K.; Panopoulos, K.; Doukelis, A.; Koumanakos, A.; Kakaras, E. Cryogenic method for H2 and CH4 recovery from a rich CO2 stream in pre-combustion carbon capture and storage schemes. Energy 2013, 53, 106–113. [Google Scholar] [CrossRef]
- Ana, G.; Cristescu, I.; Draghia, M.; Bucur, C.; Balteanu, O.; Vijulie, M.; Popescu, G.; Costeanu, C.; Sofilca, N.; Stefan, I.; et al. Construction and commissioning of a hydrogen cryogenic distillation system for tritium recovery at ICIT Rm. Valcea. Fusion Eng. Des. 2016, 106, 51–55. [Google Scholar] [CrossRef]
- Yun, S.; Ted Oyama, S. Correlations in palladium membranes for hydrogen separation: A Review. J. Membr. Sci. 2011, 375, 28–45. [Google Scholar] [CrossRef]
- Liemberger, W.; Groß, M.; Miltner, M.; Harasek, M. Experimental analysis of membrane and pressure swing adsorption (PSA) for the hydrogen separation from natural gas. J. Clean. Prod. 2017, 167, 896–907. [Google Scholar] [CrossRef]
- Al-Mufachi, N.; Rees, N.; Steinberger-Wilkens, R. Hydrogen selective membranes: A review of palladium-based dense metal membranes. Renew. Sustain. Energy Rev. 2015, 47, 540–551. [Google Scholar] [CrossRef]
- Federici, G.; Bachmann, C.; Barucca, L.; Biel, W.; Boccaccini, L.; Brown, R.; Bustreo, C.; Ciattaglia, S.; Cismondi, F.; Coleman, M.; et al. DEMO design activity in Europe: Progress and updates. Fusion Eng. Des. 2018, 136, 729–741. [Google Scholar] [CrossRef]
- Okazaki, J.; Tanaka, D.A.P.; Tanco, M.A.L.; Wakui, Y.; Mizukami, F.; Suzuki, T.M. Hydrogen permeability study of the thin Pd-Ag alloy membranes in the temperature range across the α-β phase transition. J. Membr. Sci. 2006, 282, 370–374. [Google Scholar] [CrossRef]
- Darling, A.S. Thermal and electrolytic palladium alloy diffusion cells. Platinum. Met. Rev. 1963, 7, 126–129. [Google Scholar]
- Tosti, S.; Borgognoni, F.; Santucci, A. Electrical resistivity, strain, and permeability of Pd-Ag membrane tubes. Int. J. Hydrog. Energy 2010, 35, 7796–7802. [Google Scholar] [CrossRef]
- McNicholl, R.A.; Lewis, F.A. Hydrogen contents and electrical resistivities of palladium-silver alloys. Int. J. Altern. Energy Ecol. 2004, 3, 32–33. [Google Scholar]
- Carson, A.W.; Lewis, F.A.; Schurter, W.H. Relationships between the hydrogen content and electrical resistance of palladium + silver alloys. Trans. Faraday Soc. 1967, 63, 1447–1452. [Google Scholar] [CrossRef]
- Tóth, J.; Garaguly, J.; Péter, L.; Tompa, K. Resistivity changes during hydrogenation of Pd80Ag20 alloy in non-equilibrium circumstances. J. Alloy. Compd. 2000, 312, 117–120. [Google Scholar] [CrossRef]
- Pozio, A.; Jovanovic, Z.; Presti, R.L.; De Francesco, M.; Tosti, S. Pd-Ag hydrogen content and electrical resistivity: Temperature and pressure effect. Int. J. Hydrog. Energy 2012, 37, 7925–7933. [Google Scholar] [CrossRef]
- Jovanovic, Z.; De Francesco, M.; Tosti, S.; Pozio, A. Structural modification of PdAg alloy induced by electrolytic hydrogen absorption. Int. J. Hydrogen Energy 2011, 36, 7728–7736. [Google Scholar] [CrossRef]
- Jovanovic, Z.; De Francesco, M.; Tosti, S.; Pozio, A. Influence of surface activation on the hydrogen permeation properties of PdAg cathode membrane. Int. J. Hydrogen Energy 2011, 36, 15364–15371. [Google Scholar] [CrossRef]
- Lai, T.; Lind, M.L. Heat treatment driven surface segregation in Pd77Ag23 membranes and the effect on hydrogen permeability. Int. J. Hydrogen Energy 2015, 40, 373–382. [Google Scholar] [CrossRef]
- Fukai, Y. The Metal-Hydrogen System, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Karakaya, I.; Thompson, W. The Ag-Pd (Silver-Palladium) system. Bull. All. Ph. Diagr. 1988, 9, 237–242. [Google Scholar] [CrossRef]
- Chowdhury, M.R.; Ross, D.K. A neutron scattering study of the vibrational modes of hydrogen in the β-phases of Pd-H, Pd-10Ag-H and Pd-20Ag-H. Solid State Commun. 1973, 13, 229–234. [Google Scholar] [CrossRef]
- Chowdhury, M.R. Band modes of hydrogen in Pd-10AgH and Pd-20AgH by inelastic neutron scattering. J. Phys. F Metal Phys. 1974, 4, 1657–1664. [Google Scholar] [CrossRef]
- Fratzl, P.; Blaschko, O.; Walker, E. Lattice dynamics and phonon line shapes of Pd0.9Ag0.1D0.61 at 100 K. Phys. Rev. B 1986, 34, 164–168. [Google Scholar] [CrossRef]
- Kolesnikov, A.I.; Antonov, V.E.; Eckold, G.; Prager, M.; Tomkinson, J. Inelastic neutron scattering study of the ordered Pd-Ag-H hydrides. J. Phys. Condens. Matter 1993, 5, 7075–7086. [Google Scholar] [CrossRef]
- Catti, M.; Fabelo, O.; Filabozzi, A.; Pietropaolo, A.; Tosti, S.; Pozio, A.; Santucci, A. Neutron diffraction study of the Pd0.772Ag0.228Dν membrane for hydrogen separation. Int. J. Hydrog. Energy 2017, 42, 6787–6792. [Google Scholar] [CrossRef]
- Catti, M.; Fabelo, O.; Filabozzi, A.; Pietropaolo, A.; Santucci, A.; Tosti, S. Kinetics of deuteration of the Pd0.772Ag0.228 alloy with α/β phase transition by in-situ neutron diffraction. J. All. Comp. 2019, 790, 502–508. [Google Scholar] [CrossRef]
- Cai, Y.-Y.; Collins, S.S.E.; Gallagher, M.J.; Bhattacharjee, U.; Zhang, R.; Chow, T.H.; Ahmadivand, A.; Ostovar, B.; Al-Zubeidi, A.; Wang, J.; et al. Single-Particle Emission Spectroscopy Resolves d-Hole Relaxation in Copper Nanocubes. ACS Energy Lett. 2019, 4, 2458–2465. [Google Scholar] [CrossRef]
- Bée, M. Quasi-elastic Neutron Scattering Principles and Application in Solid State. In Chemistry, Biology and Material Science; Adam Hilger: Bristol, UK, 1988. [Google Scholar]
- Mitchell, P.C.H.; Parker, S.F.; Ramirez-Cuesta, A.J.; Tomkinson, J. Vibrational Spectroscopy with Neutrons. With Applications in Chemistry, Biology, Materials Science and Catalysis; World Scientific: Singapore, 2005. [Google Scholar]
- Lovesey, S.W. Theory of Neutron Scattering from Condensed Matter; Oxford University Press: Oxford, UK, 1987; Volume 1. [Google Scholar]
- Sears, V.F. Slow-neutron multiple scattering. Adv. Phys. 1975, 24, 1–45. [Google Scholar] [CrossRef]
- Arnold, O.; Bilheux, J.; Borreguero, J.; Buts, A.; Campbell, S.; Chapon, L.C.; Doucet, M.E.; Draper, N.R.; Leal, R.F.; Gigg, M.; et al. Mantid—Data analysis and visualization package for neutron scattering and μSR experiments. Nucl. Instr. Meth. A 2014, 764, 156–166. [Google Scholar] [CrossRef] [Green Version]
- Sköld, K. Diffusion of Hydrogen in Metals. In Hydrogen in Metals I; Alefeld, G., Volkl, J., Eds.; Springer: Berlin, Germany, 1978. [Google Scholar]
- Sköld, K.; Nelin, G. Diffusion of hydrogen in the α-phase of Pd-H studied by small energy transfer neutron scattering. J. Phys. Chem. Sol. 1967, 28, 2369–2380. [Google Scholar] [CrossRef]
- Rowe, J.M.; Rush, J.J.; De Graaf, L.A.; Ferguson, G.A. Neutron Quasielastic Scattering Study of Hydrogen Diffusion in a Single Crystal of Palladium. Phys. Rev. Lett. 1972, 29, 1250–1253. [Google Scholar] [CrossRef]
- Hall, P.L.; Ross, D. Incoherent neutron scattering function for molecular diffusion in lamellar systems. Mol. Phys. 1978, 36, 1549–1554. [Google Scholar] [CrossRef]
- Hall, P.L.; Ross, D. Incoherent neutron scattering functions for random jump diffusion in bounded and infinite media. Mol. Phys. 1981, 42, 673–682. [Google Scholar] [CrossRef]
- Jobic, H.; Theodorou, D.N. Quasi-elastic neutron scattering and molecular dynamics simulation as complementary techniques for studying diffusion in zeolites. Microporous Mesoporous Mater. 2007, 102, 21–50. [Google Scholar] [CrossRef]
- Kofu, M.; Hashimoto, N.; Akiba, H.; Kobayashi, H.; Kitagawa, H.; Tyagi, M.; Faraone, A.; Copley, J.R.D.; Lohstroh, W.; Yamamuro, O. Hydrogen diffusion in bulk and nanocrystalline palladium: A quasielastic neutron scattering study. Phys. Rev. B 2016, 94, 064303. [Google Scholar] [CrossRef] [Green Version]
- Romanelli, G.; Hewer, B.; Krzystyniak, M.; Gigg, M.; Tolchenov, R.; Mukhopadhyay, S.; Fernández-Alonso, F. Data analysis of neutron Compton scattering experiments using MANTID. J. Phys. Conf. Ser. 2018, 1055, 012016. [Google Scholar] [CrossRef]
- West, G.B. Electron scattering from atoms, nuclei and nucleons. Phys. Rep. 1975, 18, 263–323. [Google Scholar] [CrossRef]
- Andersen, K.H. Resolution function of the neutron time-of-flight spectrometer MARI. Nucl. Instr. Meth. A 1996, 371, 472–479. [Google Scholar] [CrossRef]
- Isis MARI software. Available online: https://www.isis.stfc.ac.uk/Pages/MARI-software.aspx (accessed on 25 November 2020).
- Telling, M.T.F.; Campbell, S.I.; Engberg, D.; Martin y Marero, D.; Andersen, K.H. Correction: Spectroscopic characteristics of the OSIRIS near-backscattering crystal analyzer spectrometer on the ISIS pulsed neutron source. Phys. Chem. Chem. Phys. 2016, 18, 8243. [Google Scholar] [CrossRef] [Green Version]
- Serra, E.; Kemali, M.; Perujo, A.; Ross, D.K. Hydrogen and deuterium in Pd-25 pct Ag alloy: Permeation, diffusion, solubilization, and surface reaction. Metallurg. Mater. Trans. A 1998, 29, 1023–1028. [Google Scholar] [CrossRef]
- Pietropaolo, A.; Senesi, R. Electron volt neutron spectrometers. Phys. Rep. 2011, 508, 45–90. [Google Scholar] [CrossRef] [Green Version]
- Schooneveld, E.M.; Pietropaolo, A.; Andreani, C.; Cippo, E.P.; Rhodes, N.J.; Senesi, R.; Tardocchi, M.; Gorini, G. Radiative neutron capture as a counting technique at pulsed spallation neutron sources: A review of current progress. Rep. Prog. Phys. 2016, 79, 094301. [Google Scholar] [CrossRef] [Green Version]
- Schooneveld, E.M.; Mayers, J.; Rhodes, N.J.; Pietropaolo, A.; Andreani, C.; Senesi, R.; Gorini, G.; Cippo, E.P.; Tardocchi, M. Foil cycling technique for the VESUVIO spectrometer operating in the resonance detector configuration. Rev. Sci. Instrum. 2006, 77, 095103. [Google Scholar] [CrossRef] [Green Version]
- Pietropaolo, A.; Andreani, C.; Filabozzi, A.; Pace, E.; Senesi, R. Resolution function in deep inelastic neutron scattering using the Foil Cycling Technique. Nucl. Instr. Meth. A 2007, 570, 498–510. [Google Scholar] [CrossRef] [Green Version]
- Romanelli, G.; Krzystyniak, M.; Senesi, R.; Raspino, D.; Boxall, J.; Pooley, D.; Moorby, S.; Schooneveld, E.M.; Rhodes, N.J.; Andreani, C.; et al. Characterisation of the incident beam and current diffraction capabilities on the VESUVIO spectrometer. Meas. Sci. Technol. 2017, 28, 095501. [Google Scholar] [CrossRef]
- Andreani, C.; Krzystyniak, M.; Romanelli, G.; Senesi, R.; Fernandez-Alonso, F. Electron-volt neutron spectroscopy: Beyond fundamental systems. Adv. Phys. 2017, 66, 1–73. [Google Scholar] [CrossRef]
- Rodríguez Palomino, L.A.; Dawidowski, J.; Márquez Damián, J.I.; Cuello, G.J.; Romanelli, G.; Krzystyniak, M. Neutron total cross-section of hydrogenous and deuterated 1- and 2-propanol and n-butanol measured using the VESUVIO spectrometer. Nucl. Inst. Meth. A 2017, 870, 84–89. [Google Scholar] [CrossRef] [Green Version]
- Romanelli, G.; Rudić, S.; Zanetti, M.; Andreani, C.; Fernandez-Alonso, F.; Gorini, G.; Krzystyniak, M.; Škoro, G. Measurement of the para-hydrogen concentration in the ISIS moderators using neutron transmission and thermal conductivity. Nucl. Inst. Meth. A 2018, 888, 88–95. [Google Scholar] [CrossRef] [Green Version]
- Singwi, K.S.; Tosi, M.P. Sum Rules for a Generalized Frequency Distribution Function. Phys. Rev. 1966, 149, 70–72. [Google Scholar] [CrossRef]
- Long, D.; Li, M.; Meng, D.; He, Y.; Yoon, I.T.; Ahuja, R.; Luo, W. Accounting for the thermo-stability of PdHx (x = 1-3) by density functional theory. Int. J. Hydrogen Energy 2018, 43, 18372–18381. [Google Scholar] [CrossRef]
- Holleck, G.L. Diffusion and solubility of hydrogen in palladium and palladium-silver alloys. J. Phys. Chem. 1970, 74, 503–511. [Google Scholar] [CrossRef]
- Jemaa, N.; Grandjean, B.P.A.; Kaliaguine, S. Diffusion coefficient of hydrogen in a Pd-Ag membrane: Effect of hydrogen solubility. Can. J. Chem. Eng. 1995, 73, 405–410. [Google Scholar] [CrossRef]
- Krzystyniak, M.; Romanelli, G.; Fernandez-Alonso, F. Non-destructive quantitation of hydrogen via mass-resolved neutron spectroscopy. Analyst 2019, 144, 3936–3941. [Google Scholar] [CrossRef]
- Paxton, A.T.; Katzarov, I. Quantum and isotope effects on hydrogen diffusion, trapping and escape in iron. Acta Mater. 2016, 103, 71–76. [Google Scholar] [CrossRef] [Green Version]



| No. | T (K) | p (bar) | r (%) | I.C. (μA h) |
|---|---|---|---|---|
| (1) | 453 | 0.0 | 0.0 | 600.04 |
| (2) | 373 | 0.0 | 0.0 | 600.01 |
| (3) | 333 | 0.0 | 0.0 | 554.24 |
| (4) | 453 | 1.0 | 9.2 [21] | 1112.95 |
| (5) | 413 | 1.0 | 16.1 [21] | 1295.43 |
| (6) | 373 | 1.0 | 31 [21] | 1802.51 |
| (7) | 333 | 1.0 | 34 [21] | 1362.43 |
| (8) | 453 | 2.0 | 19.8 [21] | 800.85 |
| (9) | 413 | 2.0 | 18.4 [21] | 1442.39 |
| (10) | 373 | 2.0 | 35.0 [21] | 852.24 |
| (11) | 333 | 2.0 | 41.8 [21] | 750.39 |
| (12) | 333 | 4.0 | 39.8 [31] | 1117.21 |
| Sample | T (K) | p (bar) | r (%) | I.C. (μA h) |
|---|---|---|---|---|
| S1 | 473 | 0.0 | - | 1240 |
| 573 | 2.0 | 3.3 [21] | 1730 | |
| 523 | 2.0 | 7.4 [21] | 1900 | |
| 473 | 2.0 | 18.9 [40] | 750 | |
| 423 | 2.0 | 20.3 [21] | 750 | |
| 343 | 2.0 | 37.1 [21] | 1460 | |
| S2 | 673 | 0.0 | - | 1050 |
| 673 | 2.0 | 0.4 [21] | 1800 | |
| 573 | 2.0 | 3.3 [21] | 1380 | |
| 473 | 2.0 | 18.9 [21] | 1800 | |
| S3 | 673 | 0.0 | - | 720 |
| 673 | 4.0 | 3.2 [40] | 2100 | |
| 573 | 4.0 | 7.9 [40] | 1620 | |
| 473 | 4.0 | 35.1 [40] | 1690 | |
| 373 | 4.0 | 58.4 [40] | 1500 | |
| S4 | 373 | 0.0 | 2490 | |
| 523 | 4.0 | 20.7 [40] | 1500 | |
| 423 | 4.0 | 48.3 [40] | 1620 |
| T (K) | p (bar) | <Ek>H (meV) | <u2>H (Å2) |
|---|---|---|---|
| 453 | 1.0 | 72.1± 0.9 | 0.173 ± 0.003 |
| 413 | 1.0 | 67.8 ± 0.7 | 0.171 ± 0.002 |
| 373 | 1.0 | 63.6 ± 0.5 | 0.159 ± 0.001 |
| 333 | 1.0 | 60.4 ± 0.4 | 0.145 ± 0.001 |
| 453 | 2.0 | 72.0 ± 0.9 | 0.176 ± 0.003 |
| 413 | 2.0 | 68.0 ± 0.6 | 0.160 ± 0.002 |
| 373 | 2.0 | 60.5 ± 0.6 | 0.151 ± 0.002 |
| 333 | 2.0 | 60.6 ± 0.6 | 0.139 ± 0.001 |
| 333 | 4.0 | 60.7± 0.5 | 0.138 ± 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colognesi, D.; Demmel, F.; Filabozzi, A.; Pietropaolo, A.; Pozio, A.; Romanelli, G.; Santucci, A.; Tosti, S. Proton Dynamics in Palladium–Silver: An Inelastic Neutron Scattering Investigation. Molecules 2020, 25, 5587. https://doi.org/10.3390/molecules25235587
Colognesi D, Demmel F, Filabozzi A, Pietropaolo A, Pozio A, Romanelli G, Santucci A, Tosti S. Proton Dynamics in Palladium–Silver: An Inelastic Neutron Scattering Investigation. Molecules. 2020; 25(23):5587. https://doi.org/10.3390/molecules25235587
Chicago/Turabian StyleColognesi, Daniele, Franz Demmel, Alessandra Filabozzi, Antonino Pietropaolo, Alfonso Pozio, Giovanni Romanelli, Alessia Santucci, and Silvano Tosti. 2020. "Proton Dynamics in Palladium–Silver: An Inelastic Neutron Scattering Investigation" Molecules 25, no. 23: 5587. https://doi.org/10.3390/molecules25235587
APA StyleColognesi, D., Demmel, F., Filabozzi, A., Pietropaolo, A., Pozio, A., Romanelli, G., Santucci, A., & Tosti, S. (2020). Proton Dynamics in Palladium–Silver: An Inelastic Neutron Scattering Investigation. Molecules, 25(23), 5587. https://doi.org/10.3390/molecules25235587










