Partitioning of Selected Anisole and Veratrole Derivatives between Water and Anionic Surfactant Micelles
Abstract
:1. Introduction
2. Results
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Calkin, R.R.; Jellinek, J.S. Perfumery—Practice and Principles; Wiley-Interscience: New York, NY, USA, 1994. [Google Scholar]
- Sell, C. (Ed.) The Chemistry of Fragrances, 2nd ed.; RSC: Cambridge, NA, USA, 2006. [Google Scholar]
- Herman, S. Fragrance in emulsions and surfactant systems. Cosmet. Toilet. 2006, 121, 59–67. [Google Scholar]
- Aikens, P.; Friberg, S.E. Organised assemblies of cosmetics and transdermal drug delivery. Curr. Opin. Coll. Interface Sci. 1996, 1, 672–676. [Google Scholar] [CrossRef]
- Sikora, E.; Małgorzata, M.; Wolińska-Kennard, K.; Lasoń, E. Nanoemulsions as a Form of Perfumery Products. Cosmetics 2018, 5, 63. [Google Scholar] [CrossRef] [Green Version]
- Rao, J.; McClements, D.J. Lemon oil solubilization in mixed surfactant solutions: Rationalizing microemulsion & nanoemulsion formation. Food Hydrocoll. 2012, 26, 268–276. [Google Scholar] [CrossRef]
- Rosen, J.M. Surfactants and Interfacial Phenomena, 3rd ed.; Wiley Interscience: New York, NY, USA, 2004. [Google Scholar]
- Fan, Y.; Tang, H.; Strand, R.; Wang, Y. Modulation of partition and localization of perfume molecules in sodium dodecyl sulfate micelles. Soft Matter 2016, 12, 219–227. [Google Scholar] [CrossRef] [PubMed]
- Vinarov, Z.; Katev, V.; Radeva, D.; Tcholakova, S.; Denkov, N.D. Micellar solubilization of poorly water-soluble drugs: Effect of surfactant and solubilizate molecular structure. Drug Dev. Ind. Pharm. 2018, 44, 677–686. [Google Scholar] [CrossRef] [PubMed]
- Penfold, J.; Tucker, I.; Green, A.; Grainger, D.; Jones, C.; Ford, G.; Roberts, C.; Hubbard, J.; Petkov, J.; Thomas, R.K.; et al. Impact of Model Perfumes on Surfactant and Mixed Surfactant Self-Assembly. Langmuir 2008, 24, 12209–12220. [Google Scholar] [CrossRef]
- Fieber, W.; Frank, S.; Herrero, C. Competition between surfactants and apolar fragrances in micelle cores. Colloids Surfaces A Physicochem. Eng. Asp. 2018, 539, 310–318. [Google Scholar] [CrossRef]
- Tang, X.; Zou, W.; Koenig, P.H.; Mcconaughy, S.D.; Weaver, M.R.; Eike, D.M.; Schmidt, M.J.; Larson, R.G. Multiscale Modeling of the Effects of Salt and Perfume Raw Materials on the Rheological Properties of Commercial Threadlike Micellar Solutions. J. Phys. Chem. B 2017, 121, 2468–2485. [Google Scholar] [CrossRef]
- Alizadeh, M.N.; Shayanfar, A.; Jouyban, A. Solubilization of drugs using sodium lauryl sulfate: Experimental data and modeling. J. Mol. Liq. 2018, 268, 410–414. [Google Scholar] [CrossRef]
- Schramm, L.L.; Stasiuk, E.N.; Marangoni, D.G. Surfactants and their applications. Annu. Rep. Prog. Chem. Sect. C 2003, 99, 3–48. [Google Scholar] [CrossRef]
- Martin, K.; Hellsten, E.; Klingberg, A.W.; Karlsson, B.T.G. Liquid detergents from cationic, anionic and nonionic surfactants. adsorption, detergency and antistatic properties. J. Am. Oil Chem. Soc. 1989, 66, 1381–1385. [Google Scholar] [CrossRef]
- Singh, A.; Sharma, P.; Bansal, S.; Sharma, P. Comparative interaction study of amylase and surfactants for potential detergent formulation. J. Mol. Liq. 2018, 261, 397–401. [Google Scholar] [CrossRef]
- Caracciolo, A.B.; Cardoni, M.; Pescatore, T.; Patrolecco, L. Characteristics and environmental fate of the anionic surfactant sodium lauryl ether sulphate (SLES) used as the main component in foaming agents for mechanized tunnelling. Environ. Pollut. 2017, 226, 94–103. [Google Scholar] [CrossRef]
- Al-Soufi, W.; Piñeiro, L.; Novo, M. A model for monomer and micellar concentrations in surfactant solutions: Application to conductivity, NMR, diffusion, and surface tension data. J. Colloid Interface Sci. 2012, 370, 102–110. [Google Scholar] [CrossRef]
- Piñeiro, L.; Freire, S.; Bordello, J.; Novo, M.; Al-Soufi, W. Dye exchange in micellar solutions. Quantitative analysis of bulk and single molecule fluorescence titrations. Soft Matter 2013, 9, 10779–10790. [Google Scholar] [CrossRef]
- Demissie, H.; Duraisamy, R. Effects of electrolytes on the surface and micellar characteristics of sodium dodecyl sulphate surfactant solution. J. Sci. Innov. Res. 2016, 5, 208–214. [Google Scholar]
- Kaur, R.; Rani, A.; Banipal, P.K.; Banipal, T.S. Study on interactions of vitamin B1 with sodium dodecyl sulfate for potential food applications: Conductometric, volumetric, calorimetric and spectroscopic approach. J. Mol. Liq. 2019, 285, 616–625. [Google Scholar] [CrossRef]
- Naderi, O.; Sadeghi, R. Soluting effect of amino acids on 1 decyl 3 methylimidazolium bromide and 1 dodecyl 3 methylimidazolium bromide as cationic surfactants and sodium dodecyl sulfate as anionic surfactant in aqueous solutions. J. Mol. Liq. 2019, 275, 616–628. [Google Scholar] [CrossRef]
- Shirzad, S.; Sadeghi, R. Efects of addition of short chain alcohol solvents on micellization and thermodynamic properties of anionic surfactants sodium dodecyl sulfate and sodium dodecyl sulfonate in aqueous solutions. J. Iran. Chem. Soc. 2018, 15, 1365–1375. [Google Scholar] [CrossRef]
- Chauhan, G.S.; Kumar, K.; Singh, K.; Jyoti, J. Volumetric, Compressibility, and Surface Tension Studies on Micellization Behavior of SDS in Aqueous Medium: Effect of Sugars. J. Surfactants Deterg. 2013, 17, 169–175. [Google Scholar] [CrossRef]
- Niraula, T.P.; Shah, S.K.; Chatterjee, S.K.; Bhattarai, A. Effect of methanol on the surface tension and viscosity of sodiumdodecyl sulfate (SDS) in aqueous medium at 298.15–323.15 K. Karbala Int. J. Mod. Sci. 2018, 4, 26–34. [Google Scholar] [CrossRef]
- Vleugels, L.F.W.; Pollet, J.; Tuinier, R. Polycation–Sodium Lauryl Ether Sulfate-Type Surfactant Complexes: Influence of Ethylene Oxide Length. J. Phys. Chem. B 2015, 119, 6338–6347. [Google Scholar] [CrossRef] [PubMed]
- Aoudia, M.; Al-Maamari, T.; Al-Salmi, F. Intramolecular and intermolecular ion–dipole interactions in sodium lauryl ether sulfates (SLES) self-aggregation and mixed micellization with Triton X-100. Colloids Surfaces A Physicochem. Eng. Asp. 2009, 335, 55–61. [Google Scholar] [CrossRef]
- Petrović, L.B.; Milinković, J.; Fraj, J.; Bučko, S.Đ.; Katona, J.; Spasojević, L. Study of interaction between chitosan and sodium lauryl ether sulfate. Colloid Polym. Sci. 2017, 295, 2279–2285. [Google Scholar] [CrossRef]
- Fischer, E.; Fieber, W.; Navarro, C.; Sommer, H.; Benczédi, D.; Velazco, M.I.; Schönhoff, M. Partitioning and Localization of Fragrances in Surfactant Mixed Micelles. J. Surfactants Deterg. 2008, 12, 73–84. [Google Scholar] [CrossRef]
- Tokuoka, Y.; Uchiyama, H.; Abe, M.; Ogino, K. Solubilization of synthetic perfumes by nonionic surfactants. J. Colloid Interface Sci. 1992, 152, 402–409. [Google Scholar] [CrossRef]
- Normand, V.; Tang, J.; Struillou, A. Modelling perfume deposition on fabric during a washing cycle: Theoretical approach. Flavour Fragr. J. 2008, 23, 49–57. [Google Scholar] [CrossRef]
- Kim, S.; Chen, J.; Cheng, T.; Gindulyte, A.; He, J.; He, S.; Li, Q.; Shoemaker, B.A.; Thiessen, P.A.; Yu, B.; et al. Pubchem 2019 update: Improved access to chemical data. Nucleic Acids Res. 2019, 47, D1102–D1109. [Google Scholar] [CrossRef] [Green Version]
- VCCLAB, Virtual Computional Chemistry Laboratory. Available online: http://vcclab.org (accessed on 9 October 2020).
- Bonar-Law, R.P. Porphyrin Synthesis in Surfactant Solution: Multicomponent Assembly in Micelles. J. Org. Chem. 1996, 61, 3623–3634. [Google Scholar] [CrossRef]
- Micke, G.A.; Moraes, E.P.; Farah, J.P.; Tavares, M.F.M. Assessing the separation of neutral plant secondary metabolites by micellar electrokinetic chromatography. J. Chromatogr. A 2003, 1004, 131–143. [Google Scholar] [CrossRef]
- Aoudia, M.; Al-Haddabi, B.; Al-Harthi, Z.; Al-Rubkhi, A. Sodium Lauryl Ether Sulfate Micellization and Water Solubility Enhancement Towards Naphthalene and Pyrene: Effect of the Degree of Ethoxylation. J. Surfactants Deterg. 2009, 13, 103–111. [Google Scholar] [CrossRef]
- Schick, M.J. Nonionic Surfactants, Physical Chemistry, Surfactant Science Series; Marcel Dekker, Inc.: New York, NY, USA, 1987. [Google Scholar]
- Eini, D.E.; Barry, B.; Rhodes, C. Micellar size, shape, and hydration of long-chain polyoxyethylene nonionic surfactants. J. Colloid Interface Sci. 1976, 54, 348–351. [Google Scholar] [CrossRef]
- Desai, T.R.; Dixit, S.G. Interaction and Viscous Properties of Aqueous Solutions of Mixed Cationic and Nonionic Surfactants. J. Colloid Interface Sci. 1996, 177, 471–477. [Google Scholar] [CrossRef]
- Tyrode, E.; Johnson, C.M.; Kumpulainen, A.; Rutland, M.W.; Claesson, P.M. Hydration State of Nonionic Surfactant Monolayers at the Liquid/Vapor Interface: Structure Determination by Vibrational Sum Frequency Spectroscopy. J. Am. Chem. Soc. 2005, 127, 16848–16859. [Google Scholar] [CrossRef] [PubMed]
- Barber, V.P.; Newby, J.J. Jet-Cooled Fluorescence Spectroscopy of a Natural Product: Anethole. J. Phys. Chem. A 2013, 117, 12831–12841. [Google Scholar] [CrossRef] [PubMed]
- Jabbari, M.; Teymoori, F. An insight into effect of micelle-forming surfactants on aqueous solubilization and octanol/water partition coefficient of the drugs gemfibrozil and ibuprofen. J. Mol. Liq. 2018, 262, 1–7. [Google Scholar] [CrossRef]
- Martins, M.A.; Silva, L.P.; Ferreira, O.; Schröder, I.B.; Coutinho, J.A.; Pinho, S.P. Terpenes solubility in water and their environmental distribution. J. Mol. Liq. 2017, 241, 996–1002. [Google Scholar] [CrossRef] [Green Version]
- De Wolf, E.; Ruelle, P.; Broeke, J.V.D.; Deelman, B.-J.; Van Koten, G. Prediction of Partition Coefficients of Fluorous and Nonfluorous Solutes in Fluorous Biphasic Solvent Systems by Mobile Order and Disorder Theory. J. Phys. Chem. B 2004, 108, 1458–1466. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are not available from the authors. |
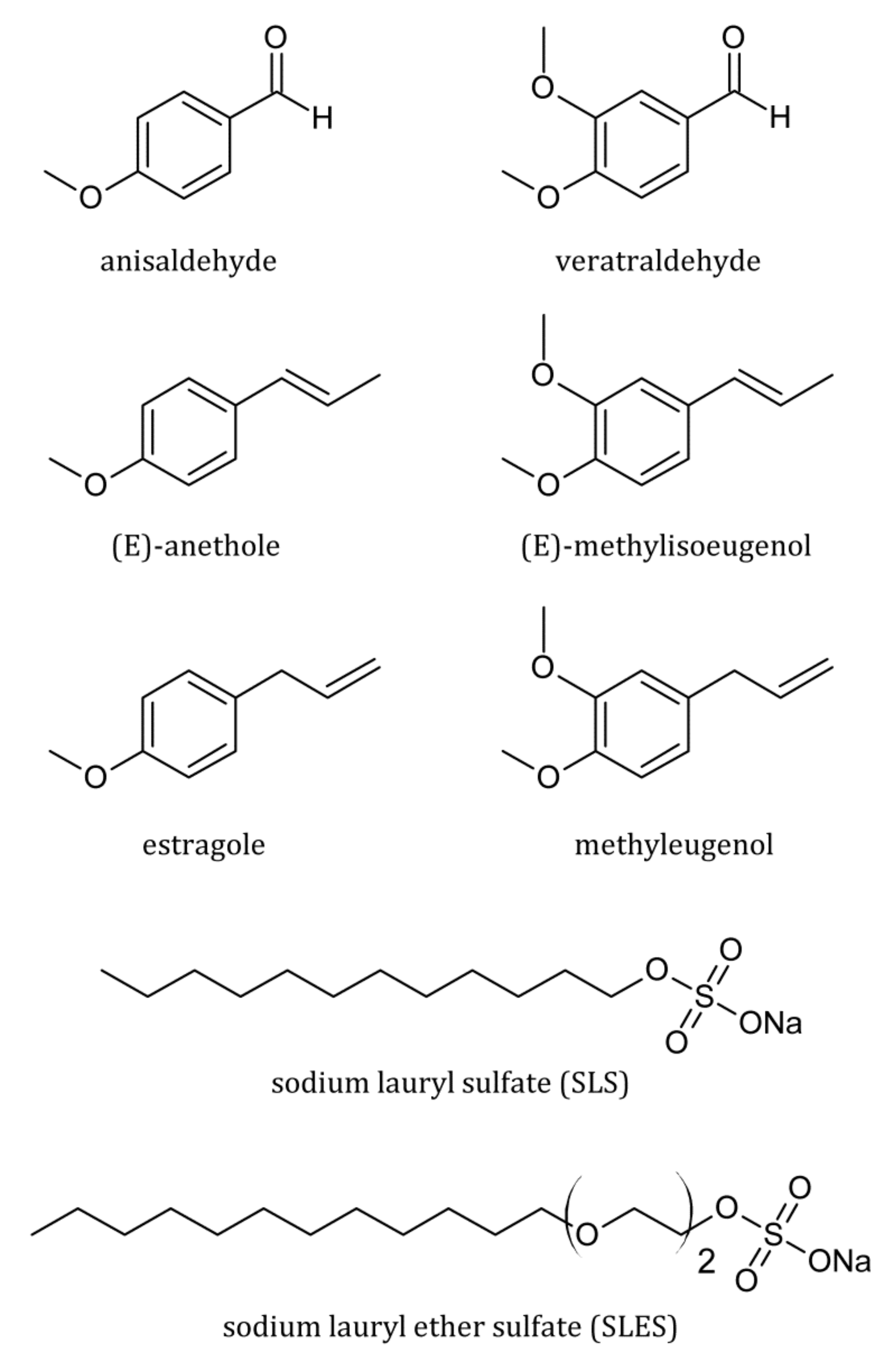
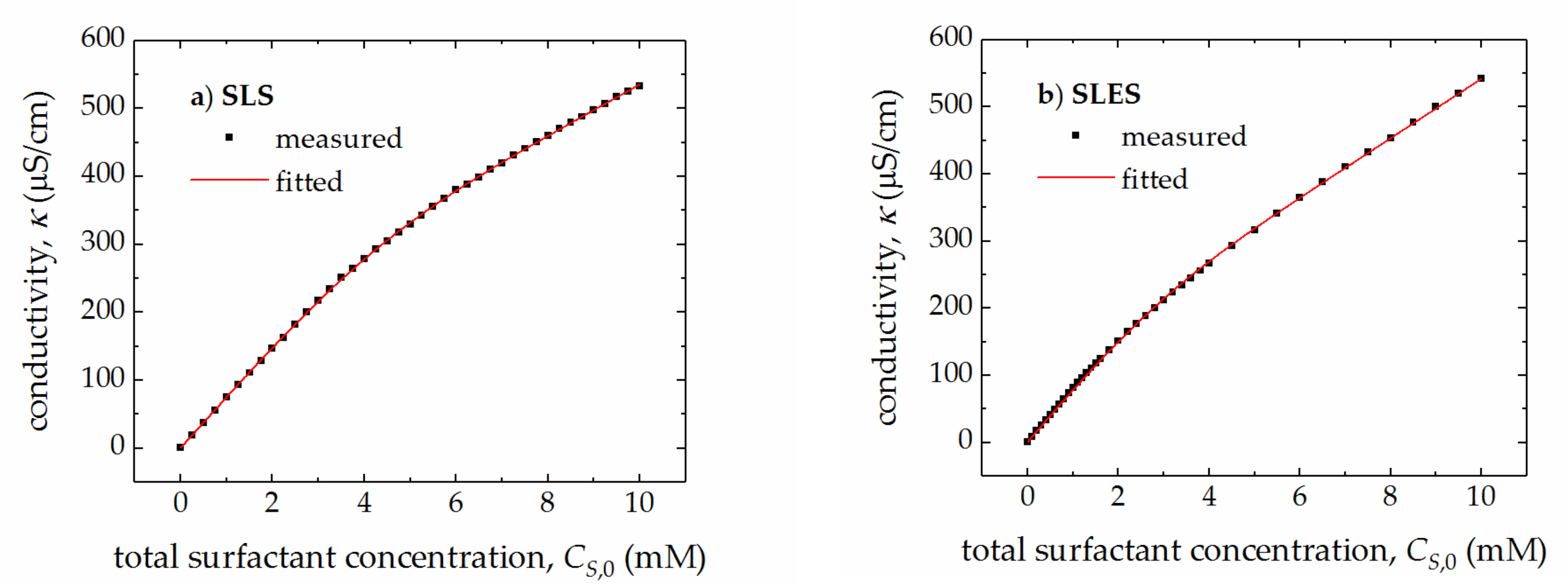
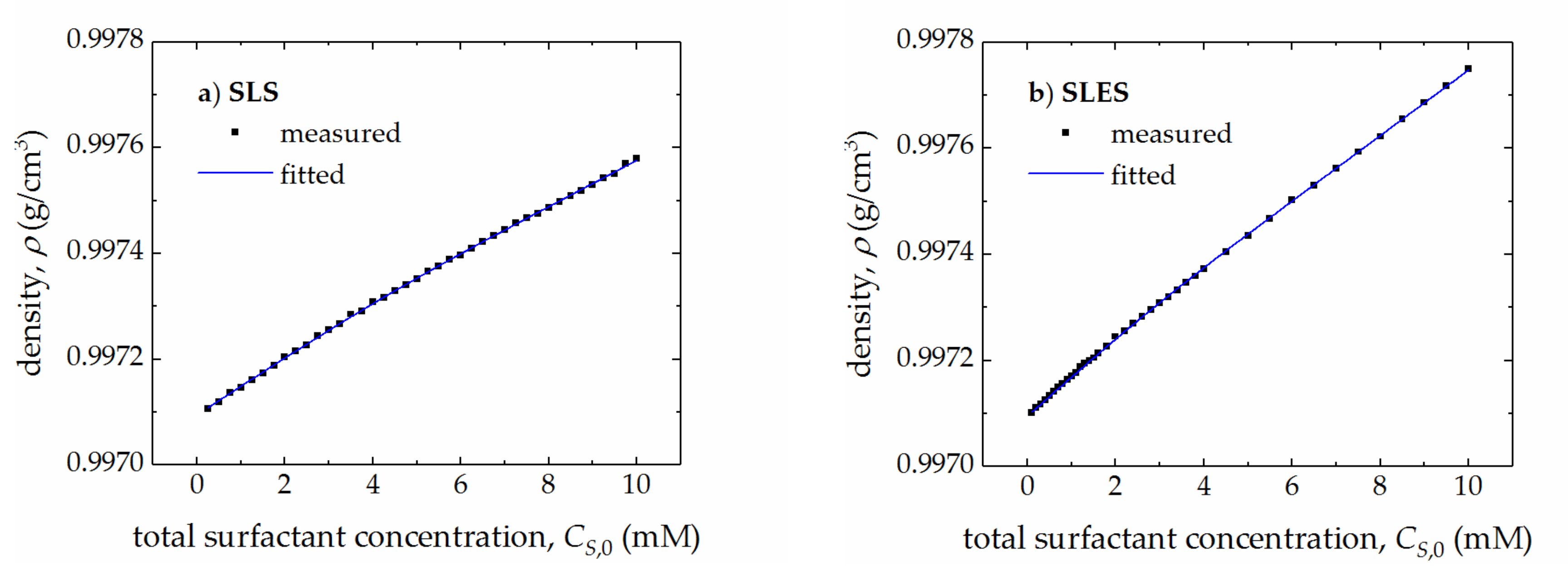

| Surfactant | CMC (mM) | r (–) | (S cm2/mol) | (S cm2/mol) | (cm3/mol) | (cm3/mol) |
|---|---|---|---|---|---|---|
| SLS | 4.17 ± 0.06 | 0.45 ± 0.02 | 75.6 ± 0.7 | 37.6 ± 0.4 | 243.5 ± 0.2 | 254.1 ± 0.2 |
| SLES | 2.74 ± 0.02 | 0.56 ± 0.03 | 80.1 ± 0.5 | 44.2 ± 0.3 | 308.2 ± 0.3 | 321.2 ± 0.2 |
| Materials | (SLS) | (SLES) | ||
|---|---|---|---|---|
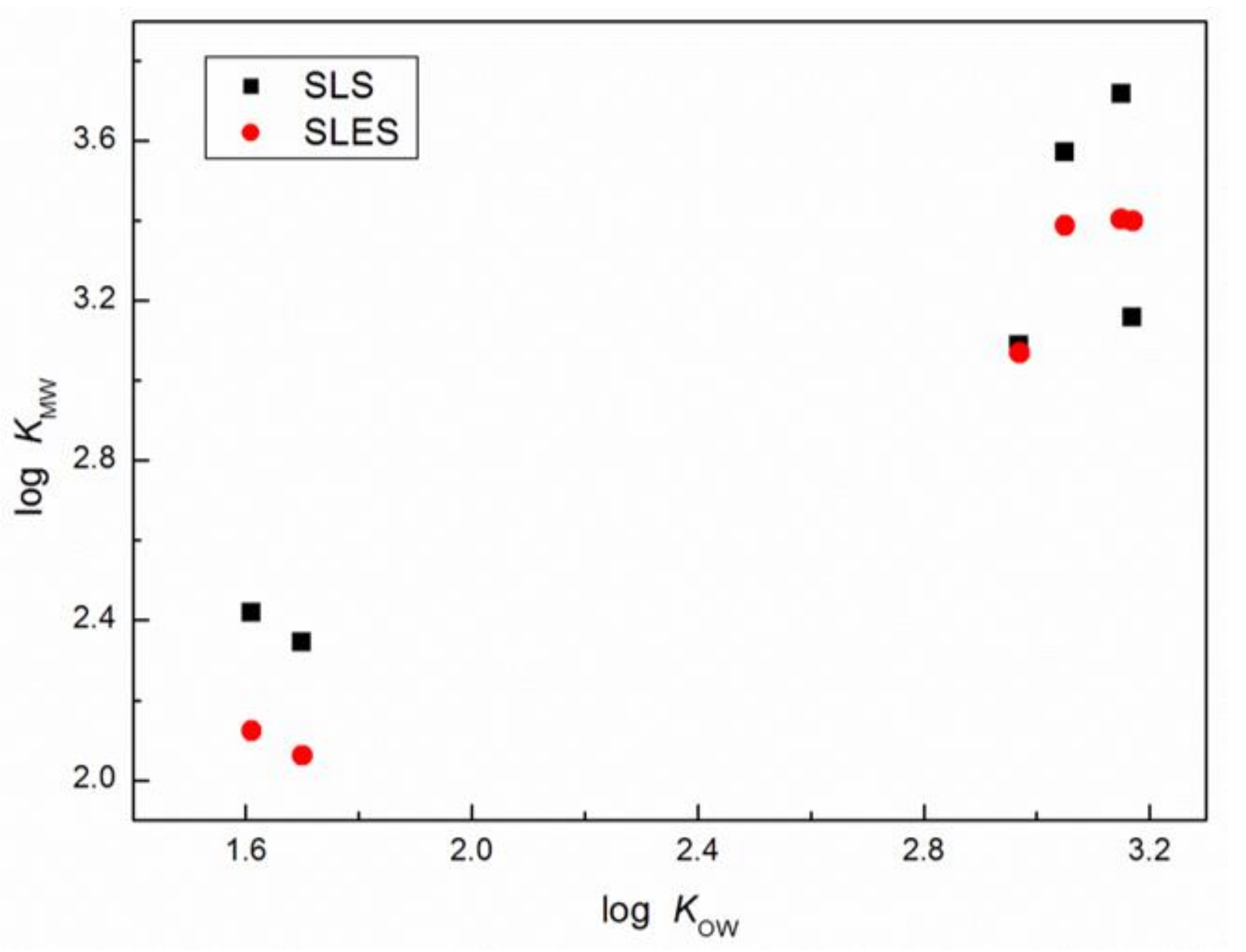
| Veratraldehyde | 2.42 ± 0.02 | 2.12 ± 0.02 | 1.61 ± 0.27 | 1.22 |
| Methyleugenol | 3.09 ± 0.06 | 3.07 ± 0.06 | 2.97 ± 0.24 | 3.03 |
| (E)-methylisoeugenol | 3.57 ± 0.07 | 3.39 ± 0.07 | 3.05 ± 0.24 | 3.47 |
| Anisaldehyde | 2.34 ± 0.02 | 2.06 ± 0.02 | 1.70 ± 0.26 | 1.76 |
| Estragole | 3.72 ± 0.05 | 3.40 ± 0.05 | 3.15 ± 0.22 | 3.47 |
| (E)-anethole | 3.16 ± 0.05 | 3.40 ± 0.04 | 3.17 ± 0.22 | 3.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lewandowski, A.; Szymczyk, K. Partitioning of Selected Anisole and Veratrole Derivatives between Water and Anionic Surfactant Micelles. Molecules 2020, 25, 5818. https://doi.org/10.3390/molecules25245818
Lewandowski A, Szymczyk K. Partitioning of Selected Anisole and Veratrole Derivatives between Water and Anionic Surfactant Micelles. Molecules. 2020; 25(24):5818. https://doi.org/10.3390/molecules25245818
Chicago/Turabian StyleLewandowski, Andrzej, and Katarzyna Szymczyk. 2020. "Partitioning of Selected Anisole and Veratrole Derivatives between Water and Anionic Surfactant Micelles" Molecules 25, no. 24: 5818. https://doi.org/10.3390/molecules25245818
APA StyleLewandowski, A., & Szymczyk, K. (2020). Partitioning of Selected Anisole and Veratrole Derivatives between Water and Anionic Surfactant Micelles. Molecules, 25(24), 5818. https://doi.org/10.3390/molecules25245818







