Computational and Experimental 1H-NMR Study of Hydrated Mg-Based Minerals
Abstract
1. Introduction
2. Results and Discussion
2.1. Model Hydroxylated and Hydrated Magnesium Compounds
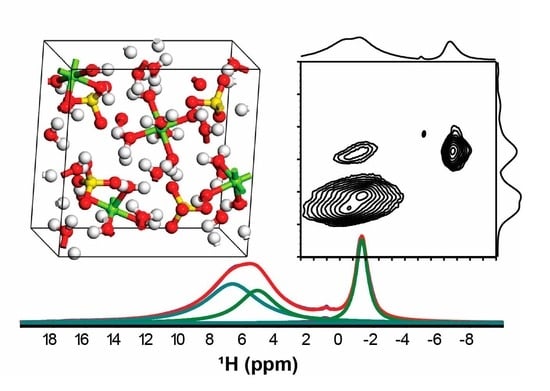
Two-Dimensional Double Quantum NMR
2.2. Computational 1H-NMR
2.2.1. Chemical Shift Referencing
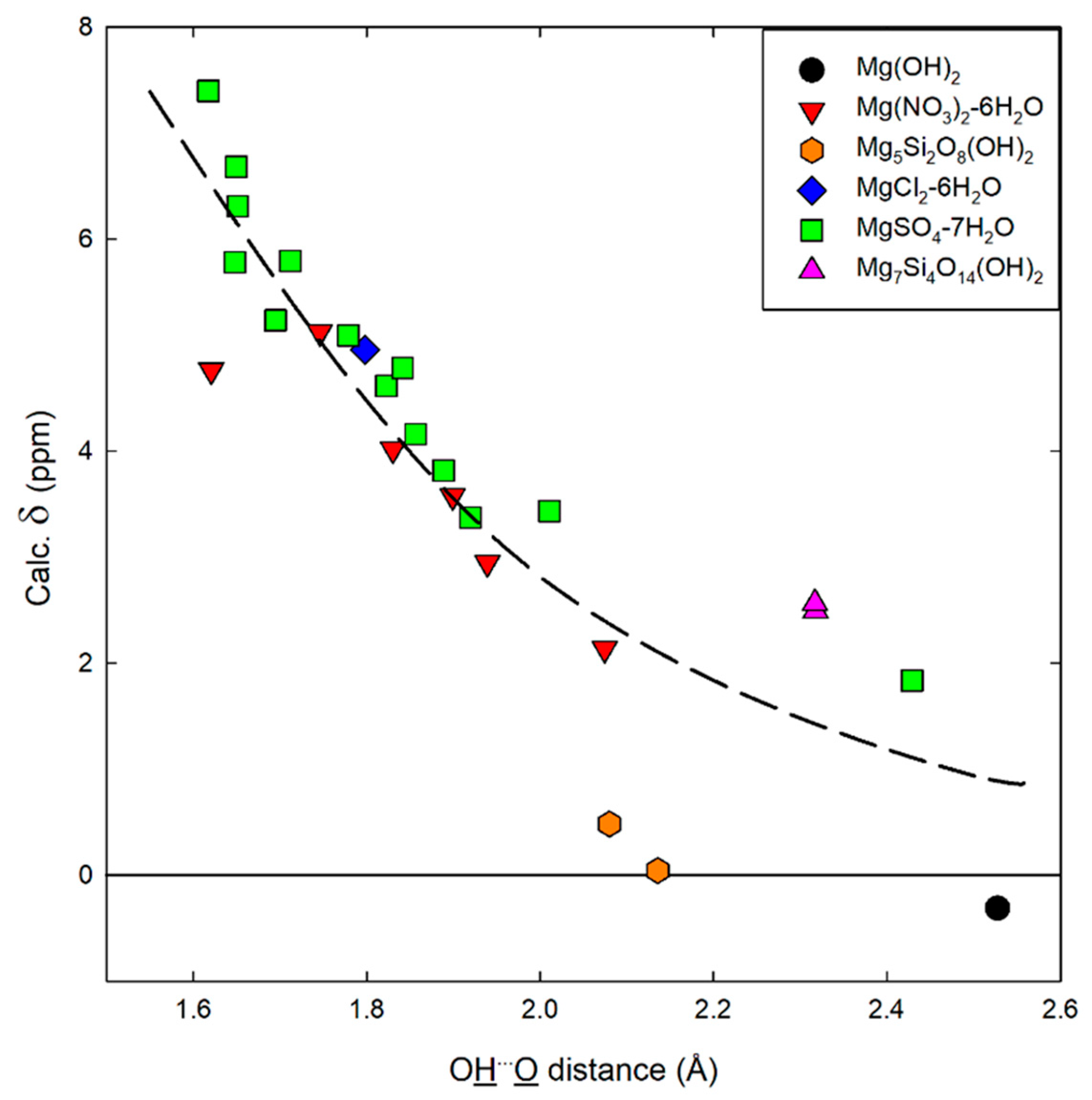
2.2.2. Predicted Chemical Shifts for Hydrogen Containing MgO Phases
3. Materials and Methods
3.1. Materials
3.2. Experimental NMR
3.3. Computational NMR
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Amaral, L.; Oliveira, I.; Salomao, R.; Frollini, E.; Pandolfelli, V. Temperature and Common-Ion Effect on Magnesium Oxide (MgO) Hydration. Ceram. Int. 2010, 36, 1047–1054. [Google Scholar] [CrossRef]
- Chizallet, C.; Costentin, G.; Lauron-Pernot, H.; Che, M.; Bonhomme, C.; Maquet, J.; Delbecq, F.; Sautet, P. Study of the Structure of OH Groups on MgO by 1D and 2D 1H MAS NMR Combined with DFT Cluster Calculations. J. Phys. Chem. C 2007, 111, 18279–18287. [Google Scholar] [CrossRef]
- Chizallet, C.; Costentin, G.; Lauron-Pernot, H.; Maquet, J.; Che, M. 1H MAS NMR Study of the Coordination of Hydroxyl Groups Generated Upon Adsorption of H2O and CD3OH on Clean MgO Surfaces. Appl. Catal. A 2006, 307, 239–244. [Google Scholar] [CrossRef]
- Arenas, C.G.; Marrero, M.; Leiva, C.; Solís-Guzmán, J.; Arenas, L.F.V. High Fire Resistance in Blocks Containing Coal Combustion Fly Ashes and Bottom Ash. Waste Manag. 2011, 31, 1783–1789. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; De Schutter, G.; Deng, D.; Yu, Z. Micro-Analysis of the Role of Interfacial Transition Zone in “Salt Weathering” on Concrete. Constr. Build. Mater. 2010, 24, 2052–2059. [Google Scholar] [CrossRef]
- Stankic, S.; Müller, M.; Diwald, O.; Sterrer, M.; Knözinger, E.; Bernardi, J. Size-Dependent Optical Properties of MgO Nanocubes. Angew. Chem. Int. Ed. 2005, 44, 4917–4920. [Google Scholar] [CrossRef]
- Abrinaei, F. Nonlinear Optical Response of Mg/MgO Structures Prepared by Laser Ablation Method. J. Eur. Opt. Soc. Rapid Publ. 2017, 13, 15. [Google Scholar] [CrossRef]
- Ponnuvelu, D.V.; Selvaraj, A.; Suriyaraj, S.P.; Selvakumar, R.; Pulithadathail, B. Ultrathin Hexagonal MgO Nanoflakes Coated Medical Textiles and Their Enhanced Antibacterial Activity. Mater. Res. Express 2016, 3, 105005. [Google Scholar] [CrossRef]
- Bindhu, M.R.; Umadevi, M.; Kavin Micheal, M.; Arasu, M.V.; Abdullah Al-Dhabi, N. Structural, Morphological and Optical Properties of MgO Nanoparticles for Antibacterial Applications. Mater. Lett. 2016, 166, 19–22. [Google Scholar] [CrossRef]
- Senbayram, M.; Gransee, A.; Wahle, V.; Thiel, H. Role of Magnesium Fertilisers in Agriculture: Plant–Soil Continuum. Crop. Pasture Sci. 2015, 66, 1219–1229. [Google Scholar] [CrossRef]
- Hayashi, K.; Matsuishi, S.; Kamiya, T.; Hirano, M.; Hosono, H. Light-Induced Conversion of an Insulating Refractory Oxide into a Persistent Electronic Conductor. Nature 2002, 419, 462–465. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Gila, B.; Mehandru, R.; Johnson, J.W.; Shin, J.H.; Lee, K.P.; Luo, B.; Onstine, A.; Abernathy, C.R.; Pearton, S.J.; et al. Electrical Characterization of GaN Metal Oxide Semiconductor Diodes Using MgO as the Gate Oxide. J. Electrochem. Soc. 2002, 149, G482–G484. [Google Scholar] [CrossRef]
- Selvamani, T.; Sinhamahapatra, A.; Bhattacharjya, D.; Mukhopadhyay, I. Rectangular MgO Microsheets with Strong Catalytic Activity. Mater. Chem. Phys. 2011, 129, 853–861. [Google Scholar] [CrossRef]
- Singh, B.; Prasad, G.K.; Pandey, K.S.; Danikhel, R.K.; Vijayaraghavan, R. Decontamination of Chemical Warfare Agents. Def. Sci. J. 2010, 60, 428–441. [Google Scholar] [CrossRef]
- Yang, P.; Lieber, C.M. Nanorod-Superconductor Composites: A Pathway to Materials with High Critical Current Densities. Science 1996, 273, 1836–1840. [Google Scholar] [CrossRef]
- Wan, L.F.; Liu, Y.-S.; Cho, E.S.; Forster, J.D.; Jeong, S.; Wang, H.-T.; Urban, J.J.; Guo, J.; Prendergast, D. Atomically Thin Interfacial Suboxide Key to Hydrogen Storage Performance Enhancements of Magnesium Nanoparticles Encapsulated in Reduced Graphene Oxide. Nano Lett. 2017, 17, 5540–5545. [Google Scholar] [CrossRef]
- Mojica-Sánchez, J.P.; Zarate-López, T.I.; Flores-Álvarez, J.M.; Reyes-Gómez, J.; Pineda-Urbina, K.; Gómez-Sandoval, Z. Magnesium Oxide Clusters as Promising Candidates for Hydrogen Storage. Phys. Chem. Chem. Phys. 2019, 21, 23102–23110. [Google Scholar] [CrossRef]
- Helton, J.; Anderson, D.; Jow, H.-N.; Marietta, M.; Basabilvazo, G. Performance Assessment in Support of the 1996 Compliance Certification Application for the Waste Isolation Pilot Plant. Risk Anal. 1999, 19, 959–986. [Google Scholar] [CrossRef]
- Xiong, Y.; Deng, H.; Nemer, M.; Johnsen, S. Experimental Determination of the Solubility Constant for Magnesium Chloride Hydroxide Hydrate (Mg3Cl(OH)5·4H2O, phase 5) at Room Temperature, and its Importance to Nuclear Waste Isolation in Geological Repositories in Salt Formations. Geochim. Cosmochim. Acta 2010, 74, 4605–4611. [Google Scholar] [CrossRef]
- Rimsza, J.M.; Sorte, E.G.; Alam, T.M. Hydration and Hydroxylation of MgO in Solution: NMR Identification of Proton-Containing Intermediate Phases. ACS Omega 2019, 4, 1033–1044. [Google Scholar] [CrossRef]
- Aramendía, M.A.; Benítez, J.A.; Borau, V.; Jiménez, C.; Marinas, J.M.; Ruiz, J.R.; Urbano, F. Study of MgO and Pt/MgO Systems by XRD, TPR, and 1H MAS NMR. Langmuir 1999, 15, 1192–1197. [Google Scholar] [CrossRef]
- Aramendía, M.A.; Benítez, J.A.; Borau, V.; Jiménez, C.; Marinas, J.M.; Ruiz, J.R.; Urbano, F. Characterization of Various Magnesium Oxides by XRD and 1H MAS NMR Spectroscopy. J. Solid State Chem. 1999, 144, 25–29. [Google Scholar] [CrossRef]
- Chizallet, C.; Petitjean, H.; Costentin, G.; Lauron-Pernot, H.; Maquet, J.; Bonhomme, C.; Che, M. Identification of the OH Groups Responsible for Kinetic Basicity on MgO Surfaces by 1H MAS NMR. J. Catal. 2009, 268, 175–179. [Google Scholar] [CrossRef]
- Xue, X.; Kanzaki, M.; Shatskiy, A. Dense Hydrous Magnesium Silicates, Phase D, and Superhydrous B: New Structural Constraints from One- and Two-Dimensional 29Si and 1H NMR. Am. Mineral. 2008, 93, 1099–1111. [Google Scholar] [CrossRef]
- Phillips, B.L.; Burnley, P.C.; Worminghaus, K.; Navrotsky, A. 29Si and 1H NMR Spectroscopy of High-Pressure Hydrous Magnesium Silicates. Phys. Chem. Miner. 1997, 24, 179–190. [Google Scholar] [CrossRef]
- Yesinowski, J.P.; Eckert, H.; Rossman, G.R. Characterization of Hydrous Species in Minerals by High-Speed Proton MAS-NMR. J. Am. Chem. Soc. 1988, 110, 1367–1375. [Google Scholar] [CrossRef]
- Aramendía, M.A.; Borau, V.; Jiménez, C.; Marinas, J.M.; Ruiz, J.R.; Urbano, F.J. XRD and 1H MAS NMR Spectroscopic Study of Mixed Oxides Obtained by Calcination of Layered-Double Hydroxides. Mater. Lett. 2000, 46, 309–314. [Google Scholar] [CrossRef]
- Grüninger, H.; Schmutzler, A.; Siegel, R.; Armstrong, K.; Frost, D.J.; Senker, J. Quantitative Description of 1H SQ and DQ Coherences for the Hydroxyl Disorder within Hydrous Ringwoodite. Phys. Chem. Chem. Phys. 2018, 20, 15098–15105. [Google Scholar] [CrossRef]
- Griffin, J.M.; Miller, A.J.; Berry, A.J.; Wimperis, S.; Ashbrook, S.E. Dynamics on the Microsecond Timescale in Hydrous Silicates Studied by Solid-State 2H NMR Spectroscopy. Phys. Chem. Chem. Phys. 2010, 12, 2989–2998. [Google Scholar] [CrossRef]
- Griffin, J.M.; Berry, A.J.; Frost, D.J.; Wimperis, S.; Ashbrook, S.E. Water in the Earth’s Mantle: A Solid-State NMR Study of Hydrous Wadsleyite. Chem. Sci. 2013, 4, 1523–1538. [Google Scholar] [CrossRef]
- Moran, R.F.; McKay, D.; Pickard, C.J.; Berry, A.J.; Griffin, J.M.; Ashbrook, S.E. Hunting for Hydrogen: Random Structure Searching and Prediction of NMR Parameters of Hydrous Wadsleyite. Phys. Chem. Chem. Phys. 2016, 18, 10173–10181. [Google Scholar] [CrossRef] [PubMed]
- McKay, D.; Moran, R.F.; Dawson, D.M.; Griffin, J.M.; Sturniolo, S.; Pickard, C.J.; Berry, A.J.; Ashbrook, S.E. A Picture of Disorder in Hydrous Wadsleyite—Under the Combined Microscope of Solid-State NMR Spectroscopy and Ab Initio Random Structure Searching. J. Am. Chem. Soc. 2019, 141, 3024–3036. [Google Scholar] [CrossRef] [PubMed]
- Lide, D.R. CRC Handbook of Chemistry and Physics; CRC press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Sears, R.; Kaliaperumal, R.; Manogaran, S. 1H Shielding Anisotropy in Mg(OH)2: The Isolated OH− Group. J. Chem. Phys. 1988, 88, 2284–2288. [Google Scholar] [CrossRef]
- Xue, X.; Kanzaki, M. High-Pressure δ-Al(OH)3 and δ-AlOOH Phases and Isostructural Hydroxides/Oxyhydroxides: New Structural Insights from High-Resolution 1H and 27Al NMR. J. Phys. Chem. B 2007, 111, 13156–13166. [Google Scholar] [CrossRef]
- Vasconcelos, F.; Cristol, S.; Paul, J.F.; Montagne, L.; Mauri, F.; Delevoye, L. First-Principles Calculations of NMR Parameters for Phosphate Materials. Magn. Reson. Chem. 2010, 48, S142–S150. [Google Scholar] [CrossRef]
- Pourpoint, F.; Gervais, C.; Bonhomme-Coury, L.; Azaïs, T.; Coelho, C.; Mauri, F.; Alonso, B.; Babonneau, F.; Bonhomme, C. Calcium Phosphates and Hydroxyapatite: Solid-State NMR Experiments and First-Principles Calculations. Appl. Magn. Reson. 2007, 32, 435–457. [Google Scholar] [CrossRef]
- Xue, X.; Kanzaki, M. Proton Distributions and Hydrogen Bonding in Crystalline and Glassy Hydrous Silicates and Related Inorganic Materials: Insights from High-Resolution Solid-State Nuclear Magnetic Resonance Spectroscopy. J. Am. Ceram. Soc. 2009, 92, 2803–2830. [Google Scholar] [CrossRef]
- Schnell, I.; Spiess, H.W. High-Resolution 1H NMR Spectroscopy in the Solid State: Very Fast Sample Rotation and Multiple-Quantum Coherences. J. Magn. Reson. 2001, 151, 153–227. [Google Scholar] [CrossRef]
- Massiot, D.; Fayon, F.; Capron, M.; King, I.; Le Calvé, S.; Alonso, B.; Durand, J.O.; Bujoli, B.; Gan, Z.; Hoatson, G. Modelling One and Two-Dimensional Solid-State NMR Spectra. Magn. Reson. Chem. 2002, 40, 70–76. [Google Scholar] [CrossRef]
- Gražulis, S.; Chateigner, D.; Downs, R.T.; Yokochi, A.; Quirós, M.; Lutterotti, L.; Manakova, E.; Butkus, J.; Moeck, P.; Le Bail, A. Crystallography Open Database–An Open-Access Collection of Crystal Structures. J. Appl. Crystallogr. 2009, 42, 726–729. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Norm-Conserving and Ultrasoft Pseudopotentials for First-Row and Transition Elements. J. Phys. Condens. Matter 1994, 6, 8245. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Pickard, C.J.; Mauri, F. All-Electron Magnetic Response with Pseudopotentials: NMR Chemical Shifts. Phys. Rev. B 2001, 63, 245101. [Google Scholar] [CrossRef]
- Pedone, A.; Palazzetti, F.; Barone, V. Models of Aged Magnesium-Silicate-Hydrate Cements Based on the Lizardite and Talc Crystals: A Periodic DFT-GIPAW Investigation. J. Phys. Chem. C 2017, 121, 7319–7330. [Google Scholar] [CrossRef]
- Charpentier, T. The PAW/GIPAW Approach for Computing NMR Parameters: A New Dimension Added to NMR Study of Solids. Solid State Nucl. Magn. Reson. 2011, 40, 1–20. [Google Scholar] [CrossRef]
- Ashbrook, S.E.; McKay, D. Combining Solid-State NMR Spectroscopy with First-Principles Calculations—A Guide to NMR Crystallography. Chem. Commun. 2016, 52, 7186–7204. [Google Scholar] [CrossRef]
Sample Availability: Not available. |

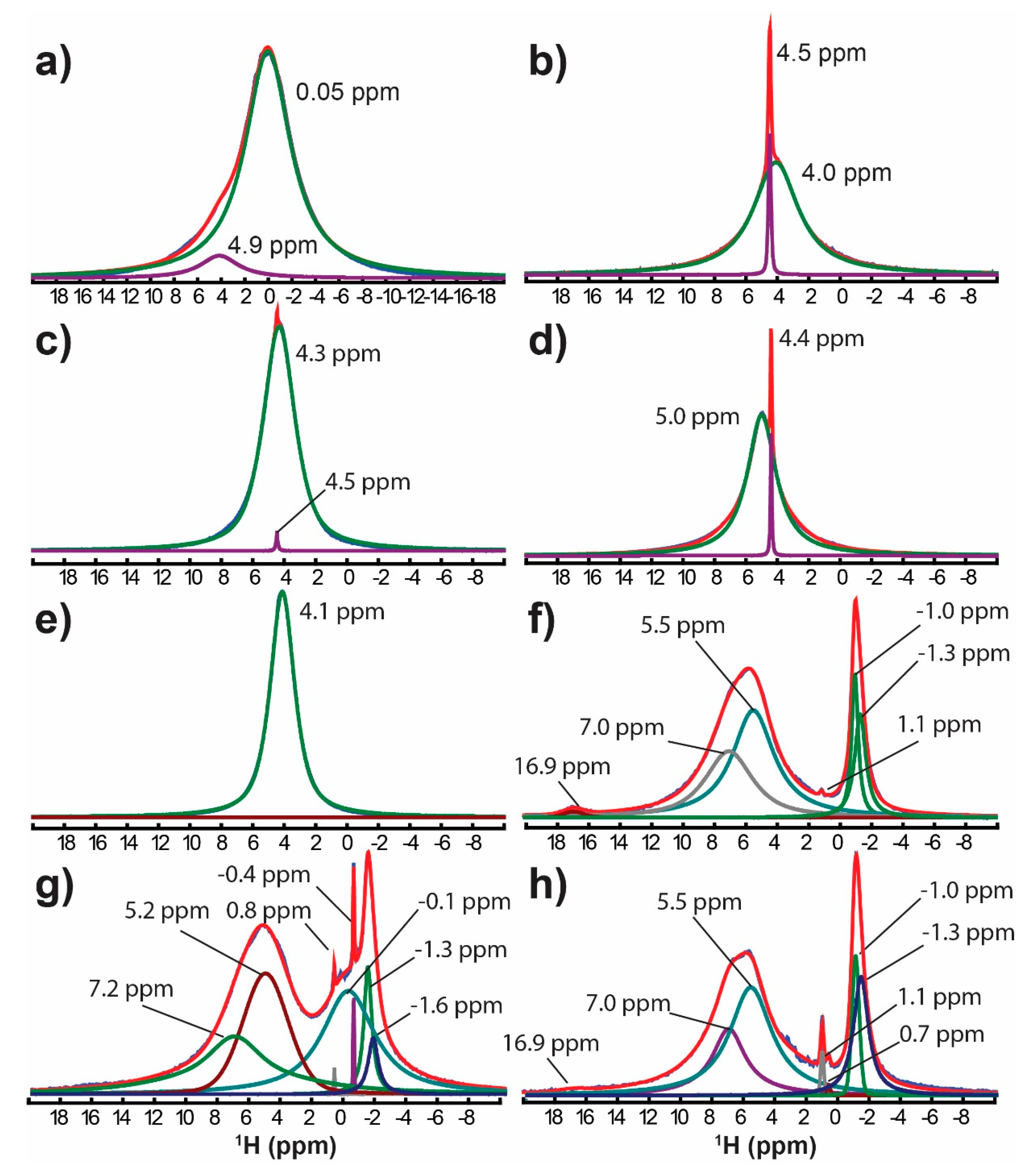



| System | 1H-NMR (ppm) [Experimental] | Conc. (%) | Average 1H-NMR [Computational] | ||
|---|---|---|---|---|---|
| σ (ppm) | δ (ppm) a | COD ID c,d | |||
| Mg(OH)2 | 0.05 | 93.2% | 30.75 | −0.31 | 1000054(ND) |
| 4.9 b | 6.8% | ||||
| −0.5 to 0.0 ± 2 Refs. [34,35,36] | |||||
| Mg(NO3)2·6H2O | 4.5 | 4.6% | 25.1 ± 0.5 | 4.6 ± 0.4 | 9011207(XD) |
| 4.0 | 95.4% | ||||
| MgCl2·6H2O | 4.5 | 2.0% | 24.0 ± 0.3 | 5.1 ± 0.2 | 9011352(ND) |
| 4.3 | 98.0% | ||||
| MgSO4·7H2O | 5.0 | 97.1% | 23.4 ± 0.5 | 5.55 ± 0.4 | 9010743(ND) |
| 4.4 b | 2.9% | ||||
| Mg7Si4O14(OH)2 | 3.9 Ref. [30] | 26.75 ± 0.04 | 2.76 ± 0.03 | 1534957(M) | |
| 4.1 Ref. [30] | |||||
| Mg5Si2O8(OH)2 | 1.1 Ref. [25] | 29.9 ± 0.3 | 0.3 ± 0.2 | 9016666(XD) | |
| MgBr2·6H2O | 4.1 | 100% | |||
| hydromagnesite [4MgCO3·Mg(OH)2·4H2O] | −1.4 | 10.6% | |||
| −1.0 | 8.5% | ||||
| 1.1 | 0.1% | ||||
| 5.5 | 48.3% | ||||
| 7.0 | 31.6% | ||||
| 16.9 | 0.9% | ||||
| artinite [MgCO3·Mg(OH)2·3H2O] | −1.6 | 1.8% | |||
| −1.3 | 3.3% | ||||
| −0.4 | 0.6% | ||||
| −0.1 | 16.9% | ||||
| 0.8 | 0.1% | ||||
| 5.2 | 39.8% | ||||
| 7.0 | 37.5% | ||||
| dypingite [4MgCO3·Mg(OH)2·5H2O] | −1.4 | 13.2% | |||
| −1.1 | 5.1% | ||||
| 0.7 | 0.2% | ||||
| 1.1 | 1.0% | ||||
| 5.5 | 52.9% | ||||
| 7.0 | 27.1% | ||||
| 16.9 | 0.5% | ||||
| NaOH | −3.2 | 72.9% | 34.5 | −3.1 | 2310820(XD) |
| 0.8 b | 20.5% | ||||
| 4.8 b | 3.0% | ||||
| 8.6 b | 3.5% | ||||
| System | 1H-NMR [Computational] | COD ID b | |
|---|---|---|---|
| σ (ppm) | δ (ppm) a | ||
| MgO Hydroxides | |||
| Mg5O4(OH)2 | 30.50 | 0.01 | 1531159 |
| Mg4O3(OH)2 | 29.56 | 0.74 | 1531161 |
| Mg3O2(OH)2 | 29.53, 30.49 | 0.02, 0.78 | 1531164 |
| Mg2O(OH)2 | 30.43 | 0.07 | 1531167 |
| Mg3O(OH)4 | 29.90, 30.25 | 0.21, 0.49 | 1531171 |
| Mg5O(OH)8 | 29.55, 29.56, 29.88, 30.25 | 0.21, 0.50, 0.76, 0.77 | 1531175 |
| Magnesium Chloride Hydrates | |||
| MgCl2·6H2O | 23.25, 23.32, 23.73, 24.15, 25.01, 25.36 | 5.69, 5.63, 5.31, 4.98, 4.31, 4.04 | 9011352 |
| MgCl2·4H2O | 24.69, 24.99, 25.08, 25.12 | 4.30, 4.33, 4.40, 4.64 | 2018339 |
| MgCl2·2H2O | 24.92 | 4.41 | 2102790 |
| MgCl2·H2O | 25.44, 25.15 | 4.05, 4.28 | 2102791 |
| Magnesium Perchlorate | |||
| Mg(ClO4)2·4H2O | 25.01, 25.02, 26.66, 26.67 | 3.07, 4.39 | 2104832 |
| Mg(ClO4)2·2H2O | 26.34 | 3.33 | 2104833 |
| Mg-Cements | |||
| 3Mg(OH)2·MgCl2·8H2O | 15.96, 22.51, 22.89, 23.27, 25.10, 25.66, 26.00, 26.16, 30.19, 30.32, 30.68 | 11.61, 6.38, 6.08, 5.78, 4.32, 3.87, 3.60, 3.47, 0.26, 0.15, −0.13 | 9010975 |
| 5Mg(OH)2·MgCl2·8H2O | 20.18, 24.20, 24.49, 24.61, 28.10, 28.32, 28.55, 28.99, 29.71, 33.42 | 8.24, 5.03, 4.80, 4.71, 1.92, 1.75, 1.56, 1.21, 0.64, −2.32 | 2103035 |
| Hydrated NaOH (Layered) | |||
| NaOH·H2O | 20.28, 20.8, 27.14 | 8.15, 7.78, 2.69 | 1532133 |
| α-NaOH·4H2O | 16.01, 18.15, 20.84, 21.03, 21.77, 25.32, 25.63, 27.67, 29.59 | 11.57, 9.86, 7.71, 7.56, 6.97, 4.14, 3.89, 2.27, 0.74 | 1532135 |
| β-NaOH·4H2O | 18.95, 21.46, 22.44, 24.13, 24.64, 26.65, 27.27, 30.33 | 9.29, 7.24, 6.45, 5.13, 4.69, 3.00, 2.60, 0.16 | 1532136 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sorte, E.G.; Rimsza, J.M.; Alam, T.M. Computational and Experimental 1H-NMR Study of Hydrated Mg-Based Minerals. Molecules 2020, 25, 933. https://doi.org/10.3390/molecules25040933
Sorte EG, Rimsza JM, Alam TM. Computational and Experimental 1H-NMR Study of Hydrated Mg-Based Minerals. Molecules. 2020; 25(4):933. https://doi.org/10.3390/molecules25040933
Chicago/Turabian StyleSorte, Eric G., Jessica M. Rimsza, and Todd M. Alam. 2020. "Computational and Experimental 1H-NMR Study of Hydrated Mg-Based Minerals" Molecules 25, no. 4: 933. https://doi.org/10.3390/molecules25040933
APA StyleSorte, E. G., Rimsza, J. M., & Alam, T. M. (2020). Computational and Experimental 1H-NMR Study of Hydrated Mg-Based Minerals. Molecules, 25(4), 933. https://doi.org/10.3390/molecules25040933