Liposome Drug Delivery System across Endothelial Plasma Membrane: Role of Distance between Endothelial Cells and Blood Flow Rate
Abstract
1. Introduction
2. Computational Details
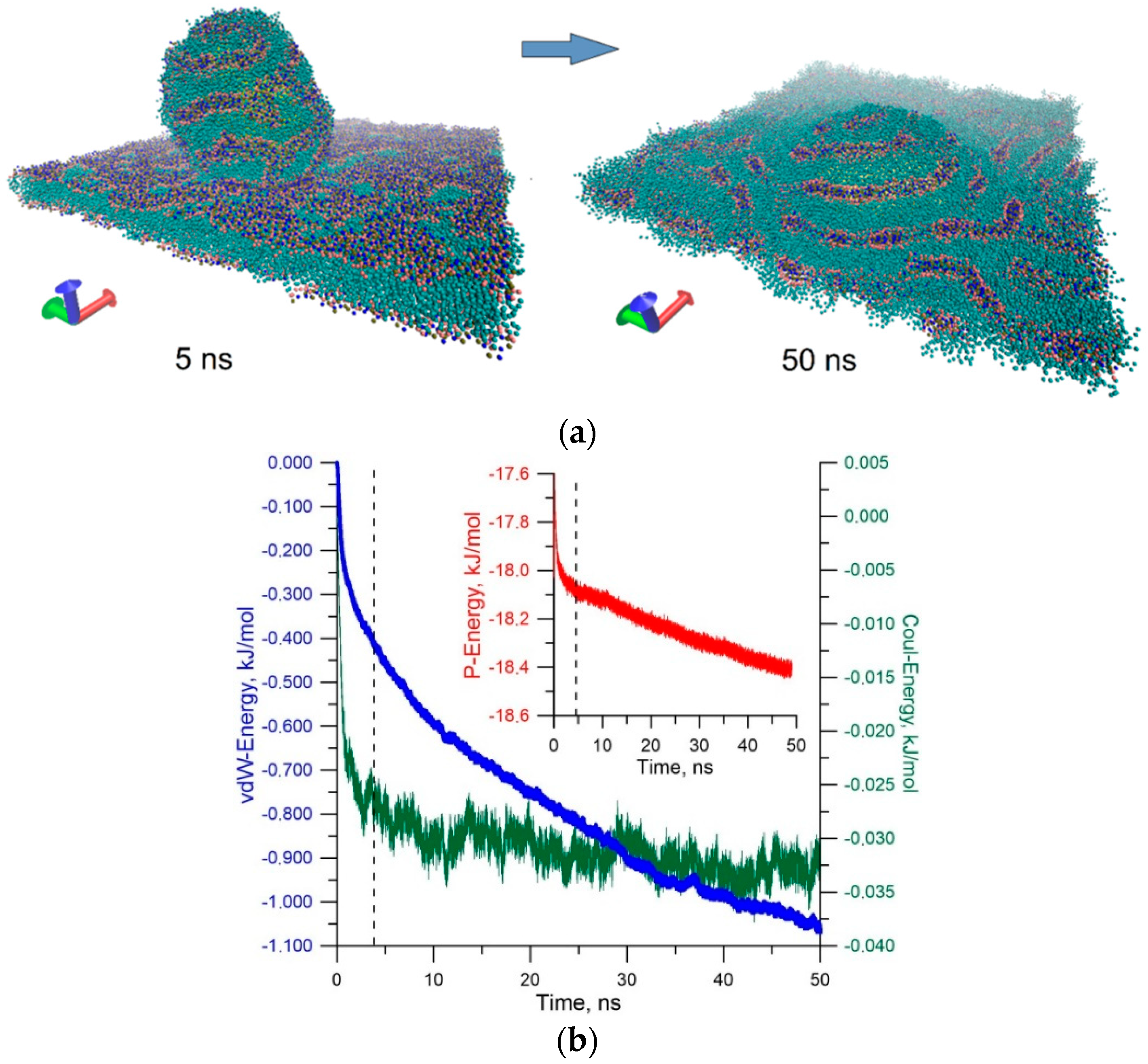
3. Results and Discussion
4. Conclusions
Funding
Conflicts of Interest
References
- Fahr, A.; Liu, X. Drug Delivery Strategies for Poorly Water-Soluble Drugs. Expert Opin. Drug Deliv. 2007, 4, 403–416. [Google Scholar] [CrossRef]
- Al-Jamal, W.T.; Kostarelos, K. Liposomes: From a Clinically Established Drug Delivery System to a Nanoparticle Platform for Theranostic Nanomedicine. Acc. Chem. Res. 2011, 44, 1094–1104. [Google Scholar] [CrossRef]
- Zhang, Y.; Chan, H.F.; Leong, K.W. Advanced Materials and Processing for Drug Delivery: The Past and the Future. Adv. Drug Deliv. Rev. 2013, 65, 104–120. [Google Scholar] [CrossRef] [PubMed]
- Mignani, S.; El Kazzouli, S.; Bousmina, M.; Majoral, J.-P. Expand Classical Drug Administration Ways by Emerging Routes Using Dendrimer Drug Delivery Systems: A Concise Overview. Adv. Drug Deliv. Rev. 2013, 65, 1316–1330. [Google Scholar] [CrossRef] [PubMed]
- Bangham, A.D.; Standish, M.M.; Watkins, J.C. Diffusion of Univalent Ions across the Lamellae of Swollen Phospholipids. J. Mol. Biol. 1965, 13, 238–252. [Google Scholar] [CrossRef]
- Allen, T.M.; Cullis, P.R. Liposomal Drug Delivery Systems: From Concept to Clinical Applications. Adv. Drug Deliv. Rev. 2013, 65, 36–48. [Google Scholar] [CrossRef] [PubMed]
- Johnsen, K.B.; Moos, T. Revisiting nanoparticle technology for blood-brain barrier transport: Unfolding at the endothelial gate improves the fate of transferrin receptor-targeted liposomes. J. Control. Release 2016, 222, 32–46. [Google Scholar] [CrossRef] [PubMed]
- Federman, N.; Denny, C.T. Targeting liposomes toward novel pediatric anticancer therapeutics. Pediatr. Res. 2010, 67, 514–519. [Google Scholar] [CrossRef]
- Wang, X.; Lu, W. Active Targeting Liposomes: Promising Approach for Tumor-Targeted Therapy. J. Bioequiv. Availab. 2016, 8, 13–14. [Google Scholar] [CrossRef]
- Zheng, C.; Ma, C.; Bai, E.; Yang, K.; Xu, R. Transferrin and cell-penetrating peptide dual-functioned liposome for targeted drug delivery to glioma. Int. J. Clin. Exp. Med. 2015, 8, 1658–1668. [Google Scholar]
- Gabizon, A.; Horowitz, A.T.; Goren, D.; Tzemach, D.; Shmeeda, H.; Zalipsky, S. In vivo fate of folate-targeted polyethylene-glycol liposomes in tumor-bearing mice. Clin. Cancer Res. 2003, 9, 6551–6559. [Google Scholar]
- Chang, D.K.; Lin, C.T.; Wu, C.H.; Wu, H.C. A novel peptide enhances therapeutic efficacy of liposomal anti-cancer drugs in mice models of human lung cancer. PLoS ONE 2009, 4, e4171. [Google Scholar] [CrossRef] [PubMed]
- Lammers, T.; Kiessling, F.; Hennink, W.E.; Storm, G. Drug targeting to tumors: Principles, pitfalls and (pre-) clinical progress. J. Control. Release 2012, 161, 175–187. [Google Scholar] [CrossRef] [PubMed]
- Torchilin, V. Passive and active drug targeting: Drug delivery to tumors as an example. Handb. Exp. Pharmacol. 2010, 197, 3–53. [Google Scholar]
- Zylberberg, C.; Matosevic, S. Pharmaceutical liposomal drug delivery: A review of new delivery systems and a look at the regulatory landscape. Drug Deliv. 2016, 23, 3319–3329. [Google Scholar] [CrossRef] [PubMed]
- Bulbake, U.; Doppalapudi, S.; Kommineni, N.; Khan, W. Liposomal Formulations in Clinical Use: An Updated Review. Pharmaceutics 2017, 9, 12. [Google Scholar] [CrossRef]
- Pattni, B.S.; Chupin, V.V.; Torchilin, V.P. New Developments in Liposomal Drug Delivery. Chem. Rev. 2015, 115, 10938–10966. [Google Scholar] [CrossRef]
- Dimov, N.; Kastner, E.; Hussain, M.; Perrie, Y.; Szita, N. Formation and purifcation of tailored liposomes for drug delivery using a module-based micro continuous-fow system. Sci. Rep. 2017, 7, 12045. [Google Scholar] [CrossRef]
- Fathi, S.; Oyelere, A.K. Liposomal drug delivery systems for targeted cancer therapy: Is active targeting the best choice? Future Med. Chem. 2016, 8, 2091–2112. [Google Scholar] [CrossRef]
- Deshpande, P.P.; Biswas, S.; Torchilin, V.P. Current trends in the use of liposomes for tumor targeting. Nanomedicine 2013, 8, 1509–1528. [Google Scholar] [CrossRef]
- Torchilin, V. Tumor delivery of macromolecular drugs based on the EPR effect. Adv. Drug. Deliv. Rev. 2011, 63, 131–135. [Google Scholar] [CrossRef] [PubMed]
- Kale, A.A.; Torchilin, V.P. Environment-responsive multifunctional liposomes. Methods Mol. Biol. 2010, 605, 213–242. [Google Scholar] [PubMed]
- Maeda, H. Macromolecular therapeutics in cancer treatment: The EPR effect and beyond. J. Control. Release 2012, 164, 138–144. [Google Scholar] [CrossRef] [PubMed]
- Maeda, H.; Nakamura, H.; Fang, J. The EPR effect for macromolecular drug delivery to solid tumors: Improvement of tumor uptake, lowering of systemic toxicity, and distinct tumor imaging in vivo. Adv. Drug. Deliv. Rev. 2012, 65, 71–79. [Google Scholar] [CrossRef] [PubMed]
- Riaz, M.K.; Riaz, M.A.; Zhang, X.; Lin, C.; Wong, K.H.; Chen, X.; Zhang, G.; Lu, A.; Yang, Z. Surface Functionalization and Targeting Strategies of Liposomes in Solid Tumor Therapy: A Review. Int. J. Mol. Sci. 2018, 19, 195. [Google Scholar] [CrossRef] [PubMed]
- Haley, B.; Frenkel, E. Nanoparticles for drug delivery in cancer treatment. Urol. Oncol. 2008, 26, 57–64. [Google Scholar] [CrossRef] [PubMed]
- Genheden, S.; Eriksson, L.A. Estimation of Liposome Penetration Barriers of Drug Molecules with All-Atom and Coarse-Grained Models. J. Chem. Theory Comput. 2016, 12, 4651–4661. [Google Scholar] [CrossRef]
- Vieira, D.B.; Gamarra, L.F. Getting into the brain: Liposome-based strategies for effective drug delivery across the blood–brain barrier. Int. J. Nanomed. 2016, 11, 5381–5414. [Google Scholar] [CrossRef]
- Agrawal, M.; Tripathi, D.K.; Saraf, S.; Saraf, S.; Antimisiaris, S.G.; Mourtas, S.; Antimisiaris, S.G.; Mourtas, S.; Hammarlund-Udenaes, M.; Alexander, A. Recent advancements in liposomes targeting strategies to cross blood-brain barrier (BBB) for the treatment of Alzheimer’s disease. J. Control. Release 2017, 260, 61–77. [Google Scholar] [CrossRef]
- Gurturk, Z.; Tezcaner, A.; Dalgic, A.D.; Korkmaz, S.; Keskin, D. Maltodextrin modified liposomes for drug delivery through the blood-brain barrier. Med. Chem. Commun. 2017, 8, 1337–1345. [Google Scholar] [CrossRef]
- Helm, F.; Fricker, G. Liposomal conjugates for drug delivery to the central nervous system. Pharmaceutics 2015, 7, 27–42. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Deng, W.; Goldys, E.M. Light-Triggerable Liposomes for Enhanced Endolysosomal Escape and Gene Silencing in PC12 Cells. Mol. Ther. Nucleic Acids 2017, 7, 366–377. [Google Scholar] [CrossRef]
- Alekseeva, A.; Kapkaeva, M.; Shcheglovitova, O.; Boldyrev, I.; Pazynina, G.; Bovin, N.; Vodovozova, E. Interactions of antitumour Sialyl Lewis X liposomes with vascular endothelial cells. Biochim. Biophys. Acta 2015, 1848, 1099–1110. [Google Scholar] [CrossRef] [PubMed]
- Jämbeck, J.P.; Eriksson, E.S.; Laaksonen, A.; Lyubartsev, A.P.; Eriksson, L.A. Molecular Dynamics Studies of Liposomes as Carriers for Photosensitizing Drugs: Development, Validation, and Simulations with a Coarse-Grained Model. J. Chem. Theory Comput. 2014, 10, 5–13. [Google Scholar] [CrossRef] [PubMed]
- Giupponi, G.; Martini, M.F.; Pickholz, M. Molecular Dynamics Study on the Encapsulation of Prilocaine in Liposomes at Physiological pH. J. Biomater. Tissue Eng. 2013, 3, 1–7. [Google Scholar] [CrossRef]
- Da Rocha, E.L.; Caramori, G.F.; Rambo, C.R. Nanoparticle translocation through a lipid bilayer tuned by surface chemistry. Phys. Chem. Chem. Phys. 2013, 15, 2282–2290. [Google Scholar] [CrossRef]
- Prates Ramalho, J.P.; Gkeka, P.; Sarkisov, L. Structure and Phase Transformations of DPPC Lipid Bilayers in the Presence of Nanoparticles: Insights from Coarse-Grained Molecular Dynamics Simulations. Langmuir 2011, 27, 3723–3730. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, H.; Chen, Z.; Zheng, Y. Penetration of Lipid Membranes by Gold Nanoparticles: Insights into Cellular Uptake, Cytotoxicity, and Their Relationship. ACS Nano 2010, 4, 5421–5429. [Google Scholar] [CrossRef]
- Lin, J.Q.; Zheng, Y.G.; Zhang, H.W.; Chen, Z. A simulation study on nanoscale holes generated by gold nanoparticles on negative lipid bilayers. Langmuir 2011, 27, 8323–8332. [Google Scholar] [CrossRef]
- Sevink, G.J.A.; Charlaganova, M.; Fraaijea, J.G.E.M. Coarse-grained hybrid simulation of liposomes. Soft Matter 2013, 9, 2816–2831. [Google Scholar] [CrossRef]
- Hu, M.; Stanzione, F.; Sum, A.K.; Faller, R.; Deserno, M. Design Principles for Nanoparticles Enveloped by a Polymer-Tethered Lipid Membrane. ACS Nano 2015, 9, 9942–9954. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zhang, Y.; Ma, J.; Meng, Q.; Fan, J. Modeling Interactions between Liposomes and Hydrophobic Nanosheets. Small 2019, 15, 1804992. [Google Scholar] [CrossRef] [PubMed]
- Glukhova, O.E.; Prytkova, T.R.; Savostyanov, G.V. Simulation of High Density Lipoprotein Behavior on a Few Layer Graphene Undergoing Non-Uniform Mechanical Load. J. Phys. Chem. B 2016, 120, 3593–3600. [Google Scholar] [CrossRef]
- Verma, A.; Stellacci, F. Effect of surface properties on nanoparticle-cell interactions. Small 2010, 6, 12–21. [Google Scholar] [CrossRef]
- Shi, X.; von dem Bussche, A.; Hurt, R.H.; Kane, A.B.; Gao, H. Cell entry of one-dimensional nanomaterials occurs by tip recognition and rotation. Nat. Nanotechnol. 2011, 6, 714–719. [Google Scholar] [CrossRef]
- Woo, S.Y.; Lee, H. All-atom simulations and free-energy calculations of coiled-coil peptides with lipid bilayers: Binding strength, structural transition, and effect on lipid dynamics. Sci. Rep. 2016, 6, 22299. [Google Scholar] [CrossRef]
- Rossi, G.; Monticelli, L. Simulating the interaction of lipid membranes with polymer and ligand-coated nanoparticles. Adv. Phys. X 2016, 1, 276–296. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Pall, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1-2, 19–25. [Google Scholar] [CrossRef]
- de Jong, D.H.; Singh, G.; Bennett, W.F.D.; Arnarez, C.; Wassenaar, T.A.; Schäfer, L.V.; Periole, X.; Tieleman, D.P.; Marrink, S.J. Improved Parameters for The Martini Coarse-Grained Protein Force Field. J. Chem. Theory Comput. 2013, 9, 687–697. [Google Scholar] [CrossRef]
- Evans, D.J.; Holian, B.L. The Nose–Hoover thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
- Qi, L.; Zhu, J.; Hancock, A.M.; Dai, C.; Zhang, X.; Frostig, R.D.; Chen, Z. Fully distributed absolute blood flow velocity measurement for middle cerebral arteries using Doppler optical coherence tomography. Biomed. Opt. Express 2016, 7, 601–615. [Google Scholar] [CrossRef] [PubMed]
- Brown, B.H.; Smallwood, R.H.; Barber, D.C.; Lawford, P.V.; Hose, D.R. Medical Physics and Biomedical Engineering, 1st ed.; Taylor & Francis Group: New York, NY, USA, 1998; pp. 615–629. [Google Scholar]
- Mogalicherla, A.K.; De, M.; Kunzru, D. Effect of Distributor on Gas-Liquid Downward Flow in Capillaries. Ind. Eng. Chem. Res. 2007, 46, 8406–8412. [Google Scholar] [CrossRef]
- Deutsch, S.; Tarbell, S.J.M.; Manning, K.B.; Rosenberg, G.; Fontaine, A.A. Artificial Heart Fluid Dynamics: Positive Displacement Pumps. In Encyclopedia of Biomaterials and Biomedical Engineering, 2nd ed.; Wnek, G.E., Bowlin, G.L., Eds.; Taylor & Francis Group: Boca Raton, FL, USA, 2008; pp. 95–107. [Google Scholar]
- Schäfer, E.; Kliesch, T.-T.; Janshoff, A. Mechanical Properties of Giant Liposomes Compressed between Two Parallel Plates: Impact of Artificial Actin Shells. Langmuir 2013, 29, 10463–10474. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, E.; Vache, M.; Kliesch, T.-T.; Janshoff, A. Mechanical response of adherent giant liposomes to indentation with a conical AFM-tip. Soft Matter 2015, 11, 4487–4495. [Google Scholar] [CrossRef] [PubMed]
- Et-Thakafy, O.; Delorme, N.; Gaillard, C.; Mériadec, C.; Artzner, F.; Lopez, C.; Guyomarc’h, F. Mechanical Properties of Membranes Composed of Gel-Phase or Fluid-Phase Phospholipids Probed on Liposomes by Atomic Force Spectroscopy. Langmuir 2017, 33, 5117–5126. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Samples of the compounds are not available from the authors. |





© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glukhova, O.E. Liposome Drug Delivery System across Endothelial Plasma Membrane: Role of Distance between Endothelial Cells and Blood Flow Rate. Molecules 2020, 25, 1875. https://doi.org/10.3390/molecules25081875
Glukhova OE. Liposome Drug Delivery System across Endothelial Plasma Membrane: Role of Distance between Endothelial Cells and Blood Flow Rate. Molecules. 2020; 25(8):1875. https://doi.org/10.3390/molecules25081875
Chicago/Turabian StyleGlukhova, Olga E. 2020. "Liposome Drug Delivery System across Endothelial Plasma Membrane: Role of Distance between Endothelial Cells and Blood Flow Rate" Molecules 25, no. 8: 1875. https://doi.org/10.3390/molecules25081875
APA StyleGlukhova, O. E. (2020). Liposome Drug Delivery System across Endothelial Plasma Membrane: Role of Distance between Endothelial Cells and Blood Flow Rate. Molecules, 25(8), 1875. https://doi.org/10.3390/molecules25081875





