Radiative Colloidal Investigation for Thermal Transport by Incorporating the Impacts of Nanomaterial and Molecular Diameters (dNanoparticles, dFluid): Applications in Multiple Engineering Systems
Abstract
1. Introduction
2. Results and Discussion
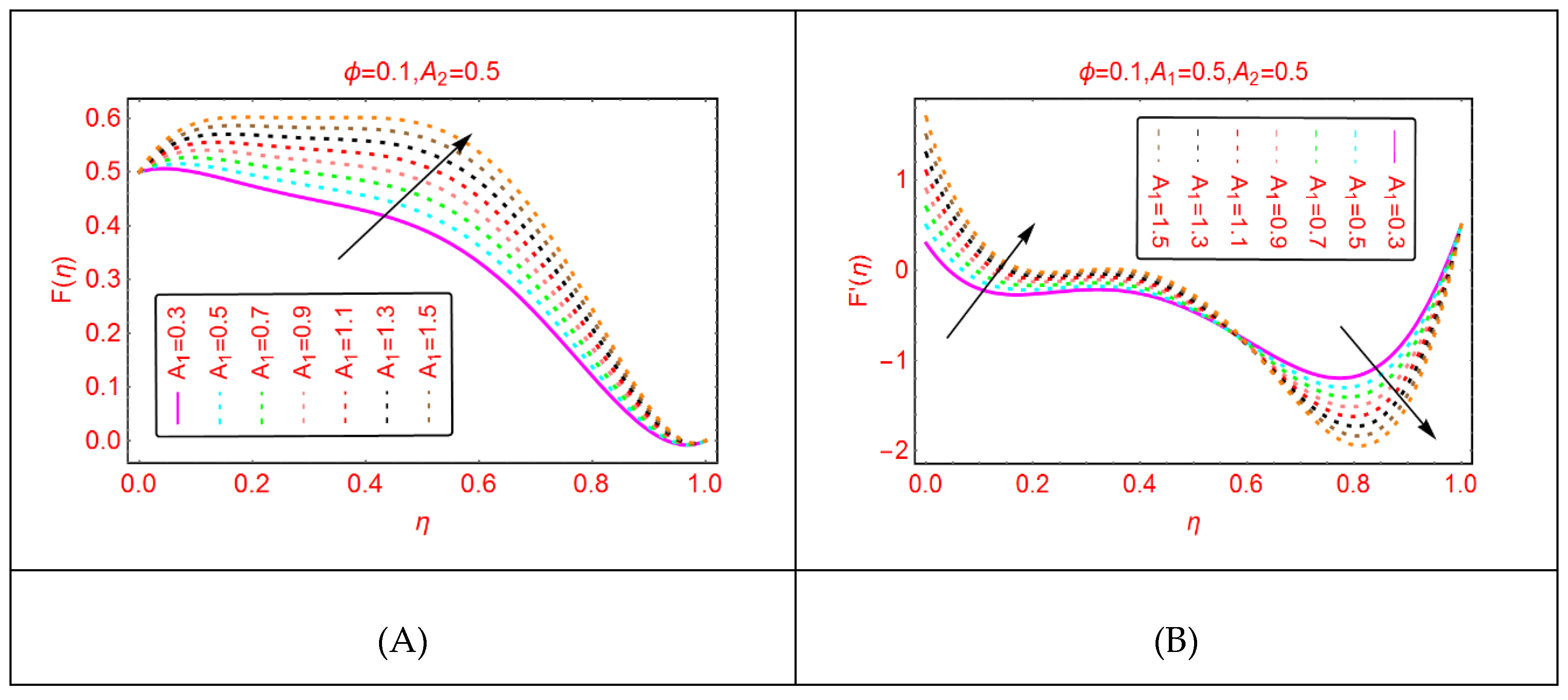
2.1. Axial and Radial Velocity Behavior
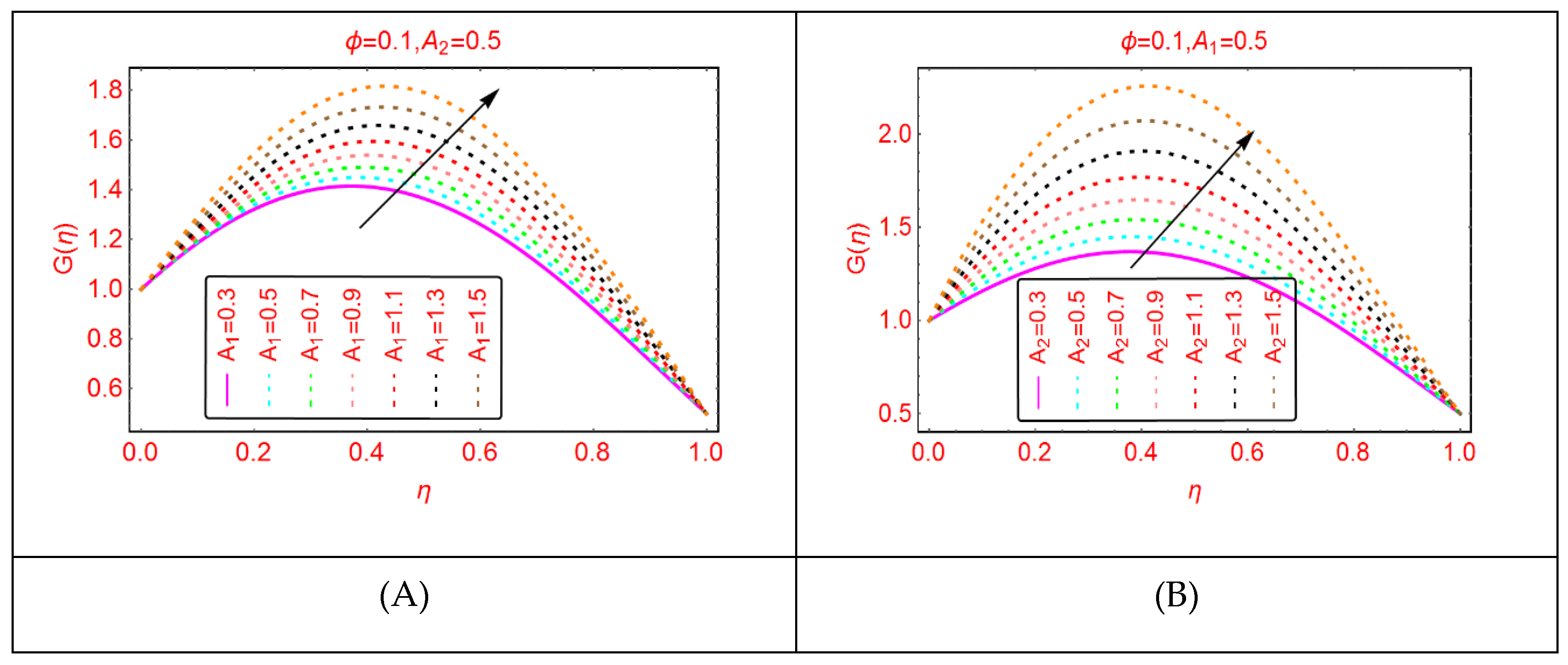
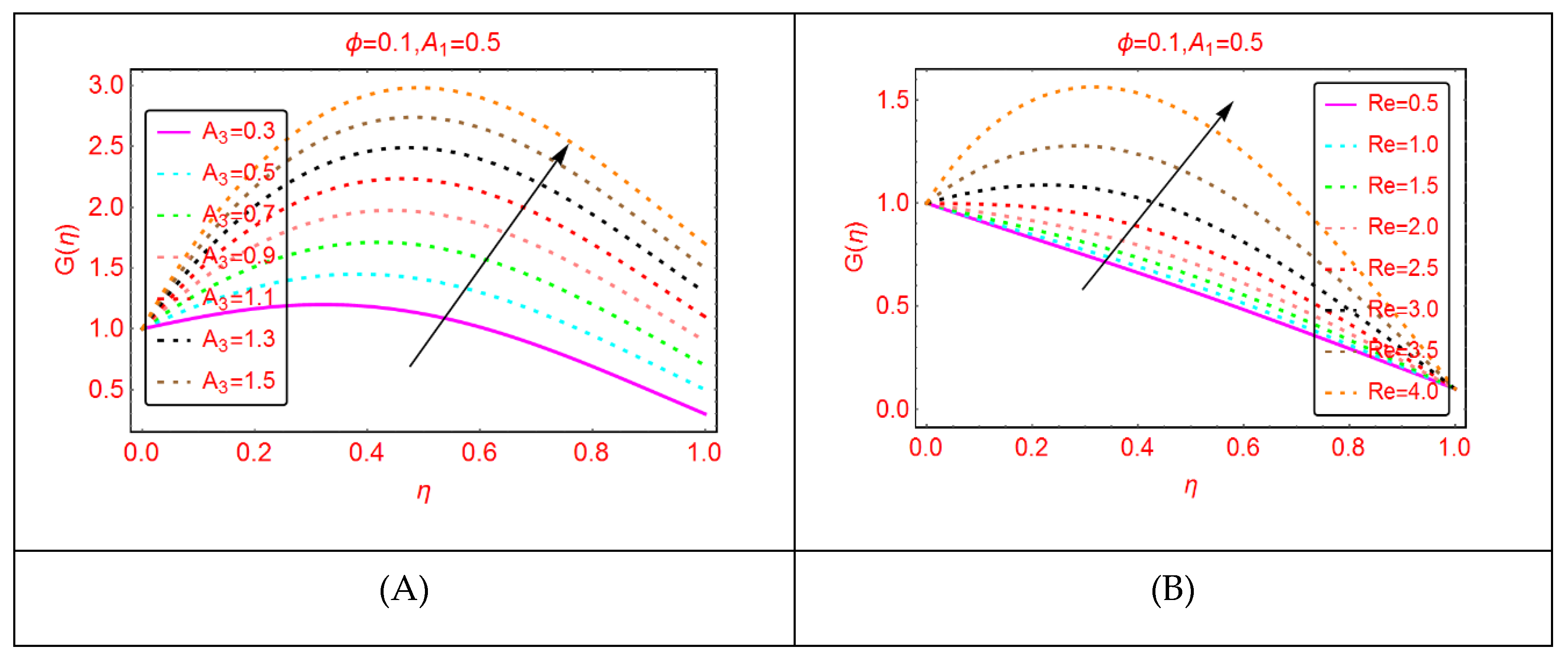
2.2. Tangential Velocity Behavior
2.3. Thermal Behavior
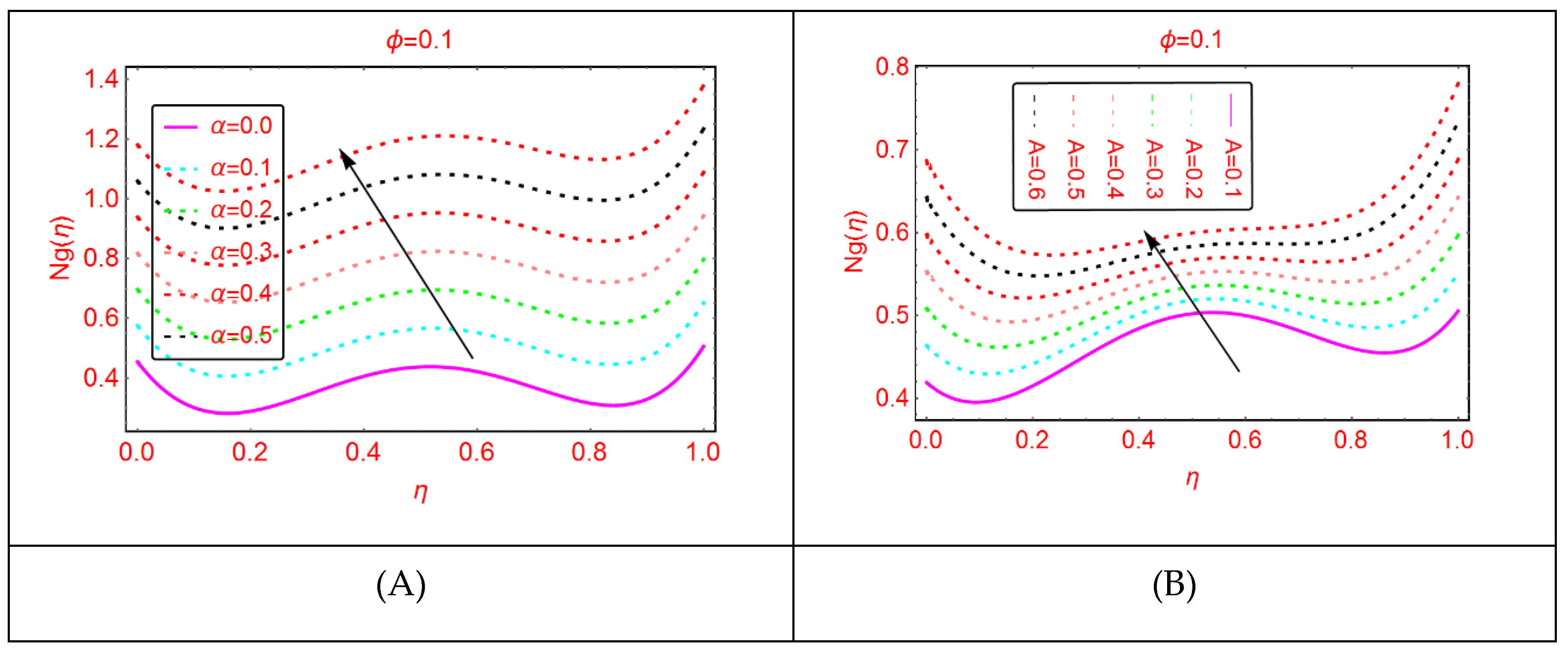
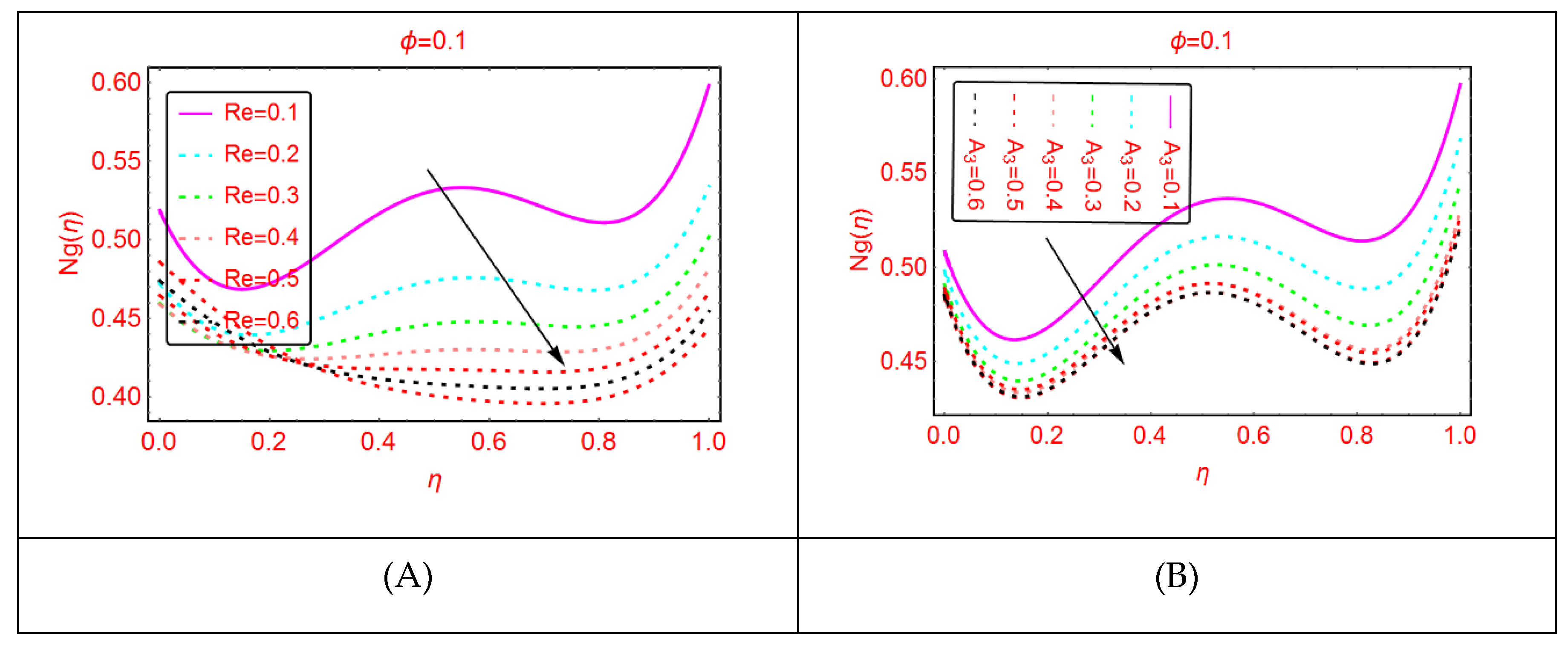
2.4. Bejan Effects and Entropy Generation
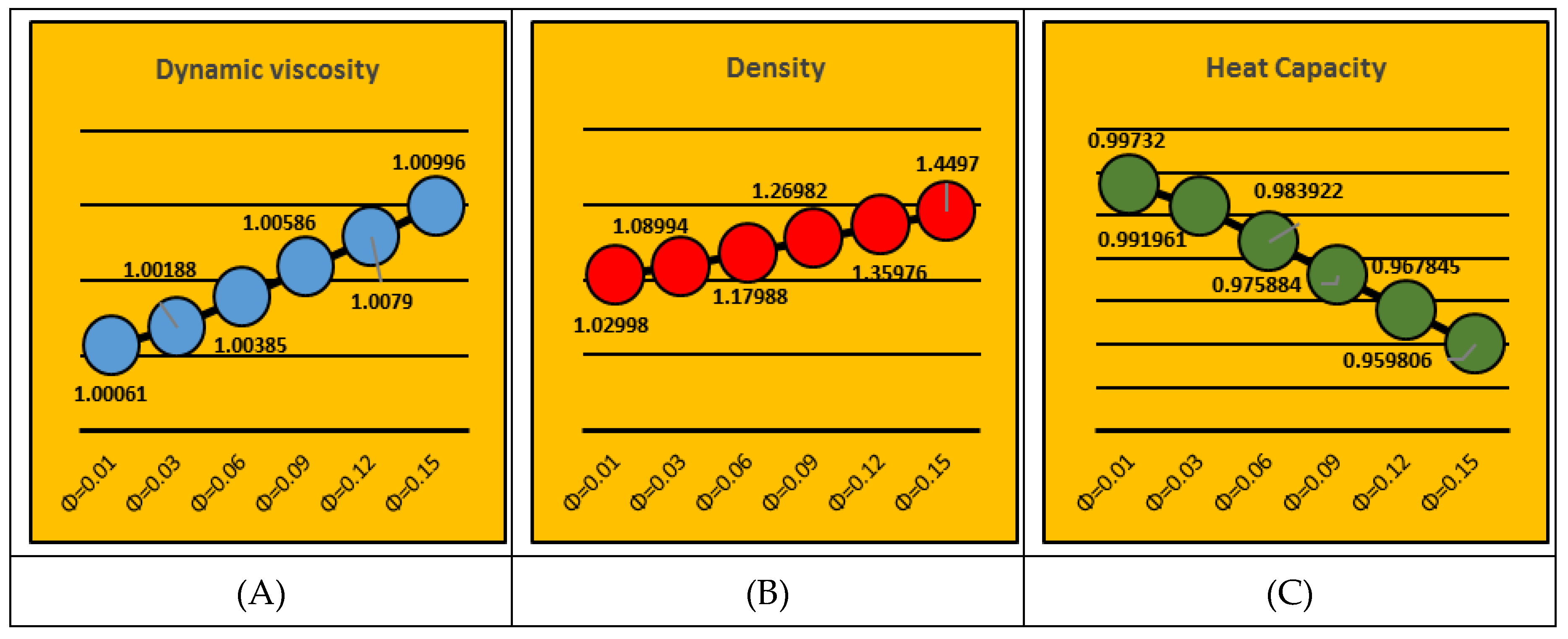
2.5. Thermophysical Characteristics
2.6. Engineering Quantities
3. Materials and Methods
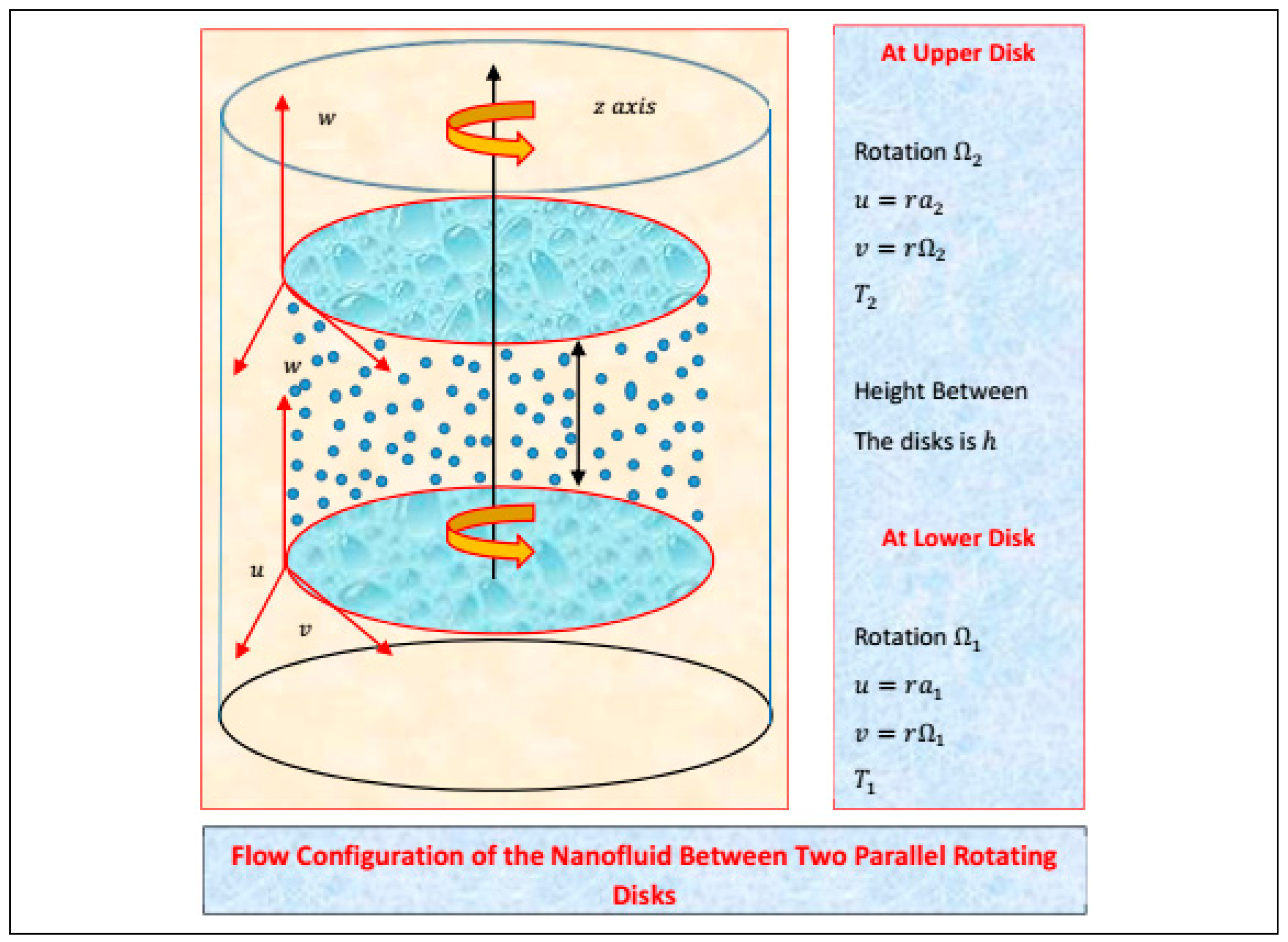
3.1. Statement and Geometry of the Model
3.2. Governing Colloidal Model
- The flow is viscous and incompressible;
- H2O is taken as host liquid;
- The nanomaterial of Al2O3 is taken;
- The host liquid and nanomaterial are thermally in equilibrium;
- There is no slip condition;
- Thermal radiations are imposed on the nanofluid flow.
3.3. Effective Characteristics
3.4. Nondimensional Nanofluid Model
3.5. Significant Quantities from for Engineers
3.6. Bejan Effects Modelling
3.7. Mathematical Analysis
4. Outcomes
- The axial velocity of Al2O3-H2O upturns due to the stretching of lower end over .
- Thermal transport enhances for Br and is detected that more dissipative Al2O3-H2O colloidal fluid is better for industrial and engineering applications where huge amount of heat transfer is required to acquire the process of production.
- The entropy generation due to an irreversible process such as fluid flow and heat transfer enhances in Al2O3-H2O for multiple values of .
- The effects on the colloidal flow of Al2O3-H2O enhances for strong thermal radiations phenomena.
- The effective characteristics of the colloidal fluid enhances for fraction factor of the nanomaterial, which significantly enhances the thermal transportation in Al2O3-H2O.
- Due to stronger fraction factor, , more colloidal fluid Al2O3-H2O particles drag at the surface are detected.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| effective density | |
| effective dynamic viscosity | |
| effective thermal conductivity | |
| effective heat capacity | |
| stands for nanofluid | |
| density of nanomaterial Al2O3-H2O | |
| density of host liquid | |
| fraction factor of the nanomaterial | |
| thermal conductivity of Al2O3 | |
| thermal conductivity of the host liquid | |
| heat capacity of Al2O3 | |
| heat capacity of host liquid | |
| temperature at lower disk | |
| temperature at upper disk | |
| viscous dissipation | |
| pressure | |
| diameter of nanomaterial | |
| Stefan Boltzmann coefficient | |
| similarity variable | |
| axial velocity | |
| radial velocity | |
| dimensionless temperature field | |
| Eckert number | |
| Reynolds number | |
| Radiation parameter | |
| Prandtl number | |
| Bejan number | |
| Entropy generation |
References
- Bhatti, M.M.; Khalique, C.M.; Tasveer, A.B.; Anwar, B.; Ali, K. Numerical study of slip and radiative effects on magnetic Fe 3 O 4-water-based nanofluid flow from a nonlinear stretching sheet in porous media with Soret and Dufour diffusion. Mod. Phys. Lett. B 2020, 34. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bhatti, M.M.; Sheikholeslami, M. Peristaltic Propulsion of Jeffrey Nanofluid with Thermal Radiation and Chemical Reaction Effects. Inventions 2019, 4. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Yousif, M.A.; Mishra, S.R.; Shahid, A. Simultaneous influence of thermo-diffusion and diffusion-thermo on non-Newtonian hyperbolic tangent magnetised nanofluid with Hall current through a nonlinear stretching surface. Pramana 2019, 93. [Google Scholar] [CrossRef]
- Machrafi, H.; Lebon, G. The role of several heat transfer mechanisms on the enhancement of thermal conductivity in nanofluids. Continuum Mech. Thermodyn. 2016, 28, 1461–1475. [Google Scholar] [CrossRef]
- Hayat, T.; Ahmad, M.W.; Khan, M.I.; Alsaedi, A. Entropy optimization in CNTs based nanomaterial flow induced by rotating disks: A study on the accuracy of statistical declaration and probable error. Comput. Methods Programs Biomed. 2020, 184. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, H.L.; Crosser, O.K. Thermal Conductivity of Heterogeneous Two-Component Systems. Ind. Eng. Chem. Fund 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. A new thermal conductivity model for nanofluids. J. Nano Res. 2004, 6, 577–588. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. Laminar nanofluid flow in micro-heat sinks. Int. J. Heat Mass Trans. 2005, 48, 2652–2661. [Google Scholar] [CrossRef]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer konstanten von heterogenen substanzen, I—Dielektrizitatskonstanten und leitfahigkeiten der mischkorper aus isotropen substanzen. Annalen. Physik. Leipzig. 1935, 24, 636–679. [Google Scholar] [CrossRef]
- Li, C.H.; Peterson, G.P. Experimental investigation of temperature and volume fraction variations on the effective thermal conductivity of nanoparticle suspensions (nanofluids). J. Appl. Phys. 2006, 99, 084314. [Google Scholar] [CrossRef]
- Patel, H.E.; Sundararajan, T.; Das, S.K. An experimental investigation into the thermal conductivity enhancement in oxide and metallic nanofluids. J. Nano Res. 2010, 12, 1015–1031. [Google Scholar] [CrossRef]
- Corcione, M. Rayleigh–Be’nard convection heat transfer in nanoparticle suspensions. Int. J. Heat Fluid Flow 2011, 32, 65–77. [Google Scholar] [CrossRef]
- Godson, R.L.; Mohan, L.B.; Wongwises, D.S. Experimental investigation on the thermal conductivity and viscosity of silver—deionized water nanofluid. Exp. Heat Transf. 2010, 23, 317–332. [Google Scholar] [CrossRef]
- Bhatta, D.P.; Mishra, S.R.; Dash, J.K. Unsteady squeezing flow of water-based nanofluid between two parallel disks with slip effects: Analytical approach. Heat Trans. 2019, 48, 1575–1594. [Google Scholar] [CrossRef]
- Sobamowo, M.G.; Akinshilo, A.T.; Yinusa, A.A. Thermo-Magneto-Solutal Squeezing Flow of Nanofluid between Two Parallel Disks Embedded in a Porous Medium: Effects of Nanoparticle Geometry, Slip and Temperature Jump Conditions. Model. Simul. Eng. 2018. [Google Scholar] [CrossRef]
- Das, K.; Jana, S.; Acharya, N. Slip effects on squeezing flow of nanofluid between two parallel disks. Int. J. Appl. Mech. Eng. 2016, 21, 5–20. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Khan, S.I.U.; Darus, M.; Hassan, S.M. Unsteady mixed convection squeezing flow of nanofluid between parallel disks. Newt. Non-Newt. Mod. Nano 2016. [Google Scholar] [CrossRef]
- Ahmed, N.; Adnan; Khan, U.; Mohyud-Din, S.T. Influence of shape factor on flow of magneto-nanofluid squeezed between parallel disks. Alex. Eng. J. 2018, 57, 1893–1903. [Google Scholar] [CrossRef]
- Azimi, M.; Riazi, R. Heat transfer analysis of GO-water nanofluid flow between two parallel disks. Prop. Power Res. 2015, 4, 23–30. [Google Scholar] [CrossRef]
- Vajravelu, K.; Prasad, K.V.; Ng, C.O.; Vaidya, H. MHD squeeze flow and heat transfer of a nanofluid between parallel disks with variable fluid properties and transpiration. Int. J. Mech. Mater. Eng. 2017. [Google Scholar] [CrossRef]
- Ahmed, N.; Adnan; Khan, U.; Mohyud-Din, S.T. Influence of an Effective Prandtl number Model on Squeezed Flow of γAl2O3-H2O and γAl2O3-C2H6O2 Nanofluids. J. Mol. Liq. 2017, 238, 447–454. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Sheremet, M.A.; Chamkha, A.J.; Hashim, I. MHD convective heat transfer in a discretely heated square cavity with conductive inner block using two-phase nanofuid model. Sci. Rep. 2018, 8, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Corcione, M. Empirical correlating equations for predicting the efective thermal conductivity and dynamic viscosity of nanofluids. Energy Convers. Manag. 2011, 52, 789–793. [Google Scholar] [CrossRef]
- Khan, U.; Adnan; Ahmed, N.; Mohyud-Din, S.T. 3D Squeezed Flow of γAl2O3-H2O and γAl2O3-C2H6O2 Nanofluids: A Numerical Study. Int. J. Hydrogen Energy 2017, 42, 24620–24633. [Google Scholar] [CrossRef]
- Ahmed, N.; Adnan; Khan, U.; Mohyud-Din, S.T. Unsteady Radiative Flow of Chemically reacting Fluid over a Convectively Heated Stretchable Surface with Cross-Diffusion Gradients. Int. J. Therm. Sci. 2017, 121, 182–191. [Google Scholar] [CrossRef]
Sample Availability: Materials for method are available from the authors. |














| Properties | |||||||
|---|---|---|---|---|---|---|---|
| Al2O3 | 33 | --------- |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, N.; Adnan; Khan, U.; Mohyud-Din, S.T.; Chu, Y.-M.; Khan, I.; Nisar, K.S. Radiative Colloidal Investigation for Thermal Transport by Incorporating the Impacts of Nanomaterial and Molecular Diameters (dNanoparticles, dFluid): Applications in Multiple Engineering Systems. Molecules 2020, 25, 1896. https://doi.org/10.3390/molecules25081896
Ahmed N, Adnan, Khan U, Mohyud-Din ST, Chu Y-M, Khan I, Nisar KS. Radiative Colloidal Investigation for Thermal Transport by Incorporating the Impacts of Nanomaterial and Molecular Diameters (dNanoparticles, dFluid): Applications in Multiple Engineering Systems. Molecules. 2020; 25(8):1896. https://doi.org/10.3390/molecules25081896
Chicago/Turabian StyleAhmed, Naveed, Adnan, Umar Khan, Syed Tauseef Mohyud-Din, Yu-Ming Chu, Ilyas Khan, and Kottakkaran Sooppy Nisar. 2020. "Radiative Colloidal Investigation for Thermal Transport by Incorporating the Impacts of Nanomaterial and Molecular Diameters (dNanoparticles, dFluid): Applications in Multiple Engineering Systems" Molecules 25, no. 8: 1896. https://doi.org/10.3390/molecules25081896
APA StyleAhmed, N., Adnan, Khan, U., Mohyud-Din, S. T., Chu, Y.-M., Khan, I., & Nisar, K. S. (2020). Radiative Colloidal Investigation for Thermal Transport by Incorporating the Impacts of Nanomaterial and Molecular Diameters (dNanoparticles, dFluid): Applications in Multiple Engineering Systems. Molecules, 25(8), 1896. https://doi.org/10.3390/molecules25081896







