Electronic and Magnetic Structures of New Interstitial Boron Sub-Oxides B12O2:X (X = B, C, N, O)
Abstract
1. Introduction
2. Computational Framework
3. Results from Energy Calculations
3.1. Trends of Cohesive Energies
3.2. Trends of Valence Electron Count VEC
3.3. Geometry Optimization Results
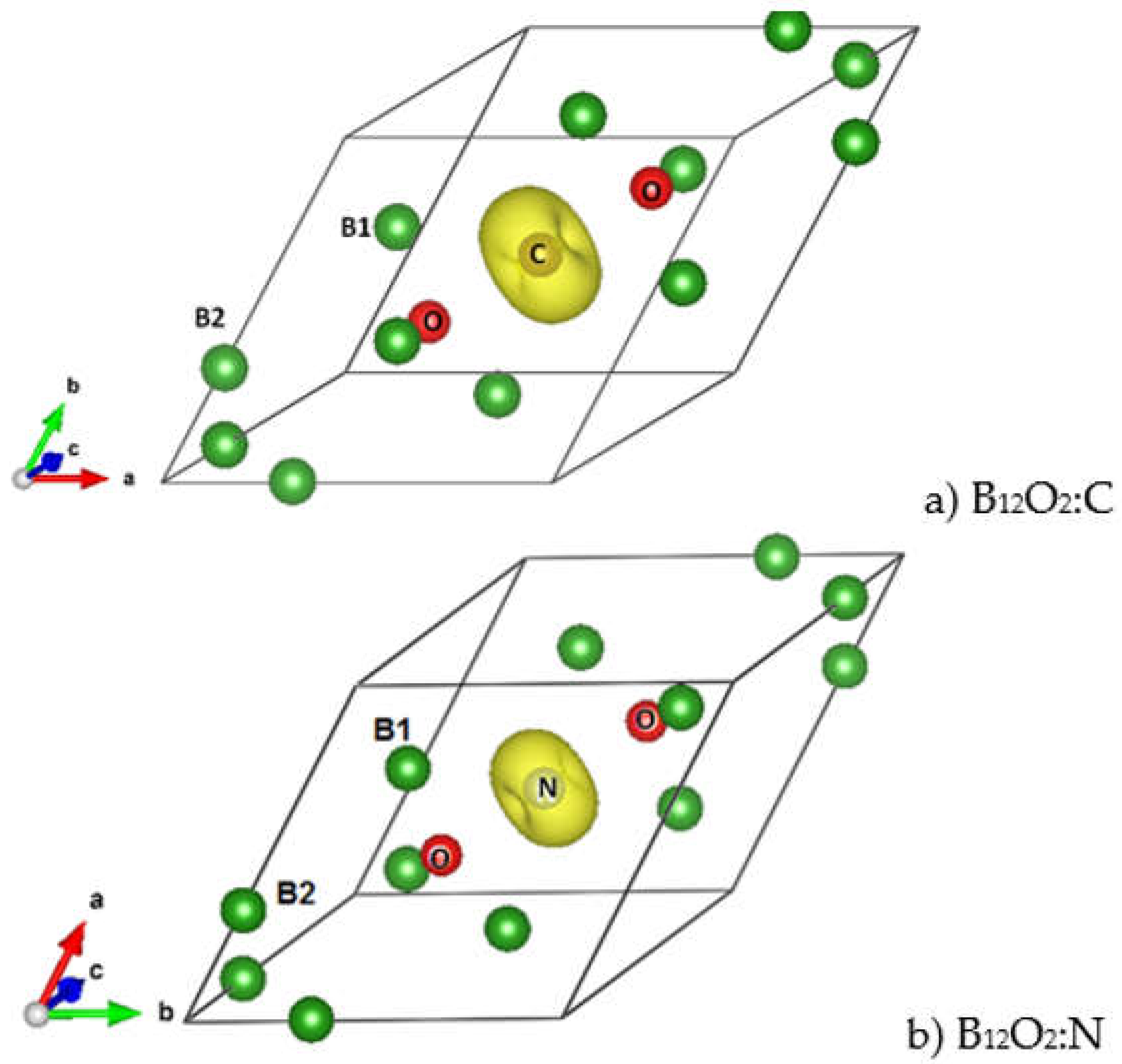
3.4. Electron Localization ELF Representations
3.5. Total and Magnetic Charge Densities
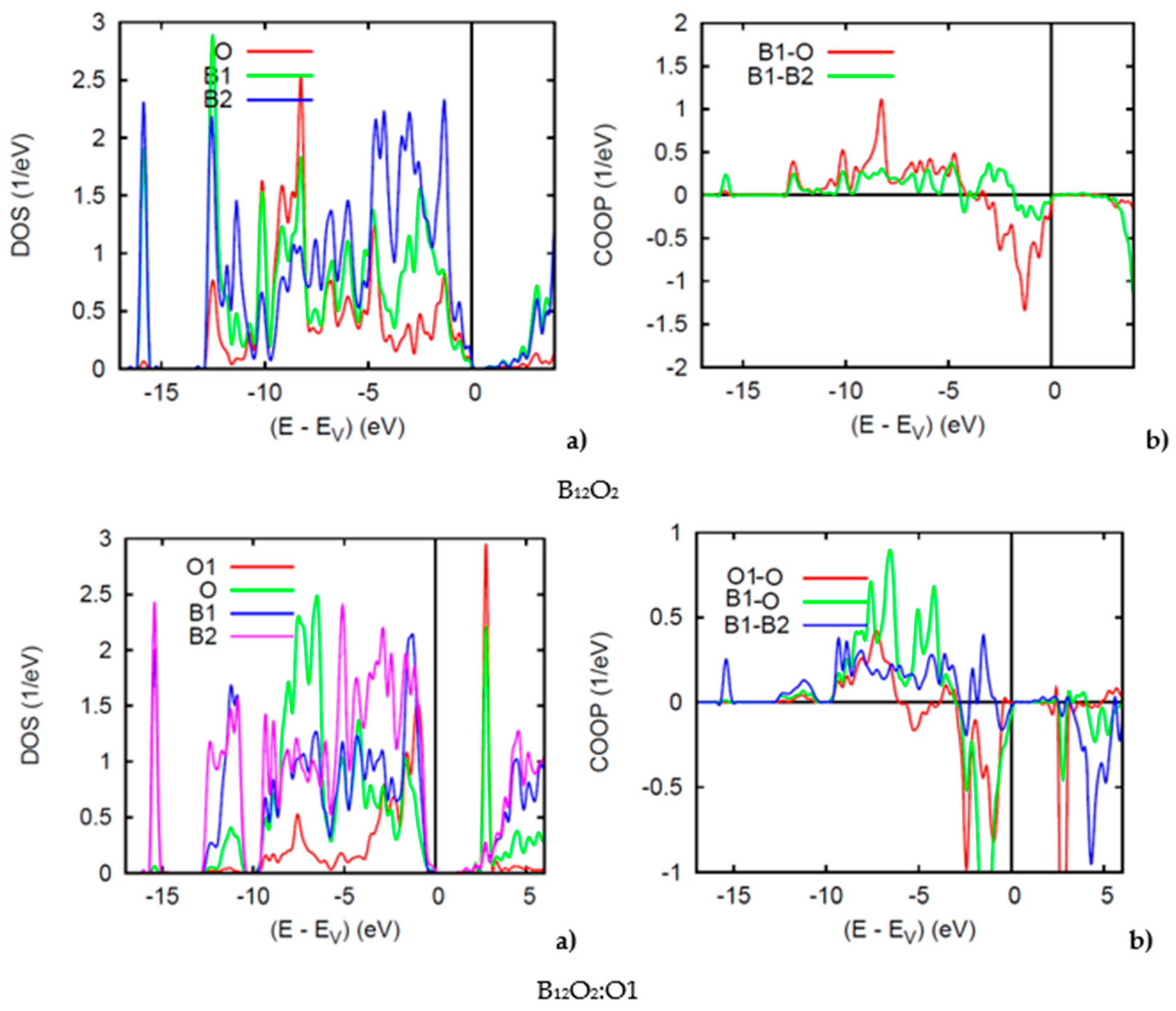
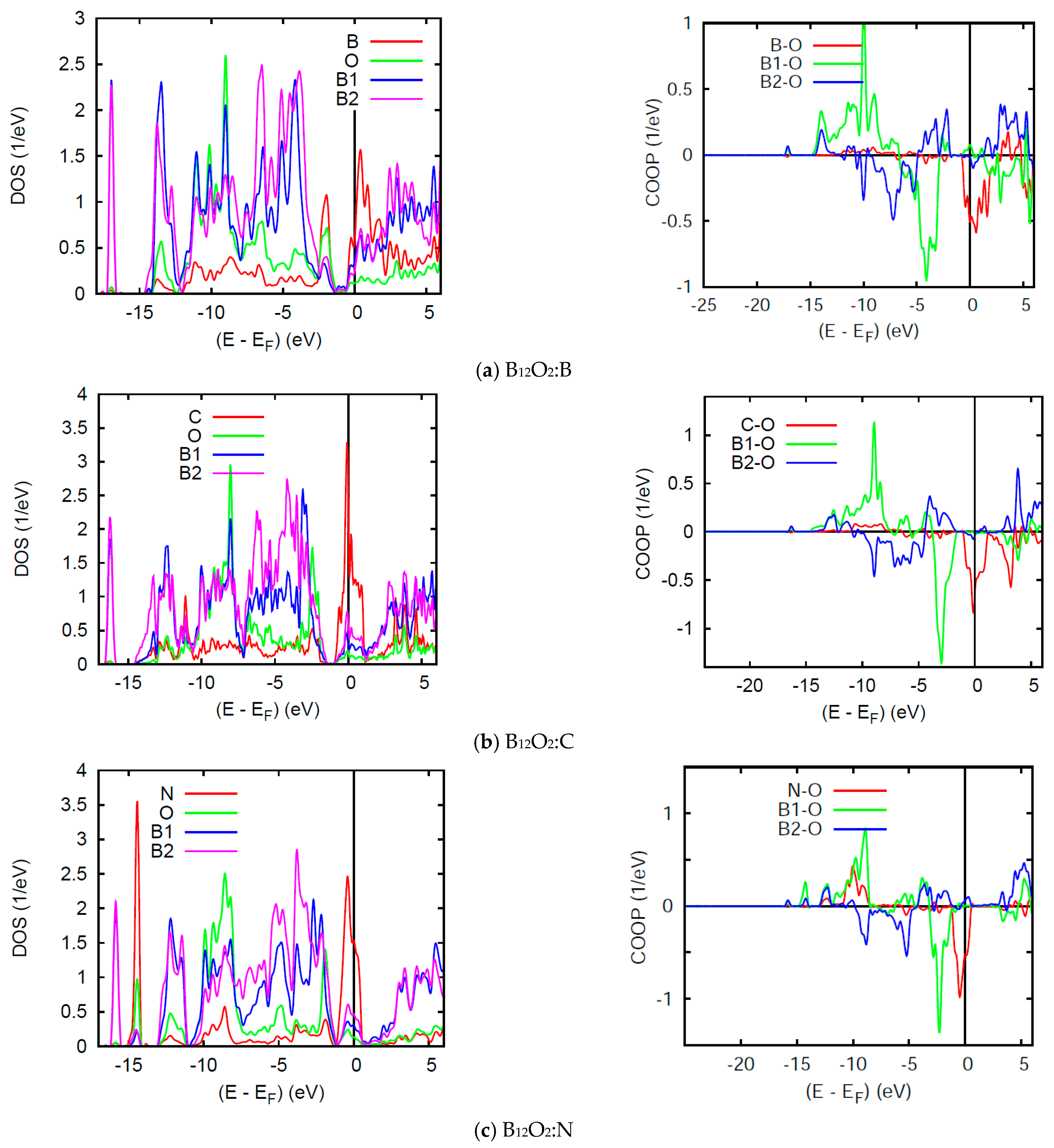
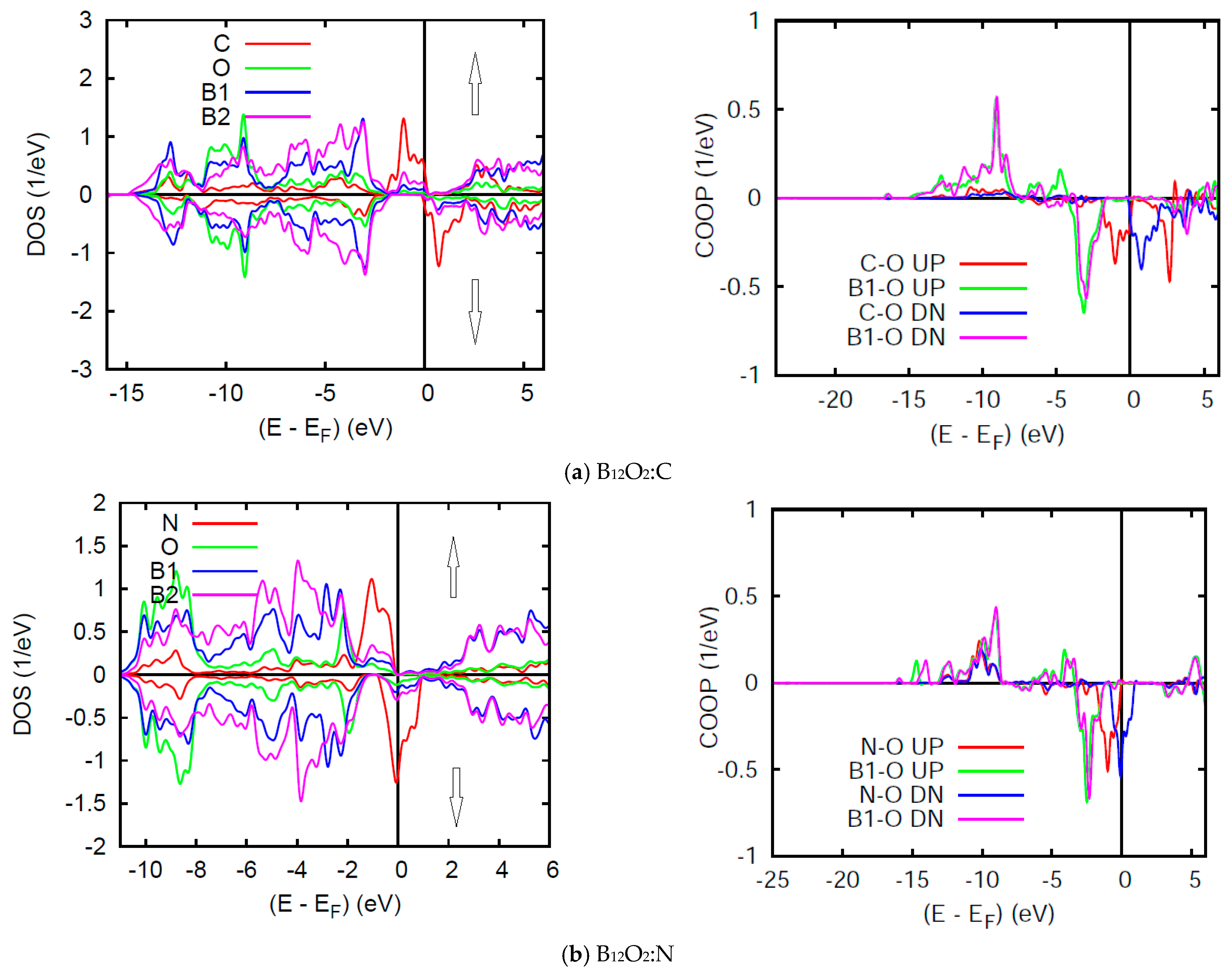
4. Electronic Structure and Bonding
4.1. NSP Calculations
4.2. SP Calculations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Turkevich, V.Z.; Turkevich, D.V.; Solozhenko, V.L. Phase Diagram of the B-B2O3 System at Pressures to 24 GPa. J. Superhard Mater. 2016, 38, 216–218. [Google Scholar] [CrossRef]
- Blomgren, H.; Lundstroem, T.; Okada, S. Structure refinement of the boron sub-oxide B6O by the Rietveld methods. AIP Conf. Proc. 1991, 231, 197. [Google Scholar]
- Decker, B.F.; Kasper, J.S. The crystal structure of a simple rhombohedral form of boron. Acta Cryst. 1959, 12, 503–506. [Google Scholar] [CrossRef]
- Olofsson, M.; Lundström, T. Synthesis and structure of non-stoichiometric B6O. J. Alloys Compd. 1997, 257, 91–95. [Google Scholar] [CrossRef]
- Endo, T.; Sato, T.; Shimada, M. High-pressure synthesis of B2O with diamond-like structure. J. Mater. Sci. Lett. 1987, 6, 683. [Google Scholar] [CrossRef]
- Grumbach, M.P.; Sankey, O.F.; McMillan, P.F. Properties of B2O: An unsymmetrical analog of carbon. Phys. Rev. B 1995, 52, 15807. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, 864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, 1133. [Google Scholar] [CrossRef]
- Etourneau, J.; Matar, S.F. rh.-B12 as host of interstitial atoms: Review of a large family with illustrative study of B12{CN2} from first-principles. Prog. Solid State Chem. 2020, 100296. [Google Scholar] [CrossRef]
- Kurakevych, O.O.; Solozhenko, V.L. Rhombohedral boron subnitride, B13N2, by X-ray powder diffraction. Acta Cryst. C 2007, 63, i80–i82. [Google Scholar] [CrossRef]
- Matar, S.F.; Solozhenko, V.L. First-principles studies of the electronic and magnetic structures and bonding properties of boron sub-nitride B13N2. J. Solid State Chem. 2020, 121840. [Google Scholar] [CrossRef]
- Kirfel, A.; Gupta, A.; Will, G. The Nature of the Chemical Bonding in Boron Carbide B13C2. I. Structure and Refinement. Acta Cryst. 1979, 35, 1052–1059. [Google Scholar] [CrossRef]
- Clark, H.K.; Hoard, J.L. The Crystal Structure of Boron Carbide. J. Am. Chem. Soc. 1943, 65, 2115–2119. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, J. From ultrasoft pseudopotentials to the projector augmented wave. Phys. Rev. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground State of the Electron Gas by a Stochastic Method. Phys. Rev. Lett. 1980, 45, 566–569. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes, 2nd ed.; Cambridge University Press: New York, NY, USA, 1986. [Google Scholar]
- Blöchl, P.E.; Jepsen, O.; Anderson, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. 1994, 49, 16223–16226. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special k-points for Brillouin Zone integration. Phys. Rev. 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Becke, D.; Edgecombe, K.E. A simple measure of electron localization. J. Chem. Phys. 1990, 92, 5397–5401. [Google Scholar] [CrossRef]
- Savin, A.; Jepsen, O.; Flad, J.; Andersen, O.K.; Preuss, H.; von Schneering, H.G. The ELF perspective of chemical bonding. Angew. Chem. Int. Ed. 1992, 31, 187–191. [Google Scholar] [CrossRef]
- Eyert, V. Basic notions, and applications of the augmented spherical wave ASW method. Int. J. Quantum Chem. 2000, 77, 1007–1012. [Google Scholar] [CrossRef]
- Hoffmann, R. Chemistry and Physics Meet in the Solid State. Angew. Chem. Int. Ed. 1987, 26, 846–878. [Google Scholar] [CrossRef]
- Marx, R.; Iberson, R.M. Powder diffraction study on solid ozone. Solid State Sci. 2001, 3, 195–202. [Google Scholar] [CrossRef]
- Mohn, P. Magnetism in the solid state: An introduction; Cardona, M., Fulde, P., von Klitzing, K., Merlin, R., Queisser, H.J., Störmer, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Matar, S.F.; Mavromaras, A. Band magnetism in A2T2Sn (A = Ce, U.; T = Ni, Pd) from local spin density functional calculations. J. Solid State Chem. 2000, 149, 449. [Google Scholar] [CrossRef]
- Matar, S.F.; Demazeau, G.; Sticht, J.; Eyert, V.; Kübler, J. Étude de la structure électronique et magnétique de CrO2. J. Phys. I 1992, 2, 315–328. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Casalot, A.; Hagenmuller, P. Les Oxydes des Métaux de Transition. Monographies de Chimie Minérale. Gauthiers-Villars: Paris, France, 1973. [Google Scholar]
- Manière, C.h.; Lee, G.; Olevsky, E.O. All-Materials-Inclusive Flash Spark Plasma Sintering. Sci. Rep. 2017, 7, 15071. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
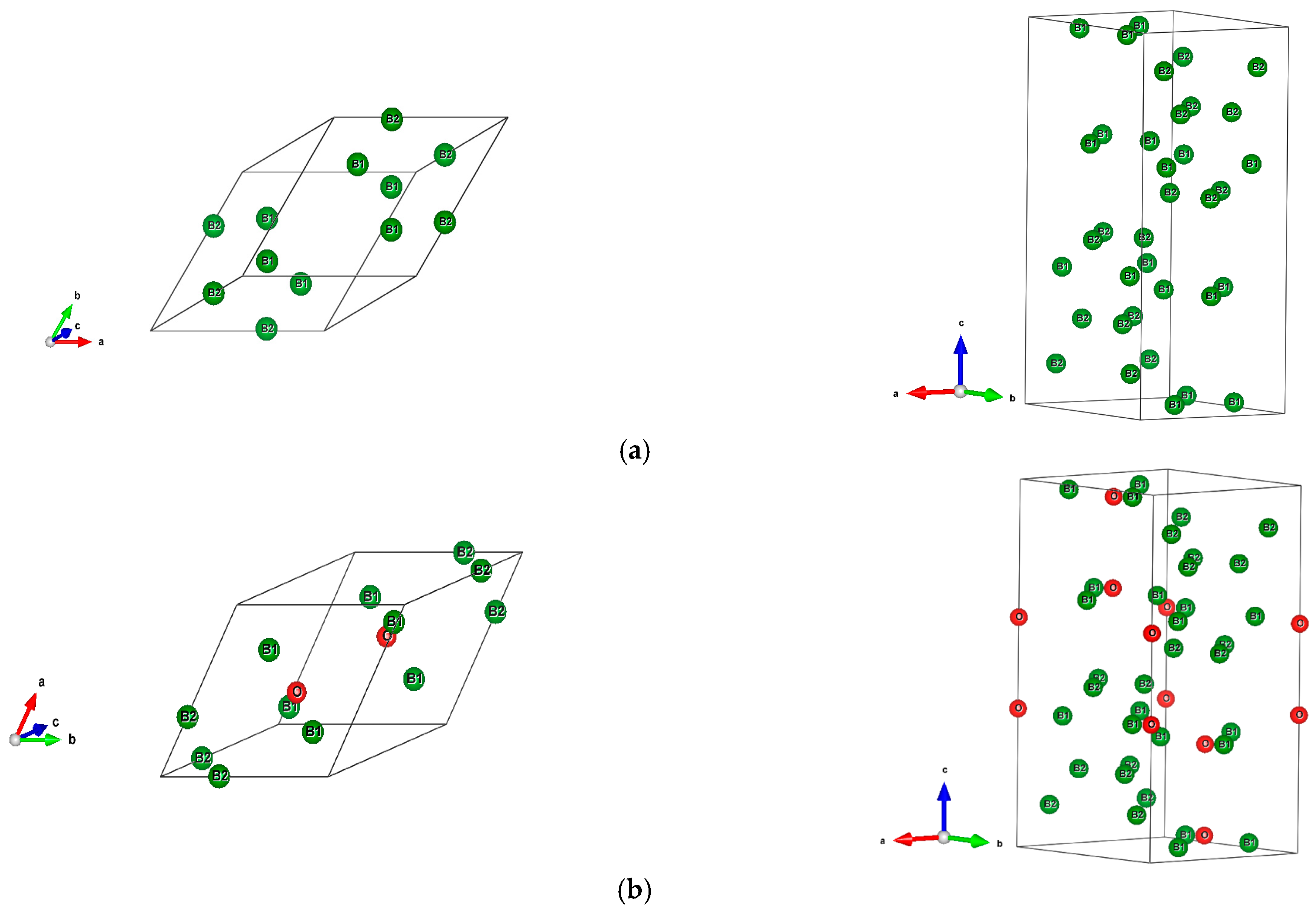
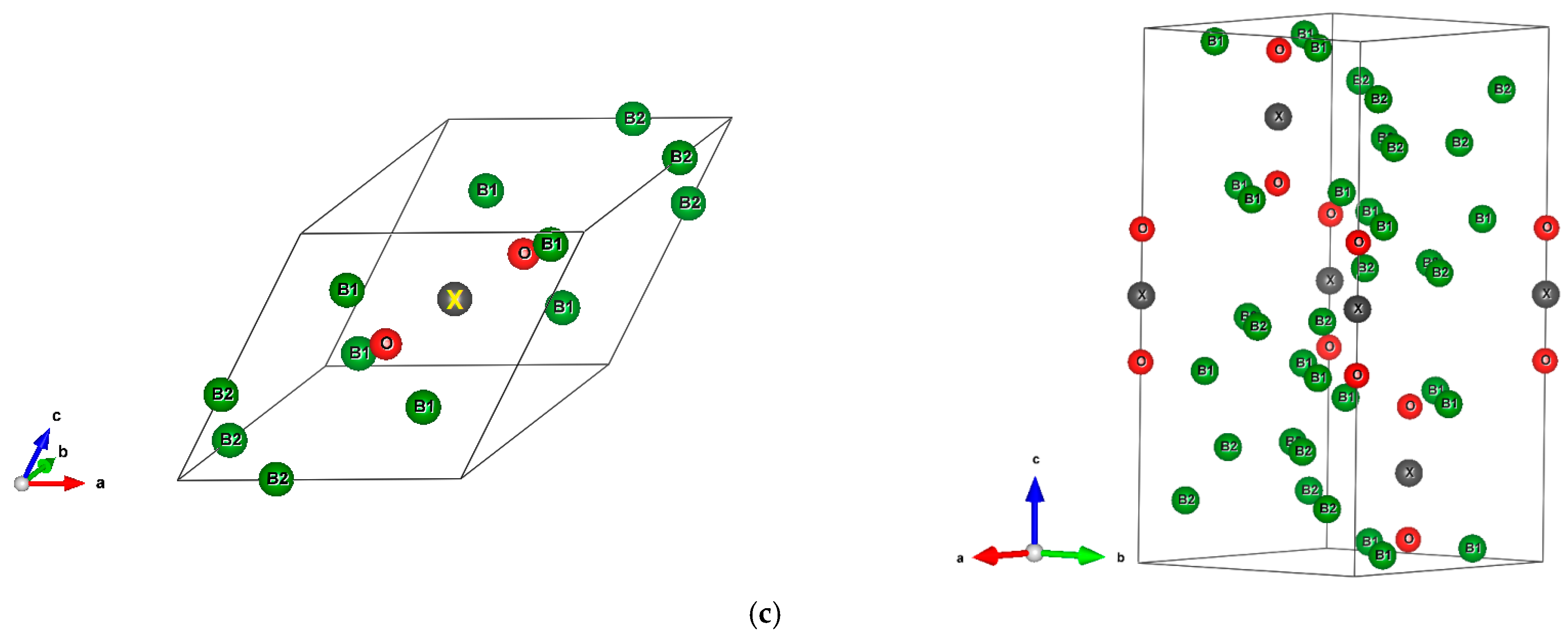
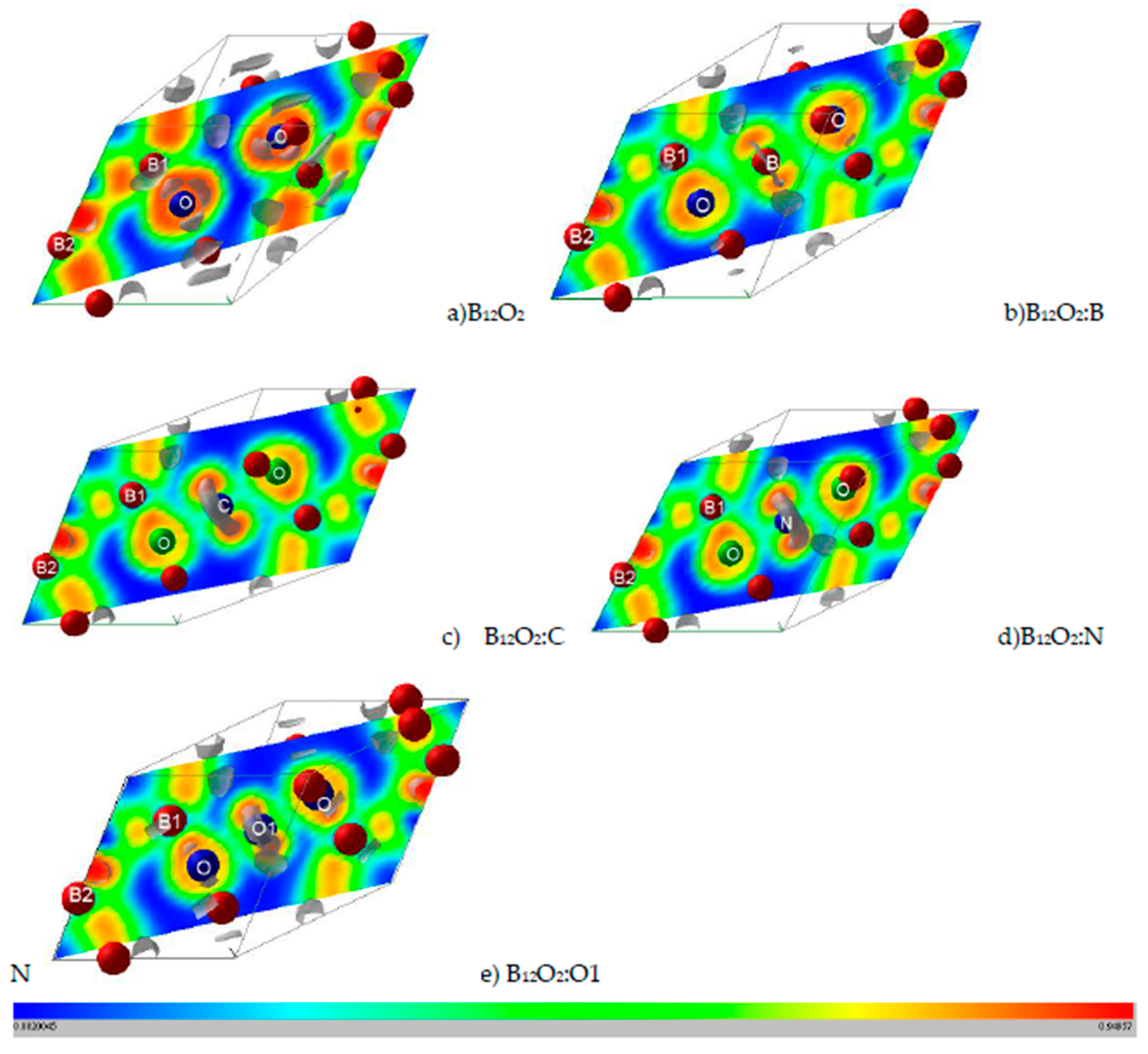
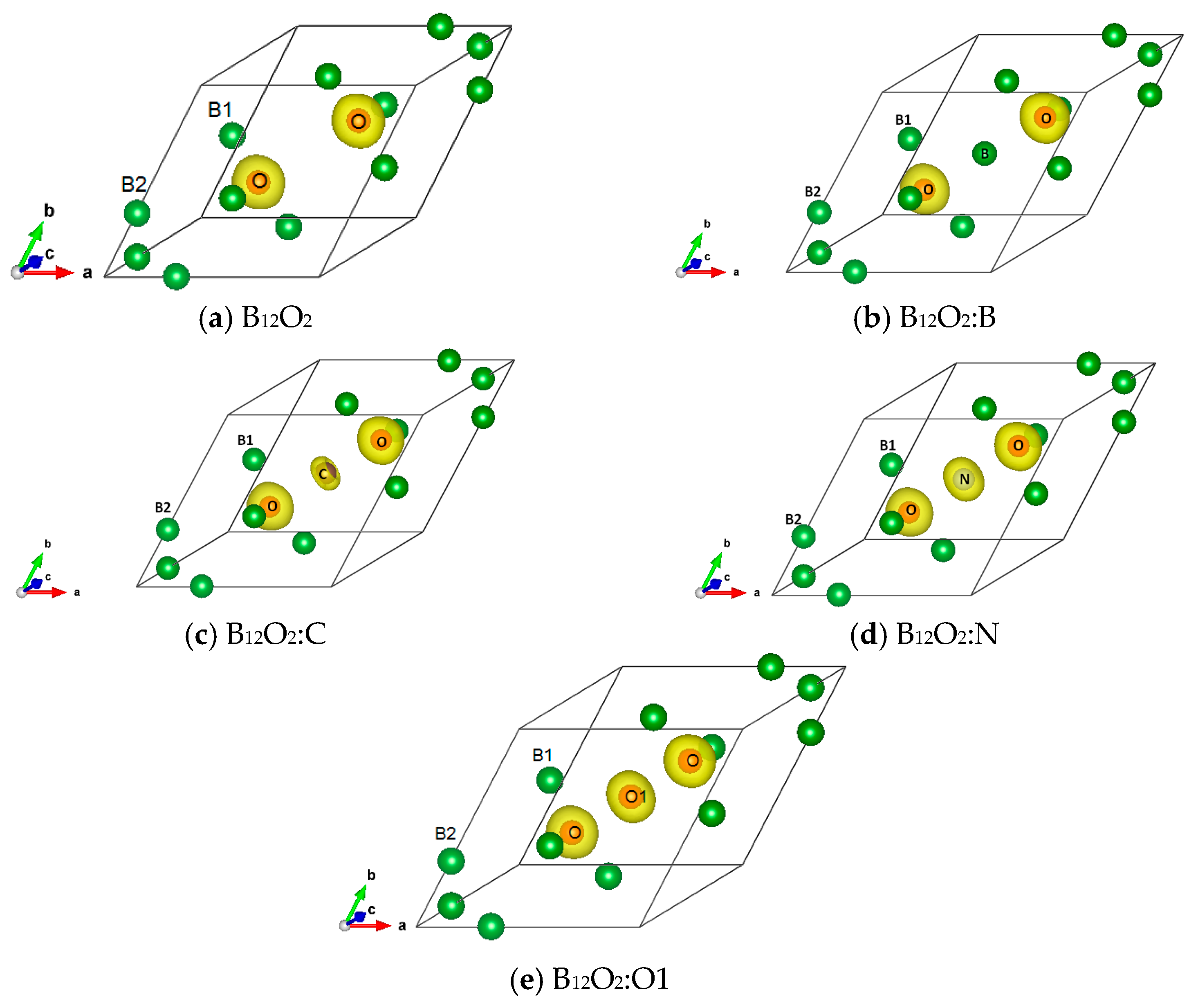
| Atom | Wyckoff | x | y | z |
|---|---|---|---|---|
| B1 | 6h | 0.800 (0.804) | 0.323 (0.323) | x |
| B2 | 6h | 0.347 (0.333) | 0.002 (0.003) | y |
| O | 2c | 0.376 (0.377) | x | x |
| Atom | Wyckoff | x | y | z |
|---|---|---|---|---|
| B1 | 6h | 0.806 | 0.321 | x |
| B2 | 6h | 0.333 | 0.003 | y |
| O | 2c | 0.348 | x | x |
| Atom | Wyckoff | x | y | z |
|---|---|---|---|---|
| B1 | 6h | 0.805 | 0.323 | x |
| B2 | 6h | 0.333 | 0.004 | y |
| O | 2c | 0.352 | x | x |
| Atom | Wyckoff | x | y | z |
|---|---|---|---|---|
| B1 | 6h | 0.804 | 0.321 | x |
| B2 | 6h | 0.333 | 0.003 | y |
| O | 2c | 0.357 | x | x |
| Atom | Wyckoff | x | y | z |
|---|---|---|---|---|
| B1 | 6h | 0.804 | 0.320 | x |
| B2 | 6h | 0.332 | 0.003 | y |
| O | 2c | 0.363 | x | x |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matar, S.F.; Etourneau, J. Electronic and Magnetic Structures of New Interstitial Boron Sub-Oxides B12O2:X (X = B, C, N, O). Molecules 2021, 26, 123. https://doi.org/10.3390/molecules26010123
Matar SF, Etourneau J. Electronic and Magnetic Structures of New Interstitial Boron Sub-Oxides B12O2:X (X = B, C, N, O). Molecules. 2021; 26(1):123. https://doi.org/10.3390/molecules26010123
Chicago/Turabian StyleMatar, Samir F., and Jean Etourneau. 2021. "Electronic and Magnetic Structures of New Interstitial Boron Sub-Oxides B12O2:X (X = B, C, N, O)" Molecules 26, no. 1: 123. https://doi.org/10.3390/molecules26010123
APA StyleMatar, S. F., & Etourneau, J. (2021). Electronic and Magnetic Structures of New Interstitial Boron Sub-Oxides B12O2:X (X = B, C, N, O). Molecules, 26(1), 123. https://doi.org/10.3390/molecules26010123








