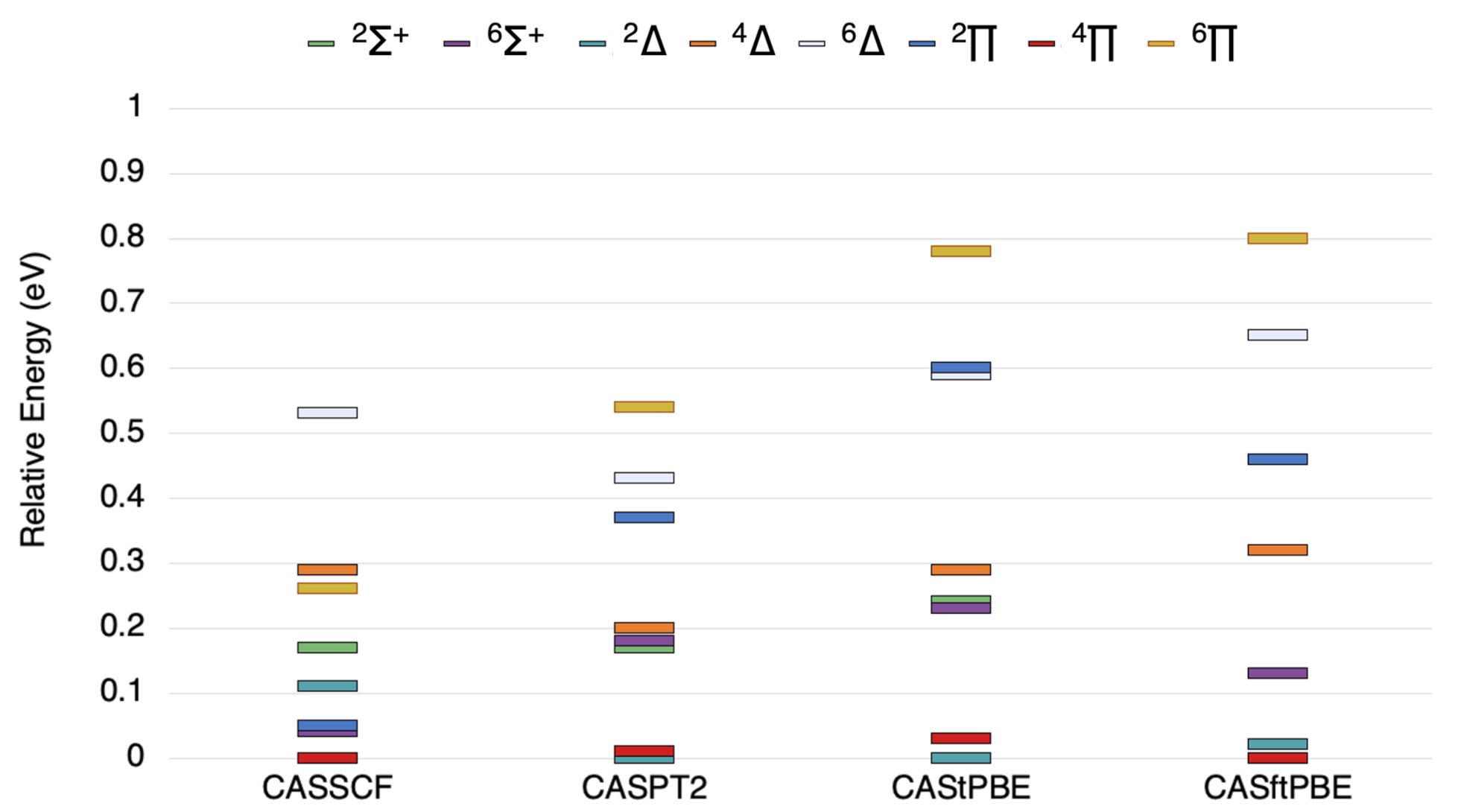
Figure 1.
The state ordering (in eV) of the lowest , , , , , , , and states of VSi as computed by the methods indicated.
Figure 1.
The state ordering (in eV) of the lowest , , , , , , , and states of VSi as computed by the methods indicated.
Figure 2.
The state ordering of the lowest , , , , , , , , and states states of NbSi as computed by the methods outlined above.
Figure 2.
The state ordering of the lowest , , , , , , , , and states states of NbSi as computed by the methods outlined above.
Figure 3.
The state ordering of the lowest , , , , , , and states of TaSi as computed by the methods indicated.
Figure 3.
The state ordering of the lowest , , , , , , and states of TaSi as computed by the methods indicated.
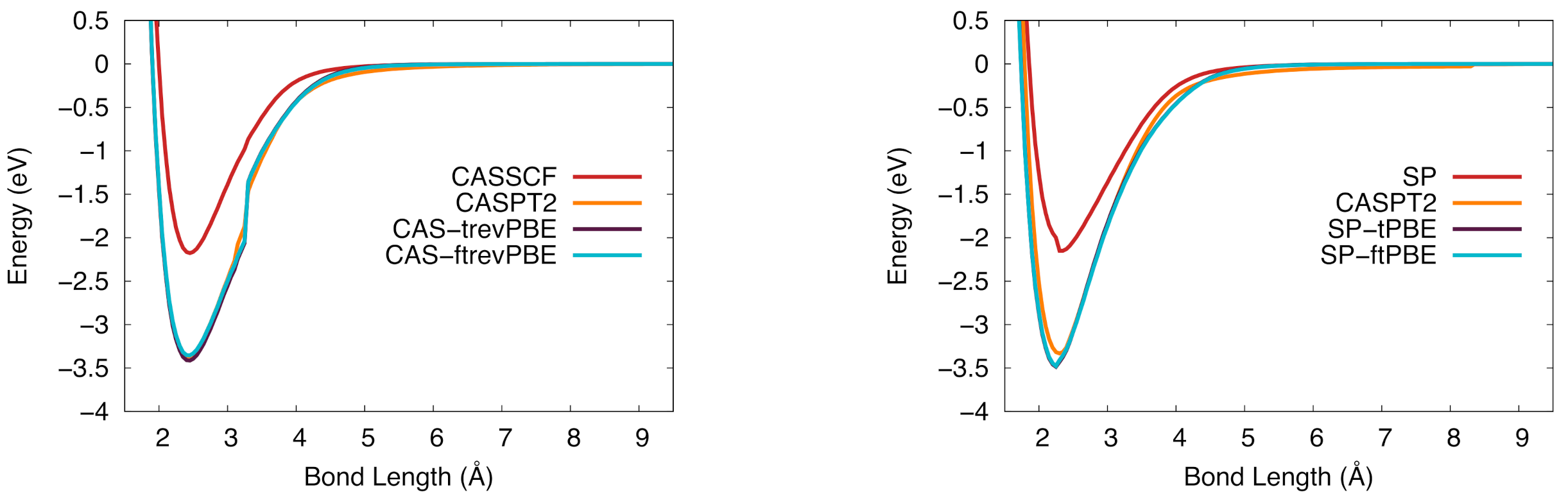
Figure 4.
The potential energy curve for vanadium silicide in the ground state. (Left): CASSCF (red), CASPT2 (orange), CAS-tPBE (purple), CAS-ftPBE (blue). (Right): Computed with SP (red), SP-tPBE (purple), SP-ftPBE (blue), and CASPT2 (orange).
Figure 4.
The potential energy curve for vanadium silicide in the ground state. (Left): CASSCF (red), CASPT2 (orange), CAS-tPBE (purple), CAS-ftPBE (blue). (Right): Computed with SP (red), SP-tPBE (purple), SP-ftPBE (blue), and CASPT2 (orange).
Figure 5.
The potential energy curve for vanadium silicide in the ground state. (Left): CASSCF (red), CASPT2 (orange), CAS-tPBE (purple), CAS-ftPBE (blue). (Right): SP (red), SP-tPBE (purple), SP-ftPBE (blue), CASPT2 (orange).
Figure 5.
The potential energy curve for vanadium silicide in the ground state. (Left): CASSCF (red), CASPT2 (orange), CAS-tPBE (purple), CAS-ftPBE (blue). (Right): SP (red), SP-tPBE (purple), SP-ftPBE (blue), CASPT2 (orange).
Figure 6.
The potential energy curve for niobium silicide in the ground state. (Left): CASSCF (red), CASPT2 (orange), CAS-tPBE (purple), CAS-ftPBE (blue). (Right): SP (red), SP-tPBE (purple), SP-ftPBE (blue), CASPT2 (orange).
Figure 6.
The potential energy curve for niobium silicide in the ground state. (Left): CASSCF (red), CASPT2 (orange), CAS-tPBE (purple), CAS-ftPBE (blue). (Right): SP (red), SP-tPBE (purple), SP-ftPBE (blue), CASPT2 (orange).
Figure 7.
The potential energy curve for niobium silicide in the ground state. (Left): Computed with CASSCF (red), CASPT2 (orange), CAS-tPBE (purple), CAS-ftPBE (blue) with a (7,10) active space. (Right): Computed with SP (red), SP-tPBE (purple), SP-ftPBE (blue) with a GAS5(7,10) active space. CASPT2 (orange) is included for comparison.
Figure 7.
The potential energy curve for niobium silicide in the ground state. (Left): Computed with CASSCF (red), CASPT2 (orange), CAS-tPBE (purple), CAS-ftPBE (blue) with a (7,10) active space. (Right): Computed with SP (red), SP-tPBE (purple), SP-ftPBE (blue) with a GAS5(7,10) active space. CASPT2 (orange) is included for comparison.
Figure 8.
The potential energy curve for tantalum silicide in the ground state. (Left): Computed with CASSCF (red), CASPT2 (orange), CAS-tPBE (purple), CAS-ftPBE (blue) with a (7,10) active space. (Right): Computed with SP (red), SP-tPBE (purple), SP-ftPBE (blue) with a GAS5(7,10) active space. CASPT2 (orange) is included for comparison.
Figure 8.
The potential energy curve for tantalum silicide in the ground state. (Left): Computed with CASSCF (red), CASPT2 (orange), CAS-tPBE (purple), CAS-ftPBE (blue) with a (7,10) active space. (Right): Computed with SP (red), SP-tPBE (purple), SP-ftPBE (blue) with a GAS5(7,10) active space. CASPT2 (orange) is included for comparison.
Table 1.
The dominant configuration and the number of configuration state functions for the active spaces of each state.
Table 1.
The dominant configuration and the number of configuration state functions for the active spaces of each state.
| | | # CSFs |
|---|
| State | Dominant Configuration | CASSCF | SP |
| 1211311 | 3480 | 152 |
| 1211311 | 2280 | - |
| 1211311 | 504 | 80 |
| 1211311 | 3460 | 336 |
| 12111311 | 2320 | - |
| 121111311 | 492 | - |
| 1211311 | 3460 | - |
| 1211311 | 2320 | 272 |
| 12111311 | 492 | - |
Table 2.
The SP approximation subspaces listed by state.
Table 2.
The SP approximation subspaces listed by state.
| State | GAS1 | GAS2 | GAS3 | GAS4 | GAS5 |
|---|
| (2e,2o) | (1e,2o) | (2e,2o) | (2e,2o) | |
| | 2,2 | 3,3 | 1,1 | 1,1 |
| (2e,2o) | (1e,2o) | (1e,2o) | (2e,2o) | (1e,2o) |
| | 2,2 | 3,3 | 1,1 | 1,1 | 1,1 |
| (2e,2o) | (2e,2o) | (1e,2o) | (2e,2o) |
| | 2,2 | 1,1 | 1,1 | 1,1 |
| (2e,2o) | (1e,2o) | (1e,2o) | (1e,2o) | (2e,2o) |
| | 2,2 | 3,3 | 1,1 | 1,1 | 1,1 |
Table 3.
The experimental bond dissociation energy, D, and the presently used values for spin-orbit contributions to the energies where A is V, Nb, or Ta, and B is Si. All entries are in eV, and the numbers in parentheses are the experimental uncertainties in the last digit.
Table 3.
The experimental bond dissociation energy, D, and the presently used values for spin-orbit contributions to the energies where A is V, Nb, or Ta, and B is Si. All entries are in eV, and the numbers in parentheses are the experimental uncertainties in the last digit.
| Molecule (AB) | D(exp.) | SOC(A) | SOC(B) | SOC(AB) |
|---|
| VSi | 2.234(2) | −0.07 | −0.019 | −0.014 |
| NbSi | 3.080(3) | −0.13 | −0.019 | 0 |
| TaSi | 2.999(3) | −0.70 | −0.019 | −0.421 |
Table 4.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for VSi in the molecular state, computed with a CASSCF wave function.
Table 4.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for VSi in the molecular state, computed with a CASSCF wave function.
| Method | r | D | D | | ZPE |
|---|
| Exp [6] | - | - | 2.234(2) | - | - |
| B3LYP [6] | 2.433 | - | 2.54 | 0.31 | - |
| CASSCF | 2.472 | 0.99 | 0.90 | −1.33 | 116.6 |
| CASPT2 | 2.284 | 2.29 | 2.19 | −0.04 | 220.3 |
| CAS-tBLYP | 2.276 | 2.14 | 2.04 | −0.19 | 236.5 |
| CAS-ftBLYP | 2.270 | 2.13 | 2.03 | −0.20 | 233.3 |
| CAS-tOreLYP | 2.261 | 2.35 | 2.25 | 0.01 | 242.2 |
| CAS-ftOReLYP | 2.261 | 2.27 | 2.17 | −0.07 | 234.1 |
| CAS-tPBE | 2.274 | 2.38 | 2.27 | 0.04 | 238.1 |
| CAS-ftPBE | 2.280 | 2.33 | 2.23 | −0.01 | 231.7 |
| CAS-trevPBE | 2.265 | 2.52 | 2.43 | 0.20 | 234.9 |
| CAS-ftrevPBE | 2.266 | 2.51 | 2.40 | 0.17 | 225.2 |
| MUE (CAS-PDFT) | | | | 0.12 | |
Table 5.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for VSi in the molecular state, computed with a SP wave function.
Table 5.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for VSi in the molecular state, computed with a SP wave function.
| Method | R | D | D | D | ZPE |
|---|
| Exp [6] | - | - | 2.234(2) | - | - |
| SP | 2.490 | 1.24 | 1.15 | −1.08 | 115.0 |
| SP-tBLYP | 2.276 | 2.14 | 2.04 | −0.19 | 234.9 |
| SP-ftBLYP | 2.265 | 2.07 | 1.97 | −0.27 | 232.5 |
| SP-tOreLYP | 2.271 | 2.13 | 2.02 | −0.21 | 235.7 |
| SP-ftOReLYP | 2.257 | 2.18 | 2.07 | −0.16 | 234.1 |
| SP-tPBE | 2.270 | 2.38 | 2.28 | 0.04 | 237.3 |
| SP-ftPBE | 2.276 | 2.34 | 2.23 | −0.01 | 230.9 |
| SP-trevPBE | 2.261 | 2.55 | 2.45 | 0.21 | 233.3 |
| SP-ftrevPBE | 2.262 | 2.50 | 2.40 | 0.17 | 224.4 |
| MUE (SP-PDFT) | | | | 0.16 | |
Table 6.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for VSi in the molecular state, computed with a CASSCF wave function.
Table 6.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for VSi in the molecular state, computed with a CASSCF wave function.
| Method | r | D | D | | ZPE |
|---|
| Exp [6] | - | - | 2.234(2) | - | - |
| CASSCF | 2.545 | 1.14 | 1.05 | −1.19 | 126.4 |
| CASPT2 | 2.233 | 2.26 | 2.16 | −0.07 | 181.4 |
| CAS-tBLYP | 2.241 | 1.95 | 1.85 | −0.38 | 195.2 |
| CAS-ftBLYP | 2.231 | 2.03 | 1.93 | −0.31 | 200.9 |
| CAS-tOreLYP | 2.189 | 2.22 | 2.11 | −0.12 | 217.1 |
| CAS-ftOReLYP | 2.200 | 2.22 | 2.12 | −0.12 | 204.1 |
| CAS-tPBE | 2.219 | 2.42 | 2.32 | 0.08 | 202.5 |
| CAS-ftPBE | 2.225 | 2.44 | 2.34 | 0.11 | 196.8 |
| CAS-trevPBE | 2.222 | 2.26 | 2.16 | −0.08 | 259.2 |
| CAS-ftrevPBE | 2.242 | 2.39 | 2.20 | −0.04 | 186.3 |
| MUE (CAS-PDFT) | | | | 0.16 | |
Table 7.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for VSi in the molecular state, computed with a SP wave function.
Table 7.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for VSi in the molecular state, computed with a SP wave function.
| Method | R | D | D | D | ZPE |
|---|
| Exp [6] | - | - | 2.234(2) | - | - |
| SP | 2.531 | 1.27 | 1.18 | −1.05 | 138.5 |
| SP-tBLYP | 2.381 | 1.87 | 1.77 | −0.47 | 196.8 |
| SP-ftBLYP | 2.362 | 1.94 | 1.84 | −0.39 | 202.5 |
| SP-tOreLYP | 2.365 | 2.02 | 1.92 | −0.31 | 200.1 |
| SP-ftOReLYP | 2.350 | 2.08 | 1.98 | −0.25 | 204.1 |
| SP-tPBE | 2.370 | 2.27 | 2.17 | −0.06 | 200.9 |
| SP-ftPBE | 2.359 | 2.32 | 2.22 | −0.01 | 203.3 |
| SP-trevPBE | 2.337 | 2.12 | 2.03 | −0.21 | 283.5 |
| SP-ftrevPBE | 2.373 | 2.18 | 2.08 | −0.15 | 197.6 |
| MUE (SP-PDFT) | | | | 0.23 | |
Table 8.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for NbSi in the ground state, computed with a CASSCF wave function.
Table 8.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for NbSi in the ground state, computed with a CASSCF wave function.
| Method | State | R | D | D | D | ZPE |
|---|
| Exp [6] | - | - | - | 3.080(3) | - | - |
| B3LYP [6] | | 2.496 | - | 2.42 | −0.66 | - |
| CASSCF | | 2.449 | 2.18 | 2.00 | −1.08 | 190.4 |
| CASPT2 | | 2.502 | 3.48 | 3.31 | 0.23 | 191.2 |
| CAS-tBLYP | | 2.548 | 3.03 | 2.86 | −0.22 | 172.5 |
| CAS-ftBLYP | | 2.542 | 2.91 | 2.73 | −0.35 | 181.4 |
| CAS-tOreLYP | | 2.521 | 3.18 | 3.01 | −0.07 | 179.0 |
| CAS-ftOReLYP | | 2.513 | 3.16 | 2.98 | −0.10 | 179.8 |
| CAS-tPBE | | 2.522 | 3.52 | 3.35 | 0.27 | 181.4 |
| CAS-ftPBE | | 2.517 | 3.45 | 3.28 | 0.20 | 181.4 |
| CAS-trevPBE | | 2.531 | 3.34 | 3.17 | 0.09 | 179.0 |
| CAS-ftrevPBE | | 2.525 | 3.31 | 3.14 | 0.06 | 179.8 |
| MUE (CAS-PDFT) | | | | | 0.17 | |
Table 9.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for NbSi in the ground state, computed with a SP wave function.
Table 9.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for NbSi in the ground state, computed with a SP wave function.
| Method | State | R | D | D | D | ZPE |
|---|
| Exp [6] | - | - | 3.080(3) | - | - | - |
| SP | | 2.455 | 2.42 | 2.24 | −0.84 | 190.4 |
| SP-tBLYP | | 2.502 | 2.57 | 2.40 | −0.68 | 173.3 |
| SP-ftBLYP | | 2.488 | 2.64 | 2.47 | −0.61 | 173.3 |
| SP-tOreLYP | | 2.475 | 2.83 | 2.66 | −0.42 | 178.2 |
| SP-ftOReLYP | | 2.465 | 2.86 | 2.69 | −0.39 | 179.8 |
| SP-tPBE | | 2.481 | 3.00 | 2.83 | −0.26 | 181.4 |
| SP-ftPBE | | 2.471 | 3.03 | 2.86 | −0.22 | 181.4 |
| SP-trevPBE | | 2.492 | 2.85 | 2.68 | −0.40 | 179.0 |
| SP-ftrevPBE | | 2.482 | 2.88 | 2.71 | −0.37 | 179.8 |
| MUE (SP-PDFT) | | | | | 0.42 | |
Table 10.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for TaSi in the molecular state, computed with a CASSCF wave function.
Table 10.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for TaSi in the molecular state, computed with a CASSCF wave function.
| Method | R | D | D | D | ZPE |
|---|
| Exp [6] | - | - | - | 2.999(3) | - |
| B3LYP [6] | 2.375 | - | 2.68 | −0.39 | |
| CASSCF | 2.391 | 2.07 | 1.75 | −1.25 | 191.2 |
| CASPT2 | 2.344 | 3.17 | 2.85 | −0.15 | 205.7 |
| CAS-tBLYP | 2.384 | 2.80 | 2.48 | −0.52 | 192.0 |
| CAS-ftBLYP | 2.377 | 2.85 | 2.53 | −0.47 | 195.2 |
| CAS-tOreLYP | 2.357 | 3.08 | 2.75 | −0.25 | 200.9 |
| CAS-ftOReLYP | 2.356 | 3.03 | 2.71 | −0.29 | 200.1 |
| CAS-tPBE | 2.364 | 3.25 | 2.93 | −0.07 | 200.0 |
| CAS-ftPBE | 2.362 | 3.23 | 2.90 | −0.10 | 200.1 |
| CAS-trevPBE | 2.371 | 3.09 | 2.77 | −0.23 | 197.6 |
| CAS-ftrevPBE | 2.370 | 3.05 | 2.72 | −0.28 | 196.8 |
| MUE (CAS-PDFT) | | | | 0.27 | |
Table 11.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for TaSi in the molecular state, computed with a SP wave function.
Table 11.
Dissociation energies (eV), equilibrium bond lengths (Å), and zero point energies (in cm) for TaSi in the molecular state, computed with a SP wave function.
| Method | R | D | D | D | ZPE |
|---|
| Exp [6] | - | - | - | 2.999(3) | - |
| SP | 2.392 | 2.31 | 1.99 | −1.01 | 191.2 |
| SP-tBLYP | 2.381 | 2.76 | 2.44 | −0.56 | 191.2 |
| SP-ftBLYP | 2.373 | 2.78 | 2.46 | −0.54 | 194.4 |
| SP-tOreLYP | 2.354 | 2.99 | 2.66 | −0.34 | 200.9 |
| SP-ftOReLYP | 2.353 | 2.95 | 2.67 | −0.37 | 200.9 |
| SP-tPBE | 2.360 | 3.24 | 2.92 | −0.08 | 200.1 |
| SP-ftPBE | 2.358 | 3.21 | 2.89 | −0.11 | 200.1 |
| SP-trevPBE | 2.368 | 3.07 | 2.75 | −0.25 | 196.8 |
| SP-ftrevPBE | 2.367 | 3.03 | 2.71 | −0.29 | 196.8 |
| MUE (SP-PDFT) | | | | 0.32 | |
Table 12.
The mean unsigned errors (eV) of ground state bond dissociation energies of transition metal diatomics as computed with CAS-PDFT and SP-PDFT/ESP-PDFT with various on-top pair-density functionals.
Table 12.
The mean unsigned errors (eV) of ground state bond dissociation energies of transition metal diatomics as computed with CAS-PDFT and SP-PDFT/ESP-PDFT with various on-top pair-density functionals.
| | tPBE | trevPBE | tBLYP | tOreLYP | ftPBE | ftrevPBE | ftBLYP | ftOreLYP | Overall |
|---|
| CAS | 0.30 | 0.25 | 0.30 | 0.26 | 0.28 | 0.23 | 0.28 | 0.26 | 0.27 |
| SP/ESP | 0.31 | 0.28 | 0.35 | 0.22 | 0.29 | 0.28 | 0.28 | 0.21 | 0.28 |