Determining Preexponential Factor in Model-Free Kinetic Methods: How and Why?
Abstract
:1. Introduction
2. How to Determine the Preexponential Factor
3. Why to Determine the Preexponential Factor
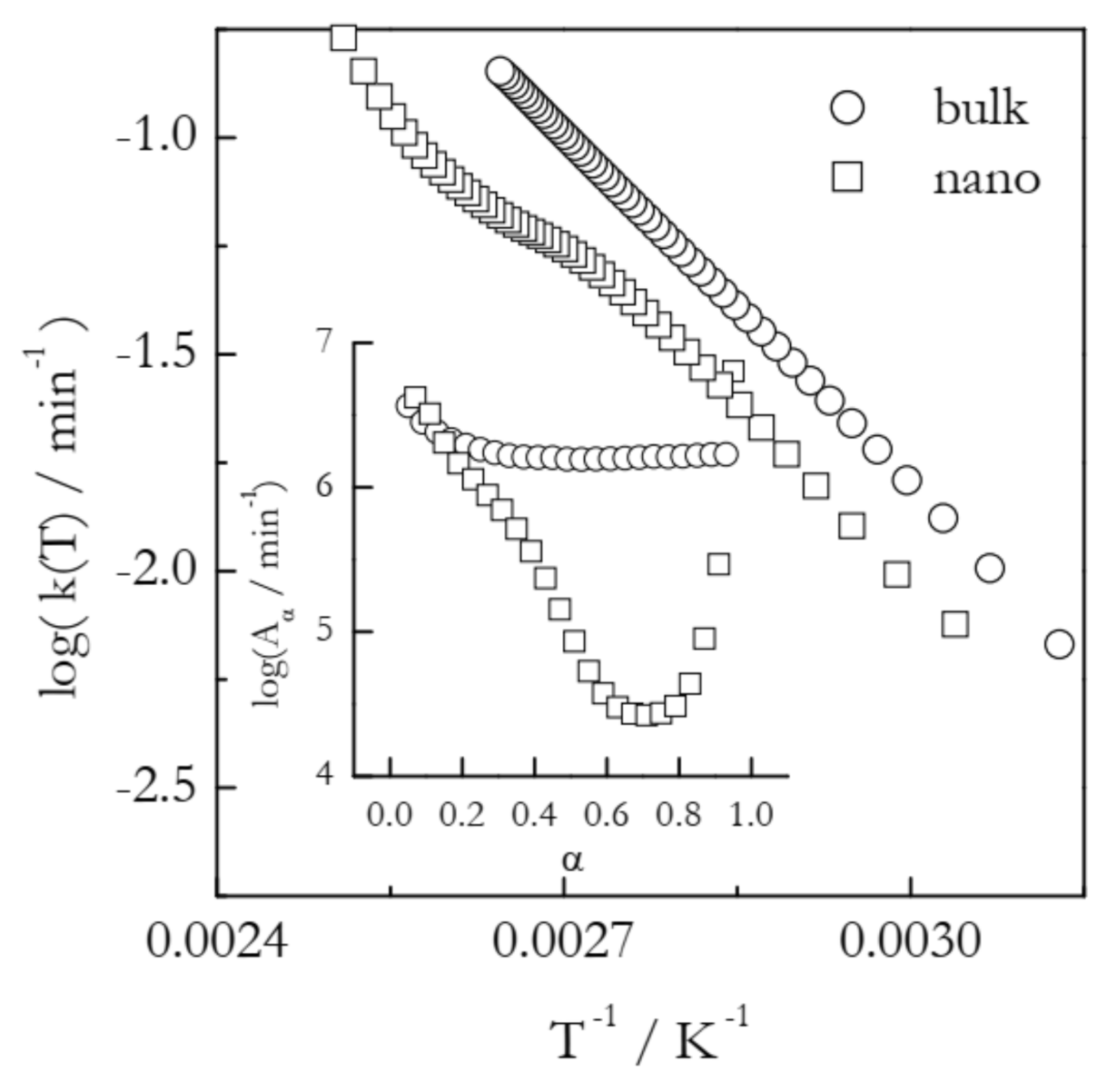
3.1. Preexponential Factor for Understanding Reaction Temperature Shifts
3.2. Entropic Interpretation of Changes in the Preexponential Factor
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee Recommendations for Performing Kinetic Computations on Thermal Analysis Data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Favergeon, L.; Koga, N.; Moukhina, E.; Pérez-Maqueda, L.A.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for analysis of multi-step kinetics. Thermochim. Acta 2020, 689, 178597. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction kinetics in differential thermal analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Vyazovkin, S. Isoconversional Kinetics of Thermally Stimulated Processes; Springer: Heidelberg, Germany, 2015. [Google Scholar]
- Vyazovkin, S. Isoconversional kinetics of polymers: The decade past. Macromol. Rapid Commun. 2017, 38, 1600615. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.mdpi.com/journal/molecules/special_issues/thermal_analysis_kinetics (accessed on 27 April 2021).
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. Part C 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Vyazovkin, S. A unified approach to kinetic processing of nonisothermal data. Int. J. Chem. Kinet. 1996, 28, 95–101. [Google Scholar] [CrossRef]
- Sbirrazzuoli, N. Model-free isothermal and nonisothermal predictions using advanced isoconversional methods. Thermochim. Acta 2021, 697, 178855. [Google Scholar] [CrossRef]
- Granado, L.; Sbirrazzuoli, N. Isoconversional computations for nonisothermal kinetic predictions. Thermochim. Acta 2021, 697, 178859. [Google Scholar] [CrossRef]
- Vyazovkin, S. A time to search: Finding the meaning of variable activation energy. Phys. Chem. Chem. Phys. 2016, 18, 18643–18656. [Google Scholar] [CrossRef]
- Vyazovkin, S. Kinetic concepts of thermally stimulated reactions in solids: A view from a historical perspective. Int. Rev. Phys. Chem. 2000, 19, 45–60. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Clawson, J.S.; Wight, C.A. Thermal dissociation kinetics of solid and liquid ammonium nitrate. Chem. Mater. 2001, 13, 960–966. [Google Scholar] [CrossRef]
- Vyazovkin, S.V.; Lesnikovich, A.I. Estimation of the pre-exponential factor in the isoconversional calculation of the effective kinetic parameters. Thermochim. Acta 1988, 128, 297–300. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Linert, W. False isokinetic relationships found in the nonisothermal decomposition of solids. Chem. Phys. 1995, 193, 109–118. [Google Scholar] [CrossRef]
- Sbirrazzuoli, N. Determination of pre-exponential factor and reaction mechanism in a model-free way. Thermochim. Acta 2020, 691, 178707. [Google Scholar] [CrossRef]
- Sbirrazzuoli, N. Determination of Pre-exponential Factors and of the Mathematical Functions f(α) or G(α) that Describe the Reaction Mechanism in a Model-free Way. Thermochim. Acta 2013, 564, 59–69. [Google Scholar] [CrossRef]
- Chen, S.; Xiao, M.; Sun, L.; Meng, Y. Study on Thermal Decomposition Behaviors of Terpolymers of Carbon Dioxide, Propylene Oxide, and Cyclohexene Oxide. Int. J. Mol. Sci. 2018, 19, 3723. [Google Scholar] [CrossRef] [Green Version]
- Zhao, M.; Raheem, A.; Memon, Z.M.; Vuppaladadiyam, A.K.; Ji, G. Iso-conversional kinetics of low-lipid micro-algae gasification by air. J. Clean. Prod. 2019, 207, 618–629. [Google Scholar] [CrossRef]
- Streltsov, D.R.; Buzin, A.I.; Dmitryakov, P.V.; Savinov, D.V.; Chvalun, S.N. A study of 2,3-dichloro-p-xylylene polymerization kinetics using high-vacuum in situ differential scanning calorimetry. Thermochim. Acta 2021, 699, 178890. [Google Scholar] [CrossRef]
- Vieira, J.C.B.; Villetti, M.A.; Frizzo, C.P. Thermal stability and decomposition mechanism of dicationic imidazolium-based ionic liquids with carboxylate anions. J. Mol. Liq. 2021, 330, 115618. [Google Scholar] [CrossRef]
- Ozawa, T. A new method of analyzing thermogravimetric data. Bull. Chem. Soc. Japan 1965, 38, 1881–1886. [Google Scholar] [CrossRef] [Green Version]
- Flynn, J.H.; Wall, L.A. A quick, direct method for the determination of activation energy from thermogravimetric data. J. Polym. Sci. B Polym. Lett. 1966, 4, 323–328. [Google Scholar] [CrossRef]
- Akahira, T.; Sunose, T. Method of determining activation deterioration constant of electrical insulating materials. Res. Rep. Chiba Inst. Technol. (Sci. Technol.) 1971, 16, 22–31. [Google Scholar]
- Vyazovkin, S. Modern isoconversional kinetics: From Misconceptions to Advances. In The Handbook of Thermal Analysis & Calorimetry, Vol.6: Recent Advances, Techniques and Applications, 2nd ed.; Vyazovkin, S., Koga, N., Schick, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 131–172. [Google Scholar]
- Vyazovkin, S. Modification of the integral isoconversional method to account for variation in the activation energy. J. Comput. Chem. 2001, 22, 178–183. [Google Scholar] [CrossRef]
- Ortega, A. A simple and precise linear integral method for isoconversional data. Thermochim. Acta 2008, 474, 81–86. [Google Scholar] [CrossRef]
- Balarin, M. Is Kissinger’s rule true? Thermochim. Acta 1979, 33, 341–343. [Google Scholar] [CrossRef]
- Vyazovkin, S. Kissinger Method in Kinetics of Materials: Things to Beware and Be Aware of. Molecules 2020, 25, 2813. [Google Scholar] [CrossRef] [PubMed]
- Stanford, V.L.; Liavitskaya, T.; Vyazovkin, S. Effect of inert gas pressure on reversible solid-state decomposition. J. Phys. Chem. C 2019, 123, 21059–21065. [Google Scholar] [CrossRef]
- Liavitskaya, T.; Birx, L.; Vyazovkin, S. Thermal stability of malonic acid dissolved in polyvinylpyrrolidone and other polymeric matrices. Ind. Eng. Chem. Res. 2018, 57, 5228–5233. [Google Scholar] [CrossRef]
- Ekawa, B.; Stanford, V.; Vyazovkin, S. Isoconversional kinetics of vaporization of nanoconfined liquids. J. Mol. Liq. 2021, 327, 114824. [Google Scholar] [CrossRef]
- Ben Osman, Y.; Liavitskaya, T.; Vyazovkin, S. Polyvinylpyrrolidone affects thermal stability of drugs in solid dispersions. Int. J. Pharm. 2018, 551, 111–120. [Google Scholar] [CrossRef]
- Jelić, D.; Liavitskaya, T.; Vyazovkin, S. Thermal stability of indomethacin increases with the amount of polyvinylpyrrolidone in solid dispersion. Thermochim. Acta 2019, 676, 172–176. [Google Scholar] [CrossRef]
- Wang, X.; Huang, Z.; Wei, M.; Lu, T.; Nong, D.; Zhao, J.; Gao, X.; Teng, L. Catalytic effect of nanosized ZnO and TiO2 on thermal degradation of poly (lactic acid) and isoconversional kinetic analysis. Thermochim. Acta 2019, 672, 14–24. [Google Scholar] [CrossRef]
- Galukhin, A.; Liavitskaya, T.; Vyazovkin, S. Kinetic and Mechanistic Insights into Thermally Initiated Polymerization of Cyanate Esters with Different Bridging Groups. Macromol. Chem. Phys. 2019, 220, 1900141. [Google Scholar] [CrossRef]
- Deng, J.; Bai, Z.-J.; Xiao, Y.; Laiwang, B.; Shu, C.-M.; Wang, C.-P. Thermogravimetric analysis of the effects of four ionic liquids on the combustion characteristics and kinetics of weak caking coal. J. Mol. Liq. 2019, 277, 876–885. [Google Scholar] [CrossRef]
- Adil, S.; Murty, B.S. Effect of milling on the oxidation kinetics of Aluminium + Boron mixture and nanocrystalline Aluminium Boride (AlB12). Thermochim. Acta 2019, 678, 178306. [Google Scholar] [CrossRef]
- Galukhin, A.; Taimova, G.; Nosov, R.; Liavitskaya, T.; Vyazovkin, S. Polymerization Kinetics of Cyanate Ester Confined to Hydrophilic Nanopores of Silica Colloidal Crystals with Different Surface-Grafted Groups. Polymers 2020, 12, 2329. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, X.; Lu, T.; Nong, D.; Gao, X.; Zhao, J.; Wei, M.; Teng, L. Isoconversional kinetic analysis of thermal decomposition of 1-butyl-3-methylimidazolium hexafluorophosphate under inert nitrogen and oxidative air atmospheres. J. Therm. Anal. Calorim. 2020, 140, 695–712. [Google Scholar] [CrossRef]
- Glasstone, S.; Laidler, K.J.; Eyring, H. The Theory of Rate Processes; McGraw-Hill Book Co.: New York, NY, USA, 1941. [Google Scholar]
- Benson, S.W. Thermochemical Kinetics; Wiley: New York, NY, USA, 1968. [Google Scholar]
- Prado, J.R.; Chen, J.; Kharlampieva, E.; Vyazovkin, S. Melting of gelatin gels confined to silica nanopores. Phys. Chem. Chem. Phys. 2016, 18, 29056–29063. [Google Scholar] [CrossRef]
- Yancey, B.; Vyazovkin, S. The kinetics and mechanism of nanoconfined molten salt reactions: Trimerization of potassium and rubidium dicyanamide. Phys. Chem. Chem. Phys. 2015, 17, 10209–10217. [Google Scholar] [CrossRef]
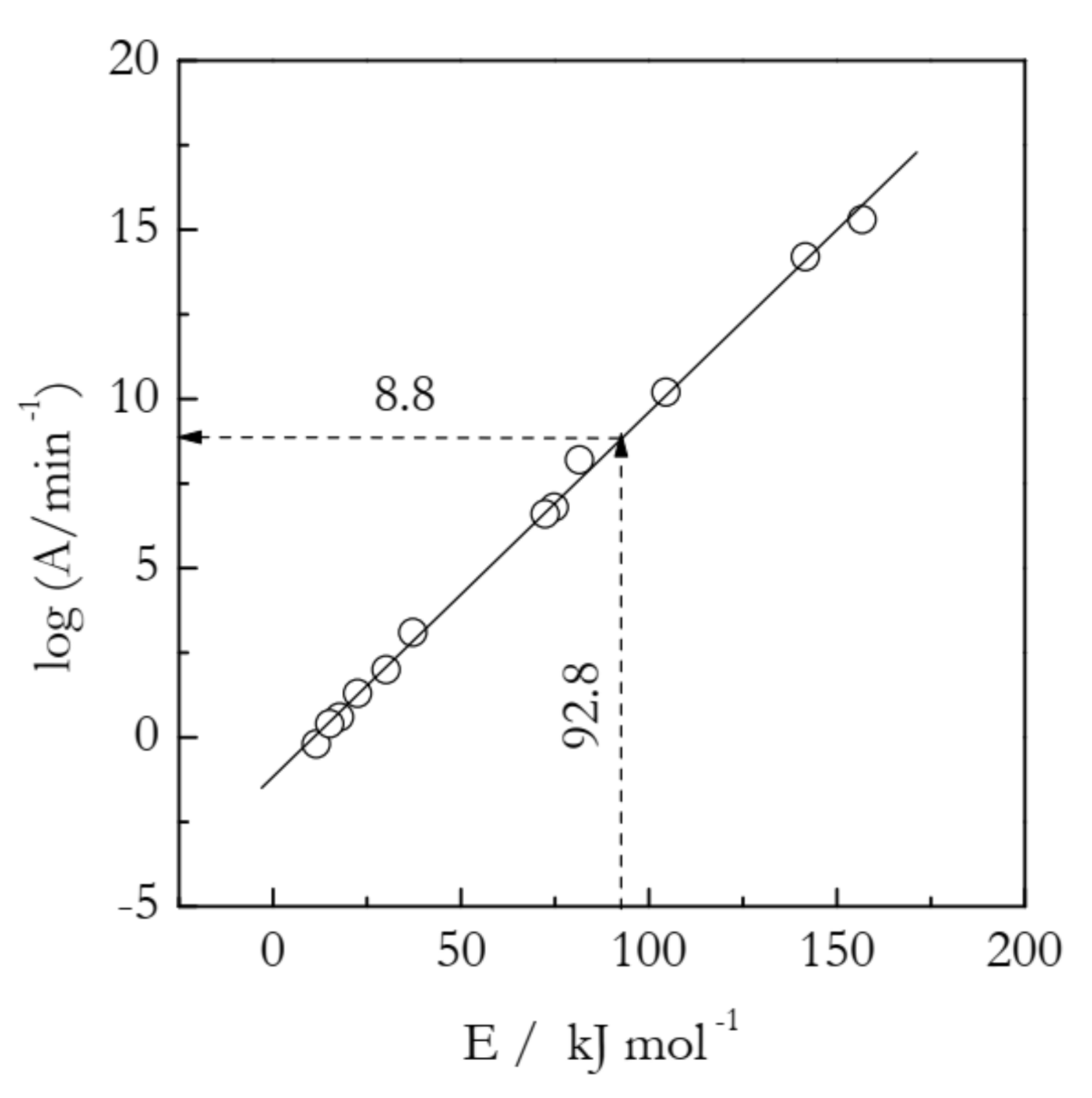



| i | Reaction Model | gi(α) | Ei/kJ mol−1 | log(Ai/min−1) |
|---|---|---|---|---|
| 1 | power law | α1/4 | 11.5 | −0.2 |
| 2 | power law | α1/3 | 17.7 | 0.6 |
| 3 | power law | α1/2 | 30.1 | 2.0 |
| 4 | power law | α3/2 | 104.5 | 10.2 |
| 5 | one-dimensional diffusion | α2 | 141.6 | 14.2 |
| 6 | Mampel (first order) | −ln(1 − α) | 81.5 | 8.2 |
| 7 | Avrami–Erofeev | [−ln(1 − α)]1/4 | 15.1 | 0.4 |
| 8 | Avrami–Erofeev | [−ln(1 − α)]1/3 | 22.5 | 1.3 |
| 9 | Avrami–Erofeev | [−ln(1 − α)]1/2 | 37.2 | 3.1 |
| 10 | three-dimensional diffusion | [1 − (1 − α)1/3]2 | 156.7 | 15.3 |
| 11 | contracting sphere | 1 − (1 − α)1/3 | 74.8 | 6.8 |
| 12 | contracting cylinder | 1 − (1 − α)1/2 | 72.4 | 6.6 |
| System | E/kJ mol−1 | log(A/s−1) | ΔS≠/J mol−1 K−1 |
|---|---|---|---|
| Bulk KDCA | 54.5 ± 1.8 | 2.4 ± 0.1 | −206 |
| 30 nm KDCA | 93.3 ± 6.8 | 5.7 ± 0.1 | −142 |
| 4 nm KDCA | 101.6 ± 7.4 | 6.8 ± 0.2 | −121 |
| Bulk RbDCA | 50.1 ± 4.5 | 2.4 ± 0.1 | −205 |
| 30 nm RbDCA | 92.3 ± 9.4 | 6.8 ± 0.1 | −120 |
| 4 nm RbDCA | 91.9 ± 5.3 | 6.7 ± 0.1 | −122 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vyazovkin, S. Determining Preexponential Factor in Model-Free Kinetic Methods: How and Why? Molecules 2021, 26, 3077. https://doi.org/10.3390/molecules26113077
Vyazovkin S. Determining Preexponential Factor in Model-Free Kinetic Methods: How and Why? Molecules. 2021; 26(11):3077. https://doi.org/10.3390/molecules26113077
Chicago/Turabian StyleVyazovkin, Sergey. 2021. "Determining Preexponential Factor in Model-Free Kinetic Methods: How and Why?" Molecules 26, no. 11: 3077. https://doi.org/10.3390/molecules26113077
APA StyleVyazovkin, S. (2021). Determining Preexponential Factor in Model-Free Kinetic Methods: How and Why? Molecules, 26(11), 3077. https://doi.org/10.3390/molecules26113077






