The Investigation on Ultrafast Pulse Formation in a Tm–Ho-Codoped Mode-Locking Fiber Oscillator
Abstract
1. Introduction
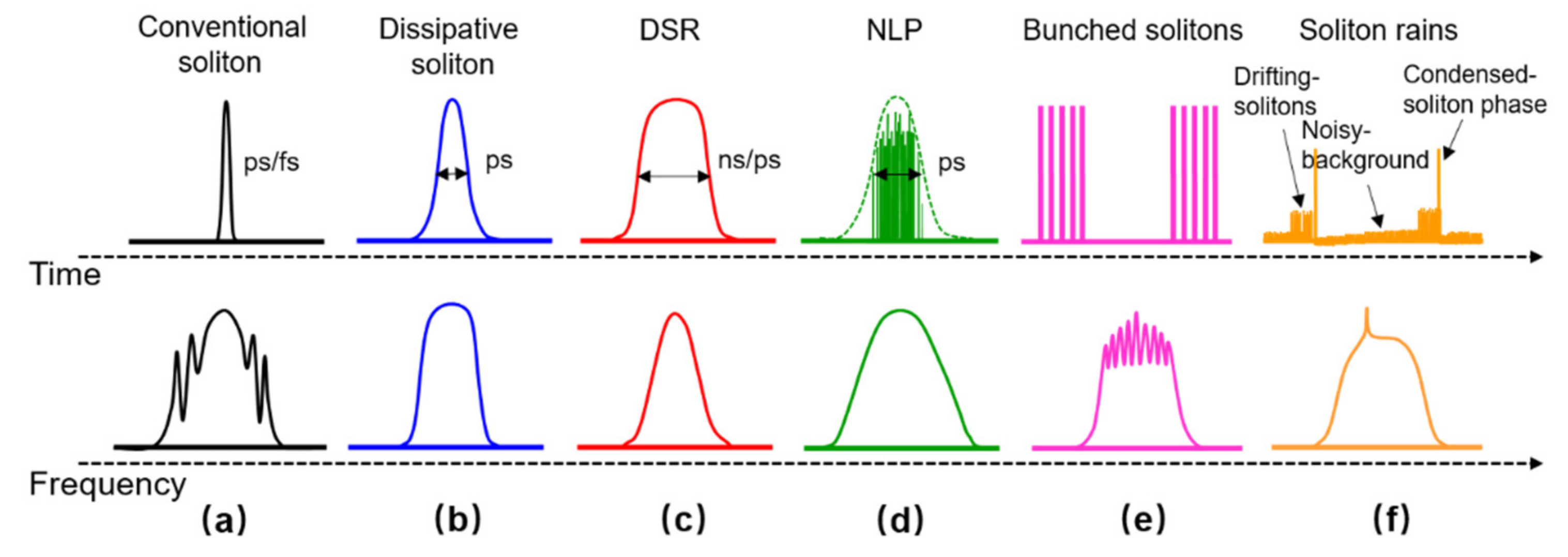
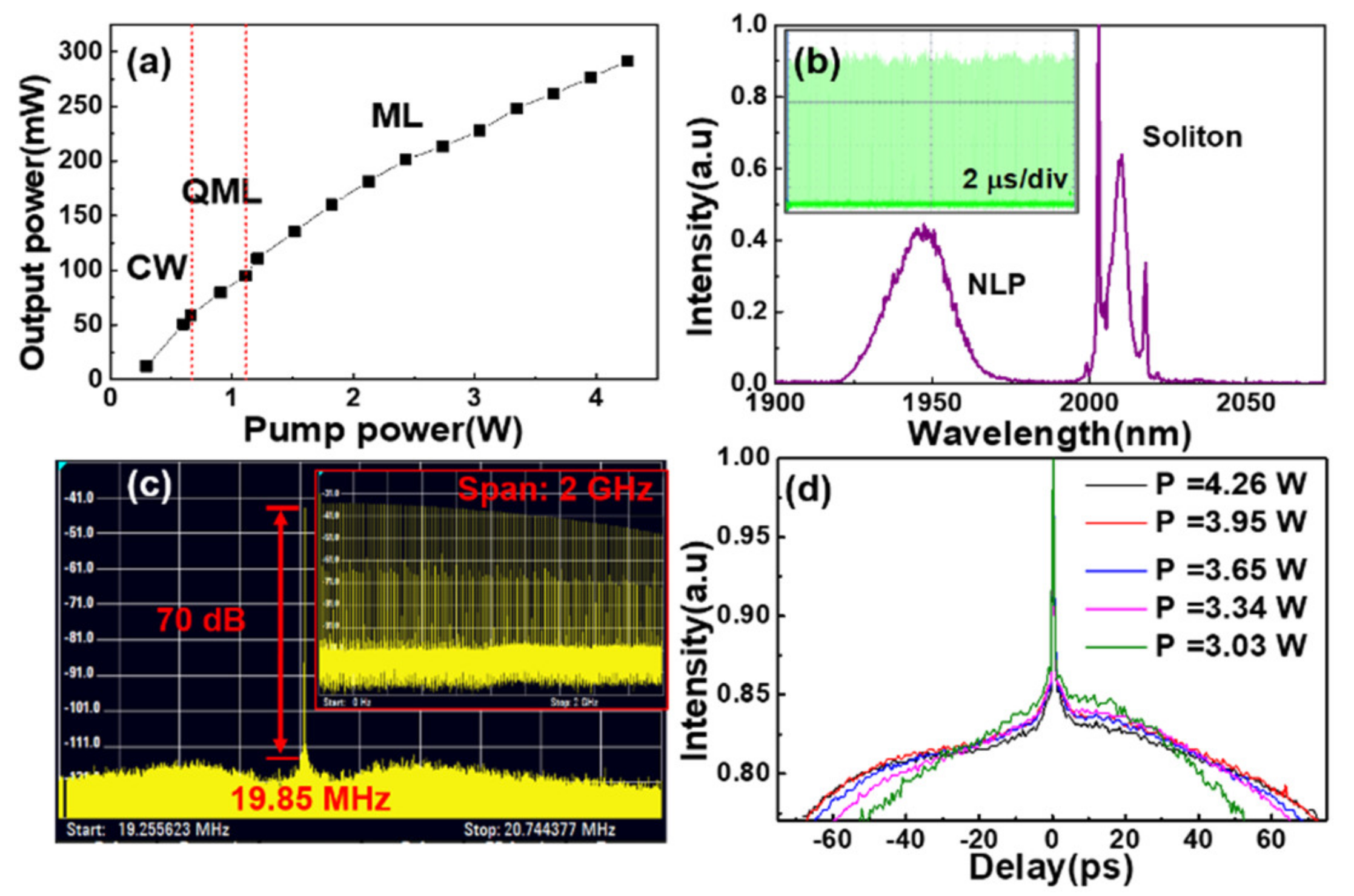
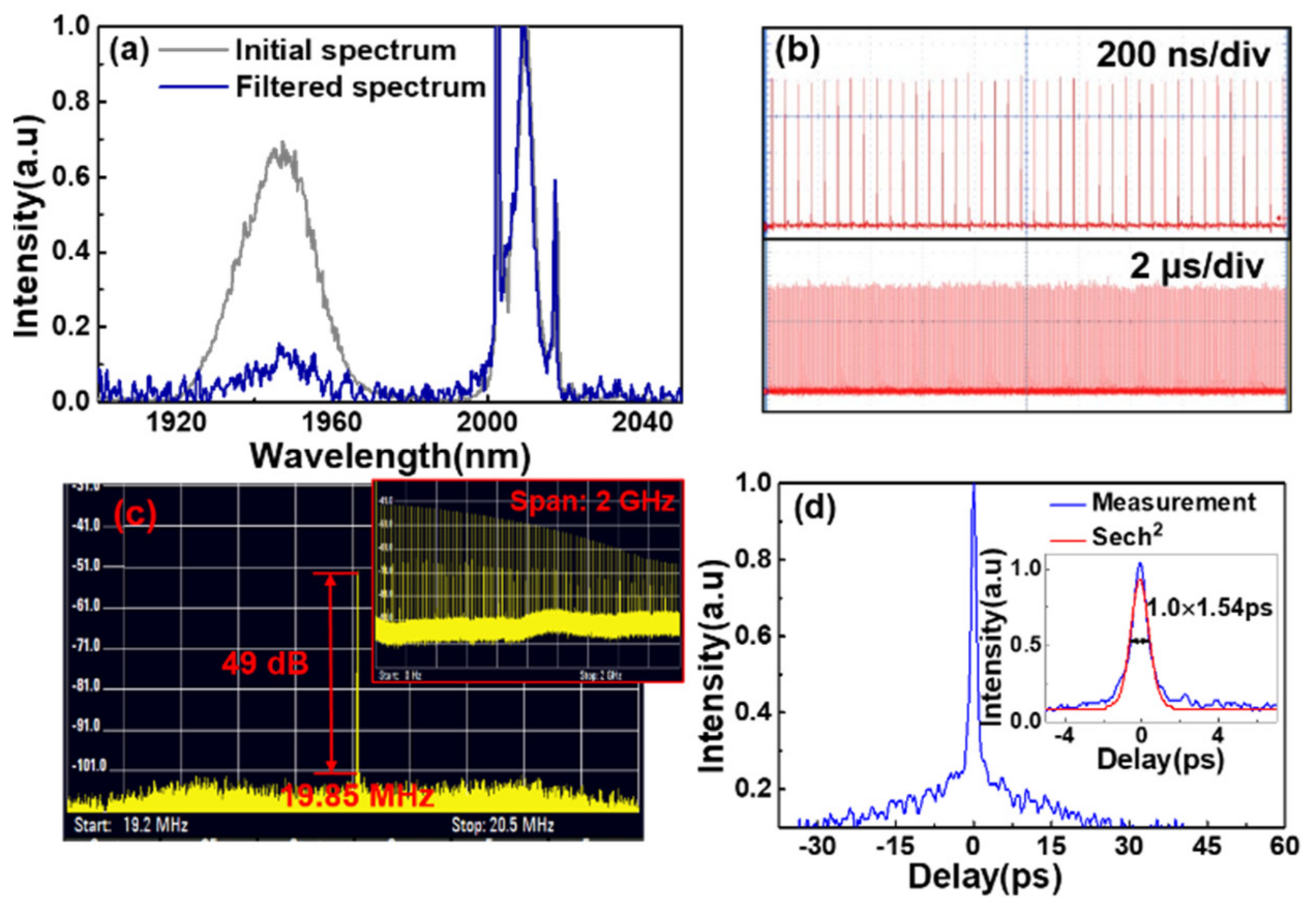
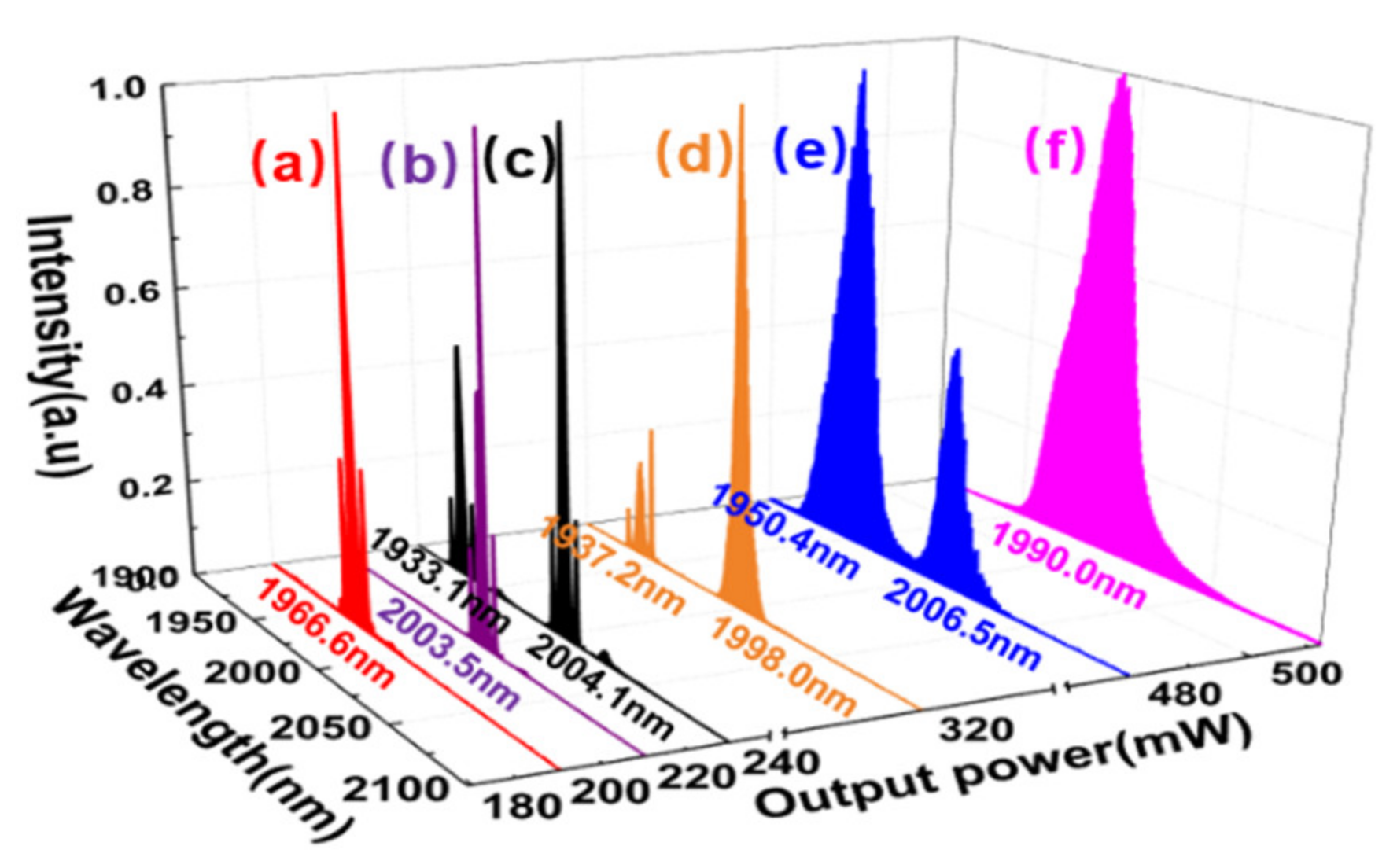
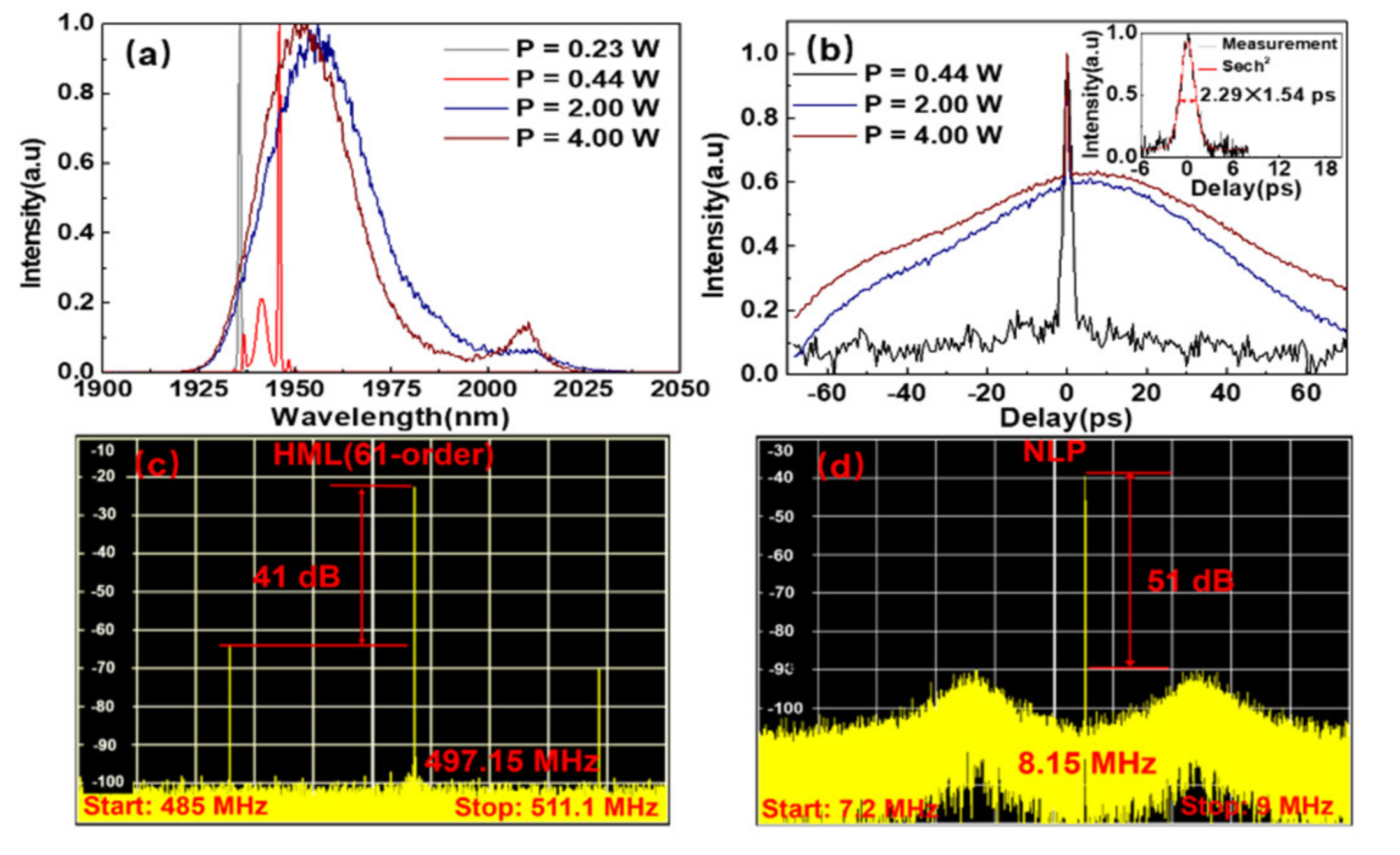
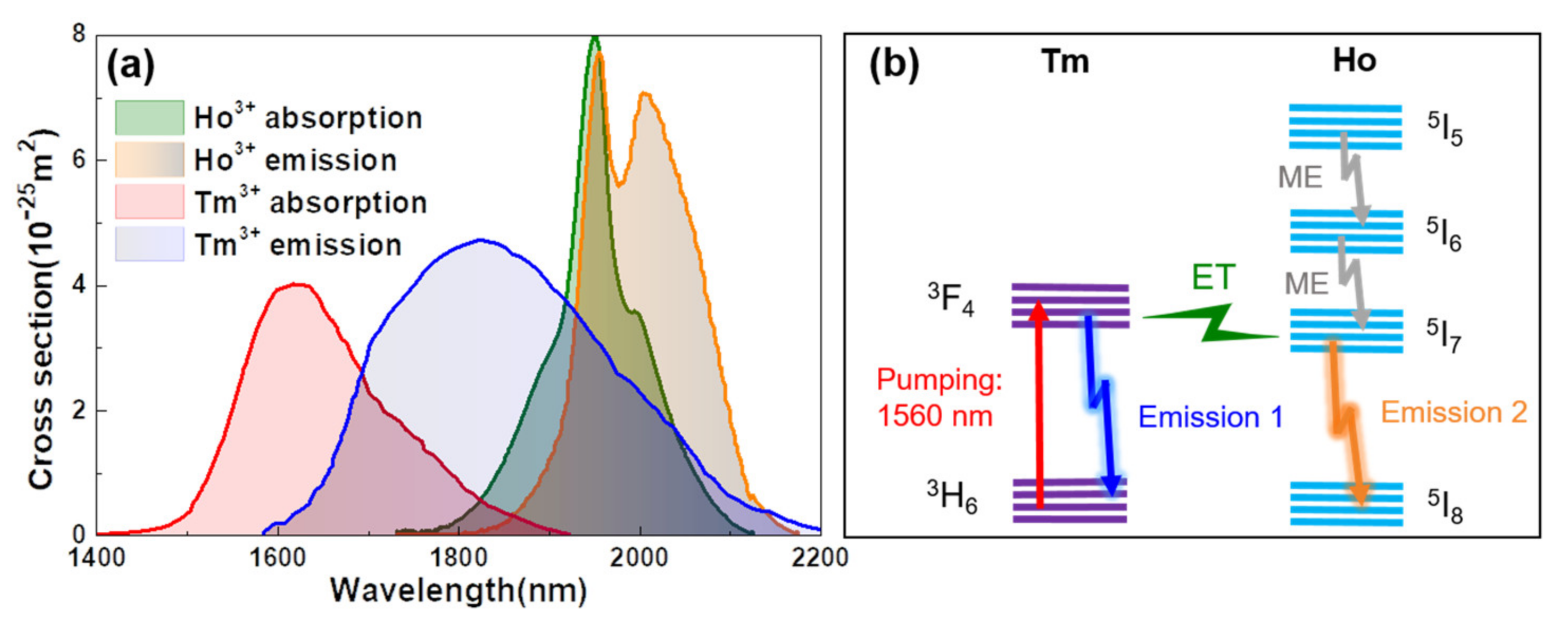
2. Results and Discussion
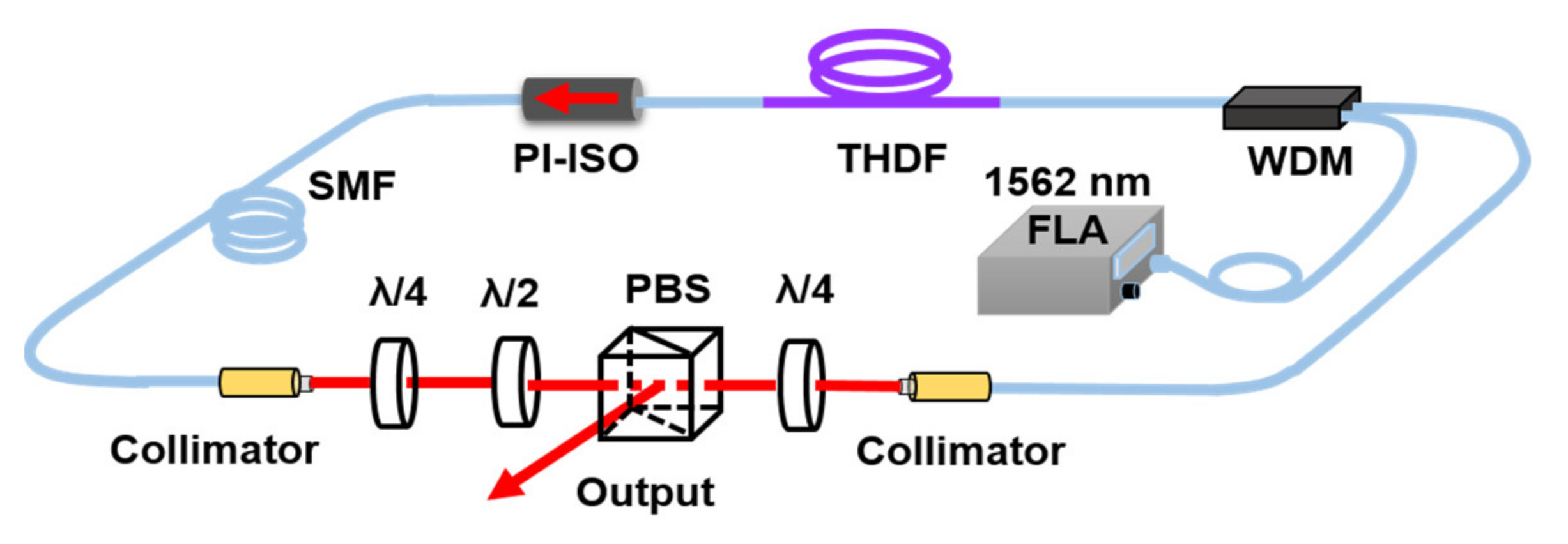
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Ma, W.X.; Chen, M. Direct search for exact solutions to the nonlinear Schrödinger equation. Appl. Math. Comput. 2009, 215, 2835–2842. [Google Scholar] [CrossRef]
- Chabchoub, A.; Kibler, B.; Finot, C.; Millot, G.; Onorato, M.; Dudley, J.M.; Babanin, A.V. The nonlinear Schrödinger equation and the propagation of weakly nonlinear waves in optical fibers and on the water surface. Ann. Phys. 2015, 361, 490. [Google Scholar] [CrossRef]
- Kobtsev, S.M.; Kukarin, S.V.; Smirnov, S.V.; Fedotov, Y.S. High-energy mode-locked all-fiber laser with ultralong resonator. Laser Phys. 2010, 20, 351–356. [Google Scholar] [CrossRef]
- Tang, D.; Zhao, L.; Zhao, B. Soliton collapse and bunched noise-like pulse generation in a passively mode-locked fiber ring laser. Opt. Express 2005, 13, 2289–2294. [Google Scholar] [CrossRef]
- Ma, W.X. N-soliton solutions and the Hirota conditions in (2+1)-dimensions. Opt. Quant. Electron. 2020, 52, 511. [Google Scholar] [CrossRef]
- Yu, S.J.; Toda, K.; Sasa, K.; Fukuyama, T. N soliton solutions to the Bogoyavlenskii-Schiff equation and a quest for the soliton solution in (3+1) dimensions. J. Phys. A Math. Gen. 1998, 31, 3337. [Google Scholar] [CrossRef]
- Zhou, Y.; Manukure, S.; Ma, W.X. Lump and lump-soliton solutions to the Hirota–Satsuma–Ito equation. Commun. Nonlinear Sci. Numer. Simulat. 2019, 68, 56–62. [Google Scholar] [CrossRef]
- Mitschke, F.M.; Mollenauer, L.F. Ultrashort pulses from the soliton laser. Opt. Lett. 1987, 12, 407–409. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Luo, H.; Liu, Y.; Yan, Z.; Sun, Z.; Zhang, L. Kelly sideband suppression and wavelength tuning of a conventional soliton in a Tm-doped hybrid mode-locked fiber laser with an all-fiber Lyot filter. Photon. Res. 2019, 7, 103–109. [Google Scholar] [CrossRef]
- Wang, M.; Wei, R.; Zhu, Z.; Ruan, S.; Yan, P.; Wang, J.; Hasan, T.; Sun, Z. 172 fs, 24.3 kW peak power pulse generation from a Ho-doped fiber laser system. Opt. Lett. 2018, 43, 4619–4622. [Google Scholar] [CrossRef]
- Luo, Z.; Li, Y.; Huang, Y.; Zhong, M.; Wan, X. Graphene mode-locked and Q-switched 2-μm Tm/Ho codoped fiber lasers using 1212-nm high-efficient pumping. Opt. Eng. 2016, 55, 081310. [Google Scholar] [CrossRef]
- Grelu, P.; Akhmediev, N. Dissipative solitons for mode-locked lasers. Nat. Photonics 2012, 6, 84–92. [Google Scholar] [CrossRef]
- Yang, N.; Tang, Y.; Xu, J. High-energy harmonic mode-locked 2 μm dissipative soliton fiber lasers. Laser Phys. Lett. 2015, 12, 085102. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, D.Y.; Wu, X.; Zhao, L.M. Multi-wavelength dissipative soliton operation of an erbium-doped fiber laser. Opt. Express 2009, 17, 12692–12697. [Google Scholar] [CrossRef]
- Chang, W.; Ankiewicz, A.; Soto-Crespo, J.M.; Akhmediev, N. Dissipative soliton resonances. Phys. Rev. A 2008, 78, 023830. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, H.; Wang, P. Simulation of generation of dissipative soliton, dissipative soliton resonance and noise-like pulse in Yb-doped mode-locked fiber lasers. Opt. Express 2015, 23, 5972–5981. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Wang, T.; Song, G.; Ma, W. Generation of Dissipative Soliton Resonance Pulse in 2 um All-Polarization-Maintaining Mode-Locked Fiber Laser. In Proceedings of the 2020 IEEE 5th Optoelectronics Global Conference (OGC), Shenzhen, China, 7–11 September 2020. [Google Scholar]
- Duan, L.; Liu, X.; Mao, D.; Wang, L.; Wang, G. Experimental observation of dissipative soliton resonance in an anomalous-dispersion fiber laser. Opt. Express 2012, 20, 265–270. [Google Scholar] [CrossRef]
- Chernykh, A.I.; Turitsyn, S.K. Soliton and collapse regimes of pulse generation in passively mode-locking laser systems. Opt. Lett. 1995, 20, 398–400. [Google Scholar] [CrossRef]
- Jeong, Y.; Vazquez-Zuniga, L.A.; Lee, S.; Kwon, Y. On the formation of noise-like pulses in fiber ring cavity configurations. Opt. Fiber Technol. 2014, 20, 575–592. [Google Scholar] [CrossRef]
- Zhao, L.M.; Tang, D.Y.; Wu, J.; Fu, X.Q.; Wen, S.C. Noise-like pulse in a gain-guided soliton fiber laser. Opt. Express 2007, 15, 2145–2150. [Google Scholar] [CrossRef]
- Ahmad, H.; Ahmed, M.H.M.; Samion, M.Z. Generation of mode-locking noise-like pulses in double-clad Tm-doped fibre laser with nonlinear optical loop mirror. J. Mod. Optic. 2020, 67, 146–152. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Z.; Sun, Z.; Luo, H.; Liu, Y.; Yan, Z.; Mou, C.; Zhang, L.; Turitsyn, S.K. All-fiber Passively Mode-locking Tm-Doped NOLM-Based Oscillator Operating at 2-μm in Both Soliton and Noisy-Pulse Regimes. Opt. Express 2014, 22, 7875–7882. [Google Scholar]
- Malomed, B.A. Bound solitons in coupled nonlinear Schrödinger equations. Phys. Rev. A 1992, 45, R8321–R8323. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.Q.; Hu, Z.A.; Cui, H.; Luo, Z.C.; Luo, A.P.; Xu, W.C. Coexistence of harmonic soliton molecules and rectangular noise-like pulses in a figure-eight fiber laser. Opt. Lett. 2016, 41, 4056–4059. [Google Scholar] [CrossRef] [PubMed]
- Kokhanovskiy, A.; Kuprikov, E.; Ivanenko, A.; Kobtsev, S. All-polarisation-maintaining modified figure-of-8 fibre laser as a source of soliton molecules. Laser Phys. Lett. 2020, 17, 085101. [Google Scholar] [CrossRef]
- Luo, W.; Liu, X.; Li, X.; Li, S.; Xu, W.; Wang, L.; Shi, Z.; Zhang, C. SnSe2 realizes soliton rain and harmonic soliton molecules in erbium-doped fiber lasers. Nanotechnology 2021, 32, 165203. [Google Scholar] [CrossRef]
- Chouli, S.; Grelu, P. Rains of solitons in a fiber laser. Opt. Express 2009, 17, 11776–11781. [Google Scholar] [CrossRef]
- Akhmediev, N.; Soto-Crespo, J.M.; Town, G. Pulsating solitons, chaotic solitons, period doubling, and pulse coexistence in mode-locked lasers: Complex Ginzburg-Landau equation approach. Phys. Rev. E 2001, 63, 056602. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Zhang, E.; Mo, K.; Wang, Y.; Liu, F.; Zhou, X.; Liu, Y. Coexistence of noise-like pulse and high repetition rate harmonic mode-locking in a dual-wavelength mode-locked Tm-doped fiber laser. Opt. Express 2017, 25, 17192–17200. [Google Scholar] [CrossRef]
- Liu, X. Coexistence of strong and weak pulses in a fiber laser with largely anomalous dispersion. Opt. Express 2011, 19, 5874–5887. [Google Scholar] [CrossRef]
- Esterowitz, L. Diode pumped holmium, thulium and erbium lasers between 2 and 3 micrometers operating cw at room temperature. Opt. Eng. 1990, 29, 676–680. [Google Scholar] [CrossRef]
- Hanna, D.C.; Jauncey, I.M.; Percival, R.M.; Perry, I.R.; Smart, R.G.; Suni, P.J.; Townsend, J.E.; Tropper, A.C. Continuous-wave oscillation of a monomode thulium-doped fibre laser. Electron. Lett. 1988, 24, 1222–1223. [Google Scholar] [CrossRef]
- Kadel, R.; Washburn, B.R. All-fiber passively mode-locked thulium/holmium laser with two center wavelengths. Appl. Opt. 2012, 51, 6465–6470. [Google Scholar] [CrossRef][Green Version]
- Filatova, S.A.; Kamynin, V.A.; Arutyunyan, N.R.; Pozharov, A.S.; Obraztsova, E.D.; Itrin, P.A.; Tsvetkov, V.B. Comparison of mode-locking regimes in a holmium fibre laser. Quantum Electron. 2018, 48, 1113–1117. [Google Scholar] [CrossRef]
- Salzenstein, P.; Pavlyuchenko, E. Uncertainty Evaluation on a 10.52 GHz (5 dBm) Optoelectronic Oscillator Phase Noise Performance. Micromachines 2021, 12, 474. [Google Scholar] [CrossRef]
- Yan, Z.; Li, X.; Tang, Y.; Shum, P.P.; Yu, X.; Zhang, Y.; Wang, Q.J. Tunable and switchable dual-wavelength Tm-doped mode-locked fiber laser by nonlinear polarization evolution. Opt. Express 2015, 23, 4369–4376. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Sun, B.; Li, X.; Luo, J.; Shum, P.P.; Yu, X.; Zhang, Y.; Wang, Q. Widely tunable Tm-doped mode-locked all-fiber laser. Sci. Rep. 2016, 6, 27245. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Tang, Y.; Sun, B.; Liu, T.; Li, X.; Ping, P.S.; Yu, X.; Zhang, Y.; Wang, Q.J. Switchable multi-wavelength Tm-doped mode-locked fiber laser. Opt. Lett. 2015, 40, 1916–1919. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Zhai, B.; Hu, Y.; Mo, K.; Lu, R.; Liu, Y. Tunable and switchable dual-wavelength mode-locked Tm3+-doped fiber laser based on a fiber taper. Opt. Express 2016, 24, 15299–15306. [Google Scholar] [CrossRef]
- Zhao, N.; Liu, M.; Liu, H.; Zheng, X.W.; Ning, Q.Y.; Luo, A.P.; Luo, Z.C.; Xu, W.C. Dual-wavelength rectangular pulse Yb-doped fiber laser using a microfiber-based graphene saturable absorber. Opt. Express 2014, 22, 10906–10913. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Tam, H.; Wai, P.K.A. Stable and uniform multi wavelength erbium-doped fiber laser using nonlinear polarization rotation. Opt. Express 2006, 14, 8205–8210. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.; Luo, J.; Yan, Z.; Liu, K.; Ji, J.; Zhang, Y.; Wang, Q.J.; Yu, X. 1867–2010 nm tunable femtosecond thulium-doped all-fiber laser. Opt. Express 2017, 25, 8997–9002. [Google Scholar] [CrossRef] [PubMed]
- Talaverano, L.; Abad, S.; Jarabo, S.; Lopez-Amo, M. Multiwavelength fiber laser sources with Bragg-grating sensor multiplexing capability. J. Lightwave Technol. 2001, 19, 553–558. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, J.; Liu, Y.; Zhao, S.; Zhao, Y.; Song, Y.; Li, T.; Feng, T. The Investigation on Ultrafast Pulse Formation in a Tm–Ho-Codoped Mode-Locking Fiber Oscillator. Molecules 2021, 26, 3460. https://doi.org/10.3390/molecules26113460
Shang J, Liu Y, Zhao S, Zhao Y, Song Y, Li T, Feng T. The Investigation on Ultrafast Pulse Formation in a Tm–Ho-Codoped Mode-Locking Fiber Oscillator. Molecules. 2021; 26(11):3460. https://doi.org/10.3390/molecules26113460
Chicago/Turabian StyleShang, Jingcheng, Yizhou Liu, Shengzhi Zhao, Yuefeng Zhao, Yuzhi Song, Tao Li, and Tianli Feng. 2021. "The Investigation on Ultrafast Pulse Formation in a Tm–Ho-Codoped Mode-Locking Fiber Oscillator" Molecules 26, no. 11: 3460. https://doi.org/10.3390/molecules26113460
APA StyleShang, J., Liu, Y., Zhao, S., Zhao, Y., Song, Y., Li, T., & Feng, T. (2021). The Investigation on Ultrafast Pulse Formation in a Tm–Ho-Codoped Mode-Locking Fiber Oscillator. Molecules, 26(11), 3460. https://doi.org/10.3390/molecules26113460




