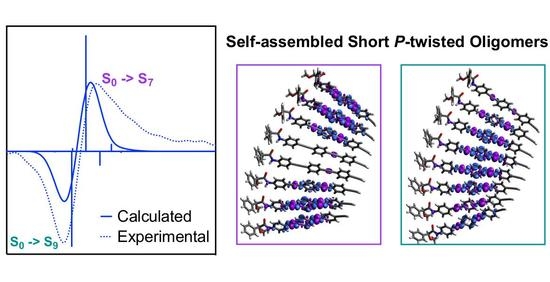
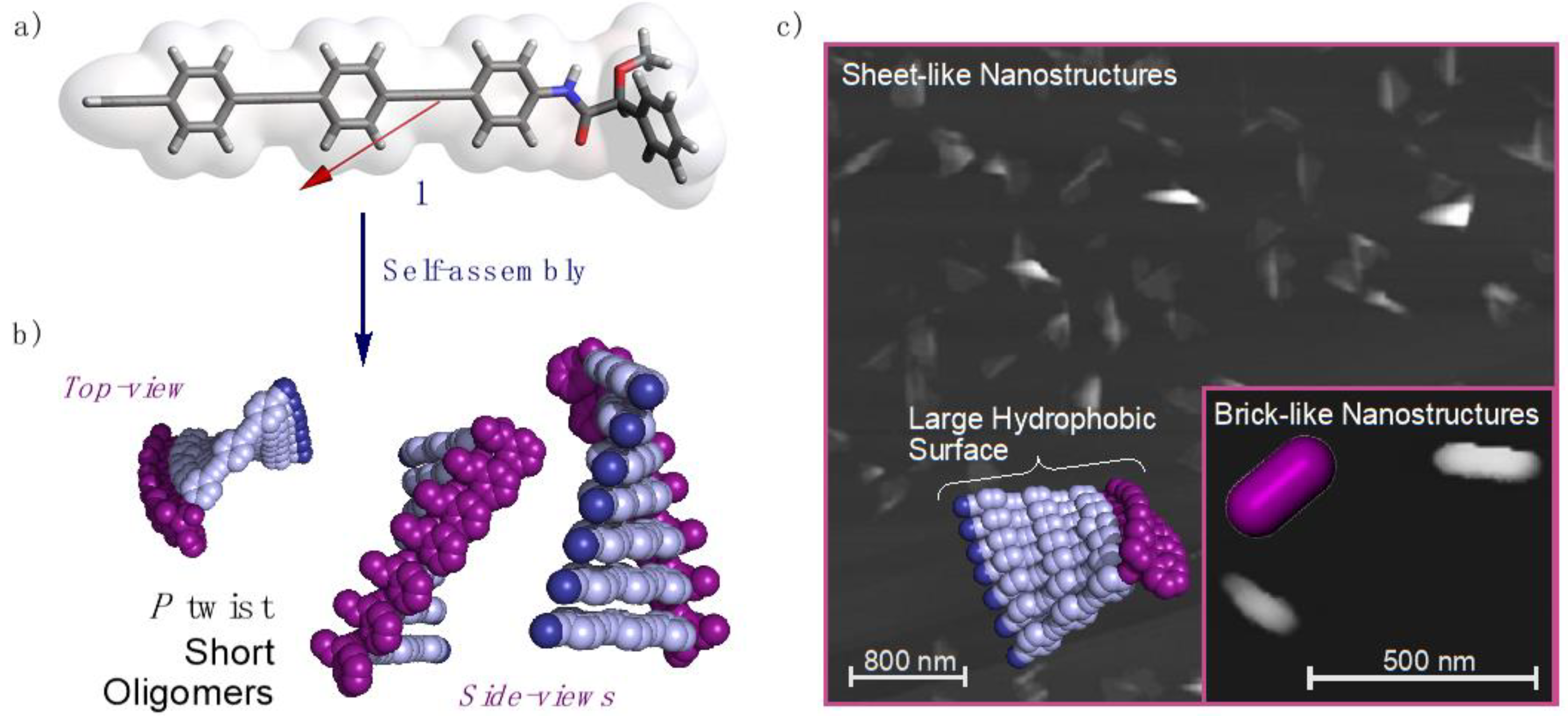
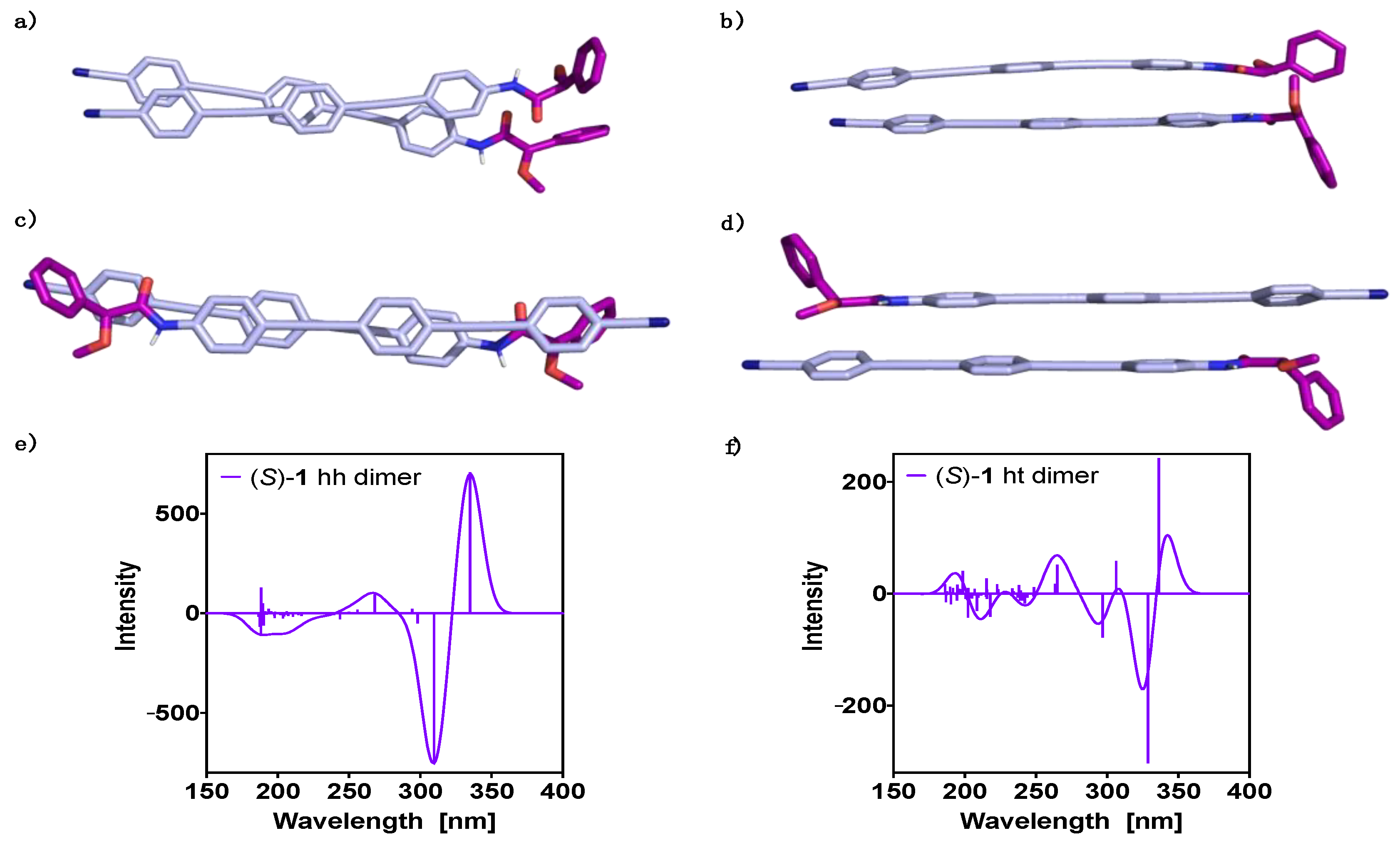
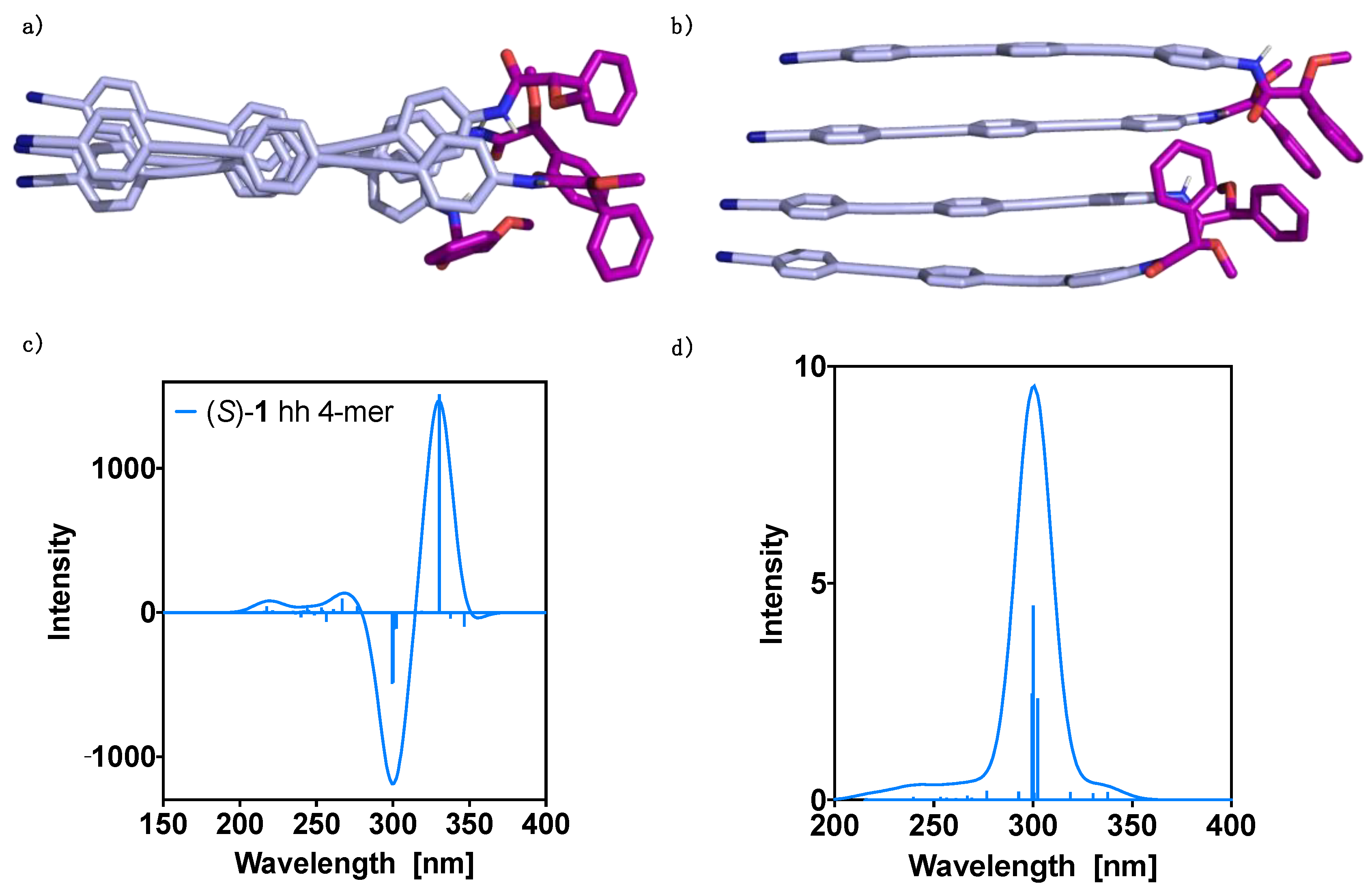
From Oligo(Phenyleneethynylene) Monomers to Supramolecular Helices: The Role of Intermolecular Interactions in Aggregation
Abstract
:1. Introduction
2. Computational Details
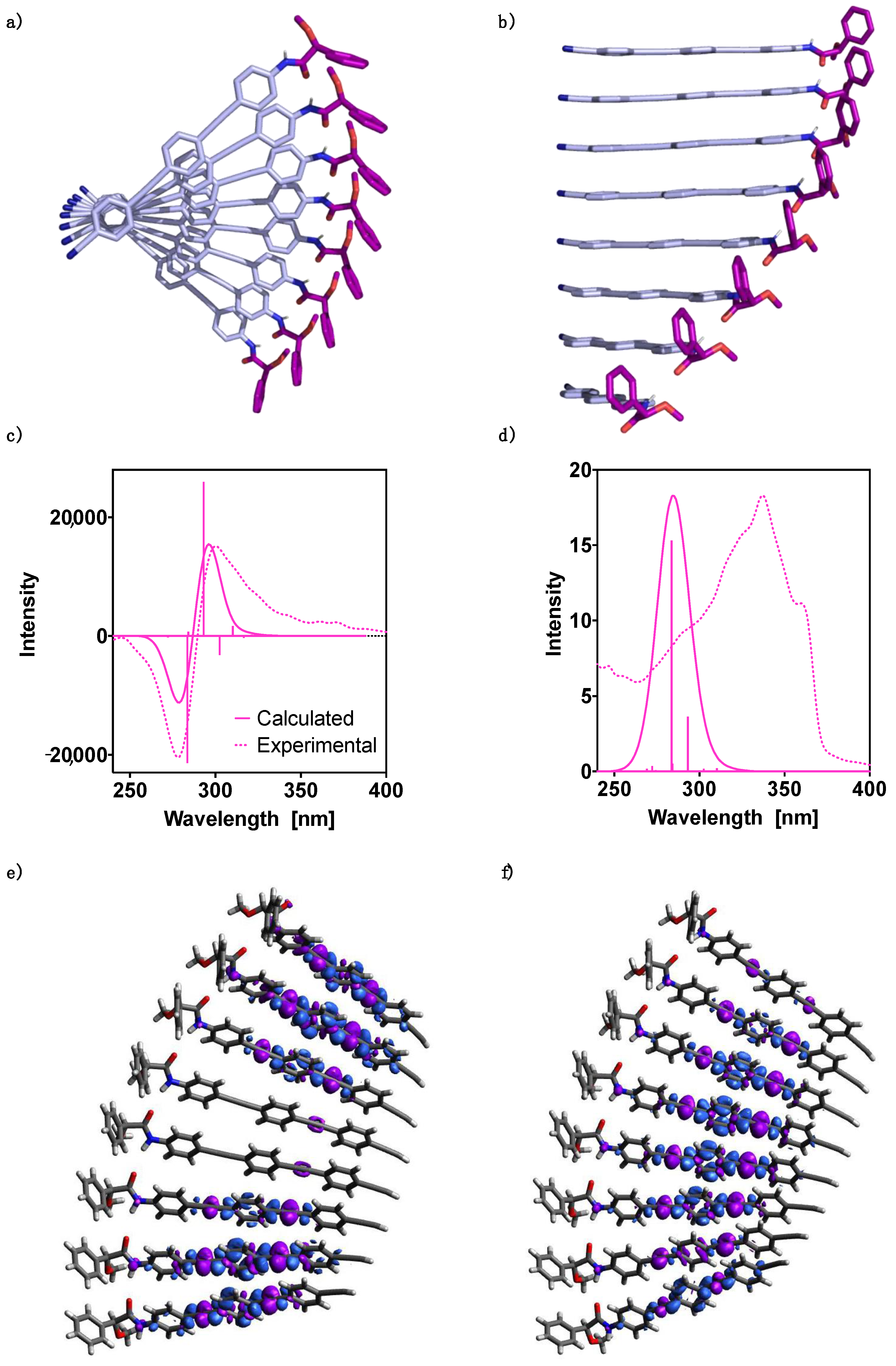
3. Results and Discussion
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Sample Availability
Geometry Availability
References
- Li, Y.; Hammoud, A.; Bouteiller, L.; Raynal, M. Emergence of homochiral benzene-1,3,5-tricarboxamide helical assemblies and catalysts upon addition of an achiral monomer. J. Am. Chem. Soc. 2020, 142, 5676–5688. [Google Scholar] [CrossRef]
- Raynal, M.; Portier, F.; van Leeuwen, P.W.N.M.; Bouteiller, L. Tunable asymmetric catalysis through ligand stacking in chiral rigid rods. J. Am. Chem. Soc. 2013, 135, 17687–17690. [Google Scholar] [CrossRef] [PubMed]
- Huerta, E.; van Genabeek, B.; Lamers, B.A.G.; Koenigs, M.M.E.; Meijer, E.W.; Palmans, A.R.A. Triggering activity of catalytic rod-like supramolecular polymers. Chem. Eur. J. 2015, 21, 3682–3690. [Google Scholar] [CrossRef]
- Desmarchelier, A.; Caumes, X.; Raynal, M.; Vidal-Ferran, A.; van Leeuwen, P.W.N.M.; Bouteiller, L. Correlation between the selectivity and the structure of an asymmetric catalyst built on a chirally amplified supramolecular helical scaffold. J. Am. Chem. Soc. 2016, 138, 4908–4916. [Google Scholar] [CrossRef]
- Saint-Denis, T.G.; Zhu, R.-Y.; Chen, G.; Wu, Q.-F.; Yu, J.-Q. Enantioselective C(sp3)-H bond activation by chiral transition metal catalysts. Science 2018, 359, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dumele, O.; Chen, J.; Passarelli, J.V.; Stupp, S.I. Supramolecular Energy Materials. Adv. Mater. 2020, 32, 1907247. [Google Scholar] [CrossRef]
- Schenning, A.P.H.J.; Meijer, E.W. Supramolecular electronics; nanowires from self-assembled π-conjugated systems. Chem. Commun. 2005, 26, 3245–3258. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Ochi, Y.; Miyamura, S.; Tanaka, T.; Kobayashi, S.; Wakamiya, T.; Matsubara, Y.; Yoshida, Z. Rigid molecular architectures that comprise a 1,3,5-trisubstituted benzene core and three oligoaryleneethynylene arms: Light-emitting characteristics and π conjugation between the arms. J. Am. Chem. Soc. 2006, 128, 4504–4505. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Fukushima, T.; Suna, Y.; Ishii, N.; Saeki, A.; Seki, S.; Tagawa, S.; Taniguchi, M.; Kawai, T.; Aida, T. Photoconductive coaxial nanotubes of molecularly connected electron donor and acceptor layers. Science 2006, 314, 1761–1764. [Google Scholar] [CrossRef]
- Tovar, J.D. Supramolecular Construction of Optoelectronic Biomaterials. Acc. Chem. Res. 2013, 46, 1527–1537. [Google Scholar] [CrossRef]
- Zhang, J.; Dong, S.; Zhang, K.; Liang, A.; Yang, X.; Huang, F.; Cao, Y. A series of blue supramolecular polymers with different counterions for polymer light-emitting diodes. Chem. Commun. 2014, 50, 8227–8230. [Google Scholar] [CrossRef]
- Goor, O.J.G.M.; Hendrikse, S.I.S.; Dankers, P.Y.W.; Meijer, E.W. From supramolecular polymers to multi-component bio- materials. Chem. Soc. Rev. 2017, 46, 6621–6637. [Google Scholar] [CrossRef] [Green Version]
- Biswas, S.; Kinbara, K.; Oya, N.; Ishii, N.; Taguchi, H.; Aida, T. A Tubular Biocontainer: Metal Ion-Induced 1D Assembly of a Molecularly Engineered Chaperonin. J. Am. Chem. Soc. 2009, 131, 7556–7557. [Google Scholar] [CrossRef]
- Aida, T.; Meijer, E.W.; Stupp, S.I. Functional Supramolecular Polymers. Science 2012, 335, 813–817. [Google Scholar] [CrossRef] [Green Version]
- Bakker, M.H.; Lee, C.C.; Meijer, E.W.; Dankers, P.Y.W.; Albertazzi, L. Multicom-ponent Supramolecular Polymers as a Modular Platform for Intracellular Delivery. ACS Nano 2016, 10, 1845–1852. [Google Scholar] [CrossRef] [PubMed]
- Kulkarni, C.; Meijer, E.W.; Palmans, A.R.A. Cooperativity Scale: A Structure-Mechanism Correlation in the Self-Assembly of Benzene-1,3,5-tricarboxiamides. Acc. Chem. Res. 2017, 50, 1928–1936. [Google Scholar] [CrossRef]
- de Greef, T.F.A.; Smulders, M.M.J.; Wolffs, M.; Schenning, A.P.H.J.; Sijbesma, R.P.; Meijer, E.W. Supramolecular Polymerization. Chem. Rev. 2009, 109, 5687–5754. [Google Scholar] [CrossRef]
- Rodríguez, R.; Ignés-Mullol, J.; Sagués, F.; Quiñoá, E.; Riguera, R.; Freire, F. Helical sense selective domains and enantiomeric superhelices generated by Langmuir-Schaefer deposition of an axially racemic chiral helical polymer. Nanoscale 2016, 8, 3362–3367. [Google Scholar] [CrossRef] [PubMed]
- Sakurai, S.-I.; Okoshi, K.; Kumaki, J.; Yashima, E. Two-Dimensional Surface Chirality Control by Solvent-Induced Helicity Inversion of a Helical Polyacetylene on Graphite. J. Am. Chem. Soc. 2006, 128, 5650–5651. [Google Scholar] [CrossRef] [PubMed]
- Okoshi, K.; Sakurai, S.-I.; Ohsawa, J.K.; Yashima, E. Two-Dimensional Hierarchical Self-Assembly of One-Handed Helical Polymers on Graphite. Angew. Chem. Int. Ed. 2006, 45, 1245–1248. [Google Scholar]
- Díaz-Cabrera, S.; Dorca, Y.; Calbo, J.; Aragó, J.; Gómez, R.; Ortí, E.; Sánchez, L. Hierarchy of Asymmetry at Work; Chain-Dependent Helix-to-Helix Interactions in Supramolecular Polymers. Chem. Eur. J. 2018, 24, 2826–2831. [Google Scholar] [CrossRef]
- Greciano, E.E.; Calbo, J.; Ortí, E.; Sánchez, L. N-Annulated Perylene Bisimides to Bias the Differentiation of Metastable Supramolecular Assemblies into J- and H-Aggregates. Angew. Chem. Int. Ed. 2020, 132, 17670–17677. [Google Scholar] [CrossRef]
- Wehner, M.; Röhr, M.I.S.; Bühler, M.; Stepanenko, V.; Wagner, W.; Würthner, F. Supramolecular Polymorphism in One-Di- mensional Self-Assembly by Kinetic Pathway Control. J. Am. Chem. Soc. 2019, 141, 6092–6107. [Google Scholar] [CrossRef]
- Ogi, S.; Stepanenko, V.; Sugiyasu, K.; Takeuchi, M.; Würthner, F. Mechanism of Self-Assembly Process and Seeded Supramolecular Polymerization of Perylene Bisimide Organogelator. J. Am. Chem. Soc. 2015, 137, 3300–3307. [Google Scholar] [CrossRef]
- Würthner, F.; Möller, C.R.S.; Fimmel, B.; Ogi, S.; Leowanawat, P.; Schmidt, D. Perylene Bisimide Dye Assemblies as Archetype Functional Supramolecular Materials. Chem. Rev. 2016, 116, 962–1052. [Google Scholar] [CrossRef]
- Weyandt, E.; ter Huurne, G.M.; Vantomme, G.; Markvoort, A.J.; Palmans, A.R.A.; Meijer, E.W. Photodynamic Control of the Chain Length in Supramolecular Polymers: Switching an Intercalator into a Chain Capper. J. Am. Chem. Soc. 2020, 142, 6295–6303. [Google Scholar] [CrossRef] [Green Version]
- Smulders, M.M.J.; Filot, I.A.W.; Leenders, J.M.A.; van der Schoot, P.; Palmans, A.R.A.; Schenning, A.P.H.J.; Meijer, E.W. Tuning the Extent of Chiral Amplification by Temperature in a Dynamic Supramolecular Polymer. J. Am. Chem. Soc. 2010, 132, 611–619. [Google Scholar] [CrossRef] [Green Version]
- Smulders, M.M.J.; Stals, P.J.M.; Mes, T.; Paffen, T.F.E.; Schenning, A.P.H.J.; Palmans, A.R.A.; Meijer, E.W. Probing the Limits of the Majority-Rules Principle in a Dynamic Supramolecular Polymer. J. Am. Chem. Soc. 2010, 132, 620–626. [Google Scholar] [CrossRef] [PubMed]
- Hifsudheen, M.; Mishra, R.K.; Vedhanarayanan, B.; Praveen, V.K.; Ajayaghosh, A. The Helix to Super-Helix Transition in the Self-Assembly of π-Systems: Superseding of Molecular Chirality at Hierarchical Level. Angew. Chem. Int. Ed. 2017, 56, 12634–12638. [Google Scholar] [CrossRef]
- García, F.; Fernández, G.; Sánchez, L. Modulated Morphology in the Self-Organization of a Rectangular Amphiphile. Chem. Eur. J. 2009, 15, 6740–6747. [Google Scholar] [CrossRef]
- Fernández, G.; García, F.; Aparicio, F.; Matesanz, E.; Sánchez, L. Two-dimensional self-organization of rectangular OPE amphiphiles into microcrystalline lamellae. Chem. Commun. 2009, 46, 7155–7157. [Google Scholar] [CrossRef] [PubMed]
- Aparicio, F.; García, F.; Fernández, G.; Matesanz, E.; Sánchez, L. Mirror Helices and Helicity Switch at Surfaces Based on Chiral Triangular-Shape Oligo(phenylene ethynylenes). Chem. Eur. J. 2011, 17, 2769–2776. [Google Scholar] [CrossRef] [PubMed]
- García, F.; Korevaar, P.A.; Verlee, A.; Meijer, E.W.; Palmans, A.R.A.; Sánchez, L. The influence of π-conjugated moieties on the thermodynamics of cooperatively self-assembling tricarboxamides. Chem. Commun. 2013, 49, 8674–8676. [Google Scholar] [CrossRef]
- Buendía, J.; Calbo, J.; García, F.; Aragó, J.; Viruela, P.M.; Ortí, E.; Sánchez, L. Helical supramolecular polymerization of C3-symmetric amides and retroamides: On the origin of cooperativity and handedness. Chem. Commun. 2016, 52, 6907–6910. [Google Scholar] [CrossRef]
- Buendía, J.; García, F.; Yélamos, B.; Sánchez, L. Transfer and amplification of chirality in Phe-based C3-symmetric non-ionic amphiphiles. Chem. Commun. 2016, 52, 8830–8833. [Google Scholar] [CrossRef]
- Zhang, W.; Jin, W.; Fukushima, T.; Ishii, N.; Aida, T. Dynamic or Nondynamic? Helical Trajectory in Hexabenzocoronene Nanotubes Biased by a Detachable Chiral Auxiliary. J. Am. Chem. Soc. 2013, 135, 114–117. [Google Scholar] [CrossRef]
- Jin, W.; Fukushima, T.; Niki, M.; Kosaka, A.; Ishii, N.; Aida, T. Self-Assembled Graphitic Nanotubes with One-Handed Helical Arrays of a Chiral Amphiphilic Molecular Graphene. Proc. Natl. Acad. Sci. USA 2005, 102, 10801–10806. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Jin, W.; Fukushima, T.; Ishii, N.; Aida, T. Metal-Ion-Coated Graphitic Nanotubes: Controlled Self-Assembly of a Pyridyl-Appended Gemini-Shaped Hexabenzocoronene Amphiphile. Angew. Chem. Int. Ed. 2009, 48, 4747–4750. [Google Scholar] [CrossRef]
- Dorca, Y.; Greciano, E.E.; Valera, J.S.; Gómez, R.; Sánchez, L. Hierarchy of Asymmetry in Chiral Supramolecular Polymers: To- ward Functional, Helical Supramolecular Structures. Chem. Eur. J. 2019, 25, 5848–5864. [Google Scholar] [CrossRef]
- Jagtap, S.P.; Mukhopadhyay, S.; Coropceanu, V.; Brizius, G.L.; Brédas, J.-L.; Collard, D.M. Closely Stacked Oligo(phenylene ethynylene)s: Effect of π-Stackingon the Electronic Properties of Conjugated Chromophores. J. Am. Chem. Soc. 2012, 134, 7176–7185. [Google Scholar] [CrossRef]
- Xiao, X.; Nagahara, L.A.; Rawlett, A.M.; Tao, N. Electrochemical Gate-Controlled Conductance of Single Oligo(phenylene ethynylene)s. J. Am. Chem. Soc. 2005, 127, 9235–9240. [Google Scholar] [CrossRef] [PubMed]
- Philips, D.S.; Kartha, K.K.; Politi, A.T.; Krügger, T.; Albuquerque, R.Q.; Fernández, G. Interplay between H-Bonding and Preorganization in the Evolution of Self-Assembled Systems. Angew. Chem. Int. Ed. 2019, 58, 4732–4736. [Google Scholar] [CrossRef] [PubMed]
- Mayoral, M.J.; Rest, C.; Schellheimer, J.; Stepanenko, V.; Fernández, G. Narcissistic versus Social Self-Sorting of Oligophenyleneethynylene Derivatives: From Isodesmic Self-Assembly to Cooperative Co-Assembly. Chem. Eur. J. 2012, 18, 15607–15611. [Google Scholar] [CrossRef] [PubMed]
- Rudolph, T.; Allampally, N.K.; Fernández, G.; Schacher, F.H. Controlling Aqueous Self-Assembly Mechanisms by Hydrophobic Interactions. Chem. Eur. J. 2014, 20, 13871–13875. [Google Scholar] [CrossRef] [PubMed]
- Albert, S.K.; Golla, M.; Thelu, H.V.P.; Krishnan, N.; Varghese, R. A pH-Responsive DNAsome from the Self-Assembly of DNA-Phenyleneethynylene Hybrid Amphiphile. Chem. Eur. J. 2017, 23, 8348–8352. [Google Scholar] [CrossRef]
- Langenstroer, A.; Kartha, K.K.; Dorca, Y.; Dröste, J.; Stepanenko, V.; Albuquerque, R.Q.; Hansen, M.R.; Sanchez, L.; Fernán-dez, G. Unraveling Concomitant Packing Polymorphism in Metallosupramolecular Polymers. J. Am. Chem. Soc. 2019, 141, 5192–5200. [Google Scholar] [CrossRef]
- Fernández, Z.; Fernández, B.; Quiñoá, E.; Freire, F. Dynamic and Individual Supramolecular Helices: The Complex Aggregation Pathway of a Short, Asymmetric and Chiral Oligo(p-phenyleneethynylene). Angew. Chem. Int. Ed. 2021. [Google Scholar] [CrossRef]
- Fernández, B.; Rodríguez, R.; Rizzo, A.; Quiñoá, E.; Riguera, R.; Freire, F. Predicting the Helical Sense of Poly(phenylacetylene)s from their Electron Circular Dichroism Spectra. Angew. Chem. Int. Ed. 2018, 57, 3666–3670. [Google Scholar] [CrossRef]
- Grimme, S. Conformer-Rotamer Ensemble Sampling Tool (CREST). J. Chem. Theor. Comput. 2019, 15, 2847–2862. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density functional thermochemistry. III. The role of exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [Green Version]
- Baranowska, A.; Zawada, A.; Fernández, B.; Bartkowiak, W.; Kedziera, D.; Kaczmarek-Kedziera, A. Interaction-induced electric properties and cooperative effects in model systems. Phys. Chem. Chem. Phys. 2010, 12, 852–862. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. Hydrogen Bonding: A Theoretical Perspective; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Fernández, B.; Rodríguez, R.; Quiñoá, E.; Riguera, R.; Freire, F. Decoding the ECD spectra of Poly(phenylacetylene)s: Structural significance. ACS Omega 2019, 4, 5233–5240. [Google Scholar] [CrossRef] [Green Version]
- Runge, E.; Gross, E.K.U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar] [CrossRef]
- Yanai, Y.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange-Correlation Fuctional Using the Coulomb-attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2005, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Binkley, J.S.; Pople, J.A.; Hehre, W.J. Self-consistent Molecular Orbital Methods. 21. Small Split-valence Basis Sets for First-row Elements. J. Am. Chem. Soc. 1980, 102, 939–947. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Neese, F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Allouche, A.R. Gabedit—A Graphical User Interface for Computational Chemistry Softwares. J. Comput. Chem. 2011, 32, 174–182. [Google Scholar] [CrossRef]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An Advanced Semantic Chemical Editor, Visualization, and Analysis Platform. J. Cheminform. 2012, 4, 17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fernández, Z.; Fernández, B.; Quiñoá, E.; Freire, F. Chiral information harvesting in helical poly(acetylene) derivatives using oligo(p-phenyleneethynylene)s as spacers. Chem. Sci. 2020, 11, 7182–7187. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, Q. Intermolecular interaction characteristics of the all-carboatomic ring, cyclo[18]carbon: Focusing on molecular absorption and stacking. Carbon 2021, 171, 514–523. [Google Scholar] [CrossRef]


| Energy (H) | ||
|---|---|---|
| monomer | Conformer 1 | −1476.4953010 |
| Conformer 2 | −1476.4953009 | |
| dimer | hh | −2953.0435193 |
| ht | −2953.0400134 | |
| 4-mer | ||
| hh | −5906.1562241 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández, B.; Fernández, Z.; Quiñoá, E.; Freire, F. From Oligo(Phenyleneethynylene) Monomers to Supramolecular Helices: The Role of Intermolecular Interactions in Aggregation. Molecules 2021, 26, 3530. https://doi.org/10.3390/molecules26123530
Fernández B, Fernández Z, Quiñoá E, Freire F. From Oligo(Phenyleneethynylene) Monomers to Supramolecular Helices: The Role of Intermolecular Interactions in Aggregation. Molecules. 2021; 26(12):3530. https://doi.org/10.3390/molecules26123530
Chicago/Turabian StyleFernández, Berta, Zulema Fernández, Emilio Quiñoá, and Félix Freire. 2021. "From Oligo(Phenyleneethynylene) Monomers to Supramolecular Helices: The Role of Intermolecular Interactions in Aggregation" Molecules 26, no. 12: 3530. https://doi.org/10.3390/molecules26123530