H/D Exchange Processes in Flavonoids: Kinetics and Mechanistic Investigations

Abstract

Several classes of flavonoids, such as anthocyanins, flavonols, flavanols, and flavones, undergo a slow H/D exchange on aromatic ring A, leading to full deuteration at positions C(6) and C(8). Within the flavanol class, H-C(6) and H-C(8) of catechin and epicatechin are slowly exchanged in D₂O to the corresponding deuterated analogues. Even quercetin, a relevant flavonol representative, shows the same behaviour in a D₂O/DMSOd₆ 1:1 solution. Detailed kinetic measurements of these H/D exchange processes are here reported by exploiting the time-dependent changes of their peak areas in the ¹H-NMR spectra taken at different temperatures. A unifying reaction mechanism is also proposed based on our detailed kinetic observations, even taking into account pH and solvent effects. Molecular modelling and QM calculations were also carried out to shed more light on several molecular details of the proposed mechanism.

1. Introduction

Flavonoids are polyphenolic compounds that are diverse in both chemical structure and properties. Since flavonoids are naturally present in fruits, vegetable, and tea, they are an integral part of the human diet. It is generally accepted that diary flavonoids have important biological effects [1,2].

Flavonoids often demonstrate phytoalexin and antioxidant properties, important for promoting abiotic and biotic stress tolerance. The antioxidant activity of flavonoids depends upon the arrangement of functional groups on the molecular skeleton [3,4]. Flavonoids are divided into several classes of compounds based on substituents and the functional groups pattern on the shared backbone (Scheme 1).

The key feature that gives flavonoids most of their characteristic properties seems to be an unusually high local concentration of ortho-phenolic hydroxyl groups [5]. In later years, great importance has been given to the reactivity of the aromatic rings of flavonoids, due to their peculiar hydroxyl substitution pattern towards other organic and inorganic molecules. Two o-hydroxyl groups and an ether-oxygen atom are attached to ring A, in an alternated fashion, and two or more hydroxyl groups are attached to ring B generating a very unique reactivity on the carbon sites of the aromatic rings. Based on polyhydroxyl configuration on the benzene rings of flavonoids, the B ring is considered to be prone to redox processes (catechol to o-quinone conversion) [6,7], whilst ring A would be much more reactive to electrophilic substitutions at the strongly activated nucleophilic sites C(6) and C(8). Among the flavonoids, structural changes in the B ring are also considered to influence the antioxidant activity.

We recently described, within the class of flavan-3-ols, an interesting case of ring C reactivity towards sulfite addition leading to the corresponding 4-sulfonated analogues [8]. During this investigation, we also observed the slow disappearance of the NMR signals of H-C(6) and H-C(8) in ring A when D₂O was used as a solvent for the flavan-3-ol substrates, evidently due to solvent-mediated H/D exchange at these positions. In fact, during kinetic measurements of sulfonation and thermal-induced isomerization of these flavanols [8], we observed that H/D exchange occurred, within a daytime scale, on both the aromatic protons of ring A.

We were not the first to observe this phenomenon in polyphenols. Several studies already reported on the modification of the H-NMR spectra of different flavonoids in the presence of deuterated solvent [9]. This exchange was first observed in catechin-like substrates by Kolar et al. [10], after cleavage of methylated procyanidin in a D₂O-dioxane solvent mixture. It was also reported that specifically sites 6 and 8 of ring A of pelargonidin and malvidin undergo the same exchange process in acidified D₂O and/or acidified CD₃OD, apparently following a keto-enol tautomerism pathway, while sites in other rings remain unlabelled [11,12,13].

The reactivity of ring A can be chemically related to that of phloroglucinol (1,3,5-trihydroxybenzene), which is well-known to undergo both O- and C- alkylation indicating an aromatic or carbonylic structure of phloroglucinol, respectively. The position of this keto-enol equilibrium implies several tautomeric forms and species distribution depends on specific medium and reaction conditions [14,15]. Similarly, deuteration at C(6) and/or C(8) on ring A can be interpreted, in acidic media, as a first electrophilic attack of D₃O⁺ (or of D₂O in neutral conditions) on activated sites of the ring A aromatic structure or as the result of solvent-mediated acid-base exchange at the α-carbonyl positions of the ring A keto structure. Totlani et al. [16] suggested that catechin-like substrates could essentially react via electrophilic aromatic substitution leading to H/D exchange [17,18]. Moreover, the two active sites (6 and 8) on ring A have been proven to have different behaviours towards H/D exchange. Other reports have found different rates of exchange for the two sites [12,19,20], which can reflect differences in their electron density, triggered by the acidity of the hydroxyl groups in position 5 and 7. Nam et al. [21] demonstrated that flavonoids undergo an exchange reaction in deuterated protic solvents (such as CD₃OD or D₂O) under acidic conditions. This reaction occurs much more slowly under neutral conditions as observed by following the reaction pathway during storage of the samples at −20 °C over a period of 12 months [21]. These results suggested the existence of different intermediate species (mono-deuterated species) in addition to the initial substrate and di-deuterated product. Moreover, other studies converged on the same main outcome leading to different rates for the process at the two sites C(6) and C(8), indicating a quite different electron density on them [22].

However, since detailed kinetic data on this H/D exchange process for flavanols in pure D₂O at neutral pH have never been reported, we decided to exploit the NMR technique to obtain robust kinetic measurements that would allow us, in turn, not only to reliably assess the kinetic parameters of the process but also to shed light on the mechanistic details of the process.

2. Results and Discussion

2.1. H/D Isotopic Exchange on Ring-A Protons at Positions C(6) and C(8) of Flavanols

Although the solubility in water of simple flavanols, such as catechin (1) or epicatechin (2) is low (≈10 mM), aqueous homogeneous solutions can be prepared and investigated through NMR without any apparent phase separation along several days. When they are dissolved in deuterated water (D₂O), all phenolic O-H protons are quickly exchanged by deuterium ions leading to 4a or 5a O-D labelled substrates (Scheme 2). At the concentrations of the homogenous solutions of 1 and 2 achievable in D₂O (≈10 mM) the pH was measured to be 6.9 (pD = 7.3) using ¹H-NMR signals of imidazole as pH indicator [23]. We found that catechin 4a undergoes a slow process of deuterium incorporation leading to the fully deuterated ring A species 4d through the partially deuterated intermediates 4b-4c. Similarly, the O-D labelled epicatechin species 5a in D₂O is slowly converted into 5d, through the intermediates 5b-5c.

Although the standard Gibbs free energy difference (∆G⁰) of the overall equilibrium process (1):

$$4a+2{\mathrm{D}}_2\mathrm{O}\rightleftarrows 4d+2\mathrm{HDO}$$

(1)

is expected to be about zero due to self-compensating enthalpic and entropic effects, the equilibrium position is completely shifted towards the products since D₂O is present in the reacting system in a much larger molar excess than 4a, thus leading to complete irreversible conversion of 4a into 4d. Since the free energy of activation (∆G^‡) of the process (1) is not so high as it would be expected for any C-H/C-D exchange, its rate can be evaluated at r.t. (or within a small T range around it) by following the time (t) and temperature (T) dependence of the ¹H-NMR signals of ring A aromatic protons.

In fact, at T = 310 K, 4a was observed to undergo in a few hours a significant D-labelling at C(6) and C(8) as highlighted in Figure 1a (blue dotted boxes) by the significant decrease of the ¹H-NMR signals H-C(6) (δ_H6 = 6.13) and H-C(8) (δ_H8 = 6.05). The same behaviour was shown (Figure 1b, blue dotted box) by the corresponding signals of epicatechin (5a) (δ_H6 = 6.15 and δ_H8 = 6.13).

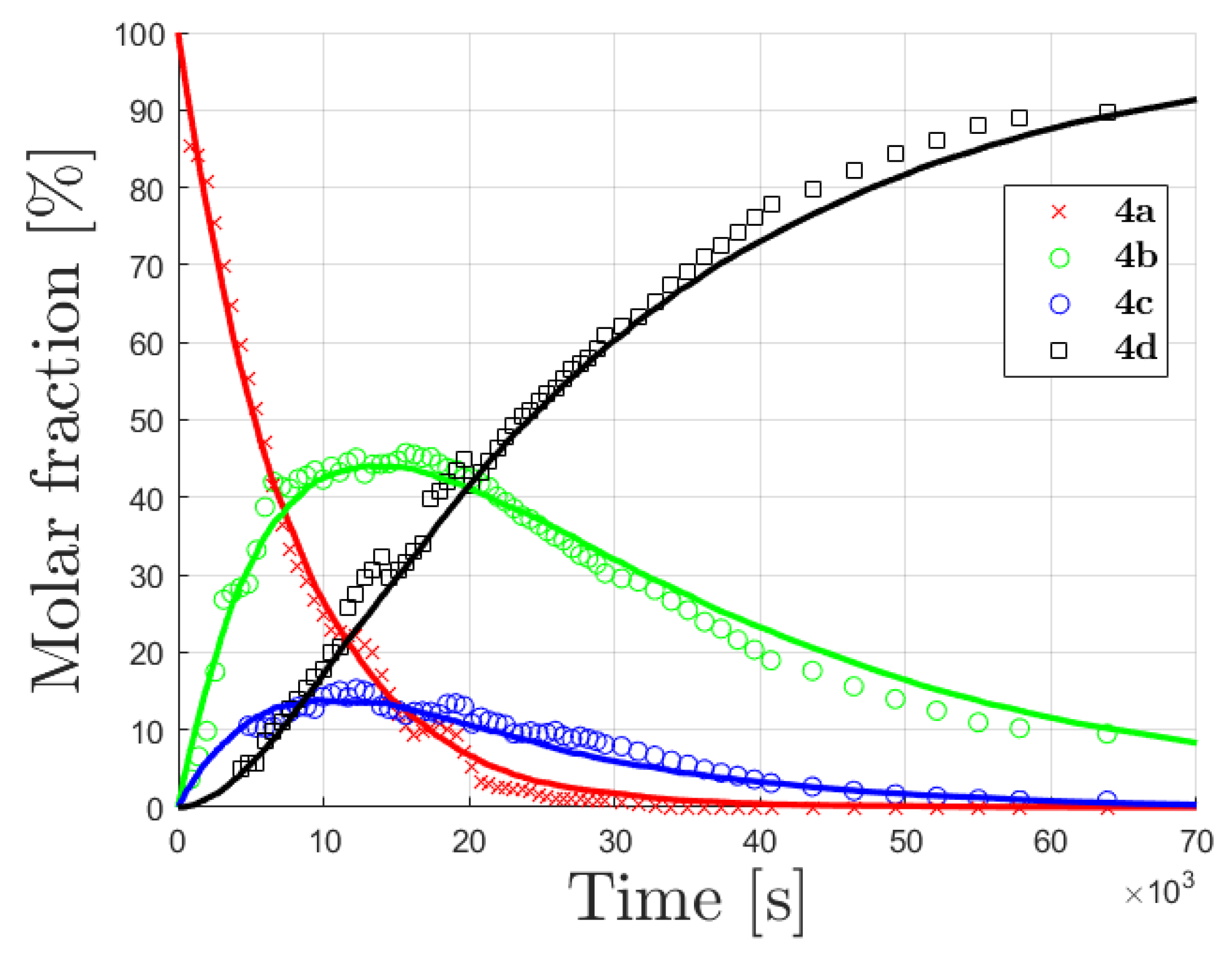
For the overall process 4a → 4d (Figure 2a) the time-varying amount of (4a + 4b) and (4a + 4c) were obtained from the NMR area integration of the signals H-C(6) and H-C(8), respectively, and were normalized to the unperturbed area of the ring B protons.

By integrating the area of these signals, we evaluated not only the time dependence of the disappearance of 4a but also of the appearance/disappearance of the monodeuterated D8 (4b) and the monodeuterated D6 intermediates (4c).

In fact, at a given time of any kinetics run (Figure 3, t = 500 min, T = 305 K), the peak deconvolution of the signal of H-C(6) at δ_H = 6.07 allows establishing the relative contributions of the residual H-C(6) of 4a (doublet, J = 2.1 Hz) and a new singlet signal (centred at almost the same frequency as the former) attributable to D-8 monodeuterated species 4b.

By normalizing to the initial concentration of 4a, the % molar fraction of these two species (x_4a + x_4b) was evaluated to be 60% and peak deconvolution leads to x_4a ≈ 2x_4b.

Correspondingly, the peak deconvolution of the signal of H-C(8) at δ_H = 5.98 allows establishing the relative contribution of the residual H-C(8) of 4a (doublet, J = 2.1 Hz) and a new singlet signal attributable to 4c. The % molar fraction of these two species (x_4a + x_4c = 52%) can be obtained by the relative area integration, whilst the peak deconvolution leads to x_4a ≈ 4x_4c.

To fulfil the mass balance constrain, the overall normalized % distribution was evaluated to be x_4a:x_4b:x_4c:x_4d = 42:20:1:28, indicating different specific rate constants (i.e., regioselectivity) at the two different sites with a faster H/D exchange at C(8) than at C(6). In principle, the relative amount of 4a–4d species can be evaluated at any time and any fixed temperature during the kinetic run. Actually, several ¹H-NMR spectra taken in kinetic runs carried out at higher temperature do not have sufficient resolution to allow an adequate deconvolution of H(6) and H(8) signals, but this outcome did not hinder our analysis so much. The peak deconvolution of the H-C(6) and H-C(8) signals allowed us to separate the time-dependent contribution of the intermediates 4b and 4c, reaching maximum values of x_4b ≈ 0.20 and x_4c ≈ 0.10 at about the same time (Figure 4a t_max ≈ 500 min). More importantly, a single exponential fitting (Figure 4) of time, the varying x_4a (t), was obtained with an observed rate constant (T = 305 K) k_obs (4a) = 3.90 × 10⁻⁵ s⁻¹ (t_½ (4a) = 17,800 s) suggesting that all the processes contributing to the disappearance of 4a are (pseudo) first-order processes, only depending on the initial concentration of 4a (Figure 4b).

Similar data were also obtained for the 5a → 5d process. However, deuteration of aromatic protons of 5a in D₂O (Figure 2b) does not show any site selectivity. In fact, the overall rate of disappearance of the H-6 signals (5a + 5b) was almost the same as that of the H-8 signals (5a + 5c). In this case, we were not able to evaluate at a given time point the relative contribution of monodeuterated 5b and 5c by peak deconvolution since from one side the difference of chemical shift between H-C(6) and H-C(8) in epicatechin is so small to become comparable to the J(6,8) coupling constant (leading to non-first order NMR signals) and, from the other side, the signal lineshape was not good enough to allow reliable fittings.

Initially, we thought that the kinetic behaviour showed by deuteration of 4a could be rationalized by assuming two competitive pseudo-first-order conversions starting from the same substrate (4a → 4b in competition with 4a → 4c) followed by two convergent pseudo-first-order processes leading to the same end product (4b → 4d in addition to 4c → 4d). To evaluate the four unknown rate constants (k₁, k₂, k₃, k₄), we resorted to the Kinetiscope software using, as the initial guess for the fitting, the values roughly estimated from our raw kinetic data shown in Figure 2. However, we soon realized that it was almost impossible to find a set of four k_i able to adequately fulfil our experimental x_i(t) data. No set of four k_i was able to fit the general trend of these curves and to be in agreement with several significant constraints imposed by experimental measures, such as the time of the crossing points of the curve x_4d(t) with that of x_4a(t) (26,800 s) and/or the time of the crossing point of the curve of x_4b(t) with those of x_4a(t) (73,000 s), x_4b(t) (42,200 s), and x_4c(t) (≈80,000 s). To find an optimal fitting of our data, another process needed to come into play, i.e., a process able to convert 4a into 4d without any detectable intermediate. Thus, we were somehow forced by experimental findings to suppose the kinetic pathway drawn in Scheme 3, based on competitive-consecutive pseudo-first-order processes. The time dependence of all the stable species is regulated by a system of linear differential equations (Scheme 3, top) that, with the appropriate boundary conditions and the mass balance constrain, lead to the integrated solution x_i(t) here reported (Scheme 3, bottom).

The fitting of these integrated equations with the stochastic simulator Kinetiscope leads to the following best fitting values at T = 305 K: k₁ = 1.7 × 10⁻⁵ s⁻¹, k₂ = 0.85 × 10⁻⁵ s⁻¹, k₃ = 1.35 × 10⁻⁵ s⁻¹, k₄ = 2.5 × 10⁻⁵ s⁻¹, and k₅ = 2.4 × 10⁻⁵ s⁻¹, fulfilling the condition k_obs = (k₁ + k₂+ k₃) = 3.90 × 10⁻⁵ s⁻¹. By introducing these values into integrated equations, we found that the calculated curves were almost superimposable to our experimental kinetic data (Figure 4b).

Since, in principle, the molar fraction of every species can be evaluated at every time (and temperature), we carried out a detailed kinetic analysis following the time dependence of the NMR-sensitive species 4a/4b/4c performing ¹H-NMR measurements at five different temperatures (300–320 K). Unfortunately, the peak deconvolution of the H-C(6) and H-C(8) signals was possible only at 300 (Figure 4a) and 305 K (Figure 4b) since at higher temperatures the peak resolution of these signals was not sufficient to allow reproducible deconvolutions.

Thus, the kinetic parameters reported in

Table 1. Kinetic data for deuterium ion incorporation process by heavy water (D₂O) on catechin and epicatechin substrates. The values of Gibbs free energy of activation (∆G^‡) in the case of epicatechin are theoretically calculated based on a given temperature by the Eyring equation, as the qualitative contribution division into enthalpy and entropy of activations.

Site	T [K]	k’obs [s−1]	EA [kJ/mol]	ΔH‡ [kJ/mol]	ΔS‡ [kJ/mol K]	(1) ΔG‡ [kJ/mol]
	300	(1.48 ± 0.01) × 10−5
	305	(2.42 ± 0.01) × 10−5
(2) C(6)	310	(3.60 ± 0.02) × 10−5	79.7 ± 5.5	77.2 ± 5.5	−0.081 ± 0.017	102.1 ± 7.6
	315	(6.72 ± 0.12) × 10−5
	320	(10.8 ± 0.5) × 10−5
	300	(2.17 ± 0.01) × 10−5
	305	(3.05 ± 0.01) × 10−5
(2) C(8)	310	(4.49 ± 0.02) × 10−5	74.4 ± 9.2	71.9 ± 9.2	−0.095 ± 0.030	101.9 ± 13.1
	315	(8.91 ± 0.11) × 10−5
	320	(13.1 ± 0.6) × 10−5
(3) C(6)	310	(2.93 ± 0.01) × 10−5	/	/	/	102.9
(3) C(8)	310	(2.71 ± 0.01) × 10−5	/	/	/	103.1

⁽¹⁾ Values calculated at T = 310 K. ⁽²⁾ Catechin. ⁽³⁾ Epicatechin.

have just an empirical significance, representing the observed time dependence (k’_obs) of the peak area of the H-C(6) (Figure 5a) and H-C(8) (Figure 5b) at fixed temperatures and not the true rate constants controlling the time changes of x_4a(t). In other words, k’_obs (and the corresponding activation energies) are not simply related to the true values of the three processes, whereby 4a is converted to the intermediates 4b and 4c and/or to the final product 4d. Anyhow, these empirical data are quite useful since they allow us to estimate how and how much the average site selectivity of deuteration depends on temperature. If we define the ratio (k’_(C6) − k’_(C8))/(k’_(C6) + k’_(C8)) at a given temperature as an empirical descriptor of this selectivity, we can notice that it significantly decreases by increasing the temperature, ranging from ≈0.2 (T = 300 K) until ≈0.1 (T = 320 K). This is largely expected since increasing T, the differential exponential factors regulating the rate constants ΔΔG^‡/RT (ΔΔG^‡ = ΔG^‡_(C6) − ΔG^‡_(C8)) must decrease.

It is worth noting that the average ΔG^‡ ≈ 100 kJmol⁻¹ of the two competitive processes is quite similar and dominated by the contribution of the enthalpic term (75–80%). As already pointed out, however, these values simply represent the time dependence of the deuterium ion attack both to 4a and 4b for the H/D exchange at C(8) and both to 4a and 4c for the H/D exchange at C(6). While in the early part the contributions of 4b and 4c can be neglected, this is not true in the middle or late steps of these kinetic runs.

A deeper insight into the mechanistic details of the pathway proposed in Scheme 3 can be achieved by considering the kinetic data for all the elementary steps obtained at two different temperatures, 300 and 305 K. For the former, the fitting of the curve x_4a (t) leads to k_obs (4a, T = 300 K) = 2.71 × 10⁻⁵ s⁻¹ (t_½ (4a) = 25,000 s), with a 30% decrease with respect to the value evaluated at T = 305 K. The simulation of all the experimental evaluated x_i(t) affords the following best fitting values at 300 K: k₁ = 1.5 × 10⁻⁵ s⁻¹, k₂ = 0.75 × 10⁻⁵ s⁻¹_, k₃ = 0.45 × 10⁻⁵ s⁻¹, k₄ = 2.2 × 10⁻⁵ s⁻¹, and k₅ = 2.2 × 10⁻⁵ s⁻¹ (Figure 4a).

Thus, k₃ decreases with the decrease of temperature significantly more than the other four rate constants pointing out that 4a undergoes a different molecular rearrangement before leading the end-product 4d. By inserting these k_i values into the Eyring equation we obtained the corresponding ΔG^‡, although we cannot estimate the relative contribution of enthalpic and entropic activation terms.

Another interesting feature is the pH-dependence of these rate constants. By lowering the pH (addition of CD₃COOD) in the 4a/D₂O reacting system, we observed as expected that the rate of the deuteration process increases. Thus, whilst the half-lifetime of 4a at 300 K in neutral solution was found at about 25 min, it decreased at about 6 min at pH 3.0. However, we noticed that k₃ became significantly lower than observed in neutral pH conditions. At pH 3.0 (300 K), this effect is largely offset (Figure 6) by the increase of k₁ and k₂ leading to an observed rate constant significantly larger than in neutral conditions. Another striking feature, related to the pH-induced changes of these rate constants, is represented by the significant increase of the maximum of the curves x_4b(t) and x_4c(t), speaking for a longer lifetime of the key-intermediates 4b and 4c.

To summarize, our explanation relies on the evidence that D₂O is strong enough as an acid to promote deuteration by the D⁺ transfer to C(8) and strong enough as a base to accept the D⁺ ion from DO-C(7). The effect of acidic catalyst seem to rely on (i) a relevant increase of the rate of the competitive processes 4a → 4b and 4a → 4c leading to higher relative amounts of the monodeuterated intermediates 4b and 4c, (ii) a large decrease of the rate of the process 4a → 4d, and iii) an almost unperturbed site selectivity of deuterium ion attack at C(6) or C(8).

Finally, we carried out kinetic runs at 300 K on 4a using CD₃OD in place of D₂O as a deuterium ion source for the H/D exchange. The observed rate constant controlling the disappearance of 4a/CD₃OD was found much lower than that of 4a/D₂O.

2.2. Mechanistic Considerations

In a Frontier Molecular Orbital approach (FMO), the mechanism of the rate-determining steps can be considered as the addition of an electrophilic species (D₃O⁺/D₂O) to the highest nucleophilic centres of flavanols, i.e., C(6) or C(8) which are electrons enriched by the multiple ortho and para mesomeric effect of the oxygen atoms on ring A. This attack will occur at the nucleophilic site having the largest electron density. According to ¹H and ¹³C-NMR experimental spectra of 4a, no matter the solvent, both H-C(8) and C(8) are slightly shielded with respect to H-C(6) and C(6) confirming their higher nucleophilicity (Figure 1a). Similar data were also obtained for the 5a → 5d process (Figure 1b).

The main outcomes of our kinetic data on deuteration of simple flavanols such as 4a and 5a in D₂O are here summarized: (i) In a first preliminary step, all O-H bonds are deuterium ion exchanged through a very fast process; (ii) at r.t., flavanols undergo slow H/D exchange at C(6) and C(8) or at both sites; (iii) the first step of deuteration occurs at a slightly higher specific rate at C(8) than at C(6); (iv) the second step of deuteration occurs at both sites with quite similar specific rates (k₃ ≈ k₄), but slightly faster than the first step; (v) the average ΔG^‡ (≈102 kJmol⁻¹) of all these deuteration processes is mainly determined by enthalpic effects; (vi) in other protic, but less polar, solvents (such as CD₃OD), these processes occur on a significantly longer time-scale.

With this kinetic information, we can propose a reasonable reaction mechanism (Scheme 4). It relies on sequential elementary steps, involving a slow, solvent-mediated, C-D bond formation/O-D bond-breaking followed by a fast, solvent-mediated, C-H bond breaking/O-D bond formation where ring-A can regain its aromaticity. Although our observed rate constants (k_i, i = 1, 2, 3, 4, 5) and the corresponding ΔG^‡ values are not related to true elementary reaction steps (i.e., involving single transition states), they can be considered a simple sequence of elementary steps with one of them as the rate-determining step. Assuming the well-known and largely accepted mechanism involving keto-enol tautomerism of 1,3,5 activated aromatic systems [24], we propose that deuterated keto-analogues (4ab and 4ac) could be the putative transient intermediates leading to the detectable intermediates 4b (k₁) and 4c (k₂) in the two competitive divergent processes 4a → 4b and 4a → 4c, respectively. Similarly, 4bd and 4cd could be the transient putative intermediates of the two convergent pathways, 4b → 4d regulated by k₄ and 4c → 4d regulated by k₅ leading to the end-product 4d. However, as already discussed, our data suggest a relevant role played by the direct process 4a → 4d, implying the putative intermediate 5,7-diketo derivative 4ad.

Although we can only speculate about the structures of the transition states leading to the above-cited putative intermediates, since the elementary steps dealing with C-D formation/O-D breaking and loss of aromaticity are highly endothermic, they are also expected to be the rate-limiting steps and the structure/energy of the relevant TS similar to the structure/energy of the putative intermediates.

The plausibility of the termolecular elementary process 4a → 4d relies on the need to introduce another step converting 4a into 4d in addition to the bimolecular elementary steps of mono-deuteration. Practically speaking, this termolecular process is feasible due to the interaction between three molecules (4a + 2D₂O) and could be energetically comparable (if not favourable) over the sequential competing bimolecular mono-deuteration processes [22], leading to lower enthalpic contribution (ΔH^‡) of the step 4a → 4ad (assuming within the Hammond postulate that the corresponding transition state has a structure similar to 4ad), only partially counterbalanced by a greater entropic term contribution (−TΔS^‡), in agreement with the lower probability to arrange two D₂O molecules in the correct positions for the H/D exchange event.

The relevant outcome that deuteration processes of 4a occur much more slowly in CD₃OD than in D₂O [25] can be explained in our view by the proton/deuterium acid-base properties of flavanols in methanol (pK_a ≈ 13–14) with respect to water (pK_a ≈ 9–10) [26]. The lower acidity of the O-H(D) groups in methanol reflects the reduced thermodynamic ability of methanol to solvate the ions produced by the proton-transfer reaction. However, since the loss of proton/deuterium ions is also involved in all the transition states leading to the putative intermediates, we believe that it can play a relevant role also in the kinetics.

2.3. H/D Isotopic Exchange on Ring-A Proton at Position C(8) of Quercetin

The solubility of quercetin (3) in water is so low (≈3 mM at 300 K) [27] to hinder the NMR measurement of deuterium ion incorporation by D₂O, which is expected to be slower than in flavanols. However, in D₂O/d₆-DMSO 1:1 solution, the solubility can be enhanced and 10 mM solutions of quercetin in this solvent mixture were appropriate to carry out a full kinetic analysis in the temperature range T = 313–333 K. The 4-keto group on ring B strongly affects the electron density on ring-A positions, in particular at C(6) position, in as much that only deuteration at C(8) can be observed in our conditions. Following the similar approach described above for flavanols, we were able to evaluate the Gibbs free energies of activation (Figure 7) for H/D exchange at C(8) in 3 by running the same reaction at different temperatures (

Table 2. Kinetic data for H/D exchange at C(8) by D₂O in quercetin 3 (D₂O/DMSO_d6 1:1 mixture).

Site	T [K]	k’obs [s−1]	EA [kJ/mol]	ΔH‡ [kJ/mol]	ΔS‡ [kJ/mol K]	(1) ΔG‡ [kJ/mol]
	313	(1.48 ± 0.01) × 10−5
	318	(2.42 ± 0.01) × 10−5
C(8)	323	(3.60 ± 0.02) ×10−5	80.3 ± 8.7	77.6 ± 8.7	−0.101 ± 0.027	110.3 ± 12.3
	328	(6.72 ± 0.12) × 10−5
	333	(10.8 ± 0.5) × 10−5

⁽¹⁾ Values calculated at T = 323 K.

).

The deuteration rate constants for 3 are about a magnitude order lower (and the corresponding ΔG^‡ values about 10 kJ/mol higher) than those discussed above for 4 and 5. In our hands, deuteration at C(6) occurs at a so low rate to be considered negligible. Findings by Faizi et al. [9] of C(6) deuteration for 3 quercetin in CF₃COOD are not in contrast with our results, since in these acidic conditions deuteration at C(8) is so fast that at the start of the analysis it was already completely exchanged.

2.4. Results from ab Initio DFT Calculations

To get further molecular details on our kinetic investigations, we resorted to density functional theory (DFT) calculations through codes implemented in the Gaussian 16 software [27]. To arrive at the energy minima of all the structures of flavanols here reported, a full conformational search with the aid of the GMMX add-on (GaussView program) was undertaken. Conformational searching was carried out, allowing both ring C flipping and single-bond rotations through the use of the default values of the program. The MM-minimized rotamers were used as initial input structures, and the geometry was energy-minimized using the DFT/B3LYP 6–311G level of theory [28].

Regarding the catechin system, calculations carried out at the B3LYP/6-311G level of theory confirmed the higher Mulliken negative charge at C(8) (−0.20) with respect to that at C(6) (−0.17). Then, ab initio calculations (geometry optimization followed by frequency calculations) were used to estimate the relative energies of all the species participating in this pathway. A set of simulations were also performed to optimize structures and energies of the corresponding transition states. The calculated energy profile is summarized in Figure 8.

Energies of the mono- and di-deuterated keto forms 4ab, 4ac, 4ad, 4bd, and 4cd were evaluated by QM calculations to be significantly higher than the corresponding mono- and di-deuterated enol forms 4a, 4b, 4c, and 4d. Importantly, the intermediate 4ad was found more stable (by 16 kJmol⁻¹, even after corrections of their different thermal contributions) than the competitive intermediates 4ab and 4ac, thus giving further support to its existence along the pathway of the overall exchange process, as already guessed by the overall fitting of our kinetic data. The transition states (4ab^‡, 4ac^‡, 4ad^‡) of the three competitive deuteration processes were found about 130 kJmol⁻¹ above the energy of reactant 4a. All the structures associated to 4ab^‡, 4ac^‡, 4ad^‡ species showed only one imaginary frequency thus ensuring we were dealing with true transition states. Interestingly, the calculations were also in agreement with the experimental evidence that specific rates of deuteration are lower in deuterated methanol than in deuterated water. In fact, the energy of the 4ab^‡ analogue obtained by deuterium ion transfer from CD₃OD was found about 35 kJmol⁻¹ higher than that of 4ab^‡ itself. The intrinsic reaction coordinate (IRC) calculation performed on 4ab^† (Supplementary Figure S1) afforded reactant 4a and product 4b showing that during the process there is a synchronous breaking of the bond D-OC(7) and formation of the bond D-C(8).

Even the bond length O-C(7) is a fine reaction coordinate since, as expected, it undergoes a significant shortening ongoing from the enol form 4a to the keto form 4b.

The calculated rate constants are of course largely lower than the experimental ones (10⁻¹⁰ s⁻¹ versus 10⁻⁵ s⁻¹) since the calculated free energies of activation are about 30 kJ/mol higher than those experimentally measured. However, we are confident that, by putting two and not only one D₂O molecules in the reactive site of these TS, their energy would become significantly lower due to the well-documented assistance [29] of the 2nd D₂O molecule enhancing the deuterium ion donor and deuterium ion acceptor capability of the first reacting D₂O molecule. Basically, in our approach, the energy profile reported in Figure 8 is aimed to just provide an approximate agreement (in terms of minimum energy of all species playing a role in the process, such as reactants, products, putative, and isolated intermediates) with our experimental findings. Thus, activation energies of processes 4a → 4b and 4a → 4c were calculated to be almost the same (in fact k₁ ≈ k₂), as well as the processes 4a → 4b and/or 4c → 4d were also calculated to have quite similar activation energies as process 4a → 4d, (in fact k₃ ≈ k₁, k₂, k₄, and k₅).

3. Materials and Methods

Each sample was prepared directly in the NMR glass tube. In addition, 10.0 ± 0.3 mM solutions of starting material 1 and 2 were prepared by dissolving 2 mg of pure compounds in 0.750 mL of D₂O with the help of a sonic bath. For compound 3, a 1:1 (0.325:0.325 mL) mixture of D₂O and DMSO_d6 was necessary to solubilize the pure quercetin, without altering the reaction conditions, since D₂O is maintained in extremely large molar excess with respect to 3. The pH of the solution was controlled directly via NMR utilizing pure imidazole ca. 0.2 mM, following the procedure described by Orgovàn et al. [23].

Kinetics of deuteration of catechin and epicatechin by D₂O at T = 300–320 K (variable temperature unit ensure δT accuracy within ± 0.1 K) were performed using Bruker Avance 400 MHz NMR spectrometer. ¹H-NMR measurements were carried out using a 5 mm BBI probe with a 90° proton pulse length of 8.7 μs at a transmission power of 0 dB and equipped with pulsed gradient field utility. ¹H-NMR spectra were recorded every ~10 min and automatic peak integration of the reference signal, which maintained the same area (100%) throughout the whole experiment and of the signals of the two hydrogen atoms that are being substituted by deuterium was performed. The chemical shift scale (δ) was calibrated on the residual proton signal of trimethylsilyl-propionic-2,2,3,3-d4 acid sodium salt (TSP) that was used as reference standard (δ_H = 0.00 ppm).

¹H-NMR of catechin (D₂O, 300K): 6.86 (d, J = 1.9, 1H, H-2′); 6.84 (dd, J = 1.9, 8.1 Hz, 1H, H-6′); 6.76 (d, J = 8.1 Hz, 1H, H5′); 6.01 (d, J = 2.3, 1H, H-6); 5.91(d, J = 2.3, 1H, H-8); 4.60 (d, J = 7.9, 1H, H-2); 4.06 (ddd, J = 8.3, 7.9, 5.4, 1H, H-3); 2.78 (dd, J = 16.0, 5.4, 1H, H4a); 2.42 (dd, J = 16.0, 8.3, 1H, H4b).

¹H-NMR of epicatechin (D₂O, 300 K); 6.86 (d, J = 1.9, 1H, H-2′); 6.84 (dd, J = 1.9, 8.1 Hz, 1H, H-6′); 6.76 (d, J = 8.1 Hz, 1H, H5′); 6.02 (d, J = 2.3, 1H, H-6); 6.00 (d, J = 2.3, 1H, H-8); 4.82 (brs, 1H, H-2); 4.22 (m, 1H, H-3); 2.82 (dd, J = 17.0, 4.3,1H, H4a); 2.67 (dd, J = 17.0, 2.1, 1H, H4b).

The molar percentage ratio of the decrease of the former and increase of the latter was plotted for each compound analysed (catechin and epicatechin) and for each proton. Using Eyring and Arrhenius plots and kinetic equations, it was possible to obtain all the meaningful kinetic and energetic quantities (rate constants, half-life times, activation energy, and Gibbs free energy of activation). A qualitative separation of Gibbs free energy of activation into its two contributions was also carried out using the best fitting curve. The reaction can be considered a pseudo-first-order process since D₂O is in large excess with respect to flavan-3-ols monomers. The same reasoning was employed also for flavonol quercetin 3 and its related kinetic analysis. The only difference for the latter is its poor solubility in pure D₂O leading to the need for the use of D₂O/DMSO_d6 1:1 solution, as solvent.

Peak deconvolution was performed using the MestReNova v12 global spectral deconvolution tool (GSD) with default parameters. Automatic peak identification and integration were also performed to obtain molar ratios of the involved structures. Rate constants guess for best curve fitting of the reaction kinetics was performed with the help of the Kinetiscope software. Molecules’ geometry, energetics and properties simulations were performed via the Gaussian 16 suite of programs [27]. All simulations were performed with DFT at the B3LYP level of theory, at first with a 6-31G basis set, which was then expanded to 6-311G to improve results accuracy. The chemistry of these molecules and processes was modelled in the solution, using the IEFPCM continuous solvent model. Standard optimization and frequency calculations were performed on all molecules, together with transition state optimization and IRC calculation to complete the computational landscape.

4. Conclusions

A careful kinetic analysis of the H/D exchange processes occurring at C(6) and/or C(8) of flavanols (1 and 2) or flavonol (3) has been carried out by joining information deriving both from experimental ¹H-NMR spectra taken at different temperatures, pH and protic solvents (D₂O, CD₃OD, D₂O/DMSOd₆), and from theoretical QM calculations (DFT, B3LYP 6-311G). For the first time, we report here on: (a) The existence, along the reaction coordinate leading from 1 (4a) to the 6,8 di-deuterated analogues 4d, of the monodeuterated species 4b and 4c; (b) different rates of formation of 4b and 4c as established by the peak deconvolution of the H-C(6) and H-C(8) NMR signals during the kinetics; (c) the relevant role played by termolecular processes whereby 4a is converted in 4d without passing through intermediates 4b and 4c; (d) the complex dependence of the overall rate constant on the pH imposed to the reacting system due to the opposite pH-response of the (two steps) route (4a → 4b → 4d) with respect to the (one step) route (4a → 4d).