Quantification and Optimization of Ethanolic Extract Containing the Bioactive Flavonoids from Millettia pulchra Radix
Abstract
:1. Introduction
2. Results and Discussion
2.1. Extraction and Isolation of Major Compounds
2.2. Simultaneous Quantification of Four Major Compounds
2.2.1. Optimized HPLC Condition
2.2.2. HPLC-PDA Method Validation
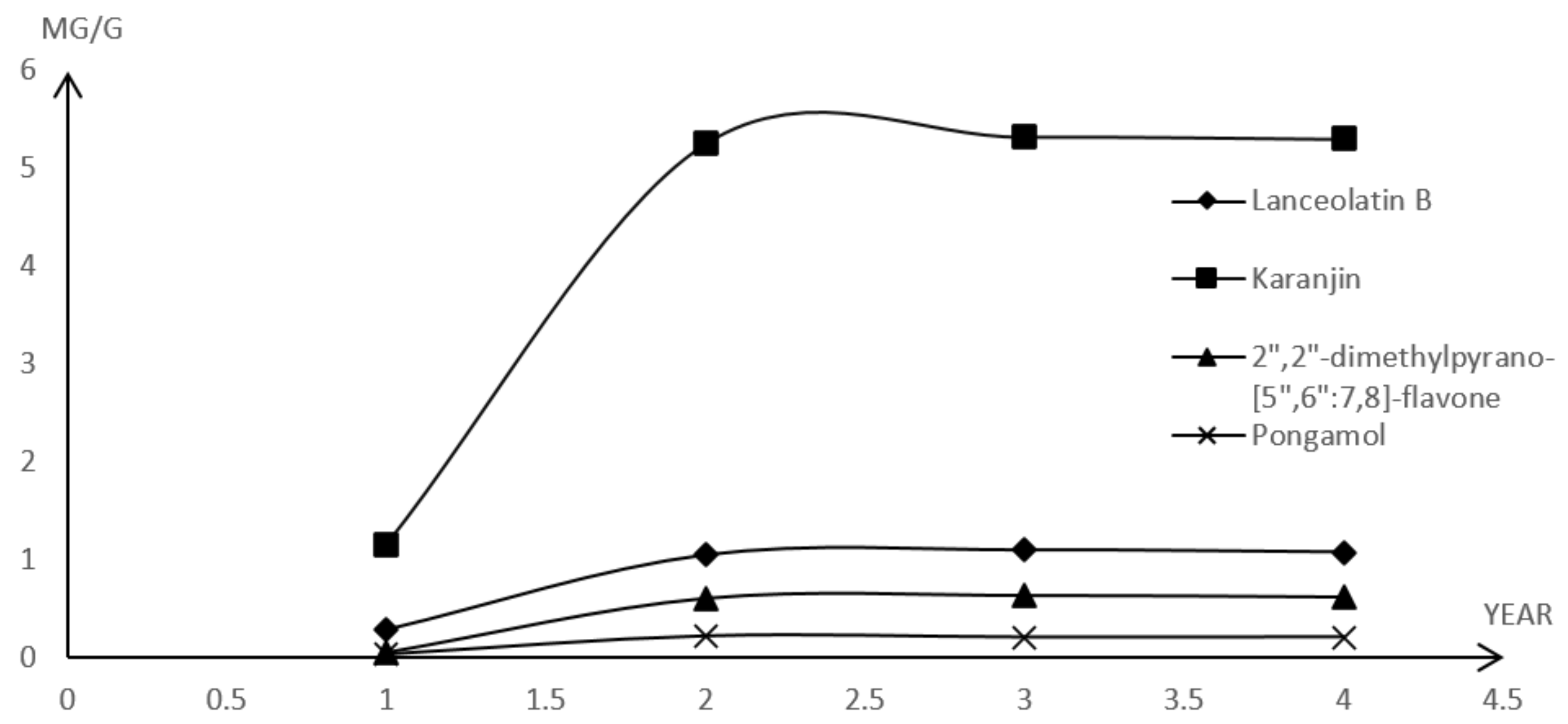
2.2.3. Determination of Major Components in M. pulchra Radix
2.3. Optimization of Extraction
2.3.1. RSM Modelling
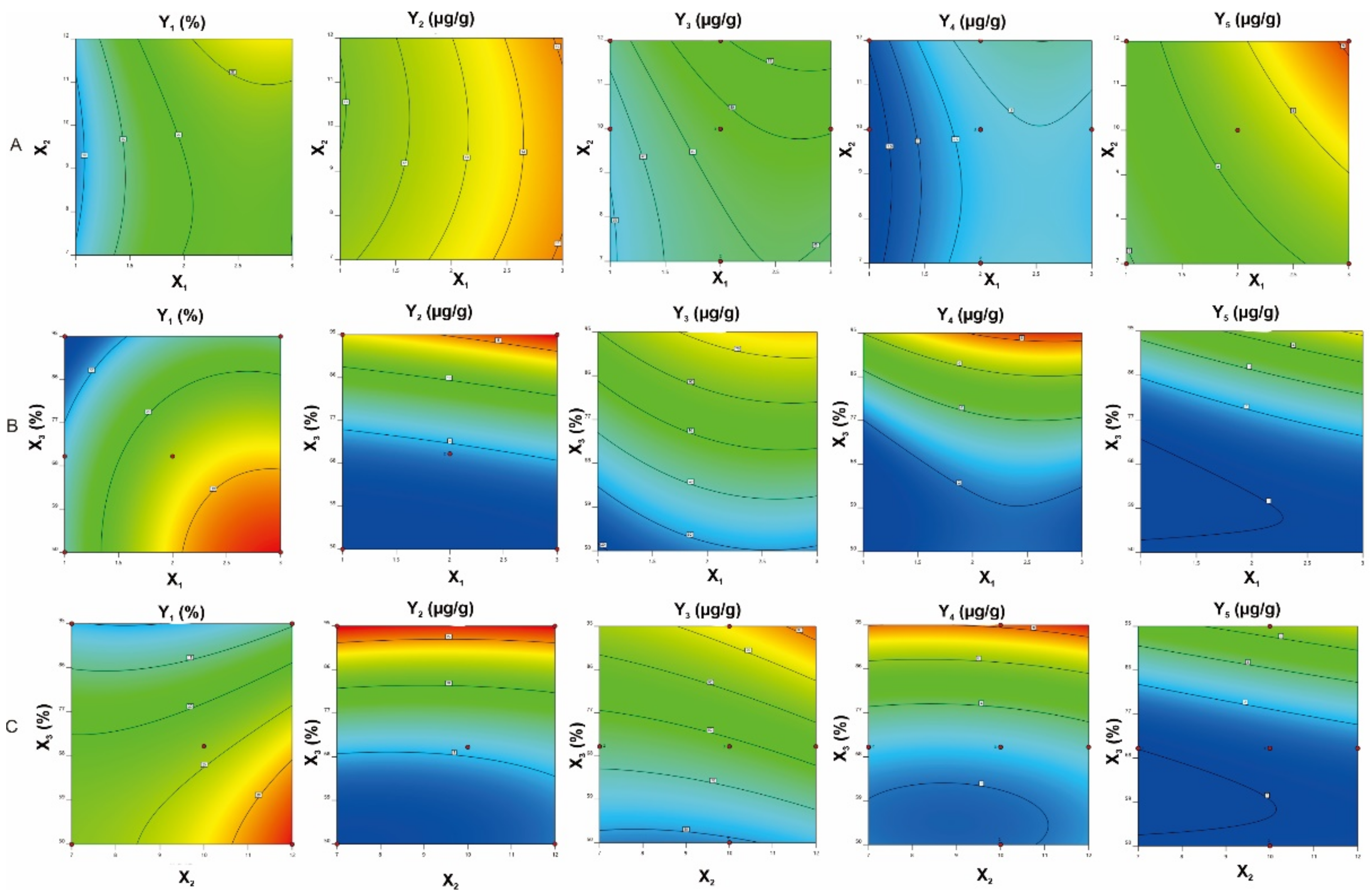
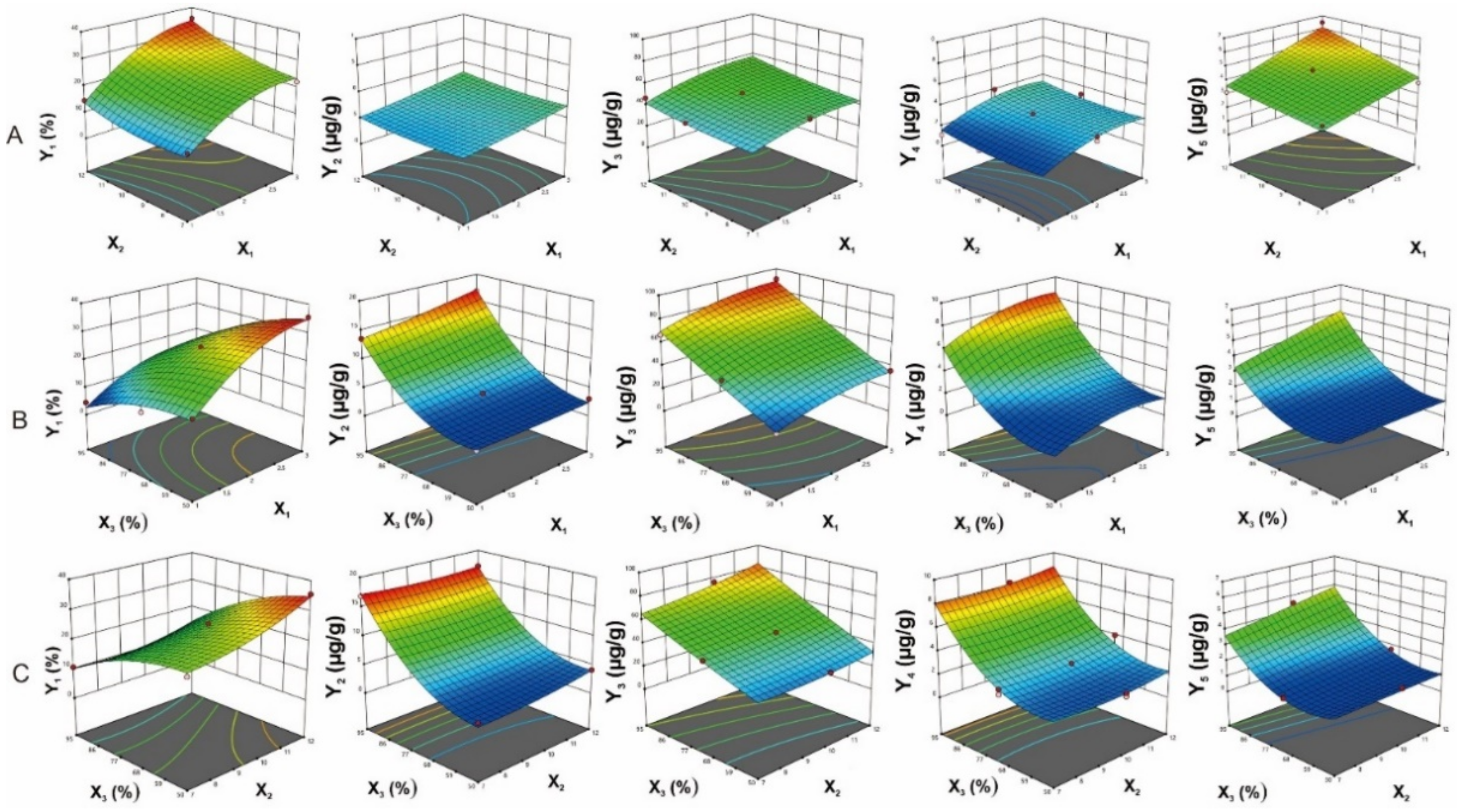
2.3.2. The Influence of Process Variables on The Extraction Yield
2.3.3. The influence of Process Variables on The Major Components’ Contents
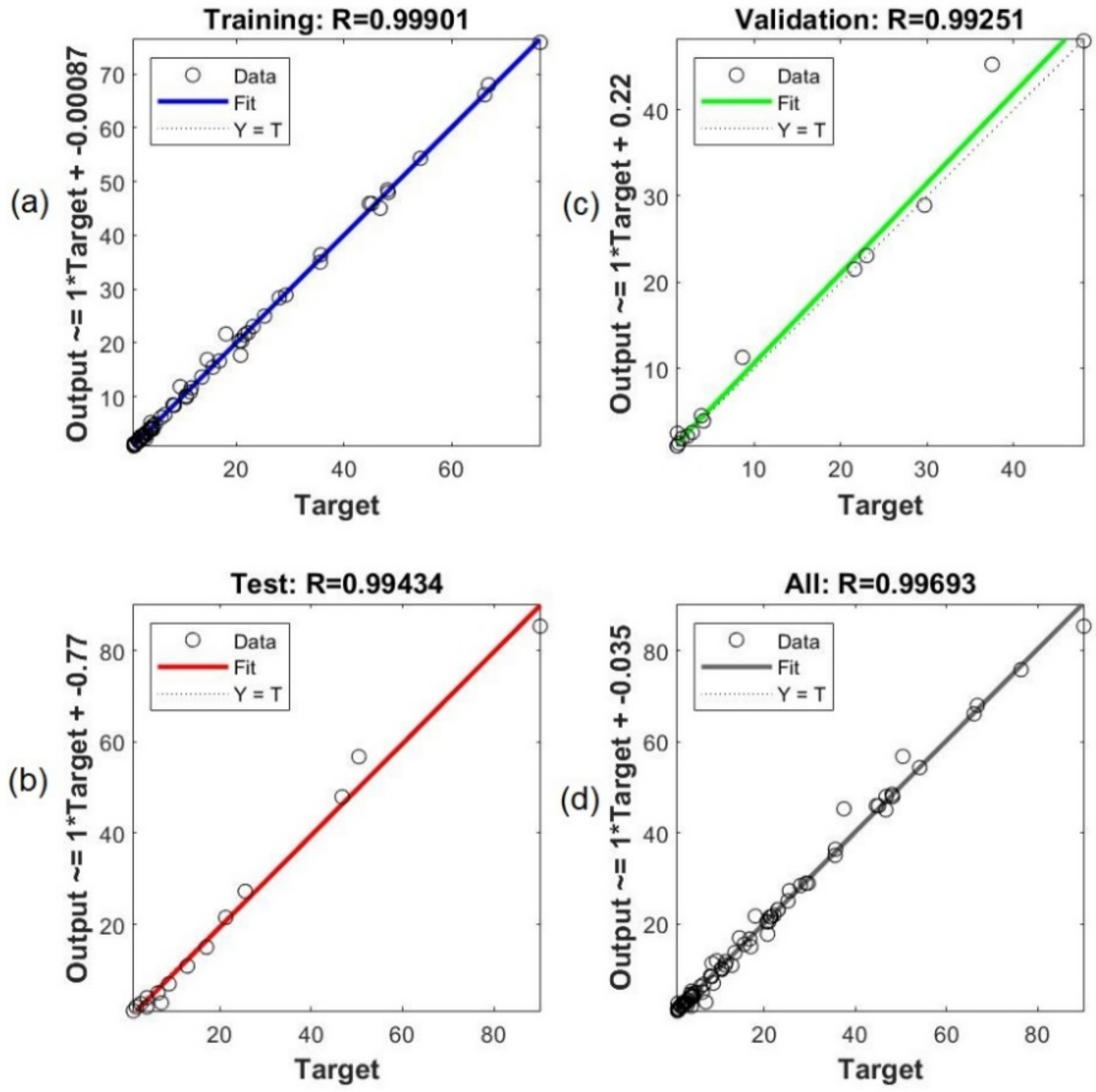
2.3.4. ANN Modelling
2.3.5. Verification and Comparison Between RSM and ANN Models
3. Materials and Methods
3.1. Chemicals and Reagents
3.2. Plant Material
3.3. Extraction and Isolation
3.4. Simultaneous Quantification of Four Major Compounds in M. pulchra Radix
3.4.1. Sample Preparation
3.4.2. Reference Solutions
3.4.3. HPLC Apparatus and Conditions
3.4.4. Method Validation
3.4.5. Simultaneous Quantification of Major Compounds in M. pulchra Radix
3.5. Optimization of Extraction
3.5.1. Sample Extraction
3.5.2. Experimental Design
3.5.3. Artificial Neural Network (ANN) Modelling
3.5.4. Verification Experiments, Comparison Between RSM and ANN Models
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Guo, Y.; Liang, X.; Meng, M.; Chen, H.; Wei, X.; Li, M.; Li, J.; Huang, R.; Wei, J. Hepatoprotective effects of Yulangsan flavone against carbon tetrachloride (CCl4)-induced hepatic fibrosis in rats. Phytomedicine 2017, 33, 28–35. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, X.; Qin, F.; Li, Y.; Duan, X.; Jian, J.; Li, Y.; Chen, J.; Huang, R. Protective effects of Millettia pulchra flavonoids on myocardial ischemia in vitro and in vivo. Cell Physiol. Biochem. 2015, 35, 516–528. [Google Scholar] [CrossRef]
- Wang, W.; Wang, J.; Li, N.; Zhang, X.; Zhao, W.; Li, J.; Si, Y. Chemopreventive flavonoids from Millettia pulchra Kurz var-laxior (Dunn) Z. Wei (Yulangsan) function as Michael reaction acceptors. Bioorg. Med. Chem. Lett. 2015, 25, 1078–1081. [Google Scholar] [CrossRef]
- Chang, L.C.; Gerhäuser, C.; Song, L.; Farnsworth, N.R.; Pezzuto, J.M.; Kinghorn, A.D. Activity-guided isolation of constituents of Tephrosia purpurea with the potential to induce the phase II enzyme, quinone reductase. J. Nat. Prod. 1997, 60, 869–873. [Google Scholar] [CrossRef]
- Huo, X.; Zhang, L.; Gao, L.; Guo, Y.; Zhang, L.; Li, L.; Si, J.; Cao, L. Anti-inflammatory and analgesic activities of ethanol extract and isolated compounds from Millettia pulchra. Biol. Pharm. Bull. 2015, 38, 1328–1336. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Singh, A.; Bhatt, G.; Gujre, N.; Mitra, S.; Swaminathan, R.; Limaye, A.M.; Rangan, L. Karanjin. Phytochemistry 2021, 183, 112641. [Google Scholar] [CrossRef]
- Sharma, R.; Williams, I.S.; Gatchie, L.; Sonawane, V.R.; Chaudhuri, B.; Bharate, S.B. Furanoflavones pongapin and lanceolatin B blocks the cell cycle and induce senescence in CYP1A1-overexpressing breast cancer cells. Bioorg. Med. Chem. 2018, 26, 6076–6086. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tamrakar, A.K.; Yadav, P.P.; Tiwari, P.; Maurya, R.; Srivastava, A.K. Identification of pongamol and karanjin as lead compounds with antihyperglycemic activity from Pongamia pinnata fruits. J. Ethnopharmacol. 2008, 118, 435–439. [Google Scholar] [CrossRef] [PubMed]
- Tamrakar, A.K.; Jaiswal, N.; Yadav, P.P.; Maurya, R.; Srivastava, A.K. Pongamol from Pongamia pinnata stimulates glucose uptake by increasing surface GLUT4 level in skeletal muscle cells. Mol. Cell Endocrinol. 2011, 339, 98–104. [Google Scholar] [CrossRef]
- Huang, J.; Tang, X.; Liang, X.; Wen, Q.; Zhang, S.; Xuan, F.; Jian, J.; Lin, X.; Huang, R. The effects of 17-methoxy-7-hydroxy-benzene-furanchalcone on the pressure overload-induced progression of cardiac hypertrophy to cardiac failure. PLoS ONE 2014, 9, e91834. [Google Scholar]
- Jian, J.; Qing, F.; Zhang, S.; Huang, J.; Huang, R. The effect of 17-methoxy-7-hydroxy-benzene-furanchalcone isolated from Millettia pulchra on myocardial ischemia in vitro and in vivo. Planta Med. 2012, 78, 1324–1331. [Google Scholar]
- Al Muqarrabun, L.M.; Ahmat, N.; Ruzaina, S.A.; Ismail, N.H.; Sahidin, I. Medicinal uses, phytochemistry and pharmacology of Pongamia pinnata (L.) Pierre: A review. J. Ethnopharmacol. 2013, 150, 395–420. [Google Scholar] [CrossRef]
- Bilgin, M.; Elhussein, E.A.A.; Özyürek, M.; Güçlü, K.; Şahin, S. Optimizing the extraction of polyphenols from Sideritis montana L. using response surface methodology. J. Pharm. Biomed. Anal. 2018, 158, 137–143. [Google Scholar] [CrossRef]
- Yu, H.C.; Huang, S.M.; Lin, W.M.; Kuo, C.H.; Shieh, C.J. Comparison of artificial neural networks and response surface methodology towards an efficient ultrasound-assisted extraction of chlorogenic acid from Lonicera japonica. Molecules 2019, 24, 2304. [Google Scholar] [CrossRef] [Green Version]
- Xi, J.; Xue, Y.; Xu, Y.; Shen, Y. Artificial neural network modeling and optimization of ultrahigh pressure extraction of green tea polyphenols. Food Chem. 2013, 141, 320–326. [Google Scholar] [CrossRef]
- Ciric, A.; Krajnc, B.; Heath, D.; Ogrinc, N. Response surface methodology and artificial neural network approach for the optimization of ultrasound-assisted extraction of polyphenols from garlic. Food Chem. Toxicol. 2020, 135, 110976. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.; Cao, D. Optimization of the silica-gel adsorption technique for the extraction of phytosterol glycosides from soybean lecithin powder using response surface methodology and artificial neural network models. J. Food Sci. 2020, 85, 1971–1982. [Google Scholar] [CrossRef] [PubMed]
- Parmar, S.P.; Rathore, J.S.; Jain, R.; Henderson, D.A.; Malone, J.F. Occurrence of pongamol as the enol structure in Tephrosia purpurea. Phytochemistry 1989, 28, 591–593. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, Y.; Huang, R.; Qin, S.; Yi, T.; Xu, F.; Tang, Y.; Qu, X.; Chen, H.; Miao, J. Determination of five flavonoids in different parts of Fordia cauliflora by ultra performance liquid chromatography/triple-quadrupole mass spectrometry and chemical comparison with the root of Millettia pulchra var. laxior. Chem. Cent. J. 2012, 7, 126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, L.L.; Yi, T.; Xu, F.; Zhang, Y.Z.; Zhang, J.Y.; Li, D.P.; Xie, Y.J.; Qin, S.D.; Chen, H.B. Characterization of flavonoids in the ethomedicine Fordiae Cauliflorae Radix and its adulterant Millettiae Pulchrae Radix by HPLC-DAD-ESI-IT-TOF-MSn. Molecules 2013, 18, 15134–15152. [Google Scholar] [CrossRef] [Green Version]
- Lin, X.; Huang, Z.; Chen, X.; Rong, Y.; Zhang, S.; Jiao, Y.; Huang, Q.; Huang, R. Protective effect of Millettia pulchra polysaccharide on cognitive impairment induced by D-galactose in mice. Carbohydr. Polym. 2014, 101, 533–543. [Google Scholar] [CrossRef] [PubMed]
- Pakrokh, G.P. The extraction process optimization of antioxidant polysaccharides from Marshmallow (Althaea officinalis L.) roots. Int. J. Biol. Macromol. 2015, 75, 51–57. [Google Scholar] [CrossRef] [PubMed]
- International Council for Harmonization. Validation of analytical procedures: Text and methodology Q2 (R1). In Proceedings of the International Conference on Harmonization, Geneva, Switzerland, 9–10 May 2005; pp. 1–13. [Google Scholar]
- Gharibzahedi, S.M.T.; Mousavi, S.M.; Hamedi, M.; Khodaiyan, F. Application of response surface modeling to optimize critical structure components of walnut-beverage emulsion with respect to analysis of the physicochemical aspects. Food Bioprocess Technol. 2013, 6, 456–469. [Google Scholar] [CrossRef]




| Markers | Retention Time (min) | Regression Equation a | R2 | Standard Curve (µg/mL) | LOD b (µg/mL) | LOQ c (µg/mL) |
|---|---|---|---|---|---|---|
| Lanceolatin B | 12.4 | ŷ = 46992523.93x − 161288.07 | 0.9976 | 5–120 | 0.006 | 0.020 |
| Karanjin | 14.0 | ŷ = 40497797.83x | 0.9984 | 5–120 | 0.006 | 0.020 |
| 2,2-Dimethylpyrano-[5,6:7,8]-flavone | 19.1 | ŷ = 41233664.76x | 0.9976 | 10–130 | 0.012 | 0.040 |
| Pongamol | 24.0 | ŷ = 27135799.19x | 0.9998 | 5–80 | 0.002 | 0.006 |
| Markers | Theoretical Conc. (µg/mL) | Found Conc. (µg/mL) | RSD (%) | Recovery (%) | |||
|---|---|---|---|---|---|---|---|
| Intra-Day a | Inter-Day b | Intra-Day a | Inter-Day b | Intra-Day a | Inter-Day b | ||
| Lanceolatin B | 40 | 36.70 | 37.98 | 0.55 | 3.08 | 91.76 | 94.94 |
| 60 | 58.67 | 58.74 | 1.43 | 2.25 | 97.78 | 97.89 | |
| 80 | 77.87 | 79.67 | 0.39 | 2.07 | 97.33 | 99.59 | |
| Karanjin | 40 | 37.06 | 38.76 | 1.92 | 3.94 | 92.65 | 96.90 |
| 60 | 61.36 | 61.11 | 1.22 | 0.57 | 102.27 | 101.84 | |
| 80 | 78.31 | 77.38 | 1.15 | 1.13 | 97.88 | 96.73 | |
| 2″,2″-Dimethylpyrano-[5″,6″:7,8]-flavone | 40 | 42.49 | 41.78 | 1.04 | 1.82 | 106.23 | 104.44 |
| 60 | 60.28 | 60.16 | 0.75 | 0.53 | 100.47 | 100.27 | |
| 80 | 81.73 | 82.25 | 0.69 | 0.73 | 102.16 | 102.82 | |
| Pongamol | 20 | 19.82 | 19.86 | 3.77 | 1.59 | 99.12 | 99.28 |
| 40 | 40.46 | 40.71 | 1.37 | 0.83 | 101.16 | 101.77 | |
| 60 | 60.50 | 59.99 | 0.59 | 1.04 | 100.83 | 99.98 | |
| Markers | Precision RSD (%) | Repeatability RSD c (%) | Stability RSD (%) b,* | |
|---|---|---|---|---|
| Intra-Day a | Inter-Day b | |||
| Lanceolatin B | 0.07 | 1.13 | 1.04 | 1.53 |
| Karanjin | 0.37 | 0.79 | 0.71 | 1.10 |
| 2,2-Dimethylpyrano-[5,6:7,8]-flavone | 0.52 | 1.59 | 1.75 | 3.13 |
| Pongamol | 0.13 | 0.56 | 0.96 | 1.54 |
| M. pulchra Radix | Age (Year) | Contents [(µg/g), n = 3 (RSD)] | |||
|---|---|---|---|---|---|
| Lanceolatin B | Karanjin | 2″,2″-Dimethylpyrano-[5″,6″:7,8]-flavone | Pongamol | ||
| Sample A | 1 | 0.2946 (0.14) | 1.1521 (1.17) | 0.0519 (0.87) | 0.0376 (0.35) |
| Sample B | 2 | 1.0499 (0.44) | 5.2534 (0.44) | 0.6021 (1.00) | 0.2194 (0.24) |
| Sample C | 3 | 1.1002 (0.18) | 5.3234 (0.19) | 0.6321 (0.12) | 0.2079 (0.43) |
| Sample D | 4 | 1.0793 (0.32) | 5.3017 (0.67) | 0.6150 (0.30) | 0.2100 (0.20) |
| Independent Variables | Unit | Symbols | Code Values | ||
|---|---|---|---|---|---|
| −1 | 0 | +1 | |||
| Extraction time | - | X1 | 1 | 2 | 3 |
| Solvent-to-material ratio | mL/g | X2 | 7 | 10 | 12 |
| Concentration of ethanol | (%) | X3 | 50 | 70 | 95 |
| Run | Independent Variables | Yield (%) | Content of Major Components (µg/g) | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | Y1, expa | Y1, pre.b | Y1, pre.c | Y2, exp. a | Y2, pre.b | Y2, pre.c | Y3, exp. a | Y3, pre.b | Y3, pre.c | Y4, exp. a | Y4, pre.b | Y4, pre.c | Y5, exp. a | Y5, pre.b | Y5, pre.c | |
| 1 | 2 | 7 | 70 | 20.58 ± 1.34 | 20.48 | 20.56 | 4.42 ± 0.18 | 4.69 | 4.43 | 44.67 ± 1.20 | 43.95 | 44.66 | 2.37 ± 0.90 | 2.40 | 2.48 | 1.15 ± 0.03 | 1.09 | 1.00 |
| 2 | 2 | 10 | 95 | 11.46 ± 1.18 | 10.75 | 11.48 | 15.66 ± 1.00 | 13.83 | 15.70 | 76.39 ± 1.97 | 74.91 | 76.40 | 8.28 ± 0.43 | 8.53 | 8.20 | 4.53 ± 0.22 | 4.39 | 4.59 |
| 3 | 2 | 12 | 70 | 25.56 ± 1.24 | 25.40 | 25.56 | 5.23 ± 0.90 | 4.98 | 5.21 | 50.44 ± 2.00 | 54.42 | 50.45 | 4.01 ± 0.09 | 3.19 | 4.01 | 1.71 ± 0.12 | 1.43 | 1.75 |
| 4 | 2 | 10 | 50 | 23.00 ± 2.30 | 24.30 | 22.99 | 2.24 ± 0.72 | 2.54 | 2.27 | 29.69 ± 0.92 | 28.59 | 29.69 | 1.62 ± 0.10 | 1.85 | 1.75 | 1.25 ± 0.05 | 1.78 | 1.04 |
| 5 | 1 | 7 | 95 | 4.22 ± 0.82 | 4.61 | 4.22 | 13.59 ± 0.98 | 13.60 | 13.59 | 54.16 ± 1.56 | 54.47 | 54.16 | 6.07 ± 0.10 | 5.94 | 6.07 | 3.28 ± 0.80 | 2.95 | 3.28 |
| 6 | 3 | 12 | 50 | 35.58 ± 2.31 | 34.90 | 35.58 | 4.14 ± 0.02 | 4.07 | 4.14 | 35.66 ± 1.00 | 34.81 | 35.67 | 1.90 ± 0.21 | 2.16 | 1.88 | 1.00 ± 0.12 | 1.32 | 1.02 |
| 7 | 3 | 7 | 95 | 10.73 ± 1.16 | 10.86 | 10.72 | 16.86 ± 1.00 | 17.41 | 16.84 | 66.08 ± 2.00 | 66.72 | 66.09 | 8.50 ± 0.78 | 8.38 | 8.53 | 3.84 ± 0.38 | 4.23 | 3.82 |
| 8 | 1 | 10 | 70 | 8.63 ± 1.11 | 9.27 | 8.63 | 3.88 ± 0.22 | 3.66 | 3.88 | 37.50 ± 0.90 | 37.01 | 37.50 | 1.09 ± 0.05 | 1.28 | 1.11 | 1.04 ± 0.09 | 1.03 | 1.02 |
| 9 | 2 | 10 | 70 | 21.60 ± 1.15 | 21.35 | 21.34 | 4.12 ± 0.91 | 4.22 | 4.04 | 48.12 ± 1.02 | 48.34 | 46.81 | 2.82 ± 0.10 | 2.71 | 2.57 | 1.09 ± 0.07 | 1.33 | 1.26 |
| 10 | 2 | 10 | 70 | 21.32 ± 2.20 | 21.35 | 21.34 | 4.05 ± 0.12 | 4.22 | 4.04 | 46.79 ± 1.25 | 48.34 | 46.81 | 2.69 ± 0.28 | 2.71 | 2.57 | 1.10 ± 0.10 | 1.33 | 1.26 |
| 11 | 2 | 10 | 50 | 23.10 ± 2.30 | 24.31 | 22.99 | 2.3 ± 0.08 | 2.54 | 2.27 | 29.21 ± 1.25 | 28.59 | 29.69 | 1.89 ± 0.12 | 1.85 | 1.75 | 1.32 ± 0.12 | 1.18 | 1.04 |
| 12 | 1 | 7 | 50 | 10.68 ± 2.00 | 10.00 | 10.68 | 2.19 ± 0,11 | 2.21 | 2.19 | 18.10 ± 1.90 | 18.98 | 18.10 | 1.03 ± 0.10 | 0.89 | 0.98 | 1.00 ± 0.10 | 1.19 | 1.06 |
| 13 | 3 | 7 | 50 | 22.16 ± 1.21 | 22.94 | 22.20 | 3.04 ± 0.42 | 2.70 | 3.00 | 28.00 ± 0.97 | 27.98 | 28.12 | 1.70 ± 0.08 | 1.75 | 1.67 | 1.04 ± 0.05 | 0.93 | 1.13 |
| 14 | 1 | 12 | 50 | 14.60 ± 1.29 | 13.39 | 14.27 | 3.22 ± 0.50 | 3.08 | 2.61 | 20.79 ± 1.10 | 22.22 | 21.23 | 1.07 ± 0.05 | 0.95 | 2.14 | 1.08 ± 0.02 | 0.98 | 1.91 |
| 15 | 2 | 10 | 70 | 21.54 ± 1.16 | 21.35 | 21.34 | 4.10 ± 0.22 | 4.22 | 4.04 | 48.20 ± 1.00 | 48.34 | 46.81 | 2.550.10 | 2.71 | 2.57 | 1.15 ± 0.14 | 1.33 | 1.26 |
| 16 | 3 | 12 | 95 | 12.91 ± 2.19 | 14.09 | 12.90 | 17.10 ± 0.62 | 17.27 | 17.09 | 90.17 ± 1.55 | 87.86 | 90.18 | 8.90 ± 0.28 | 9.55 | 8.95 | 6.48 ± 0.11 | 6.22 | 6.44 |
| 17 | 3 | 10 | 70 | 25.23 ± 1.31 | 23.35 | 25.24 | 5.00 ± 0.37 | 5.20 | 5.03 | 48.08 ± 2.00 | 50.47 | 48.08 | 3.20 ± 0.10 | 2.62 | 3.17 | 1.92 ± 0.21 | 1.60 | 1.93 |
| 18 | 2 | 7 | 70 | 21.00 ± 1.05 | 20.48 | 20.56 | 4.08 ± 0.21 | 4.34 | 4.43 | 45.12 ± 2.30 | 43.94 | 44.66 | 2.81 ± 0.21 | 2.81 | 2.48 | 1.05 ± 0.17 | 1.09 | 1.00 |
| 19 | 1 | 12 | 70 | 9.61 ± 1.18 | 11.15 | 12.87 | 4.49 ± 0.07 | 4.30 | 3.44 | 46.70 ± 1.27 | 41.70 | 46.70 | 1.10 ± 0.03 | 1.56 | 1.16 | 1.01 ± 0.05 | 1.00 | 1.07 |
| 20 | 1 | 12 | 95 | 4.52 ± 0.93 | 3.93 | 4.52 | 11.65 ± 0.87 | 12.71 | 11.65 | 66.80 ± 0.96 | 69.42 | 66.79 | 6.76 ± 0.10 | 6.32 | 6.76 | 3.15 ± 0.10 | 3.50 | 3.15 |
| Parameters | RSM | ANN | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y1 | Y2 | Y3 | Y4 | Y5 | Y1 | Y2 | Y3 | Y4 | Y5 | |
| R2 | 0.9875 | 0.9917 | 0.9889 | 0.9767 | 0.9678 | 0.9923 | 0.9951 | 0.9931 | 0.9918 | 0.9771 |
| RMSE | 0.87 | 0.53 | 1.89 | 0.33 | 0.25 | 0.74 | 0.28 | 0.47 | 0.26 | 0.22 |
| Y1 (%) | Y2 (µg/g) | Y3 (µg/g) | Y4 (µg/g) | Y5 (µg/g) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RSM | ANN | Exp. a | RSM | ANN | Exp. | RSM | ANN | Exp. | RSM | ANN | Exp. | RSM | ANN | Exp. |
| 20.22 | 20.05 | 20.05 ± 0.07 | 3.96 | 3.99 | 4.05 ± 0.05 | 48.87 | 46.99 | 46.99 ± 0.22 | 4.28 | 4.25 | 4.22 ± 0.19 | 1.22 | 1.10 | 1.05 ± 0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vo, T.-H.; Liaw, C.-C.; Lin, Y.-C.; Nguyen, D.H.; Nguyen, T.T.N.; Lee, C.-K.; Kuo, Y.-H. Quantification and Optimization of Ethanolic Extract Containing the Bioactive Flavonoids from Millettia pulchra Radix. Molecules 2021, 26, 3641. https://doi.org/10.3390/molecules26123641
Vo T-H, Liaw C-C, Lin Y-C, Nguyen DH, Nguyen TTN, Lee C-K, Kuo Y-H. Quantification and Optimization of Ethanolic Extract Containing the Bioactive Flavonoids from Millettia pulchra Radix. Molecules. 2021; 26(12):3641. https://doi.org/10.3390/molecules26123641
Chicago/Turabian StyleVo, Thanh-Hoa, Chia-Ching Liaw, Yu-Chi Lin, Duc Hanh Nguyen, Thi Tuyet Nhung Nguyen, Ching-Kuo Lee, and Yao-Haur Kuo. 2021. "Quantification and Optimization of Ethanolic Extract Containing the Bioactive Flavonoids from Millettia pulchra Radix" Molecules 26, no. 12: 3641. https://doi.org/10.3390/molecules26123641







