Theoretical Prediction of Structures, Vibrational Circular Dichroism, and Infrared Spectra of Chiral Be4B8 Cluster at Different Temperatures
Abstract
:1. Introduction
2. Theoretical Methods and Computational Details
2.1. Global Minimum Search and Computational Details
2.2. Thermochemistry Properties
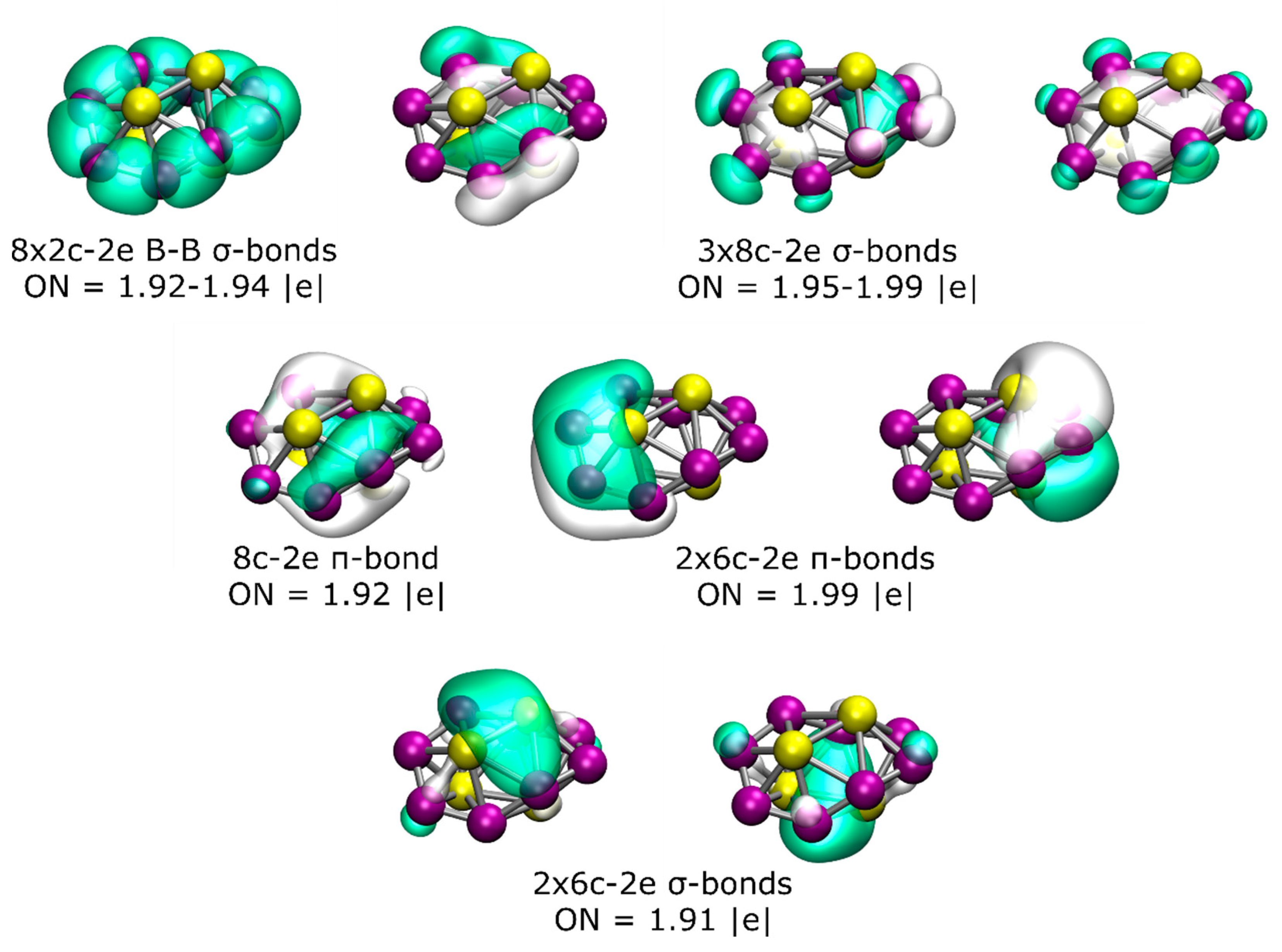
3. Results and Discussion
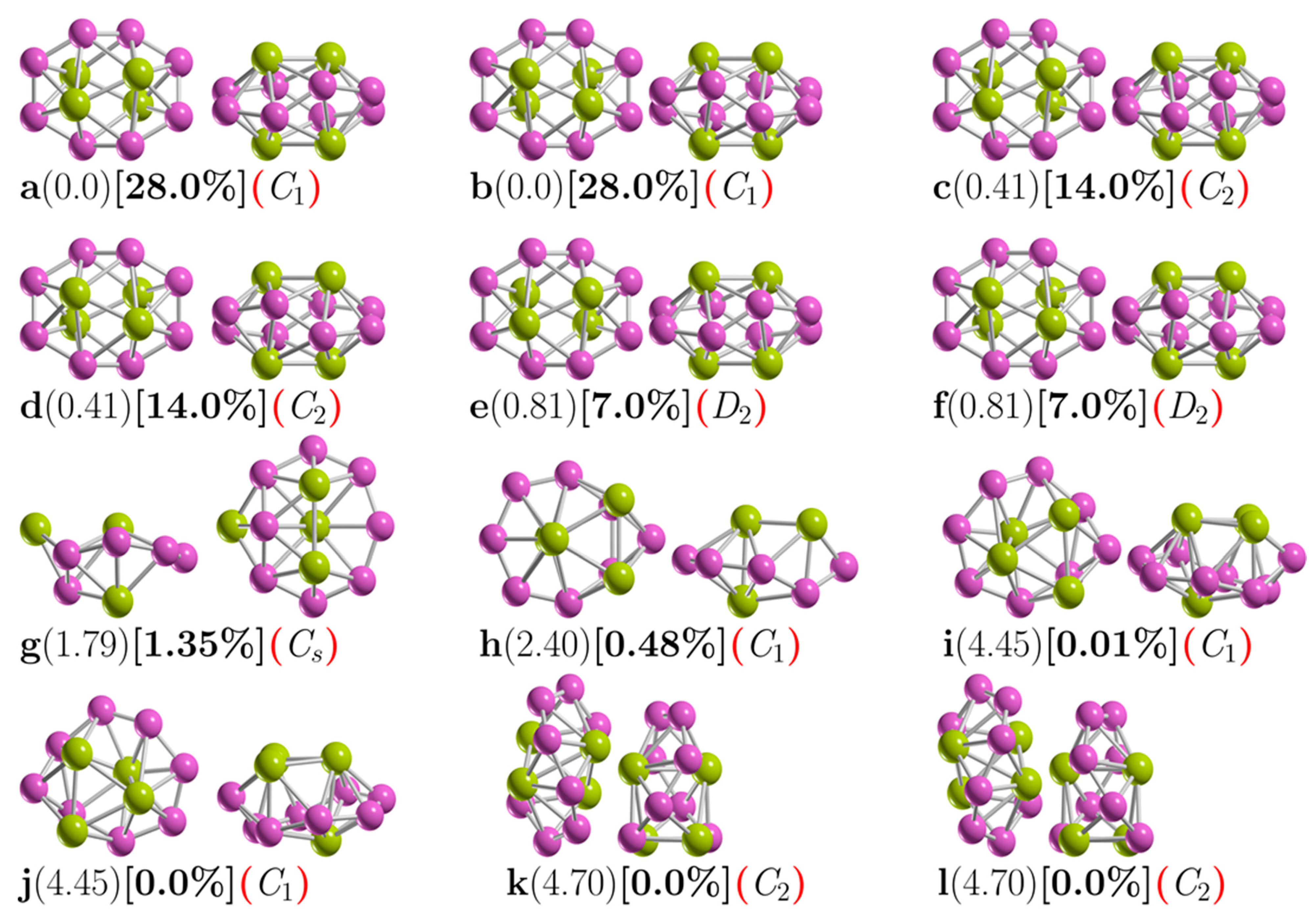
3.1. The Lowest Energy Structures and Energetics
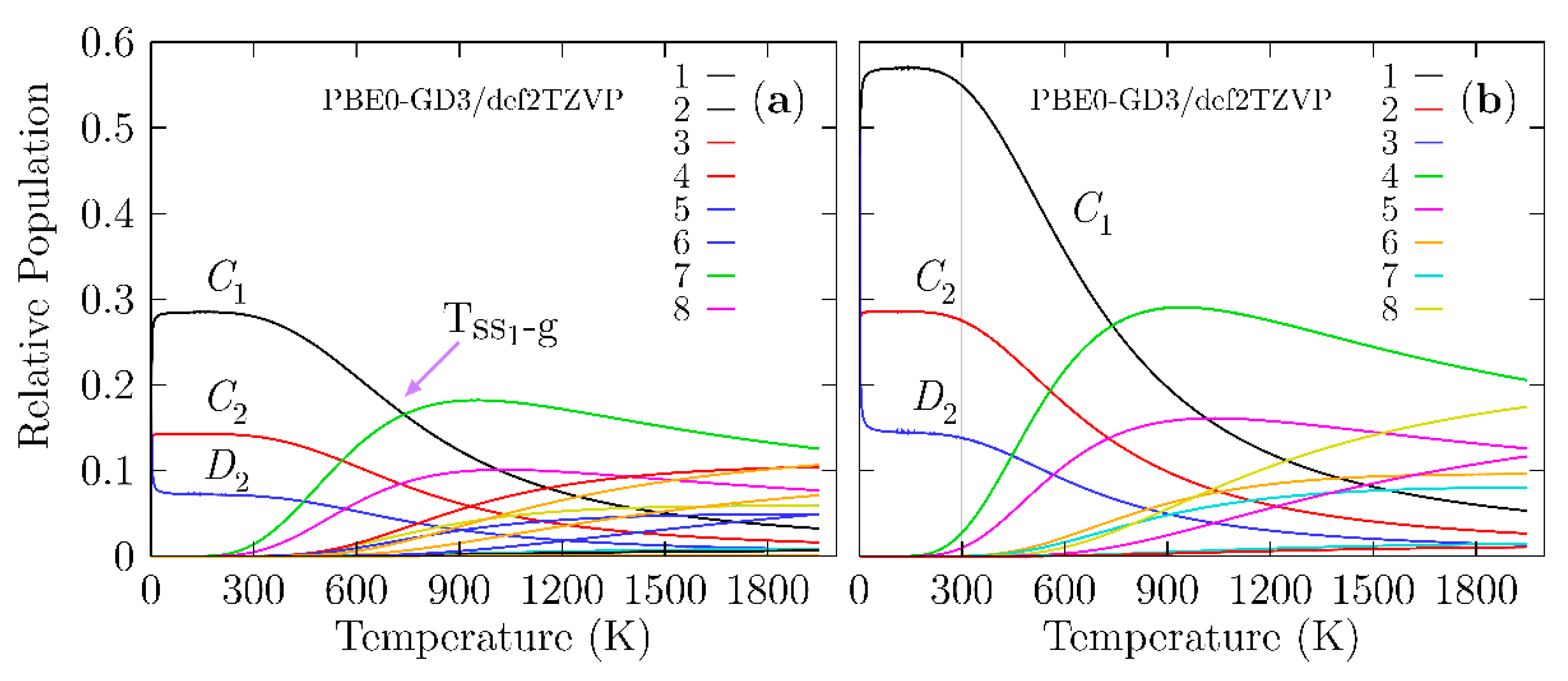
3.2. Structures and Stability at Finite Temperature
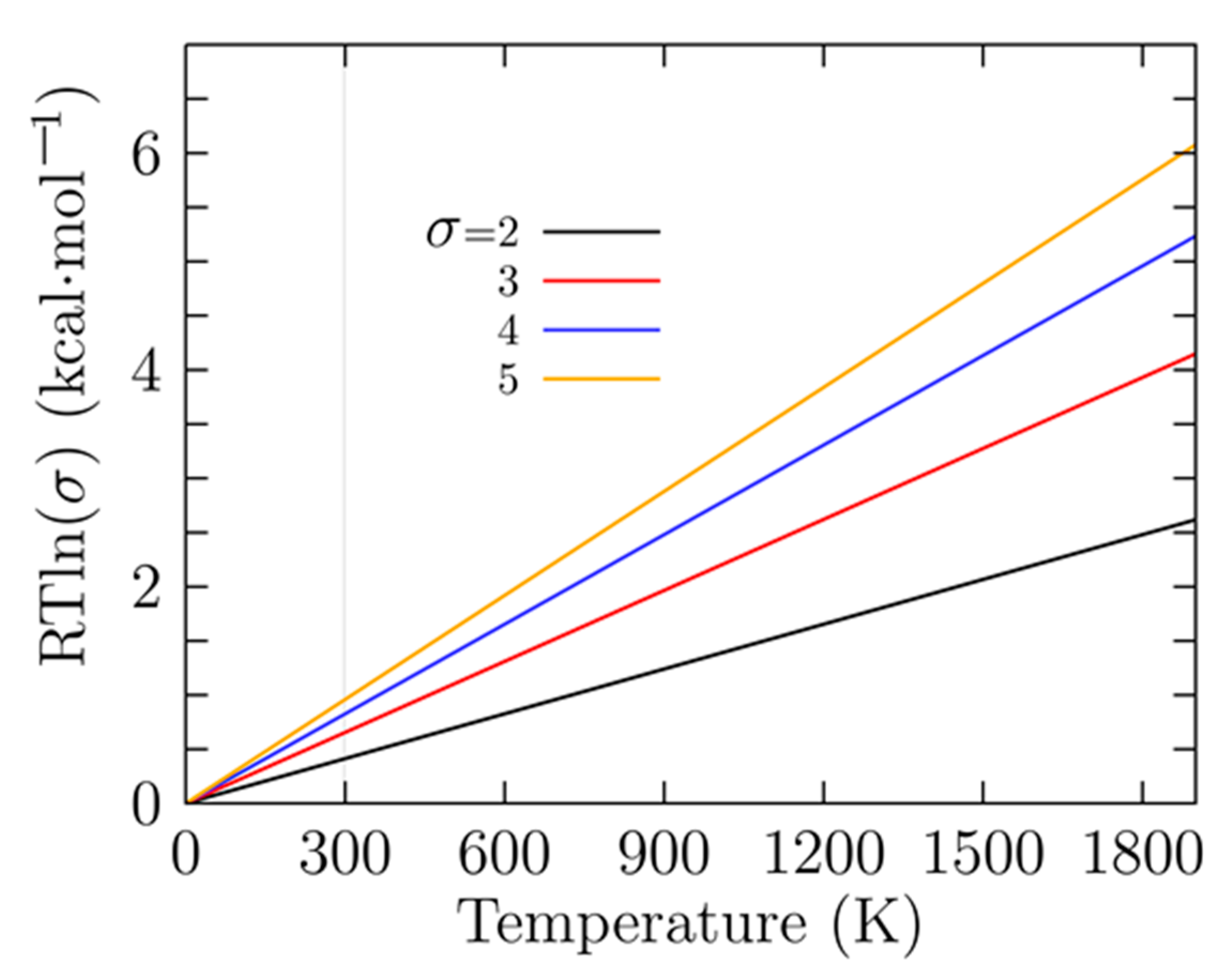
3.3. Enantiomerization Energy Barrier at Finite Temperature
3.4. Height of the Energy Barrier between Chiral and Achiral Structures at Finite Temperature
3.5. VCD and IR Spectra
3.6. Molecular Dynamics
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Abbreviations
| DFT | Density functional theory |
| CCSD(T) | Coupled cluster single-double and perturbative triple |
| DLPNO-CCSD(T) | Domain-based local pair natural orbital coupled-cluster theory |
| ZPE | Zero-point energy |
| VCD | Vibrational circular dichroism |
| IR | Vibrational infrared spectrum |
| BOFA | Boltzmann Optics Full Ader code (module nanothermodynamics) |
| GALGOSON | Global genetic algorithm of University of Sonora |
| SSh | Sandwich structure hollow |
| AdNDP | Adaptive natural density partitioning |
References
- Kondo, T. Recent progress in boron nanomaterials. Sci. Technol. Adv. Mater. 2017, 18, 780–804. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pan, S.; Barroso, J.; Jalife, S.; Heine, T.; Asmis, K.R.; Merino, G. Fluxional Boron Clusters: From Theory to Reality. Acc. Chem. Res. 2019, 52, 2732–2744. [Google Scholar] [CrossRef] [PubMed]
- Kabay, N.; Bryjak, M.; Hilal, N. Boron Separation Processes; Elsevier Science: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Kheshti, T.; Mahdavifar, Z.; Noorizadeh, S. Umbrella-shaped vs. planar; evolutionary search for BnQ, Be c BnQ (n = 6–12, Q = 0, −1) clusters. J. Mol. Liq. 2021, 328, 115389. [Google Scholar] [CrossRef]
- DeFrancesco, H.; Dudley, J.; Coca, A. Boron Chemistry: An Overview. In Boron Reagents in Synthesis; ACS Publications: Washington, DC, USA, 2016; Chapter 1; pp. 1–25. [Google Scholar] [CrossRef]
- Zhai, H.J.; Zhao, Y.F.; Li, W.L.; Chen, Q.; Bai, H.; Hu, H.S.; Piazza, Z.A.; Tian, W.J.; Lu, H.G.; Wu, Y.B.; et al. Observation of an all-boron fullerene. Nat. Chem. 2014, 727–731. [Google Scholar] [CrossRef]
- Piazza, Z.A.; Hu, H.S.; Li, W.L.; Zhao, Y.F.; Li, J.; Wang, L.S. From planar boron clusters to borophenes and metalloborophenes. Nat. Rev. Chem. 2017, 1, 0071. [Google Scholar] [CrossRef]
- Kiran, B.; Bulusu, S.; Zhai, H.J.; Yoo, S.; Zeng, X.C.; Wang, L.S. Planar-to-tubular structural transition in boron clusters: B20 as the embryo of single-walled boron nanotubes. Proc. Natl. Acad. Sci. USA 2005, 102, 961–964. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dong, X.; Jalife, S.; Vásquez-Espinal, A.; Ravell, E.; Pan, S.; Cabellos, J.L.; Liang, W.y.; Cui, Z.h.; Merino, G. Li2 B12 and Li3 B12: Prediction of the Smallest Tubular and Cage-like Boron Structures. Angew. Chem. Int. Ed. 2018, 57, 4627–4631. [Google Scholar] [CrossRef]
- Wang, Y.J.; Zhao, Y.F.; Li, W.L.; Jian, T.; Chen, Q.; You, X.R.; Ou, T.; Zhao, X.Y.; Zhai, H.J.; Li, S.D.; et al. Observation and characterization of the smallest borospherene, B28 and B28. J. Chem. Phys. 2016, 144, 064307. [Google Scholar] [CrossRef] [Green Version]
- Lv, J.; Wang, Y.; Zhang, L.; Lin, H.; Zhao, J.; Ma, Y. Stabilization of fullerene-like boron cages by transition metal encapsulation. Nanoscale 2015, 7, 10482–10489. [Google Scholar] [CrossRef]
- Piazza, Z.A.; Hu, H.S.; Li, W.L.; Zhao, Y.F.; Li, J.; Wang, L.S. Planar hexagonal B36 as a potential basis for extended single-atom layer boron sheets. Nat. Commun. 2014, 1, 3113. [Google Scholar] [CrossRef] [PubMed]
- Li, W.L.; Zhao, Y.F.; Hu, H.S.; Li, J.; Wang, L.S. B30-: A Quasiplanar Chiral Boron Cluster. Angew. Chem. Int. Ed. 2014, 53, 5540–5545. [Google Scholar] [CrossRef]
- An, W.; Bulusu, S.; Gao, Y.; Zeng, X.C. Relative stability of planar versus double-ring tubular isomers of neutral and anionic boron cluster B20 and B20-. J. Chem. Phys. 2006, 124, 154310. [Google Scholar] [CrossRef] [Green Version]
- Dong, X.; Jalife, S.; Vásquez-Espinal, A.; Barroso, J.; Orozco-Ic, M.; Ravell, E.; Cabellos, J.L.; Liang, W.y.; Cui, Z.h.; Merino, G. Li2 B24: The simplest combination for a three-ring boron tube. Nanoscale 2019, 11, 2143–2147. [Google Scholar] [CrossRef]
- Feng, L.Y.; Guo, J.C.; Li, P.F.; Zhai, H.J. Boron-Based Chiral Helix Be6 B10 and Be6 B11 Clusters: Structures, Chemical Bonding, and Formation Mechanism. Chem. Asian J. 2020, 15, 1094–1104. [Google Scholar] [CrossRef]
- Chen, Q.; Li, W.L.; Zhao, Y.F.; Zhang, S.Y.; Hu, H.S.; Bai, H.; Li, H.R.; Tian, W.J.; Lu, H.G.; Zhai, H.J.; et al. Experimental and Theoretical Evidence of an Axially Chiral Borospherene. ACS Nano 2015, 9, 754–760. [Google Scholar] [CrossRef]
- Yañez, O.; Inostroza, D.; Usuga-Acevedo, B.; Vásquez-Espinal, A.; Pino-Rios, R.; Tabilo-Sepulveda, M.; Garza, J.; Barroso, J.; Merino, G.; Tiznado, W. Evaluation of restricted probabilistic cellular automata on the exploration of the potential energy surface of Be6 B11. Theor. Chem. Acc. 2020, 139, 139–147. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, T.T.; Li, H.R.; Zhao, X.Y.; Chen, W.J.; Zhai, H.J.; Li, S.D.; Wang, L.S. B31 and B32: Chiral quasi-planar boron clusters. Nanoscale 2019, 11, 9698–9704. [Google Scholar] [CrossRef] [PubMed]
- Tai, T.B.; Nguyen, M.T. A new chiral boron cluster B44 containing nonagonal holes. Chem. Commun. 2016, 52, 1653–1656. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.C.; Feng, L.Y.; Wang, Y.J.; Jalife, S.; Vásquez-Espinal, A.; Cabellos, J.L.; Pan, S.; Merino, G.; Zhai, H.J. Coaxial Triple-Layered versus Helical Be6B11− Clusters: Dual Structural Fluxionality and Multifold Aromaticity. Angew. Chem. Int. Ed. 2017, 56, 10174–10177. [Google Scholar] [CrossRef] [PubMed]
- Merino, G.; Heine, T. And Yet It Rotates: The Starter for a Molecular Wankel Motor. Angew. Chem. Int. Ed. 2012, 51, 10226–10227. [Google Scholar] [CrossRef]
- Jimenez-Halla, J.; Islas, R.; Heine, T.; Merino, G. B19−: An Aromatic Wankel Motor. Angew. Chem. Int. Ed. 2010, 49, 5668–5671. [Google Scholar] [CrossRef]
- Martínez-Guajardo, G.; Sergeeva, A.P.; Boldyrev, A.I.; Heine, T.; Ugalde, J.M.; Merino, G. Unravelling phenomenon of internal rotation in B13+ through chemical bonding analysis. Chem. Commun. 2011, 47, 6242–6244. [Google Scholar] [CrossRef]
- Moreno, D.; Pan, S.; Zeonjuk, L.L.; Islas, R.; Osorio, E.; Martínez-Guajardo, G.; Chattaraj, P.K.; Heine, T.; Merino, G. B18: A quasi-planar bowl member of the Wankel motor family. Chem. Commun. 2014, 50, 8140–8143. [Google Scholar] [CrossRef]
- Cervantes-Navarro, F.; Martínez-Guajardo, G.; Osorio, E.; Moreno, D.; Tiznado, W.; Islas, R.; Donald, K.J.; Merino, G. Stop rotating! One substitution halts the B19 motor. Chem. Commun. 2014, 50, 10680–10682. [Google Scholar] [CrossRef]
- Jalife, S.; Liu, L.; Pan, S.; Cabellos, J.L.; Osorio, E.; Lu, C.; Heine, T.; Donald, K.J.; Merino, G. Dynamical behavior of boron clusters. Nanoscale 2016, 8, 17639–17644. [Google Scholar] [CrossRef]
- Wang, Y.J.; Feng, L.Y.; Zhai, H.J. Starting a subnanoscale tank tread: Dynamic fluxionality of boron-based B10Ca alloy cluster. Nanoscale Adv. 2019, 1, 735–745. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Guajardo, G.; Cabellos, J.L.; Díaz-Celaya, A.; Pan, S.; Islas, R.; Chattaraj, P.K.; Heine, T.; Merino, G. Dynamical behavior of Borospherene: A Nanobubble. Sci. Rep. 2015, 22, 11287–11297. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gu, F.L.; Yang, X.; Tang, A.C.; Jiao, H.; Schleyer, P.v.R. Structure and stability of B+13 clusters. J. Comput. Chem. 1998, 19, 203–214. [Google Scholar] [CrossRef]
- Yu, X.; Xu, C.; Cheng, L. Theoretical investigation on anti-sandwich beryllium-boron clusters Be2m Bn (m = 1–3): Fluxionality and multi-aromaticity. Comput. Theor. Chem. 2020, 1188, 112949. [Google Scholar] [CrossRef]
- Baletto, F.; Ferrando, R. Structural properties of nanoclusters: Energetic, thermodynamic, and kinetic effects. Rev. Mod. Phys. 2005, 77, 371–423. [Google Scholar] [CrossRef] [Green Version]
- Buelna-Garcia, C.E.; Cabellos, J.L.; Quiroz-Castillo, J.M.; Martinez-Guajardo, G.; Castillo-Quevedo, C.; de Leon-Flores, A.; Anzueto-Sanchez, G.; Martin-del Campo-Solis, M.F. Exploration of Free Energy Surface and Thermal Effects on Relative Population and Infrared Spectrum of the Be6B11− Fluxional Cluster. Materials 2021, 14, 112. [Google Scholar] [CrossRef] [PubMed]
- Axtell, J.C.; Saleh, L.M.A.; Qian, E.A.; Wixtrom, A.I.; Spokoyny, A.M. Synthesis and Applications of Perfunctionalized Boron Clusters. Inorg. Chem. 2018, 57, 2333–2350. [Google Scholar] [CrossRef]
- Ali, F.; Hosmane, N.S.; Zhu, Y. Boron Chemistry for Medical Applications. Molecules 2020, 25, 828. [Google Scholar] [CrossRef] [Green Version]
- Hawthorne, M.F. The Role of Chemistry in the Development of Boron Neutron Capture Therapy of Cancer. Angew. Chem. Int. Ed. Engl. 1993, 32, 950–984. [Google Scholar] [CrossRef]
- Pizzorno, L. Nothing Boring About Boron. Integr. Med. 2015, 14, 35–48. [Google Scholar]
- Yang, Y.; Jia, D.; Wang, Y.J.; Zhai, H.J.; Man, Y.; Li, S.D. A universal mechanism of the planar boron rotors B11-, B13+, B15+, and B19-: Inner wheels rotating in pseudo-rotating outer bearings. Nanoscale 2017, 9, 1443–1448. [Google Scholar] [CrossRef] [PubMed]
- Oganov, A.R.; Solozhenko, V.L. Boron: A hunt for superhard polymorphs. J. Superhard Mater. 2009, 31, 285. [Google Scholar] [CrossRef]
- Fakioğlu, E.; Yürüm, Y.; Nejat Veziroğlu, T. A review of hydrogen storage systems based on boron and its compounds. Int. J. Hydrog. Energy 2004, 29, 1371–1376. [Google Scholar] [CrossRef]
- Jiang, H.; Lu, Z.; Wu, M.; Ciucci, F.; Zhao, T. Borophene: A promising anode material offering high specific capacity and high rate capability for lithium-ion batteries. Nano Energy 2016, 23, 97–104. [Google Scholar] [CrossRef]
- Liang, P.; Cao, Y.; Tai, B.; Zhang, L.; Shu, H.; Li, F.; Chao, D.; Du, X. Is borophene a suitable anode material for sodium ion battery? J. Alloy. Compd. 2017, 704, 152–159. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Z.F.; Gao, P.F.; Zhang, S.L.; Wen, Y.H. Could Borophene Be Used as a Promising Anode Material for High-Performance Lithium Ion Battery? ACS Appl. Mater. Interfaces 2016, 8, 22175–22181. [Google Scholar] [CrossRef] [PubMed]
- Jiang, N.; Li, B.; Ning, F.; Xia, D. All boron-based 2D material as anode material in Li-ion batteries. J. Energy Chem. 2018, 27, 1651–1654. [Google Scholar] [CrossRef] [Green Version]
- Mir, S.H.; Chakraborty, S.; Jha, P.C.; Wärnå, J.; Soni, H.; Jha, P.K.; Ahuja, R. Two-dimensional boron: Lightest catalyst for hydrogen and oxygen evolution reaction. Appl. Phys. Lett. 2016, 109, 053903. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, S.; Dewhurst, R.D.; Ignat’ev, N.V.; Finze, M.; Braunschweig, H. Boron: Its Role in Energy-Related Processes and Applications. Angew. Chem. Int. Ed. 2020, 59, 8800–8816. [Google Scholar] [CrossRef]
- Ayuso, D.; Neufeld, O.; Ordonez, A.F.; Decleva, P.; Lerner, G.; Cohen, O.; Ivanov, M.; Smirnova, O. Synthetic chiral light for efficient control of chiral light-matter interaction. Nat. Photonics 2019, 13, 866–871. [Google Scholar] [CrossRef] [Green Version]
- Ayuso, D.; Ordonez, A.; Decleva, P.; Ivanov, M.; Smirnova, O. Polarization of chirality. arXiv 2020, arXiv:2004.05191. [Google Scholar]
- Guo, P.; Yang, B.; Zhang, L.; Zhao, L. Temperature dependent chiroptical response of sigmoidal gold clusters: Probing the stability of chiral metal clusters. Chem. Sci. 2018, 9, 5614–5622. [Google Scholar] [CrossRef] [Green Version]
- Kaspi-Kaneti, A.W.; Barroso, J.; Merino, G.; Avnir, D.; Garzón, I.L.; Tuvi-Arad, I. Head to Tail Distortion Wave Characterizes the Enantiomerization of Helicenes. J. Org. Chem. 2020, 85, 15415–15421. [Google Scholar] [CrossRef]
- Barroso, J.; Cabellos, J.L.; Pan, S.; Murillo, F.; Zarate, X.; Fernandez-Herrera, M.A.; Merino, G. Revisiting the racemization mechanism of helicenes. Chem. Commun. 2018, 54, 188–191. [Google Scholar] [CrossRef]
- Ebeling, D.; Šekutor, M.; Stiefermann, M.; Tschakert, J.; Dah, J.E.P.; Carlson, R.M.K.; Schirmeisen, A.; Schreiner, P.R. Assigning the absolute configuration of single aliphatic molecules by visual inspection. Nat. Commun. 2018, 9, 2420. [Google Scholar] [CrossRef] [Green Version]
- Cui, Z.h.; Yang, W.s.; Zhao, L.; Ding, Y.h.; Frenking, G. Unusually Short Be-Be Distances with and without a Bond in Be2 F2 and in the Molecular Discuses Be2 B8 and Be2 B7−. Angew. Chem. Int. Ed. 2016, 55, 7841–7846. [Google Scholar] [CrossRef]
- Hermann, A.; Ashcroft, N.W.; Hoffmann, R. Binary Compounds of Boron and Beryllium: A Rich Structural Arena with Space for Predictions. Chem. A Eur. J. 2013, 19, 4184–4197. [Google Scholar] [CrossRef]
- Feng, L.Y.; Guo, J.C.; Li, P.F.; Zhai, H.J. Boron-based binary Be6 B210− cluster: Three-layered aromatic sandwich, electronic transmutation, and dynamic structural fluxionality. Phys. Chem. Chem. Phys. 2018, 20, 22719–22729. [Google Scholar] [CrossRef]
- Han, L.H.; Wang, Y.J.; Zhai, H.J. Boron-based Be2B5+0- alloy clusters: Inverse sandwiches with pentagonal boron ring and reduction-induced structural transformation to molecular wheel structure. New J. Chem. 2021, 45, 4675–4682. [Google Scholar] [CrossRef]
- Dongliang, K.; Weiguo, S.; Hongxiao, S.; Cheng, L.; Xiaoyu, K. Probing the structure and electronic properties of beryllium doped boron clusters: A planar BeB16 cluster motif for metallo-borophene. Sci. Rep. 2019, 9, 14367–14387. [Google Scholar] [CrossRef] [Green Version]
- Gribanova, T.N.; Minyaev, R.M.; Minkin, V.I. Stabilization of non-typical forms of boron clusters by beryllium doping. Chem. Phys. 2019, 522, 44–54. [Google Scholar] [CrossRef]
- Gribanova, T.N.; Minyaev, R.M.; Minkin, V.I.; Boldyrev, A.I. Novel architectures of boron. Struct. Chem. 2020, 31, 2105–2128. [Google Scholar] [CrossRef]
- Li, H.R.; Liu, H.; Tian, X.X.; Zan, W.Y.; Mu, Y.W.; Lu, H.G.; Li, J.; Wang, Y.K.; Li, S.D. Structural transition in metal-centered boron clusters: From tubular molecular rotors Ta@B21 and Ta@B22+ to cage-like endohedral metalloborospherene Ta@B22−. Phys. Chem. Chem. Phys. 2017, 19, 27025–27030. [Google Scholar] [CrossRef]
- Stephens, P.; Devlin, F.; Cheeseman, J. VCD Spectroscopy for Organic Chemists; Taylor & Francis: Boca Raton, FL, USA, 2012. [Google Scholar]
- Biedermann, P.U.; Cheeseman, J.R.; Frisch, M.J.; Schurig, V.; Gutman, I.; Agranat, I. Conformational Spaces and Absolute Configurations of Chiral Fluorinated Inhalation Anaesthetics. A Theoretical Study. J. Org. Chem. 1999, 64, 3878–3884. [Google Scholar] [CrossRef]
- Aamouche, A.; Devlin, F.J.; Stephens, P.J.; Drabowicz, J.; Bujnicki, B.; Mikołajczyk, M. Vibrational Circular Dichroism and Absolute Configuration of Chiral Sulfoxides: Tert-Butyl Methyl Sulfoxide. Chem. Eur. J. 2000, 6, 4479–4486. [Google Scholar] [CrossRef]
- Nicu, V.P.; Mándi, A.; Kurtán, T.; Polavarapu, P.L. On the Complementarity of ECD and VCD Techniques. Chirality 2014, 26, 525–531. [Google Scholar] [CrossRef]
- Castiglioni, E.; Biscarini, P.; Abbate, S. Experimental aspects of solid state circular dichroism. Chirality 2009, 21, E28–E36. [Google Scholar] [CrossRef]
- Avilés Moreno, J.R.; Quesada Moreno, M.M.; López González, J.J.; Claramunt, R.M.; López, C.; Alkorta, I.; Elguero, J. Self-Assembly Structures of 1H-Indazoles in the Solution and Solid Phases: A Vibrational (IR, FIR, Raman, and VCD) Spectroscopy and Computational Study. ChemPhysChem 2013, 14, 3355–3360. [Google Scholar] [CrossRef] [Green Version]
- Aviles-Moreno, J.R.; Urena Horno, E.; Partal Urena, F.; López González, J.J. IR-Raman-VCD study of R-(+)-Pulegone: Influence of the solvent. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2011, 79, 767–776. [Google Scholar] [CrossRef]
- Partal Ureña, F.; Avilés Moreno, J.R.; López González, J.J. Conformational Flexibility in Terpenes: Vibrational Circular Dichroism (VCD), Infrared and Raman Study of S-Perillaldehyde. J. Phys. Chem. A 2008, 112, 7887–7893. [Google Scholar] [CrossRef] [PubMed]
- Huet, T.; Aviles Moreno, J.R.; Pirali, O.; Tudorie, M.; Partal Ureña, F.; Lopez Gonzalez, J.J. Terpenes in the gas phase: The Far-IR spectrum of perillaldehyde. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 1261–1265. [Google Scholar] [CrossRef]
- Yang, G.; Xu, Y. Vibrational Circular Dichroism Spectroscopy of Chiral Molecules. In Electronic and Magnetic Properties of Chiral Molecules and Supramolecular Architectures; Springer: Berlin/Heidelberg, Germany, 2011; pp. 189–236. [Google Scholar] [CrossRef]
- Nafie, L.A.; Cheng, J.C.; Stephens, P.J. Vibrational circular dichroism of 2,2,2-trifluoro-1-phenylethanol. J. Am. Chem. Soc. 1975, 97, 3842–3843. [Google Scholar] [CrossRef]
- Sherer, E.C.; Lee, C.H.; Shpungin, J.; Cuff, J.F.; Da, C.; Ball, R.; Bach, R.; Crespo, A.; Gong, X.; Welch, C.J. Systematic Approach to Conformational Sampling for Assigning Absolute Configuration Using Vibrational Circular Dichroism. J. Med. Chem. 2014, 57, 477–494. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Pan, J.J. The determination of the absolute configurations of chiral molecules using vibrational circular dichroism (VCD) spectroscopy. Chirality 2008, 20, 643–663. [Google Scholar] [CrossRef] [PubMed]
- Nafie, L.A. Vibrational Circular Dichroism: A New Tool for the Solution-State Determination of the Structure and Absolute Configuration of Chiral Natural Product Molecules. Nat. Prod. Commun. 2008, 3, 451–466. [Google Scholar] [CrossRef] [Green Version]
- Stephens, P.J.; McCann, D.M.; Devlin, F.J.; Smith, A.B. Determination of the Absolute Configurations of Natural Products via Density Functional Theory Calculations of Optical Rotation, Electronic Circular Dichroism, and Vibrational Circular Dichroism The Cytotoxic Sesquiterpene Natural Products Quadrone, Suberosenone, Suberosanone, and Suberosenol A Acetate. J. Nat. Prod. 2006, 69, 1055–1064. [Google Scholar] [CrossRef]
- Dzib, E.; Cabellos, J.L.; Ortíz-Chi, F.; Pan, S.; Galano, A.; Merino, G. Eyringpy: A program for computing rate constants in the gas phase and in solution. Int. J. Quantum Chem. 2019, 119, e25686. [Google Scholar] [CrossRef] [Green Version]
- Kubicki, J.; Watts, H. Quantum Mechanical Modeling of the Vibrational Spectra of Minerals with a Focus on Clays. Minerals 2019, 9, 141. [Google Scholar] [CrossRef] [Green Version]
- Fagiani, M.R.; Song, X.; Petkov, P.; Debnath, S.; Gewinner, S.; Schöllkopf, W.; Heine, T.; Fielicke, A.; Asmis, K.R. Structure and Fluxionality of B13+ Probed by Infrared Photodissociation Spectroscopy. Angew. Chem. Int. Ed. 2017, 56, 501–504. [Google Scholar] [CrossRef]
- Li, Z.H.; Truhlar, D.G. Nanothermodynamics of metal nanoparticles. Chem. Sci. 2014, 5, 2605–2624. [Google Scholar] [CrossRef]
- Li, Z.H.; Jasper, A.W.; Truhlar, D.G. Structures, Rugged Energetic Landscapes, and Nanothermodynamics of Aln (2<n<) Particles. J. Am. Chem. Soc. 2007, 129, 14899–14910. [Google Scholar] [CrossRef] [PubMed]
- Grigoryan, V.G.; Springborg, M. Temperature and isomeric effects in nanoclusters. Phys. Chem. Chem. Phys. 2019, 21, 5646–5654. [Google Scholar] [CrossRef] [PubMed]
- Sutton, C.; Levchenko, S.V. First-Principles Atomistic Thermodynamics and Configurational Entropy. Front. Chem. 2020, 8, 757. [Google Scholar] [CrossRef] [PubMed]
- Mermin, N.D. Thermal Properties of the Inhomogeneous Electron Gas. Phys. Rev. 1965, 137, A1441–A1443. [Google Scholar] [CrossRef]
- Pittalis, S.; Proetto, C.R.; Floris, A.; Sanna, A.; Bersier, C.; Burke, K.; Gross, E.K.U. Exact Conditions in Finite-Temperature Density-Functional Theory. Phys. Rev. Lett. 2011, 107, 163001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gonis, A.; Däne, M. Extension of the Kohn-Sham formulation of density functional theory to finite temperature. J. Phys. Chem. Solids 2018, 116, 86–99. [Google Scholar] [CrossRef]
- Eschrig, H. T > 0 ensemble-state density functional theory via Legendre transform. Phys. Rev. B 2010, 82, 205120. [Google Scholar] [CrossRef] [Green Version]
- Seitsonen, A.P.; Laasonen, K.; Nieminen, R.M.; Klein, M.L. Structure of CAl12. J. Chem. Phys. 1995, 103, 8075–8080. [Google Scholar] [CrossRef] [Green Version]
- Wales, D.J. Structure, Dynamics, and Thermodynamics of Clusters: Tales from Topographic Potential Surfaces. Science 1996, 271, 925–929. [Google Scholar] [CrossRef]
- Hill, T.L. Thermodynamics of Small Systems. J. Chem. Phys. 1962, 36, 3182–3197. [Google Scholar] [CrossRef]
- Fox, H.; Horsfield, A.P.; Gillan, M.J. Density functional calculations of surface free energies. J. Chem. Phys. 2006, 124, 134709. [Google Scholar] [CrossRef]
- Stephens, P.J.; Philip, J. Stephens: A scientific memoir. Theor. Chem. Acc. 2008, 119, 5–18. [Google Scholar] [CrossRef]
- Nafie, L. Vibrational Optical Activity: Principles and Applications; John Wiley & Sons: Chichester, UK, 2011. [Google Scholar]
- Nafie, L.A. Infrared and Raman Vibrational Optical Activity: Theoretical and Experimental Aspects. Ann. Rev. Phys. Chem. 1997, 48, 357–386. [Google Scholar] [CrossRef]
- He, Y.; Wang, B.; Dukor, R.K.; Nafie, L.A. Determination of Absolute Configuration of Chiral Molecules Using Vibrational Optical Activity: A Review. Appl. Spectrosc. 2011, 65, 699–723. [Google Scholar] [CrossRef]
- Calvo, F. Thermodynamics of nanoalloys. Phys. Chem. Chem. Phys. 2015, 17, 27922–27939. [Google Scholar] [CrossRef]
- Teague, S.J. Implications of protein flexibility for drug discovery. Nat. Rev. Drug Discov. 2003, 2, 527–541. [Google Scholar] [CrossRef]
- Dharma-wardana, M.W.C. Current Issues in Finite-T Density-Functional Theory and Warm-Correlated Matter. Computation 2016, 4, 16. [Google Scholar] [CrossRef]
- Pickard, C.J.; Needs, R.J. Ab initio random structure searching. J. Phys. Condens. Matter. 2011, 23, 053201. [Google Scholar] [CrossRef] [Green Version]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Y.; Gong, X.G. Efficiency of generalized simulated annealing. Phys. Rev. E 2000, 62, 4473–4476. [Google Scholar] [CrossRef] [PubMed]
- Xiang, Y.; Gubian, S.; Suomela, B.; Hoeng, J. Generalized Simulated Annealing for Global Optimization: The GenSA Package for R. R J. 2013, 5, 13–29. [Google Scholar] [CrossRef] [Green Version]
- Vlachos, D.; Schmidt, L.; Aris, R. Comparison of small metal clusters: Ni, Pd, Pt, Cu, Ag, Au. Z. Phys. D—Atoms. Mol. Clust. 1993, 26, 156–158. [Google Scholar] [CrossRef]
- Granville, V.; Krivanek, M.; Rasson, J.P. Simulated annealing: A proof of convergence. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 652–656. [Google Scholar] [CrossRef]
- Pan, S.; Moreno, D.; Cabellos, J.L.; Romero, J.; Reyes, A.; Merino, G.; Chattaraj, P.K. In Quest of Strong Be-Ng Bonds among the Neutral Ng-Be Complexes. J. Phys. Chem. A 2014, 118, 487–494. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.h.; Ding, Y.h.; Cabellos, J.L.; Osorio, E.; Islas, R.; Restrepo, A.; Merino, G. Planar tetracoordinate carbons with a double bond in CAl3E clusters. Phys. Chem. Chem. Phys. 2015, 17, 8769–8775. [Google Scholar] [CrossRef] [PubMed]
- Vargas-Caamal, A.; Pan, S.; Ortiz-Chi, F.; Cabellos, J.L.; Boto, R.A.; Contreras-Garcia, J.; Restrepo, A.; Chattaraj, P.K.; Merino, G. How strong are the metallocene–metallocene interactions? Cases of ferrocene, ruthenocene, and osmocene. Phys. Chem. Chem. Phys. 2016, 18, 550–556. [Google Scholar] [CrossRef] [PubMed]
- Vargas-Caamal, A.; Cabellos, J.L.; Ortiz-Chi, F.; Rzepa, H.S.; Restrepo, A.; Merino, G. How Many Water Molecules Does it Take to Dissociate HCl? Chem. A Eur. J. 2016, 22, 2812–2818. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.h.; Vassilev-Galindo, V.; Luis Cabellos, J.; Osorio, E.; Orozco, M.; Pan, S.; Ding, Y.h.; Merino, G. Planar pentacoordinate carbon atoms embedded in a metallocene framework. Chem. Commun. 2017, 53, 138–141. [Google Scholar] [CrossRef]
- Vargas-Caamal, A.; Ortiz-Chi, F.; Moreno, D.; Restrepo, A.; Merino, G.; Cabellos, J.L. The rich and complex potential energy surface of the ethanol dimer. Theor. Chem. Acc. 2015, 134, 16. [Google Scholar] [CrossRef]
- Flórez, E.; Acelas, N.; Ibargüen, C.; Mondal, S.; Cabellos, J.L.; Merino, G.; Restrepo, A. Microsolvation of NO3−: Structural exploration and bonding analysis. RSC Adv. 2016, 6, 71913–71923. [Google Scholar] [CrossRef]
- Ravell, E.; Jalife, S.; Barroso, J.; Orozco-Ic, M.; Hernandez-Juarez, G.; Ortiz-Chi, F.; Pan, S.; Cabellos, J.L.; Merino, G. Structure and Bonding in CE5-(E = Al-Tl) Clusters: Planar Tetracoordinate Carbon versus Pentacoordinate Carbon. Chem. Asian J. 2018, 13, 1467–1473. [Google Scholar] [CrossRef]
- Hadad, C.Z.; Florez, E.; Merino, G.; Cabellos, J.L.; Ferraro, F.; Restrepo, A. Potential Energy Surfaces of WC6 Clusters in Different Spin States. J. Phys. Chem. A 2014, 118, 5762–5768. [Google Scholar] [CrossRef]
- Saunders, M. Stochastic search for isomers on a quantum mechanical surface. J. Comput. Chem. 2004, 25, 621–626. [Google Scholar] [CrossRef]
- Saunders, M. Stochastic exploration of molecular mechanics energy surfaces. Hunting for the global minimum. J. Am. Chem. Soc. 1987, 109, 3150–3152. [Google Scholar] [CrossRef]
- Grande-Aztatzi, R.; Martínez-Alanis, P.R.; Cabellos, J.L.; Osorio, E.; Martínez, A.; Merino, G. Structural evolution of small gold clusters doped by one and two boron atoms. J. Comput. Chem. 2014, 35, 2288–2296. [Google Scholar] [CrossRef]
- Mondal, S.; Cabellos, J.L.; Pan, S.; Osorio, E.; Torres-Vega, J.J.; Tiznado, W.; Restrepo, A.; Merino, G. 10-π-Electron arenes a la carte: Structure and bonding of the [E-(Cn Hn)-E]n-6 (E = Ca, Sr, Ba; n = 6–8) complexes. Phys. Chem. Chem. Phys. 2016, 18, 11909–11918. [Google Scholar] [CrossRef]
- Rodríguez-Kessler, P.L.; Pan, S.; Florez, E.; Cabellos, J.L.; Merino, G. Structural Evolution of the Rhodium-Doped Silver Clusters AgnRh (n <15) and Their Reactivity toward NO. J. Phys. Chem. C 2017, 121, 19420–19427. [Google Scholar] [CrossRef]
- Alexandrova, A.N.; Boldyrev, A.I.; Fu, Y.J.; Yang, X.; Wang, X.B.; Wang, L.S. Structure of the Nax Clx (x = 1,4) clusters via ab-initio genetic algorithm and photoelectron spectroscopy. J. Chem. Phys. 2004, 121, 5709–5719. [Google Scholar] [CrossRef] [Green Version]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Cabellos, J.L.; Ortiz-Chi, F.; Ramirez, A.; Merino, G. Glomos 2.0. Cinvestav-Merida 2018, 1, 1–10. [Google Scholar]
- Hernández-Juárez, G.; Ravell, E.; Arcudia, J.; Zarate, X.; Cui, Z.h.; Merino, G.; Barroso, J. Structural effects of alkali-metals on the B12 skeleton. Phys. Chem. Chem. Phys. 2020, 22, 17344–17350. [Google Scholar] [CrossRef] [PubMed]
- Castro, A.C.; Osorio, E.; Cabellos, J.L.; Cerpa, E.; Matito, E.; Solà, M.; Swart, M.; Merino, G. Exploring the Potential Energy Surface of E2 P4 Clusters (E = Group 13 element): The Quest for Inverse Carbon-Free Sandwiches. Chem. A Eur. J. 2014, 20, 4583–4590. [Google Scholar] [CrossRef] [PubMed]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Dunning, T.H.J.; Hay, P.J. Modern Theoretical Chemistry. In Methods of Electronic Structure Theory; Schaefer, H.F., III, Ed.; Springer US: Plenum, NY, USA, 1977; Volume 3, Chapter 1; pp. 1–28. [Google Scholar]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Schafer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Lee, T.J.; Taylor, P.R. A diagnostic for determining the quality of single-reference electron correlation methods. Int. J. Quantum Chem. 1989, 36, 199–207. [Google Scholar] [CrossRef] [Green Version]
- Liakos, D.G.; Guo, Y.; Neese, F. Comprehensive Benchmark Results for the Domain Based Local Pair Natural Orbital Coupled Cluster Method (DLPNO-CCSD(T)) for Closed- and Open-Shell Systems. J. Phys. Chem. A 2020, 124, 90–100. [Google Scholar] [CrossRef] [Green Version]
- Zubarev, D.Y.; Boldyrev, A.I. Developing paradigms of chemical bonding: Adaptive natural density partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207–5217. [Google Scholar] [CrossRef] [PubMed]
- Brehm, G.; Reiher, M.; Le Guennic, B.; Leibold, M.; Schindler, S.; Heinemann, F.W.; Schneider, S. Investigation of the low-spin to high-spin transition in a novel [Fe(pmea)(NCS)2] complex by IR and Raman spectroscopy and DFT calculations. J. Raman Spectrosc. 2006, 37, 108–122. [Google Scholar] [CrossRef]
- McQuarrie, D.A.M. Statistical Mechanics; Chemistry Series; Harper & Row: New York, NY, USA, 1975. [Google Scholar]
- Hill, T. An Introduction to Statistical Thermodynamics; Addison-Wesley Series in Chemistry; Dover Publications: New York, NY, USA, 1986. [Google Scholar]
- Bhattacharya, S.; Berger, D.; Reuter, K.; Ghiringhelli, L.M.; Levchenko, S.V. Theoretical evidence for unexpected O-rich phases at corners of MgO surfaces. Phys. Rev. Mater. 2017, 1, 071601. [Google Scholar] [CrossRef] [Green Version]
- Bhumla, P.; Kumar, M.; Bhattacharya, S. Theoretical insights into C-H bond activation of methane by transition metal clusters: The role of anharmonic effects. Nanoscale Adv. 2021, 3, 575–583. [Google Scholar] [CrossRef]
- Shortle, D. Propensities, probabilities, and the Boltzmann hypothesis. Comput. Theor. Chem. 2003, 12, 1298–1302. [Google Scholar] [CrossRef] [PubMed]
- Mendoza-Wilson, A.M.; Balandrán-Quintana, R.R.; Cabellos, J.L. Thermochemical behavior of sorghum procyanidin trimers with C4-C8 and C4-C6 interflavan bonds in the reaction with superoxide anion radical and H2O2-forming NADH-oxidase flavoenzyme. Comput. Theor. Chem. 2020, 1186, 112912. [Google Scholar] [CrossRef]
- Schebarchov, D.; Baletto, F.; Wales, D.J. Structure, thermodynamics, and rearrangement mechanisms in gold clusters insights from the energy landscapes framework. Nanoscale 2018, 10, 2004–2016. [Google Scholar] [CrossRef] [Green Version]
- Goldsmith, B.R.; Florian, J.; Liu, J.X.; Gruene, P.; Lyon, J.T.; Rayner, D.M.; Fielicke, A.; Scheffler, M.; Ghiringhelli, L.M. Two-to-three dimensional transition in neutral gold clusters: The crucialrole of van der Waals interactions and temperature. Phys. Rev. Mater. 2019, 3, 016002. [Google Scholar] [CrossRef] [Green Version]
- Moezzi, A.; Olmstead, M.M.; Power, P.P. Boron-boron double bonding in the species [B2R4]2-: Synthesis and structure of [(Et2O)Li2Mes2BB(Mes)Ph], a diborane(4) dianion analog of a substituted ethylene. J. Am. Chem. Soc. 1992, 114, 2715–2717. [Google Scholar] [CrossRef]
- Zhou, M.; Tsumori, N.; Li, Z.; Fan, K.; Andrews, L.; Xu, Q. OCBBCO: A Neutral Molecule with Some Boron-Boron Triple Bond Character. J. Am. Chem. Soc. 2002, 124, 12936–12937. [Google Scholar] [CrossRef] [PubMed]
- De la Puente, E.; Aguado, A.; Ayuela, A.; López, J.M. Structural and electronic properties of small neutral (MgO)n clusters. Phys. Rev. B 1997, 56, 7607–7614. [Google Scholar] [CrossRef] [Green Version]
- Oswald, P.; Desmet, K.; Sandra, P.; Krupcik, J.; Májek, P.; Armstrong, D.W. Determination of the enantiomerization energy barrier of some 3-hydroxy-1,4-benzodiazepine drugs by supercritical fluid chromatography. J. Chromatogr. B 2002, 779, 283–295. [Google Scholar] [CrossRef]
- Pople, J.A.; Head-Gordon, M.; Raghavachari, K. Quadratic configuration interaction. A general technique for determining electron correlation energies. J. Chem. Phys. 1987, 87, 5968–5975. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ravat, P. Carbo[n]helicenes Restricted to Enantiomerize: An Insight into the Design Process of Configurationally Stable Functional Chiral PAHs. Chem. A Eur. J. 2021, 27, 3957–3967. [Google Scholar] [CrossRef]
- Malola, S.; Häkkinen, H. Chiral Inversion of Thiolate-Protected Gold Nanoclusters via Core Reconstruction without Breaking a Au–S Bond. J. Am. Chem. Soc. 2019, 141, 6006–6012. [Google Scholar] [CrossRef] [PubMed]
- Glaesemann, K.R.; Fried, L.E. Quantitative molecular thermochemistry based on path integrals. J. Chem. Phys. 2005, 123, 034103. [Google Scholar] [CrossRef]
- Hellman, O.; Steneteg, P.; Abrikosov, I.A.; Simak, S.I. Temperature dependent effective potential method for accurate free energy calculations of solids. Phys. Rev. B 2013, 87, 104111. [Google Scholar] [CrossRef] [Green Version]
- Grimvall, G.; Magyari-Köpe, B.; Ozoliņš, V.; Persson, K.A. Lattice instabilities in metallic elements. Rev. Mod. Phys. 2012, 84, 945–986. [Google Scholar] [CrossRef] [Green Version]
- Neugebauer, J.; Hickel, T. Density functional theory in materials science. WIRES Comput. Mol. Sci. 2013, 3, 438–448. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geudtner, G.; Calaminici, P.; Carmona-Espíndola, J.; del Campo, J.M.; Domínguez-Soria, V.D.; Moreno, R.F.; Gamboa, G.U.; Goursot, A.; Köster, A.M.; Reveles, J.U.; et al. deMon2k. WIRES Comput. Mol. Sci. 2012, 2, 548–555. [Google Scholar] [CrossRef]
- Li, M.; Wang, J.; Fu, B.; Hou, Q. A molecular dynamics study of melting and dissociation of tungsten nanoparticles. AIP Adv. 2015, 5, 127131. [Google Scholar] [CrossRef] [Green Version]
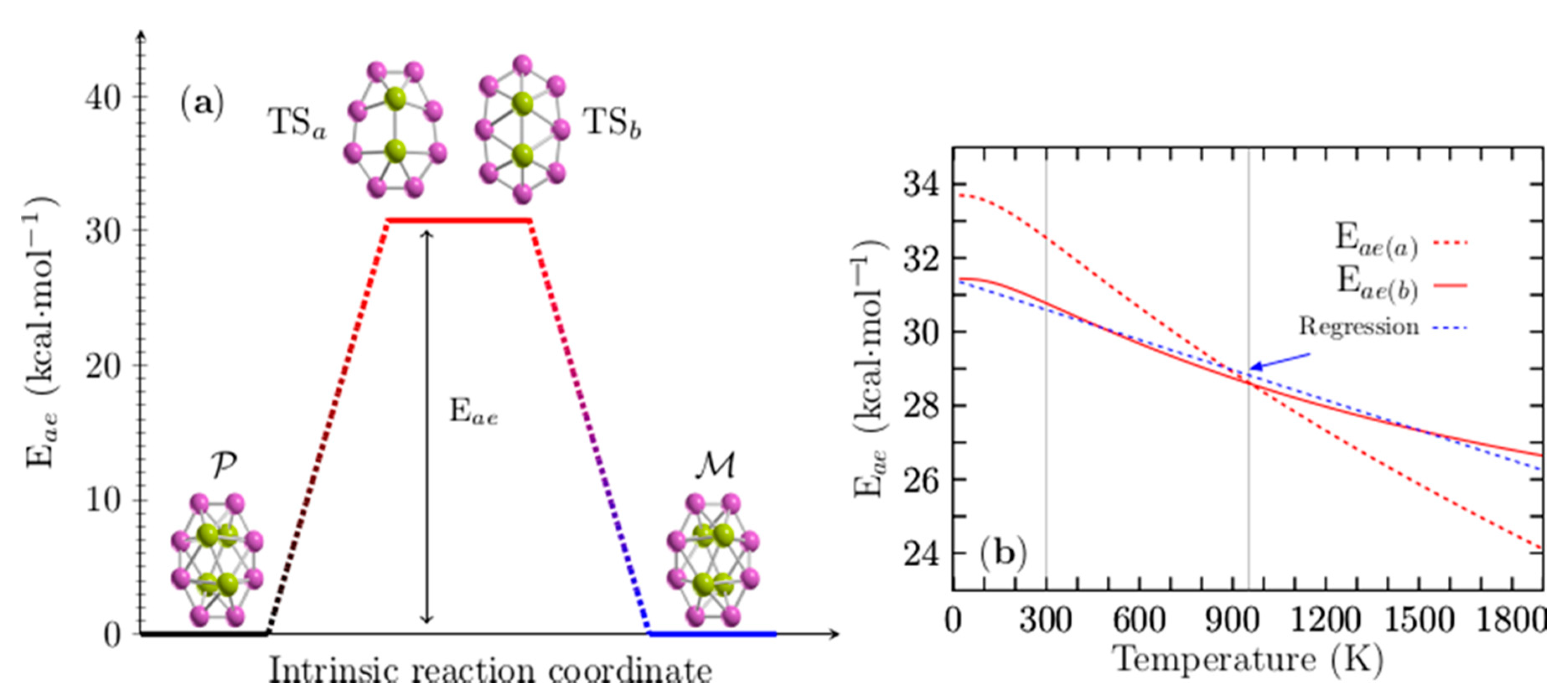
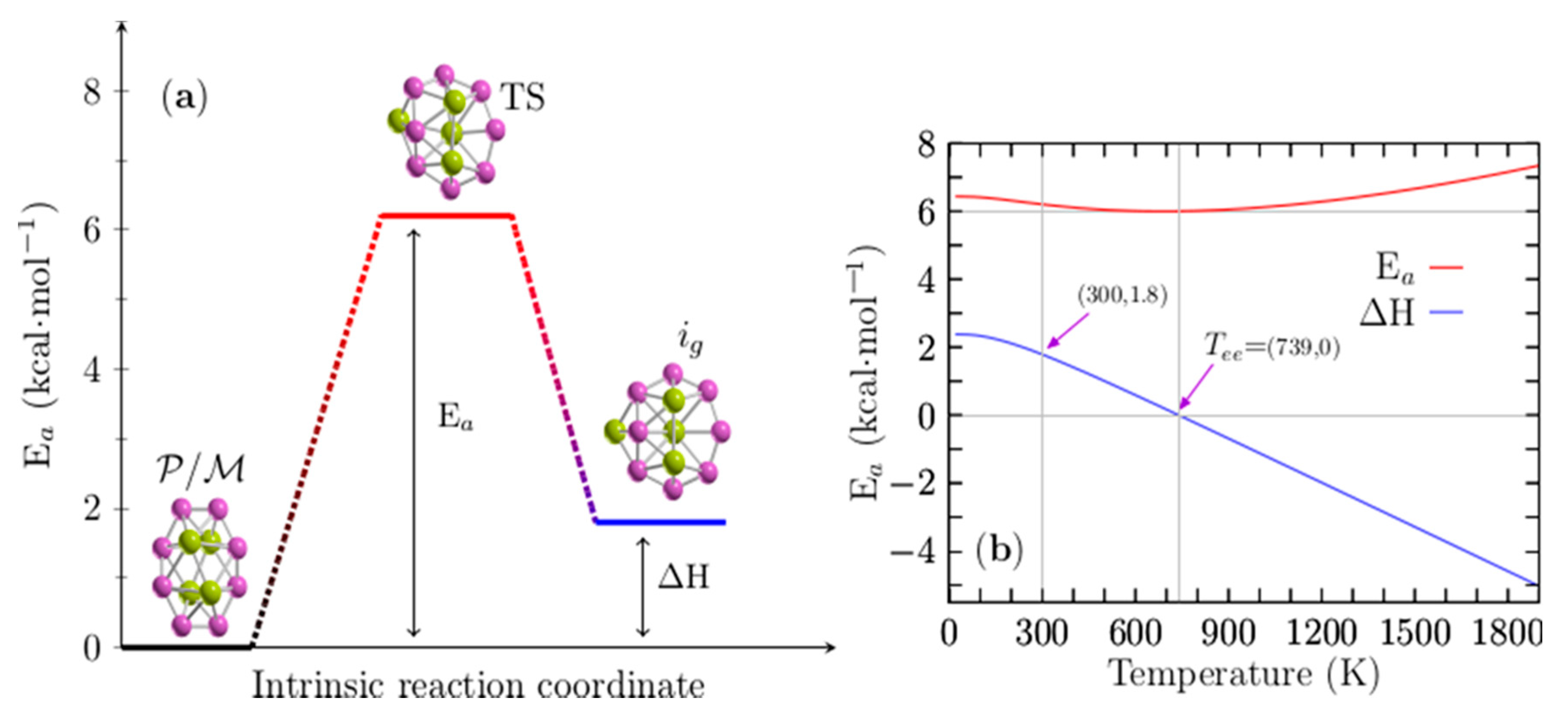
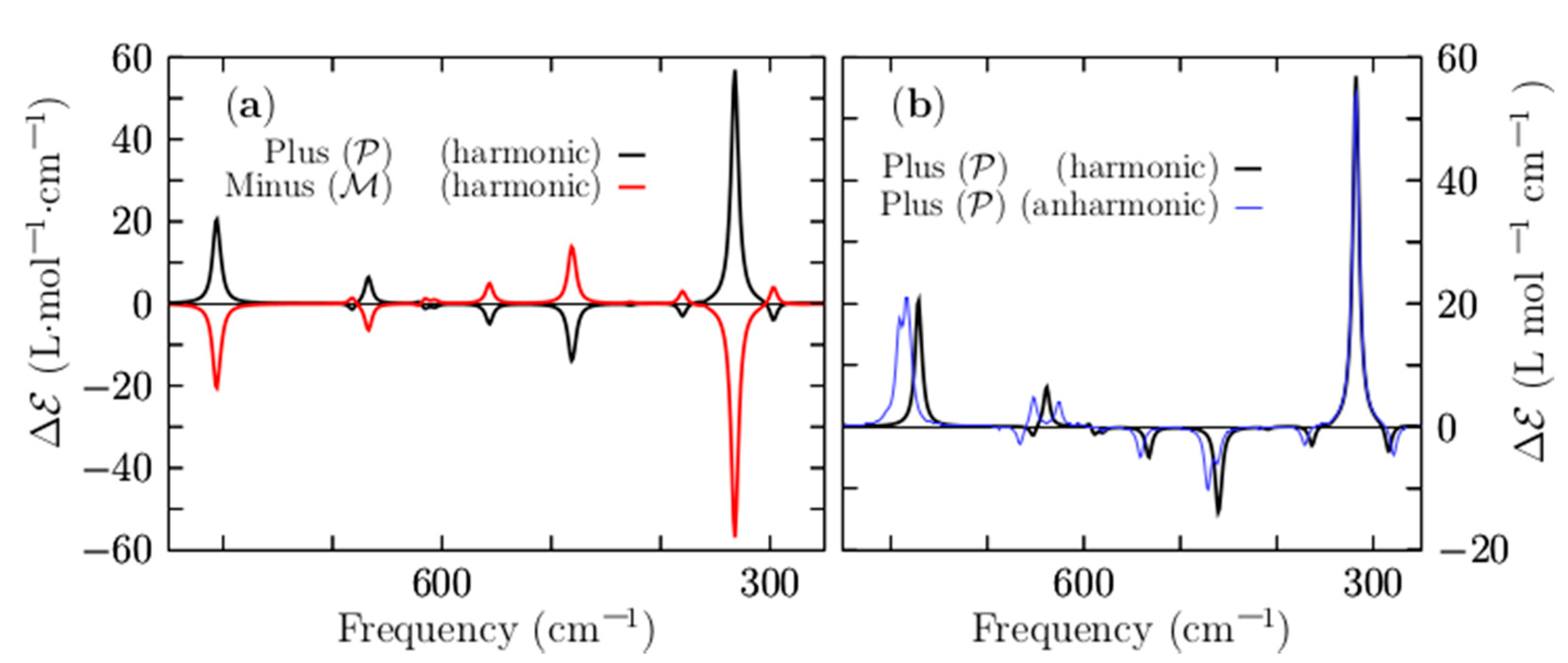
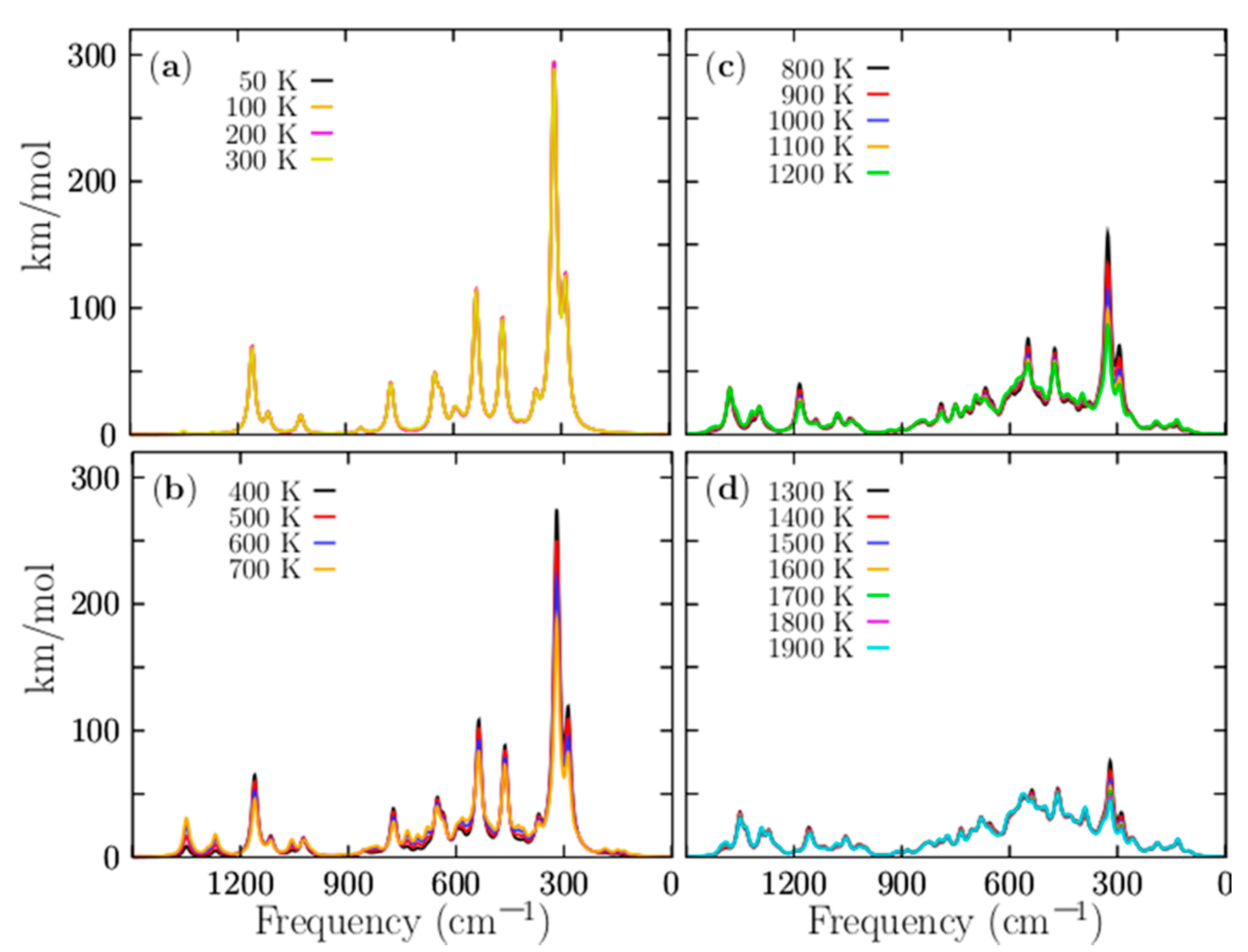
| Level | i1 | i2 | i3 | i4 | i5 | i6 | i6 | i8 | i9 | i10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.0 | 0.41 | 0.41 | 0.81 | 0.81 | 1.79 | 2.40 | 4.45 | 4.45 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3.61 | 3.38 | 5.38 | 5.38 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 2.71 | 2.51 | 4.51 | 4.51 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.75 | 1.37 | 5.0 | 5.0 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | −0.20 | 0.50 | 4.10 | 4.10 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 2.38 | 2.80 | 5.03 | 5.03 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 3.28 | 3.68 | 5.90 | 3.28 | |
| Point Group Symmetry | C1 | C1 | C2 | C2 | C1 | C1 | C1 | C1 | C2 | C2 |
| 0.019 | 0.019 | 0.019 | 0.019 | 0.019 | 0.019 | 0.019 | 0.019 | 0.019 | 0.019 |
| Temperature (K) | % (Decrease) | |||
|---|---|---|---|---|
| 0 | 33.42 | 31.42 | 0.0 | 0.0 |
| 300 | 30.60 | 31.42 | 0.81 | 2.58 |
| 600 | 29.79 | 31.42 | 1.62 | 5.17 |
| 900 | 28.97 | 31.42 | 2.44 | 7.76 |
| 1200 | 28.16 | 31.42 | 3.25 | 10.35 |
| 1500 | 27.35 | 31.42 | 4.06 | 12.94 |
| 1800 | 26.53 | 31.42 | 4.88 | 15.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buelna-García, C.E.; Robles-Chaparro, E.; Parra-Arellano, T.; Quiroz-Castillo, J.M.; del-Castillo-Castro, T.; Martínez-Guajardo, G.; Castillo-Quevedo, C.; de-León-Flores, A.; Anzueto-Sánchez, G.; Martin-del-Campo-Solis, M.F.; et al. Theoretical Prediction of Structures, Vibrational Circular Dichroism, and Infrared Spectra of Chiral Be4B8 Cluster at Different Temperatures. Molecules 2021, 26, 3953. https://doi.org/10.3390/molecules26133953
Buelna-García CE, Robles-Chaparro E, Parra-Arellano T, Quiroz-Castillo JM, del-Castillo-Castro T, Martínez-Guajardo G, Castillo-Quevedo C, de-León-Flores A, Anzueto-Sánchez G, Martin-del-Campo-Solis MF, et al. Theoretical Prediction of Structures, Vibrational Circular Dichroism, and Infrared Spectra of Chiral Be4B8 Cluster at Different Temperatures. Molecules. 2021; 26(13):3953. https://doi.org/10.3390/molecules26133953
Chicago/Turabian StyleBuelna-García, Carlos Emiliano, Eduardo Robles-Chaparro, Tristan Parra-Arellano, Jesus Manuel Quiroz-Castillo, Teresa del-Castillo-Castro, Gerardo Martínez-Guajardo, Cesar Castillo-Quevedo, Aned de-León-Flores, Gilberto Anzueto-Sánchez, Martha Fabiola Martin-del-Campo-Solis, and et al. 2021. "Theoretical Prediction of Structures, Vibrational Circular Dichroism, and Infrared Spectra of Chiral Be4B8 Cluster at Different Temperatures" Molecules 26, no. 13: 3953. https://doi.org/10.3390/molecules26133953
APA StyleBuelna-García, C. E., Robles-Chaparro, E., Parra-Arellano, T., Quiroz-Castillo, J. M., del-Castillo-Castro, T., Martínez-Guajardo, G., Castillo-Quevedo, C., de-León-Flores, A., Anzueto-Sánchez, G., Martin-del-Campo-Solis, M. F., Mendoza-Wilson, A. M., Vásquez-Espinal, A., & Cabellos, J. L. (2021). Theoretical Prediction of Structures, Vibrational Circular Dichroism, and Infrared Spectra of Chiral Be4B8 Cluster at Different Temperatures. Molecules, 26(13), 3953. https://doi.org/10.3390/molecules26133953








