Pauling’s Conceptions of Hybridization and Resonance in Modern Quantum Chemistry
Abstract
:1. Introduction
2. Computational Methods
3. Directional Hybridization
4. Resonance Delocalization
5. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Seiler, P.; Weisman, G.R.; Glendening, E.D.; Weinhold, F.; Johnson, V.B.; Dunitz, J.D. Observation of an Eclipsed C(sp3)-CH3 Bond in a Tricyclic Orthoamide: Experimental and Theoretical Evidence for C-H⋯O Hydrogen Bonds. Angew. Chem. Int. Ed. 1987, 26, 1175–1177. [Google Scholar] [CrossRef]
- Glendening, E.D.; Faust, R.; Streitwieser, A.; Vollhardt, K.P.C.; Weinhold, F. On the Role of Delocalization in Benzene. J. Am. Chem. Soc. 1993, 115, 10952–10957. [Google Scholar] [CrossRef] [Green Version]
- Suidan, L.; Badenhoop, J.K.; Glendening, E.D.; Weinhold, F. Common Textbook and Teaching Misrepresentations of Lewis Structures. J. Chem. Educ. 1995, 72, 583–586. [Google Scholar] [CrossRef]
- Glendening, E.D.; Weinhold, F. Natural Resonance Theory. I. General Formulation. J. Comput. Chem. 1998, 19, 593–609. [Google Scholar] [CrossRef]
- Glendening, E.D.; Weinhold, F. Natural Resonance Theory. II. Natural Bond Order and Valency. J. Comput. Chem. 1998, 19, 610–627. [Google Scholar] [CrossRef]
- Glendening, E.D.; Badenhoop, J.K.; Weinhold, F. Natural Resonance Theory. III. Chemical Applications. J. Comput. Chem. 1998, 19, 628–646. [Google Scholar] [CrossRef]
- Pauling, L.; Wilson, E.B., Jr. Introduction to Quantum Mechanics; McGraw-Hill: New York, NY, USA, 1935. [Google Scholar]
- Pauling, L. Nature of the Chemical Bond, 3rd ed.; Cornell University Press: Ithaca, NY, USA, 1960. [Google Scholar]
- Heitler, W.; London, F. Wechselwirkung neutraler Atome und homöpolare Bindung nach der Quantenmechanik. Z. Phys. 1927, 44, 455–472. [Google Scholar] [CrossRef]
- Pauling, L. The Application of the Quantum Mechanics to the Structure of the Hydrogen Molecule and Hydrogen Molecule-Ion and to Related Problems. Chem. Rev. 1928, 5, 173–213. [Google Scholar] [CrossRef]
- Pauling, L. The nature of the chemical bond. Application of results obtained from the quantum mechanics and from a theory of paramagnetic susceptibility to the structure of molecules. J. Am. Chem. Soc. 1931, 53, 1367–1400. [Google Scholar] [CrossRef]
- Slater, J.C. Directed valence in polyatomic molecules. Phys. Rev. 1931, 37, 481–497. [Google Scholar] [CrossRef]
- Pauling, L. The theory of resonance in chemistry. Proc. R. Soc. Lond. Ser. A 1977, 356, 433–441. [Google Scholar]
- Todd, A.R.; Cornforth, J.W. Robert Robinson, 13 September 1886–8 February 1975. Biogr. Mem. Fellows R. Soc. Lond. 1976, 22, 415–527. [Google Scholar]
- Hund, F. Zur Deutung einiger Erscheinungen in den Molekelspektre. Z. Physik 1926, 36, 657–674. [Google Scholar] [CrossRef]
- Mulliken, R.S. The Assignment of Quantum Numbers for Electrons in Molecules. I. Phys. Rev. 1928, 32, 186–222. [Google Scholar] [CrossRef]
- Lennard-Jones, J.E. The Electronic Structure of Some Diatomic Molecules Trans. Faraday Soc. 1929, 25, 668–686. [Google Scholar] [CrossRef]
- Hartree, D.R. The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part I. Theory and Method. Proc. Camb. Philos. Soc. 1928, 24, 89–110. [Google Scholar] [CrossRef]
- Fock, V. Näherungsmethode zur Lösung des quantenmechanischen Mehrkörperproblems. Z. Phys. 1930, 61, 126–148. [Google Scholar] [CrossRef]
- Slater, J.C. Note on Hartree’s Method. Phys. Rev. 1930, 35, 210–211. [Google Scholar] [CrossRef]
- Coulson, C.A. Self-consistent field for molecular hydrogen. Proc. Camb. Philos. Soc. 1938, 34, 204–212. [Google Scholar] [CrossRef]
- Roothaan, C.C.J. New Developments in Molecular Orbital Theory. Rev. Mod. Phys. 1951, 23, 69–89. [Google Scholar] [CrossRef]
- Mulliken, R.S. Spectroscopy, molecular orbitals, and chemical bonding (Nobel Prize, 1966). Science 1967, 157, 13–24. [Google Scholar] [CrossRef] [Green Version]
- Norbeck, J.M.; Gallup, G.A. Valence-bond calculation of the electronic structure of benzene. J. Am. Chem. Soc. 1974, 96, 3386–3393. [Google Scholar] [CrossRef]
- Goddard, W.A., III. Improved Quantum Theory of Many-Electron Systems. I. Construction of Eigenfunctions of S2 Which Satisfy Pauli’s Principle. Phys. Rev. 1967, 157, 73–78. [Google Scholar] [CrossRef]
- Goddard, W.A., III; Dunning, T.H., Jr.; Hunt, W.J.; Hay, P.J. Generalized valence bond description of bonding in low-lying states of molecules. Acc. Chem. Res. 1973, 6, 368–376. [Google Scholar] [CrossRef]
- Dunning, T.H.; Hay, P.J. Beyond Molecular Orbital Theory: The Impact of Generalized Valence Bond Theory in Molecular Science. In Computational Materials, Chemistry, and Biochemistry: From Bold Initiatives to the Last Mile; Shankar, S., Muller, R., Dunning, T., Chen, G.H., Eds.; Springer: Cham, Switzerland, 2021; Volume 284, pp. 55–87. [Google Scholar]
- Foresman, J.B.; Frisch, A.E. Exploring Chemistry with Electronic Structure Methods, 3rd ed.; Gaussian, Inc.: Wallingford, CT, USA, 2015. [Google Scholar]
- van’t Hoff, J.H. Sur les formules de structure dans l’espace. Arch. Neerl. Sci. Exactes Nat. 1874, 9, 445–454. [Google Scholar]
- LeBel, J.-A. Sur Les Relations Qui Existent Entre Les Formules Atomiques Des Corps Organiques et Le Pouvoir Rotatoire de Leurs Dissolutions. Bull. Soc. Chim. Paris 1874, 22, 337–347. [Google Scholar]
- Ramberg, P.J. Chemical Structure, Spatial Arrangement: The Early History of Stereochemistry, 1874–1914; Routledge: Abingdon, UK, 2017. [Google Scholar]
- Bragg, W.H.; Bragg, W.L. The structure of the diamond. Nature 1913, 91, 557. [Google Scholar] [CrossRef]
- Wierl, R. Elektronenbeugung und Molekülbau. Ann. Phys. 1931, 8, 521–564. [Google Scholar] [CrossRef]
- Jensen, W.P.; Palenik, G.J.; Suh, I.-H. The history of molecular structure determination viewed through the Nobel Prizes. J. Chem. Educ. 2003, 80, 753–761. [Google Scholar]
- Coulson, C.A. Valence, 2nd ed.; Oxford University Press: Oxford, UK, 1965. [Google Scholar]
- Kermack, W.O.; Robinson, R.R. An explanation of the property of induced polarity of atoms and an interpretion of the theory of partial valencies on an electronic basis. J. Chem. Soc. Trans. 1922, 121, 427–440. [Google Scholar] [CrossRef] [Green Version]
- Lowry, T.M. Studies of electrovalency. Part I. The polarity of double bonds. J. Chem. Soc. Trans. 1923, 123, 822–831. [Google Scholar] [CrossRef]
- Allan, J.; Oxford, A.F.; Robinson, R.; Smith, J.C. The relative directive powers of groups of the forms RO and RR’N in aromatic substitution. Part III. The nitration of some p-alkoxyanisoles. J. Chem. Soc. 1926, 129, 401–411. [Google Scholar] [CrossRef]
- Ingold, C.K.; Ingold, E.H. The nature of the alternating effect in carbon chains. Part V. A discussion of aromatic substitution with special reference to the respective roles of polar and non-polar dissociation; and a further study of the relative directive efficiencies of oxygen and nitrogen. J. Chem. Soc. 1926, 129, 1310–1328. [Google Scholar]
- Ingold, C.K. Mesomerism and tautomerism. Nature 1934, 133, 946–947. [Google Scholar] [CrossRef]
- Ingold, C.K. Principles of an electronic theory of organic reactions. Chem. Rev. 1934, 15, 225–274. [Google Scholar] [CrossRef]
- Saltzman, M.D. CK Ingold’s development of the concept of mesomerism. Bull. Hist. Chem. 1996, 19, 25–32. [Google Scholar]
- Kerber, R.C. If it’s resonance, what is resonating? J. Chem. Educ. 2006, 83, 223–227. [Google Scholar] [CrossRef]
- Coulson, C.A.; Fischer, I. Notes on the Molecular Orbital Treatment of the Hydrogen Molecule. Phil. Mag. 1949, 40, 386–393. [Google Scholar] [CrossRef]
- Grushow, A. Is it time to retire the hybrid orbital? J. Chem. Educ. 2011, 88, 860–862. [Google Scholar] [CrossRef]
- Tro, N.J. Retire the Hybrid Atomic Orbital? Not So Fast. J. Chem. Educ. 2012, 89, 567–568. [Google Scholar] [CrossRef]
- DeKock, R.L.; Strikwerda, J.R. Retire Hybrid Atomic Orbitals? J. Chem. Educ. 2012, 89, 569. [Google Scholar] [CrossRef]
- Landis, C.R.; Weinhold, F. Comments on ‘Is It Time To Retire the Hybrid Atomic Orbital?’. J. Chem. Educ. 2012, 89, 570–572. [Google Scholar] [CrossRef]
- Truhlar, D.G. Are Molecular Orbitals Delocalized? J. Chem. Educ. 2012, 89, 573–574. [Google Scholar] [CrossRef]
- Hiberty, P.C.; Volatron, F.; Shaik, S. In Defense of the Hybrid Atomic Orbitals. J. Chem. Educ. 2012, 89, 575–577. [Google Scholar] [CrossRef]
- Truhlar, D.G.; Hiberty, P.C.; Shaik, S.; Gordon, M.S.; Danovich, D. Orbitals and the Interpretation of Photoelectron Spectroscopy and (e,2e) Ionization Experiments. Angew. Chem. Int. Ed. 2019, 58, 12332–12338. [Google Scholar] [CrossRef] [PubMed]
- Graham, L.R. A Soviet Marxist view of structural chemistry: The theory of resonance controversy. Isis 1964, 55, 20–31. [Google Scholar] [CrossRef]
- The Soviet Resonance Controversy. Available online: https://paulingblog.wordpress.com/2009/03/26/paulings-theory-of-resonance-a-soviet-controversy/ (accessed on 28 May 2021).
- Frenking, G.; Krapp, A. Unicorns in the world of chemical bonding models. J. Comput. Chem. 2007, 28, 15–24. [Google Scholar] [CrossRef]
- Landis, C.R.; Hughes, R.P.; Weinhold, F. Bonding Analysis of TM(cAAC)2 (TM = Cu, Ag, Au) and the Importance of Reference State. Organometallics 2015, 34, 3442–3449. [Google Scholar] [CrossRef]
- Landis, C.R.; Hughes, R.P.; Weinhold, F. Comment on ‘Observation of alkaline earth complexes M(CO)8 (M = Ca, Sr. or Ba) that mimic transition metals’. Science 2019, 365, 553. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.T.; Thompson, J.V.K.; Dunning, T.H., Jr. Spin-coupled generalized valence bond description of group 14 species: The carbon, silicon and germanium hydrides, XHn (n = 1–4). J. Phys. Chem. A 2019, 123, 2401–2419. [Google Scholar] [CrossRef]
- Xu, L.T.; Dunning, T.H., Jr. Orbital hybridization in modern valence bond wave functions: Methane, ethylene, and acetylene. J. Phys. Chem. A 2020, 124, 204–214. [Google Scholar] [CrossRef]
- Foster, J.M.; Boys, S.F. Canonical configurational interaction procedure. Rev. Mod. Phys. 1960, 32, 300–302. [Google Scholar] [CrossRef]
- Edmiston, C.; Ruedenberg, K. Localized atomic and molecular orbitals. Rev. Mod. Phys. 1963, 35, 457–464. [Google Scholar] [CrossRef]
- Pipek, J.; Mezey, P.G. A fast intrinsic localization procedure applicable for ab initio and semiempirical linear combination of atomic orbital wave functions. J. Chem. Phys. 1989, 90, 4916–4926. [Google Scholar] [CrossRef]
- Khaliullin, R.Z.; Head-Gordon, M.; Bell, A.T. An efficient self-consistent field method for large systems of weakly interacting components. J. Chm. Phys. 2006, 124, 204105. [Google Scholar] [CrossRef] [Green Version]
- Jansík, B.; Høst, S.; Kristensen, K.; Jørgensen, P. Local orbitals by minimizing powers of the orbital variance. J. Chem. Phys. 2011, 134, 194104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. Natural Bond Orbital Methods. WIREs Comput. Mol. Sci. 2012, 2, 1–42. [Google Scholar] [CrossRef]
- Weinhold, F.; Landis, C.R.; Glendening, E.D. What is NBO Analysis and How is it Useful? Int. Rev. Phys. Chem. 2016, 35, 399–440. [Google Scholar] [CrossRef]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. Natural Bond Orbital Theory: Discovering Chemistry with NBO7. In Complementary Bonding Analysis; Grabowsky, S., Ed.; De Gruyer: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Weinhold, F.; Landis, C.R. Discovering Chemistry with Natural Bond Orbitals; John Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. Resonance Theory Reboot. J. Am. Chem. Soc. 2019, 141, 4156–4166. [Google Scholar] [CrossRef]
- Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Karafiloglou, P.; Landis, C.R.; Weinhold, F. NBO 7.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 2018. [Google Scholar]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 7.0: New Vistas in Localized and Delocalized Chemical Bonding Theory. J. Comput. Chem. 2019, 40, 2234–2241. [Google Scholar] [CrossRef] [PubMed]
- NBO. Affiliated Electronic Structure Systems and Protected Interfaces. Available online: https://nbo7.chem.wisc.edu/affil_css.htm (accessed on 2 July 2021).
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian-16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2019. [Google Scholar]
- Cooper, D.L.; Thorsteinsson, T.; Gerratt, J. Fully variational optimization of modern VB wave functions using the CASVB strategy. Int. J. Quant. Chem. 1997, 65, 439–451. [Google Scholar] [CrossRef]
- Cooper, D.L.; Thorsteinsson, T.; Gerratt, J. Modern VB representations of CASSCF wave functions and the fully-variational optimization of modern VB wave functions using the CASVB strategy. Adv. Quant. Chem. 1998, 32, 51–67. [Google Scholar]
- Werner, H.-J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M. Molpro: A general-purpose quantum chemistry program package. WIREs Comput. Mol. Sci. 2012, 2, 242–253. [Google Scholar] [CrossRef]
- Werner, H.-J.; Knowles, P.J.; Manby, F.R.; Black, J.A.; Doll, K.; Heßelmann, A.; Kats, D.; Köhn, A.; Korona, T.; Kreplin, D.A.; et al. The Molpro quantum chemistry package. J. Chem. Phys. 2020, 152, 144107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Werner, H.-J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M.; Celani, P.; Györffy, W.; Kats, D.; Korona, T.; Lindh, R.; et al. MOLPRO, 2021.1, A Package of Ab Initio Programs; Technologie-Transfer-Initiative GmbH an der Universität Stuttgart: Stuttgart, Germany, 2021. [Google Scholar]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural Population Analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Bent, H.A. Distribution of atomic s character in molecules and its chemical implications. J. Chem. Educ. 1960, 37, 616–624. [Google Scholar] [CrossRef]
- Bent, H.A. An appraisal of valence-bond structures and hybridization in compounds of the first-row elements. Chem. Rev. 1961, 61, 275–311. [Google Scholar] [CrossRef]
- Alabugin, I.V.; Bresch, S.; Manoharan, M. Hybridization trends for main group elements and the Bent’s rule beyond carbon: More than electronegativity. J. Phys. Chem. A 2014, 118, 3663–3677. [Google Scholar] [CrossRef]
- Eisenberg, D. The discovery of the α-helix and β-sheet, the principal structural features of proteins. Proc. Natl. Acad. Sci. USA 2003, 30, 11207–11210. [Google Scholar] [CrossRef] [Green Version]
- Hazra, M.K.; Chakraborty, T. Formamide tautomerization: Catalytic role of formic acid. J. Phys. Chem. A 2005, 109, 7621–7625. [Google Scholar] [CrossRef]
- Weinhold, F.; Glendening, E.D. NBO Program Manual; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 1996; p. B-82ff. Available online: https://nbo7.chem.wisc.edu/nboman.pdf (accessed on 2 July 2021).
- Jiao, Y.; Weinhold, F. NBO/NRT two-state theory of bond-shift spectral excitation. Molecules 2020, 25, 4052. [Google Scholar] [CrossRef]
- Coulson, C.A. The electronic structure of some polyenes and aromatic molecules. VII. Bonds of fractional order by the molecular orbital method. Proc. R. Soc. Lond. A 1939, 169, 413–428. [Google Scholar]
- Coulson, C.A. Bond lengths in conjugated molecules: The present position. Proc. R. Soc. Lond. A 1951, 207, 91–100. [Google Scholar]
- Mishra, P.C.; Rai, D.K. Bond order-bond length relationship in all-valence-electron molecular orbital theory. Mol. Phys. 1972, 23, 631–634. [Google Scholar] [CrossRef]
- Johnston, H.S.; Parr, C. Activation energies from bond energies. I. Hydrogen transfer reactions. J. Am. Chem. Soc. 1963, 85, 2544–2551. [Google Scholar] [CrossRef]
- Bent, H.A. Structural chemistry of donor-acceptor interactions. Chem. Rev. 1968, 68, 587–648. [Google Scholar] [CrossRef]
- Bürgi, H.; Dunitz, J.D. Fractional bonds: Relations among their lengths, strengths, and stretching force constants. J. Am. Chem. Soc. 1987, 109, 2924–2926. [Google Scholar] [CrossRef]
- Johnstone, R.A.W.; Loureiro, R.M.S.; Lurdes, M.; Cristiano, S.; Labat, G. Bond energy/bond order relationships for N-O linkages and a quantitative measure of ionicitiy: The role of nitro groups in hydrogen-bonding. ARKIVOC 2010, 2010, 142–169. [Google Scholar] [CrossRef]
- Badger, R.M. A relation between internuclear distances and bond force constants. J. Chem. Phys. 1934, 2, 128–131. [Google Scholar] [CrossRef] [Green Version]
- Boyer, M.A.; Marsalek, O.; Heindel, J.P.; Markland, T.E.; McCoy, A.B.; Xantheas, S.S. Beyond Badger’s rule: The origins and generality of the structure-spectra relationship of aqueous hydrogen bonds. J. Phys. Chem. Lett. 2019, 10, 918–924. [Google Scholar] [CrossRef]
- Gründemann, S.; Limbach, H.-H.; Buntkowsky, G.; Sabo-Etienne, S.; Chaudret, B. Distance and scalar HH-coupling correlations in transition metal dihydrides and dihydrogen complexes. J. Phys. Chem. A 1999, 103, 4752–4754. [Google Scholar] [CrossRef]
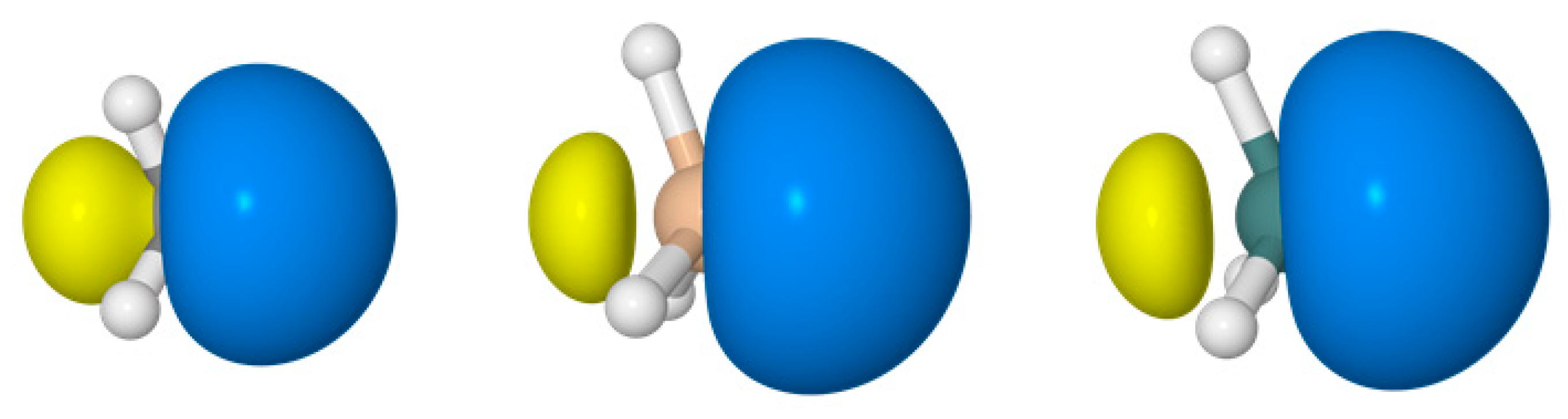


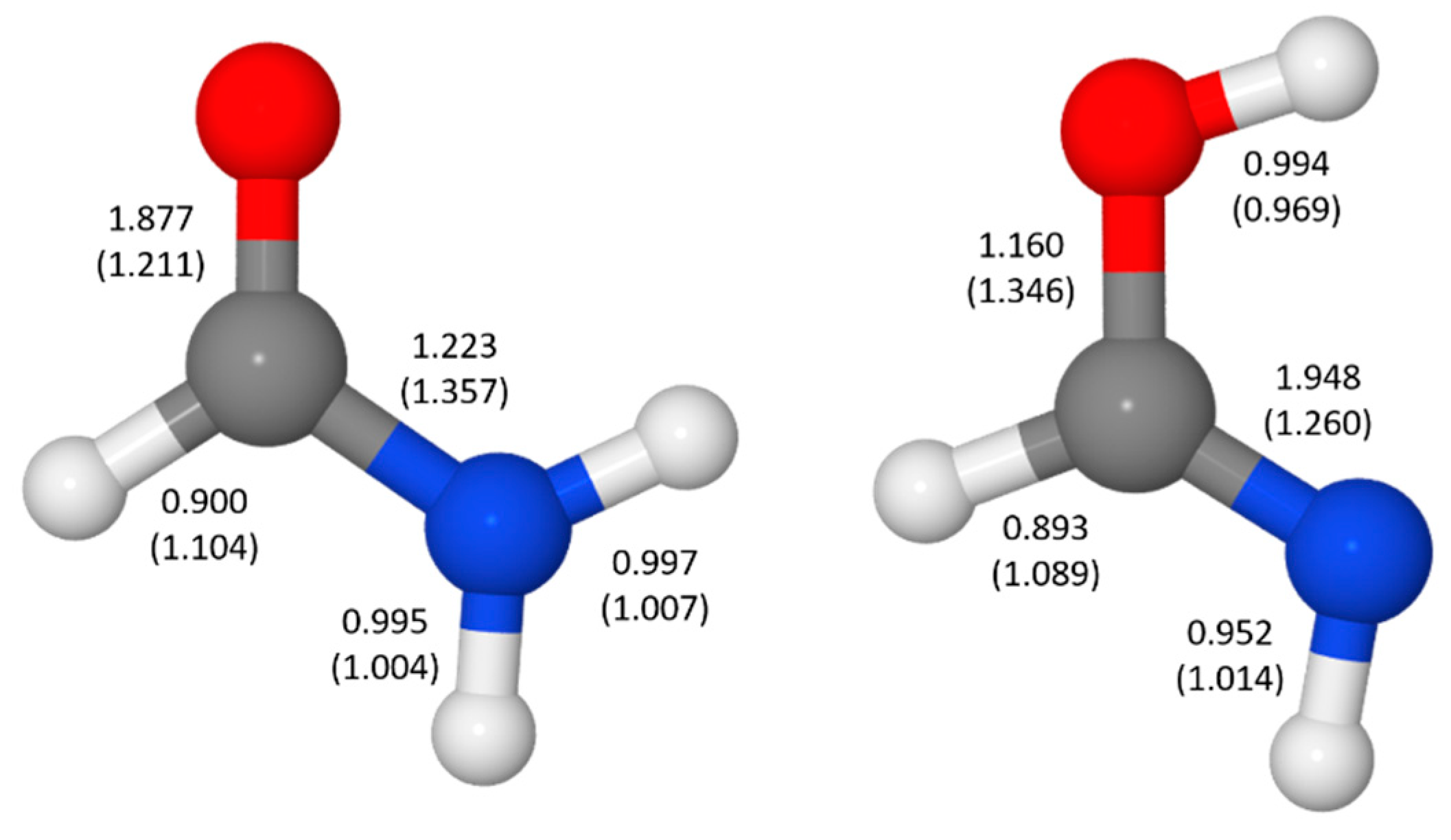
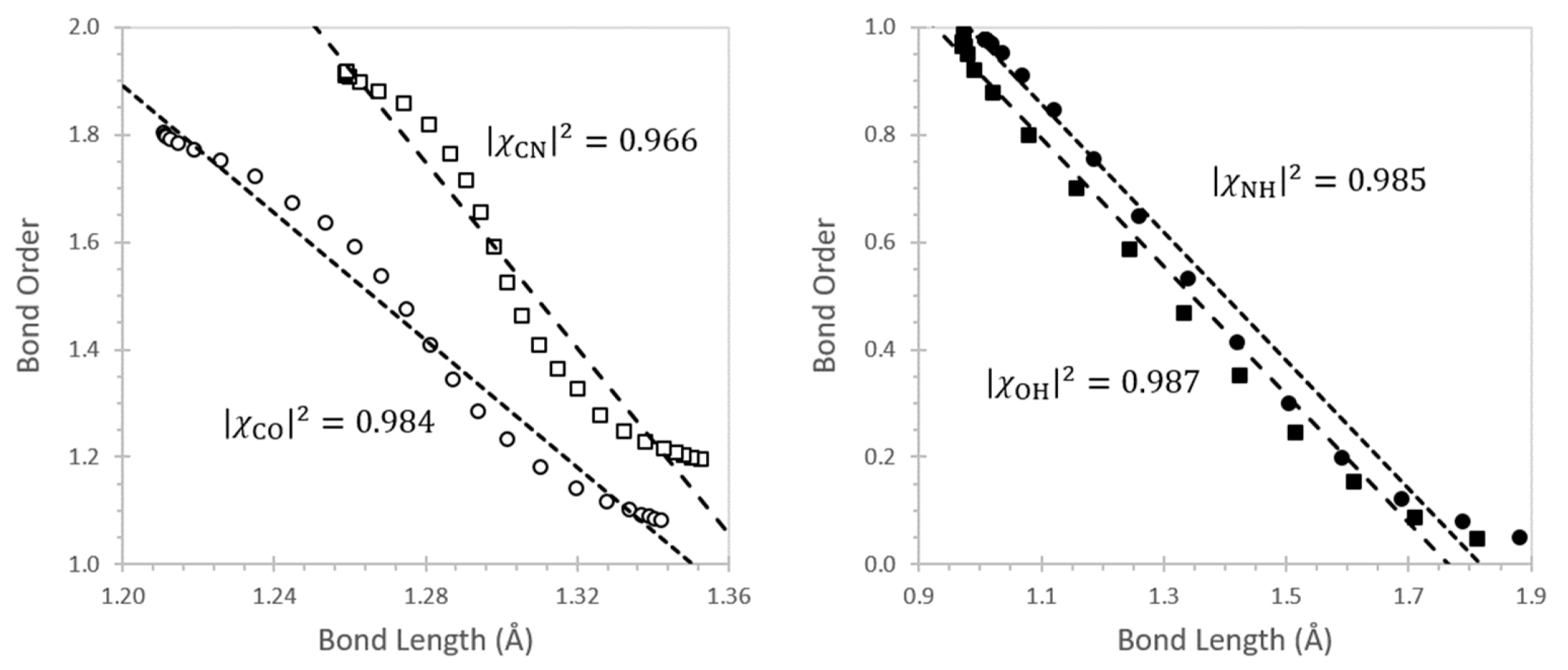
| RHF | B3LYP | SCGVB | CAS | MP2 | CCSD | |
|---|---|---|---|---|---|---|
| BH3 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 |
| CH4 | 2.99 | 3.00 | 2.99 | 2.99 | 2.99 | 2.99 |
| NH3 | 2.89 | 2.90 | 2.96 | 2.99 | 2.93 | 2.94 |
| H2O | 3.24 | 3.31 | 3.42 | 3.47 | 3.45 | 3.44 |
| HF | 3.69 | 3.86 | 4.05 | 4.09 | 4.10 | 4.08 |
| AlH3 | 1.97 | 1.98 | 1.98 | 1.98 | 1.98 | 1.98 |
| SiH4 | 2.96 | 2.98 | 2.96 | 2.96 | 2.96 | 2.96 |
| PH3 | 5.38 | 5.72 | 5.49 | 5.60 | 5.57 | 5.67 |
| H2S | 5.55 | 5.83 | 5.88 | 6.00 | 5.83 | 5.93 |
| HCl | 5.79 | 5.93 | 6.46 | 6.55 | 6.17 | 6.24 |
| GaH3 | 1.99 | 2.00 | 1.99 | 1.99 | 1.99 | 1.99 |
| GeH4 | 2.99 | 3.00 | 2.99 | 2.99 | 2.99 | 2.99 |
| AsH3 | 6.14 | 6.91 | 6.37 | 6.47 | 6.54 | 6.64 |
| H2Se | 6.43 | 7.11 | 7.00 | 7.05 | 6.95 | 7.06 |
| HBr | 6.82 | 7.27 | 7.81 | 7.80 | 7.43 | 7.52 |
| ∠HXH | α | β | |
|---|---|---|---|
| NH3 | 106.8 | 110.0 | 107.9 |
| H2O | 104.1 | 106.8 | 104.7 |
| PH3 | 93.6 | 100.3 | 98.0 |
| H2S | 92.2 | 99.9 | 95.6 |
| AsH3 | 92.5 | 98.8 | 98.8 |
| H2Se | 91.1 | 98.3 | 96.8 |
| # | Structure | Weight (%) | Donor–Acceptor Interaction b | |
|---|---|---|---|---|
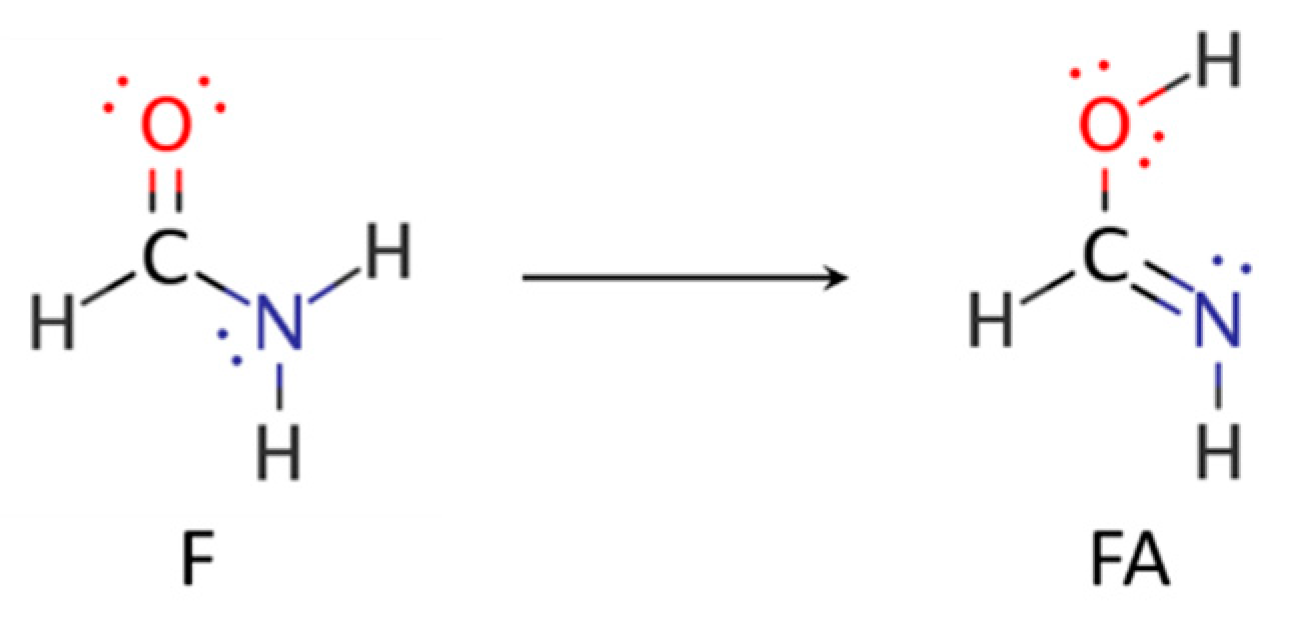
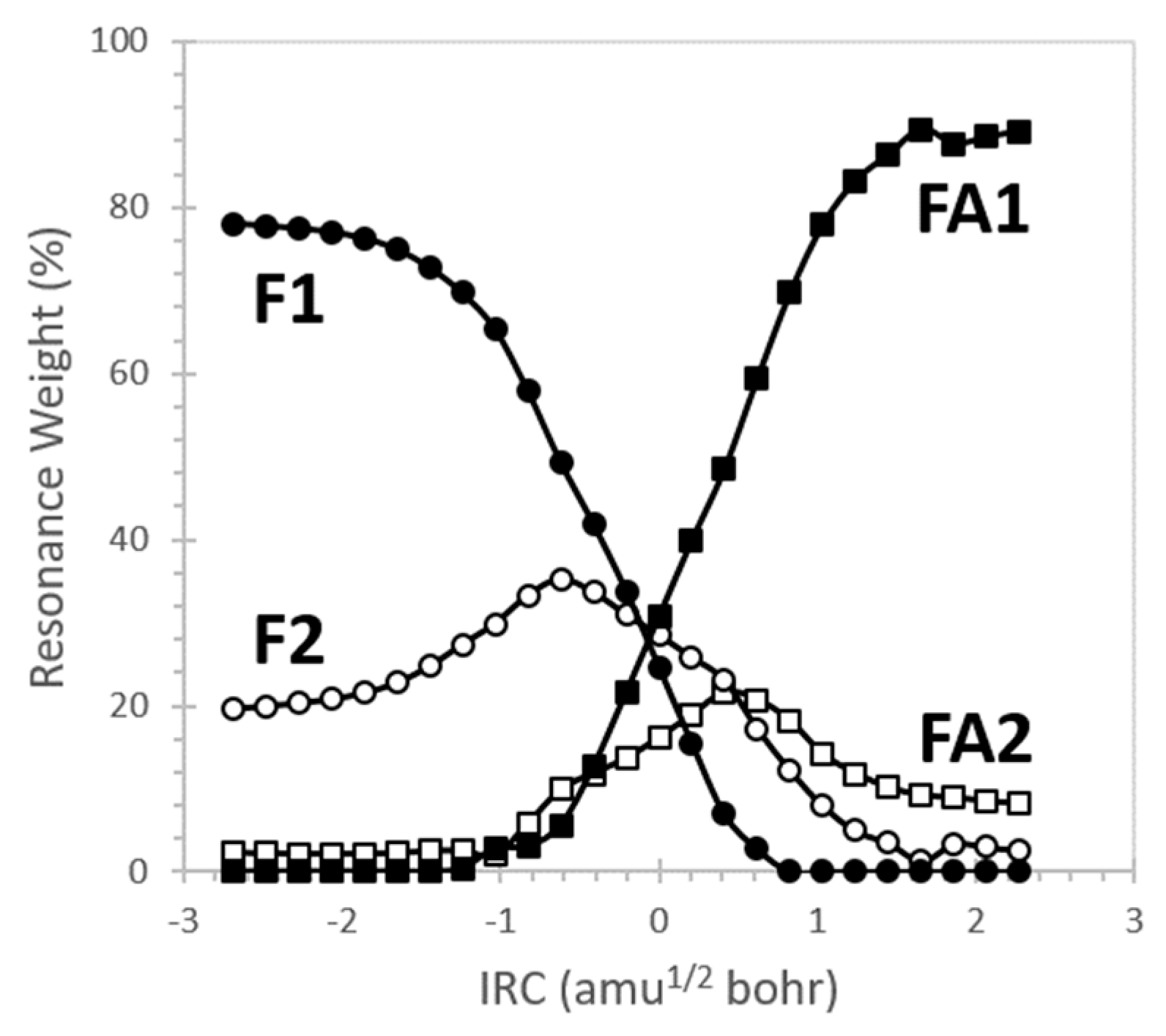
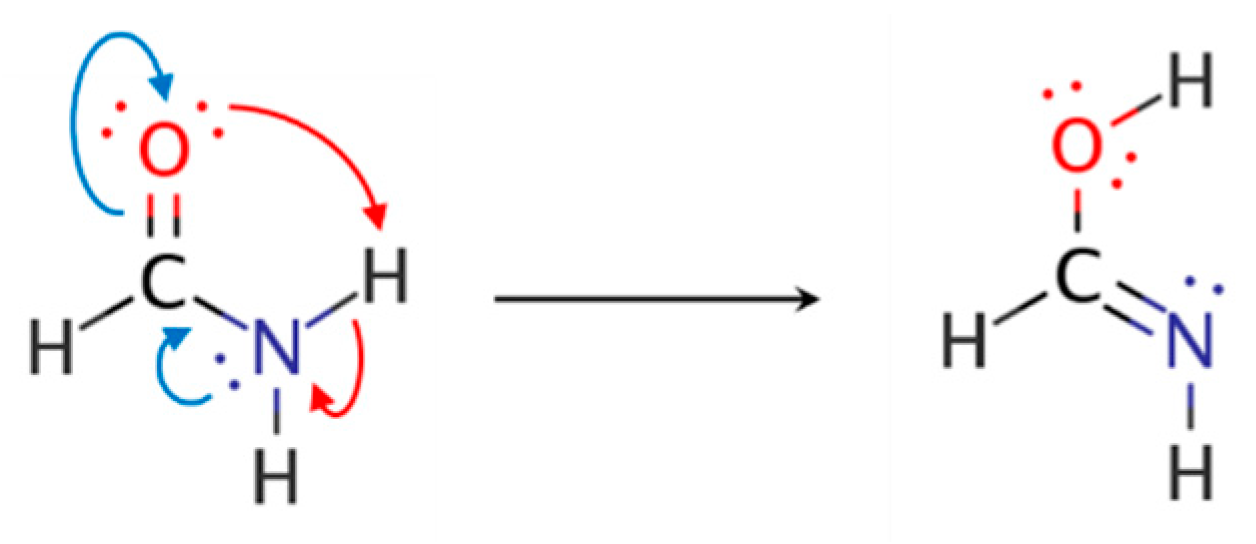
| F1 | 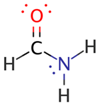 | 43.8 | ||
| F2 | 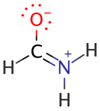 | 33.7 | nN→πCO * (61.9) | 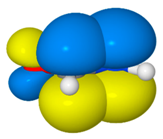 |
| F3 | 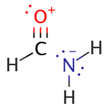 | 12.1 | nO→σCN * (26.2) | 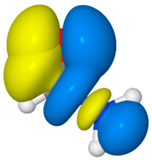 |
| F4 |  | 9.7 | nO→σCH * (22.8) | 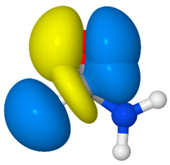 |
| # | Structure | Weight (%) | Donor–Acceptor Interaction b | |
|---|---|---|---|---|
| FA1 | 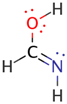 | 64.2 | ||
| FA2 | 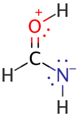 | 20.2 | nO→πCN * (40.4) | 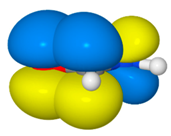 |
| FA3 | 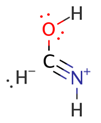 | 10.1 | nN→σCH * (10.7) | 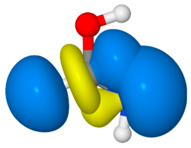 |
| FA4 |  | 3.7 | σNH→σCO * (10.6) | 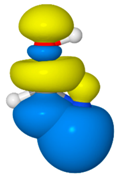 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Glendening, E.D.; Weinhold, F. Pauling’s Conceptions of Hybridization and Resonance in Modern Quantum Chemistry. Molecules 2021, 26, 4110. https://doi.org/10.3390/molecules26144110
Glendening ED, Weinhold F. Pauling’s Conceptions of Hybridization and Resonance in Modern Quantum Chemistry. Molecules. 2021; 26(14):4110. https://doi.org/10.3390/molecules26144110
Chicago/Turabian StyleGlendening, Eric D., and Frank Weinhold. 2021. "Pauling’s Conceptions of Hybridization and Resonance in Modern Quantum Chemistry" Molecules 26, no. 14: 4110. https://doi.org/10.3390/molecules26144110
APA StyleGlendening, E. D., & Weinhold, F. (2021). Pauling’s Conceptions of Hybridization and Resonance in Modern Quantum Chemistry. Molecules, 26(14), 4110. https://doi.org/10.3390/molecules26144110







