Shape and Structure Formation of Mixed Nonionic–Anionic Surfactant Micelles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Small-Angle Neutron Scattering (SANS)
2.3. Data Analysis
3. Results
3.1. Pure Micelles
3.1.1. Pure Nonionic Micelles
3.1.2. Pure SDS Micelles
3.2. Mixed Nonionic–Anionic Micelles
3.2.1. Mixed Micelles in Dilute Conditions
3.2.2. Concentrated Mixed Micelles
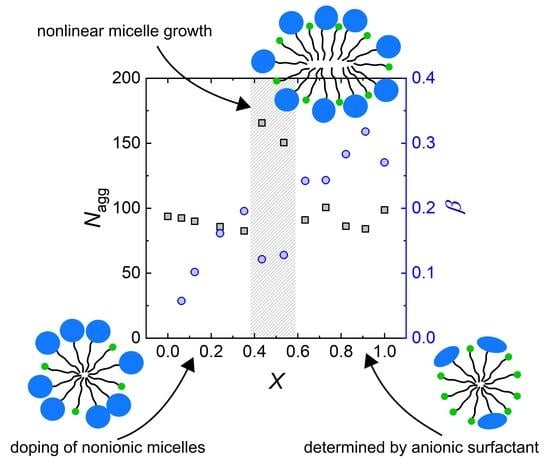
3.2.3. Non Ideal Behaviour of Mixed Nonionic–Anionic Micelles
4. Discussion
4.1. Micelle Formation
4.1.1. Nonionic Surfactants with Branched or Linear Headgroups
4.1.2. On the Nature of Mixed Micelles with Nonionic (PEO) and Anionic (Sulfate) Headgroups
4.2. Intermicellar Structuring at Various Volume Fractions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
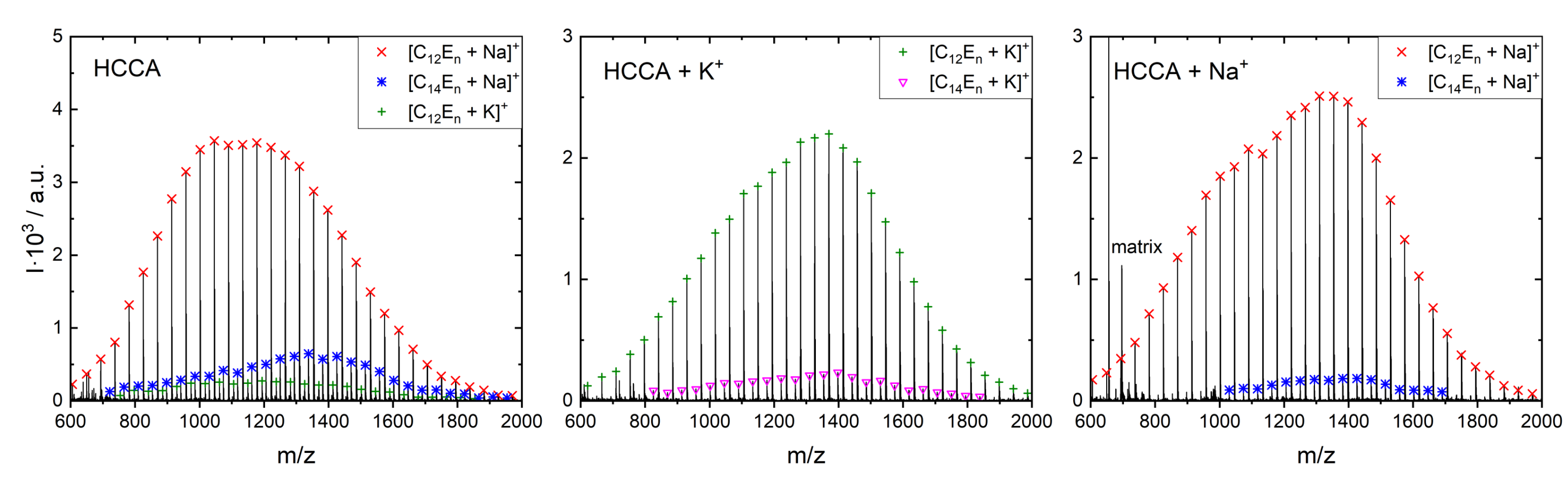
Appendix A. Mass Spectrometry of Nonionic Surfactants


| Matrix | PME:IPE | : | w + x + y + z | p + m |
|---|---|---|---|---|
| HCCA | 4.5:1 | 3.3:1 | 25.7 ± 0.1 | 10.8 ± 0.1 |
| HCCA + | 2.0:1 | 4.7:1 | 25.6 ± 0.1 | 10.7 ± 0.1 |
| HCCA + | 5.7:1 | 6.1:1 | 25.6 ± 0.1 | 10.7 ± 0.1 |
| Matrix | : | EO Groups |
|---|---|---|
| HCCA | 8:1 | 21.6 ± 0.1 |
| HCCA + | 42:1 | 23.6 ± 0.1 |
| HCCA + | 14:1 | 24.2 ± 0.1 |
Appendix B. Surfactant Properties
| Chemical/Formula | M | Density | ||
|---|---|---|---|---|
| mM | g mol | g cm | nm | |
| SDS/ | 8.3 [83] | 288.4 | 1.01 | 0.410 |
| Tween20/ | 0.059 [41] | 1128 | 1.150 | 1.805 |
| BrijL23/ | 0.09 [9] | 1198 | 1.115 | 1.809 |
| Group | ||
|---|---|---|
| nm | 10 Å | |
| 0.351 | −0.39 | |
| 0.324 | −0.39 | |
| 0.0616 | 0.67 | |
| 0.0301 | 6.34 |
References
- Tadros, T.F. Applied Surfactants: Principles and Applications, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- Kronberg, B. Surfactant mixtures. Curr. Opin. Colloid Interface Sci. 1997, 2, 456–463. [Google Scholar] [CrossRef]
- Calandra, P.; Caschera, D.; Turco Liveri, V.; Lombardo, D. How self-assembly of amphiphilic molecules can generate complexity in the nanoscale. Colloids Surf. A Physicochem. Eng. Asp. 2015, 484, 164–183. [Google Scholar] [CrossRef]
- Rosen, M.J.; Kunjappu, J.T. Surfactants and Interfacial Phenomena, 4th ed.; Engineering Professional Collection; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Calandra, P.; Nicotera, I.; Rossi, C.O.; Liveri, V.T. Dynamical properties of self-assembled surfactant-based mixtures: Triggering of one-dimensional anomalous diffusion in bis(2-ethylhexyl)phosphoric acid/n-octylamine systems. Langmuir 2013, 29, 14848–14854. [Google Scholar] [CrossRef]
- Luengo, G.S.; Fameau, A.L.; Léonforte, F.; Greaves, A.J. Surface science of cosmetic substrates, cleansing actives and formulations. Adv. Colloid Interface Sci. 2021, 290, 102383. [Google Scholar] [CrossRef]
- Myers, D. Surfactant Science and Technology, 3rd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Haque, M.E.; Das, A.R.; Rakshit, A.K.; Moulik, S.P. Properties of Mixed Micelles of Binary Surfactant Combinations. Langmuir 1996, 12, 4084–4089. [Google Scholar] [CrossRef]
- Sharma, K.S.; Patil, S.R.; Rakshit, A.K.; Glenn, K.; Doiron, M.; Palepu, R.M.; Hassan, P.A. Self-Aggregation of a Cationic–Nonionic Surfactant Mixture in Aqueous Media: Tensiometric, Conductometric, Density, Light Scattering, Potentiometric, and Fluorometric Studies. J. Phys. Chem. B 2004, 108, 12804–12812. [Google Scholar] [CrossRef]
- Funasaki, N.; Hada, S. Surface tension of aqueous solutions of surfactant mixtures. The composition of mixed micelles. J. Phys. Chem. 1979, 83, 2471–2475. [Google Scholar] [CrossRef]
- Akbaş, H.; Işcan, M.; Sidim, T. Composition of mixed anionic/nonionic surfactant micelles. J. Surfactants Deterg. 2000, 3, 77–80. [Google Scholar] [CrossRef]
- Islam, M.N.; Kato, T. Effect of temperature on the surface phase behavior and micelle formation of a mixed system of nonionic/anionic surfactants. J. Colloid Interface Sci. 2005, 282, 142–148. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Moulik, S.P. Interfacial and Micellization Behaviors of Binary and Ternary Mixtures of Amphiphiles (Tween-20, Brij-35, and Sodium Dodecyl Sulfate) in Aqueous Medium. J. Colloid Interface Sci. 1998, 208, 357–366. [Google Scholar] [CrossRef] [PubMed]
- Muñoz, M.; Rodríguez, A.; Graciani, M.D.M.; Moyá, M.L. Conductometric, surface tension, and kinetic studies in mixed SDS-Tween 20 and SDS-SB3-12 micellar solutions. Langmuir ACS J. Surf. Colloids 2004, 20, 10858–10867. [Google Scholar] [CrossRef] [PubMed]
- Moisés de Oliveira, H.P.; Gehlen, M.H. Characterization of Mixed Micelles of Sodium Dodecyl Sulfate and Tetraoxyethylene Dodecyl Ether in Aqueous Solution. Langmuir 2002, 18, 3792–3796. [Google Scholar] [CrossRef]
- Feitosa, E.; Brown, W. Mixed Micelles of the Anionic Surfactant Sodium Dodecyl Sulfate and the Nonionic Pentaethylene Glycol Mono-n-dodecyl Ether in Solution. Langmuir 1998, 14, 4460–4465. [Google Scholar] [CrossRef]
- Shiloach, A.; Blankschtein, D. Measurement and Prediction of Ionic/Nonionic Mixed Micelle Formation and Growth. Langmuir 1998, 14, 7166–7182. [Google Scholar] [CrossRef]
- Joshi, T.; Mata, J.; Bahadur, P. Micellization and interaction of anionic and nonionic mixed surfactant systems in water. Colloids Surf. A Physicochem. Eng. Asp. 2005, 260, 209–215. [Google Scholar] [CrossRef]
- Guering, P.; Nilsson, P.G.; Lindman, B. Mixed micelles of ionic and nonionic surfactants: Quasielastic light scattering and nmr self—Diffusion studies of C12E5-SDS micelles. J. Colloid Interface Sci. 1985, 105, 41–44. [Google Scholar] [CrossRef]
- Gao, H.C.; Zhao, S.; Mao, S.Z.; Yuan, H.Z.; Yu, J.Y.; Shen, L.F.; Du, Y.R. Mixed micelles of polyethylene glycol (23) lauryl ether with ionic surfactants studied by proton 1D and 2D NMR. J. Colloid Interface Sci. 2002, 249, 200–208. [Google Scholar] [CrossRef]
- Baglioni, P.; Dei, L.; Rivara-Minten, E.; Kevan, L. Mixed micelles of SDS/C12E6 and DTAC/C12E6 surfactants. J. Am. Chem. Soc. 1993, 115, 4286–4290. [Google Scholar] [CrossRef]
- Zhang, B.; Kirton, G.F.; Dubin, P.L. Compositional Heterogeneity in Anionic/Nonionic Mixed Micelles Observed by Frontal Analysis Continuous Capillary Electrophoresis. Langmuir 2002, 18, 4605–4609. [Google Scholar] [CrossRef]
- Vora, S.; George, A.; Desai, H.; Bahadur, P. Mixed micelles of some anionic-anionic, cationic-cationic, and ionic-nonionic surfactants in aqueous media. J. Surfactants Deterg. 1999, 2, 213–221. [Google Scholar] [CrossRef]
- Kralchevsky, P.A.; Danov, K.D.; Anachkov, S.E. Micellar solutions of ionic surfactants and their mixtures with nonionic surfactants: Theoretical modeling vs. Experiment. Colloid J. 2014, 76, 255–270. [Google Scholar] [CrossRef]
- Douglas, C.B.; Kaler, E.W. A Scattering Study of Mixed Micelles of Hexaethylene Glycol Mono-n-dodecyl Ether and Sodium Dodecylsulfonate in D2O. Langmuir 1994, 10, 1075–1083. [Google Scholar] [CrossRef]
- Penfold, J.; Staples, E.; Thompson, L.; Tucker, I.; Hines, J.; Thomas, R.K.; Lu, J.R.; Warren, N. Structure and Composition of Mixed Surfactant Micelles of Sodium Dodecyl Sulfate and Hexaethylene Glycol Monododecyl Ether and of Hexadecyltrimethylammonium Bromide and Hexaethylene Glycol Monododecyl Ether. J. Phys. Chem. B 1999, 103, 5204–5211. [Google Scholar] [CrossRef]
- Nettesheim, F.; Zipfel, J.; Lindner, P.; Richtering, W. Influence of sodium dodecyl sulfate on structure and rheology of aqueous solutions of the nonionic surfactant tetraethyleneglycol-monododecyl ether (C12E4). Colloids Surf. A Physicochem. Eng. Asp. 2001, 183–185, 563–574. [Google Scholar] [CrossRef]
- Penfold, J.; Staples, E.; Tucker, I. Neutron Small Angle Scattering Studies of Micellar Growth in Mixed Anionic-Nonionic Surfactants, Sodium Dodecyl Sulfate, SDS, and Hexaethylene Glycol Monododecyl Ether, C 12 E 6, in the Presence and Absence of Solubilized Alkane, Hexadecane. J. Phys. Chem. B 2002, 106, 8891–8897. [Google Scholar] [CrossRef]
- Griffiths, P.C.; Cheung, A.Y.F.; Farley, C.; Paul, A.; Heenan, R.K.; King, S.M.; Pettersson, E.; Stilbs, P.; Ranganathan, R. Small-Angle Neutron Scattering, Electron Paramagnetic Resonance, Electrophoretic NMR, and Time-Resolved Fluorescence Quenching Studies of Sodium Dodecyl Sulfate and Tetra(ethylene oxide) Dodecyl Ether Mixed Surfactant Micelles. J. Phys. Chem. B 2004, 108, 1351–1356. [Google Scholar] [CrossRef]
- Penfold, J.; Tucker, I.; Thomas, R.K.; Staples, E.; Schuermann, R. Structure of mixed anionic/nonionic surfactant micelles: Experimental observations relating to the role of headgroup electrostatic and steric effects and the effects of added electrolyte. J. Phys. Chem. B 2005, 109, 10760–10770. [Google Scholar] [CrossRef]
- Patel, T.; Ghosh, G.; Aswal, V.; Bahadur, P. Micellization of sodium dodecyl sulfate and polyoxyethylene dodecyl ethers in solution. Colloid Polym. Sci. 2009, 287, 1175–1181. [Google Scholar] [CrossRef]
- Lindner, P.; Schweins, R. The D11 Small-Angle Scattering Instrument: A New Benchmark for SANS. Neutron News 2010, 21, 15–18. [Google Scholar] [CrossRef]
- Kotlarchyk, M.; Chen, S.H. Analysis of small angle neutron scattering spectra from polydisperse interacting colloids. J. Chem. Phys. 1983, 79, 2461–2469. [Google Scholar] [CrossRef]
- Berr, S.S. Solvent isotope effects on alkytrimethylammonium bromide micelles as a function of alkyl chain length. J. Phys. Chem. 1987, 91, 4760–4765. [Google Scholar] [CrossRef]
- Hansen, J.P.; Hayter, J.B. A rescaled MSA structure factor for dilute charged colloidal dispersions. Mol. Phys. 1982, 46, 651–656. [Google Scholar] [CrossRef]
- Hayter, J.B.; Penfold, J. An analytic structure factor for macroion solutions. Mol. Phys. 1981, 42, 109–118. [Google Scholar] [CrossRef]
- Percus, J.K.; Yevick, G.J. Analysis of Classical Statistical Mechanics by Means of Collective Coordinates. Phys. Rev. 1958, 110, 1–13. [Google Scholar] [CrossRef]
- Barrat, J.L.; Hansen, J.P. Basic Concepts for Simple and Complex Liquids; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar] [CrossRef] [Green Version]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids, 3rd ed.; Elsevier/Academic Press: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Tanford, C. Micelle shape and size. J. Phys. Chem. 1972, 76, 3020–3024. [Google Scholar] [CrossRef]
- Helenius, A.; McCaslin, D.R.; Fries, E.; Tanford, C. Properties of detergents. Methods Enzymol. 1979, 56, 734–749. [Google Scholar] [CrossRef]
- Sasaki, T.; Hattori, M.; Sasaki, J.; Nukina, K. Studies of Aqueous Sodium Dodecyl Sulfate Solutions by Activity Measurements. Bull. Chem. Soc. Jpn. 1975, 48, 1397–1403. [Google Scholar] [CrossRef] [Green Version]
- Kale, K.M.; Cussler, E.L.; Evans, D.F. Characterization of micellar solutions using surfactant ion electrodes. J. Phys. Chem. 1980, 84, 593–598. [Google Scholar] [CrossRef]
- Buchner, R.; Baar, C.; Fernandez, P.; Schrödle, S.; Kunz, W. Dielectric spectroscopy of micelle hydration and dynamics in aqueous ionic surfactant solutions. J. Mol. Liq. 2005, 118, 179–187. [Google Scholar] [CrossRef]
- Prévost, S.; Gradzielski, M. SANS investigation of the microstructures in catanionic mixtures of SDS/DTAC and the effect of various added salts. J. Colloid Interface Sci. 2009, 337, 472–484. [Google Scholar] [CrossRef]
- Hayter, J.B.; Penfold, J. Self-consistent structural and dynamic study of concentrated micelle solutions. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1981, 77, 1851. [Google Scholar] [CrossRef]
- Bucci, S.; Fagotti, C.; Degiorgio, V.; Piazza, R. Small-angle neutron-scattering study of ionic-nonionic mixed micelles. Langmuir 1991, 7, 824–826. [Google Scholar] [CrossRef]
- Hassan, P.; Fritz, G.; Kaler, E.W. Small angle neutron scattering study of sodium dodecyl sulfate micellar growth driven by addition of a hydrotropic salt. J. Colloid Interface Sci. 2003, 257, 154–162. [Google Scholar] [CrossRef]
- Bergström, M.; Skov Pedersen, J. Structure of pure SDS and DTAB micelles in brine determined by small-angle neutron scattering (SANS). Phys. Chem. Chem. Phys. 1999, 1, 4437–4446. [Google Scholar] [CrossRef]
- Quina, F.H.; Nassar, P.M.; Bonilha, J.B.S.; Bales, B.L. Growth of Sodium Dodecyl Sulfate Micelles with Detergent Concentration. J. Phys. Chem. 1995, 99, 17028–17031. [Google Scholar] [CrossRef]
- Mahajan, R.K.; Chawla, J.; Vohra, K.K.; Aswal, V.K. Small angle neutron scattering study of structural aspects of nonionic surfactants (Tween 20 and Tween 80) in the presence of polyethylene glycols and triblock polymers. J. Appl. Polym. Sci. 2010, 36, 3038–3046. [Google Scholar] [CrossRef]
- Penfold, J.; Thomas, R.K.; Li, P.X.; Petkov, J.T.; Tucker, I.; Webster, J.R.P.; Terry, A.E. Adsorption at air-water and oil-water interfaces and self-assembly in aqueous solution of ethoxylated polysorbate nonionic surfactants. Langmuir 2015, 31, 3003–3011. [Google Scholar] [CrossRef]
- Nayem, J.; Zhang, Z.; Tomlinson, A.; Zarraga, I.E.; Wagner, N.J.; Liu, Y. Micellar morphology of Polysorbate 20 and 80 and their ester fractions in solution via Small Angle Neutron Scattering. J. Pharm. Sci. 2020, 109, 1498–1508. [Google Scholar] [CrossRef] [PubMed]
- Penfold, J.; Thomas, R.K.; Li, P.X.; Tucker, I.; Petkov, J.; Petkova, R.E. Nature of the Intermicellar Interactions in Ethoxylated Polysorbate Surfactants with High Degrees of Ethoxylation. Langmuir 2016, 32, 1319–1326. [Google Scholar] [CrossRef]
- Basheva, E.S.; Kralchevsky, P.A.; Danov, K.D.; Ananthapadmanabhan, K.P.; Lips, A. The colloid structural forces as a tool for particle characterization and control of dispersion stability. Phys. Chem. Chem. Phys. PCCP 2007, 9, 5183. [Google Scholar] [CrossRef]
- Phillies, G.D.J.; Hunt, R.H.; Strang, K.; Sushkin, N. Aggregation Number and Hydrodynamic Hydration Levels of Brij-35 Micelles from Optical Probe Studies. Langmuir 1995, 11, 3408–3416. [Google Scholar] [CrossRef]
- Preu, H.; Zradba, A.; Rast, S.; Kunz, W.; Hardy, E.H.; Zeidler, M.D. Small angle neutron scattering of D2O–Brij 35 and D2O–alcohol–Brij 35 solutions and their modelling using the Percus–Yevick integral equation. Phys. Chem. Chem. Phys. 1999, 1, 3321–3329. [Google Scholar] [CrossRef]
- Borbély, S. Aggregate Structure in Aqueous Solutions of Brij-35 Nonionic Surfactant Studied by Small-Angle Neutron Scattering. Langmuir 2000, 16, 5540–5545. [Google Scholar] [CrossRef]
- Tomšič, M.; Bešter-Rogač, M.; Jamnik, A.; Kunz, W.; Touraud, D.; Bergmann, A.; Glatter, O. Nonionic Surfactant Brij 35 in Water and in Various Simple Alcohols: Structural Investigations by Small-Angle X-ray Scattering and Dynamic Light Scattering. J. Phys. Chem. B 2004, 108, 7021–7032. [Google Scholar] [CrossRef]
- Tóth, G.; Madarász, A. Structure of BRIJ-35 nonionic surfactant in water: A reverse Monte Carlo study. Langmuir 2006, 22, 590–597. [Google Scholar] [CrossRef]
- Sterpone, F.; Pierleoni, C.; Briganti, G.; Marchit, M. Molecular dynamics study of temperature dehydration of a C12E6 spherical micelle. Langmuir 2004, 20, 4311–4314. [Google Scholar] [CrossRef]
- Sommer, C.; Pedersen, J.S.; Garamus, V.M. Structure and interactions of block copolymer micelles of Brij 700 studied by combining small-angle X-ray and neutron scattering. Langmuir 2005, 21, 2137–2149. [Google Scholar] [CrossRef]
- Cabane, B.; Duplessix, R. Decoration of semidilute polymer solutions with surfactant micelles. J. Phys. 1987, 48, 651–662. [Google Scholar] [CrossRef]
- Brown, W.; Fundin, J.; Miguel, M.d.G. Poly(ethylene oxide)-sodium dodecyl sulfate interactions studied using static and dynamic light scattering. Macromolecules 1992, 25, 7192–7198. [Google Scholar] [CrossRef] [Green Version]
- Rufier, C.; Collet, A.; Viguier, M.; Oberdisse, J.; Mora, S. SDS Interactions with Hydrophobically End-Capped Poly(ethylene oxide) Studied by 13 C NMR and SANS. Macromolecules 2009, 42, 5226–5235. [Google Scholar] [CrossRef]
- Fajalia, A.I.; Tsianou, M. Charging and uncharging a neutral polymer in solution: A small-angle neutron scattering investigation. J. Phys. Chem. B 2014, 118, 10725–10739. [Google Scholar] [CrossRef] [PubMed]
- Dey, J.; Sultana, N.; Kumar, S.; Aswal, V.K.; Choudhury, S.; Ismail, K. Controlling the aggregation of sodium dodecylsulphate in aqueous poly(ethylene glycol) solutions. RSC Adv. 2015, 5, 74744–74752. [Google Scholar] [CrossRef]
- Manning, G.S. Limiting Laws and Counterion Condensation in Polyelectrolyte Solutions I. Colligative Properties. J. Chem. Phys. 1969, 51, 924–933. [Google Scholar] [CrossRef]
- Treiner, C.; Khodja, A.; Fromon, M. Counterion condensation on mixed anionic/nonionic surfactant micelles: Bjerrum’s limiting condition. J. Colloid Interface Sci. 1989, 128, 416–421. [Google Scholar] [CrossRef]
- Cabane, B.; Duplessix, R. Organization of surfactant micelles adsorbed on a polymer molecule in water: A neutron scattering study. J. Phys. 1982, 43, 1529–1542. [Google Scholar] [CrossRef]
- Croce, V.; Cosgrove, T.; Dreiss, C.A.; Maitland, G.; Hughes, T. Mixed spherical and wormlike micelles: A contrast-matching study by small-angle neutron scattering. Langmuir 2004, 20, 9978–9982. [Google Scholar] [CrossRef]
- Spaar, A.; Salditt, T. Short Range Order of Hydrocarbon Chains in Fluid Phospholipid Bilayers Studied by X-Ray Diffraction from Highly Oriented Membranes. Biophys. J. 2003, 85, 1576–1584. [Google Scholar] [CrossRef] [Green Version]
- Üzüm, C.; Christau, S.; von Klitzing, R. Structuring of Polyelectrolyte (NaPSS) Solutions in Bulk and under Confinement as a Function of Concentration and Molecular Weight. Macromolecules 2011, 44, 7782–7791. [Google Scholar] [CrossRef]
- Zeng, Y.; Grandner, S.; Oliveira, C.L.P.; Thünemann, A.F.; Paris, O.; Pedersen, J.S.; Klapp, S.H.L.; von Klitzing, R. Effect of particle size and Debye length on order parameters of colloidal silica suspensions under confinement. Soft Matter 2011, 7, 10899. [Google Scholar] [CrossRef] [Green Version]
- Lindner, P.; Zemb, T. (Eds.) Neutrons, X-rays and Light: Scattering Methods Applied to Soft Condensed Matter, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Greene, D.G.; Ferraro, D.V.; Lenhoff, A.M.; Wagner, N.J. A critical examination of the decoupling approximation for small-angle scattering from hard ellipsoids of revolution. J. Appl. Crystallogr. 2016, 49, 1734–1739. [Google Scholar] [CrossRef]
- Arnim Cumme, G.; Blume, E.; Bublitz, R.; Hoppe, H.; Horn, A. Composition analysis of detergents of the polyoxyethylene type: Comparison of thin-layer chromatography, reversed-phase chromatography and matrix-assisted laser desorption/ionization mass spectrometry. J. Chromatogr. A 1997, 791, 245–253. [Google Scholar] [CrossRef]
- Ayorinde, F.O.; Gelain, S.V.; Johnson, J.H.; Wan, L.W. Analysis of some commercial polysorbate formulations using matrix-assisted laser desorption/ionization time-of-flight mass spectrometry. Rapid Commun. Mass Spectrom. 2000, 14, 2116–2124. [Google Scholar] [CrossRef]
- Frison-Norrie, S.; Sporns, P. Investigating the molecular heterogeneity of polysorbate emulsifiers by MALDI-TOF MS. J. Agric. Food Chem. 2001, 49, 3335–3340. [Google Scholar] [CrossRef] [PubMed]
- Raith, K.; Schmelzer, C.E.H.; Neubert, R.H.H. Towards a molecular characterization of pharmaceutical excipients: Mass spectrometric studies of ethoxylated surfactants. Int. J. Pharm. 2006, 319, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Hewitt, D.; Alvarez, M.; Robinson, K.; Ji, J.; Wang, Y.J.; Kao, Y.H.; Zhang, T. Mixed-mode and reversed-phase liquid chromatography–tandem mass spectrometry methodologies to study composition and base hydrolysis of polysorbate 20 and 80. J. Chromatogr. A 2011, 1218, 2138–2145. [Google Scholar] [CrossRef]
- Li, Y.; Hewitt, D.; Lentz, Y.K.; Ji, J.A.; Zhang, T.Y.; Zhang, K. Characterization and stability study of polysorbate 20 in therapeutic monoclonal antibody formulation by multidimensional ultrahigh-performance liquid chromatography-charged aerosol detection-mass spectrometry. Anal. Chem. 2014, 86, 5150–5157. [Google Scholar] [CrossRef] [PubMed]
- Danov, K.D.; Kralchevsky, P.A.; Ananthapadmanabhan, K.P. Micelle-monomer equilibria in solutions of ionic surfactants and in ionic-nonionic mixtures: A generalized phase separation model. Adv. Colloid Interface Sci. 2014, 206, 17–45. [Google Scholar] [CrossRef]
- Funasaki, N.; Hada, S.; Neya, S. Volumetric study of solubilization of hydrophobic liquids in nonionic micelles. J. Phys. Chem. 1984, 88, 1243–1248. [Google Scholar] [CrossRef]










| c | 10 | ||||||
|---|---|---|---|---|---|---|---|
| mM | nm | Å | nm | ||||
| Tween20 | 106 | 0.190 | 2.21 | 1.81 | 5.06 | 4.05 | 94 |
| 142 | 0.240 | 2.14 | 1.78 | 5.08 | 3.99 | 95 | |
| 213 | 0.333 | 1.93 | 1.72 | 5.10 | 3.85 | 92 | |
| 286 | 0.374 | 1.72 | 1.72 | 5.18 | 3.75 | 101 | |
| BrijL23 | 65.7 | 0.235 | 1.93 | 2.21 | 5.45 | 4.34 | 57 |
| 82.1 | 0.280 | 1.89 | 2.17 | 5.42 | 4.28 | 58 | |
| 123 | 0.374 | 1.77 | 2.09 | 5.38 | 4.14 | 59 | |
| 164 | 0.442 | 1.69 | 2.00 | 5.35 | 4.02 | 61 |
| c | |||||||
|---|---|---|---|---|---|---|---|
| mM | mM | nm | |||||
| SDS | 71.8 | 3.9 | 0.037 | 1.49 | 2.61 | 83 | 0.28 |
| 135 | 2.8 | 0.070 | 1.64 | 2.67 | 91 | 0.29 | |
| 180 | 1.6 | 0.090 | 1.72 | 2.71 | 99 | 0.27 | |
| 359 | 1.0 | 0.183 | 1.95 | 2.80 | 108 | 0.25 |
| X | c | 10 | ||||||
|---|---|---|---|---|---|---|---|---|
| mM | nm | Å | nm | |||||
| SDS/Tween20 | ||||||||
| 0.35 | 3.83 | 0.005 | 1.94 | 1.85 | 5.35 | 3.70 | 94 | 0.10 |
| 11.5 | 0.016 | 1.87 | 1.82 | 5.36 | 3.61 | 85 | 0.15 | |
| 38.3 | 0.053 | 1.88 | 1.74 | 5.40 | 3.63 | 88 | 0.18 | |
| 61.2 | 0.076 | 1.90 | 1.74 | 5.36 | 3.65 | 99 | 0.17 | |
| SDS/BrijL23 | ||||||||
| 0.32 | 4.22 | 0.012 | 1.89 | 2.28 | 5.78 | 4.39 | 77 | 0.12 |
| 12.7 | 0.036 | 1.80 | 2.20 | 5.71 | 4.28 | 69 | 0.17 | |
| 21.1 | 0.062 | 1.82 | 2.18 | 5.68 | 4.26 | 66 | 0.18 | |
| 42.2 | 0.128 | 1.77 | 2.18 | 5.64 | 4.24 | 63 | 0.20 |
| X | c | 10 | ||||||
|---|---|---|---|---|---|---|---|---|
| mM | nm | Å | nm | |||||
| 0.06 | 108 | 0.207 | 2.26 | 1.83 | 5.14 | 4.10 | 91 | 0.06 |
| 143 | 0.257 | 2.17 | 1.80 | 5.14 | 4.03 | 92 | 0.06 | |
| 216 | 0.343 | 2.09 | 1.77 | 5.21 | 3.96 | 98 | – | |
| 287 | 0.369 | 1.85 | 1.73 | 5.26 | 3.82 | 109 | – | |
| 0.12 | 109 | 0.215 | 2.21 | 1.85 | 5.22 | 4.10 | 88 | 0.11 |
| 146 | 0.270 | 2.17 | 1.82 | 5.21 | 4.05 | 90 | 0.10 | |
| 218 | 0.340 | 2.01 | 1.74 | 5.20 | 3.90 | 96 | 0.09 | |
| 291 | 0.390 | 1.85 | 1.67 | 5.19 | 3.76 | 100 | 0.08 | |
| 0.24 | 112 | 0.200 | 2.02 | 1.78 | 5.37 | 3.94 | 87 | 0.18 |
| 149 | 0.278 | 2.12 | 1.78 | 5.33 | 3.99 | 86 | 0.16 | |
| 224 | 0.352 | 1.99 | 1.71 | 5.30 | 3.86 | 93 | 0.13 | |
| 299 | 0.396 | 1.87 | 1.63 | 5.28 | 3.73 | 99 | 0.11 | |
| 0.35 | 115 | 0.202 | 1.92 | 1.71 | 5.44 | 3.83 | 81 | 0.21 |
| 153 | 0.268 | 1.96 | 1.71 | 5.47 | 3.85 | 82 | 0.20 | |
| 230 | 0.349 | 1.93 | 1.65 | 5.44 | 3.77 | 89 | 0.16 | |
| 306 | 0.395 | 1.83 | 1.56 | 5.37 | 3.64 | 94 | 0.13 |
| X | c | 10 | ||||||
|---|---|---|---|---|---|---|---|---|
| mM | nm | Å | nm | |||||
| 0.05 | 66.0 | 0.238 | 2.06 | 2.25 | 5.50 | 4.44 | 61 | – |
| 82.5 | 0.280 | 1.98 | 2.20 | 5.47 | 4.36 | 61 | – | |
| 124 | 0.372 | 1.87 | 2.09 | 5.40 | 4.19 | 62 | – | |
| 168 | 0.437 | 1.73 | 2.01 | 5.37 | 4.05 | 64 | – | |
| 0.11 | 66.3 | 0.223 | 1.99 | 2.27 | 5.51 | 4.43 | 65 | 0.08 |
| 82.9 | 0.272 | 1.99 | 2.24 | 5.50 | 4.40 | 65 | 0.07 | |
| 124 | 0.381 | 1.96 | 2.11 | 5.46 | 4.25 | 63 | – | |
| 165 | 0.436 | 1.82 | 2.01 | 5.38 | 4.09 | 66 | – | |
| 0.21 | 66.9 | 0.219 | 1.90 | 2.28 | 5.58 | 4.40 | 65 | 0.15 |
| 83.6 | 0.275 | 1.97 | 2.24 | 5.56 | 4.39 | 65 | 0.13 | |
| 125 | 0.372 | 2.02 | 2.15 | 5.56 | 4.32 | 69 | – | |
| 167 | 0.429 | 1.90 | 2.02 | 5.47 | 4.13 | 69 | – | |
| 0.32 | 67.5 | 0.222 | 1.79 | 2.26 | 5.64 | 4.32 | 62 | 0.19 |
| 84.4 | 0.268 | 1.85 | 2.22 | 5.66 | 4.32 | 64 | 0.17 | |
| 127 | 0.360 | 1.93 | 2.09 | 5.61 | 4.23 | 67 | 0.11 | |
| 169 | 0.416 | 1.89 | 2.00 | 5.57 | 4.11 | 71 | – |
| X | c | 10 | ||||||
|---|---|---|---|---|---|---|---|---|
| mM | nm | Å | nm | |||||
| 0.00 | 142 | 0.240 | 2.14 | 1.78 | 5.08 | 3.99 | 95 | – |
| 0.06 | 143 | 0.257 | 2.17 | 1.80 | 5.14 | 4.03 | 92 | 0.06 |
| 0.12 | 146 | 0.270 | 2.17 | 1.82 | 5.21 | 4.05 | 90 | 0.10 |
| 0.24 | 149 | 0.278 | 2.12 | 1.78 | 5.33 | 3.99 | 86 | 0.16 |
| 0.35 | 153 | 0.268 | 1.96 | 1.71 | 5.47 | 3.85 | 82 | 0.20 |
| 0.43 | 174 | 0.231 | 3.15 | 1.83 | 5.67 | 4.43 | 166 | 0.12 |
| 0.54 | 177 | 0.215 | 2.89 | 1.67 | 5.77 | 4.17 | 150 | 0.13 |
| 0.64 | 179 | 0.150 | 1.73 | 1.08 | 5.33 | 3.12 | 91 | 0.24 |
| 0.73 | 182 | 0.104 | 1.77 | 0.80 | 5.15 | 2.84 | 100 | 0.24 |
| 0.82 | 184 | 0.111 | 1.57 | 0.78 | 5.33 | 2.74 | 86 | 0.28 |
| 0.91 | 187 | 0.096 | 1.50 | 0.65 | 5.29 | 2.58 | 84 | 0.32 |
| 1.00 | 180 | 0.090 | 1.72 | 0.69 * | 6.34 * | 2.71 | 99 | 0.27 |
| S(q) | 10 | ||||||
|---|---|---|---|---|---|---|---|
| nm | Å | nm | |||||
| RMSA | 0.360 | 1.93 | 2.09 | 5.61 | 4.23 | 67 | 0.11 |
| HS-PY | 0.371 | 2.01 | 2.14 | 5.67 | 4.30 | 68 | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ludwig, M.; Geisler, R.; Prévost, S.; von Klitzing, R. Shape and Structure Formation of Mixed Nonionic–Anionic Surfactant Micelles. Molecules 2021, 26, 4136. https://doi.org/10.3390/molecules26144136
Ludwig M, Geisler R, Prévost S, von Klitzing R. Shape and Structure Formation of Mixed Nonionic–Anionic Surfactant Micelles. Molecules. 2021; 26(14):4136. https://doi.org/10.3390/molecules26144136
Chicago/Turabian StyleLudwig, Michael, Ramsia Geisler, Sylvain Prévost, and Regine von Klitzing. 2021. "Shape and Structure Formation of Mixed Nonionic–Anionic Surfactant Micelles" Molecules 26, no. 14: 4136. https://doi.org/10.3390/molecules26144136
APA StyleLudwig, M., Geisler, R., Prévost, S., & von Klitzing, R. (2021). Shape and Structure Formation of Mixed Nonionic–Anionic Surfactant Micelles. Molecules, 26(14), 4136. https://doi.org/10.3390/molecules26144136