Large Amplitude Motions of Pyruvic Acid (CH3-CO-COOH)
Abstract
1. Introduction
2. Results
2.1. Electronic Structure Calculations
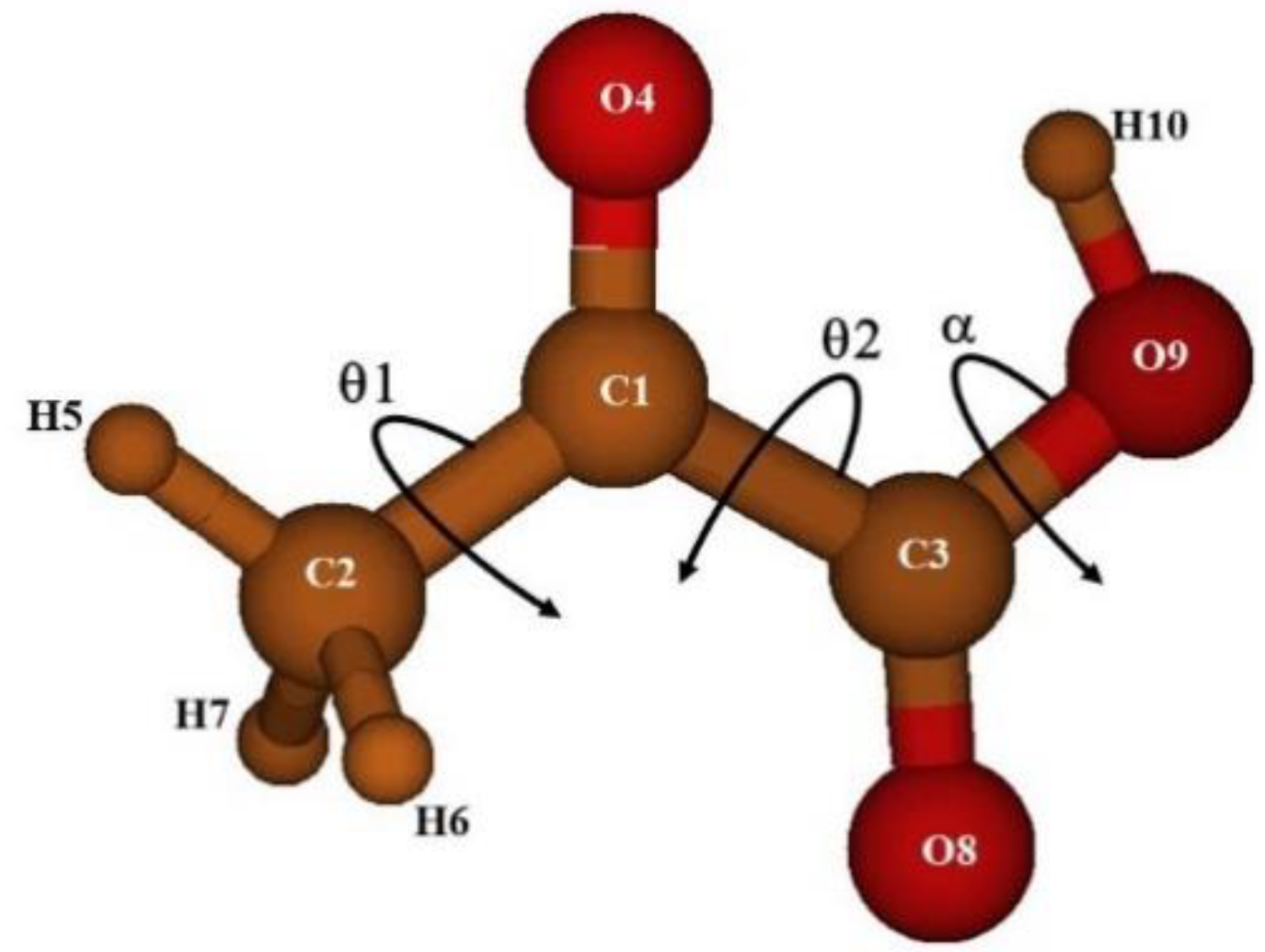
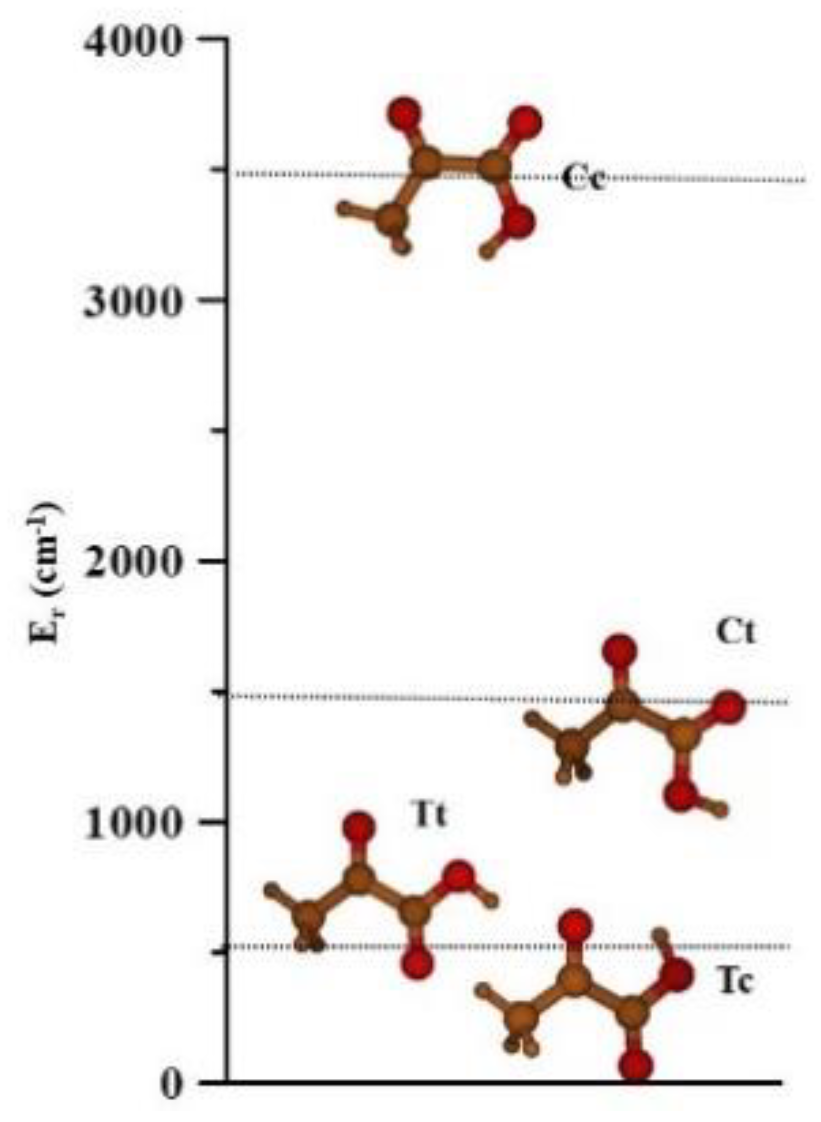
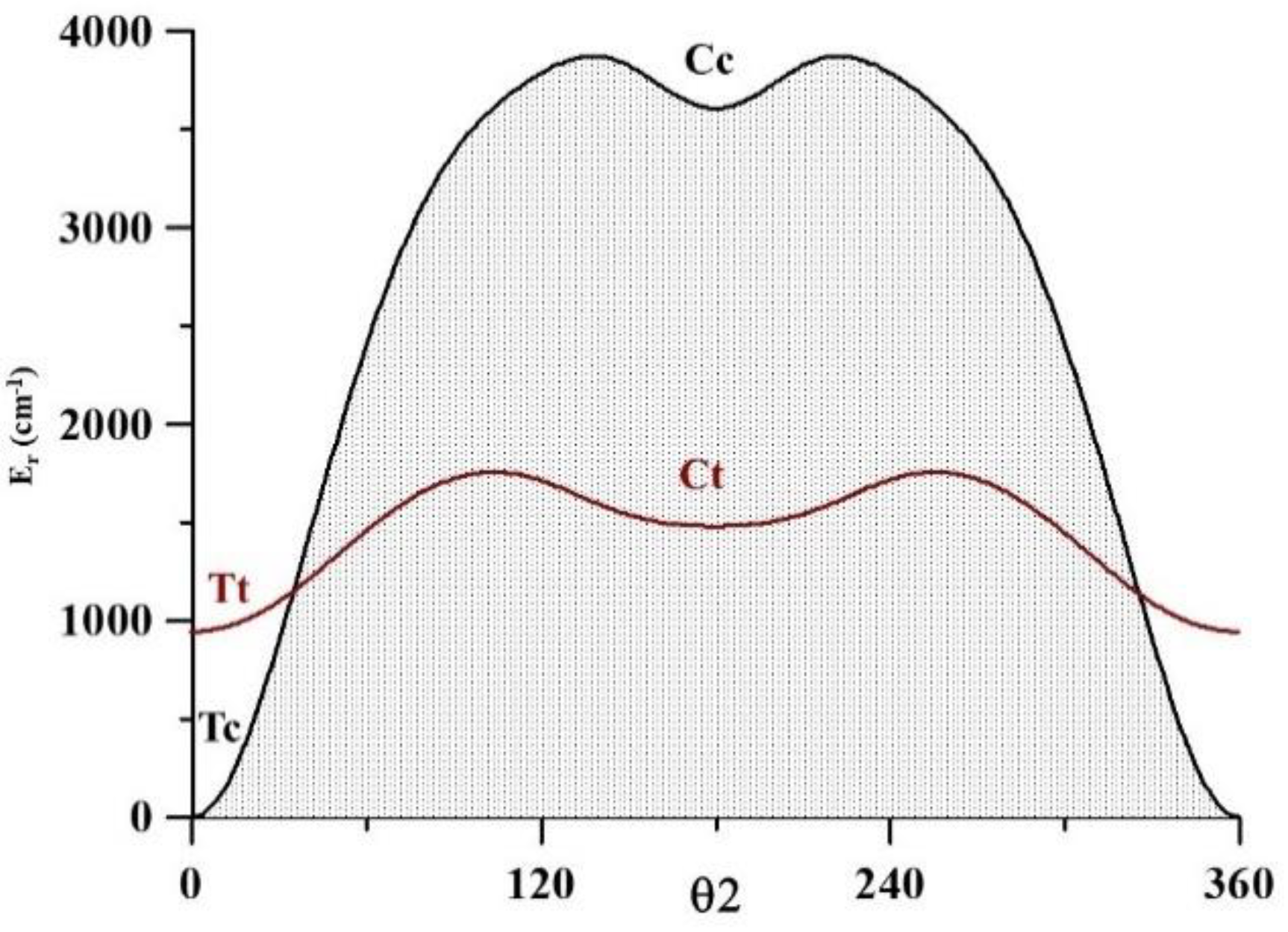
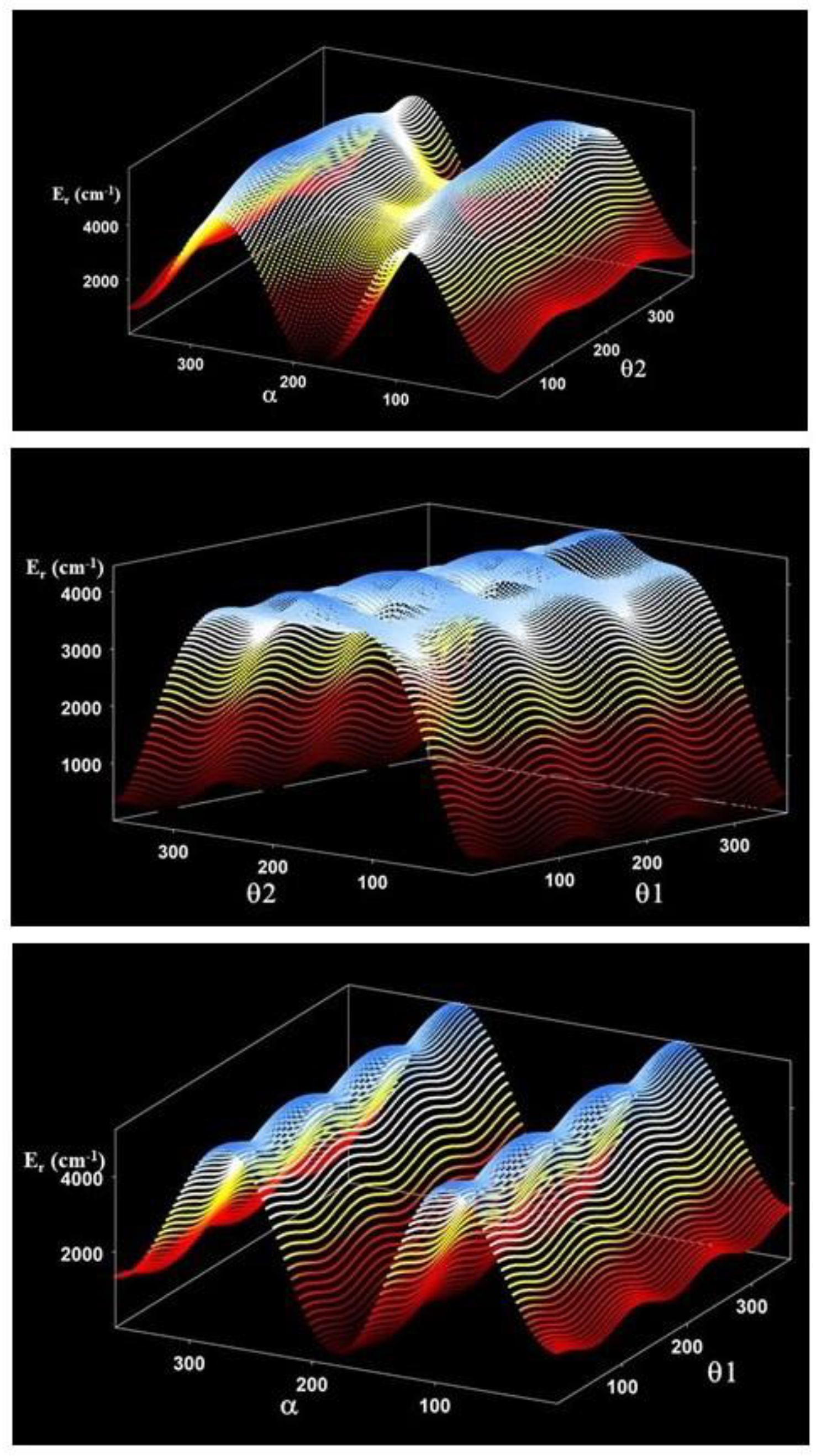
2.2. The Four Conformers of Pyruvic Acid
θ2 = O8C2C1C3 + O9C2C1C3 − 180·
α = H10O9C3O8
2.3. Ground Vibrational State: Rotational and Centrifugal Distortion Constants
+ ∆Bivib (MP2/AVTZ); i = a;.b;.c
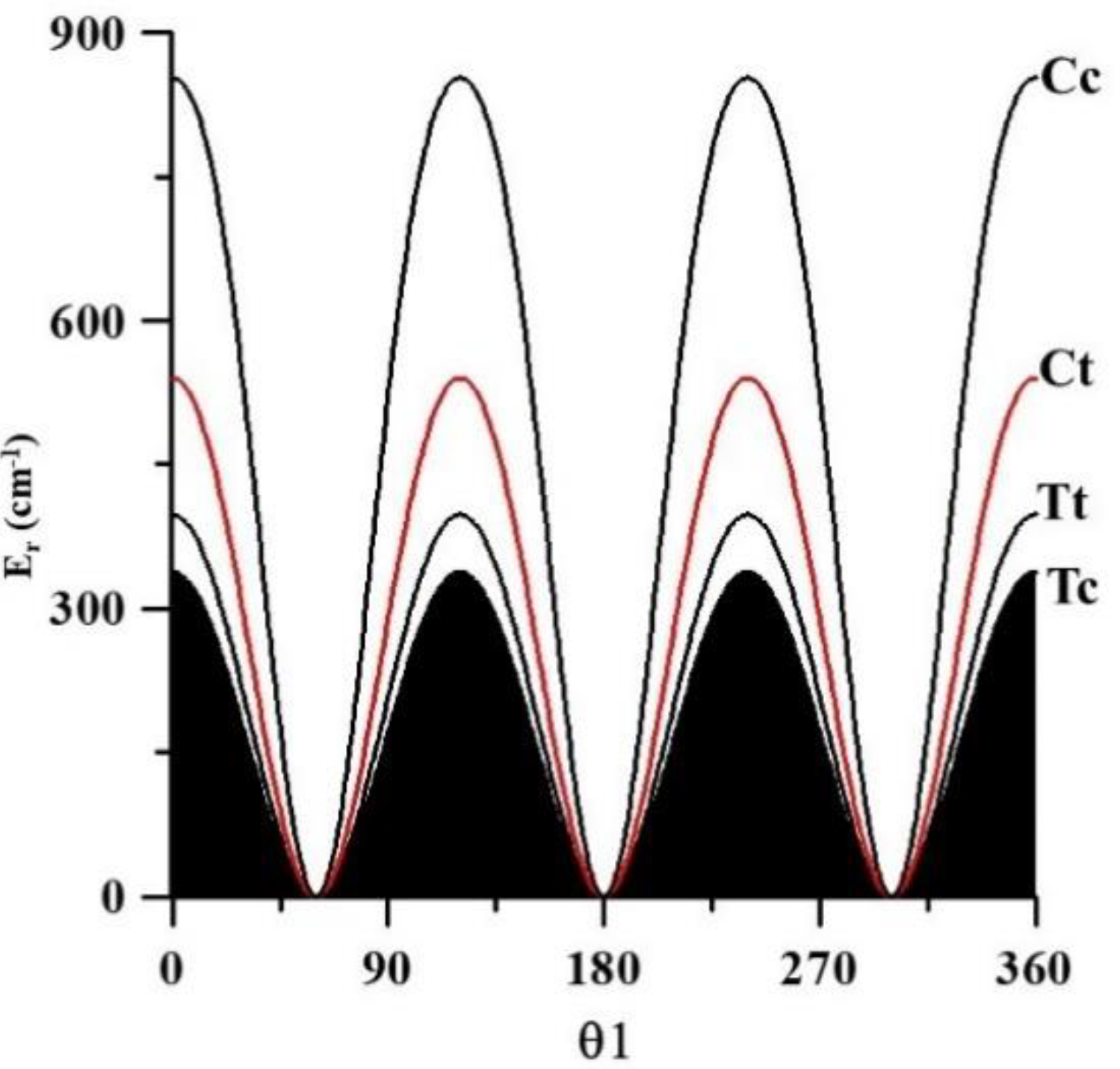
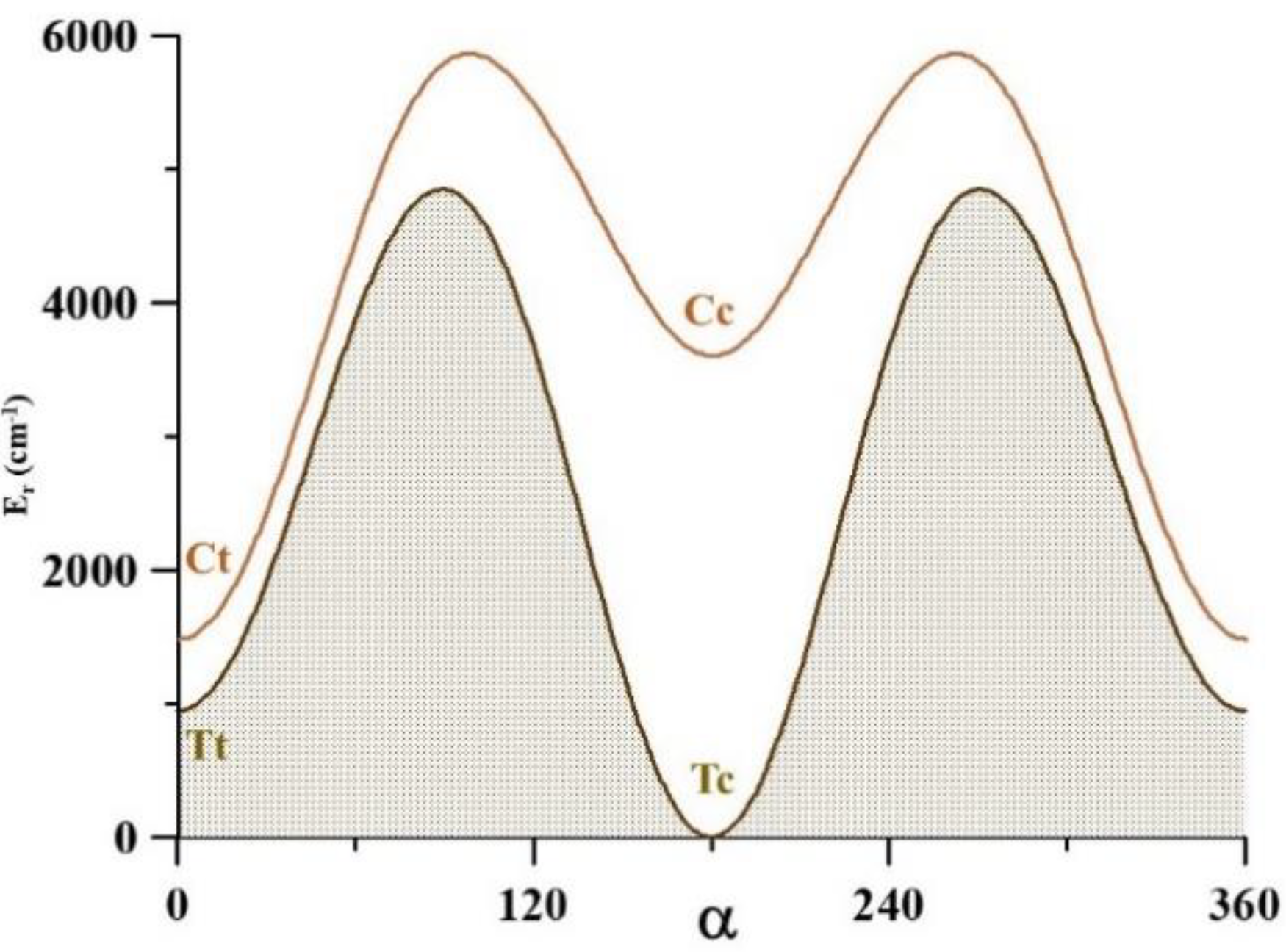
2.4. The Far Infrared Region
O8C2C1C3 = 0, 30, 60, …, 150, 180°
H10O9C3O8 = −180, −150,…, 0…, 150, 180°
3. Discussion
4. Materials and Methods
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Yu, S. Role of organic acids (formic, acetic, pyruvic and oxalic) in the formation of cloud condensation nuclei (CCN): A review. Atmos. Res. 2000, 53, 185–217. [Google Scholar] [CrossRef]
- Mellouki, A.; Wallington, T.J.; Chen, J. Atmospheric chemistry of oxygenated volatile organic compounds: Impacts on air quality and climate. Chem. Rev. 2015, 115, 3984–4014. [Google Scholar] [CrossRef]
- Nozière, B.; Kalberer, M.; Claeys, M. The molecular identification of organic compounds in the atmosphere: State of the art and challenges. Chem. Rev. 2015, 115, 3919–3983. [Google Scholar] [CrossRef]
- Reed Harris, A.E.; Pajunoja, A.; Cazaunau, M.; Gratien, A.; Pangui, E.; AMonod, A.; Griffith, E.C.; Virtanen, A.; Doussin, J.-F.; Vaida, V. Multiphase photochemistry of pyruvic acid under atmospheric conditions. J. Phys. Chem. A 2017, 121, 3327–3339. [Google Scholar] [CrossRef] [PubMed]
- Church, J.R.; Vaida, V.; Skodje, R.T. Gas-phase reaction kinetics of pyruvic acid with OH radicals: The role of tunneling, complex formation, and conformational structure. J. Phys. Chem. A 2020, 124, 790–800. [Google Scholar] [CrossRef] [PubMed]
- Church, J.R.; Vaida, V.; Skodje, R.T. Kinetic study of gas-phase reactions of pyruvic acid with HO2. J. Phys. Chem. A 2021, 125, 2232–2242. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Plath, K.L.; Skodje, R.T.; Vaida, V. Dynamics of vibrational overtone excited pyruvic acid in the gas phase: Line broadening through hydrogen-atom chattering. J. Phys. Chem. A 2008, 112, 7321–7331. [Google Scholar] [CrossRef]
- Plath, K.L.; Takahashi, K.; Skodje, R.T.; Vaida, V. Fundamental and overtone vibrational spectra of gas-phase pyruvic acid. J. Phys. Chem. A 2009, 113, 7294–7303. [Google Scholar] [CrossRef]
- Sephton, M.A. Organic compounds in carboniceous meteorites. Nat. Prod. Rep. 2002, 19, 292–311. [Google Scholar] [CrossRef]
- Mehringer, D.M.; Snyder, L.E.; Miao, Y.; Lovas, F. Detection and confirmation of interstellar acetic acid. Astrophys. J. 1997, 480, L71–L74. [Google Scholar] [CrossRef]
- Kleimeier, N.F.; Eckhardr, A.K.; Schreiner, P.R.; Kaiser, R.I. Interstellar formation of biorelevant pyruvic acid (CH3COCOOH). Chem 2020, 6, 3385–3395. [Google Scholar] [CrossRef]
- Kisiel, Z.; Pszczołkowski, L.; Białkowska-Jaworska, E.; Charnley, S.B. The millimeter wave rotational spectrum of pyruvic acid. J. Mol. Spectrosc. 2007, 241, 220–229. [Google Scholar] [CrossRef]
- Kaluza, C.E.; Bauder, A.; Günthard, H.H. The microwave spectrum of pyruvic acid. Chem. Phys. Lett. 1973, 22, 454–457. [Google Scholar] [CrossRef]
- Marstokk, K.-M.; Möllendal, H. Microwave spectrum, conformation, barrier to internal rotation and dipole moment of pyruvic acid. J. Mol. Struct. 1974, 20, 257–267. [Google Scholar] [CrossRef]
- Dyllick-Brenzinger, C.E.; Bauder, A.; Günthard, H.s.H. The substitution structure, barrier to internal rotation, and low frequency vibrations of pyruvic acid. Chem. Phys. 1977, 23, 195–206. [Google Scholar] [CrossRef]
- Meyer, R.; Bauder, A. Torsional coupling in pyruvic acid. J. Mol. Spectrosc. 1982, 94, 136–149. [Google Scholar] [CrossRef]
- Hollenstein, H.; Akermann, F.; Gunthard, H.H. Vibrational analysis of pyruvic acid and D-, 13C- and 18O-labelled species: Matrix spectra, assignments, valence force field and normal coordinate analysis. Spectrochim. Acta A 1978, 34, 1041–1063. [Google Scholar] [CrossRef]
- Reva, I.; Nunes, C.M.; Biczysko, M.; Fausto, R. Conformational switching in pyruvic acid isolated in Ar and N2 matrixes: Spectroscopic analysis, anharmonic simulation, and tunneling. J. Phys. Chem. A 2015, 119, 2614–2627. [Google Scholar] [CrossRef]
- Tarakeshwar, P.; Manogaran, S. An ab initio study of pyruvic acid. J. Mol. Struct. 1998, 430, 51–56. [Google Scholar] [CrossRef]
- Barone, V.; Biczysko, M.; Bloino, J. CC/DFT Route toward accurate structures and spectroscopic features for observed and elusive conformers of flexible molecules: Pyruvic acid as a case study. J. Chem. Theory Comput. 2015, 11, 4342–4363. [Google Scholar] [CrossRef]
- Senent, M.L. Ab initio determination of the torsional spectra of acetic acid. Mol. Phys. 2001, 99, 1311–1321. [Google Scholar] [CrossRef]
- Dalbouha, S.; Mogren Al-Mogren, M.; MLSenent, M.L. Rotational and torsional properties of various monosubstituted isotopologues of acetone (CH3-CO-CH3) from explicitly correlated ab initio methods. ACS Earth Space Chem. 2021, 5, 890–899. [Google Scholar] [CrossRef]
- Senent, M.L.; Moule, D.C.; Smeyers, Y.G.; Toro-Labbé, T.; Peñalver, F.J. A theoretical spectroscopic study of the Ã1Au(S1) ← X1Ag(S0), n → π* Transition in Biacetyl, (CH3CO)2. J. Mol. Spectrosc. 1994, 164, 66–78. [Google Scholar] [CrossRef][Green Version]
- Knizia, G.; Adler, T.B.; Werner, H.-J. Simplified CCSD(T)-F12 methods: Theory and benchmarks. J. Chem. Phys. 2009, 130, 054104. [Google Scholar] [CrossRef] [PubMed]
- Werner, H.-J.; Adler, T.B.; Manby, F.R. General orbital invariant MP2-F12 theory. J. Chem. Phys. 2007, 126, 164102. [Google Scholar] [CrossRef] [PubMed]
- Senent, M.L.; Ruiz, R.; Dominguez-Gómez, R.; Villa, M. CCSD(T) study of the far-infrared spectrum of ethyl methyl ether. J. Chem. Phys. 2009, 130, 064101. [Google Scholar] [CrossRef] [PubMed]
- Boussesi, R.; Senent, M.L. Computational analysis of the far Infrared spectral region of various deuterated varieties of Ethylene Glycol. Phys. Chem. Chem. Phys. 2020, 22, 23785–23794. [Google Scholar] [CrossRef]
- Werner, H.-J.; Knowles, P.J.; Manby, F.R.; Schütz, M.; Celani, P.; Knizia, G.; Korona, T.; Lindh, R.; Mitrushenkov, A.; Rauhut, G.; et al. MOLPRO, version 2012.1; a Package of ab Initio Programs; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 2012; Available online: http://www.molpro.net (accessed on 4 June 2021).
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Knowles, P.J.; Hampel, C.; Werner, H.-J. Coupled cluster theory for high spin, open shell reference wave functions. J. Chem. Phys. 1993, 99, 5219–5227. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. V. Core-valence basis sets for boron through neon. J. Chem. Phys. 1995, 103, 4572–4585. [Google Scholar] [CrossRef]
- Barone, V. Anharmonic vibrational properties by a fully automated second-order perturbative approach. J. Chem. Phys. 2005, 122, 014108. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision, C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Senent, M.L. ENEDIM, “A Variational Code for Non-Rigid Molecules”. 2001. Available online: http://tct1.iem.csic.es/PROGRAMAS.htm (accessed on 7 June 2021).
- Senent, M.L. Determination of the kinetic energy parameters of non-rigid molecules. Chem. Phys. Lett. 1998, 296, 299–306. [Google Scholar] [CrossRef]
- Senent, M.L. Ab initio determination of the roto-torsional energy levels of trans-1,3-butadiene. J. Mol. Spectrosc. 1998, 191, 265–275. [Google Scholar] [CrossRef]
- Watson, J.K.G. Determination of Centrifugal Distortion Coefficients of Asymmetric-Top Molecules. III. Sextic Coefficients. J. Chem. Phys. 1968, 48, 4517–4524. [Google Scholar] [CrossRef]
- Groner, P. Effective rotational Hamiltonian for molecules with two periodic large-amplitude motions. J. Chem. Phys. 1997, 107, 4483–4498. [Google Scholar] [CrossRef]
- Boussesi, R.; Senent, M.L.; Jaïdane, N. Weak intramolecular interaction effects on the low temperature spectra of ethylene glycol, an astrophysical species. J. Chem. Phys. 2016, 144, 164110. [Google Scholar] [CrossRef] [PubMed]
- Motiyenko, R.A.; Margulès, L.; Senent, M.L.; Guillemin, J.C. Internal rotation of OH group in 4-hydroxy-2-butynenitrile studied by millimeter-wave spectroscopy. J. Phys. Chem. A 2018, 122, 3163–3169. [Google Scholar] [CrossRef]
- Dalbouha, S.; Senent, M.L.; Komiha, N.; Domínguez-Gómez, R. Structural and spectroscopic characterization of methyl isocyanate methyl cyanate, methyl fulminate, and acetonitrile N-oxide using highly correlated ab initio methods. R. J. Chem. Phys. 2016, 145, 124309. [Google Scholar] [CrossRef] [PubMed]
- Gámez, V.; Senent, M.L. The formation of C3O3H6 structural isomers in the gas phase through barrierless pathways. Formation and spectroscopic characterization of methoxy acetic acid. Astrophys. J. 2021, 913, 21–37. [Google Scholar] [CrossRef]
| Tc | Tt | Ct | Cc | ||
|---|---|---|---|---|---|
| Calc. | Exp. [Ref] | Calc. | Calc. | Calc. | |
| E | 0.0 a | 960.3 | 1526.0 | 3742.6 | |
| EZPVE | 0.0 b | 877.5 | 1416.3 | 3563.5 | |
| θ1 | 180° | 180° | 180° | 180° | |
| θ2 | 0° | 0° | 180° | 180° | |
| α | 180° | 0° | 0° | 180° | |
| Ae | 5537.641 | 5640.946 | 5568.843 | 5513.683 | |
| Be | 3606.390 | 3497.767 | 3503.128 | 3483.147 | |
| Ce | 2213.503 | 2187.875 | 2179.097 | 2163.620 | |
| μa | 2.5575 | 2.27 ± 0.02 [14] | 0.3809 | 0.2021 | 2.9383 |
| μb | 0.131 | 0.35 ± 0.02 [14] | 1.353 | 4.4313 | 5.2582 |
| μc | 0.0 | 0.0 | 0.0 | 0.0 | |
| μ | 2.5609 | 2.3 ± 0.03 [14] | 1.4056 | 4.4359 | 6.0235 |
| V3 | 338.0 | 336.358(50) [12] | 397.8 | 540.2 | 852.8 |
| VOH (Tc → Tt) | 4852 | ||||
| VOH (Ct → Cc) | 4383 | ||||
| VCC (Tc → Cc) | 3871 | ||||
| VCC (Tt → Ct) | 812 | ||||
| Tc | Tt | Ct | Cc | |
|---|---|---|---|---|
| H10….O4 | 2.0030 | - | - | - |
| C1C2 | 1.4971 | 1.5008 | 1.5031 | 1.5149 |
| C1C3 | 1.5433 | 1.5408 | 1.5476 | 1.5561 |
| O4C1 | 1.2168 | 1.2063 | 1.2048 | 1.2031 |
| H5C2 | 1.0870 | 1.0863 | 1.0866 | 1.0865 |
| H6C2 | 1.0914 | 1.0908 | 1.0909 | 1.0935 |
| H7C2 | 1.0914 | 1.0908 | 1.0909 | 1.0935 |
| O8C3 | 1.2069 | 1.2054 | 1.1972 | 1.1922 |
| O9C3 | 1.3363 | 1.3353 | 1.3502 | 1.3536 |
| H10O9 | 0.9734 | 0.9670 | 0.9671 | 0.9616 |
| C2C1C3 | 116.8 | 114.7 | 117.8 | 118.8 |
| O4C1C3 | 117.8 | 120.3 | 117.8 | 118.2 |
| H5C2C1 | 109.9 | 109.2 | 109.0 | 108.9 |
| H6C2C1 | 109.3 | 109.7 | 109.9 | 110.6 |
| H7C2C1 | 109.3 | 109.7 | 109.9 | 110.6 |
| O8C3C1 | 122.9 | 122.6 | 124.2 | 122.3 |
| O9C3O8 | 124.6 | 124.8 | 124.4 | 121.6 |
| H10O9C3 | 105.3 | 106.5 | 106.6 | 110.8 |
| H6C2C1H5 | −121.9 | −121.5 | −121.3 | −119.9 |
| H7C2C1H5 | 121.9 | 121,5 | 121.3 | 119.9 |
| Tc | Tt | Ct | Cc | ||||
|---|---|---|---|---|---|---|---|
| Calc. | Exp. ref | Calc. | Exp. ref | Calc. | Calc. | ||
| ν(a’) | |||||||
| ν1 | OH st | 3426 | 3463 b | 3561 | 3579 b | 3554 | 3636 |
| ν2 | CH3 st | 3072 | 3025 b | 3072 | 3067 | 3059 | |
| ν3 | CH3 st | 2971 | 2941 b | 2973 | 2973 | 2958 | |
| ν4 | C3=0 st | 1782 | 1804 b | 1747 | 1773 | 1788 | |
| ν5 | C1=0 st | 1705 | 1737 b | 1723 | 1721 | 1721 | |
| ν6 | CH3 b | 1435 | 1424 b | 1436 | 1436 | 1447 | |
| ν7 | C-C- st | 1380 | 1391 b | 1382 | 1363 | 1355 | |
| ν8 | CH3 b | 1332 | 1360 b | 1356 | 1340 | 1273 | |
| ν9 | COH b | 1214 | 1211 b | 1203 | 1162 | 1177 | |
| ν10 | C-OH st | 1135 | 1133 b | 1120 | 1102 | 1098 | |
| ν11 | CH3 b | 971 | ~970 c | 962 | 971 | 965 | |
| ν12 | C-C st | 756 | 761 c | 731 | 724 | 738 | |
| ν13 | skeletal b | 602 | 604 c | 587 | 605 | 606 | |
| ν14 | skeletal b | 529 | 517 | 484 | 478 | ||
| ν15 | OCCb | 387 | 386 | 401 | 405 | ||
| ν16 | CCCb | 258 | 245 | 253 | 263 | ||
| ν(a”) | |||||||
| ν17 | CH3 st | 3019 | 3024 | 3026 | 3005 | ||
| ν18 | CH3 b | 1432 | 1437 | 1441 | 1458 | ||
| ν19 | CH3 b | 1017 | 1030 b | 1019 | 1020 | 1011 | |
| ν20 | skeletal b | 792 | 723 | 713 | 699 | ||
| ν21 | OH tor (+C=O) | 606 | 668 c | 601 | 601 | 461 | |
| ν22 | skeletal b | 391 | 392 c | 373 | 373 | 357 | |
| ν23 | CH3 tor | 123 | 130 | 151 | 187 | ||
| ν24 | C-C tor | 93 | 90 c | 39 | 19 | 1 | |
| Tc | Tt | Ct | Cc | ||
|---|---|---|---|---|---|
| in MHz | |||||
| Calc. | Exp. [12] | Calc. | Calc. | Calc. | |
| A0 | 5530.506 | 5535.46113 (18) | 5629.841 | 5553.752 | 5499.149 |
| B0 | 3581.177 | 3583.408634 (78) | 3473.363 | 3474.982 | 3449.328 |
| C0 | 2203.077 | 2204.858443 (63) | 2180.423 | 2173.717 | 2158.751 |
| in kHz | |||||
| ΔJ | 0.645465 | 0.675114 (35) | 0.577981 | 0.583771 | 1.831225 |
| ΔK | 1.259501 | 1.49373 (49) | 1.275684 | 1.340695 | 3.880986 |
| ΔJK | −0.550295 | −0.77911 (12) | −0.392555 | −0.469353 | −4.231851 |
| δJ | 0.252245 | 0.264241 (16) | 0.221177 | 0.225223 | 0.480955 |
| δK | 0.582614 | 0.552491 (97) | 0.601105 | 0.576154 | 5.552698 |
| in Hz | |||||
| HJ | 0.000111 | 0.0001239 (86) | 0.000116 | 0.000118 | −0.320165 |
| HK | 0.003486 | 0.00561 (48) | 0.004440 | 0.010283 | −6.821416 |
| HJK | 0.000466 | - | 0.000523 | 0.001860 | −2.315587 |
| HKJ | −0.003375 | −0.00171 (13) | −0.004398 | −0.011623 | 9.438257 |
| φJ | 0.000091 | 0.0000718 (46) | 0.000094 | 0.000098 | −0.252688 |
| φJK | 0.002459 | 0.003983 | 0.011783 | −7.667262 | |
| φK | 0.000755 | 0.002441 (76) | 0.000772 | 0.001065 | −0.425569 |
| Bθ1θ1 | 5.4904 | Bθ1θ2 | −0.1751 |
| Bθ2θ2 | 0.7411 | Bθ1α | 0.0376 |
| Bαα | 18.5985 | Bθ2α | 0.0061 |
| m n l | Variational | VPT2 | Ref. [16] | m n l | Variational | VPT2 | ||
|---|---|---|---|---|---|---|---|---|
| 0 0 0 | A1 E | 0.000 b 0.024 | - | 0.000 0.024 | 3 0 0 (3ν23) | A2 E | 327.476 278.686 | 340 |
| 0 1 0 (ν24) | A2 E | 89.754 89.709 | 93 | 90.1 90.0 | 4 0 0 (4ν23) | A1 E | 334.735 394.098 | 432 |
| 1 0 0 (ν23) | A2 E | 120.539 119.833 | 123 | 118.3 117.7 | (ν24ν16) | 348 | ||
| 0 2 0 (2ν24) | A1 E | 178.744 178.766 | 186 | 179.9 180.0 | (ν23ν16) | 380 | ||
| 1 1 0 (ν24ν23) | A1 E | 202.976 206.570 | 214 | 222.5 225.0 | 0 4 0 (4ν24) | A1 E | 355.311 355.197 | 368 |
| 2 0 0 (2ν23) | A1 E | 223.301 226.756 | 232 | 200.5 204.5 | (ν15) | 387 | ||
| (ν16) | 258 | (ν22) | 391 | |||||
| 0 3 0 (3ν24) | A2 E | 267.193 267.161 | 277 | 1 3 0 (3ν24ν23) | A1 E | 380.268 390.184 | 393 | |
| 1 2 0 (2ν24ν23) | A2 E | 291.127 298.695 | 304 | 2 2 0 (2ν232ν24) | A1 E | 408.508 421.158 | 412 | |
| 2 1 0 (2ν23ν24) | A2 E | 315.337 325.067 | 325 | 3 1 0 (3ν23ν24) | A1 E | 425.414 368.775 | 425 | |
| 0 0 1 (ν21) | A2 E | 581.306 581.327 | 680 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senent, M.L.; Dalbouha, S. Large Amplitude Motions of Pyruvic Acid (CH3-CO-COOH). Molecules 2021, 26, 4269. https://doi.org/10.3390/molecules26144269
Senent ML, Dalbouha S. Large Amplitude Motions of Pyruvic Acid (CH3-CO-COOH). Molecules. 2021; 26(14):4269. https://doi.org/10.3390/molecules26144269
Chicago/Turabian StyleSenent, María Luisa, and Samira Dalbouha. 2021. "Large Amplitude Motions of Pyruvic Acid (CH3-CO-COOH)" Molecules 26, no. 14: 4269. https://doi.org/10.3390/molecules26144269
APA StyleSenent, M. L., & Dalbouha, S. (2021). Large Amplitude Motions of Pyruvic Acid (CH3-CO-COOH). Molecules, 26(14), 4269. https://doi.org/10.3390/molecules26144269







