Excited States Symmetry Breaking and In-Plane Polarization Cause Chiral Reversal in Diastereomers
Abstract
:1. Introduction
2. Method
2.1. Computational Details
2.2. ECD
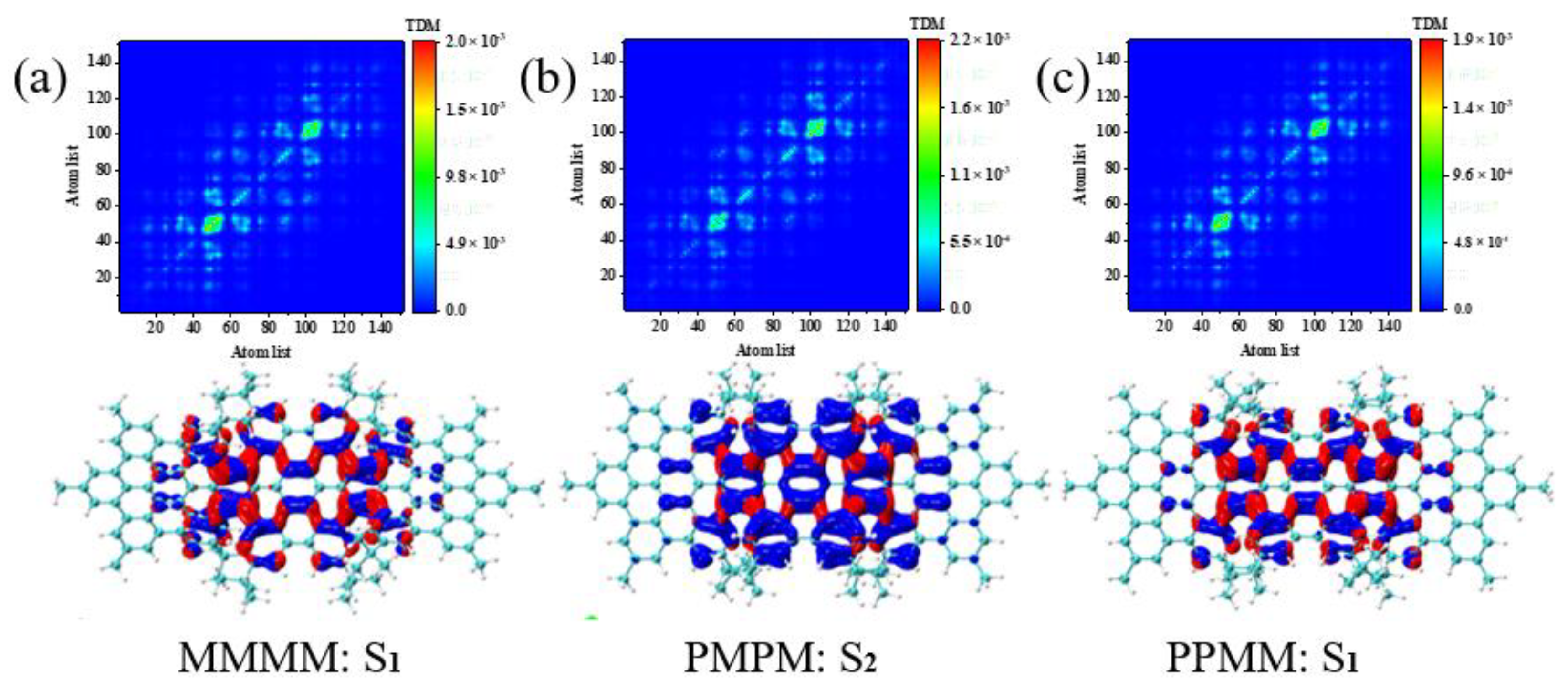
2.3. TEDMs and TMDMs
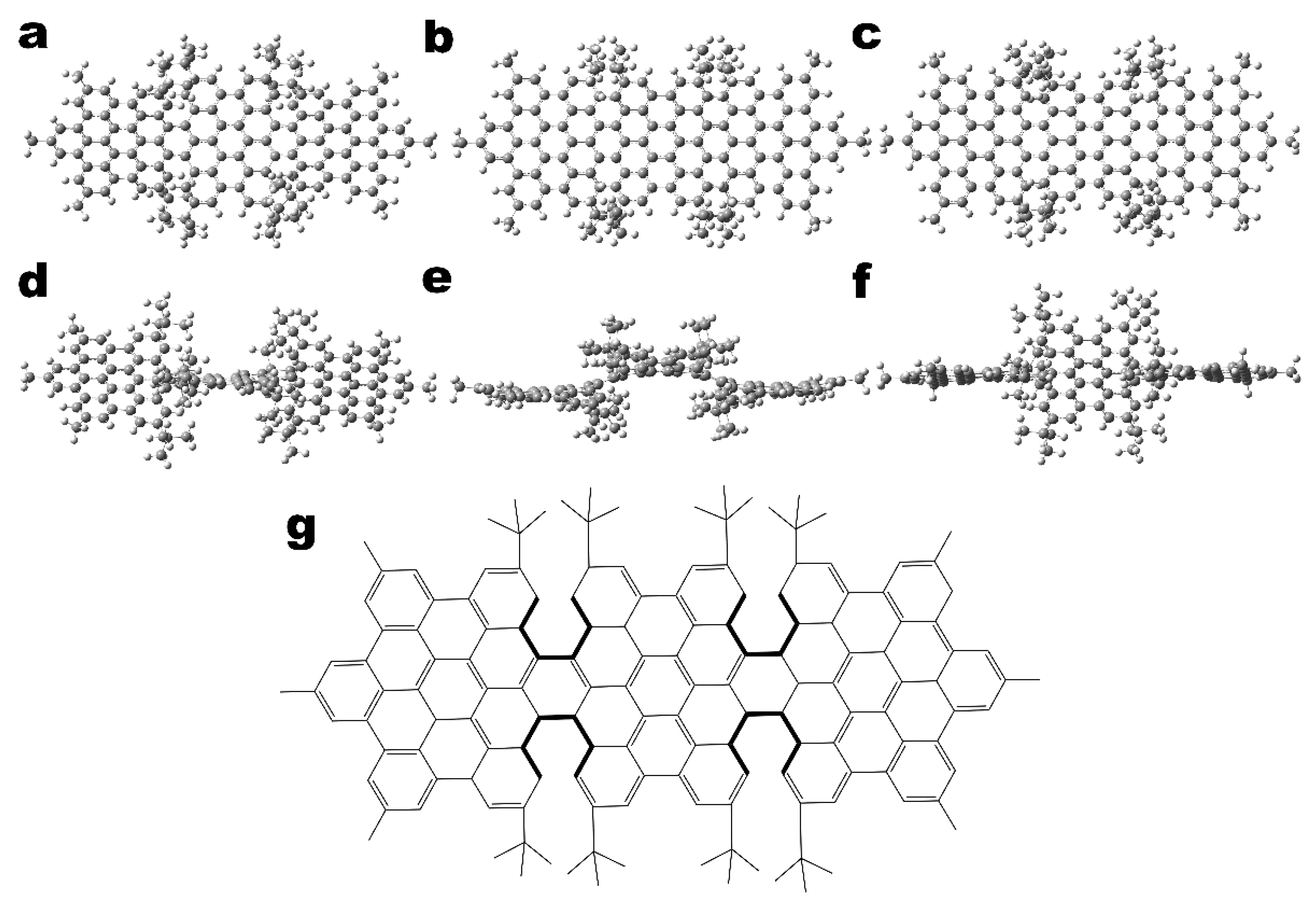
3. Results and Discussion
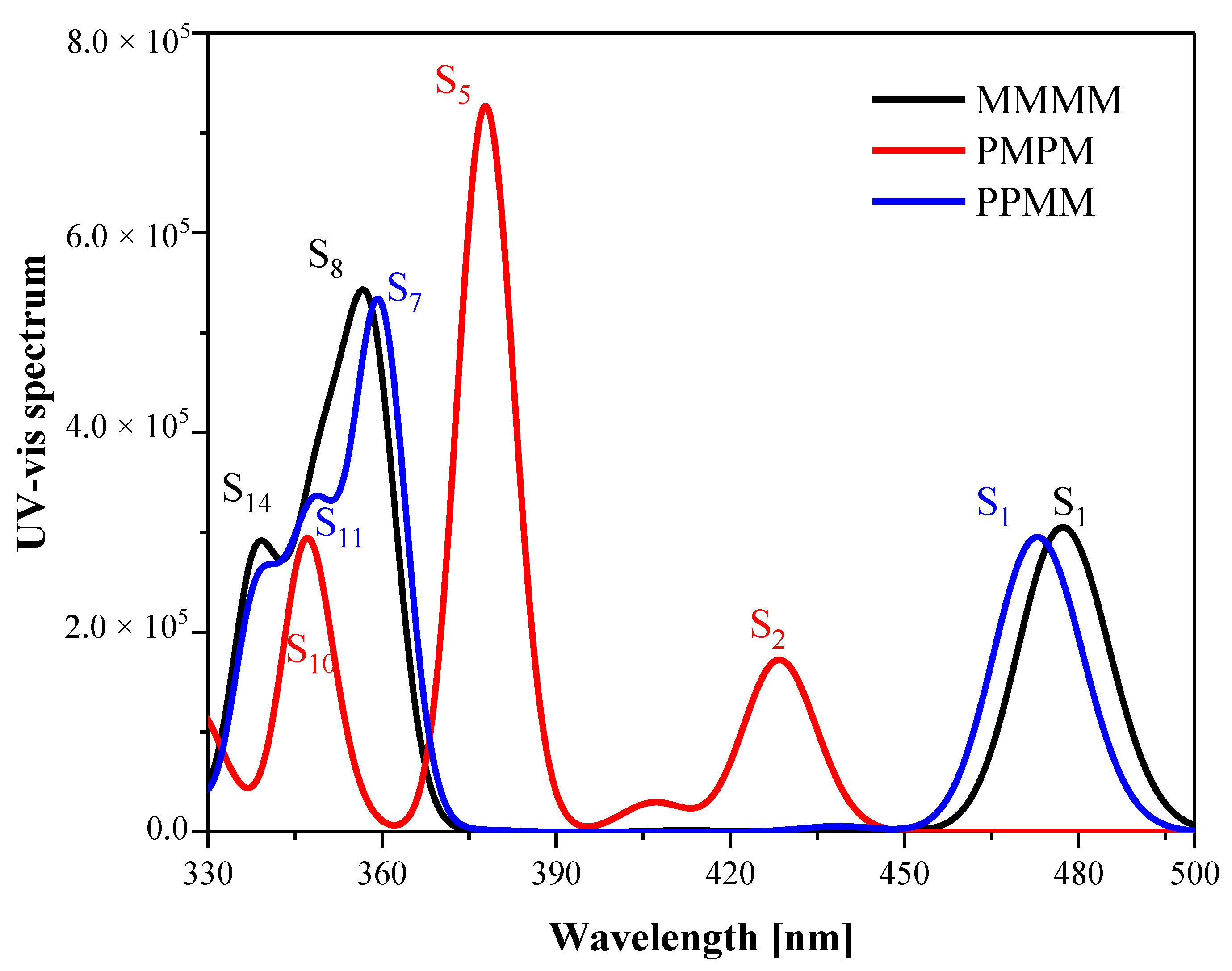
3.1. UV-Vis Absorption Spectra
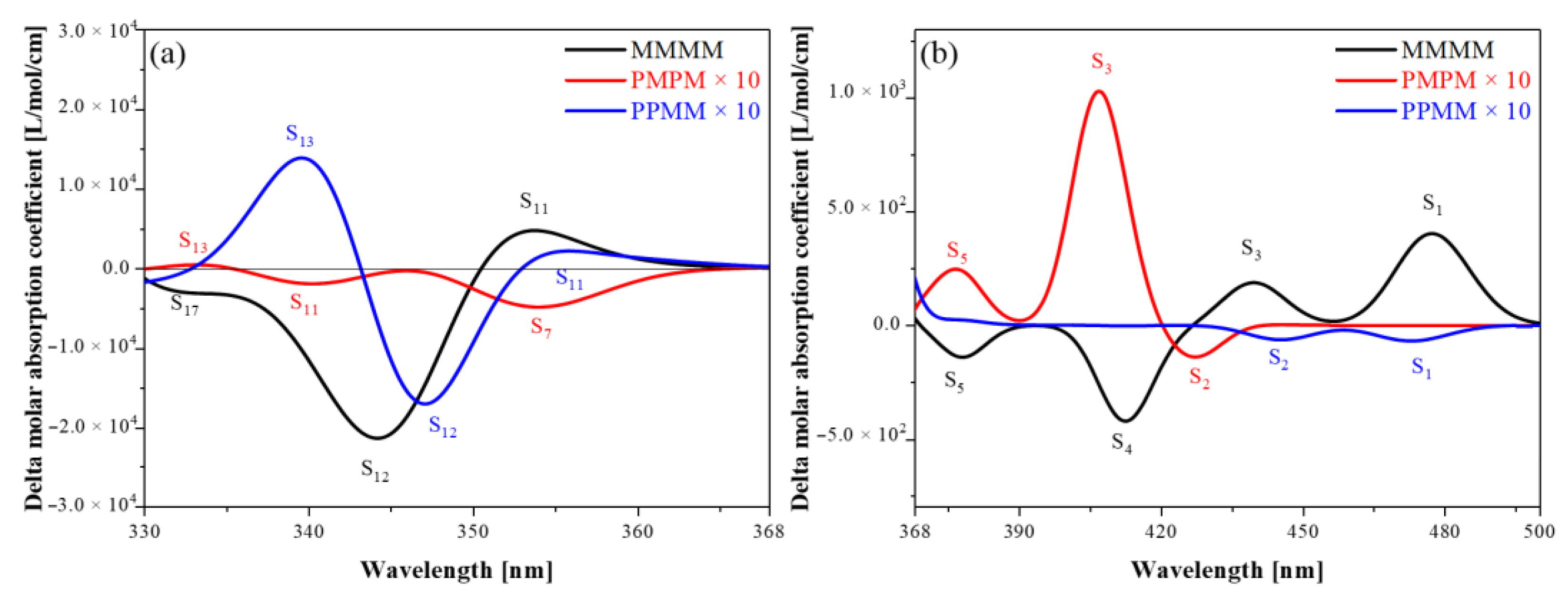
3.2. ECD Spectra
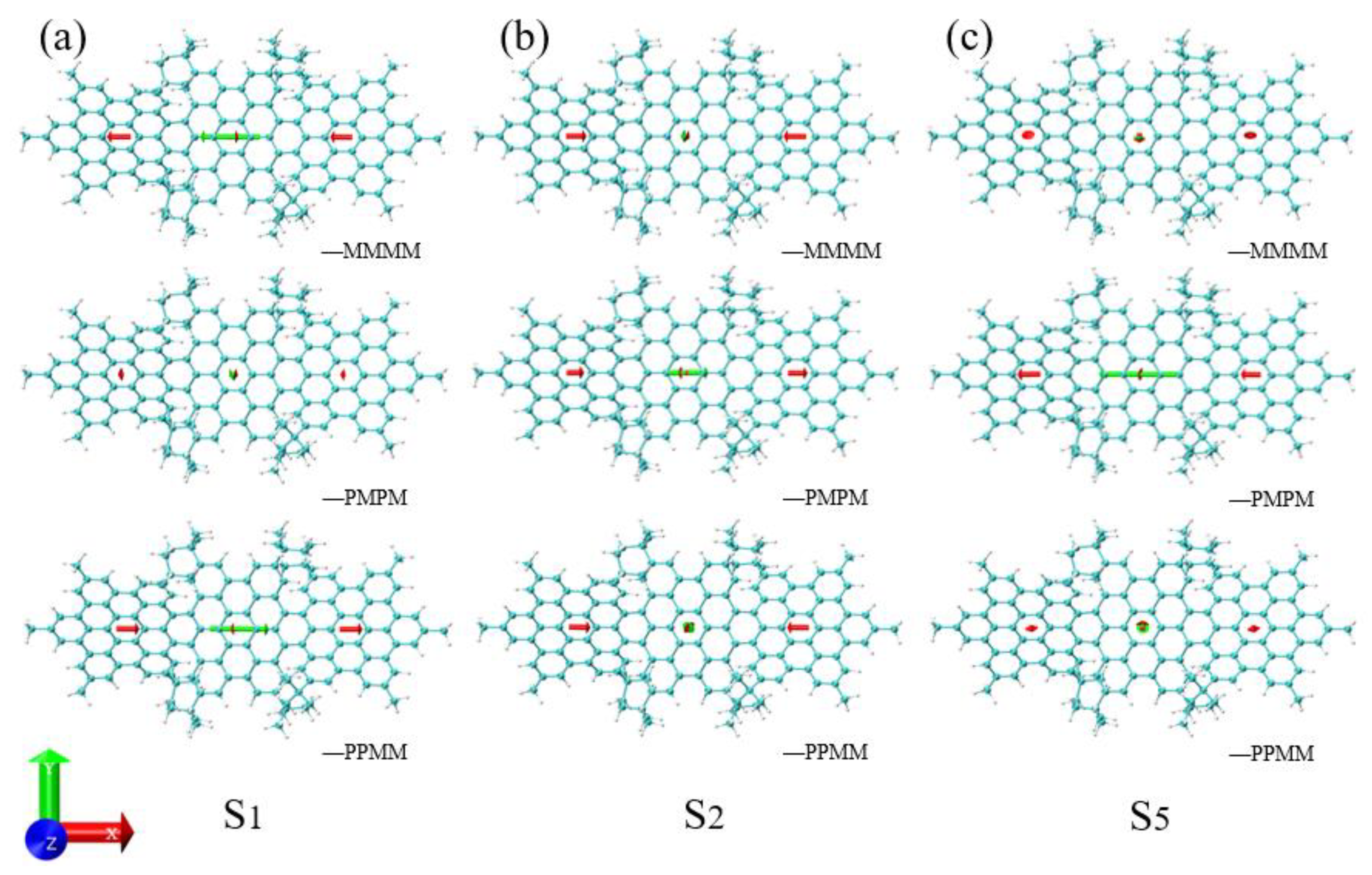
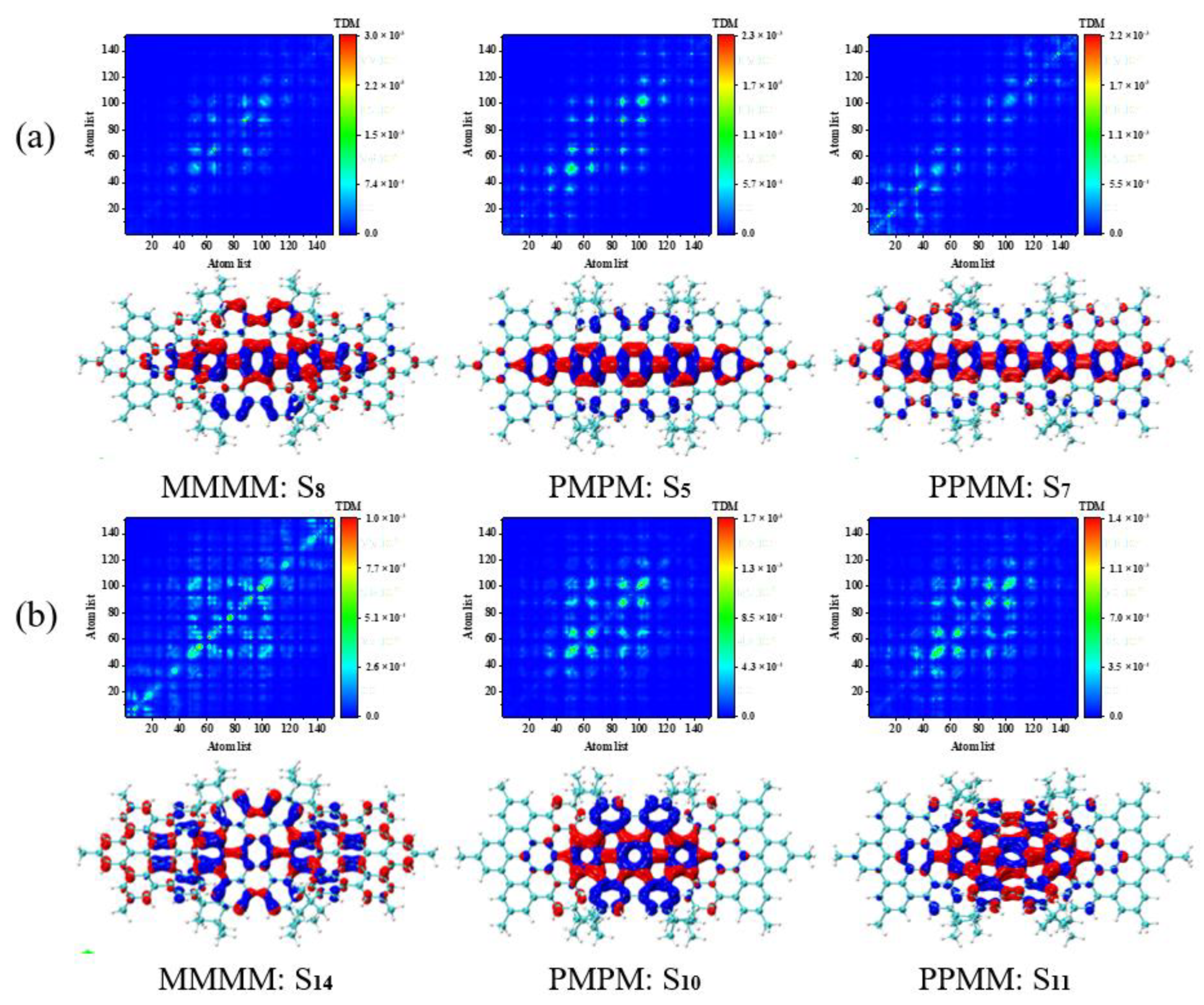
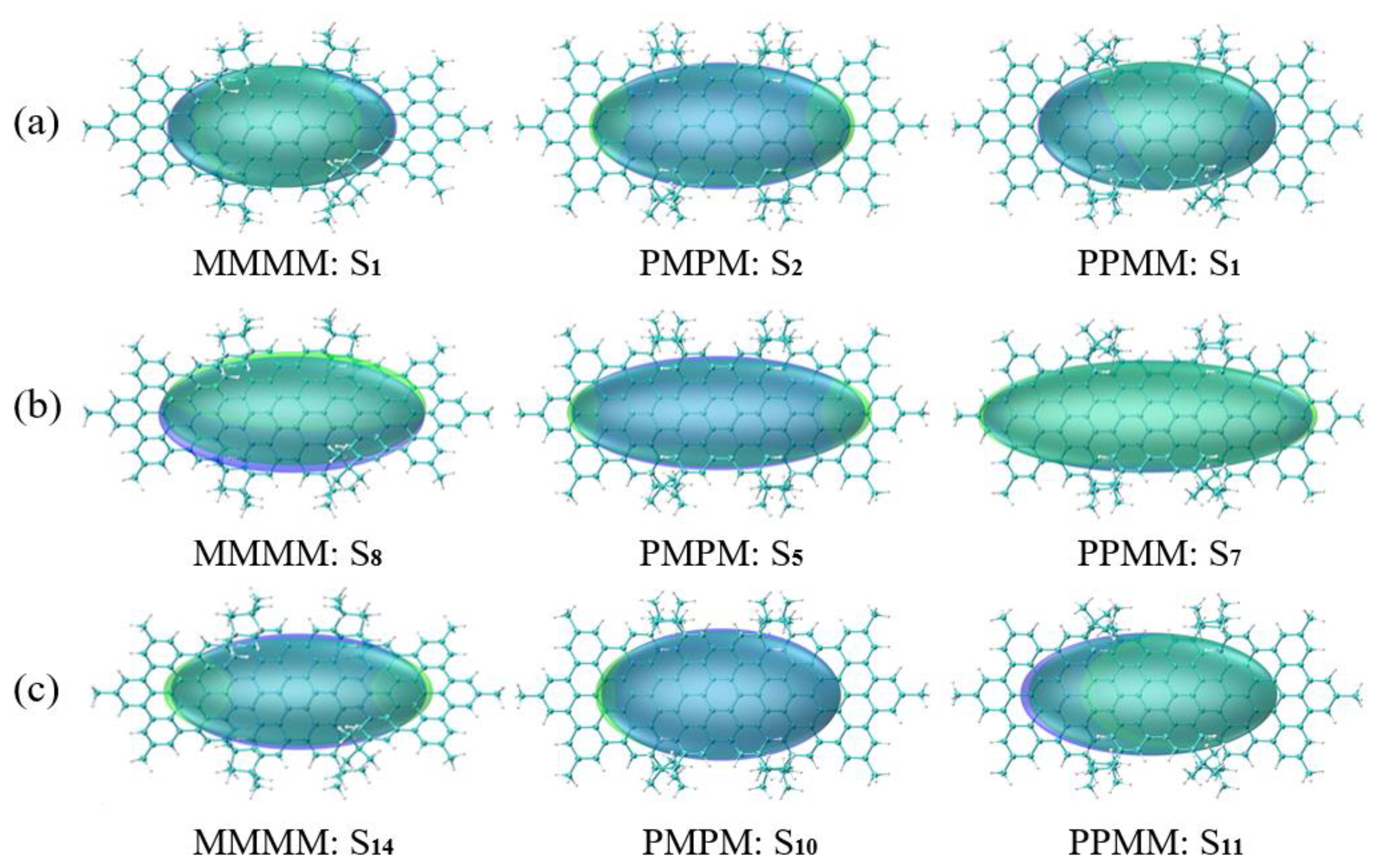
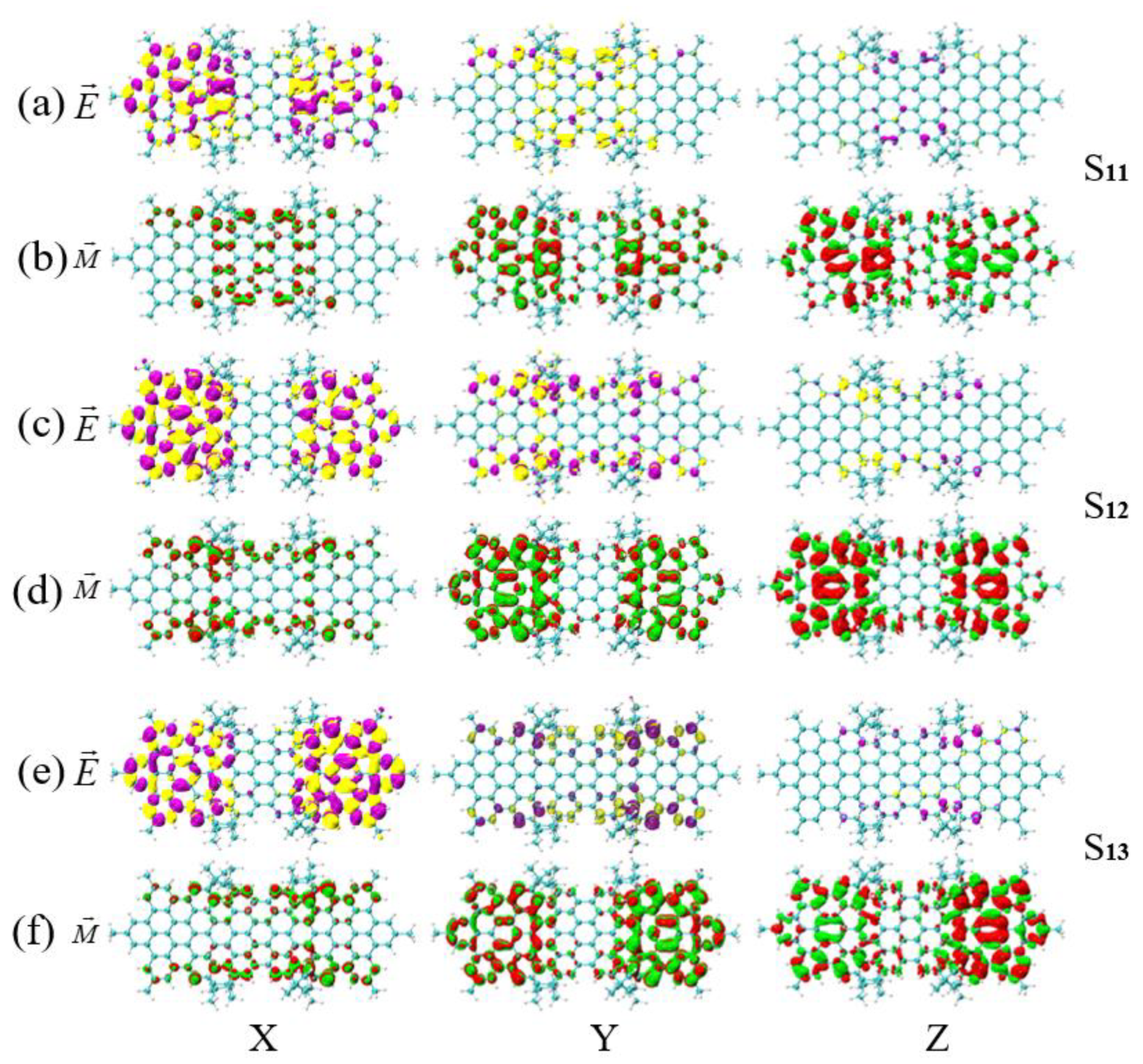
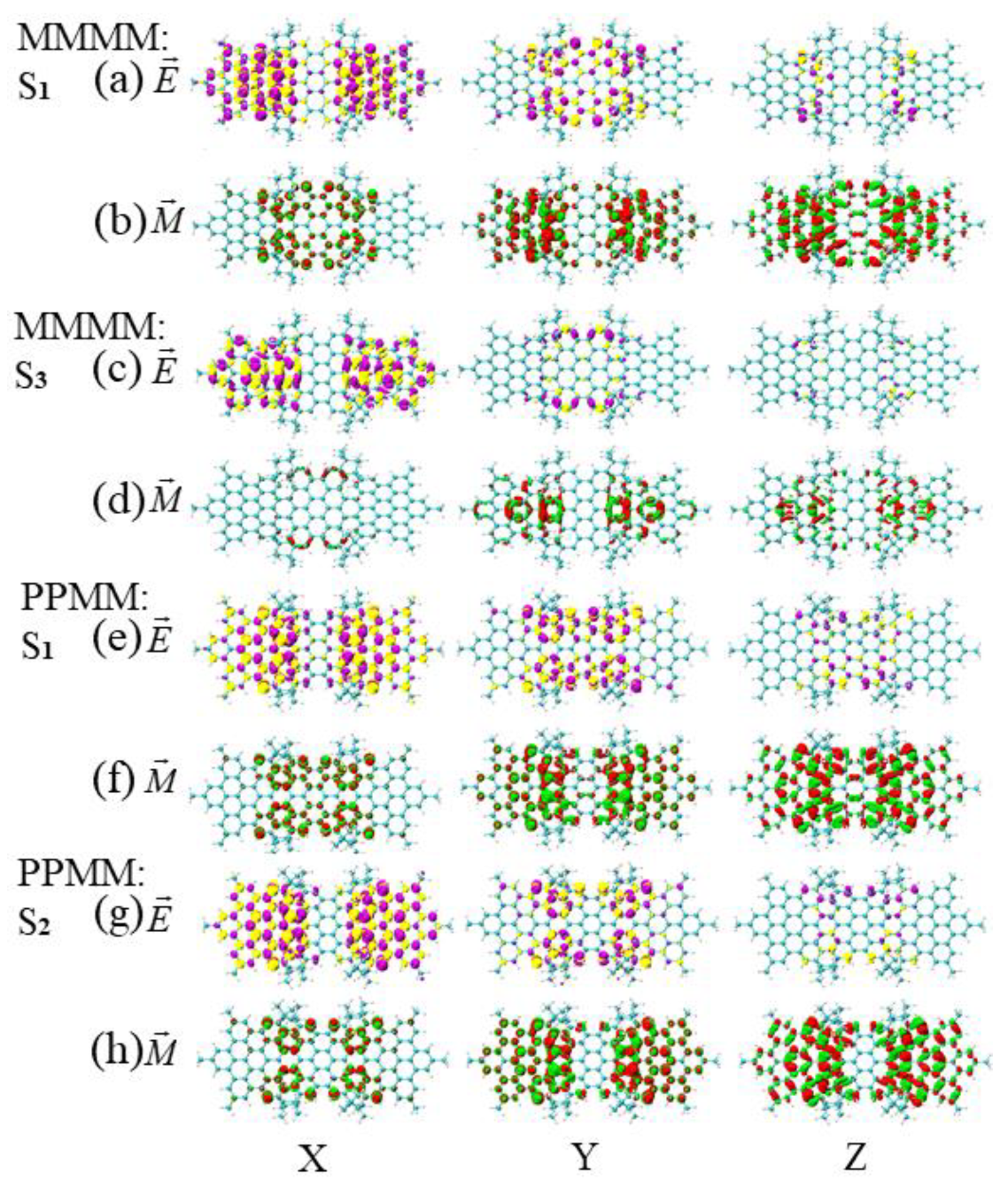
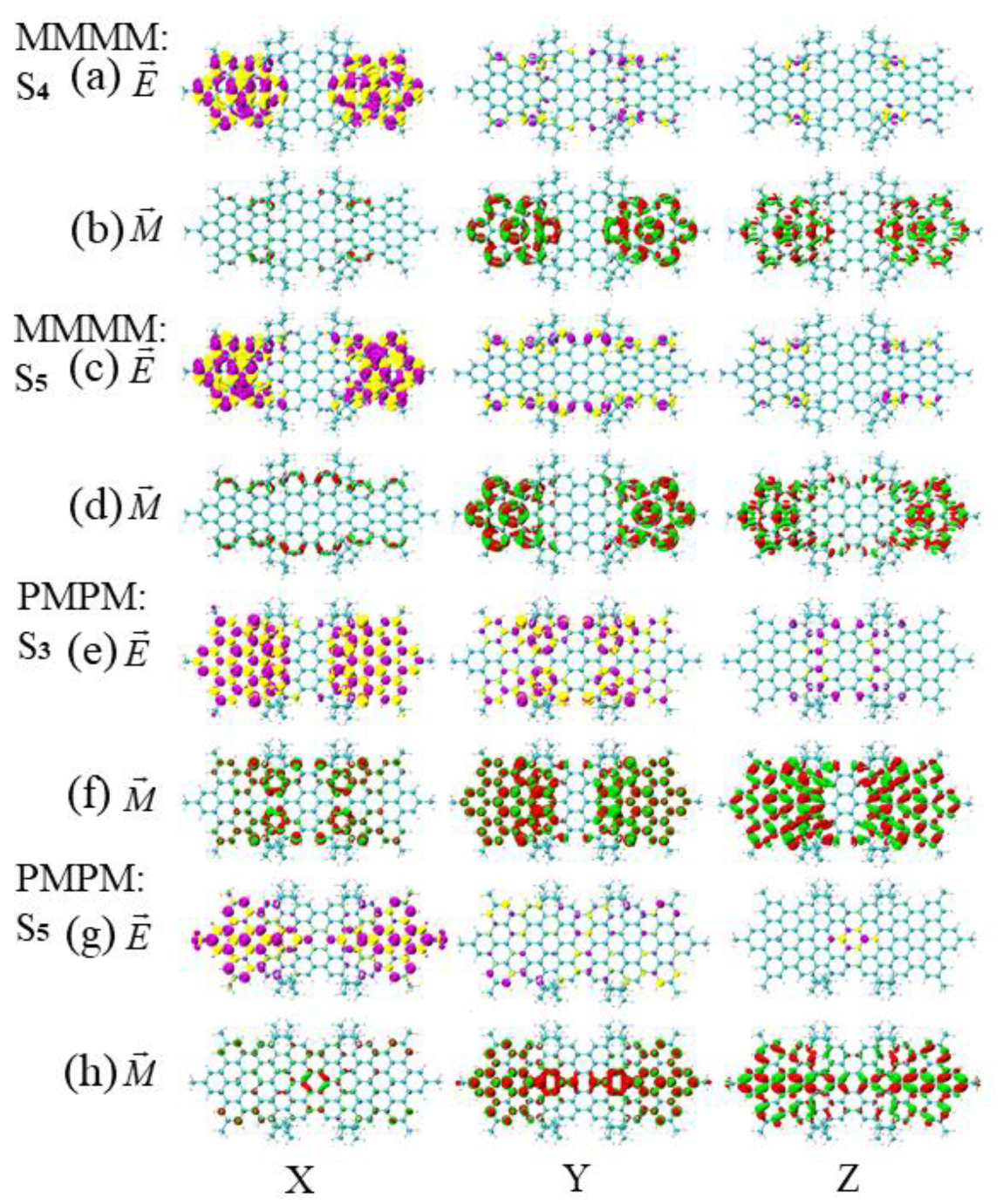
3.3. Energy-Breaking Chiral Reversal
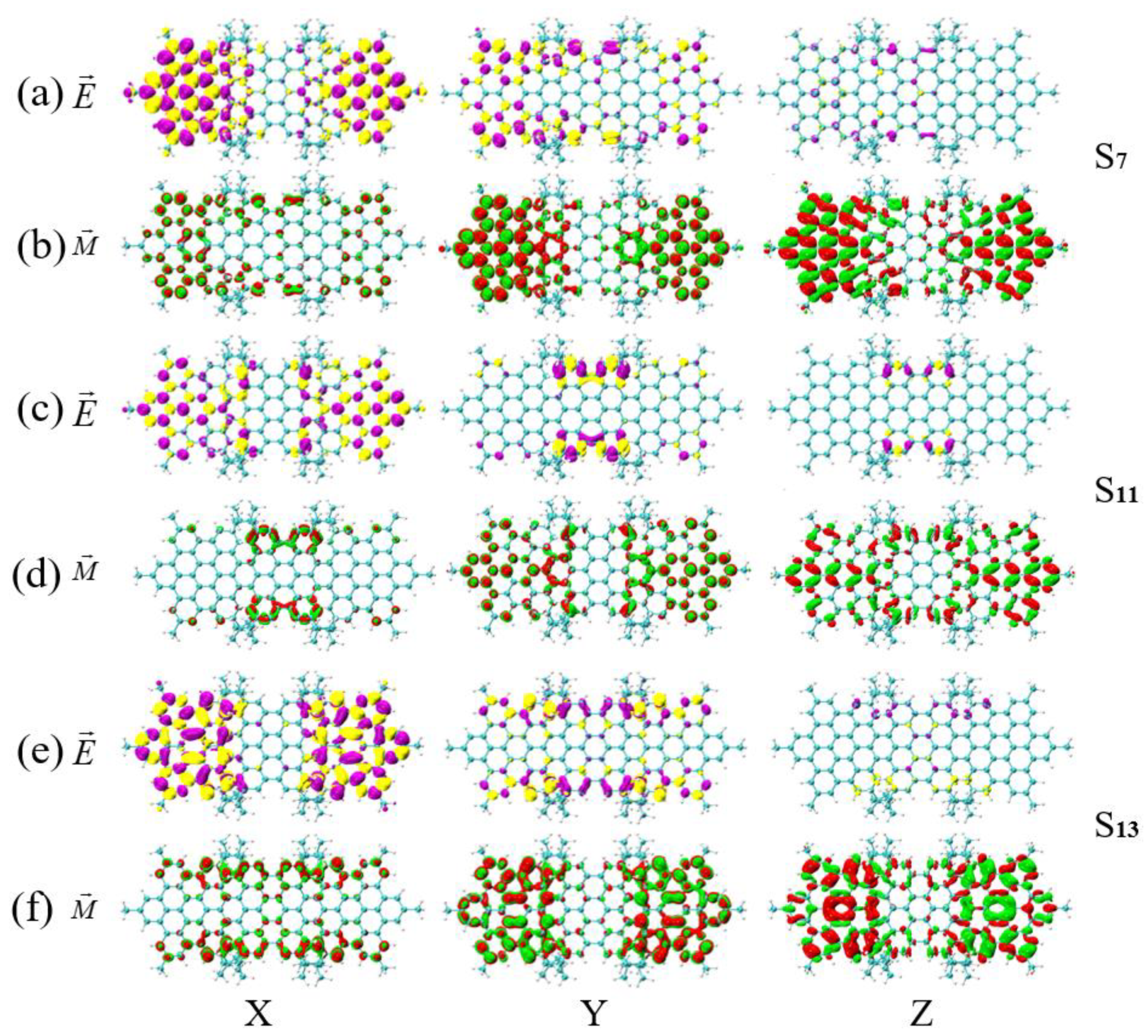
3.4. Symmetry-Breaking Chiral Reversal
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Mu, X.J.; Sun, M.T. The Linear and Nonlinear Optical Absorption and Asymmetrical Electromagnetic Interaction in Chiral Twisted Bilayer Graphene with Hybrid Edges. Mater. Today Phys. 2020, 14, 100222. [Google Scholar] [CrossRef]
- Yao, X.; Hu, Y.; Cao, B.; Peng, R.; Ding, J. Effects of surface molecular chirality on adhesion and differentiation of stem cells. Biomaterials 2013, 34, 9001–9009. [Google Scholar] [CrossRef]
- Ma, J.L.; Qiao, W.H.; Mu, X.J.; Dong, J.; Quan, J.; Tian, C.H. Optical Properties of Artemisinin and Its Derivatives. ACS Omega 2020, 5, 30849–30857. [Google Scholar] [CrossRef] [PubMed]
- Palle, D. On Chirality of the Vorticity of the Universe. Entropy 2012, 14, 958–965. [Google Scholar] [CrossRef] [Green Version]
- Kiran, M.; Yadav, P.; Deolekar, P.; Thakre, V. Chiral chemistry in pharmacology—A review. Int. J. 2012, 1, 7–10. [Google Scholar]
- Pasteur, L. On the molecular asymmetry of natural organic products. Ann. Chim. Phys. 1848, 24, 442–459. [Google Scholar]
- Spek, V.D.; Trienke, M. Selling a theory: The role of molecular models in JH van’t Hoff’s stereochemistry theory. Ann. Sci. 2006, 63, 157–177. [Google Scholar] [CrossRef]
- Salam, A. The role of chirality in the origin of life. J. Mol. Evol. 1991, 33, 105–113. [Google Scholar] [CrossRef]
- Barron, L.D. Chirality and life. Space Sci. Rev. 2008, 135, 187–201. [Google Scholar] [CrossRef]
- Riant, O.; Samuel, O.; Kagan, H.B. A general asymmetric synthesis of ferrocenes with planar chirality. J. Am. Chem. Soc. 1993, 115, 5835–5836. [Google Scholar] [CrossRef]
- Barron, L.D. True and false chirality and absolute asymmetric synthesis. J. Am. Chem. Soc. 1986, 108, 5539–5542. [Google Scholar] [CrossRef]
- Garrison, A.W. Probing the enantioselectivity of chiral pesticides. Environ. Sci. Technol. 2006, 40, 16–23. [Google Scholar] [CrossRef] [Green Version]
- Daniel, K.G.; Guida, W.C.; Brooks, W.H. The significance of chirality in drug design and development. Curr. Top. Med. Chem. 2011, 11, 760–770. [Google Scholar]
- Pirkle, W.H.; Pochapsky, T.C. Considerations of chiral recognition relevant to the liquid chromatography separation of enantiomers. Chem. Rev. 1989, 89, 347–362. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, Y.; Li, X.; Feng, Y.; Zhang, H.; Xu, J. Chiral Perovskites: Promising Materials toward Next-Generation Optoelectronics. Small 2019, 15, 1902237. [Google Scholar] [CrossRef]
- Noyori, R.; Takaya, H. BINAP: An efficient chiral element for asymmetric catalysis. Accounts. Chem. Res. 1990, 23, 345–350. [Google Scholar] [CrossRef]
- Caner, H.; Groner, E.; Levy, L.; Agranat, I. Trends in the development of chiral drugs. Drug Discov. Today 2004, 9, 105–110. [Google Scholar] [CrossRef]
- Mu, X.J.; Wang, J.G.; Duan, G.Q.; Li, Z.J.; Wen, J.X.; Sun, M.T. The nature of chirality induced by molecular aggregation and self-assembly. Spectrochim. Acta Part A 2019, 212, 188–198. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.T.; Qiao, W.H.; Miao, W.J.; Zhang, Y.; Mu, X.J.; Wang, J.W. the Dependence of implicit Solvent Model parameters and electronic Absorption Spectra and photoinduced charge transfer. Sci. Rep. 2020, 10, 1–8. [Google Scholar] [CrossRef]
- Jimeno, C. Water in asymmetric organocatalytic systems: A global perspective. Org. Biomol. Chem. 2016, 14, 6147–6164. [Google Scholar] [CrossRef] [PubMed]
- Akihiro, Y.; Xiuhua, H.; Osamu, Y.; Joji, N. Development of Fluorous Lewis Acid-Catalyzed Reactions. Molecules 2006, 11, 627–640. [Google Scholar]
- Pârvulescu, V.I.; Hardacre, C. Catalysis in ionic liquids. Chem. Rev. 2007, 107, 2615–2665. [Google Scholar] [CrossRef]
- Olmos, A.; Asensio, G.; Perez, P.J. Homogeneous metal-based catalysis in supercritical carbon dioxide as reaction medium. ACS Catal. 2016, 6, 4265–4280. [Google Scholar] [CrossRef]
- Kondru, R.K.; Wipf, P.; Beratan, D.N. Atomic contributions to the optical rotation angle as a quantitative probe of molecular chirality. Science 1998, 282, 2247–2250. [Google Scholar] [CrossRef] [Green Version]
- Bentley, R. Role of sulfur chirality in the chemical processes of biology. Chem. Soc. Rev. 2005, 34, 609–624. [Google Scholar] [CrossRef]
- Lorenzo, M.O.; Baddeley, C.J.; Muryn, C.; Raval, R. Extended surface chirality from supramolecular assemblies of adsorbed chiral molecules. Nature 2000, 404, 376–379. [Google Scholar] [CrossRef]
- Silvia, C.-F.; Cruz, C.M.; Inês, F.A.M.; Irene, R.M.; Araceli, G.C. Two-photon absorption enhancement by the inclusion of a tropone ring in distorted nanographene ribbons. Angew. Chem. 2020, 132, 7205–7211. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Li, X. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Gross, E.K.U.; Kohn, W. Local density-functional theory of frequency-dependent linear response phys. Rev. Lett. 1985, 55, 2085. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–Correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Zhao, L.; Mu, X.J. Visualization of vibrational-resolution charge transfer enhanced resonance Raman scattering spectroscopy. Spectrochim. Acta Part A 2020, 229, 117945. [Google Scholar] [CrossRef] [PubMed]
- Mu, X.J.; Chen, X.T.; Wang, J.G.; Sun, M.T. Visualizations of electric and magnetic interactions in electronic circular dichroism and raman optical activity. J. Phys. Chem. A 2019, 123, 8071–8081. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Wang, J.; Wang, C. Excited States Symmetry Breaking and In-Plane Polarization Cause Chiral Reversal in Diastereomers. Molecules 2021, 26, 4680. https://doi.org/10.3390/molecules26154680
Wang C, Wang J, Wang C. Excited States Symmetry Breaking and In-Plane Polarization Cause Chiral Reversal in Diastereomers. Molecules. 2021; 26(15):4680. https://doi.org/10.3390/molecules26154680
Chicago/Turabian StyleWang, Chenglong, Jingang Wang, and Chunyang Wang. 2021. "Excited States Symmetry Breaking and In-Plane Polarization Cause Chiral Reversal in Diastereomers" Molecules 26, no. 15: 4680. https://doi.org/10.3390/molecules26154680
APA StyleWang, C., Wang, J., & Wang, C. (2021). Excited States Symmetry Breaking and In-Plane Polarization Cause Chiral Reversal in Diastereomers. Molecules, 26(15), 4680. https://doi.org/10.3390/molecules26154680






