A Critical Look at Linus Pauling’s Influence on the Understanding of Chemical Bonding
Abstract
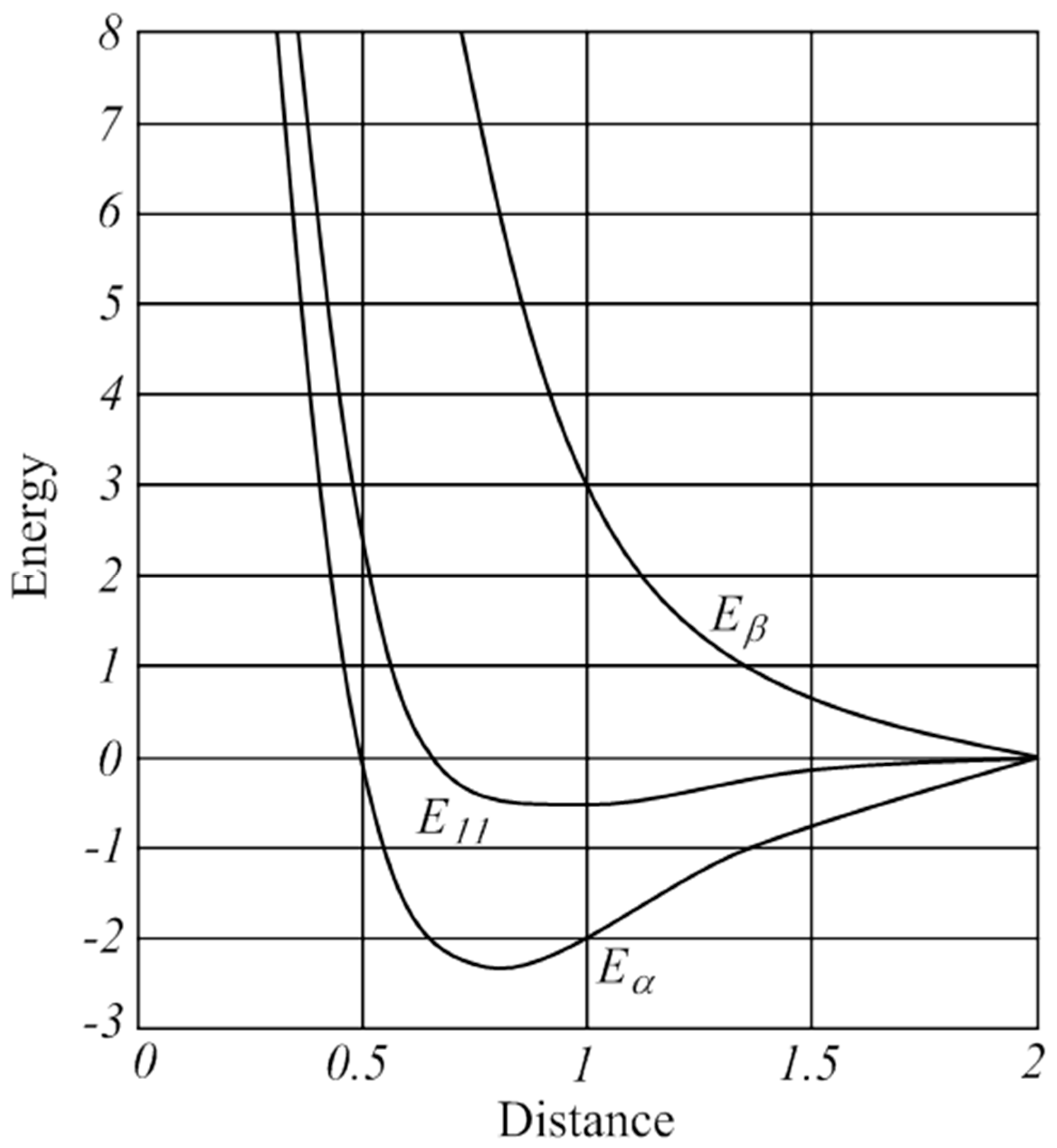
: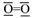 , but this is in conflict with its triplet ground state. Lewis already struggled with the triplet state of O2 in his presentation of the electron pair model, which appeared to be an anomaly for describing the bonding situation in molecules [13,14]. Pauling introduced in 1931 the concept of one-electron and three-electron bonds [96] and he suggested to write O2 with the following “structure A” (Figure 3).
, but this is in conflict with its triplet ground state. Lewis already struggled with the triplet state of O2 in his presentation of the electron pair model, which appeared to be an anomaly for describing the bonding situation in molecules [13,14]. Pauling introduced in 1931 the concept of one-electron and three-electron bonds [96] and he suggested to write O2 with the following “structure A” (Figure 3).Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References and Notes
- Serafini, A. Linus Pauling: A Man and His Science; Paragon House: New York, NY, USA, 1989. [Google Scholar]
- Newton, D.E. Linus Pauling: Scientist and Advocate; Facts on File, Inc.: New York, NY, USA, 1994. [Google Scholar]
- Goertzel, T.; Goertzel, B. Linus Pauling: A Life in Science and Politics; Basic Books: New York, NY, USA, 1995. [Google Scholar]
- Hager, T. Force of Nature: The Life of Linus Pauling; Simon and Schuster: New York, NY, USA, 1995. [Google Scholar]
- Davenport, D.A. The Many Lifes of Linus Pauling: A Review of Reviews. J. Chem. Ed. 1966, 73, A210–A212. [Google Scholar] [CrossRef] [Green Version]
- Pauling, L. The Nature of the Chemical Bond, 1st ed.; Cornell University Press: Ithaca, NY, USA, 1939; 2nd ed., 1948; 3rd ed., 1960. [Google Scholar]
- Mulliken, R. Life of a Scientist; Springer: Berlin/Heidelberg, Germany, 1989; pp. 60–61. [Google Scholar]
- Berry, S. A Little History of Atomic Theory at The University of Chicago from a Very Personal Perspective. Available online: https://sps.uchicago.edu/talks/StephenBerry1.pdf (accessed on 23 May 2021).
- Hückel, E. Ein Gelehrtenleben; Verlag Chemie: Weinheim, Germany, 1975. [Google Scholar]
- Heitler, W.; London, F. Wechselwirkung neutraler Atome und homöopolare Bindung nach der Quantenmechanik. Z. Phys. 1927, 44, 455–472. [Google Scholar] [CrossRef]
- Heisenberg, W. Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. Z. Phys. 1925, 33, 879–893. [Google Scholar] [CrossRef]
- Schrödinger, E. Quantisierung als Eigenwertproblem. Ann. Phys. 1926, 79, 361–376. [Google Scholar] [CrossRef]
- Lewis, G.N. The atom and the molecule. J. Am. Chem. Soc. 1916, 38, 762–785. [Google Scholar] [CrossRef] [Green Version]
- Lewis, G.N. Valence and the Structure of Atoms and Molecules; American Chemical Society Monograph Series: New York, NY, USA, 1923. [Google Scholar]
- Langmuir, I. The arrangement of electrons in atoms and molecules. J. Am. Chem. Soc. 1919, 41, 868–934. [Google Scholar] [CrossRef] [Green Version]
- Langmuir, I. Isomorphism, isosterism and covalence. J. Am. Chem. Soc. 1919, 41, 1543–1559. [Google Scholar] [CrossRef] [Green Version]
- Langmuir, I. The octet theory of valence and its applications with special reference to organic nitrogen compounds. J. Am. Chem. Soc. 1920, 42, 274–292. [Google Scholar] [CrossRef] [Green Version]
- Langmuir, I. Types of valence. Science 1921, 54, 59–67. [Google Scholar] [CrossRef]
- Shaik, S.; Hiberty, P.C. A Chemist’s Guide to Valence Bond Theory; John Wiley & Sons, Inc.: New York, NY, USA, 2007. [Google Scholar]
- Cooper, D. Valence Bond Theory; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Zhao, L.; Hermann, M.; Schwarz, W.H.E.; Frenking, G. The Lewis electron-pair bonding model: The physical background, a century later. Nat. Rev. Chem. 2019, 3, 35–47. [Google Scholar] [CrossRef]
- Mulliken, R.S. Electronic States and Band Spectrum Structure in Diatomic Molecules. IV. Hund’s Theory; Second Positive Nitrogen and Swan Bands; Alternating Intensities. Phys. Rev. 1927, 29, 637–649. [Google Scholar] [CrossRef]
- Mulliken, R.S. The assignment of quantum numbers for electrons in molecules. Phys. Rev. 1928, 32, 186–222. [Google Scholar] [CrossRef]
- Hund, F. Zur Deutung der Molekelspektren, Part I. Z. Phys. 1927, 40, 742–764. [Google Scholar] [CrossRef]
- Hund, F. Zur Deutung der Molekelspektren, Part II. Z. Phys. 1927, 42, 93–120. [Google Scholar] [CrossRef]
- Hund, F. Zur Deutung der Molekelspektren, Part III. Z. Phys. 1927, 43, 805–826. [Google Scholar] [CrossRef]
- Hund, F. Zur Deutung der Molekelspektren, Part IV. Z. Phys. 1928, 51, 759–795. [Google Scholar] [CrossRef]
- Hund, F. Zur Deutung der Molekelspektren, Part V. Z. Phys. 1930, 63, 719–751. [Google Scholar] [CrossRef]
- Coulson, C.A. Valence; The Book Received Two Significantly Revised Editions in 1961 and 1979, the Last One Being Edited by Roy MyWeeny and Published with the Title “Coulson”s Valence”; Oxford University: Oxford, UK, 1952. [Google Scholar]
- Pauling, L. Quantum mechanics of valence. Nature 1952, 170, 384–385. [Google Scholar] [CrossRef]
- Sidgwick, N.V. The Electronic Theory of Valency; Clarendon Press: Oxford, UK, 1927. [Google Scholar]
- Sidgwick, N.V. Some Physical Properties of the Covalent Link in Chemistry; Cornell University Press: Ithaca, NY, USA, 1933. [Google Scholar]
- Statements of Ref. [32]: Sidgwick, N.V. Some Physical Properties of the Covalent Link in Chemistry; Cornell University Press: Ithaca, NY, USA, 1933; p. 60. [Google Scholar]
- For a recent controversial discussion on the use of arrows for describing chemical bonds see the following paper and the next two references: Himmel, D.; Krossing, I.; Schnepf, A. Dative Bonds in Main-Group Compounds: A Case for Fewer Arrows! Angew. Chem. Int. Ed. 2013, 53, 370–374.
- Frenking, G. Dative Bonds in Main-Group Compounds: A Case for More Arrows! Angew. Chem. Int. Ed. 2014, 53, 6040–6046. [Google Scholar] [CrossRef]
- Himmel, D.; Krossing, I.; Schnepf, A. Dative or Not Dative? Angew. Chem. Int. Ed. 2014, 53, 6047–6048. [Google Scholar] [CrossRef] [PubMed]
- Lewis, G.N. Acids and bases. J. Frankl. Inst. 1938, 226, 293–313. [Google Scholar] [CrossRef]
- Dewar, M.J.S. A Review of π Complex Theory. Bull. Soc. Chim. Fr. 1951, 18, C79. [Google Scholar]
- Chatt, J.; Duncanson, L.A. Olefin co-ordination compounds. Part III. Infra-red spectra and structure: Attempted preparation of acetylene complexes. J. Chem. Soc. 1953, 2939–2947. [Google Scholar] [CrossRef]
- Lennard-Jones, J.E. The electronic structure of some diatomic molecules. Trans. Faraday Soc. 1929, 25, 668–686. [Google Scholar] [CrossRef]
- Fukui, K.; Yonezawa, T.; Shingu, H. A Molecular Orbital Theory of Reactivity in Aromatic Hydrocarbons. J. Chem. Phys. 1952, 20, 722–725. [Google Scholar] [CrossRef]
- Fukui, K.; Yonezawa, T.; Nagata, C. Theory of substitution in conjugated molecules. Bull. Chem. Soc. Jpn. 1954, 27, 423–427. [Google Scholar] [CrossRef] [Green Version]
- Fukui, K.; Yonezawa, T.; Nagata, C.; Shingu, H. Molecular Orbital Theory of Orientation in Aromatic, Heteroaromatic, and Other Conjugated Molecules. J. Chem. Phys. 1954, 22, 1433. [Google Scholar] [CrossRef] [Green Version]
- Fukui, K. Theory of Orientation and Stereoselection; Springer: Berlin/Heidelberg, Germany, 1975. [Google Scholar]
- Woodward, R.B.; Hoffmann, R. The Conservation of Orbital Symmetry; Verlag Chemie: Weinheim, Germany, 1970. [Google Scholar]
- Streitwieser, A. Molecular Orbital Theory for Organic Chemists; Wiley: New York, NY, USA, 1961. [Google Scholar]
- Gilchrist, T.L.; Storr, R.C. Organic Reactions and Orbital Symmetry, 2nd ed.; Cambridge University Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Borden, W.T. Modern Molecular Orbital Theory for Organic Chemists; Prentice-Hall: Englewood Cliffs, NJ, USA, 1975. [Google Scholar]
- Dewar, M.J.S. Molecular Orbital Theory for Organic Chemists; Prentice-Hall: Englewood Cliffs, NJ, USA, 1975. [Google Scholar]
- Sustmann, R. Orbital energy control of cycloaddition reactivity. Pure Appl. Chem. 1974, 40, 569–593. [Google Scholar] [CrossRef] [Green Version]
- Houk, K.N. Frontier molecular orbital theory of cycloaddition reactions. Acc. Chem. Res. 1975, 8, 361–369. [Google Scholar] [CrossRef]
- Fleming, I. Frontier Orbitals and Organic Chemical Reactions; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Albright, T.A.; Burdett, J.K.; Whangbo, M.-H. Orbital Interactions in Chemistry, 1st ed.; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Frenking, G.; Fernández, I.; Holzmann, N.; Pan, S.; Krossing, I.; Zhou, M.F. Metal-CO Bonding in Mononuclear Transition Metal Carbonyl Complexes. J. Am. Chem. Soc. 2021, 1, 623–645. [Google Scholar]
- Hoffmann, R.; Howell, J.M.; Muetterties, E.L. Molecular orbital theory of pentacoordinate phosphorus. J. Am. Chem. Soc. 1972, 94, 3047–3058. [Google Scholar] [CrossRef]
- Lein, M.; Frenking, G. Chemical Bonding in Octahedral XeF6 and SF6. Aust. J. Chem. 2004, 57, 1191–1195. [Google Scholar] [CrossRef]
- Krapp, A.; Bickelhaupt, F.M.; Frenking, G. Orbital Overlap and Chemical Bonding. Chem. Eur. J. 2006, 12, 9196–9216. [Google Scholar] [CrossRef] [PubMed]
- Huber, K.P.; Herzberg, G. Molecular Spectra and Molecular Structure IV. Constants of Diatomic Molecules; Van Nostrand-Reinhold: New York, NY, USA, 1979. [Google Scholar]
- Shaik, S.; Danovich, D.; Wu, W.; Su, P.; Rzepa, H.S.; Hiberty, P.C. Quadruple Bonding in C2 and Analogous Eight-Valence Electron Species. Nat. Chem. 2012, 4, 195–200. [Google Scholar] [CrossRef]
- Shaik, S.; Rzepa, H.S.; Hoffmann, R. One Molecule, Two Atoms, Three Views, Four Bonds? Angew. Chem. Int. Ed. 2013, 52, 3020–3033. [Google Scholar] [CrossRef] [PubMed]
- Danovich, D.; Hiberty, P.C.; Wu, W.; Rzepa, H.S.; Shaik, S. The Nature of the Fourth Bond in the Ground State of C2: The Quadruple Bond Conundrum. Chem. Eur. J. 2014, 20, 6220–6232. [Google Scholar] [CrossRef] [PubMed]
- Shaik, S.; Danovich, D.; Braida, B.; Hiberty, P.C. The Quadruple Bonding in C2 Reproduces the Properties of the Molecule. Chem. Eur. J. 2016, 22, 4116–4128. [Google Scholar] [CrossRef] [PubMed]
- Frenking, G.; Hermann, M. Critical Comments on “One Molecule, Two Atoms, Three Views, Four Bonds?”. Angew. Chem. Int. Ed. 2013, 52, 5922–5925. [Google Scholar] [CrossRef] [PubMed]
- Danovich, D.; Shaik, S.; Rzepa, H.S.; Hoffmann, R. A Response to the Critical Comments on “One Molecule, Two Atoms, Three Views, Four Bonds?”. Angew. Chem. Int. Ed. 2013, 52, 5926–5928. [Google Scholar] [CrossRef] [PubMed]
- Frenking, G.; Hermann, M. Comment on “The Quadruple Bonding in C2 Reproduces the Properties of the Molecule”. Chem. Eur. J. 2016, 22, 18975–18976. [Google Scholar] [CrossRef] [PubMed]
- Shaik, S.; Danovich, D.; Braida, B.; Hiberty, P.C. A Response to a Comment by G. Frenking and M. Hermann on: “The Quadruple Bonding in C2 Reproduces the Properties of the Molecule”. Chem. Eur. J. 2016, 22, 18977–18980. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hermann, M.; Frenking, G. The Chemical Bond in C2. Chem. Eur. J. 2016, 22, 4100–4108. [Google Scholar] [CrossRef]
- Zou, W.; Cremer, D. C2 in a Box: Determining Its Intrinsic Bond Strength for the X1Σg+ Ground State. Chem. Eur. J. 2016, 22, 4087–4099. [Google Scholar] [CrossRef]
- Piris, M.; Lopez, X.; Ugalde, J.M. The Bond Order of C2 from a Strictly N-Representable Natural Orbital Energy Functional Perspective. Chem. Eur. J. 2016, 22, 4109–4115. [Google Scholar] [CrossRef]
- Cooper, D.L.; Ponec, R.; Kohout, M. New insights from domain-averaged Fermi holes and bond order analysis into the bonding conundrum in C2. Mol. Phys. 2016, 114, 1270–1284. [Google Scholar] [CrossRef]
- Xu, L.T.; Dunning, T.H., Jr. Insights into the Perplexing Nature of the Bonding in C2 from Generalized Valence Bond Calculations. J. Chem. Theory Comput. 2014, 10, 195–201. [Google Scholar] [CrossRef]
- de Sousa, D.W.O.; Nascimento, M.A.C. Is There a Quadruple Bond in C2? J. Chem. Theory Comput. 2016, 12, 2234–2241. [Google Scholar] [CrossRef]
- Zhong, R.; Zhang, M.; Xu, H.; Su, Z. Latent harmony in dicarbon between VB and MO theories through orthogonal hybridization of 3σg and 2σu. Chem. Sci. 2016, 7, 1028–1032. [Google Scholar] [CrossRef] [Green Version]
- West, A.C.; Schmidt, M.W.; Gordon, M.S.; Ruedenberg, K. Intrinsic Resolution of Molecular Electronic Wave Functions and Energies in Terms of Quasi-atoms and Their Interactions. J. Phys. Chem. A 2017, 121, 1086–1105. [Google Scholar] [CrossRef]
- Liu, Y.; Frankcombe, T.J.; Schmidt, T.W. Chemical bonding motifs from a tiling of the many-electron wavefunction. Phys. Chem. Chem. Phys. 2016, 18, 13385–13394. [Google Scholar] [CrossRef]
- Hiberty, P.C.; Braida, B. Pleading for a Dual Molecular-Orbital/Valence-Bond Culture. Angew. Chem. Int. Ed. 2018, 57, 5994–6002. [Google Scholar] [CrossRef]
- Laws, B.A.; Gibson, S.T.; Lewis, B.R.; Field, R.W. The dicarbon bonding puzzle viewed with photoelectron imaging. Nature Commun. 2019, 10, 5199. [Google Scholar] [CrossRef]
- Koopmans, T. Über die Zuordnung von Wellenfunktionen und Eigenwerten zu den einzelnen Elektronen eines Atoms. Physica 1934, 1, 104–113. [Google Scholar] [CrossRef]
- Ballard, E. Photoelectron Spectroscopy and Molecular Orbital Theory; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Hund, F. Zur Frage der chemischen Bindung. Z. Phys. 1932, 73, 1–30. [Google Scholar] [CrossRef]
- Hund, F. Bemerkung zu meiner Arbeit: Zur Frage der chemischen Bindung. Z. Phys. 1932, 74, 429–430. [Google Scholar] [CrossRef]
- Hund, F. Zur Frage der chemischen Bindung. II. Zum Verständnis der organischen Chemie. Z. Phys. 1932, 73, 565–577. [Google Scholar] [CrossRef]
- Dewar, M.J.S. Chemical implications of σ Conjugation. J. Am. Chem. Soc. 1984, 106, 669–682. [Google Scholar] [CrossRef]
- Mulliken, R.S. Electronic Structure of Polyatomic Molecule and Valence. Phys. Rev. 1932, 40, 55–62. [Google Scholar] [CrossRef]
- Pauling, L. The Nature of the Chemical Bond. I. Application of Results Obtained from the Quantum Mechanics and from a Theory of Paramagnetic Susceptibility to the Structure of Molecules. J. Am. Chem. Soc. 1931, 53, 1367–1400. [Google Scholar] [CrossRef]
- Slater, J.C. Directed valence in polyatomic molecules. Phys. Rev. 1931, 37, 481–489. [Google Scholar] [CrossRef]
- Bethe, H.; Fermi, E. About the interaction of two electrons. Z. Phys. 1932, 77, 296–306. [Google Scholar] [CrossRef]
- Hückel, E. Quantentheoretische Beiträge zum Benzolproblem. Z. Phys. 1931, 70, 204–286. [Google Scholar] [CrossRef]
- Hellmann, H. A New Approximation Method in the Problem of Many Electrons. J. Chem. Phys. 1935, 3, 61. [Google Scholar] [CrossRef]
- Kutzelnigg, W. The Physical Mechanism, of the Chemical Bond. Angew. Chem. Int. Ed. Engl. 1973, 12, 546–562. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Ivanic, J.; Ruedenberg, K. The Physical Origin of the Chemical Bond. In The Chemical Bond. 1. Fundamental Aspects of Chemical Bonding; Frenking, G., Shaik, S., Eds.; Wiley-VCH: Weinheim, Germany, 2014; pp. 1–67. [Google Scholar]
- Ruedenberg, K. Physical nature of chemical bond. Rev. Mod. Phys. 1962, 34, 326–376. [Google Scholar] [CrossRef]
- Statements of ref. [6]: Pauling, L. The structure of molecules and complex ions involving bonds with partial double-bond character. In The Nature of the Chemical Bond, 3rd ed.; Cornell University Press: Ithaca, NY, USA, 1960; pp. 331–349. [Google Scholar]
- Statements of ref. [6]: Pauling, L. The one-electron and the three-electron bond; electron-deficient substances. In The Nature of the Chemical Bond, 3rd ed.; Cornell University Press: Ithaca, NY, USA, 1960; pp. 386–387. [Google Scholar]
- Rayón, V.M.; Frenking, G. Bis(benzene)chromium Is a δ-Bonded Molecule and Ferrocene Is a π-Bonded Molecule. Organometallics 2003, 22, 3304–3308. [Google Scholar] [CrossRef]
- Pauling, L. The Nature of the Chemical Bond. II. The One Electron Bond and the Three Electron Bond. J. Am. Chem. Soc. 1931, 53, 3225–3237. [Google Scholar] [CrossRef]
- Wheland, G.W.; Pauling, L. A Quantum Mechanical Discussion of Orientation of Substituents in Aromatic Molecules. J. Am. Chem. Soc. 1935, 57, 2086–2095. [Google Scholar] [CrossRef]
- Gerratt, J.; Cooper, D.L.; Karadakov, P.B.; Raimondi, M. Modern valence bond theory. Chem. Soc. Rev. 1997, 26, 87–100. [Google Scholar] [CrossRef]
- Shaik, S.; Shurki, A. Valence Bond Diagrams and Chemical Reactivity. Angew. Chem. Int. Ed. 1999, 38, 585–625. [Google Scholar] [CrossRef]
- Corry, T.A.; O’Malley, P.J. Localized Bond Orbital Analysis of the Bonds of O2. J. Phys. Chem. A 2020, 124, 9771–9776. [Google Scholar] [CrossRef] [PubMed]
- Statements of ref. [19]: Shaik, S.; Hiberty, P.C. Mapping molecular orbital—configuration interaction to valence bond wave functions. In A Chemist’s Guide to Valence Bond Theory; John Wiley & Sons, Inc.: New York, NY, USA, 2007; p. 94. [Google Scholar]
- Shaik, S. A Personal Story on a Renaissance in Valence Bond Theory: A Theory Coming of Age! Comp. Theor. Chem. 2017, 1116, 2–31. [Google Scholar] [CrossRef]
- Hiberty, P.C.; Shaik, S. Bridging Cultures. In The Chemical Bond: Fundamental Aspects of Chemical Bonding; Frenking, G., Shaik, S., Eds.; Wiley-VCH: Weinheim, Germany, 2014; pp. 69–90. [Google Scholar]
- Shaik, S.; Danovich, D.; Hiberty, P.C. Valence Bond Theory—Its Birth, Struggles with Molecular Orbital Theory, Its Present State and Future Prospects. Molecules 2021, 26, 1624. [Google Scholar] [CrossRef]
- In ref. [14], p. 163, Lewis calls quantum theory “the entering wedge of scientific bolshevism”.
- Shaik, S.; Maitre, P.; Sini, G.; Hiberty, P.C. The charge-shift bonding concept. Electron-pair bonds with very large ionic-covalent resonance energies. J. Am. Chem. Soc. 1992, 114, 7861–7866. [Google Scholar] [CrossRef]
- Shaik, S.; Danovich, D.; Wu, W.; Hiberty, P.C. Charge-shift bonding and its manifestations in chemistry. Nat. Chem. 2009, 1, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Shaik, S.; Danovich, D.; Galbraith, J.M.; Braida, B.; Wu, W.; Hiberty, P.C. Charge-Shift Bonding: A New and Unique Form of Bonding. Angew. Chem. Int. Ed. 2020, 59, 984–1001. [Google Scholar] [CrossRef]
- For a highly entertaining article declared to be a “Socratic-Talmudic trialogue” see: Hiberty, P.C.; Danovich, D.; Shaik, S. A Conversation on New Types of Chemical Bonds. Isr. J. Chem. 2021. [CrossRef]
- Zhang, H.; Danovich, D.; Wu, W.; Braida, B.; Hiberty, P.C.; Shaik, S. Charge-Shift Bonding Emerges as a Distinct Electron-Pair Bonding Family from Both Valence Bond and Molecular Orbital Theories. J. Chem. Theory Comput. 2014, 10, 2410–2418. [Google Scholar] [CrossRef] [PubMed]
- Gershoni-Poranne, R.; Chen, P. The Carbon–Nitrogen Bonds in Ammonium Compounds Are Charge Shift Bonds. Chem. Eur. J. 2017, 23, 4659–4668. [Google Scholar] [CrossRef]
- Frenking, G. Covalent Bonding and Charge Shift Bonds: Comment on “The Carbon–Nitrogen Bonds in Ammonium Compounds Are Charge Shift Bonds”. Chem. Eur. J. 2017, 23, 18320–18324. [Google Scholar] [CrossRef]
- Chen, P.; Gershoni-Poranne, R. Response to “Covalent Bonding and Charge Shift Bonds: Comment on ‘The Carbon–Nitrogen Bonds in Ammonium Compounds Are Charge Shift Bonds’”. Chem. Eur. J. 2017, 23, 18325–18329. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Fedik, N.; Martinez-Martinez, C.; Ciborowski, S.M.; Zhang, X.; Boldyrev, A.I.; Bowen, K.H. Realization of Lewis Basic Sodium Anion in the NaBH3− Cluster. Angew. Chem. Int. Ed. 2019, 58, 13789–13793. [Google Scholar] [CrossRef]
- Pan, S.; Frenking, G. Comment on “Realization of Lewis Basic Sodium Anion in the NaBH3− Cluster”. Angew. Chem. Int. Ed. 2020, 59, 8756–8759. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Fedik, N.; Martinez-Martinez, C.; Ciborowski, S.M.; Zhang, X.; Boldyrev, A.I.; Bowen, K.H. Reply to the Comment on “Realization of Lewis Basic Sodium Anion in the NaBH3− Cluster”. Angew. Chem. Int. Ed. 2020, 59, 8760–8764. [Google Scholar] [CrossRef] [PubMed]
- Foroutan-Nejad, C. The Na⋅⋅⋅B Bond in NaBH3−: A Different Type of Bond. Angew. Chem. Int. Ed. 2020, 59, 20900–20903. [Google Scholar] [CrossRef]
- Salvador, P.; Vos, E.; Corral, I.; Andrada, D.M. Beyond the Classical Electron-Sharing and Dative Bond Picture: Case of the Spin-Polarized Bond. Angew. Chem. Int. Ed. 2021, 60, 1498–1502. [Google Scholar] [CrossRef]
- Radenković, S.; Shaik, S.S.; Braïda, B. Na⋅⋅⋅B Bond in NaBH3−: Solving the Conundrum. Angew. Chem. Int. Ed. 2021, 60, 12723–12726. [Google Scholar] [CrossRef]
- Pino-Rios, R.; Inostroza, D.; Tiznad, W. Neither too Classic nor too Exotic: One-Electron Na·B Bond in NaBH3− Cluster. Angew. Chem. Int. Ed. 2021, 60, 12747–12753. [Google Scholar] [CrossRef] [PubMed]
- Grünenberg, J. Vielleicht sogar richtig—Aber trotzdem sinnlos. Nachr. Chem. 2016, 64, 773–775. [Google Scholar]
- The Pauling Blog. Available online: https://paulingblog.wordpress.com/category/facets-of-linus-pauling/ (accessed on 23 May 2021).
- Landis, C.R.; Weinhold, F. Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective; Cambridge University Press: Cambridge, MA, USA, 2005. [Google Scholar]
- The fundamental role of spatial symmetry in chemistry, physics and biology has been emphasized in this and the following article and further cited papers therein by Martin Quack: Quack, M. The concept of law and models in chemistry. Eur. Rev. 2014, 22, S50–S86.
- Quack, M. Molecular spectra, reaction dynamics, symmetries and life. Chimia 2003, 57, 147. [Google Scholar] [CrossRef] [Green Version]
- Truhlar, D. Valence bond theory for chemical dynamics. J. Comput. Chem. 2007, 28, 73–86. [Google Scholar] [CrossRef] [PubMed]
- Havenith, R.W.A.; Cunha, A.V.; Klein, J.E.M.N.; Perolari, F.; Feng, X. The electronic structure of carbones revealed: Insights from valence bond theory. Phys. Chem. Chem. Phys. 2021, 23, 3327–3334. [Google Scholar] [CrossRef]
- Vemulapalli, G.K. Theories of the chemical bond and its true nature. Found. Chem. 2008, 10, 167–176. [Google Scholar] [CrossRef]
- Hoffmann, R.; Shaik, S.; Hiberty, P.C. A conversation on VB vs MO theory: A never-ending rivalry? Acc. Chem. Res. 2003, 36, 750–756. [Google Scholar] [CrossRef] [PubMed]
- Murrel, J.N. The origins and later developments of molecular orbital theory. Int. J. Quantum Chem. 2012, 112, 2875–2879. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, W. Ab initio valence bond theory: A brief history, recent developments, and near future. J. Chem. Phys. 2020, 153, 090902. [Google Scholar] [CrossRef]
- Mo, Y.; Song, L.; Lin, Y. Block-Localized Wavefunction (BLW) Method at the Density Functional Theory (DFT) Level. J. Phys. Chem. A 2007, 111, 8291–8301. [Google Scholar] [CrossRef]
- Mo, Y. The Block-Localized Wavefunction (BLW) Perspective of Chemical Bonding. In The Chemical Bond. 1. Fundamental Aspects of Chemical Bonding; Frenking, G., Shaik, S., Eds.; Wiley-VCH: Weinheim, Germany, 2014; pp. 199–232. [Google Scholar]
- Grofe, A.; Zhao, R.; Wildman, A.; Stetina, T.F.; Li, X.; Bao, P.; Gao, J. Generalization of Block-Localized Wave Function for Constrained Optimization of Excited Determinants. J. Chem. Theory Comput. 2021, 17, 277–289. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, S.; Frenking, G. A Critical Look at Linus Pauling’s Influence on the Understanding of Chemical Bonding. Molecules 2021, 26, 4695. https://doi.org/10.3390/molecules26154695
Pan S, Frenking G. A Critical Look at Linus Pauling’s Influence on the Understanding of Chemical Bonding. Molecules. 2021; 26(15):4695. https://doi.org/10.3390/molecules26154695
Chicago/Turabian StylePan, Sudip, and Gernot Frenking. 2021. "A Critical Look at Linus Pauling’s Influence on the Understanding of Chemical Bonding" Molecules 26, no. 15: 4695. https://doi.org/10.3390/molecules26154695
APA StylePan, S., & Frenking, G. (2021). A Critical Look at Linus Pauling’s Influence on the Understanding of Chemical Bonding. Molecules, 26(15), 4695. https://doi.org/10.3390/molecules26154695






