Isavuconazole: Thermodynamic Evaluation of Processes Sublimation, Dissolution and Partition in Pharmaceutically Relevant Media
Abstract
:1. Introduction
2. Results and Discussion
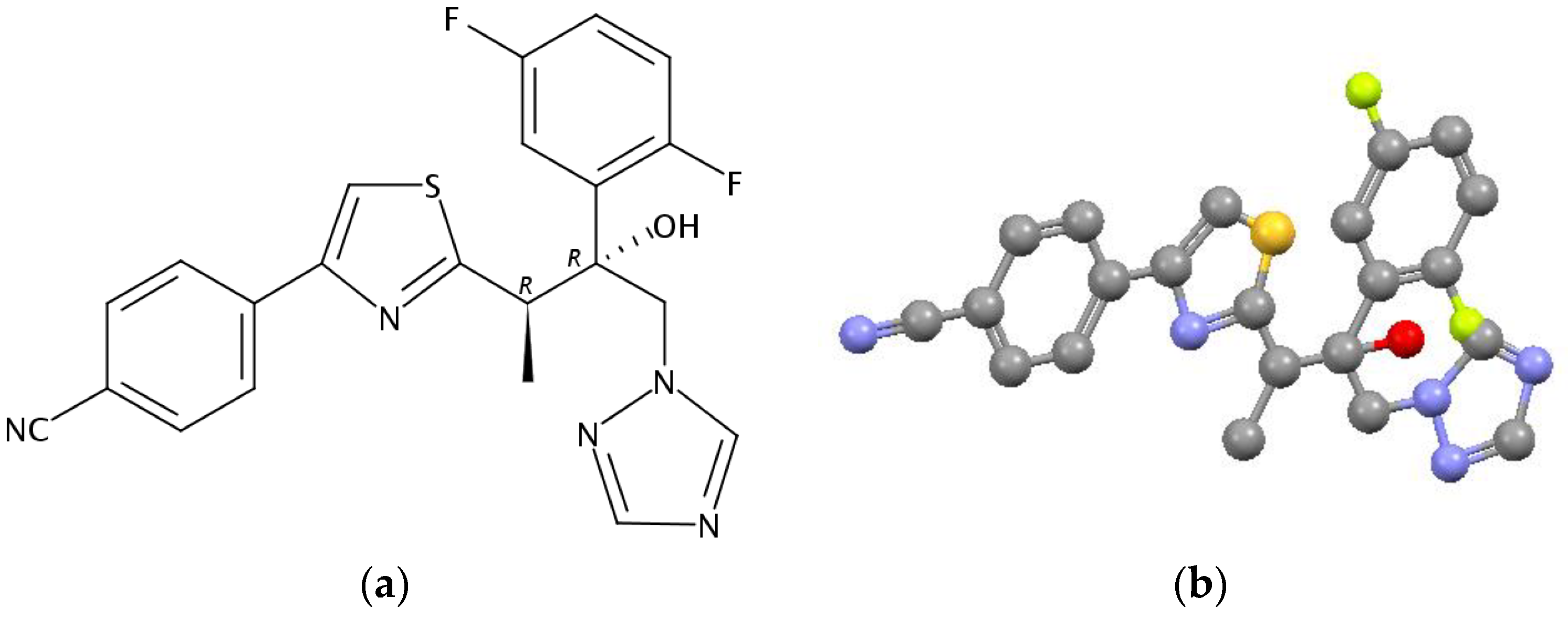
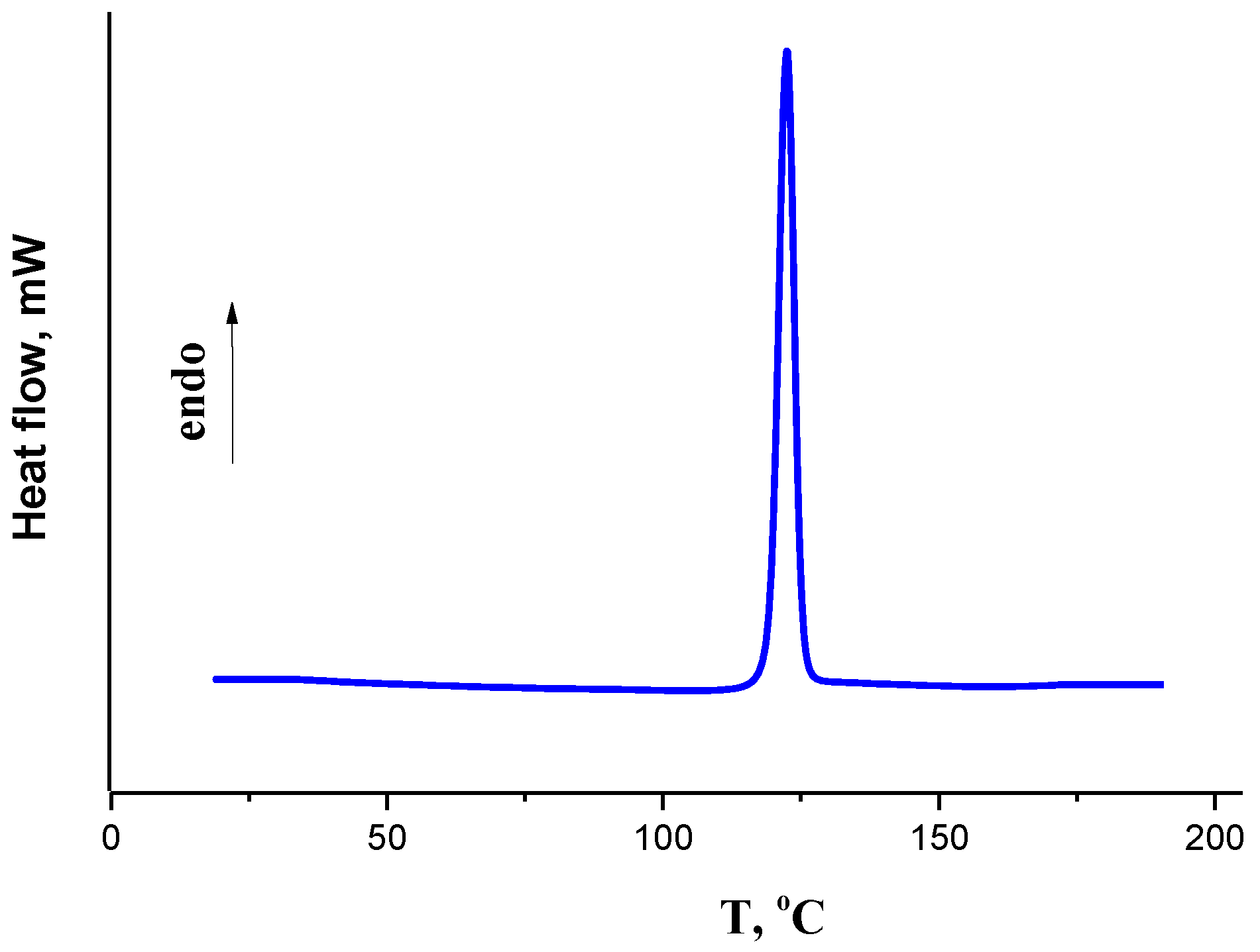
2.1. Thermophysical Properties
2.2. Sublimation
2.2.1. Experimental Results
2.2.2. Clusterization Approach
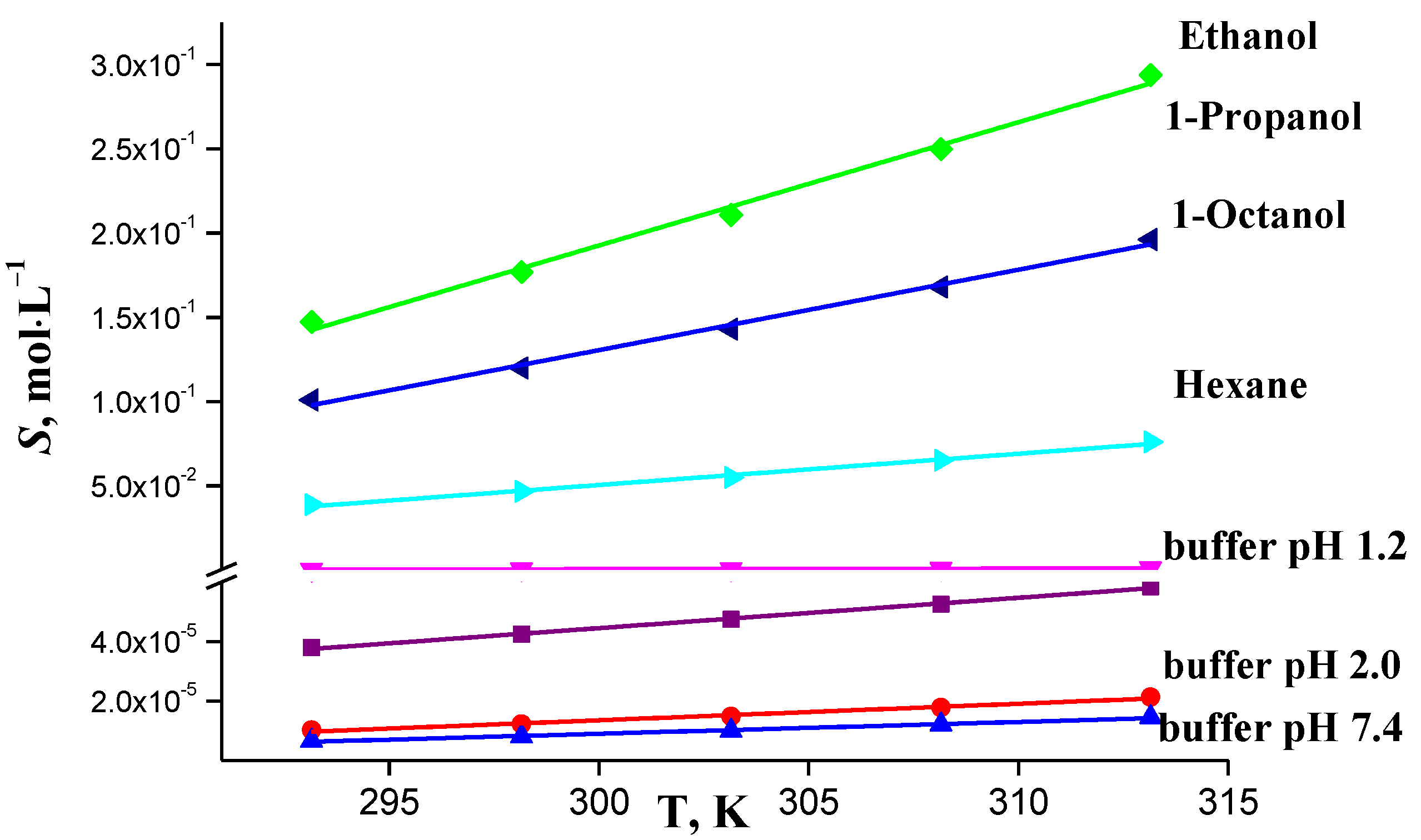
2.3. Solubility
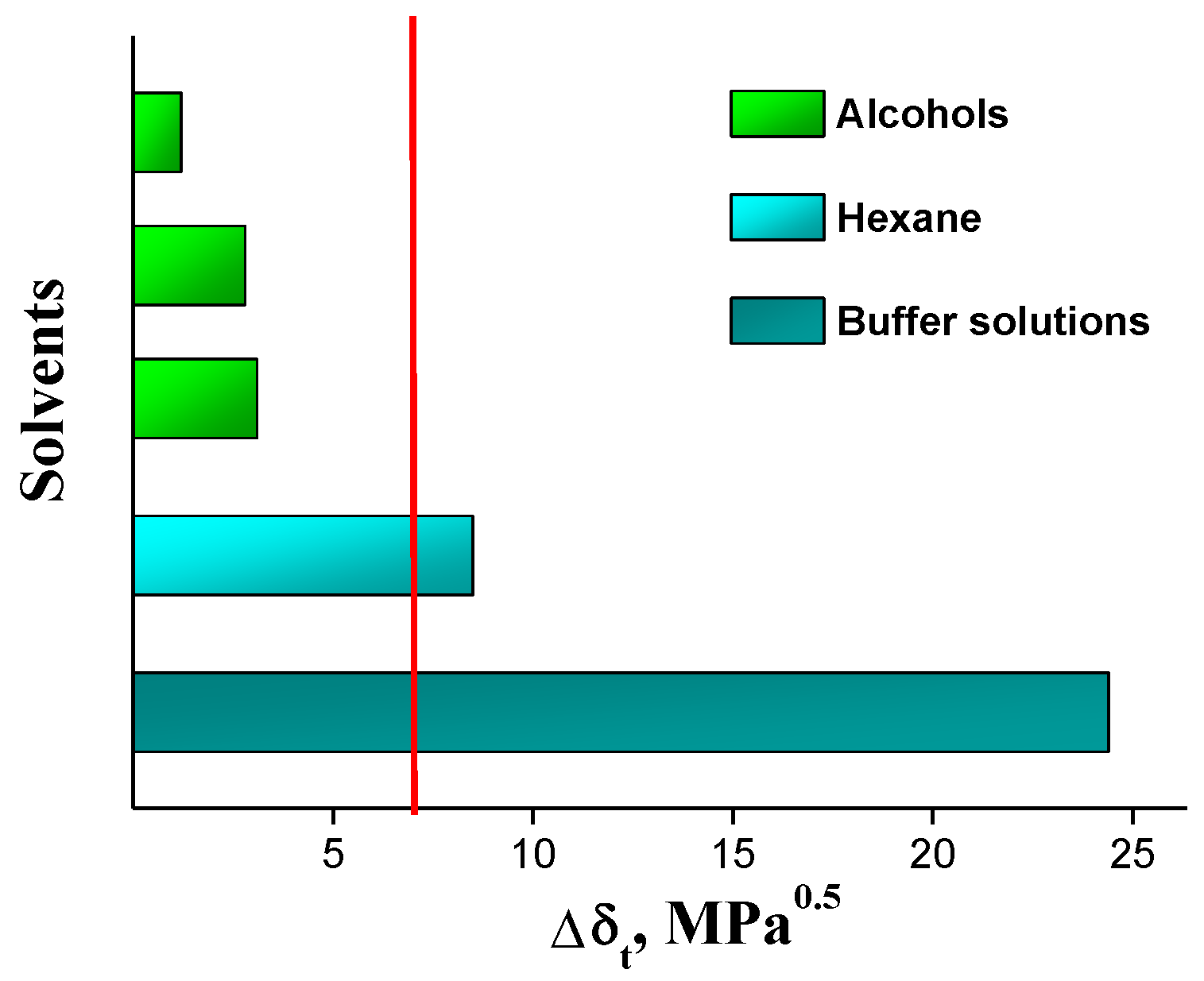
2.4. Hansen Solubility Parameters
2.5. Solubility Data Modeling
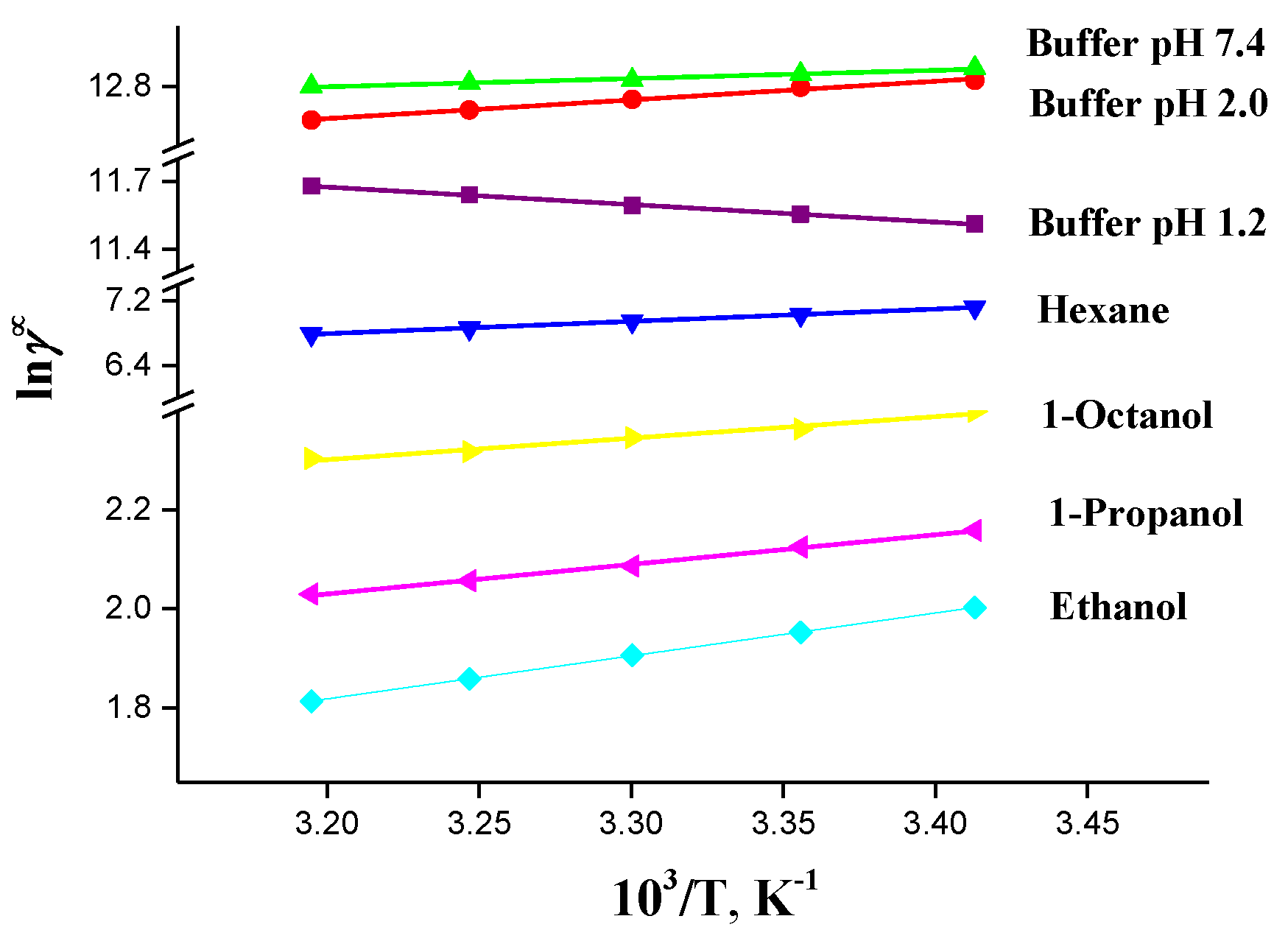
2.6. Dissolution Thermodynamics
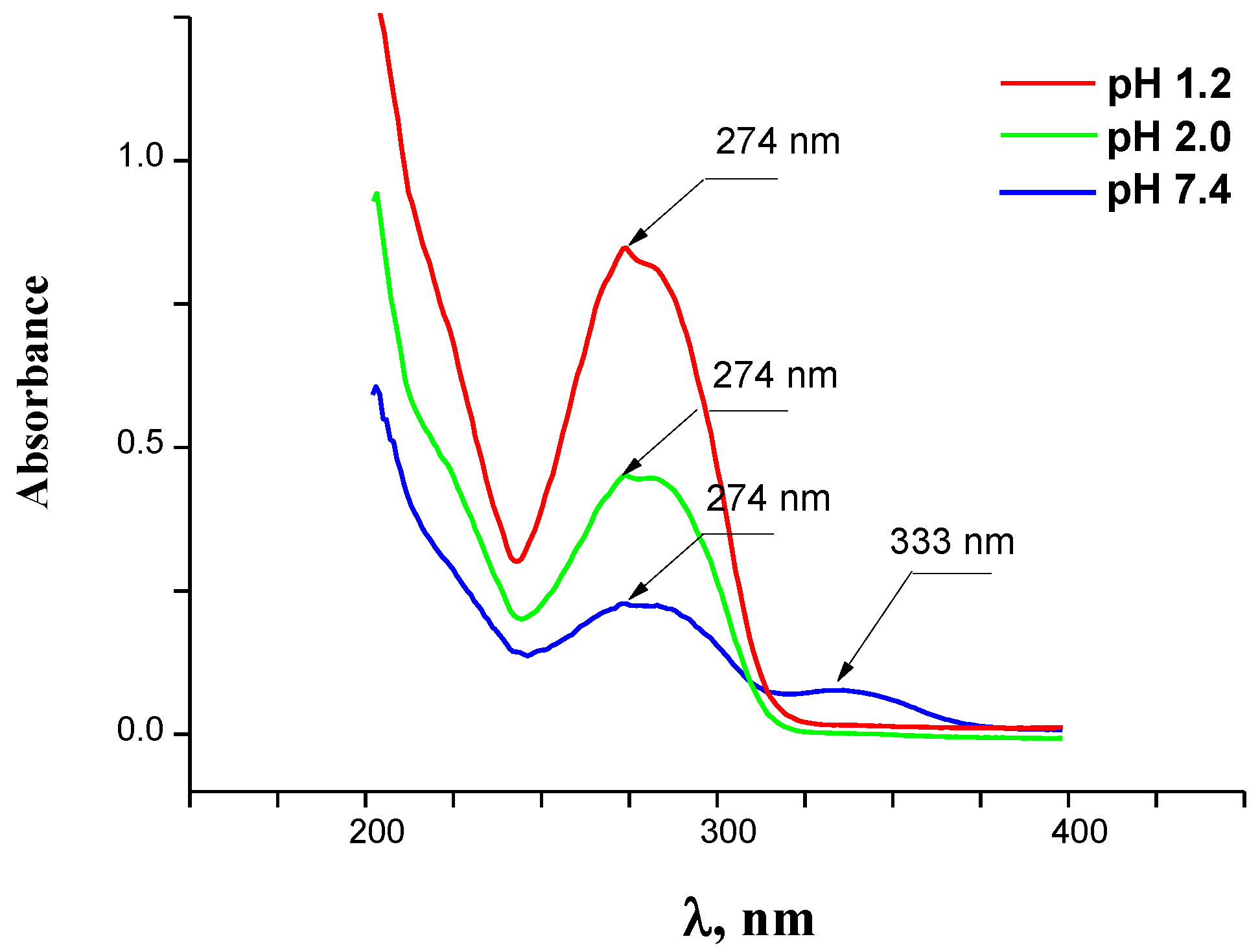
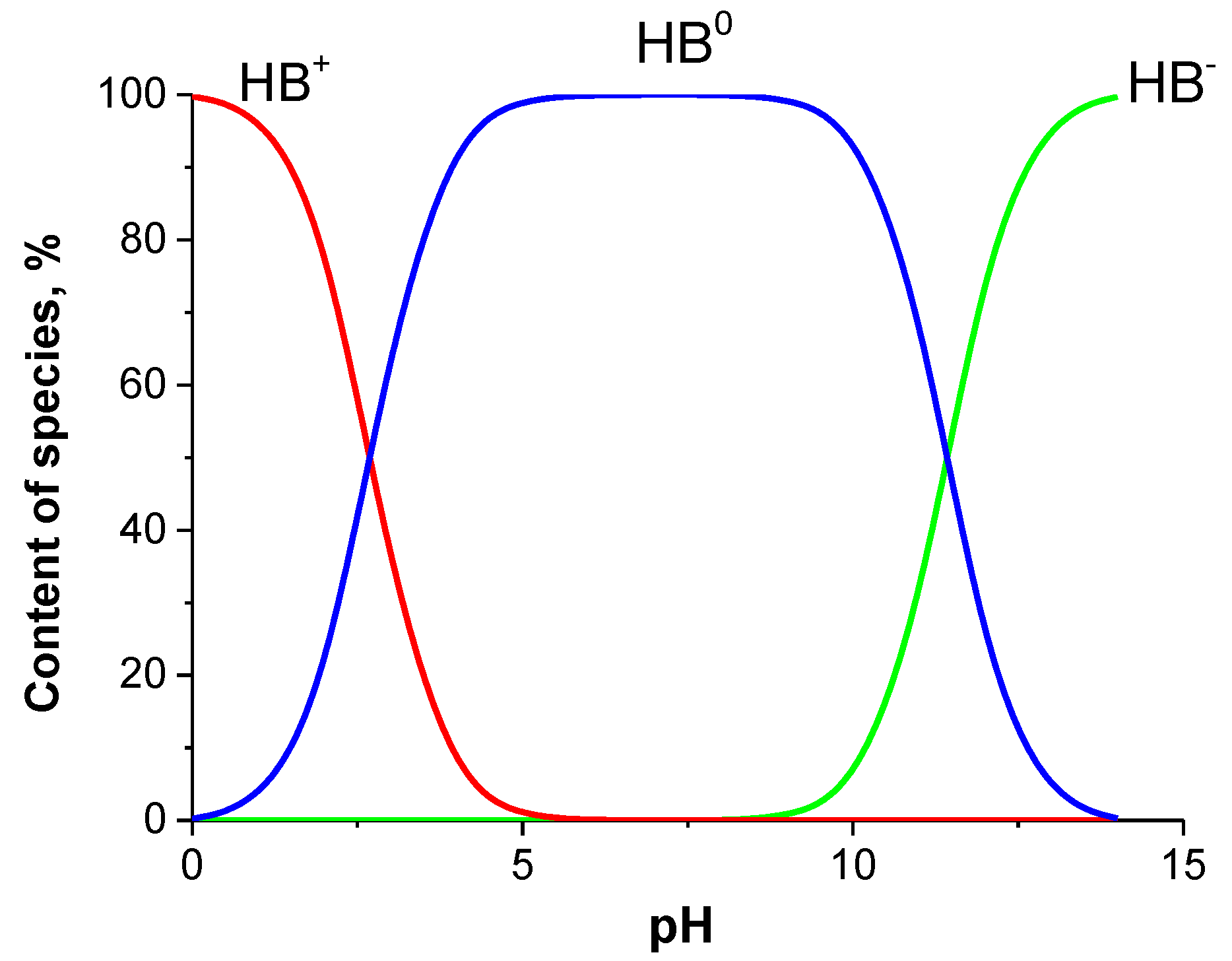
2.7. Lipophilicity
3. Materials and Methods
3.1. Materials
3.2. Differential Scanning Calorimetry
3.3. Powder X-ray Diffraction
3.4. Vapor Pressure Measurements
3.5. Solubility
3.6. Partition Experiment
3.7. Theoretical Basis
3.7.1. Hansen Solubility Parameters
3.7.2. Modified Apelblat Model
3.7.3. Van’t Hoff Equation
3.7.4. Data Correlation
3.8. Dissolution Thermodynamics
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Enoch, D.A.; Ludlam, H.A.; Brown, N.M. Invasive fungal infections: A review of epidemiology and management options. J. Med. Microbiol. 2006, 55, 809–818. [Google Scholar] [CrossRef]
- Badiee, P.; Hashemizadeh, Z. Opportunistic invasive fungal infections: Diagnosis & clinical management. Indian J. Med. Res. 2014, 139, 195–204. [Google Scholar]
- Maertens, J.; Groll, A.H.; Cordonnier, C.; De La Cámara, R.; Roilides, E.; Marchetti, O. Treatment and timing in invasive mould disease. J. Antimicrob. Chemother. 2010, 66, i37–i43. [Google Scholar] [CrossRef] [Green Version]
- Kontoyiannis, D.P.; Marr, K.A.; Park, B.J.; Alexander, B.D.; Anaissie, E.J.; Walsh, T.J.; Ito, J.; Andes, D.; Baddley, J.W.; Brown, J.M.; et al. Prospective Surveillance for Invasive Fungal Infections in Hematopoietic Stem Cell Transplant Recipients, 2001–2006: Overview of the Transplant-Associated Infection Surveillance Network (TRANSNET) Database. Clin. Infect. Dis. 2010, 50, 1091–1100. [Google Scholar] [CrossRef]
- Skiada, A.; Pagano, L.; Groll, A.; Zimmerli, S.; Dupont, B.; Lagrou, K.; Lass-Florl, C.; Bouza, E.; Klimko, N.; Gaustad, P.; et al. Zygomycosis in Europe: Analysis of 230 cases accrued by the registry of the European Confederation of Medical Mycology (ECMM) Working Group on Zygomycosis between 2005 and 2007. Clin. Microbiol. Infect. 2011, 17, 1859–1867. [Google Scholar] [CrossRef] [Green Version]
- Girmenia, C. New generation azole antifungals in clinical investigation. Expert Opin. Investig. Drugs 2009, 18, 1279–1295. [Google Scholar] [CrossRef]
- Livermore, J.; Hope, W. Evaluation of the pharmacokinetics and clinical utility of isavuconazole for treatment of invasive fungal infections. Expert Opin. Drug Metab. Toxicol. 2012, 8, 759–765. [Google Scholar] [CrossRef]
- Peyton, L.R.; Gallagher, S.; Hashemzadeh, M. Triazole antifungals: A review. Drugs Today 2015, 51, 705–718. [Google Scholar] [CrossRef]
- Pasqualotto, A.C.; Denning, D. New and emerging treatments for fungal infections. J. Antimicrob. Chemother. 2008, 61, i19–i30. [Google Scholar] [CrossRef] [Green Version]
- Kerns, E.; Di, L. Druglike Properties: Concepts, Structure Design and Methods; Wermuth, C., Ed.; Elsevier: New York, NY, USA, 2008. [Google Scholar]
- Garzón, L.C.; Martínez, F. Temperature Dependence of Solubility for Ibuprofen in Some Organic and Aqueous Solvents. J. Solut. Chem. 2004, 33, 1379–1395. [Google Scholar] [CrossRef]
- Domańska, U.; Pobudkowska, A.; Pelczarska, A.; Gierycz, P. pKa and Solubility of Drugs in Water, Ethanol, and 1-Octanol. J. Phys. Chem. B 2009, 113, 8941–8947. [Google Scholar] [CrossRef]
- Della Gatta, G.; Badea, E.; Jozwiak, M.; Barone, G. Hydrophobic−Hydrophilic Solvation of Variously Substituted N-Alkylureas in Aqueous Solution: A Calorimetric Study at a Temperature of 298.15 K. J. Chem. Eng. Data 2009, 54, 2739–2744. [Google Scholar] [CrossRef]
- Almeida, A.R.; Monte, M.J. Thermodynamic study of phase transitions of imidazoles and 1-methylimidazoles. J. Chem. Thermodyn. 2012, 44, 163–168. [Google Scholar] [CrossRef]
- Brittain, H.G.; Bogdanowich, S.J.; Bugay, D.E.; DeVincentis, J.; Lewen, G.; Newman, A.W. Physical characterization of pharmaceutical solids. Pharm. Res. 1991, 8, 963–973. [Google Scholar] [CrossRef] [PubMed]
- Testa, B.; Carrupt, P.A.; Lisa, G. Lipophilicity in Drug Action and Toxicology; VCH Publishers: Weinheim, Germany, 1996; pp. 49–71. [Google Scholar] [CrossRef]
- Clarke, E.C.W.; Glew, D.N. Evaluation of thermodynamic functions from equilibrium constants. Trans. Faraday Soc. 1966, 62, 539–547. [Google Scholar] [CrossRef]
- Perlovich, G.L. Formation Thermodynamics of Two-Component Molecular Crystals: Polymorphism, Stoichiometry, and Impact of Enantiomers. Cryst. Growth Des. 2020, 20, 5526–5537. [Google Scholar] [CrossRef]
- Allen, F.H.; Kennard, O. 3D search and research using the Cambridge Structural Database. Chem. Des. Automat. News 1993, 8, 31. [Google Scholar]
- Raevsky, O.A.; Gerasimenko, V.A.; Trepalin, S.V. MOLDIVS (MOLecular DIVersity & Similarity) Program Package. Registration by Russian State Patent Agency N 990093, 26 February 1999. [Google Scholar]
- Raevsky, O.A.; Grigor’ev, V.J.; Trepalin, S.V. HYBOT Program Package. Registration by Russian State Patent Agency N 990090, 26 February 1999. [Google Scholar]
- Liu, X.; Testa, B.; Fahr, A. Lipophilicity and Its Relationship with Passive Drug Permeation. Pharm. Res. 2010, 28, 962–977. [Google Scholar] [CrossRef]
- Völgyi, G.; Baka, E.; Box, K.J.; Comer, J.E.; Takács-Novák, K. Study of pH-dependent solubility of organic bases. Revisit of Henderson-Hasselbalch relationship. Anal. Chim. Acta 2010, 673, 40–46. [Google Scholar] [CrossRef]
- Po, H.N.; Senozan, N.M. The Henderson-Hasselbalch Equation: Its History and Limitations. J. Chem. Educ. 2001, 78, 1499–1503. [Google Scholar] [CrossRef]
- Reichardt, C. Solvents and Solvent Effects in Organic Chemistry, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2003. [Google Scholar]
- Mohammad, M.A.; Alhalaweh, A.; Velaga, S.P. Hansen solubility parameter as a tool to predict cocrystal formation. Int. J. Pharm. 2011, 407, 63–71. [Google Scholar] [CrossRef]
- Yan, Y.; Li, A.; Si, Z.; Zhang, X. Solubility measurement, correlation and molecular simulation of dabigatran etexilate mesylate polymorphs in five mono-solvents. J. Mol. Liq. 2020, 314, 113676. [Google Scholar] [CrossRef]
- Dong, X.; Cao, Y.; Wang, N.; Wang, P.; Li, M. Systematic study on solubility of chrysin in different organic solvents: The synergistic effect of multiple intermolecular interactions on the dissolution process. J. Mol. Liq. 2021, 325, 115180. [Google Scholar] [CrossRef]
- Hansch, C.; Leo, A.; Mekapati, S.B.; Kurup, A. QSAR and ADME. Bioorganic Med. Chem. 2004, 12, 3391–3400. [Google Scholar] [CrossRef]
- Comer, J.E. High throughput measurement of logD and pKa. In Methods and Principles in Medicinal Chemistry; Artursson, P., Lennernas, H., van de Waterbeemd, H., Eds.; Wiley-VCH: Weinheim, Germany, 2003. [Google Scholar]
- Sarge, S.M.; Hemminger, W.; Gmelin, E.; Höhne, G.W.H.; Cammenga, H.K.; Eysel, W. Metrologically based procedures for the temperature, heat and heat flow rate calibration of DSC. J. Therm. Anal. Calorim. 1997, 49, 1125–1134. [Google Scholar] [CrossRef]
- Archer, D.G.; Rudtsch, S. Enthalpy of Fusion of Indium: A Certified Reference Material for Differential Scanning Calorimetry†. J. Chem. Eng. Data 2003, 48, 1157–1163. [Google Scholar] [CrossRef]
- Zielenkiewicz, X.; Perlovich, G.L.; Wszelaka-Rylik, M. The Vapour Pressure and the Enthalpy of Sublimation: Determination by inert gas flow method. J. Therm. Anal. Calorim. 1999, 57, 225–234. [Google Scholar] [CrossRef]
- Blokhina, S.; Sharapova, A.; Ol’Khovich, M.; Perlovich, G. Sublimation thermodynamics of four fluoroquinolone antimicrobial compounds. J. Chem. Thermodyn. 2017, 105, 37–43. [Google Scholar] [CrossRef]
- Davies, M.; Jones, J.I. The sublimation pressures and heats of sublimation of some carboxylic acids. Trans. Faraday Soc. 1954, 50, 1042–1047. [Google Scholar] [CrossRef]
- Colomina, M.; Jimenez, P.; Turrion, C. Vapour pressures and enthalpies of sublimation of naphthalene and benzoic acid. J. Chem. Thermodyn. 1982, 14, 779–784. [Google Scholar] [CrossRef]
- Zaitsau, D.; Verevkin, S.P.; Sazonova, A.Y. Vapor pressures and vaporization enthalpies of 5-nonanone, linalool and 6-methyl-5-hepten-2-one. Data evaluation. Fluid Phase Equilibria 2015, 386, 140–148. [Google Scholar] [CrossRef]
- Cox, J.D.; Pilcher, G. Thermochemistry of Organic and Organometallic Compounds; Academic Press: London, UK, 1970. [Google Scholar]
- Blokhina, S.; Sharapova, A.; Ol’Khovich, M.; Perlovich, G. A thermodynamic study of sublimation, dissolution and distribution processes of anti-inflammatory drug Clonixin. J. Chem. Thermodyn. 2019, 132, 281–288. [Google Scholar] [CrossRef]
- Hansen, C.M. Hansen Solubility Parameters-A User’s Handbook; CRC Press LLC: New York, NY, USA, 2000. [Google Scholar]
- Lapuerta, M.; Canoira, L. The Suitability of Fatty Acid Methyl Esters (FAME) as Blending Agents in Jet A-1. In Biofuels for Aviation; Elsevier BV: Amsterdam, The Netherlands, 2016; pp. 47–84. [Google Scholar]
- Fedors, R.F. A method for estimating both the solubility parameters and molar volumes of liquids. Polym. Eng. Sci. 1974, 14, 147–154. [Google Scholar] [CrossRef]
- Van Krevelen, D.W. Properties of Polymers, Their Estimation and Correlation with Chemical Structure; Elsevier: New York, NY, USA, 1976. [Google Scholar]
- Stefanis, E.; Panayiotou, C. Prediction of Hansen Solubility Parameters with a New Group-Contribution Method. Int. J. Thermophys. 2008, 29, 568–585. [Google Scholar] [CrossRef]
- Just, S.; Sievert, F.; Thommes, M.; Breitkreutz, J. Improved group contribution parameter set for the application of solubility parameters to melt extrusion. Eur. J. Pharm. Biopharm. 2013, 85, 1191–1199. [Google Scholar] [CrossRef]
- Manzurola, E.; Apelblat, A. Solubilities of l-glutamic acid, 3-nitrobenzoic acid, p-toluic acid, calcium-l-lactate, calcium gluconate, magnesium-dl-aspartate, and magnesium-l-lactate in water. J. Chem. Thermodyn. 2002, 34, 1127–1136. [Google Scholar] [CrossRef]
- Apelblat, A.; Manzurola, E. Solubilities ofo-acetylsalicylic, 4-aminosalicylic, 3,5-dinitrosalicylic, andp-toluic acid, and magnesium-DL-aspartate in water fromT=(278 to 348) K. J. Chem. Thermodyn. 1999, 31, 85–91. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, B.; Wang, X.; Wang, H. Measurement and Correlation of the Solubilities of l-Valine in Water, Ethanol, N,N-Dimethylformamide, Acetone, and Isopropyl Alcohol between (293.15 and 343.15) K. J. Chem. Eng. Data 2014, 59, 2704–2708. [Google Scholar] [CrossRef]
- Monk, P. Physical Chemistry: Understanding Our Chemical World; Wiley: Manchester, UK, 2004. [Google Scholar]
- Atkins, P.; De Paula, J. Physical Chemistry for the Life Sciences, Eighth ed.; W.H. Freeman and Company: New York, NY, USA, 2006. [Google Scholar]
- Grant, D.J.W.; Higuchi, T. Solubility Behavior of Organic Compounds (Techniques of Chemistry); Wiley-Interscience: New York, NY, USA, 1990. [Google Scholar]
- Stanley, I. Chemical and Engineering Thermodynamics, 2rd ed.; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
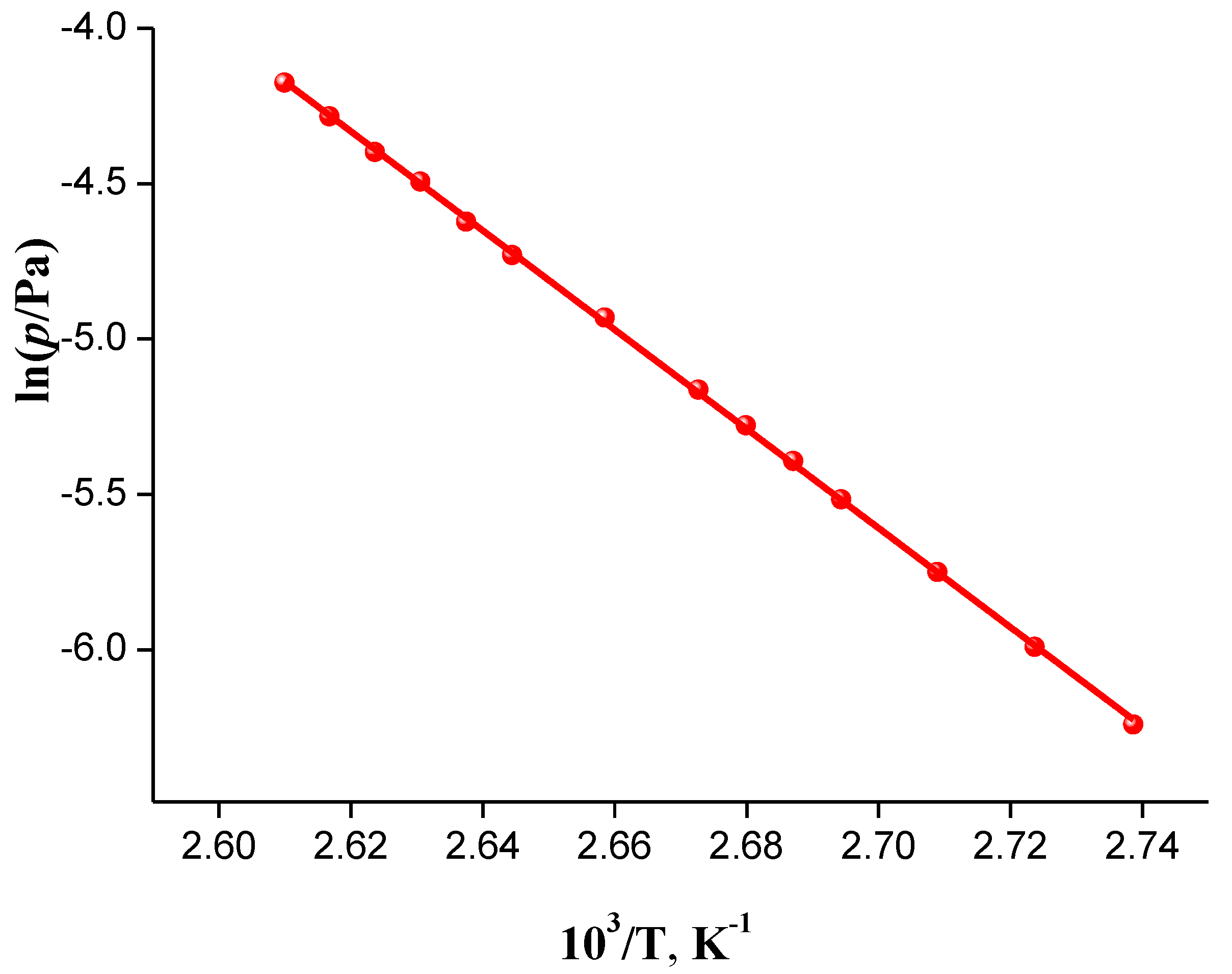
| aT/K | b 103 m/mg | cV(N2)/dm3 | dTa/K | Flow/dm3·h−1 | 103 p/Pa | lnp |
|---|---|---|---|---|---|---|
| 365.15 | 3.38 | 9.802 | 297.15 | 1.69 | 1.95 | −6.241 |
| 367.15 | 4.09 | 9.210 | 296.15 | 1.69 | 2.50 | −5.991 |
| 369.15 | 5.16 | 9.092 | 295.15 | 1.69 | 3.19 | −5.749 |
| 371.15 | 6.76 | 9.430 | 295.15 | 1.69 | 4.02 | −5.515 |
| 372.15 | 7.74 | 9.548 | 295.15 | 1.69 | 4.55 | −5.393 |
| 373.15 | 8.72 | 9.582 | 295.15 | 1.69 | 5.11 | −5.277 |
| 374.15 | 9.35 | 9.160 | 295.15 | 1.69 | 5.72 | −5.163 |
| 376.15 | 11.48 | 8.923 | 295.15 | 1.69 | 7.22 | −4.931 |
| 378.15 | 14.69 | 9.329 | 295.15 | 1.69 | 8.83 | −4.729 |
| 379.15 | 15.84 | 9.041 | 295.15 | 1.69 | 9.83 | −4.622 |
| 380.15 | 17.09 | 8.568 | 295.15 | 1.69 | 11.19 | −4.493 |
| 381.15 | 20.21 | 9.244 | 296.15 | 1.69 | 12.30 | −4.398 |
| 382.15 | 20.92 | 8.534 | 296.15 | 1.69 | 13.79 | −4.283 |
| 383.15 | 23.59 | 8.636 | 296.15 | 1.60 | 15.37 | −4.175 |
| /kJ·mol−1 | 68.9 ± 0.2 | |||||
| /kJ·mol−1 | 138.1 ± 0.5 | |||||
| /J·mol−1·K−1 | −71.8 | |||||
| /J·mol−1·K−1 | 230.4 ± 4.6 | |||||
| T/K | a Buffer pH 1.2 | b Buffer pH 2.0 | c Buffer pH 7.4 | Hexane | Ethanol | 1-Propanol | 1-Octanol |
|---|---|---|---|---|---|---|---|
| (S·105) | (S·105) | (S·106) | (S·104) | (S·101) | (S·101) | (S·102) | |
| 293.15 | 3.80 | 1.03 | 6.67 | 4.23 | 1.47 | 1.01 | 3.89 |
| 298.15 | 4.24 | 1.23 | 8.13 | 5.37 | 1.77 | 1.20 | 4.67 |
| 303.15 | 4.74 | 1.49 | 10.00 | 6.77 | 2.11 | 1.43 | 5.50 |
| 308.15 | 5.25 | 1.79 | 12.16 | 8.47 | 2.50 | 1.68 | 6.52 |
| 313.15 | 5.84 | 2.14 | 14.55 | 10.50 | 2.94 | 1.96 | 7.60 |
| Compound | V, cm3·mol−1 | δd, MPa0.5 | δp, MPa0.5 | δh, MPa0.5 | δt, MPa0.5 | e Δδt | f ∆δ | δv, MPa0.5 |
|---|---|---|---|---|---|---|---|---|
| IVZ | 389.7 | 21.8 | 4.3 | 7.3 | 23.4 | - | - | 22.2 |
| Buffer solutions | 18.0 | 15.5 | 16.0 | 42.3 | 47.8 | 24.4 | 37.4 | 22.3 |
| Hexane | 131.6 | 14.9 | 0.0 | 0.0 | 14.9 | 8.5 | 10.9 | 14.9 |
| Ethanol | 58.5 | 15.8 | 8.8 | 19.4 | 26.5 | 3.1 | 14.2 | 18.1 |
| 1-Propanol | 75.2 | 16.0 | 6.8 | 17.4 | 24.6 | 1.2 | 11.9 | 17.4 |
| 1-Octanol | 157.7 | 17.0 | 5.0 | 11.9 | 20.6 | 2.8 | 6.7 | 17.7 |
| T/K | xexp | Modified Apelblat Equation | van’t Hoff Equation | ||
|---|---|---|---|---|---|
| xcal | 103·RD | xcal | 103 RD | ||
| Buffer pH 1.2 a | |||||
| 293.15 | 6.8309·10−7 | 6.8301·10−7 | 0.1228 | 6.8234·10−7 | 1.1027 |
| 298.15 | 7.6422·10−7 | 7.6469·10−7 | −0.6118 | 7.6519·10−7 | −1.2718 |
| 303.15 | 8.5596·10−7 | 8.5388·10−7 | 2.4392 | 8.5488·10−7 | 1.2713 |
| 308.15 | 9.4893·10−7 | 9.5109·10−7 | −2.2742 | 9.5164·10−7 | −2.8588 |
| 313.15 | 10.578·10−7 | 10.568·10−7 | 0.9561 | 10.557·10−7 | 1.9519 |
| Buffer pH 2.0 b | |||||
| 293.15 | 1.8538·10−7 | 1.8489·10−7 | 2.6902 | 1.8386·10−7 | 8.2257 |
| 298.15 | 2.2156·10−7 | 2.2301·10−7 | −6.5181 | 2.2353·10−7 | −8.8859 |
| 303.15 | 2.686·10−7 | 2.6872·10−7 | −0.4723 | 2.7002·10−7 | −5.2979 |
| 308.15 | 3.2558·10−7 | 3.2354·10−7 | 6.2519 | 3.2418·10−7 | 4.2902 |
| 313.15 | 3.8771·10−7 | 3.8914·10−7 | −3.691 | 3.8694·10−7 | 1.979 |
| Buffer pH 7.4 c | |||||
| 293.15 | 1.1952·10−7 | 1.1915·10−7 | 3.1335 | 1.1936·10−7 | 1.3961 |
| 298.15 | 1.4591·10−7 | 1.4708·10−7 | −8.0535 | 1.4693·10−7 | −7.0446 |
| 303.15 | 1.8073·10−7 | 1.7998·10−7 | 4.1779 | 1.7964·10−7 | 6.0225 |
| 308.15 | 2.1892·10−7 | 2.1840·10−7 | 2.3701 | 2.1821·10−7 | 3.2370 |
| 313.15 | 2.6240·10−7 | 2.6294·10−7 | −2.0585 | 2.6341·10−7 | −3.8416 |
| Hexane | |||||
| 293.15 | 5.5224·10−5 | 5.5187·10−5 | 0.6774 | 5.5171·10−5 | 0.9647 |
| 298.15 | 7.0509·10−5 | 7.0549·10−5 | −0.5658 | 7.0584·10−5 | −1.0607 |
| 303.15 | 8.9532·10−5 | 8.9506·10−5 | 0.2907 | 8.9572·10−5 | −0.4460 |
| 308.15 | 11.287·10−5 | 11.274·10−5 | 1.1049 | 11.279·10−5 | 0.6517 |
| 313.15 | 14.101·10−5 | 14.103·10−5 | −0.1695 | 14.099·10−5 | 0.1353 |
| Ethanol | |||||
| 293.15 | 0.9236·10−2 | 0.9240·10−2 | 0.0023 | 0.9213·10−2 | 2.9608 |
| 298.15 | 1.1339·10−2 | 1.1326·10−2 | 1.2112 | 1.1348·10−2 | −0.7125 |
| 303.15 | 1.3831·10−2 | 1.3835·10−2 | −0.3595 | 1.3883·10−2 | −3.8107 |
| 308.15 | 1.6854·10−2 | 1.6844·10−2 | 0.3442 | 1.6873·10−2 | −1.3468 |
| 313.15 | 2.0450·10−2 | 2.0441·10−2 | 0.4360 | 2.0379·10−2 | 3.4562 |
| 1-Propanol | |||||
| 293.15 | 7.9034·10−3 | 7.8833·10−3 | 2.1086 | 7.8924·10−3 | 0.9592 |
| 298.15 | 9.5491·10−3 | 9.5597·10−3 | −6.2862 | 9.5750·10−3 | −2.6146 |
| 303.15 | 11.557·10−3 | 11.528·10−3 | 6.2322 | 11.542·10−3 | 1.5228 |
| 308.15 | 13.829·10−3 | 13.827·10−3 | −1.9602 | 13.830·10−3 | 0.0031 |
| 313.15 | 16.474·10−3 | 16.501·10−3 | −0.0372 | 16.475·10−3 | −0.3328 |
| 1-Octanol | |||||
| 293.15 | 6.2145·10−3 | 6.2160·10−3 | −0.9679 | 6.2245·10−3 | −2.3294 |
| 298.15 | 7.5228·10−3 | 7.4880·10−3 | 4.2499 | 7.4831·10−3 | 4.9131 |
| 303.15 | 8.9147·10−3 | 8.9532·10−3 | −4.8528 | 8.9416·10−3 | −3.5518 |
| 308.15 | 10.657·10−3 | 10.629·10−3 | 2.9069 | 10.623·10−3 | 3.4729 |
| 313.15 | 12.526·10−3 | 12.534·10−3 | −0.3032 | 12.551·10−3 | −1.6928 |
| Solvents | A | B | C | RMSD | 103 RAD |
|---|---|---|---|---|---|
| Modified Apelblat equation | |||||
| Buffer pH 1.2 | −34.28 | −788.9 | 4.01 | 1.43·10−9 | 1.3 |
| Buffer pH 2.0 | −133.86 | 2450.3 | 19.36 | 1.31·10−9 | 3.9 |
| Buffer pH 7.4 | 41.51 | −5666.2 | −6.71 | 7.28·10−10 | 3.8 |
| Hexane | −7.99 | −3725.7 | 1.92 | 5.29·10−9 | 0.6 |
| Ethanol | −72.53 | −22.3 | 11.96 | 8.08·10−6 | 0.5 |
| 1-Propanol | −12.03 | 2544.3 | 2.79 | 4.43·10−5 | 3.3 |
| 1-Octanol | 39.18 | −4720.7 | −4.96 | 2.84·10−5 | 3.6 |
| van’t Hoff equation | |||||
| Buffer pH 1.2 | −7.36 | −2003.4 | 1.69·10−9 | 1.7 | |
| Buffer pH 2.0 | −3.86 | −3415.4 | 1.47·10−9 | 5.7 | |
| Buffer pH 7.4 | −3.55 | −3633.4 | 8.70·10−10 | 4.3 | |
| Hexane | 4.88 | −4306.6 | 5.62·10−8 | 0.7 | |
| Ethanol | 7.74 | −3644.2 | 4.27·10−5 | 2.5 | |
| 1-Propanol | 6.68 | −3378.1 | 4.49·10−5 | 4.1 | |
| 1-Octanol | 5.90 | −3219.1 | 2.97·10−5 | 3.7 | |
| T/K | lnxid | lnγ∞ | ||||||
|---|---|---|---|---|---|---|---|---|
| Buffer pH 1.2 | Buffer pH 2.0 | Buffer pH 7.4 | Hexane | Ethanol | 1-Propanol | 1-Octanol | ||
| 293.15 | −2.68 | 11.51 | 12.82 | 13.26 | 7.12 | 2.00 | 2.16 | 2.40 |
| 298.15 | −2.53 | 11.55 | 12.80 | 13.21 | 7.03 | 1.95 | 2.12 | 2.36 |
| 303.15 | −2.37 | 11.59 | 12.76 | 13.15 | 6.95 | 1.91 | 2.09 | 2.34 |
| 308.15 | −2.22 | 11.64 | 12.72 | 13.11 | 6.86 | 1.86 | 2.06 | 2.32 |
| 313.15 | −2.08 | 11.67 | 12.69 | 13.08 | 6.79 | 1.81 | 2.03 | 2.30 |
| a A | 14.15 ± 0.05 | 10.69 ± 0.1 | 10.34 ± 0.1 | 1.91 ± 0.04 | −0.96 ± 0.02 | 0.11 ± 0.06 | 0.91 ± 0.11 | |
| a B | −774 ± 15 | 625 ± 31 | 854 ± 18 | 1526 ± 13 | 867 ± 5 | 598 ± 16 | 435 ± 33 | |
| b R | 0.9994 | 0.9962 | 0.9962 | 0.9999 | 0.9999 | 0.9988 | 0.9913 | |
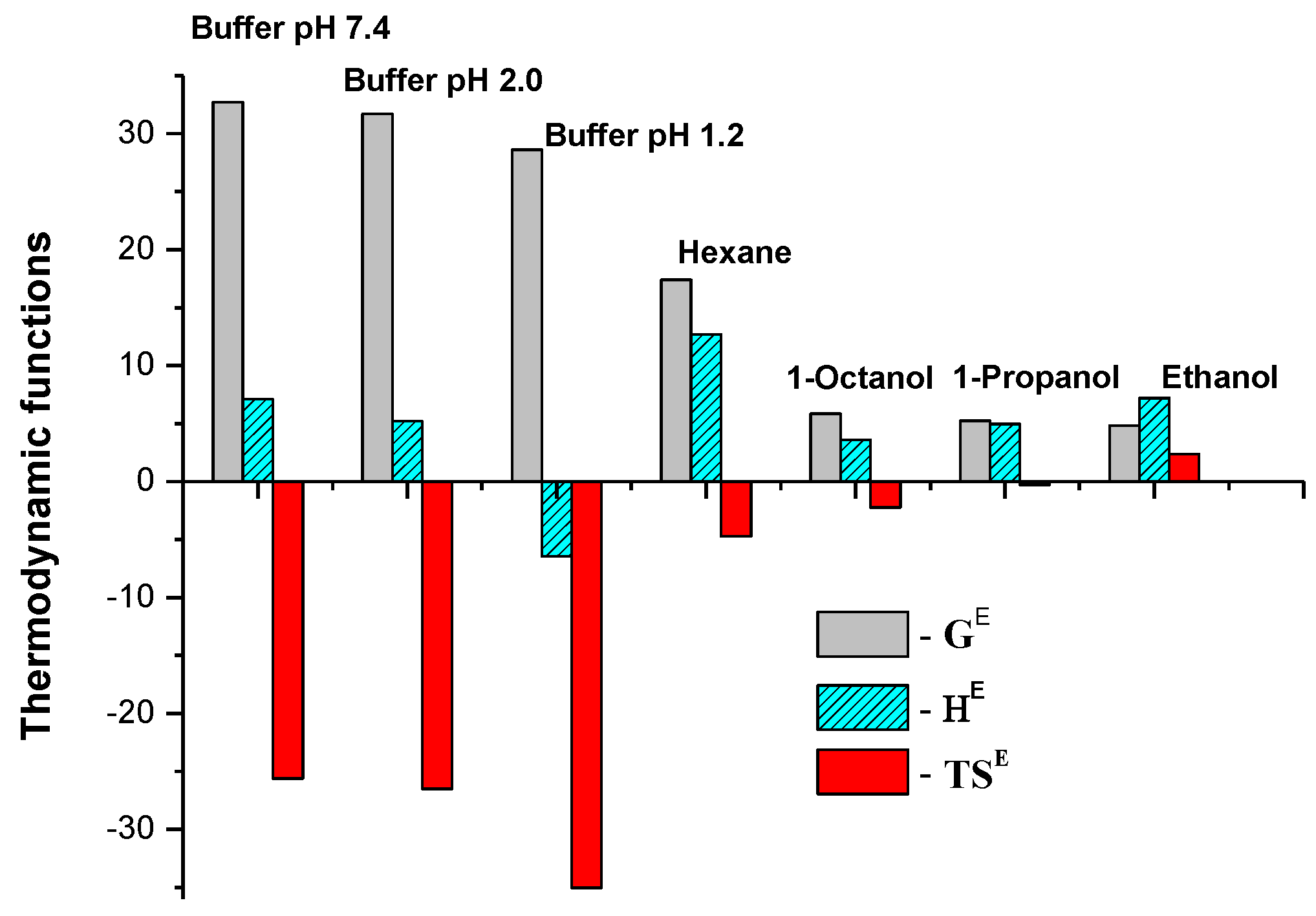
| Solvent | GE, kJ·mol−1 | HE, kJ·mol−1 | TSE, kJ·mol−1 | SE, J·mol−1·K−1 | a ςHE, % | b ςTSE,% |
|---|---|---|---|---|---|---|
| Buffer pH 1.2 | 28.6 ± 0.5 | −6.43 ± 0.1 | −35.03 | −117.5 ± 4.1 | 15.3 | 84.7 |
| Buffer pH 2.0 | 31.7 ± 0.6 | 5.20 ± 0.3 | −26.50 | −88.9 ± 5.1 | 16.4 | 83.6 |
| Buffer pH 7.4 | 32.7 ± 0.6 | 7.10 ± 0.1 | −25.6 | −85.9 ±2.9 | 21.7 | 78.3 |
| Hexane | 17.4 ± 0.3 | 12.69 ± 0.1 | −4.71 | −15.8 ± 0.4 | 72.9 | 27.1 |
| Ethanol | 4.83 ± 0.1 | 7.21 ± 0.1 | 2.38 | 8.0 ± 0.3 | 75.2 | 24.8 |
| 1-Propanol | 5.25 ± 0.2 | 4.97 ± 0.1 | −0.28 | −0.9 ± 0.04 | 94.7 | 5.3 |
| 1-Octanol | 5.85 ± 0.2 | 3.62 ± 0.1 | −2.23 | −7.5 ± 0.3 | 61.9 | 38.1 |
| T/K | sO · 103 | sB · 106 | PO/B | logPO/B | xo · 104 | xB · 107 | logP*O/B |
|---|---|---|---|---|---|---|---|
| 293.15 | 2.15 | 6.85 | 313.71 | 2.50 | 3.39 | 1.22 | 3.44 |
| 298.15 | 2.15 | 5.98 | 359.18 | 2.56 | 3.40 | 1.07 | 3.50 |
| 303.15 | 2.15 | 5.20 | 413.63 | 2.62 | 3.42 | 0.93 | 3.56 |
| 308.15 | 2.15 | 4.53 | 474.77 | 2.68 | 3.43 | 0.81 | 3.62 |
| 313.15 | 2.15 | 4.02 | 535.22 | 2.73 | 3.45 | 0.72 | 3.68 |
| Aa | 16.52 ± 0.09 | = −19.99 ± 0.4/kJ·mol−1 | |||||
| Ba | 2520 ± 26 | = 20.95 ± 0.2/kJ·mol−1 | |||||
| Rb | 0.9998 | = 40.9 ± 1.5/kJ·mol−1 | |||||
| σc | 0.8·10−2 | = 137.3 ± 5.2/J·mol−1K−1 | |||||
| Chemical Name | CAS Register No. | Formula | M/g mol−1 | Source | Initial Mass Fraction Purity | Final Mass Fraction Purity |
|---|---|---|---|---|---|---|
| Isavuconazole | 241479-67-4 | C22 H17 F2 N5 O S | 437.5 | Shanghai Send Pharmaceutical Technology | ≥0.99 a | No purification |
| Ethanol | 64-17-5 | C2H6O | 46.1 | Sigma-Aldrich | ≥0.99 b | No purification |
| 1-Propanol | 71-23-8 | C3 H8 O | 60.1 | Sigma-Aldrich | ≥0.99 b | No purification |
| 1-Octanol | 111-87-5 | C8H18O | 130.2 | Sigma-Aldrich | ≥0.99 b | No purification |
| Hexane | 110-54-3 | C6H14 | 86.2 | Sigma-Aldrich | ≥0.97 b | ≥0.98 c |
| Potassium dihydrogen phosphate | 7778-77-0 | KH2PO4 | 136.1 | Merck | ≥0.99 c | No purification |
| Disodium hydrogen phosphate dodecahydrate | 10039-32-4 | Na2HPO4·12H2O | 358.1 | Merck | ≥0.99 b | No purification |
| Potassium chloride | 7447-40-7 | KCl | 74.5 | Sigma-Aldrich | ≥0.99 b | No purification |
| Hydrochloric acid mol/dm3 fixanal | 7647-01-0 | Aldrich | - | None | No purification |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ol’khovich, M.; Sharapova, A.; Blokhina, S.; Perlovich, G. Isavuconazole: Thermodynamic Evaluation of Processes Sublimation, Dissolution and Partition in Pharmaceutically Relevant Media. Molecules 2021, 26, 4759. https://doi.org/10.3390/molecules26164759
Ol’khovich M, Sharapova A, Blokhina S, Perlovich G. Isavuconazole: Thermodynamic Evaluation of Processes Sublimation, Dissolution and Partition in Pharmaceutically Relevant Media. Molecules. 2021; 26(16):4759. https://doi.org/10.3390/molecules26164759
Chicago/Turabian StyleOl’khovich, Marina, Angelica Sharapova, Svetlana Blokhina, and German Perlovich. 2021. "Isavuconazole: Thermodynamic Evaluation of Processes Sublimation, Dissolution and Partition in Pharmaceutically Relevant Media" Molecules 26, no. 16: 4759. https://doi.org/10.3390/molecules26164759
APA StyleOl’khovich, M., Sharapova, A., Blokhina, S., & Perlovich, G. (2021). Isavuconazole: Thermodynamic Evaluation of Processes Sublimation, Dissolution and Partition in Pharmaceutically Relevant Media. Molecules, 26(16), 4759. https://doi.org/10.3390/molecules26164759







