Initial Decomposition Mechanism of 3-Nitro-1,2,4-triazol-5-one (NTO) under Shock Loading: ReaxFF Parameterization and Molecular Dynamic Study
Abstract
:1. Introduction
2. Method
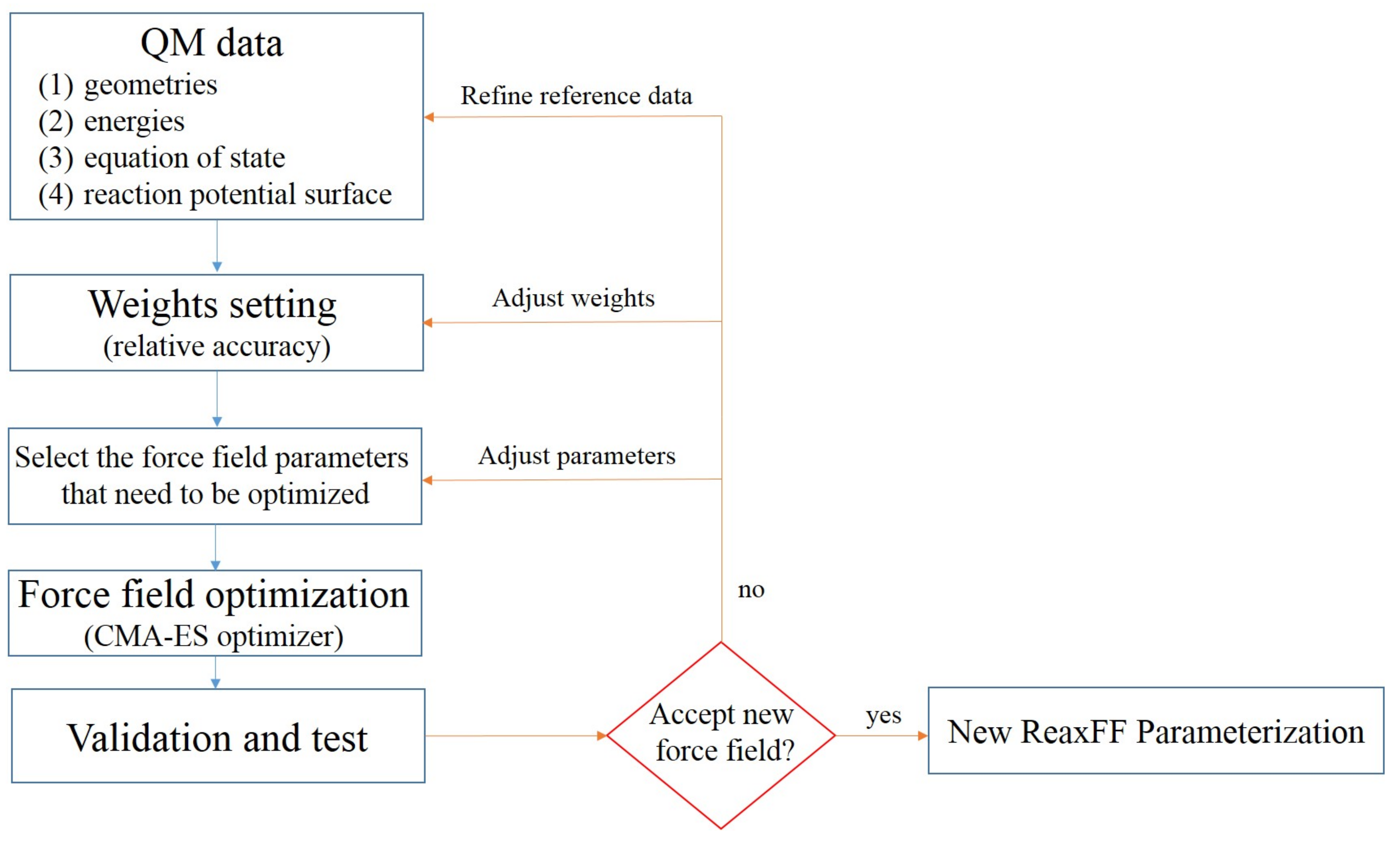
2.1. ReaxFF Parameterization
2.2. Molecular Dynamic Simulations
3. Result and Discussion
3.1. Parameterization and Verification
3.1.1. New Reaxff-Lg Parameterization for NTO
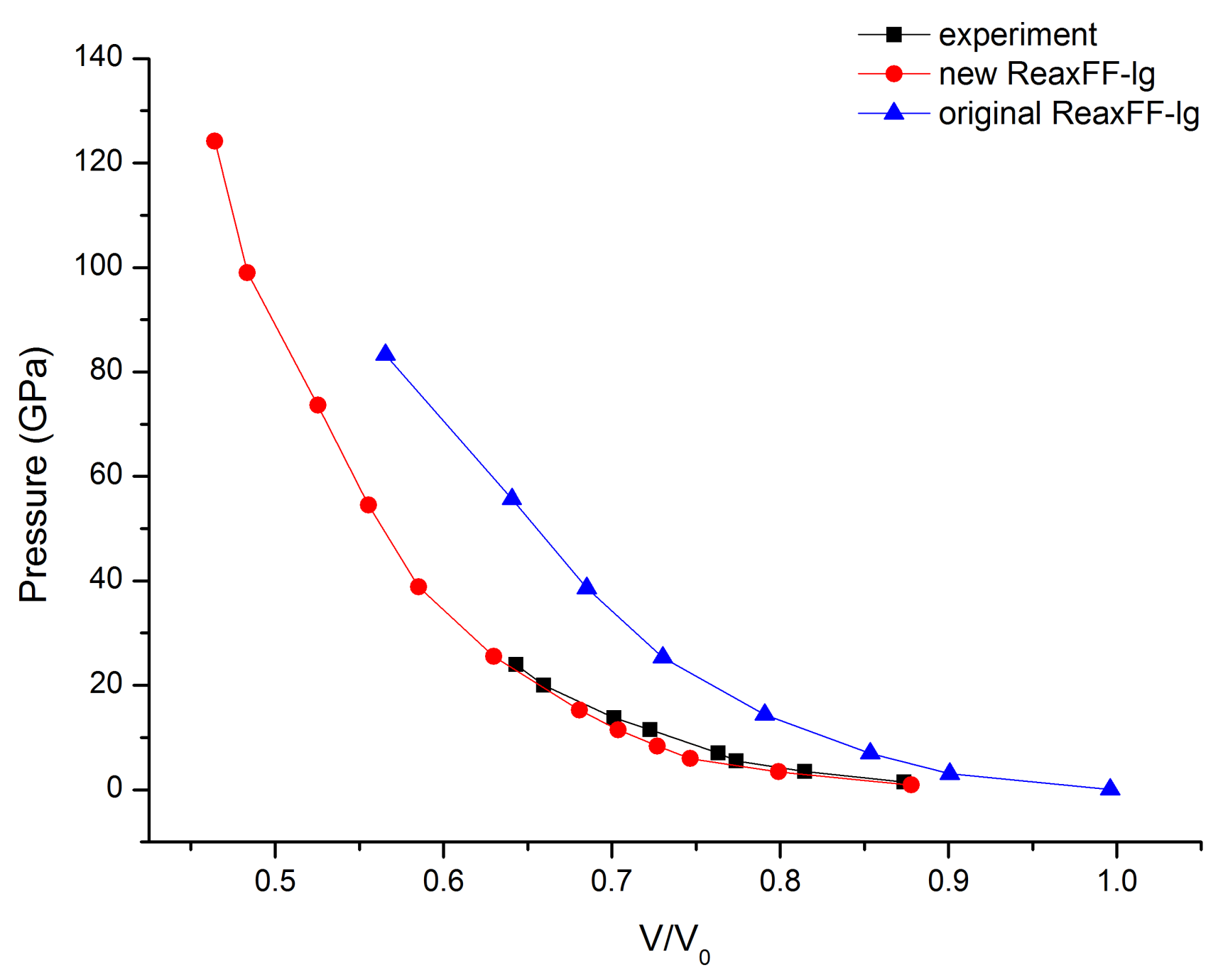
3.1.2. Description of the Crystal Properties
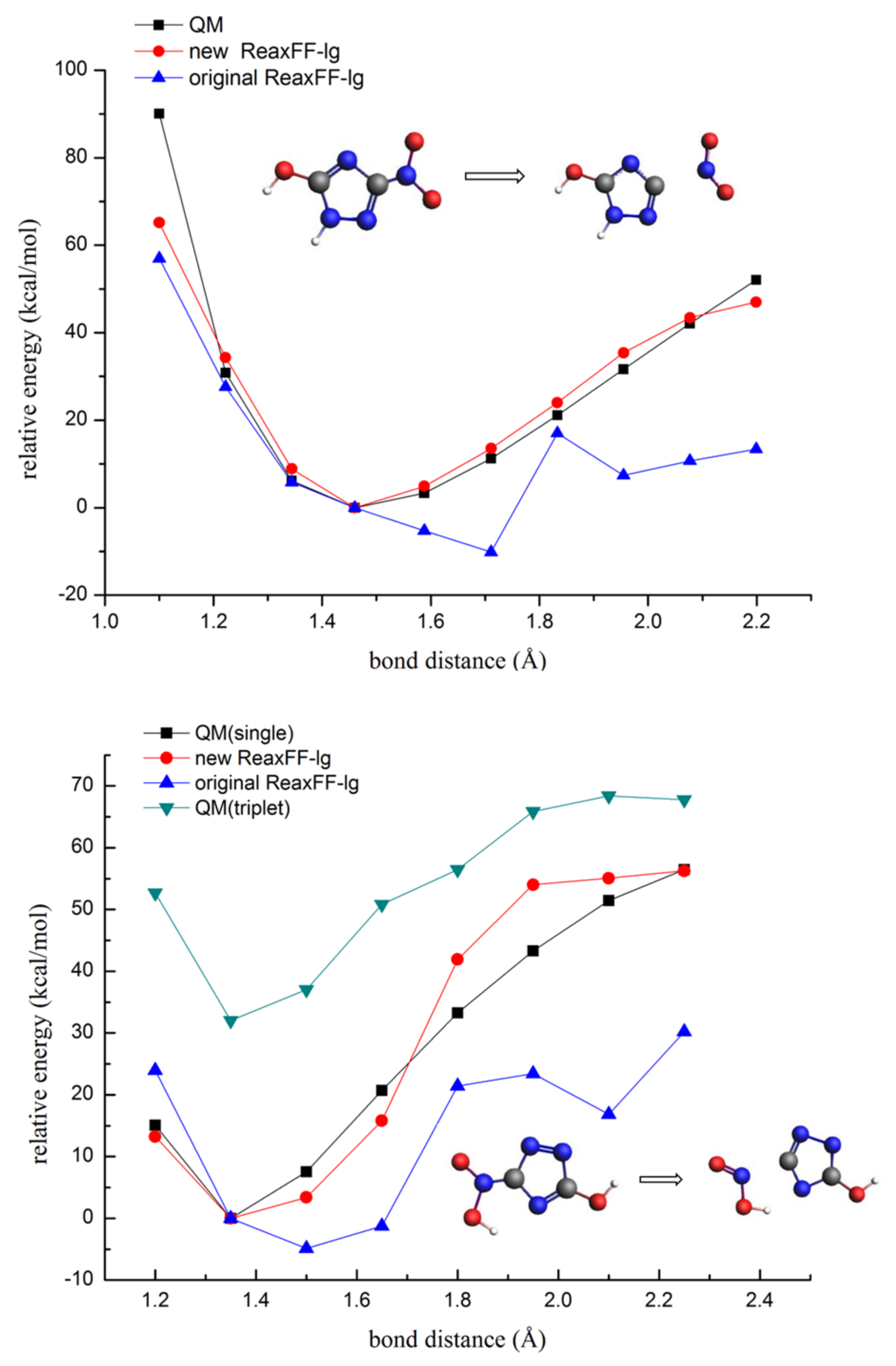
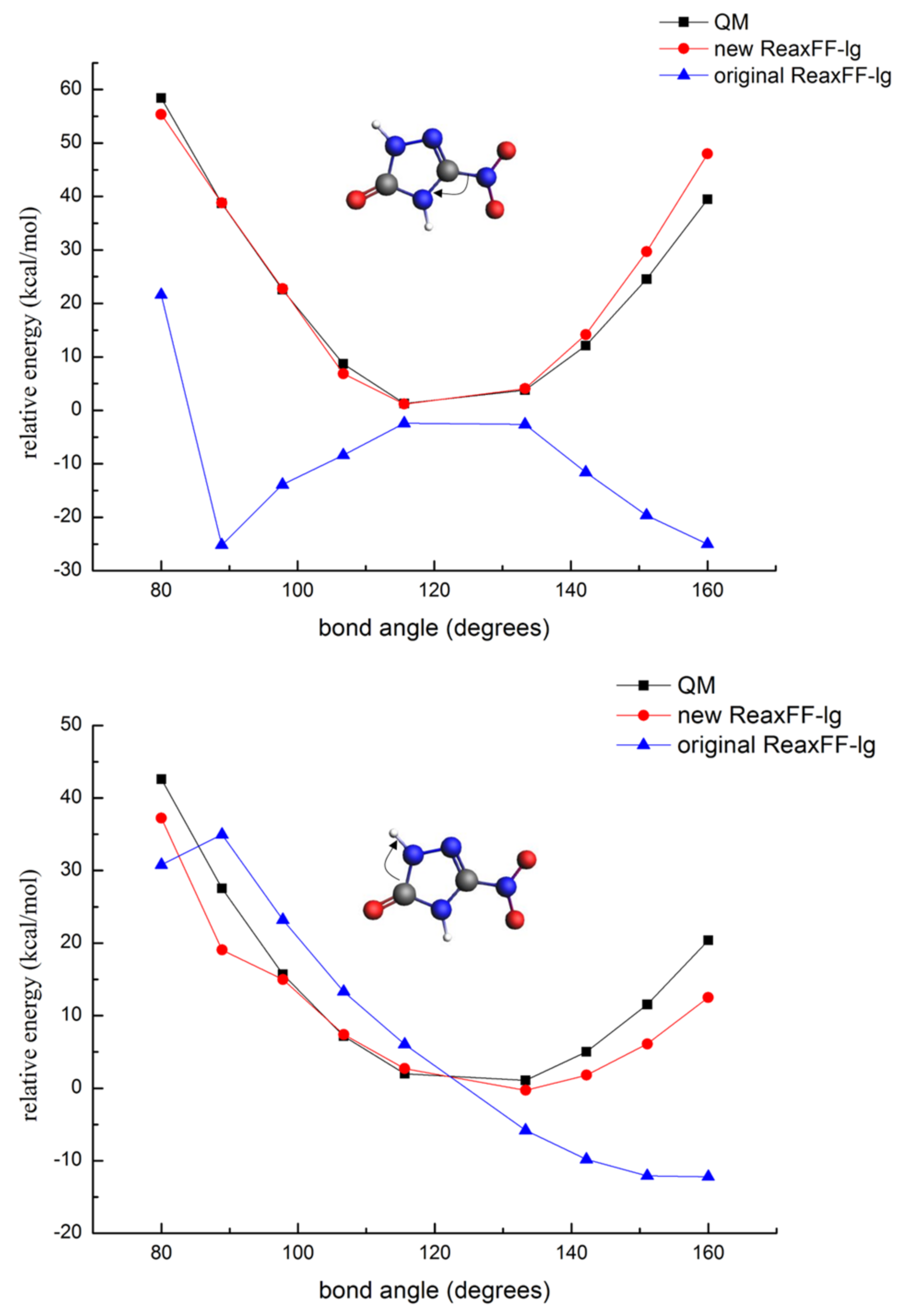
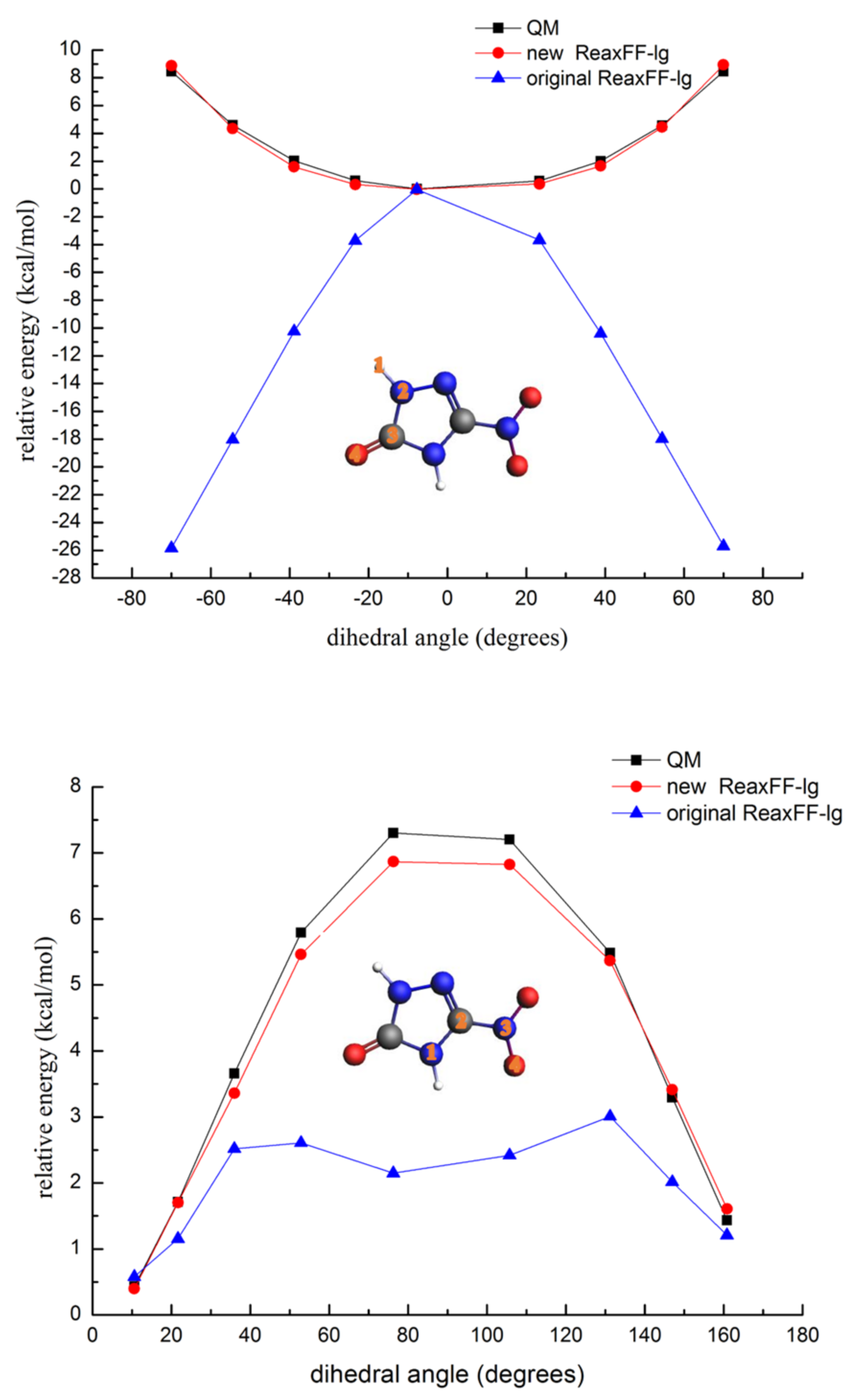
3.1.3. Description of the Potential Energy Surface
3.2. Shock-Induced Chemistry of NTO
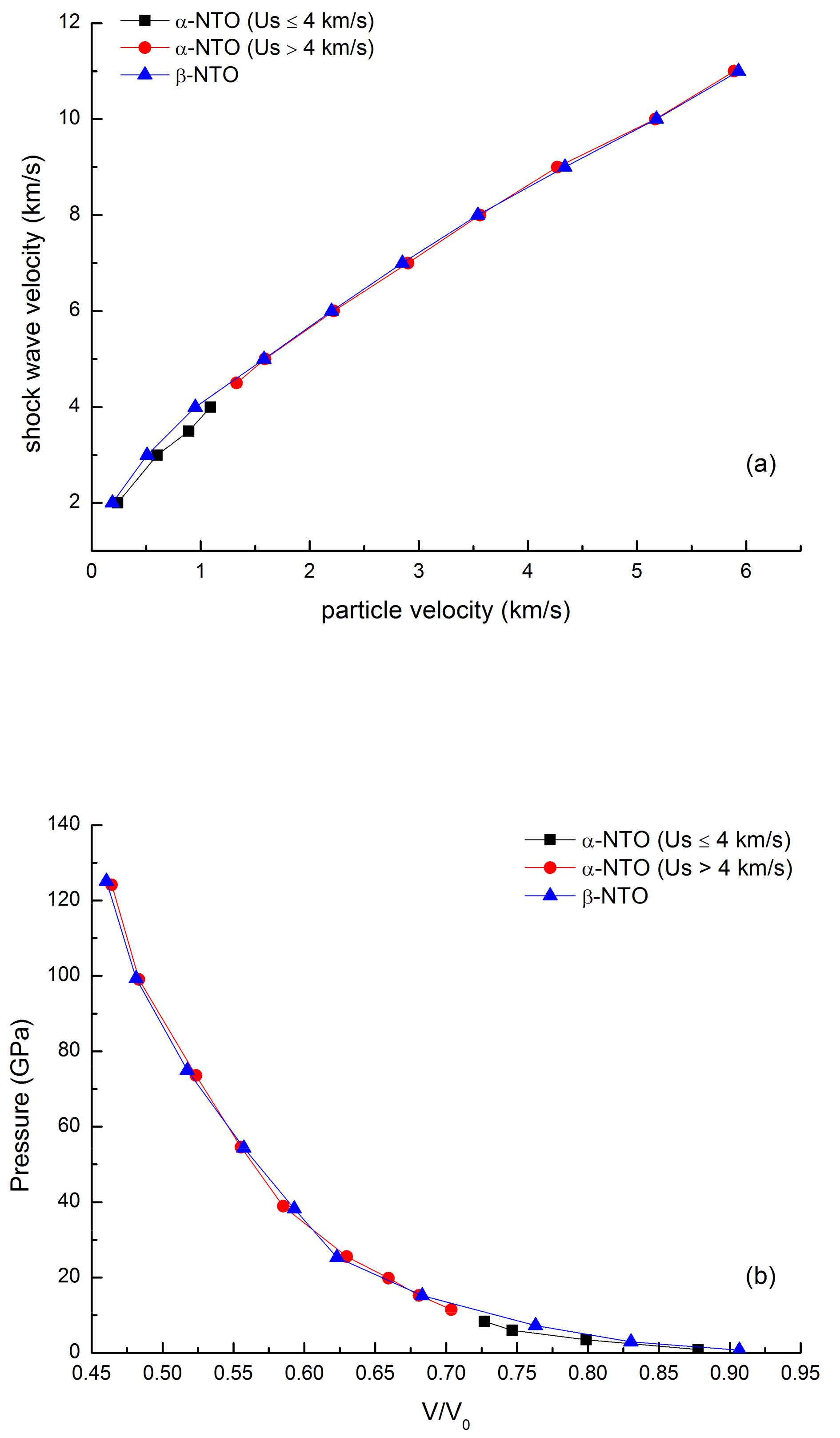
3.2.1. Shock Hugoniot State
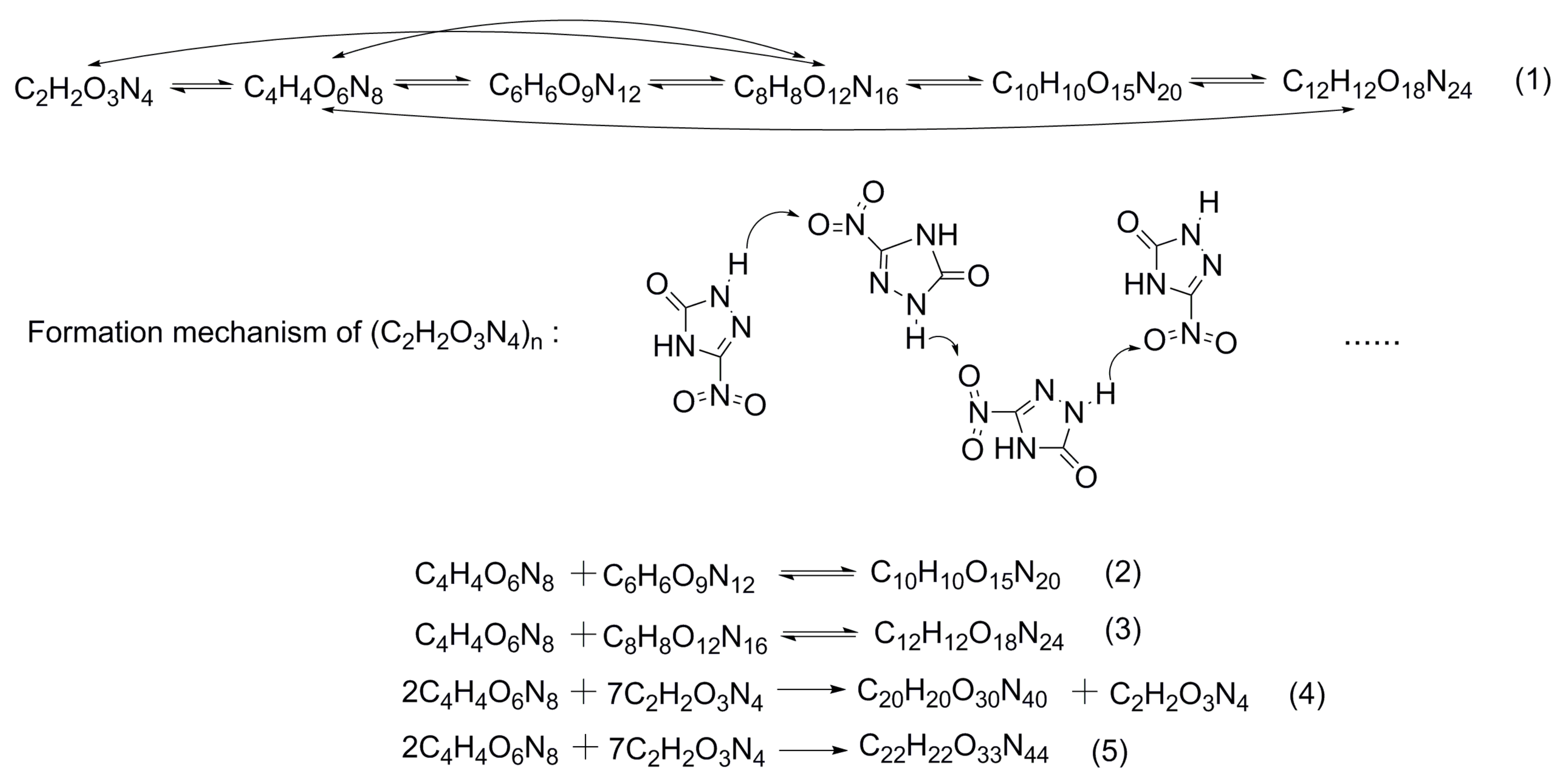
3.2.2. Initial Decomposition Mechanism
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Hanafi, S.; Trache, D.; Abdous, S.; Abdous, S.; Bensalem, Z.; Mezroua, A. 5-Nitro-1, 2, 4-triazole-3-one: A review of recent ad-vances. Chin. J. Energetic Mater. 2019, 27, 326–347. [Google Scholar]
- Nouguez, B.; Mahé, B. Achieving STANAG 4439 IM shaped charge requirements on 155 mm shells: An update. In Proceedings of the The 2010 Insensitive Munitions & Energetic Materials Technology Symposium, Munich, Germany, 11–13 October 2010; pp. 11–14. [Google Scholar]
- Corley, J.D.; Stewart, A.C. Fuzed Insensitive General Purpose Bomb Containing AFX-645; Wright Lab Eglin Afb Fl Armament Directorate, Ed.; Defense Technical Information Center: Fort Belvoir, VA, USA, 1995. [Google Scholar]
- Richard, T.; Weidhaas, J. Dissolution, sorption, and phytoremediation of IMX-101 explosive formulation constituents: 2, 4-dinitroanisole (DNAN), 3-nitro-1, 2, 4-triazol-5-one (NTO), and nitroguanidine. J. Hazard. Mater. 2014, 280, 561–569. [Google Scholar] [CrossRef]
- Du, L.X.S.; Jin, S.H.; Shu, Q.H.; Li, L.J.; Chen, K.; Chen, M.L.; Wang, J.F. The investigation of NTO/HMX-based plastic-bonded explosives and its safety performance. Def. Technol. 2021. [Google Scholar] [CrossRef]
- Long, G.T.; Brems, B.A.; Wight, C.A. Thermal activation of the high explosive NTO: Sublimation, decomposition, and autoca-talysis. J. Phys. Chem. B 2002, 106, 4022–4026. [Google Scholar] [CrossRef]
- Williams, G.K.; Palopoli, S.F.; Brill, T.B. Thermal decomposition of energetic materials 65. Conversion of insensitive explosives (NTO, ANTA) and related compounds to polymeric melon-like cyclic azine burn-rate suppressants. Combust. Flame 1994, 98, 197–204. [Google Scholar] [CrossRef]
- Singh, G.; Kapoor, I.P.S.; Tiwari, S.K.; Felix, P.S. Studies on energetic compounds: Part 16. Chemistry and decomposition mechanisms of 5-nitro-2, 4-dihydro-3H-1, 2, 4-triazole-3-one (NTO). J. Hazard. Mater. 2001, 81, 67–82. [Google Scholar] [CrossRef]
- Sinditskii, V.P.; Smirnov, S.P.; Egorshev, V.Y. Thermal decomposition of NTO: An explanation of the high activation energy. Propellants Explos. Pyrotech. Int. J. Deal. Sci. Technol. Asp. Energetic Mater. 2007, 32, 277–287. [Google Scholar] [CrossRef]
- Sinditskii, V.P.; Egorshev, V.Y.; Serushkin, V.V.; Levshenkov, A.I.; Berezin, M.V.; Filatov, S.A.; Smirnov, S.P. Evaluation of de-composition kinetics of energetic materials in the combustion wave. Thermochim. Acta 2009, 496, 1–12. [Google Scholar] [CrossRef]
- Wang, J.F. The Decomposition of TKX-50 and NTO in Confined Space; Beijing Institute of Technology: Beijing, China, 2019. [Google Scholar]
- Harris, N.J.; Lammertsma, K. Tautomerism, ionization, and bond dissociations of 5-nitro-2, 4-dihydro-3 H-1, 2, 4-triazolone. J. Am. Chem. Soc. 1996, 118, 8048–8055. [Google Scholar] [CrossRef]
- Wang, Y.M.; Chen, C.; Lin, S.T. Theoretical studies of the NTO unimolecular decomposition. J. Mol. Struct. THEOCHEM 1999, 460, 79–102. [Google Scholar] [CrossRef]
- Liu, Z.C.; Wu, Q.; Zhu, W.H.; Xiao, H.M. Vacancy-induced initial decomposition of condensed phase NTO via bimolecular hy-drogen transfer mechanisms at high pressure: A DFT-D study. Phys. Chem. Chem. Phys. 2015, 17, 10568–10578. [Google Scholar] [CrossRef]
- Van Duin, A.C.T.; Dasgupta, S.; Lorant, F.; Goddard, W.A. ReaxFF: A reactive force field for hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef] [Green Version]
- Chenoweth, K.; Van Duin, A.C.T.; Goddard, W.A. ReaxFF reactive force field for molecular dynamics simulations of hydro-carbon oxidation. J. Phys. Chem. A 2008, 112, 1040–1053. [Google Scholar] [CrossRef] [Green Version]
- Strachan, A.; Kober, E.M.; Van Duin, A.C.T.; Oxgaard, J.; Goddard, W.A. Thermal decomposition of RDX from reactive molec-ular dynamics. J. Chem. Phys. 2005, 122, 54502. [Google Scholar] [CrossRef]
- Zhang, L.Z.; Zybin, S.V.; Van Duin, A.C.T.; Dasgupta, S.; Goddard, W.A.; Kober, E.M. Carbon cluster formation during ther-mal decomposition of octahydro-1, 3, 5, 7-tetranitro-1, 3, 5, 7-tetrazocine and 1, 3, 5-triamino-2, 4, 6-trinitrobenzene high ex-plosives from ReaxFF reactive molecular dynamics simulations. J. Phys. Chem. A 2009, 113, 10619–10640. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sergeev, O.V.; Yanilkin, A.V. Hydrogen transfer in energetic materials from ReaxFF and DFT calculations. J. Phys. Chem. A 2017, 121, 3019–3027. [Google Scholar] [CrossRef]
- Rom, N.; Hirshberg, B.; Zeiri, Y.; Furman, D.; Zybin, S.V.; Goddard, W.A.; Kosloff, R. First-principles-based reaction kinetics for decomposition of hot, dense liquid TNT from ReaxFF multiscale reactive dynamics simulations. J. Phys. Chem. C 2013, 117, 21043–21054. [Google Scholar] [CrossRef]
- Liu, L.C.; Liu, Y.; Zybin, S.V.; Sun, H.; Goddard, W.A. ReaxFF-lg: Correction of the ReaxFF reactive force field for London dis-persion, with applications to the equations of state for energetic materials. J. Phys. Chem. A 2011, 115, 11016–11022. [Google Scholar] [CrossRef]
- Wang, N.; Peng, J.H.; Pang, A.M.; He, T.S.; Du, F.; Botero, A.J. Thermodynamic simulation of the RDX–aluminum interface us-ing ReaxFF molecular dynamics. J. Phys. Chem. C 2017, 121, 14597–14610. [Google Scholar] [CrossRef] [Green Version]
- Mortier, W.J.; Ghosh, S.K.; Shankar, S. Electronegativity-equalization method for the calculation of atomic charges in mole-cules. J. Am. Chem. Soc. 1986, 108, 4315–4320. [Google Scholar] [CrossRef]
- Rappe, A.K.; Goddard, W.A. Charge equilibration for molecular dynamics simulations. J. Phys. Chem. 1991, 95, 3358–3363. [Google Scholar] [CrossRef]
- Moellmann, J.; Grimme, S. DFT-D3 study of some molecular crystals. J. Phys. Chem. C 2014, 118, 7615–7621. [Google Scholar] [CrossRef]
- Chakraborty, D.; Muller, R.P.; Dasgupta, S.; Goddard, W.A. The mechanism for unimolecular decomposition of RDX (1, 3, 5-trinitro-1, 3, 5-triazine), an ab initio study. J. Phys. Chem. A 2000, 104, 2261–2272. [Google Scholar] [CrossRef] [Green Version]
- Gindulytė, A.; Massa, L.; Huang, L.L.; Karle, J. Proposed mechanism of 1, 1-diamino-dinitroethylene decomposition: A density functional theory study. J. Phys. Chem. A 1999, 103, 11045–11051. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. A thorough benchmark of density functional methods for general main group thermochemistry, ki-netics, and noncovalent interactions. Phys. Chem. Chem. Phys. 2011, 13, 6670–6688. [Google Scholar] [CrossRef] [PubMed]
- Goerigk, L.; Grimme, S. Efficient and Accurate Double-Hybrid-Meta-GGA Density Functionals—Evaluation with the Extended GMTKN30 Database for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2011, 7, 291–309. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.L.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [Green Version]
- Bučko, T.; Lebègue, S.; Hafner, J.; Angyan, J.G. Tkatchenko-Scheffler van der Waals correction method with and without self-consistent screening applied to solids. Phys. Rev. B 2013, 87, 64110. [Google Scholar] [CrossRef]
- ReaxFF 2020, SCM, Theoretical Chemistry, Vrjie Universiteit: Amsterdam, The Netherlands. Available online: https://www.scm.com (accessed on 29 July 2021).
- Furman, D.; Carmeli, B.; Zeiri, Y.; Kosloff, R. Enhanced particle swarm optimization algorithm: Efficient training of reaxff reac-tive force fields. J. Chem. Theory Comput. 2018, 14, 3100–3112. [Google Scholar] [CrossRef]
- Reed, E.J.; Fried, L.E.; Joannopoulos, J.D. A method for tractable dynamical studies of single and double shock compression. Phys. Rev. Lett. 2003, 90, 235503. [Google Scholar] [CrossRef] [Green Version]
- Aktulga, H.M.; Fogarty, J.C.; Pandit, S.A.; Grama, A.Y. Parallel reactive molecular dynamics: Numerical methods and algo-rithmic techniques. Parallel Comput. 2012, 38, 245–259. [Google Scholar] [CrossRef] [Green Version]
- Scienomics. Introduction to MAPS; Scienomics: Paris, France, 2012. [Google Scholar]
- Brady, J.E.; Smith, J.L.; Hart, C.E.; Oxley, J. Estimating Ambient Vapor Pressures of Low Volatility Explosives by Ris-ing-Temperature Thermogravimetry. Propellants Explos. Pyrotech. 2012, 37, 215–222. [Google Scholar] [CrossRef]
- Stavrou, E.; Zaug, J.M.; Bastea, S.; Bastea, S.; Crowhurst, J.C. The equation of state of 5-nitro-2, 4-dihydro-1, 2, 4,-triazol-3-one determined via in-situ optical microscopy and interferometry measurements. J. Appl. Phys. 2016, 119, 135904. [Google Scholar] [CrossRef]
- Engelke, R.; Blais, N.C.; Sheffield, S.A.; Sander, R.K. Production of a chemically-bound dimer of 2, 4, 6-TNT by transient high pressure. J. Phys. Chem. A 2001, 105, 6955–6964. [Google Scholar] [CrossRef]


| Item | New ReaxFF-lg | Original ReaxFF-lg [21] | Experiment | |
|---|---|---|---|---|
| a | 9.317 | 9.380 | 9.326 | |
| b | 5.445 | 5.482 | 5.450 | |
| c | 8.851 | 9.093 | 9.040 | |
| α | 90.0 | 90.0 | 90.0 | |
| β | 101.47 | 101.47 | 101.47 | |
| γ | 90.0 | 90.0 | 90.0 | |
| density (g/cm3) | 1.926 | 1.885 | 1.918 | |
| density error (%) | −0.417 | −1.721 | − | |
| ΔHsub (kcal/mol) | 25.62 | 39.89 | 23.42–28.65 [37] | |
| RMSD (Å) | crystal | 0.204 | 0.660 | − |
| molecule | 0.063 | 0.247 | − | |
| Us (km/s) | Up (km/s) | V/V0 | P (GPa) | |||
|---|---|---|---|---|---|---|
| α-NTO | β-NTO | α-NTO | β-NTO | α-NTO | β-NTO | |
| 2 | 0.24 | 0.19 | 0.88 | 0.91 | 0.92 | 0.73 |
| 3 | 0.6 | 0.51 | 0.80 | 0.83 | 3.45 | 2.93 |
| 4 | 1.09 | 0.95 | 0.73 | 0.76 | 8.35 | 7.29 |
| 5 | 1.59 | 1.58 | 0.68 | 0.68 | 15.23 | 15.16 |
| 6 | 2.22 | 2.20 | 0.63 | 0.63 | 25.51 | 25.32 |
| 7 | 2.90 | 2.85 | 0.59 | 0.59 | 38.88 | 38.27 |
| 8 | 3.56 | 3.54 | 0.56 | 0.56 | 54.55 | 54.32 |
| 9 | 4.27 | 4.34 | 0.53 | 0.52 | 73.61 | 74.92 |
| 10 | 5.17 | 5.18 | 0.48 | 0.48 | 99.03 | 99.35 |
| 11 | 5.89 | 5.93 | 0.46 | 0.49 | 124.15 | 125.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, L.; Jin, S.; Nie, P.; She, C.; Wang, J. Initial Decomposition Mechanism of 3-Nitro-1,2,4-triazol-5-one (NTO) under Shock Loading: ReaxFF Parameterization and Molecular Dynamic Study. Molecules 2021, 26, 4808. https://doi.org/10.3390/molecules26164808
Du L, Jin S, Nie P, She C, Wang J. Initial Decomposition Mechanism of 3-Nitro-1,2,4-triazol-5-one (NTO) under Shock Loading: ReaxFF Parameterization and Molecular Dynamic Study. Molecules. 2021; 26(16):4808. https://doi.org/10.3390/molecules26164808
Chicago/Turabian StyleDu, Lixiaosong, Shaohua Jin, Pengsong Nie, Chongchong She, and Junfeng Wang. 2021. "Initial Decomposition Mechanism of 3-Nitro-1,2,4-triazol-5-one (NTO) under Shock Loading: ReaxFF Parameterization and Molecular Dynamic Study" Molecules 26, no. 16: 4808. https://doi.org/10.3390/molecules26164808
APA StyleDu, L., Jin, S., Nie, P., She, C., & Wang, J. (2021). Initial Decomposition Mechanism of 3-Nitro-1,2,4-triazol-5-one (NTO) under Shock Loading: ReaxFF Parameterization and Molecular Dynamic Study. Molecules, 26(16), 4808. https://doi.org/10.3390/molecules26164808





