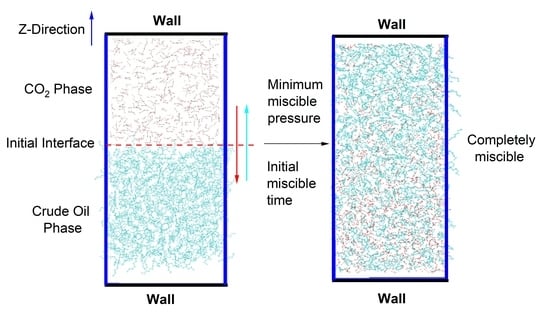
Determination of Minimum Miscibility Pressure of CO2–Oil System: A Molecular Dynamics Study
Abstract
:1. Introduction
2. Simulation Method
2.1. Simulation and Force Field
2.2. Simulation System
3. Results and Discussion
3.1. Definition of Initial Miscible Time
3.2. Reconfirmation of Initial Miscible Time
3.2.1. Solvent Accessible SURFACE Area (SASA) Analysis
3.2.2. Root Mean Square Deviation (RMSD) Analysis
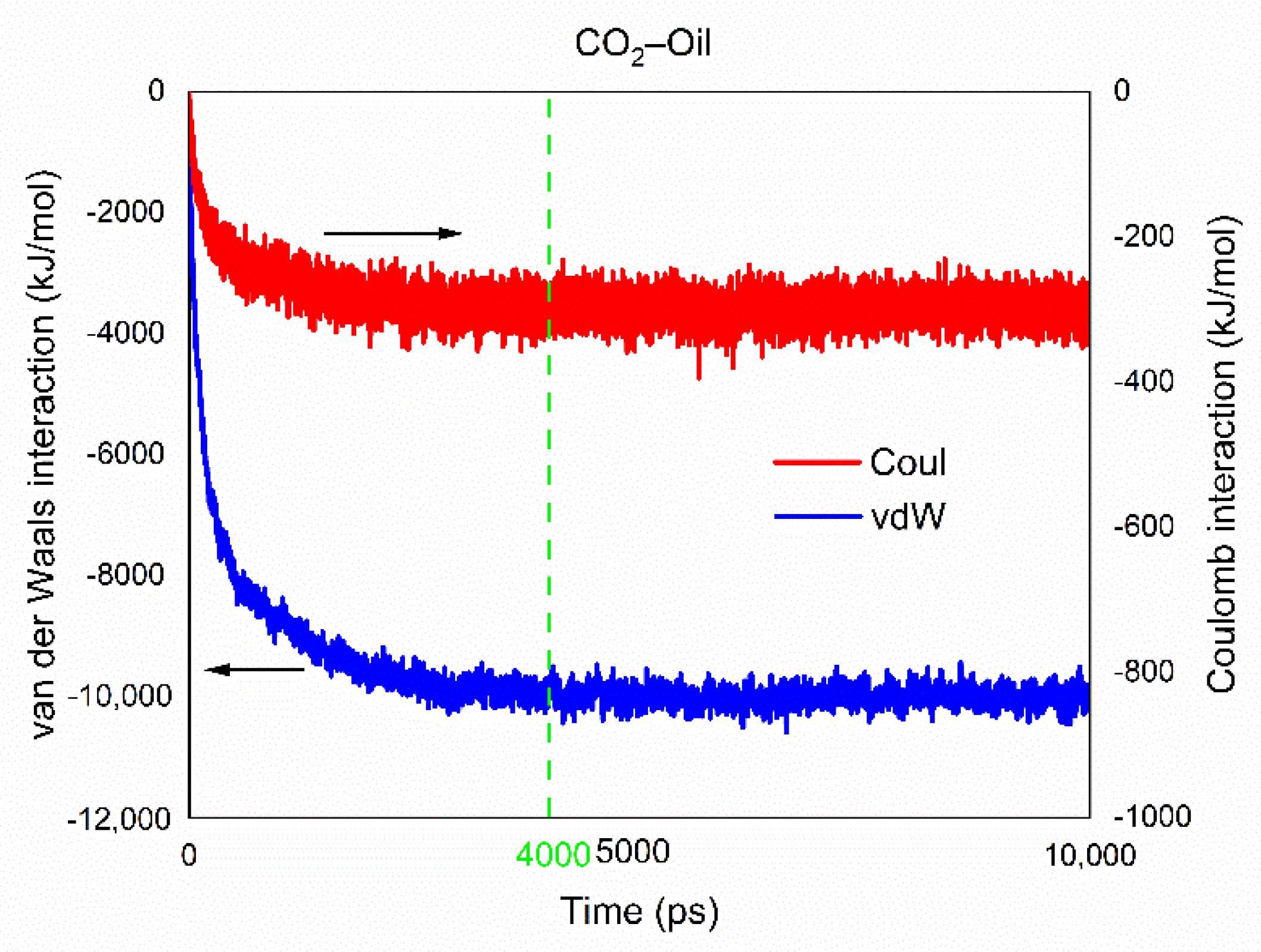
3.2.3. Interaction Energy Analysis
3.3. Acquisition of MMP
3.4. MMP in Different Temperature Systems
3.5. Model Assessment
3.6. Comparison of MMP Predicted by CO2 and Crude Oil
3.7. Relationships between TR and MMP
4. Conclusions
- (1)
- The molecular scale mixing progress of CO2 and crude oil was investigated in principle for the first time, and the research process was not affected by other external objective factors. Results showed that the ratio of CO2/crude oil atoms that passed through the initial interface to their respective totals was always the same when the system was miscible. The proposed model had good prediction capabilities.
- (2)
- In the process of the simulation, the SASA, RMSD, and interaction energy of CO2/crude oil changed obviously, thus they can be used as criteria of miscibility between both phases.
- (3)
- The MMP predicted by CO2 of the CO2–oil system were 20.31 MPa, 21.08 MPa, 22.12 MPa, 24.43 MPa, and 26.25 MPa at temperatures of 333 K, 343 K, 353 K, 363 K, and 373 K, respectively, and MMPs predicted by crude oil were 20.21 MPa, 20.89 MPa, 22.36 MPa, 23.84 MPa, and 24.52 MPa at the same temperatures. The two sets of data had a linear relationship.
- (4)
- MMP and reservoir temperature (TR) had a linear relationship in the present work, and the slope was about 0.15 MPa/K, which are in agreement with theoretical analyses and literature results.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Farajzadeh, R.; Eftekhari, A.A.; Dafnomilis, G.; Lake, L.; Bruining, J. On the sustainability of CO2 storage through CO2–Enhanced oil recovery. Appl. Energy 2020, 261, 114467. [Google Scholar] [CrossRef]
- Li, S.; Li, Z.; Dong, Q. Diffusion coefficients of supercritical CO2 in oil-saturated cores under low permeability reservoir conditions. J. CO2 Util. 2016, 14, 47–60. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, S.; Zhang, L.; Ren, S.; Guo, Q. Assessment of CO2-EOR and its geo-storage potential in mature oil reservoirs, Shengli Oilfield, China. Petrol. Explor. Dev. 2009, 36, 737–742. [Google Scholar]
- Dong, M.; Huang, S.; Srivastava, R. Effect of Solution Gas in Oil on CO2 Minimum Miscibility Pressure. Annu. Tech. Meet. 1999, 39. [Google Scholar] [CrossRef]
- Rathmell, J.; Stalkup, F.; Hassinger, R. A Laboratory Investigation of Miscible Displacement by Carbon Dioxide. Soc. Pet. Eng. AIME Pap. 1971, SPE3483, 1–10. [Google Scholar] [CrossRef]
- Zhang, K.; Jia, N.; Zeng, F.; Li, S.; Liu, L. A review of experimental methods for determining the Oil‒Gas minimum miscibility pressures. J. Pet. Sci. Eng. 2019, 183. [Google Scholar] [CrossRef]
- Glaso, O. Miscible Displacement: Recovery Tests with Nitrogen. SPE Reserv. Eng. 1990, 5, 61–68. [Google Scholar] [CrossRef]
- Zhang, K.; Gu, Y. Two different technical criteria for determining the minimum miscibility pressures (MMPs) from the slim-tube and coreflood tests. Fuel 2015, 161, 146–156. [Google Scholar] [CrossRef]
- Mogensen, K. A novel protocol for estimation of minimum miscibility pressure from slimtube experiments. J. Pet. Sci. Eng. 2016, 146, 545–551. [Google Scholar] [CrossRef]
- Christiansen, R.L.; Haines, H.K. Rapid Measurement of Minimum Miscibility Pressure with the Rising-Bubble Apparatus. SPE Reserv. Eng. 1987, 2, 523–527. [Google Scholar] [CrossRef]
- Zhang, K.; Jia, N.; Zeng, F. Application of predicted bubble-rising velocities for estimating the minimum miscibility pressures of the light crude oil–CO2 systems with the rising bubble apparatus. Fuel 2018, 220, 412–419. [Google Scholar] [CrossRef]
- Orr, F.M.; Jessen, K. An analysis of the vanishing interfacial tension technique for determination of minimum miscibility pressure. Fluid Phase Equilibria 2007, 255, 99–109. [Google Scholar] [CrossRef]
- Ghorbani, M.; Momeni, A.; Safavi, S.; Gandomkar, A. Modified vanishing interfacial tension (VIT) test for CO2–Oil minimum miscibility pressure (MMP) measurement. J. Nat. Gas Sci. Eng. 2014, 20, 92–98. [Google Scholar] [CrossRef]
- Hemmati-Sarapardeh, A.; Ayatollahi, S.; Ghazanfari, M.-H.; Masihi, M. Experimental Determination of Interfacial Tension and Miscibility of the CO2–Crude Oil System; Temperature, Pressure, and Composition Effects. J. Chem. Eng. Data 2014, 59, 61–69. [Google Scholar] [CrossRef]
- Ayirala, S.C.; Rao, D.N. Application of the parachor model to the prediction of miscibility in multi-component hydrocarbon systems. J. Phys. Condens. Matter 2004, 16, S2177–S2186. [Google Scholar] [CrossRef]
- Benham, A.; Dowden, W.; Kunzman, W. Miscible Fluid Displacement—Prediction of Miscibility. Trans. AIME 1960, 219, 229–237. [Google Scholar] [CrossRef]
- Kuo, S. Prediction of Miscibility for the Enriched-Gas Drive Process. SPE Annu. Tech. Conf. Exhib. 1985. [Google Scholar] [CrossRef]
- Orr, F.J.; Silva, M. Effect of Oil Composition on Minimum Miscibility Pressure-Part 2: Correlation. SPE Reserv. Eng. 1987, 2, 479–491. [Google Scholar] [CrossRef]
- Yuan, H.; Johns, R.T.; Egwuenu, A.M.; Dindoruk, B. Improved MMP Correlation for CO2 Floods Using Analytical Theory. SPE Reserv. Eval. Eng. 2005, 8, 418–425. [Google Scholar] [CrossRef]
- Valluri, M.K.; Mishra, S.; Schuetter, J. An improved correlation to estimate the minimum miscibility pressure of CO2 in crude oils for carbon capture, utilization, and storage projects. J. Pet. Sci. Eng. 2017, 158, 408–415. [Google Scholar] [CrossRef]
- Dong, M.; Huang, S.; Dyer, S.B.; Mourits, F.M. A comparison of CO2 minimum miscibility pressure determinations for Weyburn crude oil. J. Pet. Sci. Eng. 2001, 31, 13–22. [Google Scholar] [CrossRef]
- Chen, G.; Wang, X.; Liang, Z.; Gao, R.; Sema, T.; Luo, P.; Zeng, F.; Tontiwachwuthikul, P. Simulation of CO2-Oil Minimum Miscibility Pressure (MMP) for CO2 Enhanced Oil Recovery (EOR) using Neural Networks. Energy Procedia 2013, 37, 6877–6884. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Fu, K.; Liang, Z.; Sema, T.; Li, C.; Tontiwachwuthikul, P.; Idem, R. The genetic algorithm based back propagation neural network for MMP prediction in CO2-EOR process. Fuel 2014, 126, 202–212. [Google Scholar] [CrossRef]
- Tatar, A.; Shokrollahi, A.; Mesbah, M.; Rashid, S.; Arabloo, M.; Bahadori, A. Implementing Radial Basis Function Networks for modeling CO2-reservoir oil minimum miscibility pressure. J. Nat. Gas Sci. Eng. 2013, 15, 82–92. [Google Scholar] [CrossRef]
- Emera, M.K.; Sarma, H.K. Use of genetic algorithm to estimate CO2–oil minimum miscibility pressure—A key parameter in design of CO2 miscible flood. J. Pet. Sci. Eng. 2005, 46, 37–52. [Google Scholar] [CrossRef]
- Sayyad, H.; Manshad, A.K.; Rostami, H. Application of hybrid neural particle swarm optimization algorithm for prediction of MMP. Fuel 2013, 116, 625–633. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, C.; Jia, N.; Duncan, I.; Yang, S.; Yang, Y. A machine learning model for predicting the minimum miscibility pressure of CO2 and crude oil system based on a support vector machine algorithm approach. Fuel 2021, 290, 120048. [Google Scholar] [CrossRef]
- Ghiasi, M.M.; Mohammadi, A.H.; Zendehboudi, S. Use of hybrid-ANFIS and ensemble methods to calculate minimum miscibility pressure of CO2-reservoir oil system in miscible flooding process. J. Mol. Liq. 2021, 331, 115369. [Google Scholar] [CrossRef]
- Li, D.; Li, X.; Zhang, Y.; Sun, L.; Yuan, S. Four Methods to Estimate Minimum Miscibility Pressure of CO2-Oil Based on Machine Learning. Chin. J. Chem. 2019, 37, 1271–1278. [Google Scholar] [CrossRef]
- Karkevandi-Talkhooncheh, A.; Hajirezaie, S.; Hemmati-Sarapardeh, A.; Husein, M.M.; Karan, K.; Sharifi, M. Application of adaptive neuro fuzzy interface system optimized with evolutionary algorithms for modeling CO2-crude oil minimum miscibility pressure. Fuel 2017, 205, 34–45. [Google Scholar] [CrossRef]
- Karkevandi-Talkhooncheh, A.; Rostami, A.; Sarapardeh, A.H.; Ahmadi, M.; Husein, M.M.; Dabir, B. Modeling minimum miscibility pressure during pure and impure CO2 flooding using hybrid of radial basis function neural network and evolutionary techniques. Fuel 2018, 220, 270–282. [Google Scholar] [CrossRef]
- Ekechukwu, G.K.; Falode, O.; Orodu, O.D. Improved Method for the Estimation of Minimum Miscibility Pressure for Pure and Impure CO2–Crude Oil Systems Using Gaussian Process Machine Learning Approach. J. Energy Resour. Technol. 2020, 142, 1–14. [Google Scholar] [CrossRef]
- Zendehboudi, S.; Rezaei, N.; Lohi, A. Applications of hybrid models in chemical, petroleum, and energy systems: A systematic review. Appl. Energy 2018, 228, 2539–2566. [Google Scholar] [CrossRef]
- Zendehboudi, S.; Ahmadi, M.A.; Bahadori, A.; Shafiei, A.; Babadagli, T. A developed smart technique to predict minimum miscible pressure-eor implications. Can. J. Chem. Eng. 2013, 91, 1325–1337. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Van Der Spoel, D.; Van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; Van Der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Case, “Development and testing of a general amber force field” Journal of Computational Chemistry(2004) 25(9) 1157-1174. J. Comput. Chem. 2004, 26, 114. [Google Scholar] [CrossRef]
- Malde, A.; Zuo, L.; Breeze, M.; Stroet, M.; Poger, D.; Nair, P.; Oostenbrink, C.; Mark, A. An Automated Force Field Topology Builder (ATB) and Repository: Version 1.0. J. Chem. Theory Comput. 2011, 7, 4026–4037. [Google Scholar] [CrossRef] [PubMed]
- Koziara, K.B.; Stroet, M.; Malde, A.; Mark, A.E. Testing and validation of the Automated Topology Builder (ATB) version 2.0: Prediction of hydration free enthalpies. J. Comput. Mol. Des. 2014, 28, 221–233. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [Green Version]
- Berendsen, H.J.C.; Postma, J.P.M.; Van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Apostolakis, J.; Ferrara, P.; Caflisch, A. Calculation of conformational transitions and barriers in solvated systems: Application to the alanine dipeptide in water. J. Chem. Phys. 1999, 110, 2099–2108. [Google Scholar] [CrossRef] [Green Version]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Essmann, U.; Perera, L.; Berkowitz, M.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
- Van der Spoel, D.; Lindahl, E.; Hess, B.; Van Buuren, A.; Apol, E.; Meulenhoff, P.; Tieleman, D.; Sijbers, A.; Feenstra, K.; van Drunen, R.; et al. Gromacs User Manual Version 4.0. Manuals 2005. Available online: www.gromacs.org (accessed on 7 May 2021).
- Teklebrhan, R.B.; Ge, L.; Bhattacharjee, S.; Xu, Z.; Sjöblom, J. Probing Structure–Nanoaggregation Relations of Polyaromatic Surfactants: A Molecular Dynamics Simulation and Dynamic Light Scattering Study. J. Phys. Chem. B 2012, 116, 5907–5918. [Google Scholar] [CrossRef]
- De Lara, L.; Michelon, M.F.; Miranda, C.R. Molecular Dynamics Studies of Fluid/Oil Interfaces for Improved Oil Recovery Processes. J. Phys. Chem. B 2012, 116, 14667–14676. [Google Scholar] [CrossRef]
- Kunieda, M.; Nakaoka, K.; Liang, Y.; Miranda, C.R.; Ueda, A.; Takahashi, S.; Okabe, H.; Matsuoka, T. Self-Accumulation of Aromatics at the Oil−Water Interface through Weak Hydrogen Bonding. J. Am. Chem. Soc. 2010, 132, 18281–18286. [Google Scholar] [CrossRef]
- Song, S.; Zhang, H.; Sun, L.; Shi, J.; Cao, X.; Yuan, S. Molecular Dynamics Study on Aggregating Behavior of Asphaltene and Resin in Emulsified Heavy Oil Droplets with Sodium Dodecyl Sulfate. Energy Fuels 2018, 32, 12383–12393. [Google Scholar] [CrossRef]
- Yu, H.; Lu, X.; Fu, W.; Wang, Y.; Xu, H.; Xie, Q.; Qu, X.; Lu, J. Determination of minimum near miscible pressure region during CO2 and associated gas injection for tight oil reservoir in Ordos Basin, China. Fuel 2020, 263, 116737. [Google Scholar] [CrossRef]
- Lee, J. Effectiveness of Carbon Dioxide Displacement under Miscible and Immiscible Conditions; Petroleum Recovery Inst.: Calgary, AB, Canada, 1979. [Google Scholar]
- Alston, R.; Kokolis, G.; James, C. CO2 Minimum Miscibility Pressure: A Correlation for Impure CO2 Streams and Live Oil Systems. Soc. Pet. Eng. J. 1985, 25, 268–274. [Google Scholar] [CrossRef]
- Shokir, E.M.E.-M. CO2–oil minimum miscibility pressure model for impure and pure CO2 streams. J. Pet. Sci. Eng. 2007, 58, 173–185. [Google Scholar] [CrossRef]
- Cronquist, C. Carbon dioxide dynamic miscibility with light reservoir oils. In Proceedings of the Fourth Annual US DOE Symposium, Tulsa, OK, USA, 28 August 1978; pp. 28–30. [Google Scholar]
- Glaso, O. Generalized Minimum Miscibility Pressure Correlation (includes associated papers 15845 and 16287). Soc. Pet. Eng. J. 1985, 25, 927–934. [Google Scholar] [CrossRef]
- Yellig, W.F.; Metcalfe, R.S. Determination and Prediction of CO2 Minimum Miscibility Pressures (includes associated paper 8876). J. Pet. Technol. 1980, 32, 160–168. [Google Scholar] [CrossRef]
- Zolghadr, A.; Escrochi, M.; Ayatollahi, S. Temperature and Composition Effect on CO2 Miscibility by Interfacial Tension Measurement. J. Chem. Eng. Data 2013, 58, 1168–1175. [Google Scholar] [CrossRef]
- Zheng, L.; Ma, K.; Yuan, S.; Wang, F.; Dong, X.; Li, Y.; Du, D. Determination of the multiple-contact minimum miscibility pressure of CO2/oil system using oil droplet volume measurement method. J. Pet. Sci. Eng. 2019, 106578. [Google Scholar] [CrossRef]
- Lashkarbolooki, M.; Eftekhari, M.J.; Najimi, S.; Ayatollahi, S. Minimum miscibility pressure of CO2 and crude oil during CO2 injection in the reservoir. J. Supercrit. Fluids 2017, 127, 121–128. [Google Scholar] [CrossRef]
- Menouar, H. Discussion on Carbon Dioxide Minimum Miscibility Pressure Estimation: An Experimental Investigation. In Proceedings of the SPE Western Regional & AAPG Pacific Section Meeting 2013 Joint Technical Conference, Monterey, CA, USA, 19–25 April 2013. [Google Scholar]








| CO2 | Crude Oil | |
|---|---|---|
| 10 MPa | 0.0292 | 0.0300 |
| 15 MPa | 0.0231 | 0.0236 |
| 20 MPa | 0.0219 | 0.0221 |
| 25 MPa | 0.0216 | 0.0217 |
| 30 MPa | 0.0204 | 0.0207 |
| 35 MPa | 0.0205 | 0.0208 |
| 333 K | 343 K | 353 K | 363 K | 373 K | |
|---|---|---|---|---|---|
| 10 MPa | 4.0 | 5.0 | 3.5 | 4.0 | 3.0 |
| 15 MPa | 4.5 | 6.0 | 3.5 | 3.0 | 2.5 |
| 20 MPa | 4.5 | 5.0 | 4.0 | 3.0 | 3.0 |
| 25 MPa | 4.0 | 3.5 | 4.0 | 3.0 | 3.5 |
| 30 MPa | 3.5 | 4.0 | 4.0 | 3.0 | 4.0 |
| 35 MPa | 4.5 | 4.0 | 4.5 | 3.5 | 4.0 |
| CO2 | Crude Oil | |
|---|---|---|
| 333 K | 20.31 | 20.21 |
| 343 K | 21.08 | 20.89 |
| 353 K | 22.12 | 22.36 |
| 363 K | 24.43 | 23.84 |
| 373 K | 26.25 | 24.52 |
| Model | Number of Parameters | Predicted MMP (MPa) | Relative Error (%) |
|---|---|---|---|
| Yu et al. [51] | - | 22.75 | - |
| CO2 (this study) | 1 | 19.63 | 13.71 |
| Crude Oil (this study) | 1 | 20.81 | 8.53 |
| Lee [52] | 1 | 20.84 | 8.32 |
| Alston et al. [53] | 4 | 19.72 | 13.22 |
| Shokir [54] | 8 | 20.03 | 11.89 |
| Emera and Sarma [25] | 2 | 30.11 | 32.44 |
| Cronquist [55] | 3 | 26.59 | 16.96 |
| Glaso [56] | 2 | 27.60 | 21.41 |
| Yellig and Metcalfe [57] | 1 | 16.55 | 27.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Xie, S.; Li, X.; Zhang, Y.; Zhang, H.; Yuan, S. Determination of Minimum Miscibility Pressure of CO2–Oil System: A Molecular Dynamics Study. Molecules 2021, 26, 4983. https://doi.org/10.3390/molecules26164983
Li D, Xie S, Li X, Zhang Y, Zhang H, Yuan S. Determination of Minimum Miscibility Pressure of CO2–Oil System: A Molecular Dynamics Study. Molecules. 2021; 26(16):4983. https://doi.org/10.3390/molecules26164983
Chicago/Turabian StyleLi, Ding, Shuixiang Xie, Xiangliang Li, Yinghua Zhang, Heng Zhang, and Shiling Yuan. 2021. "Determination of Minimum Miscibility Pressure of CO2–Oil System: A Molecular Dynamics Study" Molecules 26, no. 16: 4983. https://doi.org/10.3390/molecules26164983
APA StyleLi, D., Xie, S., Li, X., Zhang, Y., Zhang, H., & Yuan, S. (2021). Determination of Minimum Miscibility Pressure of CO2–Oil System: A Molecular Dynamics Study. Molecules, 26(16), 4983. https://doi.org/10.3390/molecules26164983