Ribitol in Solution Is an Equilibrium of Asymmetric Conformations
Abstract
:1. Introduction
2. Results and Discussion
2.1. Database Analysis of Ribitol and Ribitol Phosphate
2.2. NMR Analysis
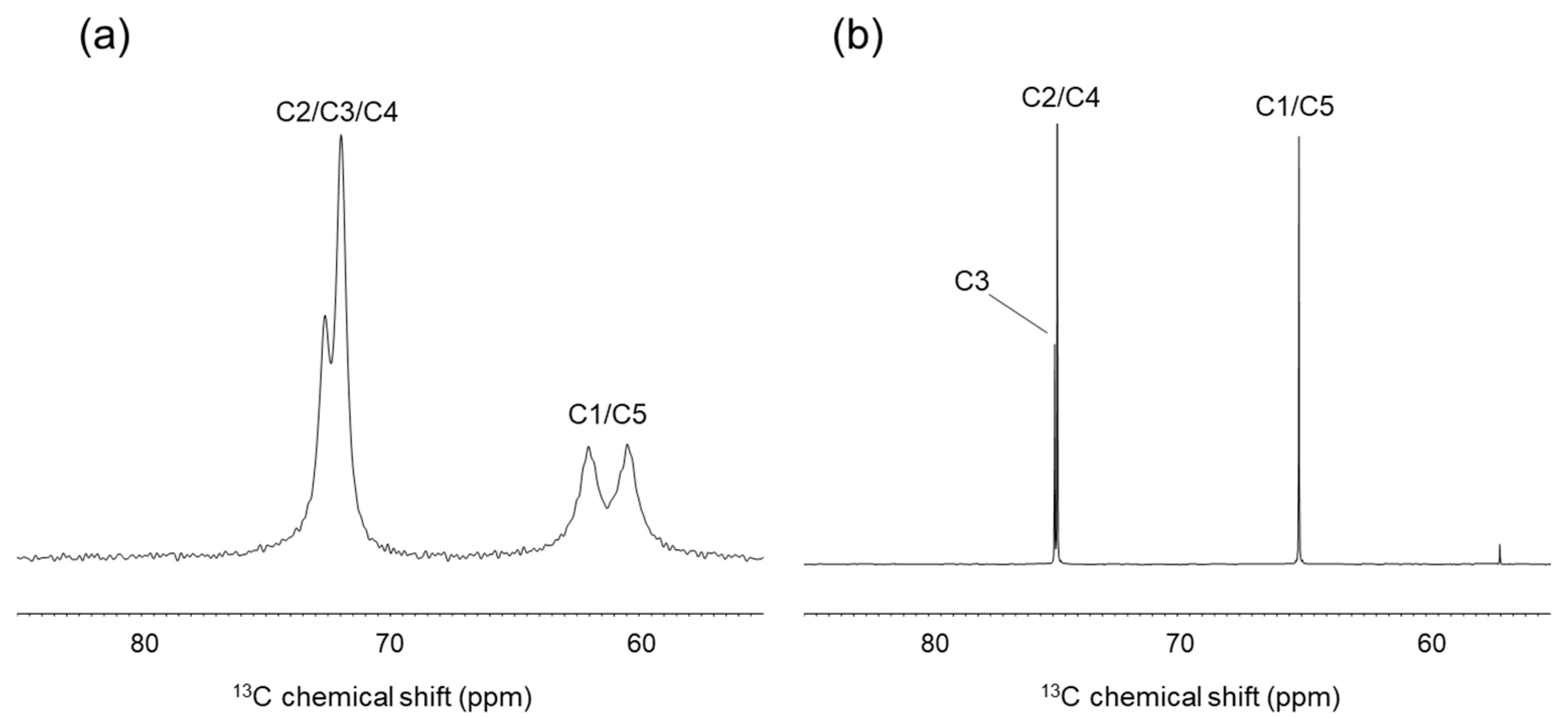
2.2.1. Solid-State 13C-NMR Analysis of Crystalline Ribitol
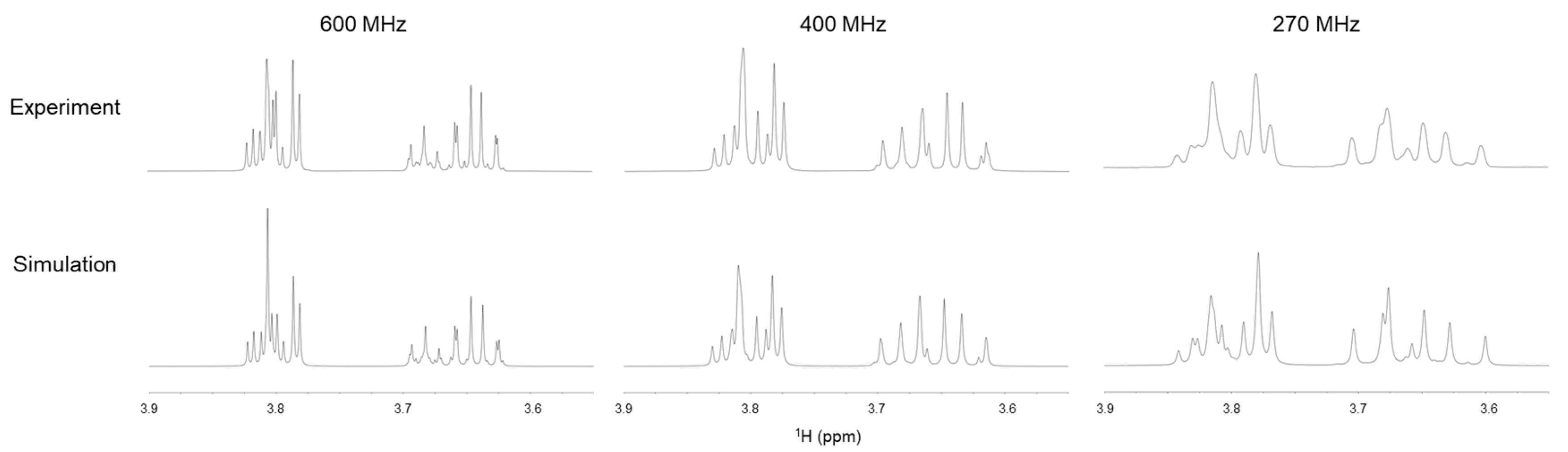
2.2.2. Solution NMR Analysis of Ribitol Based on Coupling Constant
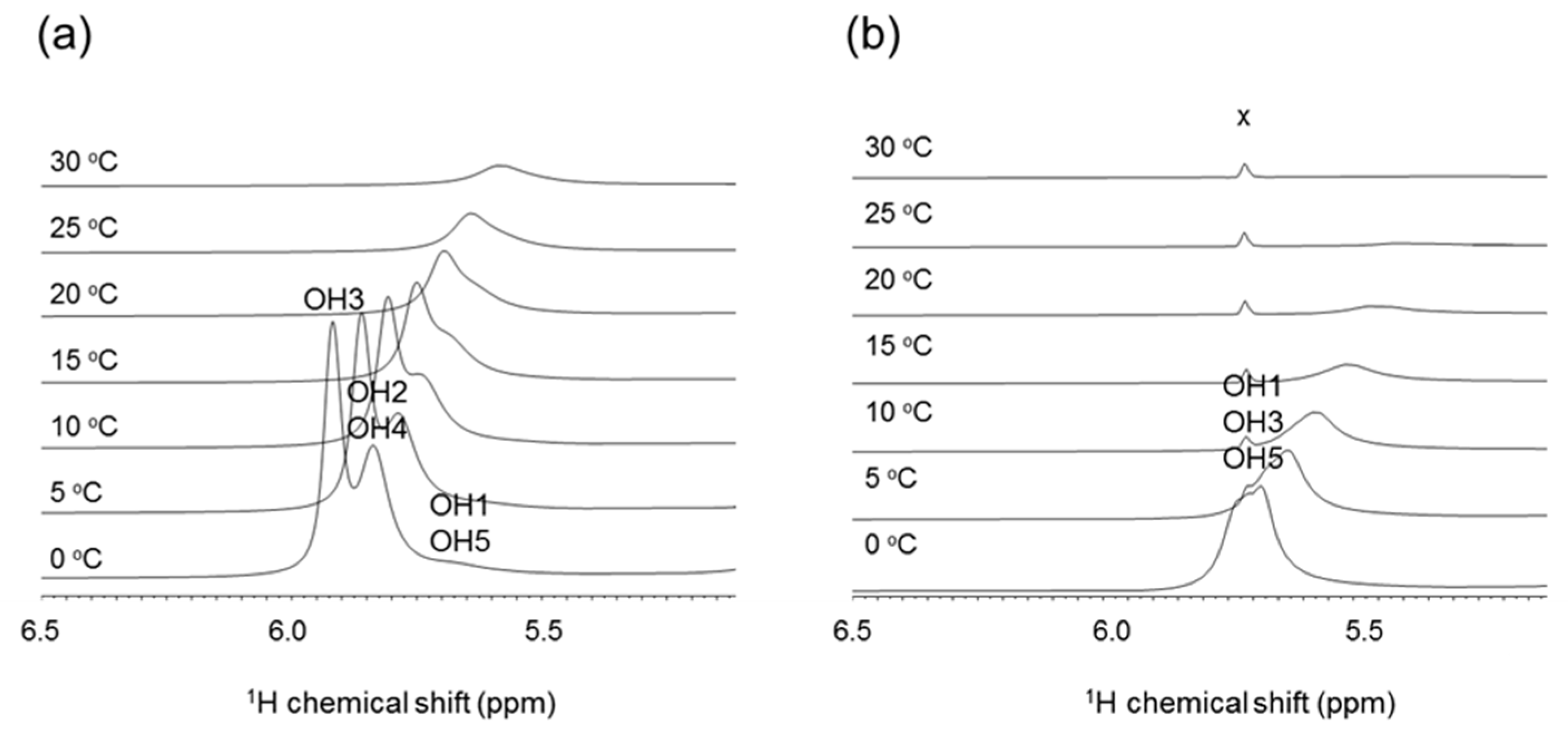
2.2.3. NMR Analysis of Hydroxy Protons
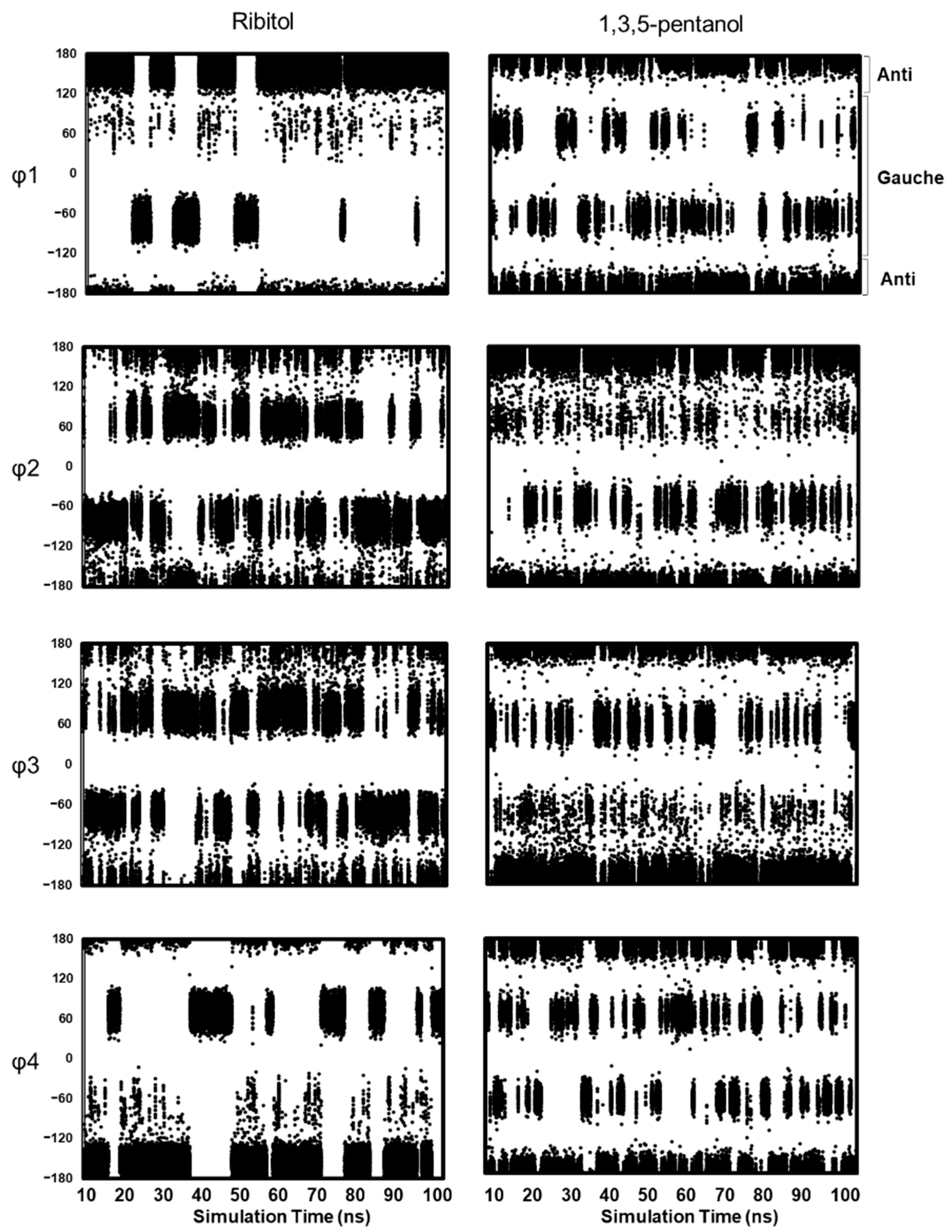
2.3. MD Simulations
Distribution of Main Chain Dihedral Angles
3. Materials and Methods
3.1. Database Analysis of Ribitol and Ribitol Phosphate
3.2. Solution NMR Analysis
3.3. Solid-State 13C-CP-MAS NMR
3.4. MD Simulation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Brown, S.; Santa Maria, J.P., Jr.; Walker, S. Wall teichoic acids of gram-positive bacteria. Annu. Rev. Microbiol. 2013, 67, 313–336. [Google Scholar] [CrossRef] [Green Version]
- Kanagawa, M.; Kobayashi, K.; Tajiri, M.; Manya, H.; Kuga, A.; Yamaguchi, Y.; Akasaka-Manya, K.; Furukawa, J.I.; Mizuno, M.; Kawakami, H.; et al. Identification of a post-translational modification with ribitol-phosphate and its defect in muscular dystrophy. Cell Rep. 2016, 14, 2209–2223. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Endo, T. Mammalian O-mannosyl glycans: Biochemistry and glycopathology. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2019, 95, 39–51. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jeffrey, G.A.; Kim, H.S. Conformations of the alditols. Carbohydr. Res. 1970, 14, 207–216. [Google Scholar] [CrossRef]
- Tanaka, N.; Ashida, T.; Sasada, Y.; Kakudo, M. The crystal structure of riboflavin hydrobromide monohydrate. Bull. Chem. Soc. Jpn. 1969, 42, 1546–1554. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tanaka, N.; Ashida, T.; Sasada, Y.; Kakudo, M. The crystal structure of riboflavin hydrobromide monohydrate. Bull. Chem. Soc. Jpn. 1967, 40, 1739. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hawkes, G.E.; Lewis, D. 1H nuclear magnetic resonance spectra and conformations of alditols in deuterium oxide. J. Chem. Soc. Perk. Trans. 1984, 2073–2078. [Google Scholar] [CrossRef]
- Garrett, E.C.; Serianni, A.S. (1-13C)Alditols: Elimination of magnetic equivalence in 1H- and 13C-n.m.r. spectra of symmetric compounds through (13C)-substitution. Carbohydr. Res. 1990, 208, 23–35. [Google Scholar] [CrossRef]
- Klein, R.A.; Hartmann, R.; Egge, H.; Behr, T.; Fischer, W. The aqueous solution structure of the tetrasaccharide-ribitol repeat-unit from the lipoteichoic acid of Streptococcus pneumoniae strain R6 determined using a combination of NMR spectroscopy and computer calculations. Carbohydr. Res. 1994, 256, 189–222. [Google Scholar] [CrossRef]
- Hatcher, E.; Guvench, O.; Mackerell, A.D., Jr. CHARMM additive all-atom force field for acyclic polyalcohols, acyclic carbohydrates and inositol. J. Chem. Theory Comput. 2009, 5, 1315–1327. [Google Scholar] [CrossRef] [Green Version]
- Imberty, A. Oligosaccharide structures: Theory versus experiment. Curr. Opin. Struct. Biol. 1997, 7, 617–623. [Google Scholar] [CrossRef]
- Kim, H.S.; Jeffrey, G.A.; Rosenste, R.D. Crystal structure of ribitol. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1969, 25, 2223–2230. [Google Scholar] [CrossRef]
- Madsen, A.O.; Larsen, S. Insight into solid-state entropy from diffraction data. Angew. Chem. Int. Ed. Engl. 2007, 46, 8609–8613. [Google Scholar] [CrossRef] [PubMed]
- Madsen, A.O.; Mattson, R.; Larsen, S. Understanding thermodynamic properties at the molecular level: Multiple temperature charge density study of ribitol and xylitol. J. Phys. Chem. A 2011, 115, 7794–7804. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, H.; Yoshihara, A.; Teraoka, M.; Terami, Y.; Takata, G.; Izumori, K.; Kamitori, S. X-ray structure of a novel L-ribose isomerase acting on a non-natural sugar L-ribose as its ideal substrate. FEBS J. 2014, 281, 3150–3164. [Google Scholar] [CrossRef] [PubMed]
- Gerlach, D.; Guo, Y.; De Castro, C.; Kim, S.H.; Schlatterer, K.; Xu, F.F.; Pereira, C.; Seeberger, P.H.; Ali, S.; Codee, J.; et al. Methicillin-resistant Staphylococcus aureus alters cell wall glycosylation to evade immunity. Nature 2018, 563, 705–709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuwabara, N.; Imae, R.; Manya, H.; Tanaka, T.; Mizuno, M.; Tsumoto, H.; Kanagawa, M.; Kobayashi, K.; Toda, T.; Senda, T.; et al. Crystal structures of fukutin-related protein (FKRP), a ribitol-phosphate transferase related to muscular dystrophy. Nat. Commun. 2020, 11, 303. [Google Scholar] [CrossRef]
- Furihata, K.; Tashiro, M.; Seto, H. High resolution-HMBC (HR-HMBC), a new method for measuring heteronuclear long-range coupling constants. Magn. Reson. Chem. 2010, 48, 179–183. [Google Scholar] [CrossRef]
- Franks, F.; Kay, R.L.; Dadok, J. A nuclear magnetic resonance study of isomeric pentitols in aqueous and non-aqueous solutions. J. Chem. Soc. Farad. Trans. 1988, 84, 2595–2602. [Google Scholar] [CrossRef]
- Haasnoot, C.A.G.; Deleeuw, F.A.A.M.; Altona, C. The relationship between proton-proton NMR coupling constants and substituent electronegativities. 1. An empirical generalization of the Karplus equation. Tetrahedron 1980, 36, 2783–2792. [Google Scholar] [CrossRef]
- Palermo, G.; Riccio, R.; Bifulco, G. Effect of electronegative substituents and angular dependence on the heteronuclear spin-spin coupling constant 3J(C-H): An empirical prediction equation derived by density functional theory calculations. J. Org. Chem. 2010, 75, 1982–1991. [Google Scholar] [CrossRef]
- Aydin, R.; Günther, H. 13C, 1H spin–spin coupling. X—Norbornane: A reinvestigation of the karplus curve for 3J(13C, 1H). Magn. Reson. Chem. 1990, 28, 448–457. [Google Scholar] [CrossRef]
- Dobson, C.M.; Lian, L.Y.; Redfield, C.; Topping, K.D. Measurement of hydrogen-exchange rates using 2D NMR-spectroscopy. J. Magn. Reson. 1986, 69, 201–209. [Google Scholar] [CrossRef]
- Sandstrom, C.; Baumann, H.; Kenne, L. The use of chemical shifts of hydroxy protons of oligosaccharides as conformational probes for NMR studies in aqueous solution. Evidence for persistent hydrogen bond interaction in branched trisaccharides. J. Chem. Soc. Perk. Trans. 1998, 2385–2393. [Google Scholar] [CrossRef]
- BIOVIA Discovery Studio. Discovery Studio 2019; Dassault Systèmes: San Diego, CA, USA, 2019. [Google Scholar]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
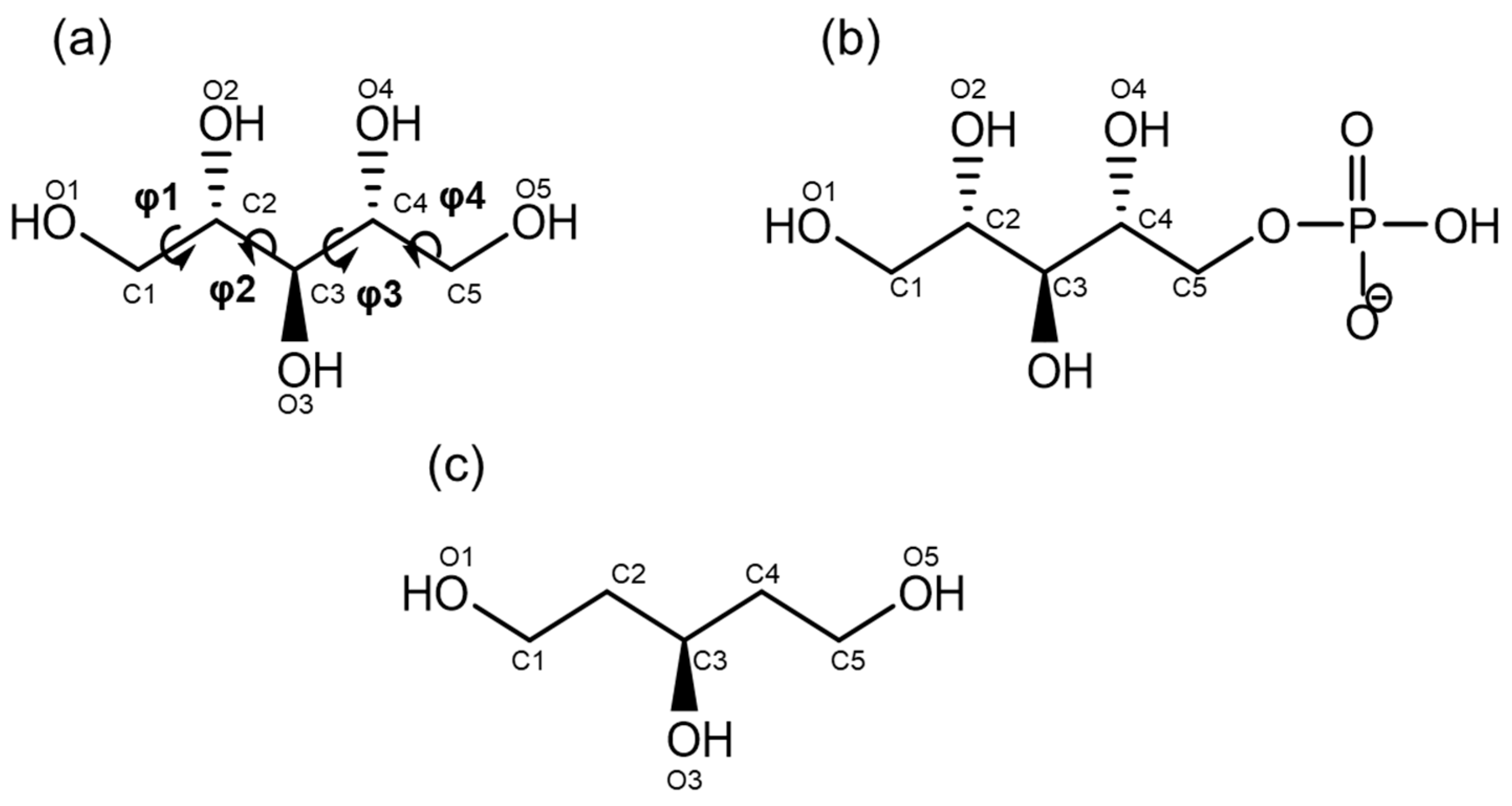
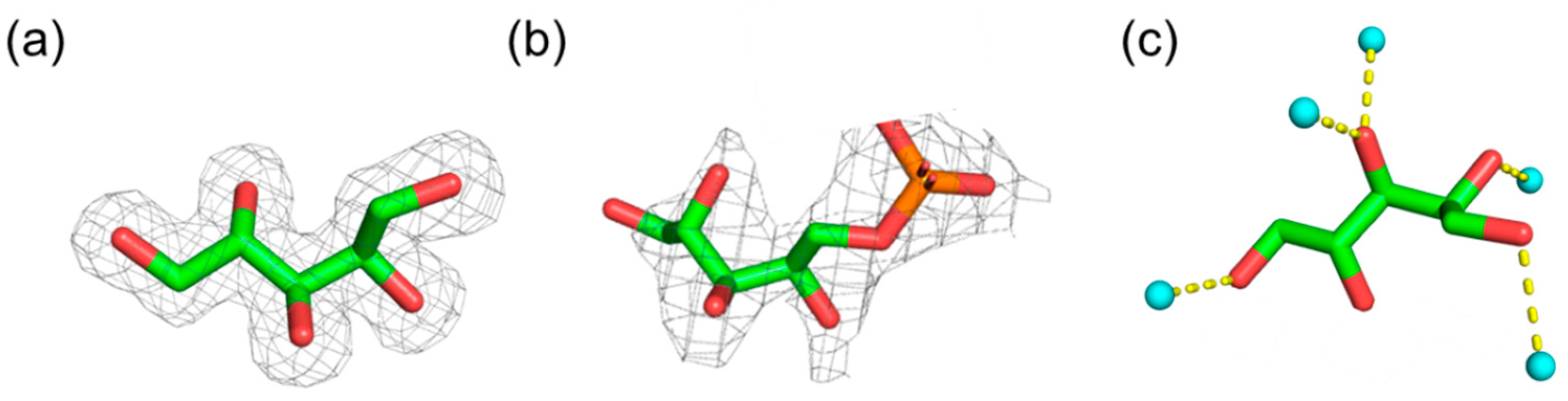
| CCDC Deposition Number/DB ID | φ1 (O1–C1–C2–C3) | φ2 (C1–C2–C3–C4) | φ3 (C2–C3–C4–C5) | φ4 (C3–C4–C5–O5) | C1–C5 Distance | Resolution | Reference |
|---|---|---|---|---|---|---|---|
| ribitol | |||||||
| 1249410 | 171 | −62 | −172 | 71 | 4.5 | - | [12] |
| 662559 | 171 | −61 | −171 | 73 | 4.6 | - | [13] |
| 1015979 | 171 | −61 | −170 | 73 | 4.6 | - | [14] |
| 5IAI | 173 | 166 | 60 | 170 | 4.5 | 1.6 | NA |
| 4Q0S | −176 | −62 | −167 | 176 | 4.5 | 1.9 | [15] |
| 4F2D | −150 | −174 | 77 | −147 | 4.5 | 2.3 | NA |
| Ribitol phosphate | |||||||
| 6H4F | 149 | 94 | 83 | 156 | 4.4 | 2.2 | [16] |
| 6H4M | 131 | −136 | −143 | −158 | 5.0 | 2.7 | [16] |
| 6HNQ | 166 | 160 | 69 | 155 | 4.6 | 2.4 | [16] |
| 6KAM | −75 | 164 | 96 | −168 | 4.8 | 2.5 | [17] |
| Chemical Shift (ppm) | |
|---|---|
| H1R(pro-R) | 3.79 |
| H1S(pro-S) | 3.64 |
| H2 | 3.81 |
| H3 | 3.68 |
| C1 | 65.1 |
| C2 | 74.8 |
| C3 | 74.9 |
| Coupling constant (Hz) | |
| 3J(H1R,H2)(pro-R) | 3.00 |
| 3J(H1S,H2)(pro-S) | 7.20 |
| 3J(H2,H3) | 6.50 |
| 2J(H1R,H1S) | −12.70 |
| 3J(C1,H3) | 3.8 * |
| 3J(C3,H1S) | 2.9 * |
| Calculated J Value (Hz) | Experimental J Value (Hz) | |
|---|---|---|
| 3J(H1R,H2)(pro-R) | 3.11 ± 0.05 | 3.00 |
| 3J(H1S,H2)(pro-S) | 7.57 ± 1.02 | 7.20 |
| 3J(H2,H3) | 6.41 ± 0.09 | 6.50 |
| 3J(C1,H3) | 4.20 ± 0.36 | 3.9 |
| 3J(C3,H1S) | 2.67 ± 0.64 | 3.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ohno, S.; Manabe, N.; Yamaguchi, T.; Uzawa, J.; Yamaguchi, Y. Ribitol in Solution Is an Equilibrium of Asymmetric Conformations. Molecules 2021, 26, 5471. https://doi.org/10.3390/molecules26185471
Ohno S, Manabe N, Yamaguchi T, Uzawa J, Yamaguchi Y. Ribitol in Solution Is an Equilibrium of Asymmetric Conformations. Molecules. 2021; 26(18):5471. https://doi.org/10.3390/molecules26185471
Chicago/Turabian StyleOhno, Shiho, Noriyoshi Manabe, Takumi Yamaguchi, Jun Uzawa, and Yoshiki Yamaguchi. 2021. "Ribitol in Solution Is an Equilibrium of Asymmetric Conformations" Molecules 26, no. 18: 5471. https://doi.org/10.3390/molecules26185471
APA StyleOhno, S., Manabe, N., Yamaguchi, T., Uzawa, J., & Yamaguchi, Y. (2021). Ribitol in Solution Is an Equilibrium of Asymmetric Conformations. Molecules, 26(18), 5471. https://doi.org/10.3390/molecules26185471






