Effects of Temperature on Enantiomerization Energy and Distribution of Isomers in the Chiral Cu13 Cluster
Abstract
:1. Introduction
2. Theoretical Methods and Computational Details
3. Results and Discussion
Energetics
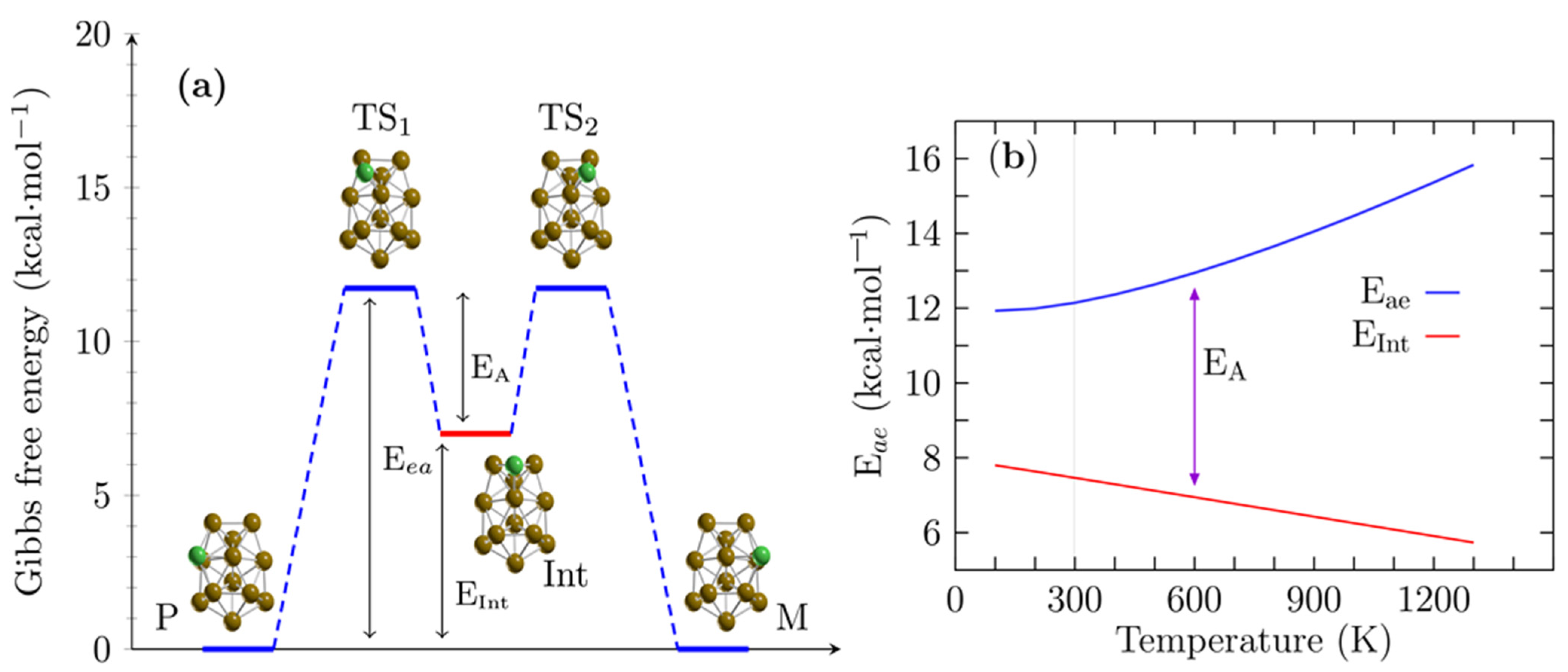
4. Enantiomerization Energy of a Pair of Enantiomers of the Cu13 Cluster at Finite Temperature
5. Relative Population of Cu13 Cluster at Finite Temperature
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Chaves, A.S.; Piotrowski, M.J.; Da Silva, J.L.F. Evolution of the structural, energetic, and electronic properties of the 3d, 4d, and 5d transition-metal clusters (30 TMn systems for n = 2–15): A density functional theory investigation. Phys. Chem. Chem. Phys. 2017, 19, 15484–15502. [Google Scholar] [CrossRef]
- Chen, W.; Chen, S. Oxygen Electroreduction Catalyzed by Gold Nanoclusters: Strong Core Size Effects. Angew. Chem. Int. Ed. 2009, 48, 4386–4389. [Google Scholar] [CrossRef]
- Henry, C.R. Surface studies of supported model catalysts. Surf. Sci. Rep. 1998, 31, 231–325. [Google Scholar] [CrossRef]
- Santiago González, B.; Rodríguez, M.J.; Blanco, C.; Rivas, J.; López-Quintela, M.A.; Martinho, J.M.G. One Step Synthesis of the Smallest Photoluminescent and Paramagnetic PVP-Protected Gold Atomic Clusters. Nano Lett. 2010, 10, 4217–4221. [Google Scholar] [CrossRef] [PubMed]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef] [PubMed]
- Cathcart, N.; Kitaev, V. Silver Nanoclusters: Single-Stage Scaleable Synthesis of Monodisperse Species and Their Chirooptical Properties. J. Phys. Chem. C 2010, 114, 16010–16017. [Google Scholar] [CrossRef]
- Ding, X.L.; Xue, W.; Ma, Y.P.; Wang, Z.C.; He, S.G. Density functional study on cage and noncage (Fe2O3)n clusters. J. Chem. Phys. 2009, 130, 014303. [Google Scholar] [CrossRef] [PubMed]
- Majid, A.; Zahid, S.; Khan, S.U.D.; Khan, S.U.D. Theoretical study of (TM)FeO3 (TM = 3d transition metals) molecular clusters. J. Nanoparticle Res. 2020, 22, 145. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, J.; Peng, Q.; Wang, X.; Li, Y. Nearly Monodisperse Cu2O and CuO Nanospheres: Preparation and Applications for Sensitive Gas Sensors. Chem. Mater. 2006, 18, 867–871. [Google Scholar] [CrossRef]
- Gawande, M.B.; Goswami, A.; Felpin, F.X.; Asefa, T.; Huang, X.; Silva, R.; Zou, X.; Zboril, R.; Varma, R.S. Cu and Cu-Based Nanoparticles: Synthesis and Applications in Catalysis. Chem. Rev. 2016, 116, 3722–3811. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, Y.; Chen, W. Sub-nanometre sized metal clusters: From synthetic challenges to the unique property discoveries. Chem. Soc. Rev. 2012, 41, 3594–3623. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Rogach, A.L. Synthesis, optical properties and applications of light-emitting copper nanoclusters. Nanoscale Horiz. 2017, 2, 135–146. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.S.; Lin, Y.F.; Nain, A.; Huang, Y.F.; Chang, H.T. A critical review of copper nanoclusters for monitoring of water quality. Sens. Actuators Rep. 2021, 3, 100026. [Google Scholar] [CrossRef]
- Itoh, M.; Kumar, V.; Adschiri, T.; Kawazoe, Y. Comprehensive study of sodium, copper, and silver clusters over a wide range of sizes 2 ≤ N ≤ 75. J. Chem. Phys. 2009, 131, 174510. [Google Scholar] [CrossRef] [Green Version]
- Jug, K.; Zimmermann, B.; Calaminici, P.; Köster, A.M. Structure and stability of small copper clusters. J. Chem. Phys. 2002, 116, 4497–4507. [Google Scholar] [CrossRef]
- Calaminici, P.; Janetzko, F.; Koster, A.M.; Mejia-Olvera, R.; Zuniga-Gutierrez, B. Density functional theory optimized basis sets for gradient corrected functionals: 3d transition metal systems. J. Chem. Phys. 2007, 126, 044108. [Google Scholar] [CrossRef] [PubMed]
- Massobrio, C.; Pasquarello, A.; Dal Corso, A. Structural and electronic properties of small Cun cluster using generalized-gradient approximations within density functional theory. J. Chem. Phys. 1998, 109, 6626–6630. [Google Scholar] [CrossRef]
- Calaminici, P.; Koster, A.M.; Russo, N.; Salahub, D.R. A density functional study of small copper clusters: Cun (n < 5). J. Chem. Phys. 1996, 105, 9546–9556. [Google Scholar] [CrossRef]
- Poater, A.; Duran, M.; Jaque, P.; Toro-Labbé, A.; Sola, M. Molecular Structure and Bonding of Copper Cluster Monocarbonyls CunCO (n = 1–9). J. Chem. Phys. B 2006, 110, 6526–6536. [Google Scholar] [CrossRef] [PubMed]
- Calaminici, P.; Koster, A.M.; Gómez-Sandoval, Z. Density Functional Study of the Structure and Properties of Cu9 and Cu9−. J. Chem. Theory Comput. 2007, 3, 905–913. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Yang, F.; Jackson, K.A.; Jellinek, J. Probing the structural evolution of CuN−, N = 9–20, through a comparison of computed electron removal energies and experimental photoelectron spectra. J. Chem. Phys. 2010, 132, 064306. [Google Scholar] [CrossRef]
- Lecoultre, S.; Rydlo, A.; Félix, C.; Buttet, J.; Gilb, S.; Harbich, W. Optical absorption of small copper clusters in neon: Cun, (n = 1–9). J. Chem. Phys. 2011, 134, 074303. [Google Scholar] [CrossRef] [Green Version]
- Binns, C. Nanoclusters deposited on surfaces. Surface Sci. Rep. 2001, 44, 1–49. [Google Scholar] [CrossRef]
- Brack, M. The physics of simple metal clusters: Self-consistent jellium model and semiclassical approaches. Rev. Mod. Phys. 1993, 65, 677–732. [Google Scholar] [CrossRef] [Green Version]
- Martin, T. Shells of atoms. Phys. Rep. 1996, 273, 199–241. [Google Scholar] [CrossRef]
- Sakurai, M.; Watanabe, K.; Sumiyama, K.; Suzuki, K. Magic numbers in transition metal (Fe, Ti, Zr, Nb, and Ta) clusters observed by time-of-flight mass spectrometry. J. Chem. Phys. 1999, 111, 235–238. [Google Scholar] [CrossRef]
- Darby, S.; Mortimer-Jones, T.V.; Johnston, R.L.; Roberts, C. Theoretical study of Cu–Au nanoalloy clusters using a genetic algorithm. J. Chem. Phys. 2002, 116, 1536–1550. [Google Scholar] [CrossRef]
- Guvelioglu, G.H.; Ma, P.; He, X.; Forrey, R.C.; Cheng, H. Evolution of Small Copper Clusters and Dissociative Chemisorption of Hydrogen. Phys. Rev. Lett. 2005, 94, 026103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Itoh, M.; Kumar, V.; Kawazoe, Y. Growth Behaviors And Electronic Structures Of Na And Cu Nanoclusters: The Role Of Sp–D Hybridization. Int. J. Mod. Phys. B 2005, 19, 2421–2426. [Google Scholar] [CrossRef]
- Yang, M.; Jackson, K.A.; Koehler, C.; Frauenheim, T.; Jellinek, J. Structure and shape variations in intermediate-size copper clusters. J. Chem. Phys. 2006, 124, 024308. [Google Scholar] [CrossRef]
- Jiang, M.; Zeng, Q.; Zhang, T.; Yang, M.; Jackson, K.A. Icosahedral to double-icosahedral shape transition of copper clusters. J. Chem. Phys. 2012, 136, 104501. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Peng, M.; Duan, T.; Wang, B. Insight into size dependence of C2 oxygenate synthesis from syngas on Cu cluster: The effect of cluster size on the selectivity. Appl. Surf. Sci. 2017, 407, 282–296. [Google Scholar] [CrossRef]
- Shuangjing, C.; Xin, C.; Hui, Z. Probing the activity of Ni13, Cu13, and Ni12Cu clusters towards the ammonia decomposition reaction by density functional theory. J. Mater. Sci. 2017, 52, 3162–3168. [Google Scholar] [CrossRef]
- Takahashi, K. First-Principles Design of Cu12 shell Fe core Core–Shell Clusters Assembled with K3O into Hexameric Rings: Implications for Gas-Storage Materials. ACS Appl. Nano Mater. 2020, 3, 55–58. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.J.; Tian, N.; Zhou, Z.Y.; Huang, R.; Liu, Z.L.; Xiao, J.; Sun, S.G. Alloy tetrahexahedral Pd-Pt catalysts: Enhancing significantly the catalytic activity by synergy effect of high-index facets and electronic structure. Chem. Sci. 2012, 3, 1157–1161. [Google Scholar] [CrossRef]
- Chou, J.P.; Hsing, C.R.; Wei, C.M.; Cheng, C.; Chang, C.M. Ab initio random structure search for 13-atom clusters of FCC elements. J. Phys. Condens. Matter 2013, 25, 125305. [Google Scholar] [CrossRef]
- Akola, J.; Häkkinen, H.; Manninen, M. Ionization potential of aluminum clusters. Phys. Rev. B 1998, 58, 3601–3604. [Google Scholar] [CrossRef] [Green Version]
- Ebeling, D.; Šekutor, M.; Stiefermann, M.; Tschakert, J.; Dah, J.E.P.; Carlson, R.M.K.; Schirmeisen, A.; Schreiner, P.R. Assigning the absolute configuration of single aliphatic molecules by visual inspection. Nat. Commun. 2018, 9, 2420. [Google Scholar] [CrossRef] [Green Version]
- Li, W.L.; Zhao, Y.F.; Hu, H.S.; Li, J.; Wang, L.S. A Quasiplanar Chiral Boron Cluster. Angew. Chem. Int. Ed. 2014, 53, 5540–5545. [Google Scholar] [CrossRef]
- Barroso, J.; Cabellos, J.L.; Pan, S.; Murillo, F.; Zarate, X.; Fernandez-Herrera, M.A.; Merino, G. Revisiting the racemization mechanism of helicenes. Chem. Commun. 2018, 54, 188–191. [Google Scholar] [CrossRef]
- Lv, P.; Lu, Z.; Yang, F.; Zhang, Y.; Yang, X.; Xu, G.; Yang, Z. A theoretical study of the lowest-energy PtPd co-doped silicon clusters: Chirality and fluxional transformation. Phys. Lett. A 2017, 381, 873–878. [Google Scholar] [CrossRef]
- Kong, Y.J.; Yan, Z.P.; Li, S.; Su, H.F.; Li, K.; Zheng, Y.X.; Zang, S.Q. Photoresponsive Propeller-like Chiral AIE Copper(I) Clusters. Angew. Chem. Int. Ed. 2020, 59, 5336–5340. [Google Scholar] [CrossRef]
- Buelna-Garcia, C.E.; Cabellos, J.L.; Quiroz-Castillo, J.M.; Martinez-Guajardo, G.; Castillo-Quevedo, C.; de Leon-Flores, A.; Anzueto-Sanchez, G.; Martin-del Campo-Solis, M.F. Exploration of Free Energy Surface and Thermal Effects on Relative Population and Infrared Spectrum of the Be6B11− Fluxional Cluster. Materials 2021, 14, 112. [Google Scholar] [CrossRef]
- Rao, Y.; Lei, Y.; Cui, X.; Liu, Z.; Chen, F. Optical and magnetic properties of Cu-doped 13-atom Ag nanoclusters. J. Alloy. Compd. 2013, 565, 50–55. [Google Scholar] [CrossRef]
- Baletto, F.; Ferrando, R. Structural properties of nanoclusters: Energetic, thermodynamic, and kinetic effects. Rev. Mod. Phys. 2005, 77, 371–423. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Longhi, G.; Abbate, S.; Lucotti, A.; Tommasini, M.; Villani, C.; Catalano, V.J.; Lykhin, A.O.; Varganov, S.A.; Chalifoux, W.A. Chiral Peropyrene: Synthesis, Structure, and Properties. J. Am. Chem. Soc. 2017, 139, 13102–13109. [Google Scholar] [CrossRef] [PubMed]
- Buelna-Garcia, C.E.; Robles-Chaparro, E.; Parra-Arellano, T.; Quiroz-Castillo, J.M.; del Castillo-Castro, T.; Martínez-Guajardo, G.; Castillo-Quevedo, C.; de León-Flores, A.; Anzueto-Sánchez, G.; Martin-del Campo-Solis, M.F.; et al. Theoretical Prediction of Structures, Vibrational Circular Dichroism, and Infrared Spectra of Chiral Be4B8 Cluster at Different Temperatures. Molecules 2021, 26, 3953. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 Revision D; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Fernández, E.; Boronat, M.; Corma, A. Trends in the Reactivity of Molecular O2 with Copper Clusters: Influence of Size and Shape. J. Phys. Chem. C 2015, 119, 19832–19846. [Google Scholar] [CrossRef]
- Jaque, P.; Toro-Labbé, A. Characterization of copper clusters through the use of density functional theory reactivity descriptors. J. Chem. Phys. 2002, 117, 3208–3218. [Google Scholar] [CrossRef]
- Cramer, C.J.; Truhlar, D.G. Density functional theory for transition metals and transition metal chemistry. Phys. Chem. Chem. Phys. 2009, 11, 10757–10816. [Google Scholar] [CrossRef]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Challenges for Density Functional Theory. Chem. Rev. 2012, 112, 289–320. [Google Scholar] [CrossRef] [PubMed]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals. J. Chem. Phys. 1985, 82, 299–310. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J. Chem. Phys. 1985, 82, 270–283. [Google Scholar] [CrossRef]
- Zeng, Q.; Wang, X.; Yang, M.L.; Fu, H.B. Interplay between geometrical and electronic stability of neutral and anionic Cu13 clusters: A first-principles study. Eur. Phys. J. D 2010, 58, 125–129. [Google Scholar] [CrossRef]
- Bardakc, T.; Kumru, M.; Altun, A. Molecular structures, charge distributions, and vibrational analyses of the tetracoordinate Cu(II), Zn(II), Cd(II), and Hg(II) bromide complexes of p-toluidine investigated by density functional theory in comparison with experiments. J. Mol. Struct. 2016, 1116, 292–302. [Google Scholar] [CrossRef]
- Matczak, P. Assessment of B3LYP combined with various ECP basis sets for systems containing Pd, Sn, and Pb. Comput. Theor. Chem. 2012, 983, 25–30. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heiles, S.; Johnston, R.L. Global optimization of clusters using electronic structure methods. Int. J. Quantum Chem. 2013, 113, 2091–2109. [Google Scholar] [CrossRef]
- Vargas-Caamal, A.; Cabellos, J.L.; Ortiz-Chi, F.; Rzepa, H.S.; Restrepo, A.; Merino, G. How Many Water Molecules Does it Take to Dissociate HCl? Chem. A Eur. J. 2016, 22, 2812–2818. [Google Scholar] [CrossRef] [PubMed]
- Ravell, E.; Jalife, S.; Barroso, J.; Orozco-Ic, M.; Hernández-Juárez, G.; Ortiz-Chi, F.; Pan, S.; Cabellos, J.L.; Merino, G. Structure and Bonding in CE5− (E = Al–Tl) Clusters: Planar Tetracoordinate Carbon versus Pentacoordinate Carbon. Chem. Asian J. 2018, 13, 1467–1473. [Google Scholar] [CrossRef]
- Pan, S.; Moreno, D.; Cabellos, J.L.; Romero, J.; Reyes, A.; Merino, G.; Chattaraj, P.K. In Quest of Strong Be–Ng Bonds among the Neutral Ng–Be Complexes. J. Phys. Chem. A 2014, 118, 487–494. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.H.; Ding, Y.H.; Cabellos, J.L.; Osorio, E.; Islas, R.; Restrepo, A.; Merino, G. Planar tetracoordinate carbons with a double bond in CAl3E clusters. Phys. Chem. Chem. Phys. 2015, 17, 8769–8775. [Google Scholar] [CrossRef]
- Vargas-Caamal, A.; Pan, S.; Ortiz-Chi, F.; Cabellos, J.L.; Boto, R.A.; Contreras-Garcia, J.; Restrepo, A.; Chattaraj, P.K.; Merino, G. How strong are the metallocene–metallocene interactions? Cases of ferrocene, ruthenocene, and osmocene. Phys. Chem. Chem. Phys. 2016, 18, 550–556. [Google Scholar] [CrossRef]
- Cui, Z.H.; Vassilev-Galindo, V.; Luis Cabellos, J.; Osorio, E.; Orozco, M.; Pan, S.; Ding, Y.h.; Merino, G. Planar pentacoordinate carbon atoms embedded in a metallocene framework. Chem. Commun. 2017, 53, 138–141. [Google Scholar] [CrossRef]
- Vargas-Caamal, A.; Ortiz-Chi, F.; Moreno, D.; Restrepo, A.; Merino, G.; Cabellos, J.L. The rich and complex potential energy surface of the ethanol dimer. Theor. Chem. Acc. 2015, 134, 16. [Google Scholar] [CrossRef]
- Florez, E.; Acelas, N.; Ibarguen, C.; Mondal, S.; Cabellos, J.L.; Merino, G.; Restrepo, A. Microsolvation of NO3−: Structural exploration and bonding analysis. RSC Adv. 2016, 6, 71913–71923. [Google Scholar] [CrossRef]
- Grande-Aztatzi, R.; Martinez-Alanis, P.R.; Cabellos, J.L.; Osorio, E.; Martínez, A.; Merino, G. Structural evolution of small gold clusters doped by one and two boron atoms. J. Comput. Chem. 2014, 35, 2288–2296. [Google Scholar] [CrossRef] [PubMed]
- Elena Navarro, R.; Serna-Medina, O.; Soberanes, Y.; Cabellos, J.L.; Inoue, M.; Santacruz, H.; Álvaro Posada-Amarillas. 1H NMR of paramagnetic Dy3+ complex with DTPA-amide p-xylylene-cyclophane; possible probing action toward d-histidine and histamine. Polyhedron 2020, 181, 114474. [Google Scholar] [CrossRef]
- Barroso, J.; Mondal, S.; Cabellos, J.L.; Osorio, E.; Pan, S.; Merino, G. Structure and Bonding of Alkali-Metal Pentalenides. Organometallics 2017, 36, 310–317. [Google Scholar] [CrossRef]
- Hadad, C.Z.; Florez, E.; Merino, G.; Cabellos, J.L.; Ferraro, F.; Restrepo, A. Potential Energy Surfaces of WC6 Clusters in Different Spin States. J. Phys. Chem. A 2014, 118, 5762–5768. [Google Scholar] [CrossRef] [PubMed]
- Contreras, M.; Pan, S.; Orozco-Ic, M.; Cabellos, J.L.; Merino, G. E3M3+ (E = C–Pb, M = Li–Cs) Clusters: The Smallest Molecular Stars. Chem. Eur. J. 2017, 23, 11430–11436. [Google Scholar] [CrossRef]
- Dong, X.; Jalife, S.; Vásquez-Espinal, A.; Ravell, E.; Pan, S.; Cabellos, J.L.; Liang, W.y.; Cui, Z.h.; Merino, G. Li2B12 and Li3B12: Prediction of the Smallest Tubular and Cage-like Boron Structures. Angew. Chem. Int. Ed. 2018, 57, 4627–4631. [Google Scholar] [CrossRef]
- Guo, J.C.; Feng, L.Y.; Wang, Y.J.; Jalife, S.; Vásquez-Espinal, A.; Cabellos, J.L.; Pan, S.; Merino, G.; Zhai, H.J. Coaxial Triple-Layered versus Helical Be6B11− Clusters: Dual Structural Fluxionality and Multifold Aromaticity. Angew. Chem. Int. Ed. 2017, 56, 10174–10177. [Google Scholar] [CrossRef]
- Dong, X.; Jalife, S.; Vásquez-Espinal, A.; Barroso, J.; Orozco-Ic, M.; Ravell, E.; Cabellos, J.L.; Liang, W.y.; Cui, Z.h.; Merino, G. Li2B24: The simplest combination for a three-ring boron tube. Nanoscale 2019, 11, 2143–2147. [Google Scholar] [CrossRef] [PubMed]
- Alexandrova, A.N.; Boldyrev, A.I. Search for the Lin0/+1/−1 (n = 5–7) Lowest-Energy Structures Using the ab Initio Gradient Embedded Genetic Algorithm (GEGA). Elucidation of the Chemical Bonding in the Lithium Clusters. J. Chem. Theory Comput. 2005, 1, 566–580. [Google Scholar] [CrossRef] [PubMed]
- Zubarev, D.Y.; Boldyrev, A.I. Developing paradigms of chemical bonding: Adaptive natural density partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207–5217. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.H.; Truhlar, D.G. Nanothermodynamics of metal nanoparticles. Chem. Sci. 2014, 5, 2605–2624. [Google Scholar] [CrossRef]
- Li, Z.H.; Jasper, A.W.; Truhlar, D.G. Structures, Rugged Energetic Landscapes, and Nanothermodynamics of Aln (2 ≤ n ≤ 65) Particles. J. Am. Chem. Soc. 2007, 129, 14899–14910. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Supramolecular Binding Thermodynamics by Dispersion-Corrected Density Functional Theory. Chem. Eur. J. 2012, 18, 9955–9964. [Google Scholar] [CrossRef]
- Dzib, E.; Cabellos, J.L.; Ortíz-Chi, F.; Pan, S.; Galano, A.; Merino, G. Eyringpy: A program for computing rate constants in the gas phase and in solution. Int. J. Quantum Chem. 2019, 119, e25686. [Google Scholar] [CrossRef] [Green Version]
- McQuarrie, D.A.M. Statistical Mechanics; Chemistry Series; Harper & Row: Manhattan, NY, USA, 1975. [Google Scholar]
- Hill, T. An Introduction to Statistical Thermodynamics; Addison-Wesley Series in Chemistry; Dover Publications: Mineola, NY, USA, 1986. [Google Scholar]
- Pracht, P.; Grimme, S. Calculation of absolute molecular entropies and heat capacities made simple. Chem. Sci. 2021, 12, 6551–6568. [Google Scholar] [CrossRef] [PubMed]
- Mendoza-Wilson, A.M.; Balandrán-Quintana, R.R.; Cabellos, J.L. Thermochemical behavior of sorghum procyanidin trimers with C4–C8 and C4–C6 interflavan bonds in the reaction with superoxide anion radical and H2O2-forming NADH-oxidase flavoenzyme. Comput. Theor. Chem. 2020, 1186, 112912. [Google Scholar] [CrossRef]
- Rodriguez-Kessler, P.L.; Rodriguez-Dominguez, A.R.; Muñoz Castro, A. Systematic cluster growth: A structure search method for transition metal clusters. Phys. Chem. Chem. Phys. 2021, 23, 4935–4943. [Google Scholar] [CrossRef]
- Limbu, D.K.; Madueke, M.U.; Atta-Fynn, R.; Drabold, D.A.; Biswas, P. Ab initio density-functional studies of 13-atom Cu and Ag clusters. J. Phys. Conf. Ser. 2019, 1252, 012009. [Google Scholar] [CrossRef]
- Guvelioglu, G.H.; Ma, P.; He, X.; Forrey, R.C.; Cheng, H. First principles studies on the growth of small Cu clusters and the dissociative chemisorption of H2. Phys. Rev. B 2006, 73, 155436. [Google Scholar] [CrossRef] [Green Version]
- Kabir, M.; Mookerjee, A.; Bhattacharya, A. Copper clusters: Electronic effect dominates over geometric effect. Eur. Phys. J. D At. Mol. Opt. Plasma Phys. 2004, 31, 477–485. [Google Scholar] [CrossRef]
- Pauling, L. On the nature of the bonding in Cu2—a Comment. J. Chem. Phys. 1983, 78, 3346. [Google Scholar] [CrossRef] [Green Version]
- Iwasa, T.; Sato, T.; Takagi, M.; Gao, M.; Lyalin, A.; Kobayashi, M.; Shimizu, K.i.; Maeda, S.; Taketsugu, T. Combined Automated Reaction Pathway Searches and Sparse Modeling Analysis for Catalytic Properties of Lowest Energy Twins of Cu13. J. Phys. Chem. A 2019, 123, 210–217. [Google Scholar] [CrossRef] [Green Version]
- Longo, R.C.; Gallego, L.J. Structures of 13-atom clusters of FCC transition metals by ab initio and semiempirical calculations. Phys. Rev. B 2006, 74, 193409. [Google Scholar] [CrossRef]
- De la Puente, E.; Aguado, A.; Ayuela, A.; López, J.M. Structural and electronic properties of small neutral (MgO)n clusters. Phys. Rev. B 1997, 56, 7607–7614. [Google Scholar] [CrossRef] [Green Version]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fernández-Ramos, A.; Ellingson, B.A.; Meana-Pañeda, R.; Marques, J.M.C.; Truhlar, D.G. Symmetry numbers and chemical reaction rates. Theor. Chem. Acc. 2007, 118, 813–826. [Google Scholar] [CrossRef] [Green Version]
- Gilson, M.K.; Irikura, K.K. Symmetry Numbers for Rigid, Flexible, and Fluxional Molecules: Theory and Applications. J. Phys. Chem. B 2010, 114, 16304–16317. [Google Scholar] [CrossRef] [Green Version]
- Ravat, P. Carbo[n]helicenes Restricted to Enantiomerize: An Insight into the Design Process of Configurationally Stable Functional Chiral PAHs. Chem. A Eur. J. 2021, 27, 3957–3967. [Google Scholar] [CrossRef]
- Jensen, B. Quantum Mechanics on Surfaces. In Some Applications of Quantum Mechanics; Pahlavani, M.R., Ed.; IntechOpen: Rijeka, Croatia, 2012. [Google Scholar] [CrossRef] [Green Version]
- Grigoryan, V.G.; Springborg, M. Temperature and isomeric effects in nanoclusters. Phys. Chem. Chem. Phys. 2019, 21, 5646–5654. [Google Scholar] [CrossRef] [PubMed]

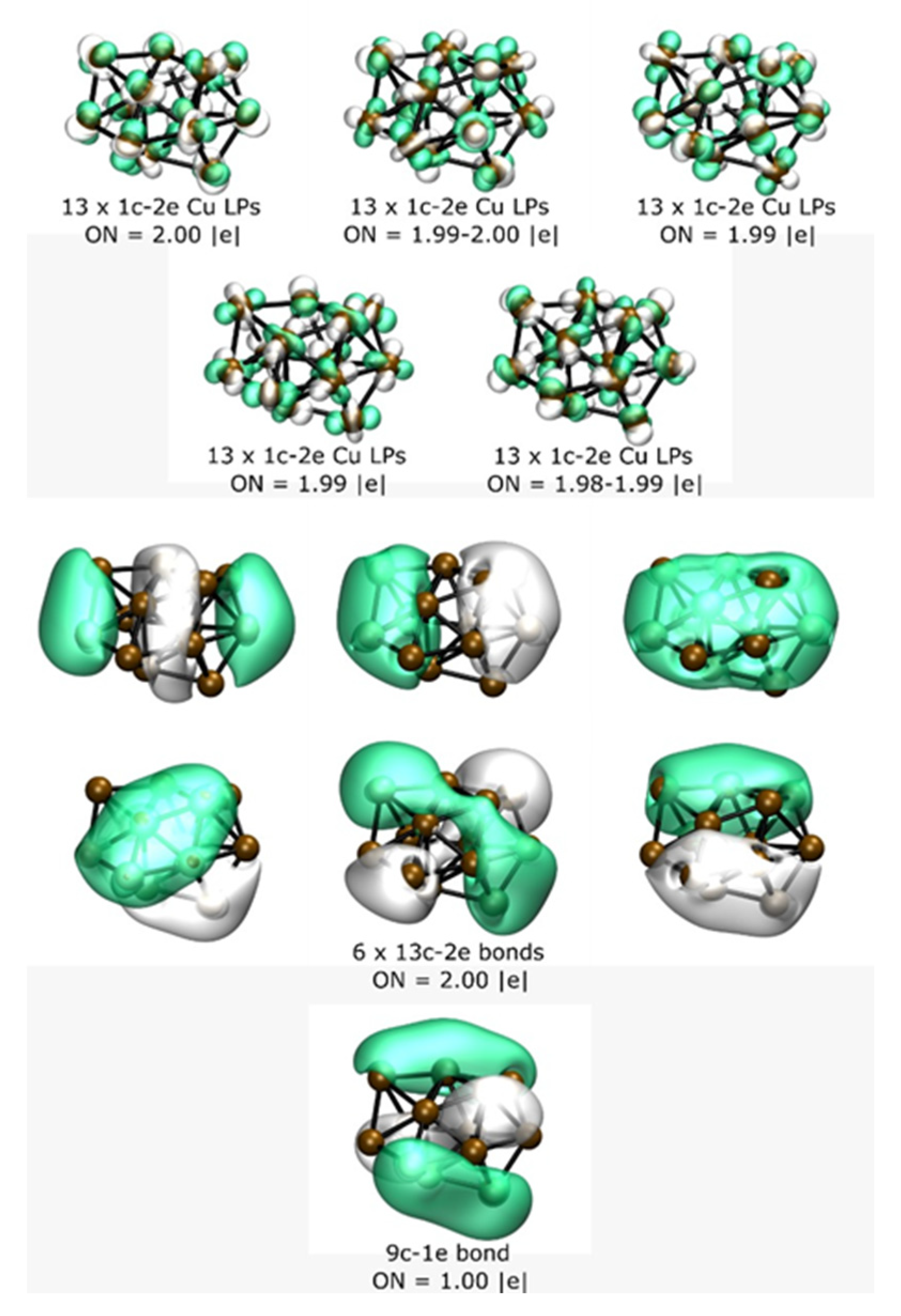

| Isomers Labeling (Figure 1) | Symmetry | Functionals | |||||
|---|---|---|---|---|---|---|---|
| B3PW91 | TPSS | PBE | BP86 | ||||
| a | C1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| b | C1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| c | C2 | 0.0 | 0.0 | 0.40 | 0.40 | 0.42 | 0.40 |
| d | C2 | 0.0 | 0.0 | 0.41 | 0.41 | 0.42 | 0.41 |
| e | Cs | 0.90 | 0.93 | 1.0 | 0.72 | 0.55 | 0.86 |
| f | C1 | 4.71 | 4.59 | 3.93 | 5.60 | 3.85 | 3.56 |
| g | C1 | 4.71 | 4.59 | 3.94 | 5.60 | 3.85 | 3.56 |
| Route A | Route B | |||||
|---|---|---|---|---|---|---|
| Level of Theory | Eea | Eint | EA | Eea | Eint | EA |
| B3PW91-D3/def2TZVP | 12.2 | 7.1 | 5.0 | 14.8 | 10.8 | 4.0 |
| B3PW91/def2TZVP | 12.3 | 6.4 | 6.0 | 15.6 | 10.3 | 4.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castillo-Quevedo, C.; Buelna-Garcia, C.E.; Paredes-Sotelo, E.; Robles-Chaparro, E.; Zamora-Gonzalez, E.; Martin-del-Campo-Solis, M.F.; Quiroz-Castillo, J.M.; del-Castillo-Castro, T.; Martínez-Guajardo, G.; de-Leon-Flores, A.; et al. Effects of Temperature on Enantiomerization Energy and Distribution of Isomers in the Chiral Cu13 Cluster. Molecules 2021, 26, 5710. https://doi.org/10.3390/molecules26185710
Castillo-Quevedo C, Buelna-Garcia CE, Paredes-Sotelo E, Robles-Chaparro E, Zamora-Gonzalez E, Martin-del-Campo-Solis MF, Quiroz-Castillo JM, del-Castillo-Castro T, Martínez-Guajardo G, de-Leon-Flores A, et al. Effects of Temperature on Enantiomerization Energy and Distribution of Isomers in the Chiral Cu13 Cluster. Molecules. 2021; 26(18):5710. https://doi.org/10.3390/molecules26185710
Chicago/Turabian StyleCastillo-Quevedo, Cesar, Carlos Emiliano Buelna-Garcia, Edgar Paredes-Sotelo, Eduardo Robles-Chaparro, Edgar Zamora-Gonzalez, Martha Fabiola Martin-del-Campo-Solis, Jesus Manuel Quiroz-Castillo, Teresa del-Castillo-Castro, Gerardo Martínez-Guajardo, Aned de-Leon-Flores, and et al. 2021. "Effects of Temperature on Enantiomerization Energy and Distribution of Isomers in the Chiral Cu13 Cluster" Molecules 26, no. 18: 5710. https://doi.org/10.3390/molecules26185710
APA StyleCastillo-Quevedo, C., Buelna-Garcia, C. E., Paredes-Sotelo, E., Robles-Chaparro, E., Zamora-Gonzalez, E., Martin-del-Campo-Solis, M. F., Quiroz-Castillo, J. M., del-Castillo-Castro, T., Martínez-Guajardo, G., de-Leon-Flores, A., Cortez-Valadez, M., Ortiz-Chi, F., Gaxiola, T., Castillo, S. J., Vásquez-Espinal, A., Pan, S., & Cabellos, J. L. (2021). Effects of Temperature on Enantiomerization Energy and Distribution of Isomers in the Chiral Cu13 Cluster. Molecules, 26(18), 5710. https://doi.org/10.3390/molecules26185710








