Structure and Undulations of Escin Adsorption Layer at Water Surface Studied by Molecular Dynamics
Abstract
:1. Introduction
2. Results and Discussion
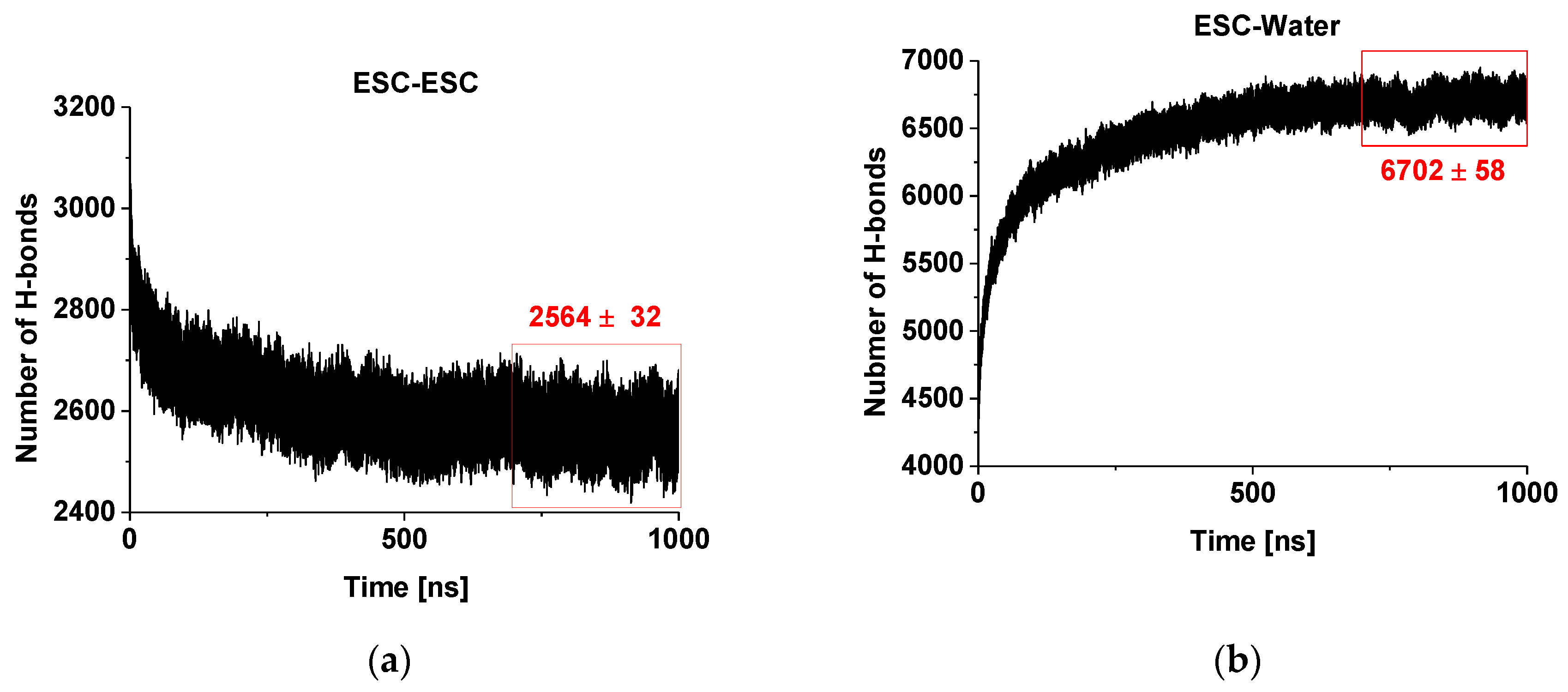
2.1. Hydrogen Bonding of Escin Molecules
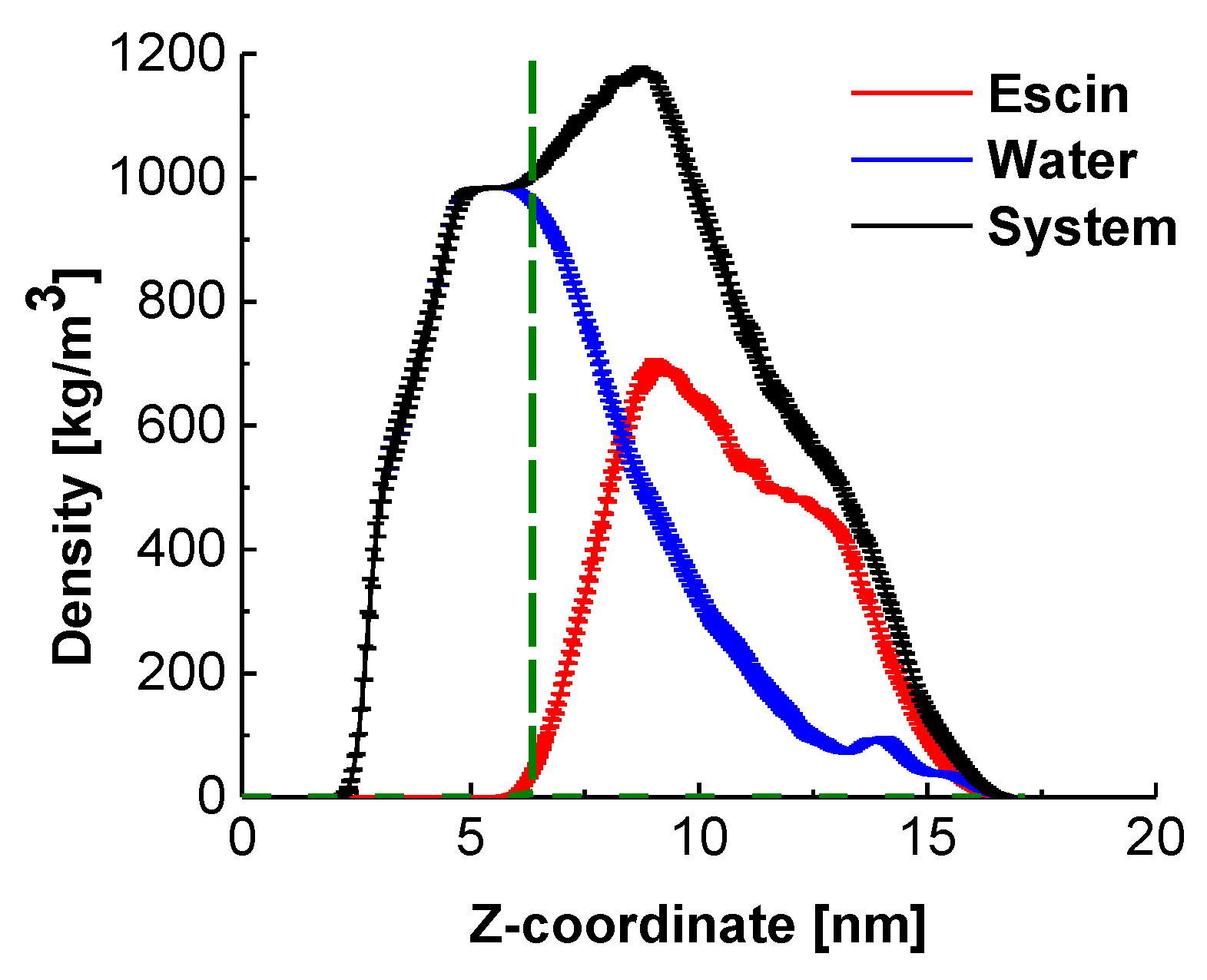
2.2. Position of the Escin Molecules Relative to Water
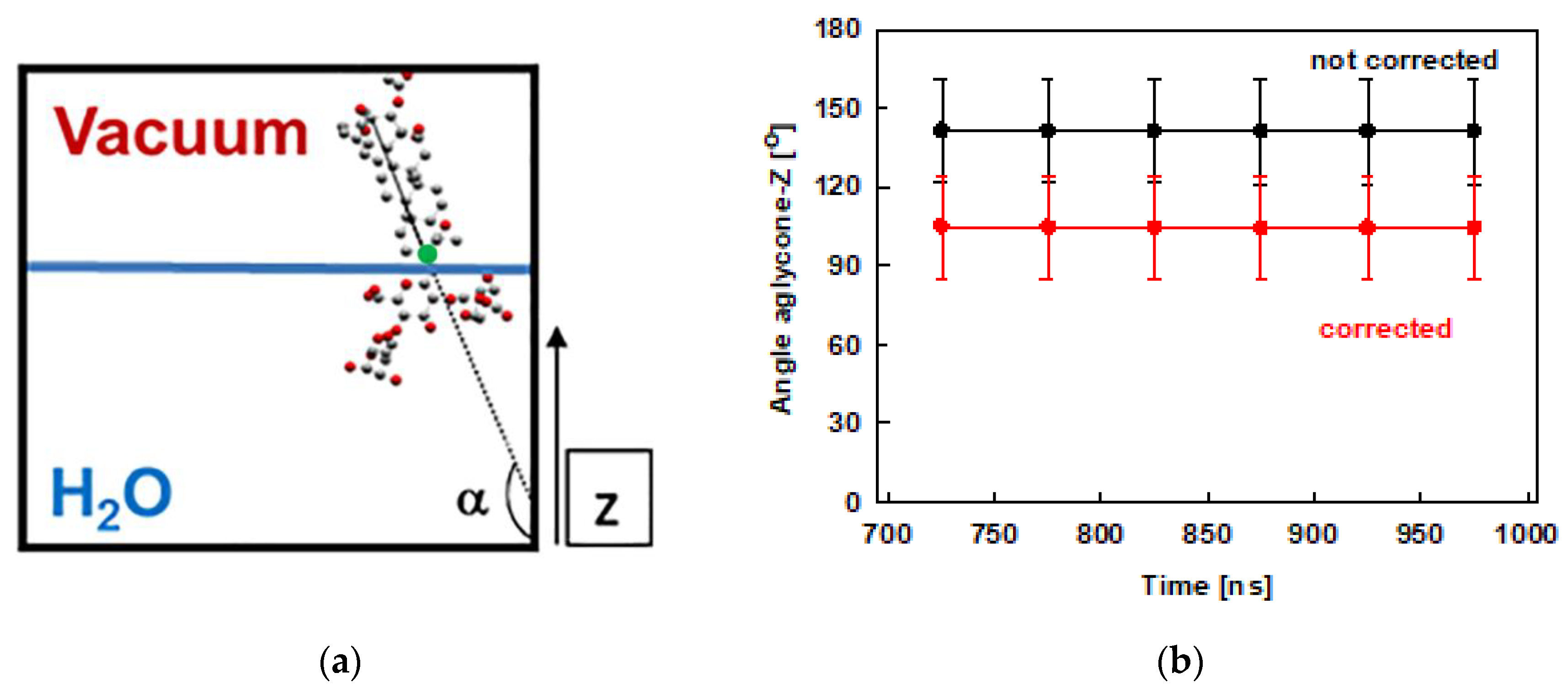
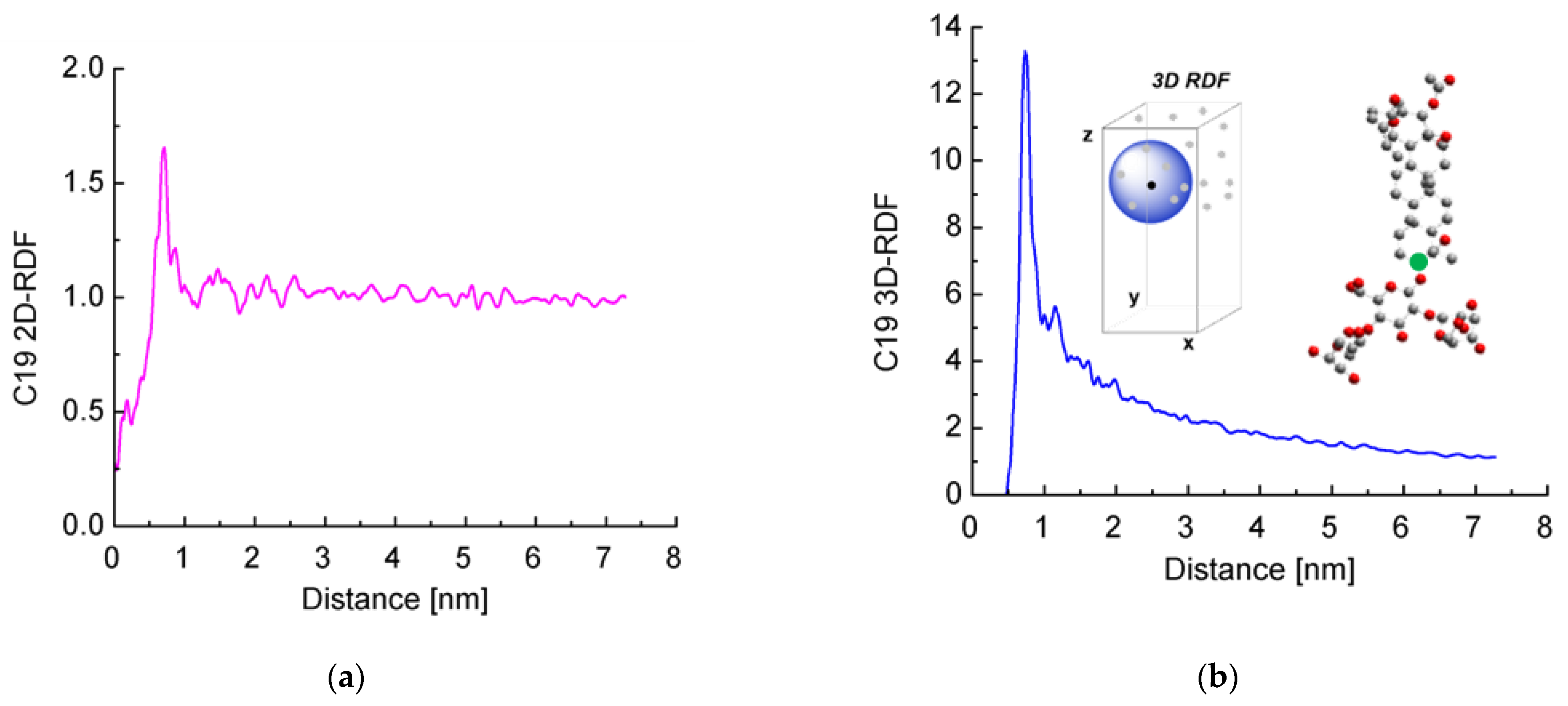
2.3. Interfacial Orientation and Intermolecular Ordering of the Escin Molecules
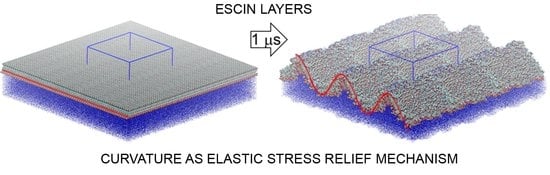
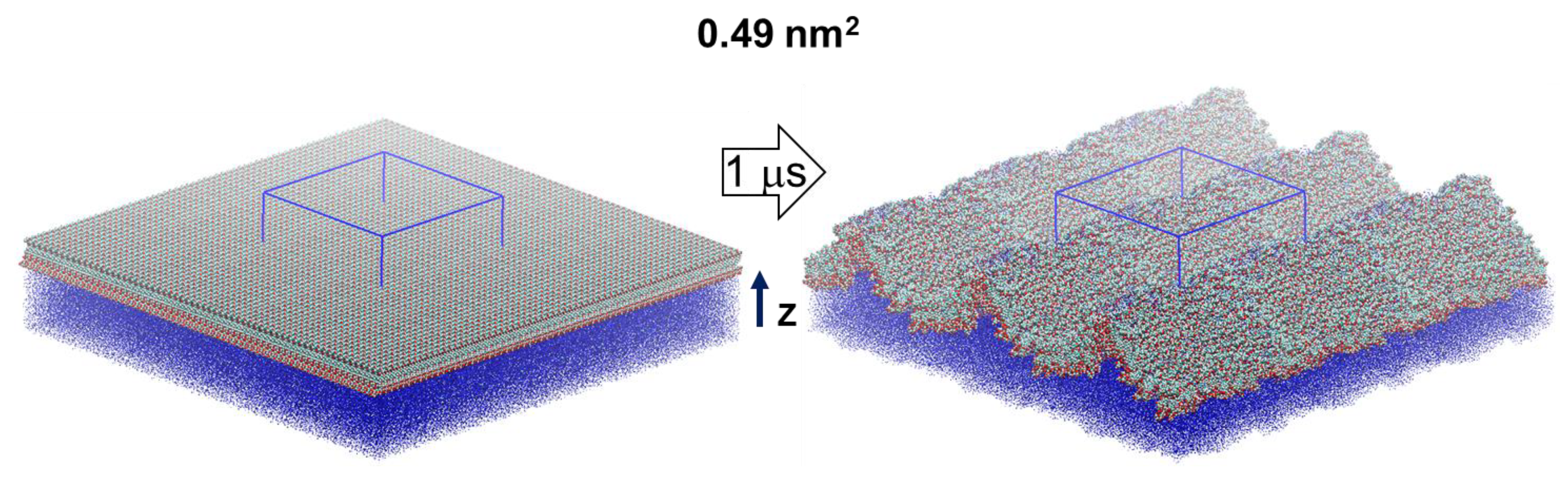
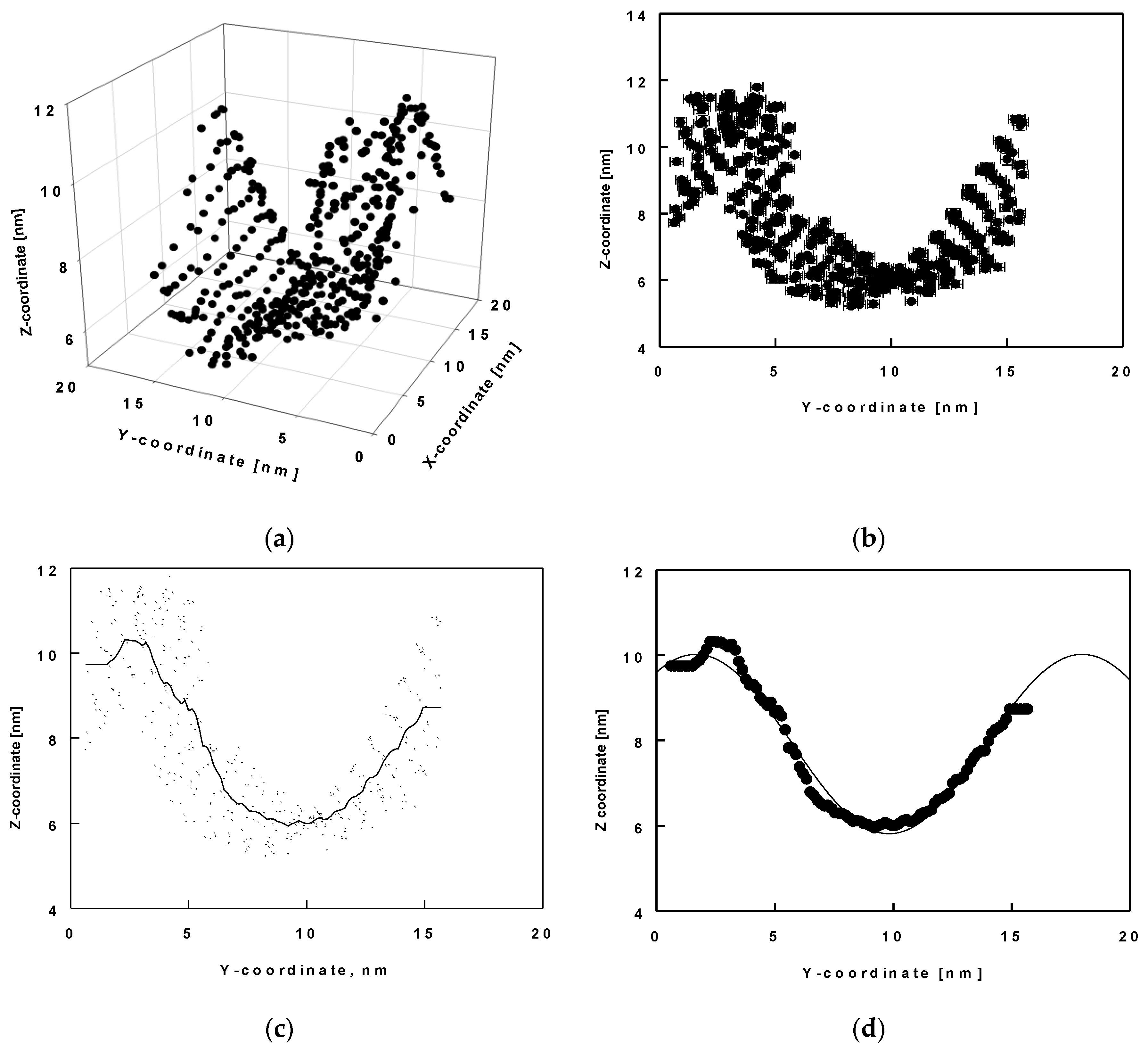
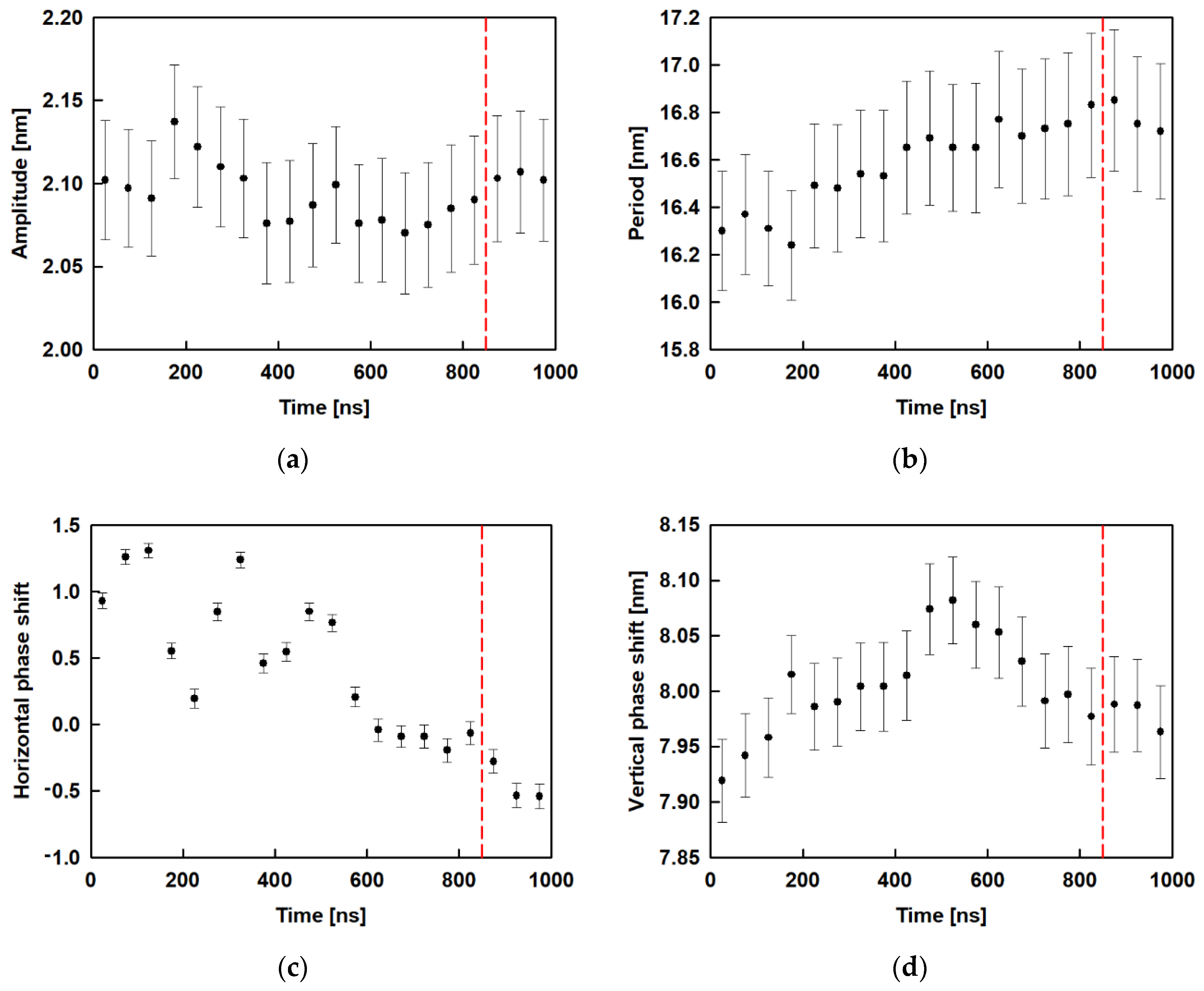
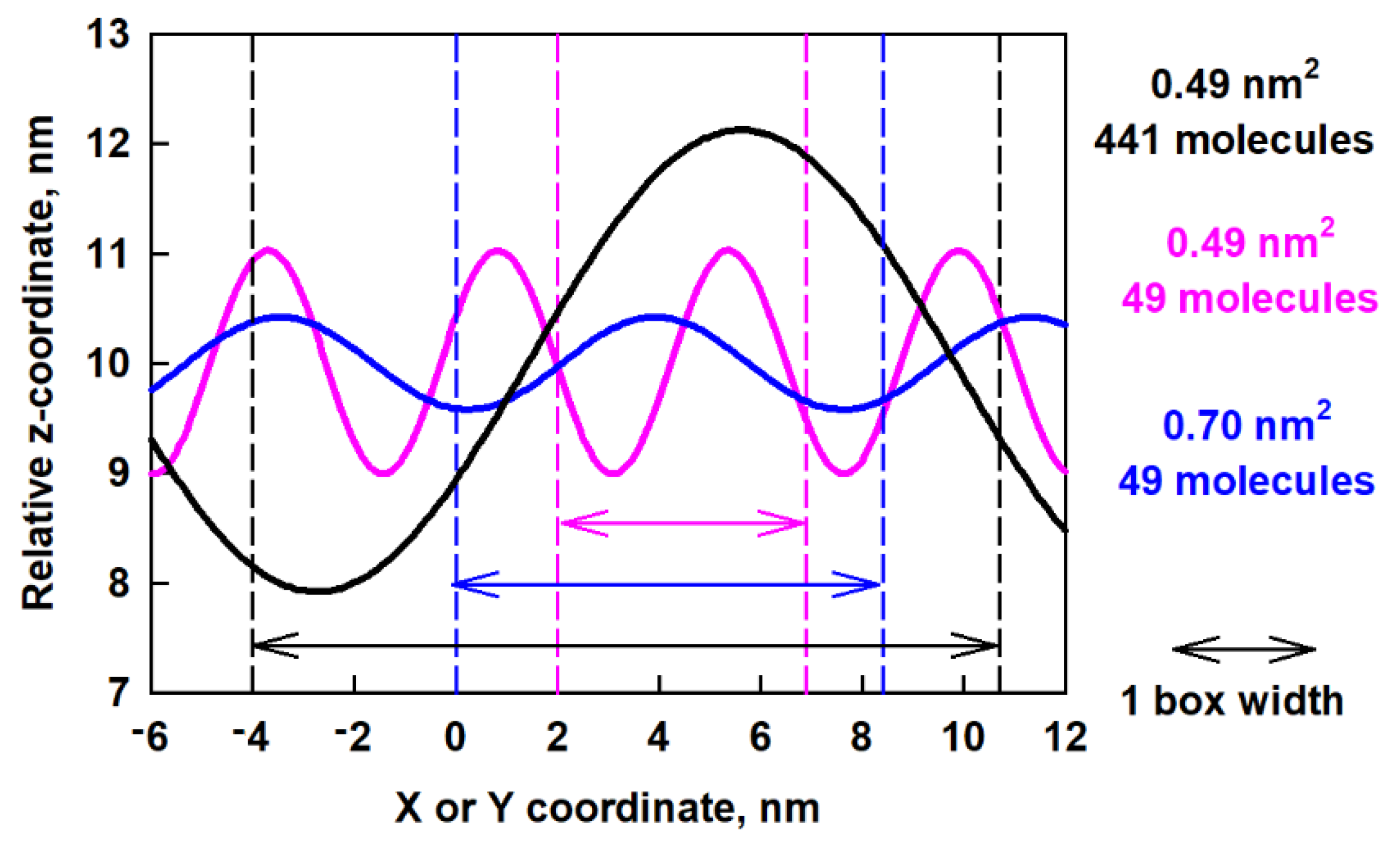
2.4. Surface Undulations and Curvature
3. Molecular Models and Computational Protocol
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sagis, L.M.C. Dynamic properties of interfaces in soft matter: Experiment and theory. Rev. Mod. Phys. 2011, 83, 1367–1403. [Google Scholar] [CrossRef]
- Kragel, J.; Derkatch, S.R. Interfacial Shear Rheology. Curr. Opin. Colloid Interface Sci. 2010, 15, 246–255. [Google Scholar] [CrossRef]
- Noskov, B.A. Dilatational surface rheology of polymer and polymer/surfactant solutions. Curr. Opin. Colloid Interface Sci. 2010, 15, 229–236. [Google Scholar] [CrossRef]
- Noskov, B.A.; Loglio, G.; Miller, R. Dilatational surface visco-elasticity of polyelectrolyte-surfactant solutions: Formation of heterogeneous absorption layers. Adv. Colloid Interface Sci. 2011, 168, 179–197. [Google Scholar] [CrossRef] [PubMed]
- Arboleya, J.-C.; Wilde, P.J. Competitive adsorption of proteins with methylcellulose and hydroxypropyl methylcellulose. Food Hydrocoll. 2005, 19, 485–491. [Google Scholar] [CrossRef]
- Erni, P.; Windhab, E.; Gunde, R.; Graber, M.; Pfister, B.; Parker, A.; Fischer, P. Interfacial rheology of surface—Active biopolymers: Acacia. Biomacromolecules 2007, 8, 3458–3466. [Google Scholar] [CrossRef] [PubMed]
- Perez-Orozco, J.; Beristain, C.; Espinosa-Paredes, G.; Lobato-Calleros, C.; Vernon-Carter, E. Interfacial shear rheology of interacting carbohydrate polyelectrolytes at the water—oil interface using an adapted conventional rheometer. Carbohyd. Polym. 2004, 57, 45–54. [Google Scholar] [CrossRef]
- Murray, B. Proteins at Liquid Interfaces, 1st ed.; Mobius, D., Miller, R., Eds.; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Lucassen-Reynders, E.; Benjamins, J.; Fainerman, V. Dilatational rheology of protein films absorbed at fluid interfaces. Curr. Opin. Colloid Interface Sci. 2010, 15, 264–270. [Google Scholar] [CrossRef]
- Freer, E.; Yim, K.; Fuller, G.; Radke, C. Interfacial rheology of globular and flexible proteins at the hexadecane/water interface: Comparison of shear and dilatation deformation. J. Phys. Chem. B 2004, 108, 3835–3844. [Google Scholar] [CrossRef]
- Dickinson, E. Absorbed protein layers at fluid interfaces. Colloids Surf. B Biointerfaces 1999, 15, 161–176. [Google Scholar] [CrossRef]
- Alexandrov, N.; Marinova, K.; Gurkov, T.; Danov, K.; Kralchevsky, P.; Stoyanov, S.; Blijdenstein, T.; Arnaudov, L.; Pelan, E.; Lips, A. Interfacial layers from the protein HFBII hydrophobin: Dynamic surface tension, dilatational elasticity and relaxation times. J. Colloid Interface Sci. 2012, 376, 296–306. [Google Scholar] [CrossRef]
- Radulova, G.; Golemanov, K.; Danov, K.; Kralchevsky, P.; Stoyanov, S.; Arnaudov, L.; Blijdenstein, T.; Pelan, E.; Lips, A. Surface shear rheology of adsorption layers from the protein HFBII hydrophobin: Effect of β-Casein. Langmuir 2012, 28, 4168–4177. [Google Scholar] [CrossRef] [PubMed]
- Caro, A.; Nino, R.; Patino, J. The effect of pH on surface dilatational amd shear properties of phospholipid monolayers. Colloids Surf. A Physicochem. Eng. Asp. 2008, 327, 79–89. [Google Scholar] [CrossRef]
- Erni, P.; Fischer, P.; Windhab, E.J. Sorbitan Tristearate Layers at the Air/Water Interface Studied by Shear and Dilatational Interfacial Rheology. Langmuir 2005, 21, 10555–10563. [Google Scholar] [CrossRef]
- Gavranovic, G.T.; Kurtz, R.E.; Golemanov, K.; Lange, A.; Fuller, G.G. Interfacial rheology and structure of straight—chain and branched hexadecanol mixtures. Ind. Eng. Chem. Res. 2006, 45, 6880–6884. [Google Scholar] [CrossRef]
- Golemanov, K.; Denkov, N.; Tcholakova, S.; Vethamuthu, M.; Lips, A. Surfactant mixtures for control of bubble surface mobility in foam studies. Langmuir 2008, 24, 9956–9961. [Google Scholar] [CrossRef] [PubMed]
- Mitrinova, Z.; Tcholakova, S.; Golemanov, K.; Denkov, N.; Vethamuthu, M.; Ananthapadmanabhan, K. Surface and foam properties of SLES + CAPB + fatty acid mixtures: Effect of pH for C12–C16 acids. Colloid Surf. A Physicochem. Eng. Asp. 2013, 438, 186–198. [Google Scholar] [CrossRef]
- Madivala, B.; Fransaer, J.; Vermant, J. Self-assembly and rheology of ellipsoidal particles at interfaces. Langmuir 2009, 25, 2718–2728. [Google Scholar] [CrossRef]
- Zang, D.; Langevin, D.; Binks, B.; Wei, B. Shearing particle monolayers: Strain—rate frequency superposition. Phys. Rev. E 2010, 81, 011604. [Google Scholar] [CrossRef]
- Safouane, M.; Langevin, D.; Binks, B. Effect of particle hydrophobicity on the properties of silica particle layers at the air-water interface. Langmuir 2007, 23, 11546–11553. [Google Scholar] [CrossRef]
- Liggieri, L.; Santini, E.; Guzman, E.; Maestro, A.; Ravera, F. Wide-frequency dilatational rheology investigation of mixed silica nanoparticle—CTAB interfacial layers. Soft Matter 2011, 7, 7699–7709. [Google Scholar] [CrossRef]
- Xu, H.; Melle, S.; Golemanov, K.; Fuller, G. Shape and buckling transitions in solid stabilized drops. Langmuir 2005, 21, 10016–10020. [Google Scholar] [CrossRef] [PubMed]
- Stanimirova, R.; Marinova, K.; Tcholakova, S.; Denkov, N.; Stoyanov, S.; Pelan, E. Surface Rheology of Saponin Adsoprtion Layers. Langmuir 2011, 27, 12486–12498. [Google Scholar] [CrossRef] [PubMed]
- Golemanov, K.; Tcholakova, S.; Denkov, N.; Pelan, E.; Stoyanov, S. Surface shear rheology of saponin adsorption layers. Langmuir 2012, 28, 12071–12084. [Google Scholar] [CrossRef]
- Golemanov, K.; Tcholakova, S.; Denkov, N.; Pelan, E.; Stoyanov, S. Remarkably high surface visco-elasticity of adsorption layers of triterpenoid saponins. Soft Matter 2013, 9, 5738–5752. [Google Scholar] [CrossRef]
- Golemanov, K.; Tcholakova, S.; Denkov, N.; Pelan, E.; Stoyanov, S. The role of the hydrophobic phase in the unique rheological properties of saponin adsorption layers. Soft Matter 2014, 10, 7034–7044. [Google Scholar] [CrossRef] [PubMed]
- Pagureva, N.; Tcholakova, S.; Golemanov, K.; Denkov, N.; Pelan, E.; Stoyanov, S. Surface properties of adsorption layers formed from triterpenoid and steroid saponins. Colloids Surf. A Physicochem. Eng. Asp. 2016, 491, 18–28. [Google Scholar] [CrossRef]
- Piotrowski, M.; Lewandowska, J.; Wojciechowski, K. Biosurfactant—Protein mixtures: Quillaja Bark Saponin at water/air and water/oil interfaces in presence of β-lactoglobulin. J. Phys. Chem. B 2012, 116, 4843–4850. [Google Scholar] [CrossRef]
- Wojciechowski, K. Surface activity of saponin from quillaja bark at the air/water and oil/water interfaces. Colloids Surf. B Biointerfaces 2013, 108, 95–102. [Google Scholar] [CrossRef]
- Wojciechowski, K.; Orczyk, M.; Marcinkowski, K.; Kobiela, T.; Trapp, M.; Gutberlet, T.; Geue, T. Effect of hydration of sugar groups on adsorption of Quillaja Bark saponin at air/water and Si/water interface. Colloid Surf. B Biointerfaces 2014, 117, 60–67. [Google Scholar] [CrossRef]
- Kezwon, A.; Wojciechowski, K. Interaction of Quillaja Bark with food-relevant proteins. Adv. Colloid Interface Sci. 2014, 209, 185–195. [Google Scholar] [CrossRef] [PubMed]
- Tsibranska, S.; Tcholakova, S.; Golemanov, K.; Denkov, N.D.; Pelan, E.; Stoyanov, S.D. Role of interfacial elasticity for the rheological properties of saponin-stabilized emulsions. J. Colloid Interface Sci. 2020, 564, 264–275. [Google Scholar] [CrossRef] [Green Version]
- Denkov, N.D.; Tcholakova, S.; Politova-Brinkova, N. Physicochemical control of foam properties. Curr. Opin. Colloid Interface Sci. 2020, 50, 101376. [Google Scholar] [CrossRef]
- Tsibranska, S.; Tcholakova, S.; Golemanov, K.; Denkov, N.; Arnaudov, L.; Pelan, E.; Stoyanov, S. Origin of the extremely high elasticity of bulk emulsions, stabilized by Yucca Schidigera saponins. Food Chem. 2020, 316, 126365. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tcholakova, S.; Mustan, F.; Pagureva, N.; Golemanov, K.; Denkov, N.D.; Pelan, E.; Stoyanov, S.D. Role of surface properties for kinetics of Ostwald ripening in saponin stabilized foams. Colloids Surf. A Physicochem. Eng. Asp. 2017, 543, 16–25. [Google Scholar] [CrossRef]
- Dudek-Makuch, M.; Studzińska-Sroka, E. Horse chestnut—Efficacy and safety in chronic venous insufficiency: An overview. Rev. Bras. Farm. 2015, 25, 533–541. [Google Scholar] [CrossRef] [Green Version]
- Wei, F.; Ma, L.Y.; Cheng, X.L.; Lin, R.C.; Jin, W.T.; Khan, I.A.; Lu, J. Preparative HPLC for Purification of Four Isomeric Bioactive Saponins from the Seeds of Aesculus chinensis. J. Liq. Chrom. Rel. Technol. 2005, 28, 763–773. [Google Scholar] [CrossRef]
- Blijdenstein, T.B.J.; De Groot, P.W.N.; Stoyanov, S.D. On the link between foam coarsening and surface rheology: Why hydrophobins are so different. Soft Matter 2010, 6, 1799–1808. [Google Scholar] [CrossRef]
- Basheva, E.S.; Kralchevsky, P.A.; Danov, K.D.; Stoyanov, S.D.; Blijdenstein, T.B.J.; Pelan, E.G.; Lips, A. Self-assembled bilayers from the protein HFBII hydrophobin: Nature of the adhesion energy. Langmuir 2011, 27, 4481–4488. [Google Scholar] [CrossRef]
- Basheva, E.S.; Kralchevsky, P.A.; Christov, N.C.; Danov, K.D.; Stoyanov, S.D.; Blijdenstein, T.B.J.; Kim, H.-J.; Pelan, E.G.; Lips, A. Unique properties of bubbles and foam films stabilized by HFBII hydrophobin. Langmuir 2011, 27, 2382–2392. [Google Scholar] [CrossRef]
- Danov, K.D.; Kralchevsky, P.A.; Stoyanov, S.D. Elastic Langmuir layers and membranes subjected to unidirectional compression: Wrinkling and collapse. Langmuir 2010, 26, 143–155. [Google Scholar] [CrossRef] [PubMed]
- Cerda, E.; Mahadevan, L. Geometry and physics of wrinkling. Phys. Rev. Lett. 2003, 90, 074302. [Google Scholar] [CrossRef] [Green Version]
- Erni, P.; Jerri, H.A.; Wong, K.; Parker, A. Interfacial viscoelasticity controls buckling, wrinkling and arrest in emulsion drops undergoing mass transfer. Soft Matter 2012, 8, 6958–6967. [Google Scholar] [CrossRef]
- Tsibranska, S.; Ivanova, A.; Tcholakova, S.; Denkov, N. Self-assembly of escin molecules at the air-water interface studied by molecular dynamics. Langmuir 2017, 33, 8330–8341. [Google Scholar] [CrossRef] [PubMed]
- Tsibranska, S.; Ivanova, A.; Tcholakova, S.; Denkov, N. Structure of Dense Adsorption Layers of Escin at the Air–Water Interface Studied by Molecular Dynamics Simulations. Langmuir 2019, 35, 12876–12887. [Google Scholar] [CrossRef]
- Pedebos, C.; Pol-Fachin, L.; Verli, H. Unrestrained conformational characterization of stenocereus eruca saponins in aqueous and nonaqueous solvents. J. Nat. Prod. 2012, 75, 1196–1200. [Google Scholar] [CrossRef] [PubMed]
- Pedebos, C.; Pol-Fachin, L.; Pons, R.; Teixeira, C.V.; Verli, H. Atomic model and micelle dynamics of QS-21 saponin. Molecules 2014, 19, 3744–3760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dai, X.; Shi, X.; Wang, Y.; Qiao, Y. Solubilization of saikosaponin a by ginsenoside Ro biosurfactant in aqueous solution: Mesoscopic simulation. J. Colloid Interface Sci. 2012, 384, 73–80. [Google Scholar] [CrossRef] [PubMed]
- Karpagam, V.; Sathishkumar, N.; Sathiyamoorthy, S.; Rasappan, P.; Shila, S.; Kim, Y.; Yang, D. Identification of BACE1 inhibitors from Panax ginseng saponins—An Insilco approach. Comput. Biol. Med. 2013, 43, 1037–1044. [Google Scholar] [CrossRef]
- Kim, O.T.P.; Le, M.D.; Trinh, H.X.; Nong, H.V. In silico studies for the interaction of tumor necrosis factor-alpha (TNF-α) with different saponins from Vietnamese ginseng (Panax vietnamesis). Biophys. Physicobiol. 2016, 13, 173–180. [Google Scholar] [CrossRef] [Green Version]
- Cui, C.; Zong, J.; Sun, Y.; Zhang, L.; Ho, C.; Wan, X.; Hou, R. Triterpenoid saponins from the genus Camellia: Structures, biological activities, and molecular simulation for structure-activity relationship. Food Funct. 2018, 9, 3069–3091. [Google Scholar] [CrossRef]
- Mimaki, Y.; Yokosuka, A.; Kuroda, M.; Sashida, Y. Cytotoxic Activities and Structure—Cytotoxic Relationships of Steroidal Saponins. Biol. Pharm. Bull. 2001, 24, 1286–1289. [Google Scholar] [CrossRef] [Green Version]
- Walkowicz, W.E.; Fernández-Tejada, A.; George, C.; Corzana, F.; Jiménez-Barbero, J.; Ragupathi, G.; Tan, D.S.; Gin, D.Y. Quillaja saponin variants with central glycosidic linkage modifications exhibit distinct conformations and adjuvant activities. Chem. Sci. 2016, 7, 2371–2380. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.Y.; Chen, Y.; Wu, C.; Tsai, H. What is the Effective Component in Suanzaoren Decoction for Curing Insomnia? Discovery by Virtual Screening and Molecular Dynamic Simulation. J. Biomol. Struct. Dyn. 2008, 26, 57–64. [Google Scholar] [CrossRef]
- Xu, H.-L.; Chen, G.-H.; Wu, Y.-T.; Xie, L.-P.; Tan, Z.-B.; Liu, B.; Fan, H.-J.; Chen, H.-M.; Huang, G.-Q.; Liu, M.; et al. Ginsenoside Ro, an oleanolic saponin of Panax ginseng, exerts anti-inflammatory effect by direct inhibiting toll like receptor 4 signaling pathway. J. Ginseng Res. 2021, in press. [Google Scholar] [CrossRef]
- Taiwo, B.J.; Olubiyi, O.O.; Wang, X.; Fisusi, F.A.; Akinniyi, G.A.; Van Heerden, F.R.; Strodel, B. Schistosomiasis: Snail-vector control, molecular modelling and dynamic studies of bioactive N-acetylglycoside saponins from Tetrapleura tetraptera. Comput. Biol. Chem. 2018, 77, 363–372. [Google Scholar] [CrossRef] [PubMed]
- Ghirardello, M.; Ruiz-de-Angulo, A.; Sacristan, N.; Barriales, D.; Jiménez-Barbero, J.; Poveda, A.; Corzana, F.; Anguita, J.; Fernández-Tejada, A. Exploiting structure–activity relationships of QS-21 in the design and synthesis of streamlined saponin vaccine adjuvants. Chem. Commun. 2020, 56, 719–722. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shahinozzaman, M.; Ishii, T.; Takano, R.; Halim, M.A.; Hossain, M.A.; Tawata, S. Cytotoxic Desulfated Saponin from Holothuria atra Predicted to Have High Binding Affinity to the Oncogenic Kinase PAK1: A Combined In Vitro and In Silico Study. Sci. Pharm. 2018, 86, 32. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, F.; Wang, R. Hemolytic mechanism of dioscin proposed by molecular dynamics simulations. J. Mol. Model. 2010, 16, 107–118. [Google Scholar] [CrossRef]
- Sahu, N.P.; Achari, B. Advances in Structural Determination of Saponins and Terpenoid Glycosides. Curr. Org. Chem. 2001, 5, 315–334. [Google Scholar] [CrossRef]
- Liangzi, F.; Qinfang, Z.; Jun, H. Research on saponin active compounds of Tuchao Baibiandouren for the treatment of type-2 diabetes based on UHPLC-Q-Exactive Orbitrap MS and network pharmacology. Digit. Chin. Med. 2021, 4, 19–31. [Google Scholar] [CrossRef]
- Castillo-Tejasa, J.; Castrejón-Gonzálezb, O.; Carroa, S.; González-Coronelc, V.; Alvarado, J.F.J.; Manero, O. Associative polymers. Part III: Shear rheology from moleculardynamics. Colloid Surf. A Physicochem. Eng. Asp. 2016, 491, 37–49. [Google Scholar] [CrossRef]
- Castrejón-González, E.O.; Márquez Baños, V.E.; Javier Alvarado, J.F.; Rico-Ramírez, V.; Castillo-Tejas, J.; Jiménez-Islas, H. Rheological model for micelles in solution from molecular dynamics. J. Mol. Liq. 2014, 198, 84–93. [Google Scholar] [CrossRef]
- Baimova, J.A.; Korznikova, E.A.; Dmitriev, S.V.; Liu, B.; Zhou, K. Review on crumpled graphene: Unique mechanical properties. Rev. Adv. Mater. Sci. 2014, 39, 69–83. [Google Scholar]
- Klaver, T.P.C.; Zhu, S.; Sluiter, M.H.F.; Janssen, G.C.A.M. Molecular dynamics simulation of graphene on Cu (100) and (111) surfaces. Carbon 2015, 82, 538–547. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.Y.; Mylvaganam, K.; Zhang, L.C. Wrinkling of monolayer graphene: A study by molecular dynamics and continuum plate theory. Phys. Rev. B 2009, 80, 155445. [Google Scholar] [CrossRef] [Green Version]
- Qingbin, Z.; Zhigang, L.; Yan, G.; Shujun, W.; Jang-Kyo, K. Molecular Dynamics Study of the Effect of Chemical Functionalization on the Elastic Properties of Graphene Sheets. J. Nanosci. Nanotechnol. 2010, 10, 7070–7074. [Google Scholar]
- Zhang, C.; Lu, C.; Pei, L.; Li, J.; Wang, R. The wrinkling and buckling of graphene induced by nanotwinned copper matrix: A molecular dynamics study. Nano Mater. Sci. 2021, 3, 95–103. [Google Scholar] [CrossRef]
- Durinck, J.; Coupeau, C.; Colin, J.; Grilhé, J. Molecular dynamics simulations of buckling-induced plasticity. Appl. Phys. Lett. 2008, 93, 221904. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Hu, N.; Ning, H.; Liu, Y.; Li, Y.; Wu, L. Molecular dynamics simulation on interfacial mechanical properties of polymer nanocomposites with wrinkled graphene. Comput. Mater. Sci. 2015, 108, 160–167. [Google Scholar] [CrossRef]
- Li, B.; Cao, Y.; Feng, X.; Gao, H. Mechanics of morphological instabilities and surface wrinkling in soft materials: A review. Soft Matter 2012, 8, 5728–5745. [Google Scholar] [CrossRef]
- Wei, Y.; Yang, R. Nanomechanics of graphene. Natl. Sci. Rev. 2019, 6, 324–348. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Allen, M.P.; Tildesley, D.J. Some tricks of the trade. In Computer Simulation of Liquids; Oxford University Press: New York, NY, USA, 1987. [Google Scholar]
- Penfold, J.; Thomas, R.K.; Tucker, I.; Petkov, J.T.; Stoyanov, S.D.; Denkov, N.; Golemanov, K.; Tcholakova, S.; Webster, J.R.P. Saponin Adsorption at the Air−Water Interface Neutron Reflectivity and Surface Tension Study. Langmuir 2018, 34, 9540–9547. [Google Scholar] [CrossRef]
- Cholakova, D.; Denkov, N. Rotator Phases in Alkane Systems: In Bulk, Surface Layers and Micro/nano-confinements. Adv. Colloid Interface Sci. 2019, 269, 7–42. [Google Scholar] [CrossRef] [PubMed]
- Bermudez, H.; Hammer, D.A.; Discher, D.E. Effect of Bilayer Thickness on Membrane Bending Rigidity. Langmuir 2004, 20, 540–543. [Google Scholar] [CrossRef] [Green Version]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M., Jr.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Cieplak, P.; Kollman., P.A. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J. Comput. Chem. 2000, 21, 1049–1074. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3691. [Google Scholar] [CrossRef] [Green Version]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
- Toukmaji, A.; Sagui, C.; Board, J.; Darden, T. Efficient PME-based approach to fixed and induced dipolar interactions. J. Chem. Phys. 2000, 113, 10913–10927. [Google Scholar] [CrossRef]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef] [Green Version]
- Miyamoto, S.; Kollman, P.A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High Performance Molecular Simulations through Multi—Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. Model. 1996, 14, 33–38. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsibranska, S.; Ivanova, A.; Tcholakova, S.; Denkov, N. Structure and Undulations of Escin Adsorption Layer at Water Surface Studied by Molecular Dynamics. Molecules 2021, 26, 6856. https://doi.org/10.3390/molecules26226856
Tsibranska S, Ivanova A, Tcholakova S, Denkov N. Structure and Undulations of Escin Adsorption Layer at Water Surface Studied by Molecular Dynamics. Molecules. 2021; 26(22):6856. https://doi.org/10.3390/molecules26226856
Chicago/Turabian StyleTsibranska, Sonya, Anela Ivanova, Slavka Tcholakova, and Nikolai Denkov. 2021. "Structure and Undulations of Escin Adsorption Layer at Water Surface Studied by Molecular Dynamics" Molecules 26, no. 22: 6856. https://doi.org/10.3390/molecules26226856
APA StyleTsibranska, S., Ivanova, A., Tcholakova, S., & Denkov, N. (2021). Structure and Undulations of Escin Adsorption Layer at Water Surface Studied by Molecular Dynamics. Molecules, 26(22), 6856. https://doi.org/10.3390/molecules26226856