Computational Investigations of a pH-Induced Structural Transition in a CTAB Solution with Toluic Acid
Abstract
:1. Introduction
2. Results and Discussion
2.1. Different Aggregation Morphologies
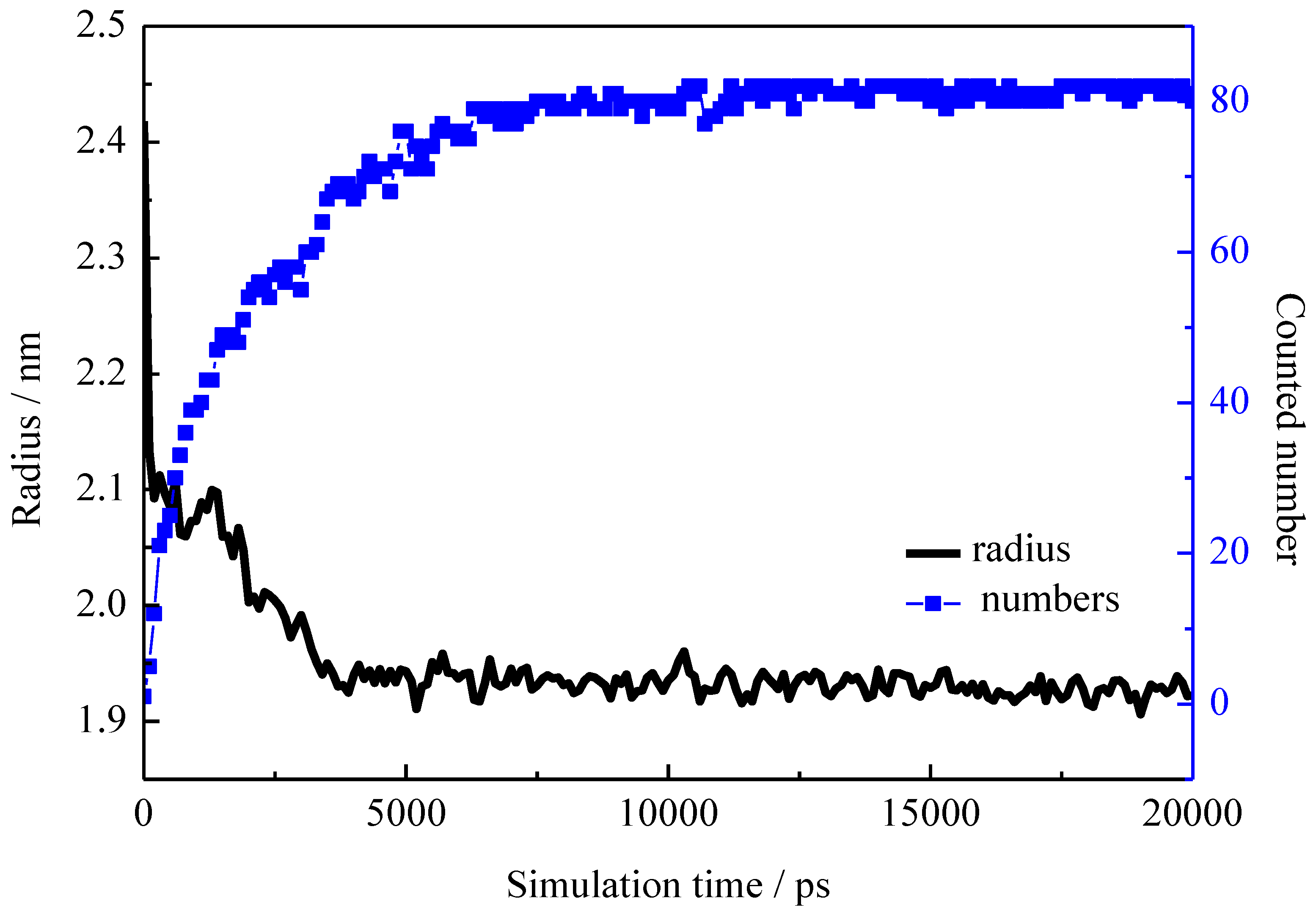
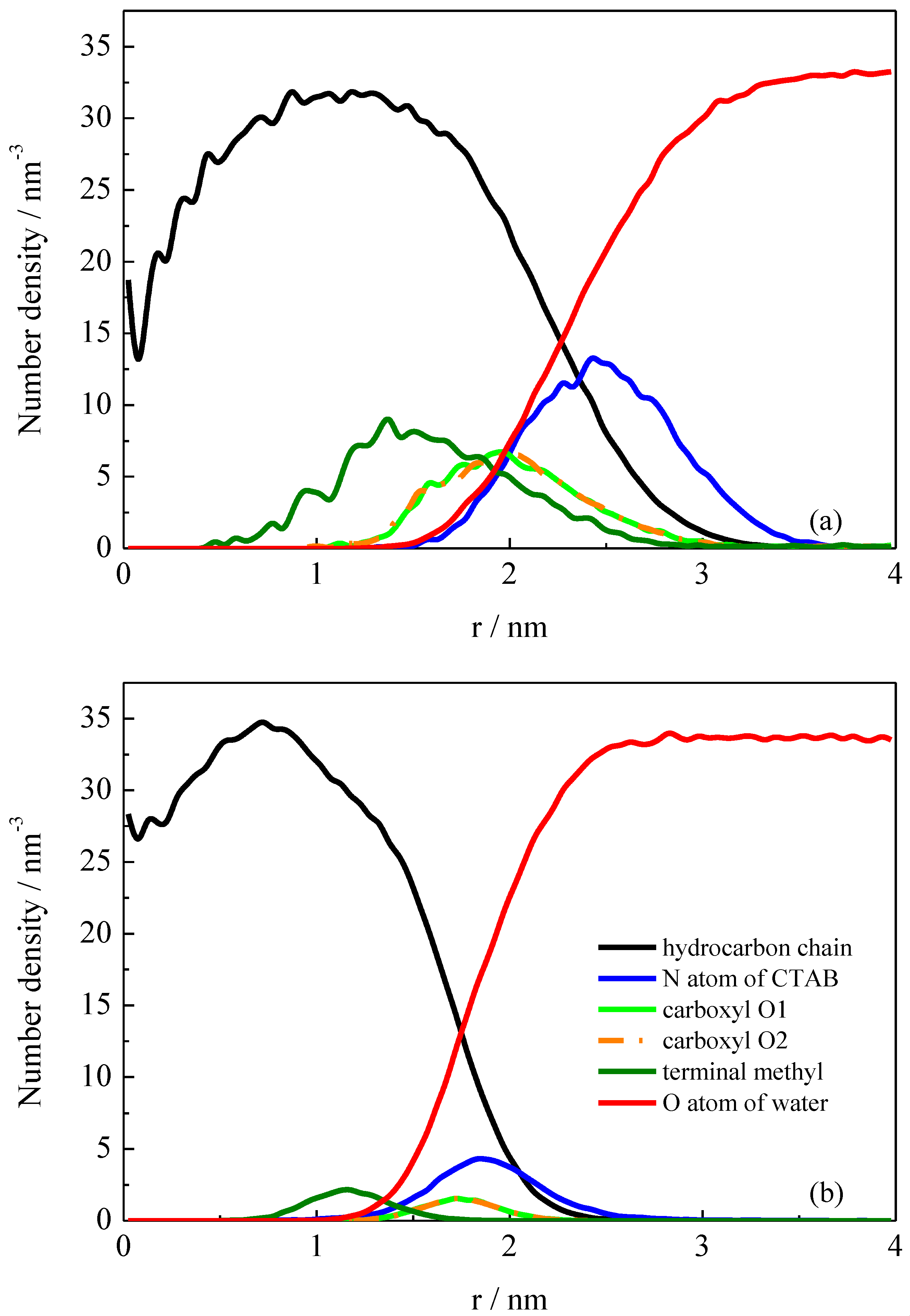
2.2. Detailed Structural Properties of the Formed Micelles
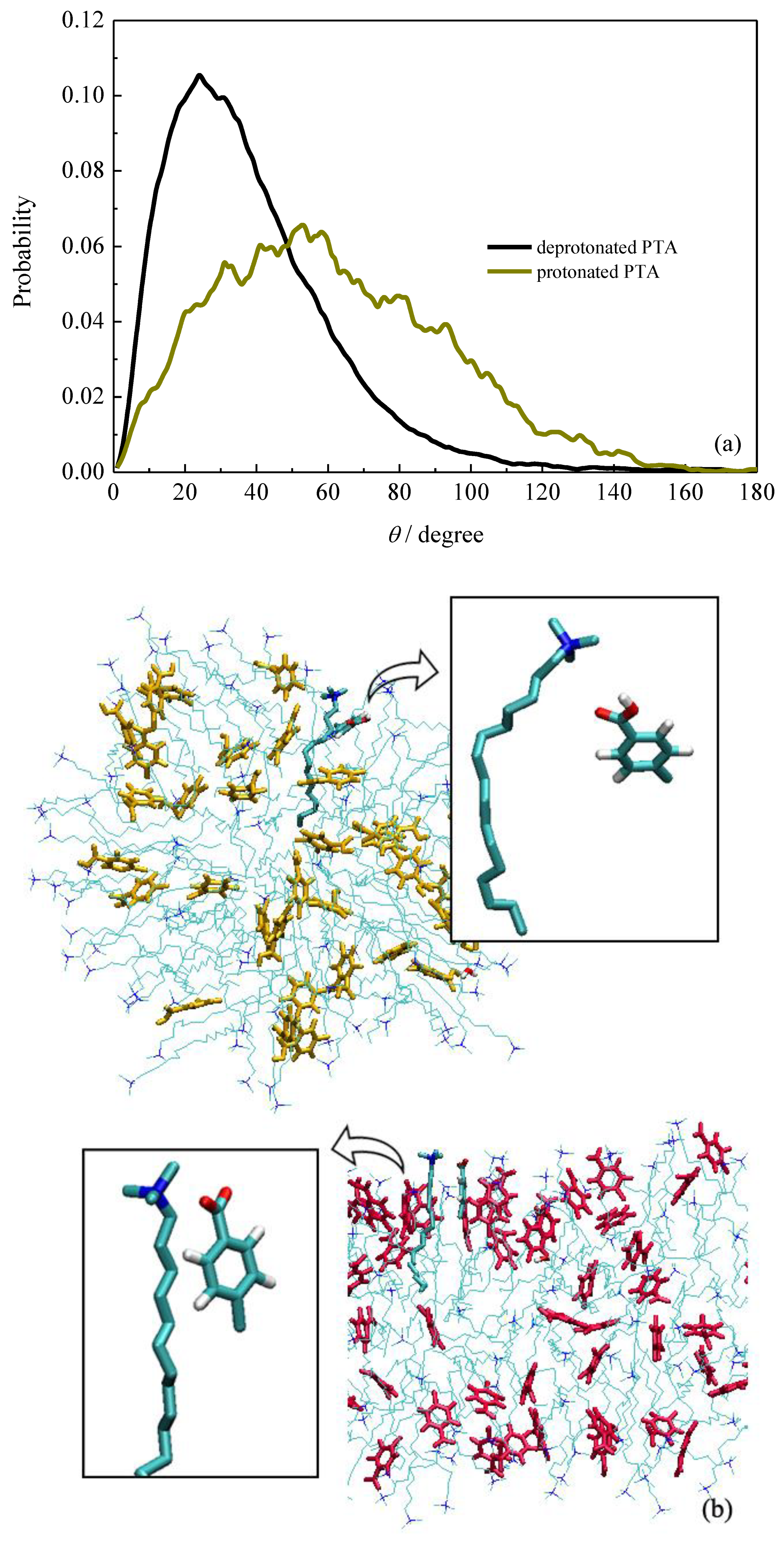
2.3. Bonding Structures of PTA−/PTA and Surfactants
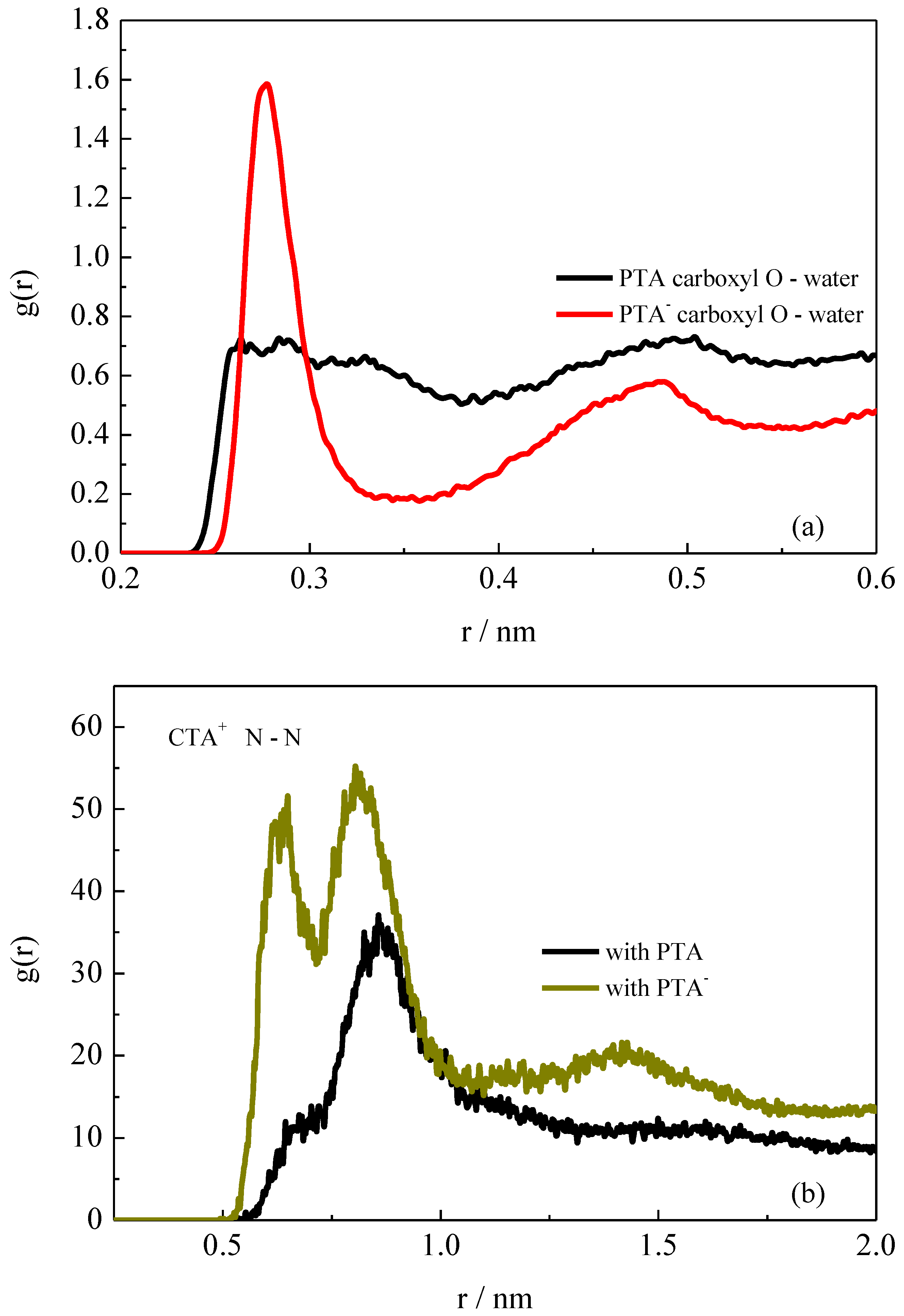
2.4. Intermolecular Interactions
3. Computational Details
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Chu, Z.; Dreiss, C.A.; Feng, Y. Smart wormlike micelles. Chem. Soc. Rev. 2013, 42, 7174–7203. [Google Scholar] [CrossRef]
- Dreiss, C.A. Wormlike micelles: Where do we stand? Recent developments, linear rheology and scattering techniques. Soft Matter 2013, 3, 956–970. [Google Scholar] [CrossRef] [PubMed]
- Patel, V.; Dharaiya, N.; Ray, D.; Aswal, V.K.; Bahadur, P. pH controlled size/shape in CTAB micelles with solubilized polar additives: A viscometry, scattering and spectral evaluation. Colloid Surf. A 2014, 455, 67–75. [Google Scholar] [CrossRef]
- De, S.; Aswal, V.K.; Goyal, P.S.; Bhattacharya, S. Role of spacer chain length in dimeric micellar organization. Small angle neutron scattering and fluorescence studies. J. Phys. Chem. 1996, 100, 11664–11671. [Google Scholar] [CrossRef]
- Varade, D.; Joshi, T.; Aswal, V.K.; Goyal, P.S.; Hassan, P.A.; Bahadur, P. Effect of salt on the micelles of cetyl pyridinium chloride. Colloids Surf. A Physicochem. Eng. Asp. 2005, 259, 95–101. [Google Scholar] [CrossRef]
- Srinivasan, V.; Blankschtein, D. Effect of counterion binding on micellar solution behavior: 1. Molecular-thermodynamic theory of micellization of ionic surfactants. Langmuir 2003, 19, 9932–9945. [Google Scholar] [CrossRef]
- Moulik, S.P.; Haque, M.E.; Jana, P.K.; Das, A.R. Micellar properties of cationic surfactants in pure and mixed states. J. Phys. Chem. 1996, 100, 701–708. [Google Scholar] [CrossRef]
- Giongo, C.V.; Bales, B.L. Estimate of the ionization degree of ionic micelles based on krafft temperature measurements. J. Phys. Chem. B 2003, 107, 5398–5403. [Google Scholar] [CrossRef]
- Lin, Z.; Cai, J.J.; Sciven, L.E.; Davis, H.T. Spherical-to-wormlike micelle transition in CTAB solution. J. Phys. Chem. 1994, 98, 5984–5993. [Google Scholar] [CrossRef]
- Imae, T.; Ikeda, S. Characteristics of rodlike micelles of cetyltrimethylammonium chloride in aqueous NaCl solutions: Their flexibility and the scaling laws in dilute and semidilute regimes. Colloid Polym. Sci. 1987, 265, 1090–1098. [Google Scholar] [CrossRef]
- Raghavan, S.R.; Kaler, E.W. Highly viscoelastic wormlike micellar solutions formed by cationic surfactants with long unsaturated tails. Langmuir 2001, 17, 300–306. [Google Scholar] [CrossRef]
- Hartmann, V.; Cressely, R. Simple salts effects on the characteristics of the shear thickening exhibited by an aqueous micellar solution of CTAB/NaSal. Europhys. Lett. 1997, 40, 691–696. [Google Scholar] [CrossRef]
- Rao, U.R.K.; Manohar, C.; Valaulikar, B.S.; Lyer, R.M. Micellar chain model for the origin of the viscoelasticity in dilute surfactant solutions. J. Phys. Chem. 1987, 91, 3286–3291. [Google Scholar] [CrossRef]
- Sakai, H.; Matsumura, A.; Yokoyama, S.; Saji, T.; Abe, M. Photochemical Switching of Vesicle Formation Using an Azobenzene-Modified Surfactant. J. Phys. Chem. B 1999, 103, 10737–10740. [Google Scholar] [CrossRef]
- Chu, Z.; Feng, Y. Thermo-switchable surfactant gel. Chem. Commun. 2011, 47, 7191–7193. [Google Scholar] [CrossRef] [PubMed]
- Dexter, A.F.; Malcolm, A.S.; Middelberg, A.P.J. Reversible active switching of the mechanical properties of a peptide film at a fluid-fluid interface. Nat. Mater. 2006, 5, 502–506. [Google Scholar] [CrossRef] [PubMed]
- Minkenberg, C.B.; Florusse, L.; Eelkema, R.; Koper, G.J.M.; van Esch, J.H. Triggered self-assembly of simple dynamic covalent surfactants. J. Am. Chem. Soc. 2009, 131, 11274–11275. [Google Scholar] [CrossRef] [PubMed]
- Jessop, P.G.; Mercer, S.M.; Heldebrant, D.J. CO2-triggered switchable solvents, surfactants, and other materials. Energy Env. Sci. 2012, 5, 7240–7253. [Google Scholar] [CrossRef]
- Sambasivam, A.; Dhakal, S.; Sureshkumar, R. Structure and rheology of self-assembled aqueous suspensions of nanoparticles and wormlike micelles. Mol. Simul. 2018, 44, 485–493. [Google Scholar] [CrossRef]
- Maillet, J.B.; Lachet, V.; Coveney, P.V. Large scale molecular dynamics simulations of self-assembly processes in short and long chain cationic surfactants. Phys. Chem. Chem. Phys. 1999, 1, 5277–5290. [Google Scholar] [CrossRef] [Green Version]
- Marrink, S.J.; Tieleman, D.P.; Mark, A.E. Molecular dynamics simulation of the kinetics of spontaneous micelle formation. J. Phys. Chem. B 2000, 104, 12165–12173. [Google Scholar] [CrossRef] [Green Version]
- Yakovlev, D.S.; Boek, E.S. Molecular dynamics simulations of mixed cationic/anionic wormlike micelles. Langmuir 2007, 23, 6588–6597. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.W.; Larson, R.G. Molecular dynamics simulations of threadlike cetyltrimethylammonium chloride micelles: Effect of sodium chloride and sodium salicylate salts. J. Phys. Chem. B 2009, 113, 13697–13710. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, C.D.; Hsieh, C.M.; Dreiss, C.A.; Lawrence, M.J. Molecular dynamics simulations of the interfacial and structural properties of dimethyldodecylamine-N-oxide micelles. Langmuir 2011, 27, 546–553. [Google Scholar] [CrossRef]
- Aswal, V.K.; Goyal, P.S. Role of counterion distribution on the structure of micelles in aqueous salt solutions: Small-angle neutron scattering study. Chem. Phys. Lett. 2002, 357, 491–497. [Google Scholar] [CrossRef]
- Brinchi, L.; Germani, R.; Di Profio, P.; Marte, L.; Savelli, G.; Oda, R.; Berti, D. Viscoelastic solutions formed by worm-like micelles of amine oxide surfactant. J. Colloid Interface Sci. 2010, 346, 100–106. [Google Scholar] [CrossRef]
- Kumar, S.; Sharma, D.; Kabir-ud-Din. Role of partitioning site in producing vis-coelasticity in micellar solutions. J. Surf. Deterg. 2005, 8, 247–252. [Google Scholar] [CrossRef]
- Sabatino, P.; Szczygiel, A.; Sinnaeve, D.; Hakimhashemi, M.; Saveyn, H.; Martins, J.C.; Meeren, P.V. NMR study of the influence of pH on phenol sorption in cationic CTAB micellar solutions. Colloids Surf. A 2010, 370, 42–48. [Google Scholar] [CrossRef] [Green Version]
- Umeasiegbu, C.D.; Balakotaiah, V.; Krishnamoorti, R. pH-Induced re-entrant microstructural transitions in cationic surfactant-hydrotrope mixtures. Langmuir 2016, 32, 655–663. [Google Scholar] [CrossRef]
- Yan, H.; Wang, Y.; Zhang, L.; Li, G.; Wei, X.; Liu, C. Molecular dynamics simulation of spherical-to-threadlike transition in a cationic surfactant solution. Mol. Simulat. 2019, 45, 797–805. [Google Scholar] [CrossRef]
- Yan, H.; Han, Z.; Li, K.; Li, G.; Wei, X. Molecular dynamics simulation of the pH-induced structural transitions in CTAB/NaSal solution. Langmuir 2018, 34, 351–358. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Páll, S.; Abraham, M.J.; Kutzner, C.; Hess, B.; Lindahl, E. Tackling exascale software challenges in molecular dynamics simulations with GROMACS. Solving Softw. Chall. Exascale 2015, 8759, 3–27. [Google Scholar]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for highly efficient load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.; Lin, Z.; van Gunsteren, W.F. Validation of the GROMOS 54A7 force field with respect to beta-peptide folding. J. Chem. Theory Comput. 2011, 7, 1237–1243. [Google Scholar] [CrossRef] [PubMed]
- Malde, A.K.; Zuo, L.; Breeze, M.; Stroet, M.; Poger, D.; Nair, P.C.; Oostenbrink, C.; Mark, A.E. An automated force field topology builder (ATB) and repository: Version 1.0. J. Chem. Theory Comput. 2011, 7, 4026–4037. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [Green Version]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Essman, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle-mesh ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graphics. 1996, 14, 33–38. [Google Scholar] [CrossRef]


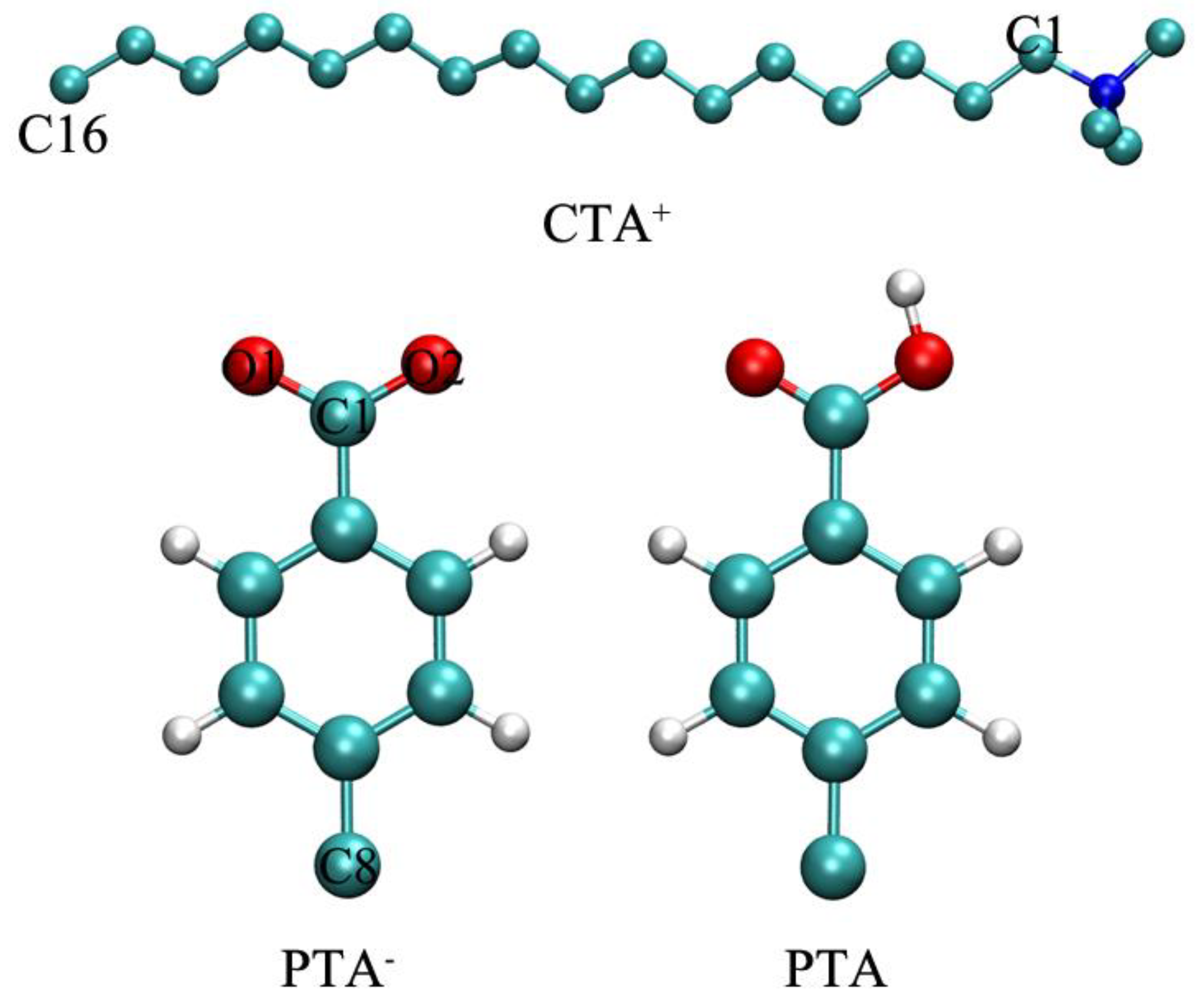
| Scheme 2. | CTA+ | Br− | PTA | PTA− | H+ | Cl− | Na+ | Water | |
|---|---|---|---|---|---|---|---|---|---|
| pH 2 | 180 | 180 | 88 | 2 | 9 | 7 | 193623 | ||
| pH 7 | 180 | 180 | 90 | 90 | 193636 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Yan, H.; Lv, L.; Xu, Y.; Zhang, L.; Jia, H. Computational Investigations of a pH-Induced Structural Transition in a CTAB Solution with Toluic Acid. Molecules 2021, 26, 6978. https://doi.org/10.3390/molecules26226978
Wang T, Yan H, Lv L, Xu Y, Zhang L, Jia H. Computational Investigations of a pH-Induced Structural Transition in a CTAB Solution with Toluic Acid. Molecules. 2021; 26(22):6978. https://doi.org/10.3390/molecules26226978
Chicago/Turabian StyleWang, Tingyi, Hui Yan, Li Lv, Yingbiao Xu, Lingyu Zhang, and Han Jia. 2021. "Computational Investigations of a pH-Induced Structural Transition in a CTAB Solution with Toluic Acid" Molecules 26, no. 22: 6978. https://doi.org/10.3390/molecules26226978
APA StyleWang, T., Yan, H., Lv, L., Xu, Y., Zhang, L., & Jia, H. (2021). Computational Investigations of a pH-Induced Structural Transition in a CTAB Solution with Toluic Acid. Molecules, 26(22), 6978. https://doi.org/10.3390/molecules26226978







