Ionic Transport Triggered by Asymmetric Illumination on 2D Nano-Membrane
Abstract
1. Introduction
2. Models and Methods
2.1. Carriers’ Diffusion Model
2.2. Model for Ion Transport Inside the Nanochannel
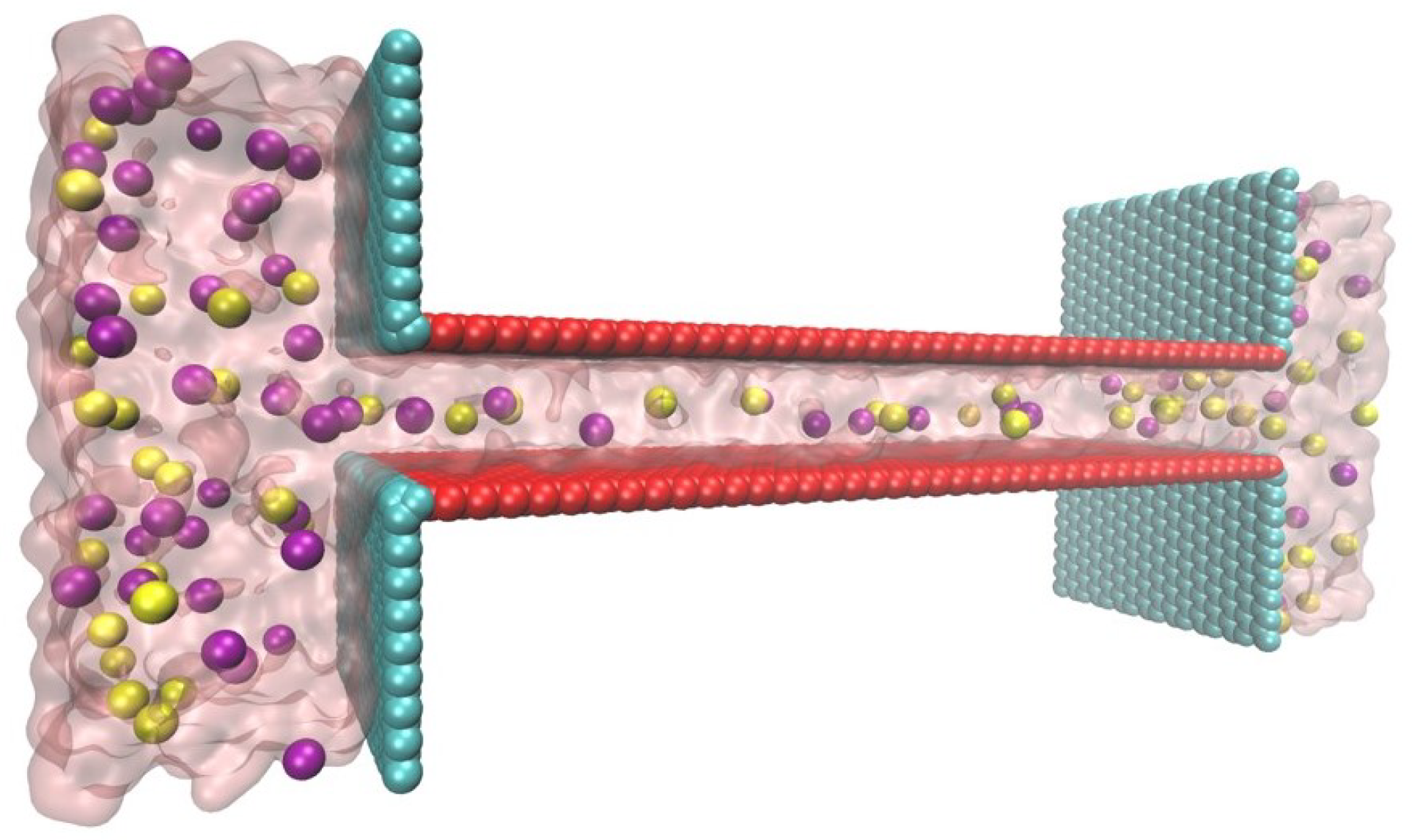
3. Results and Discussion
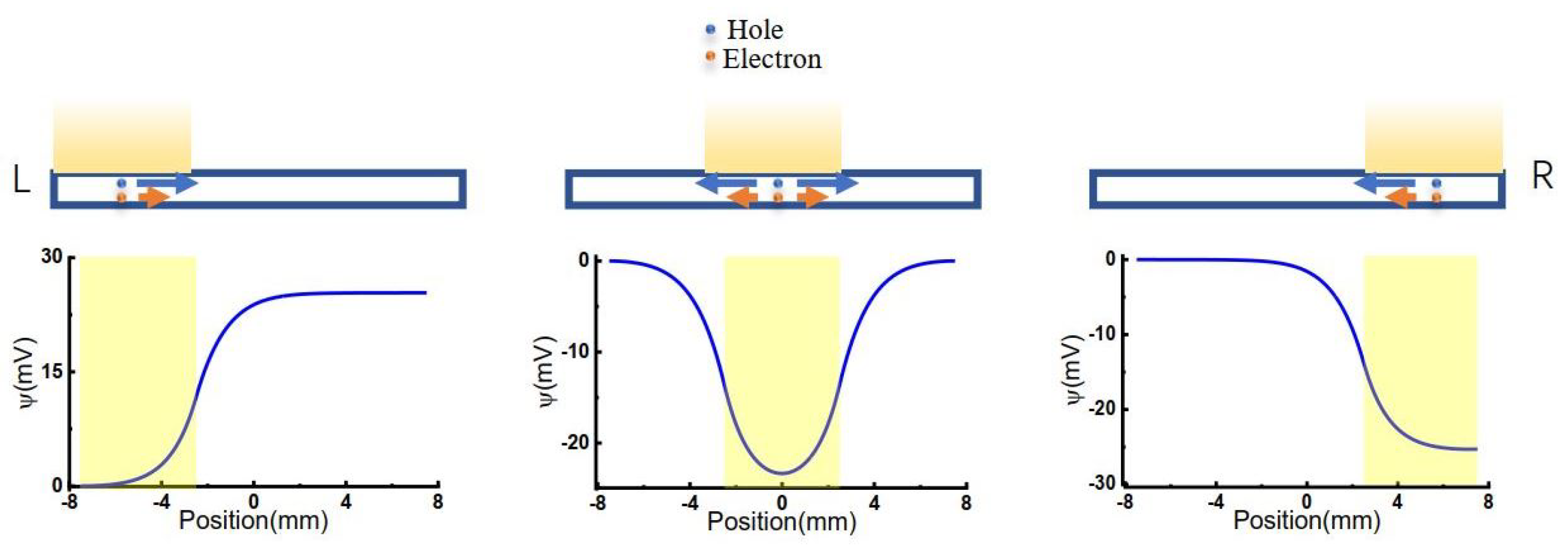
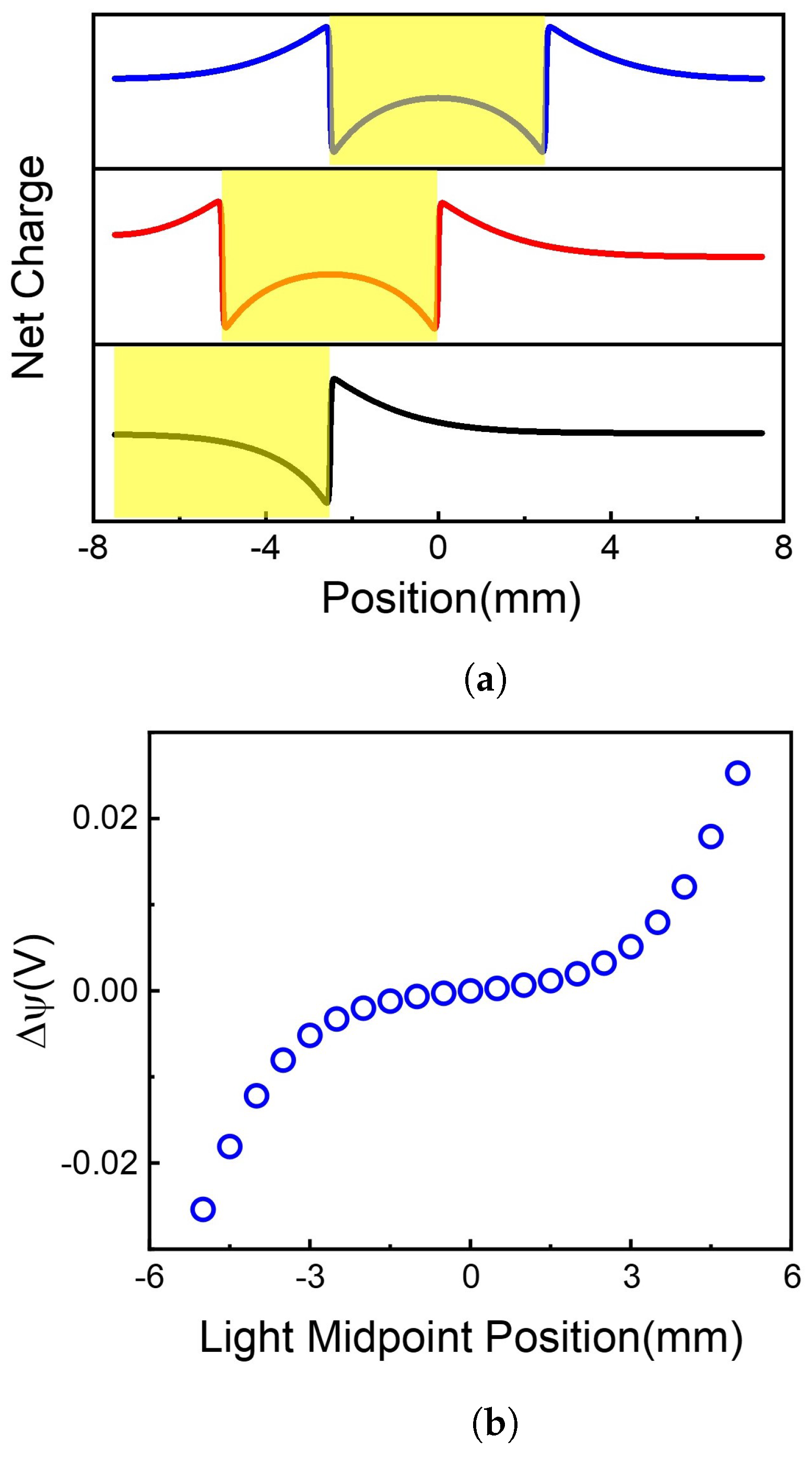
3.1. The Effect of Illuminate Position on the Voltage Difference
3.2. The Effect of Photoresponsivity on the Voltage Difference
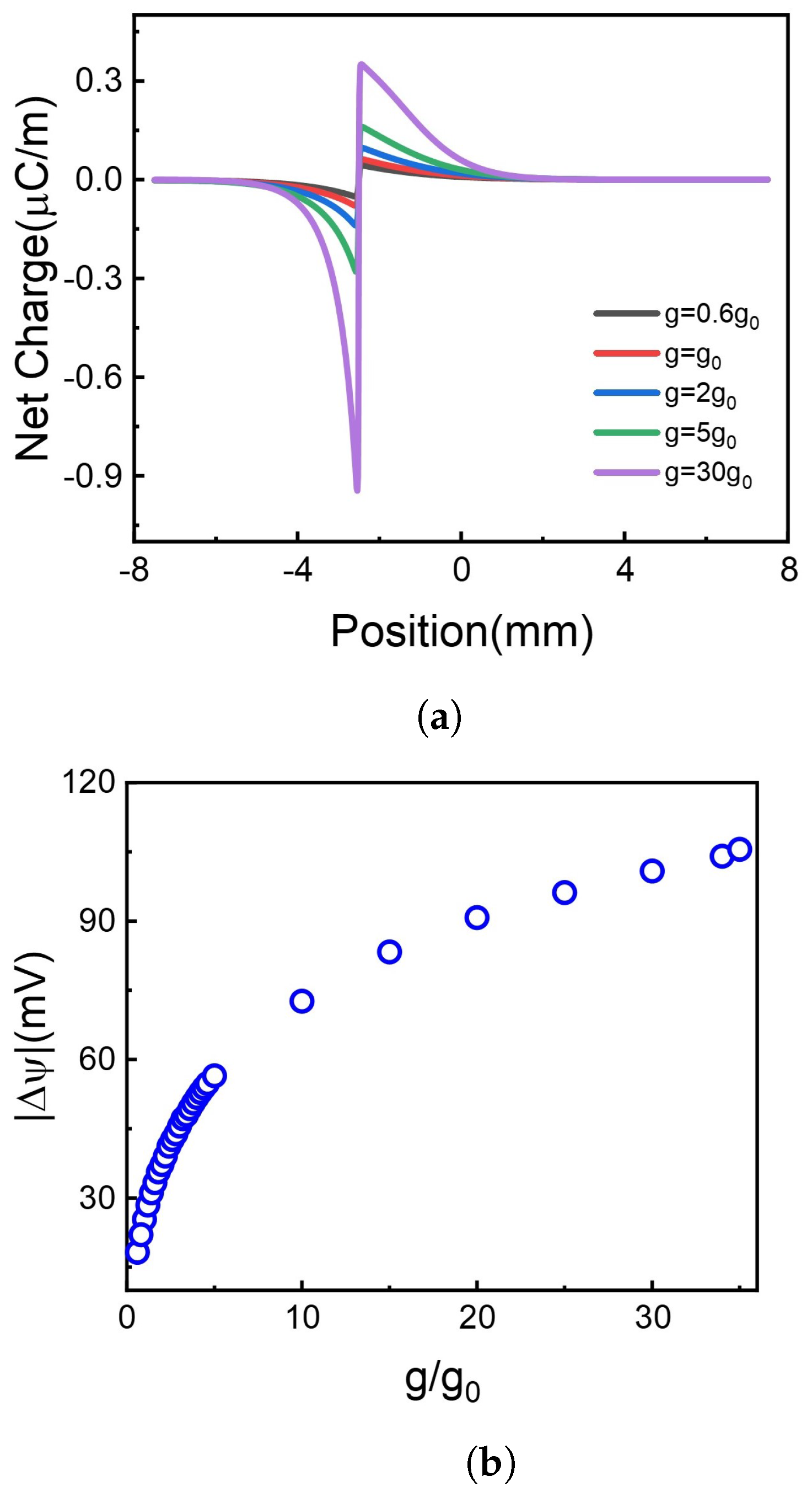
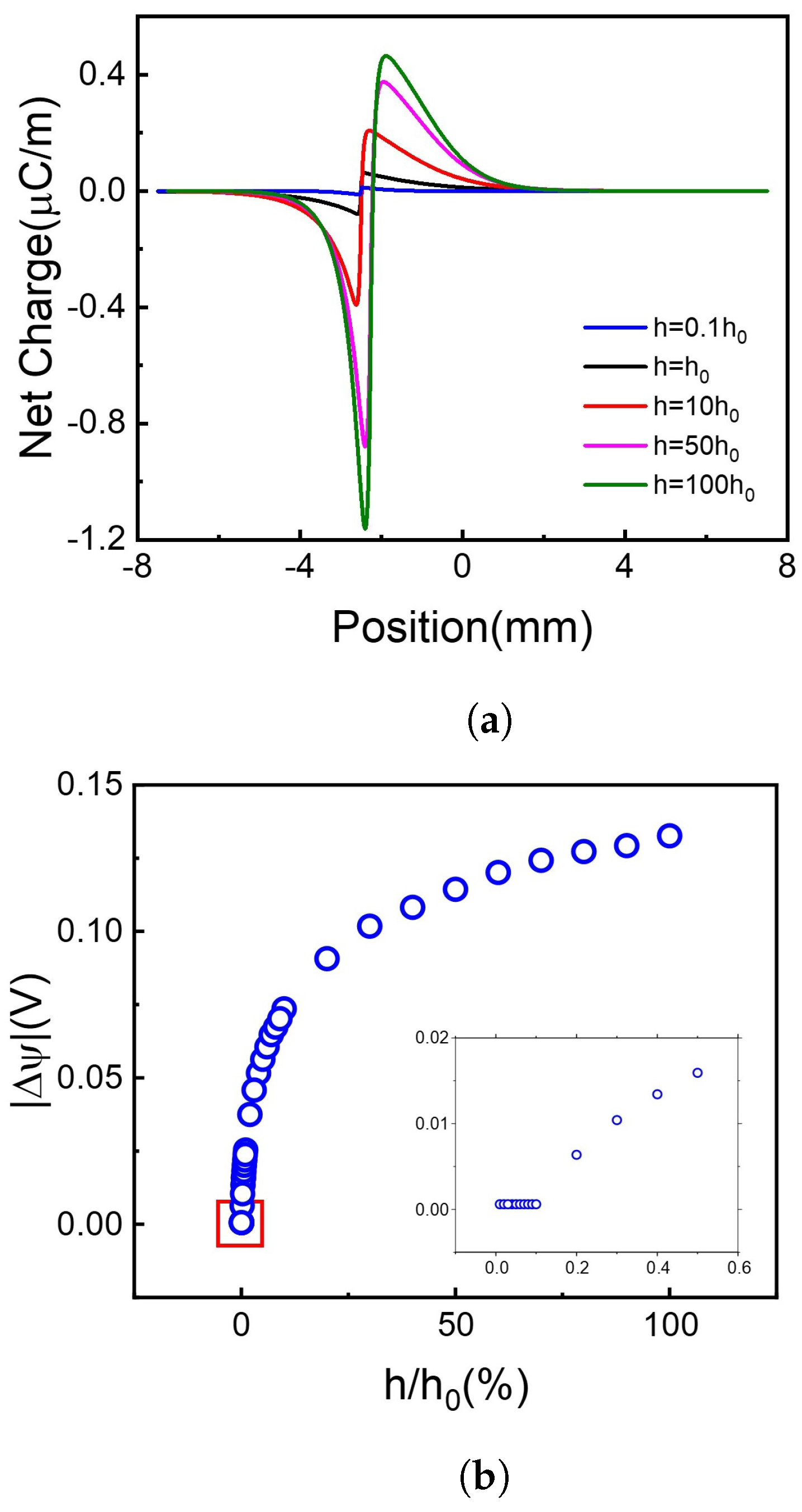
3.3. The Effect of Recombination Coefficient on the Voltage Difference
3.4. The Effect of and on the Voltage Difference
3.5. Photocurrent Induced by Illumination
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Eijkel, J.C.; Van Den Berg, A. Nanofluidics: What is it and what can we expect from it? Microfluid. Nanofluid. 2005, 1, 249–267. [Google Scholar] [CrossRef]
- Hu, X.; Lu, D. Intensification of chemical separation engineering by nanostructured channels and nanofluidics: From theories to applications. Chin. J. Chem. Eng. 2019, 27, 1439–1448. [Google Scholar] [CrossRef]
- Foquet, M.; Korlach, J.; Zipfel, W.; Webb, W.W.; Craighead, H.G. DNA fragment sizing by single molecule detection in submicrometer-sized closed fluidic channels. Anal. Chem. 2002, 74, 1415–1422. [Google Scholar] [CrossRef] [PubMed]
- Jia, Z.; Wang, B.; Song, S.; Fan, Y. Blue energy: Current technologies for sustainable power generation from water salinity gradient. Renew. Sustain. Energy Rev. 2014, 31, 91–100. [Google Scholar] [CrossRef]
- Jia, P.; Wen, Q.; Liu, D.; Zhou, M.; Jin, X.; Ding, L.; Dong, H.; Lu, D.; Jiang, L.; Guo, W. Highly Efficient Ionic Photocurrent Generation through WS2-Based 2D Nanofluidic Channels. Small 2019, 15, 1905355. [Google Scholar] [CrossRef] [PubMed]
- Yan, R.; Liang, W.; Fan, R.; Yang, P. Nanofluidic diodes based on nanotube heterojunctions. Nano Lett. 2009, 9, 3820–3825. [Google Scholar] [CrossRef] [PubMed]
- Roos, G.; Geerlings, P.; Messens, J. Enzymatic catalysis: The emerging role of conceptual density functional theory. J. Phys. Chem. B 2009, 113, 13465–13475. [Google Scholar] [CrossRef] [PubMed]
- Sparreboom, W.; van den Berg, A.; Eijkel, J.C. Principles and applications of nanofluidic transport. Nat. Nanotechnol. 2009, 4, 713. [Google Scholar] [CrossRef]
- Wang, C.; Nam, S.W.; Cotte, J.M.; Jahnes, C.V.; Colgan, E.G.; Bruce, R.L.; Brink, M.; Lofaro, M.F.; Patel, J.V.; Gignac, L.M. Wafer-scale integration of sacrificial nanofluidic chips for detecting and manipulating single DNA molecules. Nat. Commun. 2017, 8, 14243. [Google Scholar] [CrossRef]
- Brown, D. The discovery of water channels (aquaporins). Ann. Nutr. Metab. 2017, 70, 37–42. [Google Scholar] [CrossRef]
- Isaksson, J.; Kjäll, P.; Nilsson, D.; Robinson, N.; Berggren, M.; Richter-Dahlfors, A. Electronic control of Ca2+ signalling in neuronal cells using an organic electronic ion pump. Nat. Mater. 2007, 6, 673–679. [Google Scholar] [CrossRef] [PubMed]
- Uchiyama, M.; Yoshizawa, H. Nephron structure and immunohistochemical localization of ion pumps and aquaporins in the kidney of frogs inhabiting different environments. Symp. Soc. Exp. Biol. 2002, 54, 109–128. [Google Scholar]
- Bocquet, L. Nanofluidics coming of age. Nat. Mater. 2020, 19, 254–256. [Google Scholar] [CrossRef] [PubMed]
- Taniguchi, M.; Minami, S.; Ono, C.; Hamajima, R.; Morimura, A.; Hamaguchi, S.; Akeda, Y.; Kanai, Y.; Kobayashi, T.; Kamitani, W.; et al. Combining machine learning and nanopore construction creates an artificial intelligence nanopore for coronavirus detection. Nat. Commun. 2021, 12, 3726. [Google Scholar] [CrossRef]
- Ryuzaki, S.; Yasui, T.; Tsutsui, M.; Yokota, K.; Komoto, Y.; Paisrisarn, P.; Kaji, N.; Ito, D.; Tamada, K.; Ochiya, T.; et al. Rapid Discrimination of Extracellular Vesicles by Shape Distribution Analysis. Anal. Chem. 2021, 93, 7037–7044. [Google Scholar] [CrossRef]
- Liu, P.; Zhou, T.; Teng, Y.; Fu, L.; Hu, Y.; Lin, X.; Kong, X.Y.; Jiang, L.; Wen, L. Light-Induced Heat Driving Active Ion Transport Based on 2D MXene Nanofluids for Enhancing Osmotic Energy Conversion. CCS Chem. 2020, 3, 1325–1335. [Google Scholar] [CrossRef]
- Mocciaro, A.; Roth, T.L.; Bennett, H.M.; Soumillon, M.; Shah, A.; Hiatt, J.; Chapman, K.; Marson, A.; Lavieu, G. Light-activated cell identification and sorting (LACIS) for selection of edited clones on a nanofluidic device. Commun. Biol. 2018, 1, 41. [Google Scholar] [CrossRef]
- Wen, L.; Tian, Y.; Guo, Y.; Ma, J.; Liu, W.; Jiang, L. Conversion of light to electricity by photoinduced reversible pH changes and biomimetic nanofluidic channels. Adv. Funct. Mater. 2013, 23, 2887–2893. [Google Scholar] [CrossRef]
- Ajayan, P.; Kim, P.; Banerjee, K. van der Waals materials. Phys. Today 2016, 69, 9–38. [Google Scholar] [CrossRef]
- Deng, Y.; Xie, Y.; Zou, K.; Ji, X. Review on recent advances in nitrogen-doped carbons: Preparations and applications in supercapacitors. J. Mater. Chem. A 2016, 4, 1144–1173. [Google Scholar] [CrossRef]
- Wang, L.; Meric, I.; Huang, P.; Gao, Q.; Gao, Y.; Tran, H.; Taniguchi, T.; Watanabe, K.; Campos, L.; Muller, D. One-dimensional electrical contact to a two-dimensional material. Science 2013, 342, 614–617. [Google Scholar] [CrossRef] [PubMed]
- Chung, C.; Kim, Y.K.; Shin, D.; Ryoo, S.R.; Hong, B.H.; Min, D.H. Biomedical applications of graphene and graphene oxide. Acc. Chem. Res. 2013, 46, 2211–2224. [Google Scholar] [CrossRef] [PubMed]
- Kadam, V.; Kyratzis, I.L.; Truong, Y.B.; Schutz, J.; Wang, L.; Padhye, R. Electrospun bilayer nanomembrane with hierarchical placement of bead-on-string and fibers for low resistance respiratory air filtration. Sep. Purif. Technol. 2019, 224, 247–254. [Google Scholar] [CrossRef]
- Dong, Z.; Zhang, C.; Peng, H.; Gong, J.; Zhao, Q. Modular design of solar-thermal nanofluidics for advanced desalination membranes. J. Mater. Chem. A 2020, 8, 24493–24500. [Google Scholar] [CrossRef]
- Ahmadi, H.; Hosseini, E.; Cha-Umpong, W.; Abdollahzadeh, M.; Korayem, A.H.; Razmjou, A.; Chen, V.; Asadnia, M. Incorporation of natural lithium-ion trappers into graphene oxide nanosheets. Adv. Mater. Technol. 2021, 6, 2000665. [Google Scholar] [CrossRef]
- Xiao, K.; Jiang, L.; Antonietti, M. Ion transport in nanofluidic devices for energy harvesting. Joule 2019, 3, 2364–2380. [Google Scholar] [CrossRef]
- Zakertabrizi, M.; Hosseini, E.; Korayem, A.H.; Razmjou, A.; Fane, A.G.; Chen, V. Insight from perfectly selective and ultrafast proton transport through anhydrous asymmetrical graphene oxide membranes under Grotthuss mechanism. J. Membr. Sci. 2021, 618, 118735. [Google Scholar] [CrossRef]
- Alimohammadi, E.; Khedri, M.; Jahromi, A.M.; Maleki, R.; Rezaian, M. Graphene-based nanoparticles as potential treatment options for parkinson’s disease: A molecular dynamics study. Int. J. Nanomed. 2020, 15, 6887. [Google Scholar] [CrossRef]
- Hosseini, E.; Zakertabrizi, M.; Korayem, A.H.; Chen, S.; Mohsenabadi, S.K. Graphene oxide in ceramic-based layered structure: Nanosheet optimization. Constr. Build. Mater. 2019, 224, 266–275. [Google Scholar] [CrossRef]
- Huang, H.; Song, Z.; Wei, N.; Shi, L.; Mao, Y.; Ying, Y.; Sun, L.; Xu, Z.; Peng, X. Ultrafast viscous water flow through nanostrand-channelled graphene oxide membranes. Nat. Commun. 2013, 4, 2979. [Google Scholar] [CrossRef]
- Trick, J.L.; Chelvaniththilan, S.; Klesse, G.; Aryal, P.; Wallace, E.J.; Tucker, S.J.; Sansom, M.S. Functional annotation of ion channel structures by molecular simulation. Structure 2016, 24, 2207–2216. [Google Scholar] [CrossRef] [PubMed]
- El-Kady, M.F.; Strong, V.; Dubin, S.; Kaner, R.B. Laser scribing of high-performance and flexible graphene-based electrochemical capacitors. Science 2012, 335, 1326–1330. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.C.; Mou, C.Y.; Yu, S.S.F.; Chan, S.I. Heterogeneous formulation of the tricopper complex for efficient catalytic conversion of methane into methanol at ambient temperature and pressure. Energy Environ. Sci. 2016, 9, 1361–1374. [Google Scholar] [CrossRef]
- Darmanin, T.; Guittard, F. Recent advances in the potential applications of bioinspired superhydrophobic materials. J. Mater. Chem. A 2014, 2, 16319–16359. [Google Scholar] [CrossRef]
- Li, Y.; Shi, J. Hollow-structured mesoporous materials: Chemical synthesis, functionalization and applications. Adv. Mater. 2014, 26, 3176–3205. [Google Scholar] [CrossRef]
- Yang, J.; Hu, X.; Kong, X.; Jia, P.; Ji, D.; Quan, D.; Wang, L.; Wen, Q.; Lu, D.; Wu, J. Photo-induced ultrafast active ion transport through graphene oxide membranes. Nat. Commun. 2019, 10, 1171. [Google Scholar] [CrossRef]
- Lee, D.; Seo, J.; Zhu, X.; Lee, J.; Shin, H.J.; Cole, J.M.; Shin, T.; Lee, J.; Lee, H.; Su, H. Quantum confinement-induced tunable exciton states in graphene oxide. Sci. Rep. 2013, 3, 2250. [Google Scholar] [CrossRef]
- Xia, F.; Mueller, T.; Lin, Y.m.; Valdes-Garcia, A.; Avouris, P. Ultrafast graphene photodetector. Nat. Nanotechnol. 2009, 4, 839. [Google Scholar] [CrossRef]
- Ruzicka, B.A.; Wang, S.; Werake, L.K.; Weintrub, B.; Loh, K.P.; Zhao, H. Hot carrier diffusion in graphene. Phys. Rev. B 2010, 82, 195414. [Google Scholar] [CrossRef]
- Qi, X.; Zou, X.; Huang, Z.; Ren, L.; Hao, G.; Liu, Y.; Wei, X.; Zhong, J. Ultraviolet, visible, and near infrared photoresponse properties of solution processed graphene oxide. Appl. Surf. Sci. 2013, 266, 332–336. [Google Scholar] [CrossRef]
- Li, S.S.; Tu, K.H.; Lin, C.C.; Chen, C.W.; Chhowalla, M. Solution-processable graphene oxide as an efficient hole transport layer in polymer solar cells. ACS Nano 2010, 4, 3169–3174. [Google Scholar] [CrossRef] [PubMed]
- Eda, G.; Mattevi, C.; Yamaguchi, H.; Kim, H.; Chhowalla, M. Insulator to semimetal transition in graphene oxide. J. Phys. Chem. C 2009, 113, 15768–15771. [Google Scholar] [CrossRef]
- Gómez-Navarro, C.; Weitz, R.T.; Bittner, A.M.; Scolari, M.; Mews, A.; Burghard, M.; Kern, K. Electronic transport properties of individual chemically reduced graphene oxide sheets. Nano Lett. 2007, 7, 3499–3503. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef]
- Chen, Q.; Kong, X.; Li, J.; Lu, D.; Liu, Z. Electrokinetic desalination using honeycomb carbon nanotubes (HC-CNTs): A conceptual study by molecular simulation. Phys. Chem. Chem. Phys. 2014, 16, 18941–18948. [Google Scholar] [CrossRef]
- Li, J.; Kong, X.; Lu, D.; Liu, Z. Italicized carbon nanotube facilitating water transport: A molecular dynamics simulation. Sci. Bull. 2015, 60, 1580–1586. [Google Scholar] [CrossRef][Green Version]
- Lu, D. Accelerating water transport through a charged SWCNT: A molecular dynamics simulation. Phys. Chem. Chem. Phys. 2013, 15, 14447–14457. [Google Scholar] [CrossRef]
- MacKerell Jr, A.D.; Bashford, D.; Bellott, M.; Dunbrack Jr, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef]
- Kang, P.; Wang, M.C.; Knapp, P.M.; Nam, S. Crumpled Graphene Photodetector with Enhanced, Strain-Tunable, and Wavelength-Selective Photoresponsivity. Adv. Mater. 2016, 28, 4639–4645. [Google Scholar] [CrossRef]
- Gan, X.; Shiue, R.J.; Gao, Y.; Meric, I.; Heinz, T.F.; Shepard, K.; Hone, J.; Assefa, S.; Englund, D. Chip-integrated ultrafast graphene photodetector with high responsivity. Nat. Photonics 2013, 7, 883. [Google Scholar] [CrossRef]
- Mudd, G.W.; Svatek, S.A.; Hague, L.; Makarovsky, O.; Kudrynskyi, Z.R.; Mellor, C.J.; Beton, P.H.; Eaves, L.; Novoselov, K.S.; Kovalyuk, Z.D. High broad-band photoresponsivity of mechanically formed InSe–graphene van der Waals heterostructures. Adv. Mater. 2015, 27, 3760–3766. [Google Scholar] [CrossRef] [PubMed]
- Schoch, R.B.; Han, J.; Renaud, P. Transport phenomena in nanofluidics. Rev. Mod. Phys. 2008, 80, 839. [Google Scholar] [CrossRef]


| Parameters | Values | References |
|---|---|---|
| Photoresponsivity (g) | Ref. [40] | |
| Recombination coefficient (h) | Refs. [41,42] | |
| Hole mobility () | Ref. [39] | |
| Electron mobility () | Refs. [41,43] | |
| Diffusion coefficient of hole () | Equation (2) | |
| Diffusion coefficient of electron () | Equation (2) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, L.; Hu, X.; Lu, D.; Liu, Z. Ionic Transport Triggered by Asymmetric Illumination on 2D Nano-Membrane. Molecules 2021, 26, 7078. https://doi.org/10.3390/molecules26237078
Du L, Hu X, Lu D, Liu Z. Ionic Transport Triggered by Asymmetric Illumination on 2D Nano-Membrane. Molecules. 2021; 26(23):7078. https://doi.org/10.3390/molecules26237078
Chicago/Turabian StyleDu, Linhan, Xiaoyu Hu, Diannan Lu, and Zheng Liu. 2021. "Ionic Transport Triggered by Asymmetric Illumination on 2D Nano-Membrane" Molecules 26, no. 23: 7078. https://doi.org/10.3390/molecules26237078
APA StyleDu, L., Hu, X., Lu, D., & Liu, Z. (2021). Ionic Transport Triggered by Asymmetric Illumination on 2D Nano-Membrane. Molecules, 26(23), 7078. https://doi.org/10.3390/molecules26237078







