Thermodynamic Solution Properties of a Biodegradable Chelant (L-glutamic-N,N-diacetic Acid, L-GLDA) and Its Sequestering Ability toward Cd2+
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Apparatus and Procedure for the Potentiometric Measurements
2.3. Calculations
3. Results and Discussion
3.1. Acid–Base Properties of L-glutamic-N,N-diacetic Acid
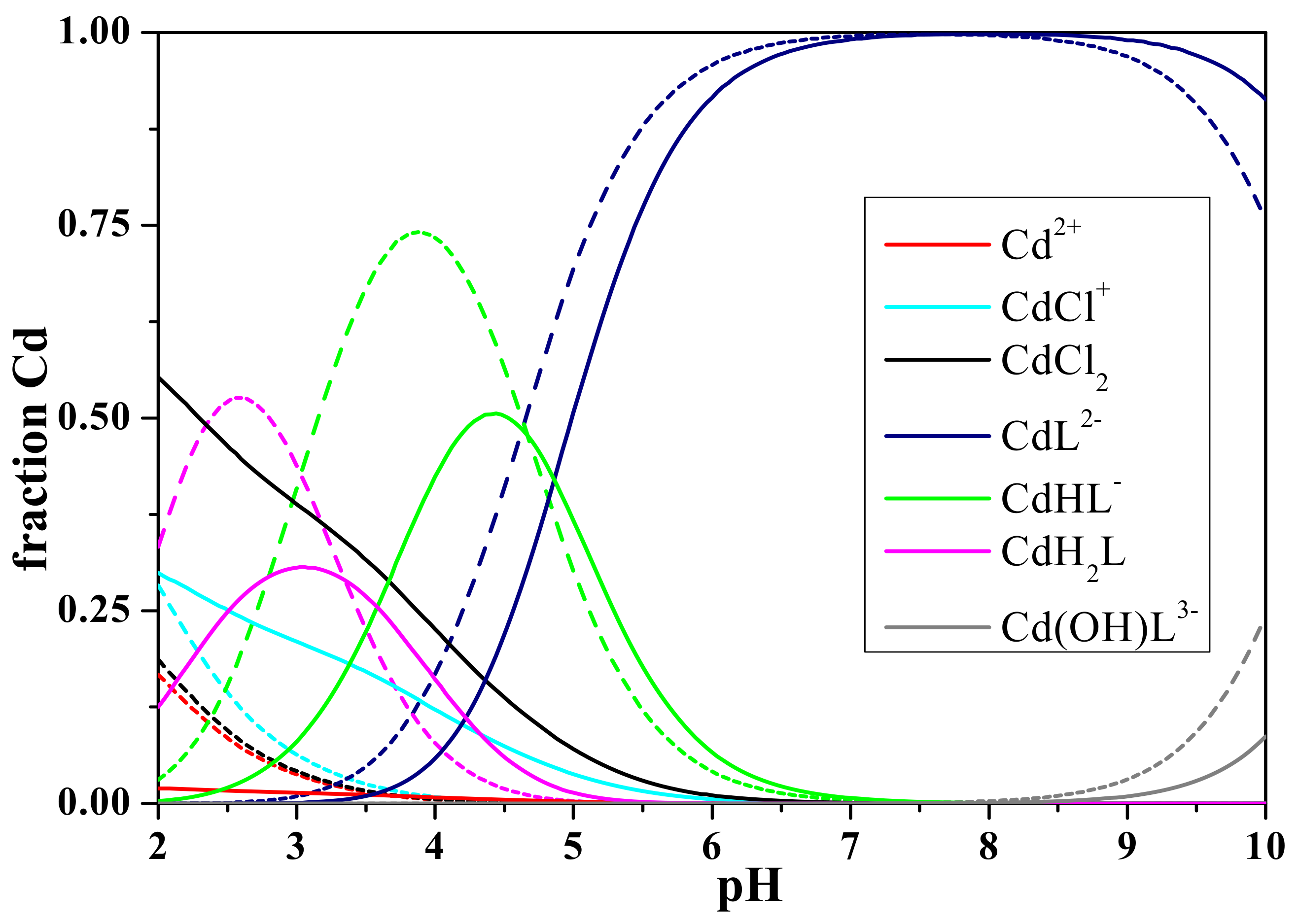
3.2. Interaction of L-glutamic-N,N-diacetic Acid with Cd2+
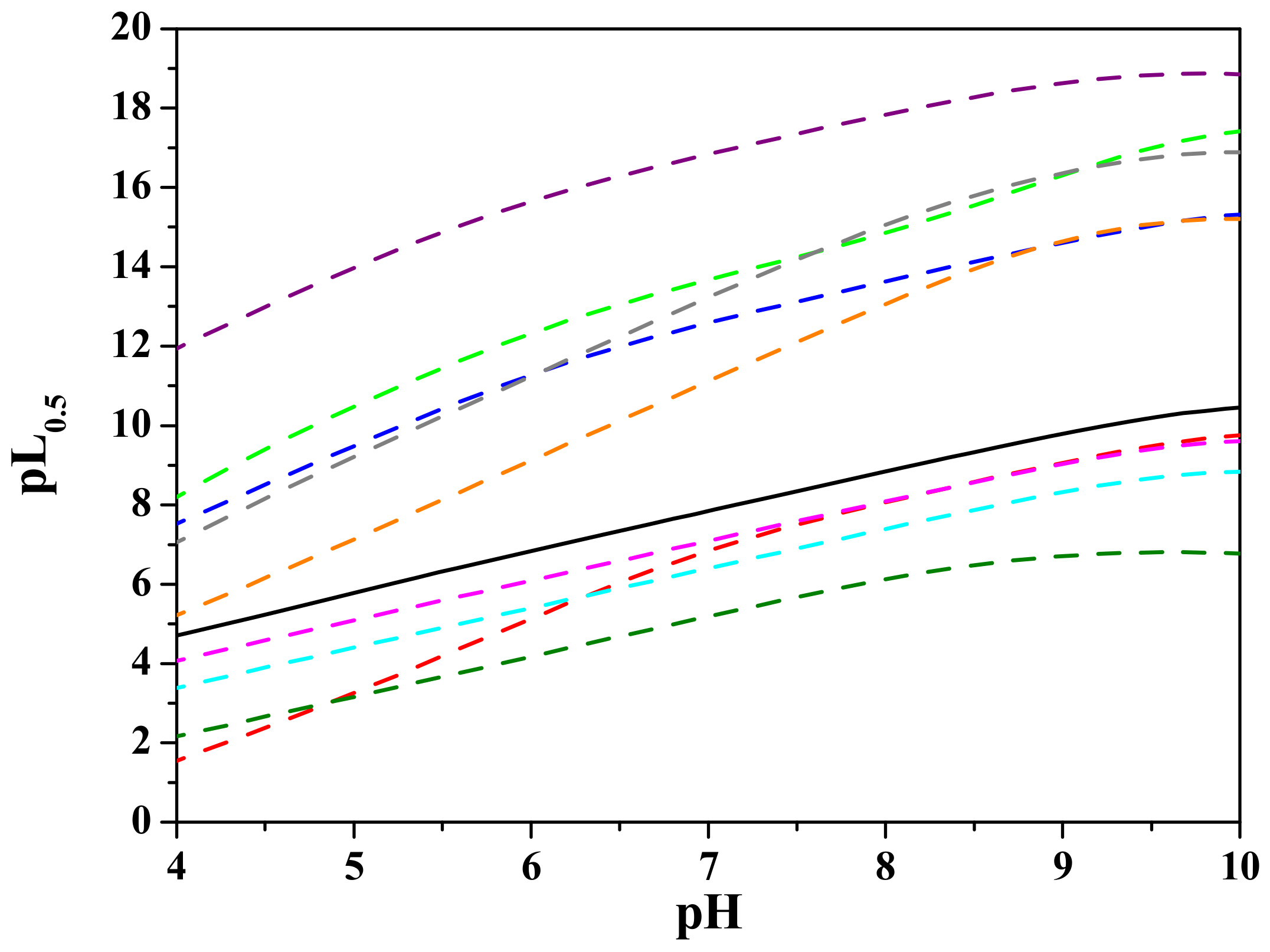
3.3. Comparisons with the Literature Data
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kołodyńska, D. Application of a New Generation of Complexing Agents in Removal of Heavy Metal Ions from Different Wastes. Environ. Sci. Pollut. Res. 2013, 20, 5939–5949. [Google Scholar] [CrossRef]
- Duo, L.; Yin, L.; Zhang, C.; Zhao, S. Ecotoxicological Responses of the Earthworm Eisenia Fetida to EDTA Addition under Turfgrass Growing Conditions. Chemosphere 2019, 220, 56–60. [Google Scholar] [CrossRef]
- Kołodyńska, D. The Chelating Agents of a New Generation as an Alternative to Conventional Chelators for Heavy Metal Ions Removal from Different Waste Waters. In Expanding Issues in Desalination; Ning, R.Y., Ed.; InTech Publishers: Zagreb, Croatia, 2011; pp. 339–371. [Google Scholar]
- Begum, Z.A.; Rahman, I.M.; Hasegawa, H. Complexation Behavior of SrII and Geochemically-Related Elements (MgII, CaII, BaII, and YIII) with Biodegradable Aminopolycarboxylate Chelators (GLDA and HIDS). J. Mol. Liq. 2017, 242, 1123–1130. [Google Scholar] [CrossRef]
- Begum, Z.A.; Rahman, I.M.M.; Sawai, H.; Tate, Y.; Maki, T.; Hasegawa, H. Stability Constants of Fe(III) and Cr(III) Complexes with dl-2-(2-Carboxymethyl)nitrilotriacetic Acid (GLDA) and 3-Hydroxy-2,2′-iminodisuccinic acid (HIDS) in Aqueous Solution. J. Chem. Eng. Data 2012, 57, 2723–2732. [Google Scholar] [CrossRef]
- Begum, Z.A.; Rahman, I.M.; Takase, T.; Hasegawa, H. Formation and Stability of the Mixed-Chelator Complexes of Sr2+, Mg2+, Ca2+, Ba2+, and Y3+ in Solution with Bio-Relevant Chelators. J. Inorg. Biochem. 2019, 195, 141–148. [Google Scholar] [CrossRef]
- Begum, Z.A.; Rahman, I.M.M.; Tate, Y.; Egawa, Y.; Maki, T.; Hasegawa, H. Formation and Stability of Binary Complexes of Divalent Ecotoxic Ions (Ni, Cu, Zn, Cd, Pb) with Biodegradable Aminopolycarboxylate Chelants (dl-2-(2-Carboxymethyl)Nitrilotriacetic Acid, GLDA, and 3-Hydroxy-2,2′-Iminodisuccinic Acid, HIDS) in Aqueous Solutions. J. Solut. Chem. 2012, 41, 1713–1728. [Google Scholar] [CrossRef]
- Pinto, I.; Neto, I.F.F.; Soares, H. Biodegradable Chelating Agents for Industrial, Domestic, and Agricultural Applications—A Review. Environ. Sci. Pollut. Res. 2014, 21, 11893–11906. [Google Scholar] [CrossRef]
- Van Ginkel, C.G.; Geerts, R.; Nguyen, P.D. Biodegradation of L-Glutamatediacetate by Mixed Cultures and an Isolate. ACS Symp. Ser. 2005, 910, 183–194. [Google Scholar] [CrossRef]
- Parsadoust, F.; Shirvani, M.; Shariatmadari, H.; Dinari, M. Effects of GLDA, MGDA, and EDTA Chelating Ligands on Pb Sorption by Montmorillonite. Geoderma 2020, 366, 114229. [Google Scholar] [CrossRef]
- Wang, G.; Pan, X.; Zhang, S.; Zhong, Q.; Zhou, W.; Zhang, X.; Wu, J.; Vijver, M.G.; Peijnenburg, W.J. Remediation of Heavy Metal Contaminated Soil by Biodegradable Chelator–Induced Washing: Efficiencies and Mechanisms. Environ. Res. 2020, 186, 109554. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, S.; Xu, X.; Zhong, Q.; Zhang, C.; Jia, Y.; Li, T.; Deng, O.; Li, Y. Heavy Metal Removal by GLDA Washing: Optimization, Redistribution, Recycling, and Changes in Soil Fertility. Sci. Total Environ. 2016, 569–570, 557–568. [Google Scholar] [CrossRef]
- Suanon, F.; Sun, Q.; Dimon, B.; Mama, D.; Yu, C.-P. Heavy Metal Removal from Sludge with Organic Chelators: Comparative Study of N, N-bis(carboxymethyl) Glutamic Acid and Citric Acid. J. Environ. Manag. 2016, 166, 341–347. [Google Scholar] [CrossRef]
- Wu, Q.; Cui, Y.; Li, Q.; Sun, J. Effective Removal of Heavy Metals from Industrial Sludge with the Aid of a Biodegradable Chelating Ligand GLDA. J. Hazard. Mater. 2015, 283, 748–754. [Google Scholar] [CrossRef]
- Gluhar, S.; Kaurin, A.; Lestan, D. Soil Washing with Biodegradable Chelating Agents and EDTA: Technological Feasibility, Remediation Efficiency and Environmental Sustainability. Chemosphere 2020, 257, 127226. [Google Scholar] [CrossRef]
- Liu, L.; Luo, D.; Yao, G.; Huang, X.; Wei, L.; Liu, Y.; Wu, Q.; Mai, X.; Liu, G.; Xiao, T. Comparative Activation Process of Pb, Cd and Tl Using Chelating Agents from Contaminated Red Soils. Int. J. Environ. Res. Public Health 2020, 17, 497. [Google Scholar] [CrossRef]
- Van Thinh, N.; Osanai, Y.; Adachi, T.; Vuong, B.T.S.; Kitano, I.; Chung, N.T.; Thai, P.K. Removal of Lead and other Toxic Metals in Heavily Contaminated Soil Using Biodegradable Chelators: GLDA, Citric Acid and Ascorbic Acid. Chemosphere 2021, 263, 127912. [Google Scholar] [CrossRef]
- Guo, X.; Chen, Y.; Han, W.; Wang, L.; Gao, L.; Zhang, G.; He, Q. Heavy Metals Removal from Sewage Sludge with Mixed Chelators of N, N-bis(carboxymethyl) Glutamic Acid and Citric Acid. Environ. Technol. 2020, 1–9. [Google Scholar] [CrossRef]
- Wang, K.; Liu, Y.; Song, Z.; Khan, Z.H.; Qiu, W. Effects of Biodegradable Chelator Combination on Potentially Toxic Metals Leaching Efficiency in Agricultural Soils. Ecotoxicol. Environ. Saf. 2019, 182, 109399. [Google Scholar] [CrossRef]
- Yan, D.; Guo, Z.; Xiao, X.; Peng, C.; He, Y.; Yang, A.; Wang, X.; Hu, Y.; Li, Z. Cleanup of Arsenic, Cadmium, and Lead in the Soil From a Smelting Site using N,N-bis(carboxymethyl)-L-glutamic Acid Combined with Ascorbic Acid: A Lab-Scale Experiment. J. Environ. Manag. 2021, 296, 113174. [Google Scholar] [CrossRef]
- WHO. IPCS Cadmium, Cadmium Chloride, Cadmium Oxide, Cadmium Sulphide, Cadmium Acetate, Cadmium Sulphate; World Health Organization: Geneva, Switzerland, 2019. [Google Scholar]
- WHO. IPCS Cadmium; World Health Organization: Geneva, Switzerland, 1992. [Google Scholar]
- Crea, F.; Foti, C.; Milea, D.; Sammartano, S. Speciation of Cadmium in the Environment. In Cadmium: From Toxicity to Essentiality; Sigel, A., Sigel, H., Sigel, R.K.O., Eds.; Springer Science + Business Media B.V.: Dordrecht, The Netherlands, 2013; Volume 11, pp. 63–83. [Google Scholar]
- Garside, M. Global Refinery Production of Cadmium by Country 2020. Available online: https://www.statista.com/statistics/1023116/refinery-production-cadmium-worldwide-by-country/ (accessed on 11 October 2021).
- UNEP. Final Review of Scientific Information on Cadmium; United Nations Environment Programme, Chemicals Branch DTIE; Version of December 2010. Available online: https://www.unep.org/resources/report/final-review-scientific-information-cadmium (accessed on 26 September 2021).
- Ding, P.; Zhuang, P.; Li, Z.; Xia, H.; Lu, H. Accumulation and Detoxification of Cadmium by Larvae of Prodenia litura (Lepidoptera: Noctuidae) feeding on Cd-enriched Amaranth Leaves. Chemosphere 2013, 91, 28–34. [Google Scholar] [CrossRef]
- Perrin, D.D.; Armarego, W.L.F. Purification of Laboratory Chemicals, 3rd ed.; Pergamon Press: Oxford, UK, 1988; p. 392. [Google Scholar]
- De Stefano, C.; Princi, P.; Rigano, C.; Sammartano, S. Computer Analysis of Equilibrium Data in Solution. ESAB2M: An Improved Version of the ESAB Program. Ann. Chim. 1987, 77, 643–675. [Google Scholar]
- De Stefano, C.; Sammartano, S.; Mineo, P.; Rigano, C. Computer Tools for the Speciation of Natural Fluids. In Marine Chemistry –An Environmental Analytical Chemistry Approach; Gianguzza, A., Pelizzetti, E., Sammartano, S., Eds.; Kluwer Academic Publishers: Amsterdam, The Netherlands, 1997; pp. 71–83. [Google Scholar]
- De Robertis, A.; De Stefano, C.; Sammartano, S.; Rigano, C. The Determination of Formation Constants of Weak Complexes by Potentiometric Measurements: Experimental Procedures and Calculation Methods. Talanta 1987, 34, 933–938. [Google Scholar] [CrossRef]
- Alderighi, L.; Gans, P.; Ienco, A.; Peters, D.; Sabatini, A.; Vacca, A. Hyperquad Simulation and Speciation (HySS): A Utility Program for the Investigation of Equilibria Involving Soluble and Partially Soluble Species. Coord. Chem. Rev. 1999, 194, 311–318. [Google Scholar] [CrossRef]
- De Stefano, C.; Foti, C.; Sammartano, S.; Gianguzza, A.; Rigano, C. Equilibrium Studies in Natural Fluids. Use of Synthetic Seawater and Other Media as Background Salts. Ann. Chim. 1994, 84, 159–175. [Google Scholar]
- Brönsted, J.N. Studies on Solubility. Iv. The Principle of the Specific Interaction of Ions. J. Am. Chem. Soc. 1922, 44, 877–898. [Google Scholar] [CrossRef]
- Ciavatta, L. The Specific Interaction Theory in the Evaluating Ionic Equilibria. Ann. Chim. 1980, 70, 551–562. [Google Scholar]
- Grenthe, I.; Puigdomenech, I. Modelling in Aquatic Chemistry; OECD-NEA: Paris, France, 1997. [Google Scholar]
- Guggenheim, E.A.; Turgeon, J.C. Specific Interaction of Ions. Trans. Faraday Soc. 1955, 51, 747–761. [Google Scholar] [CrossRef]
- Scatchard, G. Concentated Solutions of Strong Electrolytes. Chem. Rev. 1936, 19, 309–327. [Google Scholar] [CrossRef]
- Bretti, C.; Cigala, R.M.; De Stefano, C.; Lando, G.; Sammartano, S. Understanding the Bioavailability and Sequestration of Different Metal Cations in the Presence of a Biodegradable Chelant S,S-EDDS in Biological Fluids and Natural Waters. Chemosphere 2016, 150, 341–356. [Google Scholar] [CrossRef]
- Crea, F.; Stefano, C.; Foti, C.; Milea, D.; Sammartano, S. Chelating Agents for the Sequestration of Mercury(II) and Monomethyl Mercury(II). Curr. Med. Chem. 2014, 21, 3819–3836. [Google Scholar] [CrossRef]
- Bretti, C.; De Stefano, C.; Cardiano, P.; Cataldo, S.; Pettignano, A.; Arena, G.; Sgarlata, C.; Ida Grasso, G.; Lando, G.; Sammartano, S. Risedronate complexes with Mg2+, Zn2+, Pb2+, and Cu2+: Species Thermodynamics and Sequestering Ability in NaCl(aq) at Different Ionic Strengths and at T = 298.15 K. J. Mol. Liq. 2021, 343, 117699. [Google Scholar] [CrossRef]
- Irto, A.; Cardiano, P.; Chand, K.; Cigala, R.M.; Crea, F.; De Stefano, C.; Gano, L.; Sammartano, S.; Santos, M.A. Bifunctional 3-Hydroxy-4-Pyridinones as Effective aluminium chelators: Synthesis, Solution Equilibrium Studies and In Vivo Evaluation. J. Inorg. Biochem. 2018, 186, 116–129. [Google Scholar] [CrossRef]
- Cigala, R.M.; De Stefano, C.; Irto, A.; Milea, D.; Sammartano, S. Thermodynamic Data for the Modeling of Lanthanoid(III) Sequestration by Reduced Glutathione in Aqueous Solution. J. Chem. Eng. Data 2015, 60, 192–201. [Google Scholar] [CrossRef]
- Bretti, C.; Majlesi, K.; De Stefano, C.; Sammartano, S. Thermodynamic Study on the Protonation and Complexation of GLDA with Ca2+ and Mg2+ at Different Ionic Strengths and Ionic Media at 298.15 K. J. Chem. Eng. Data 2016, 61, 1895–1903. [Google Scholar] [CrossRef]
- Bretti, C.; Cigala, R.M.; De Stefano, C.; Lando, G.; Sammartano, S. Thermodynamic Solution Properties of a Biodegradable Chelant (MGDA) and its Interaction with the Major Constituents of Natural Fluids. Fluid Phase Equilibria 2017, 434, 63–73. [Google Scholar] [CrossRef]
- Bretti, C.; De Stefano, C.; Lando, G.; Majlesi, K.; Sammartano, S. Thermodynamics (Solubility and Protonation Constants) of Risedronic Acid in Different Media and Temperatures (283.15–318.15 K). J. Solut. Chem. 2017, 46, 1903–1927. [Google Scholar] [CrossRef]
- Bretti, C.; Cardiano, P.; Cigala, R.M.; De Stefano, C.; Irto, A.; Lando, G.; Sammartano, S. Exploring Various Ligand Classes for the Efficient Sequestration of Stannous Cations in the Environment. Sci. Total. Environ. 2018, 643, 704–714. [Google Scholar] [CrossRef]
- Bretti, C.; Cigala, R.M.; Giuffrè, O.; Lando, G.; Sammartano, S. Modeling Solubility and Acid-Base Properties of some Polar Side Chain Amino Acids in NaCl and (CH 3) 4 NCl Aqueous Solutions at Different Ionic Strengths and Temperatures. Fluid Phase Equilibria 2018, 459, 51–64. [Google Scholar] [CrossRef]
- Pytkowicz, R.M. (Ed.) Activity Coefficients in Electrolyte Solutions; CRC Press, Inc.: Boca Raton, FL, USA, 1979; Volume 1, p. 288. [Google Scholar]
- Pytkowicz, R.M. (Ed.) Activity Coefficients in Electrolyte Solutions; CRC Press, Inc.: Boca Raton, FL, USA, 1979; Volume 2, p. 330. [Google Scholar]
- Berto, S.; Daniele, P.G.; Lando, G.; Prenesti, E.; Sammartano, S. Methodological Aspects in the Study of Alkali Metal Ion Weak Complexes Using Different ISEs Electrodes. Int. J. Electrochem. Sci. 2012, 7, 10976–10986. [Google Scholar]
- Daniele, P.G.; Foti, C.; Gianguzza, A.; Prenesti, E.; Sammartano, S. Weak Alkali and Alkaline Earth Metal Complexes of Low Molecular Weight Ligands in Aqueous Solution. Coord. Chem. Rev. 2008, 252, 1093–1107. [Google Scholar] [CrossRef]
- Crea, F.; De Stefano, C.; Foti, C.; Lando, G.; Milea, D.; Sammartano, S. Alkali Metal Ion Complexes with Phosphates, Nucleotides, Amino Acids, and Related Ligands of Biological Relevance. Their Properties in Solution. Met. Ions Life Sci. 2016, 16, 133–166. [Google Scholar] [CrossRef] [PubMed]
- Crea, F.; De Stefano, C.; Milea, D.; Pettignano, A.; Sammartano, S. SALMO and S3M: A Saliva Model and a Single Saliva Salt Model for Equilibrium Studies. Bioinorg. Chem. Appl. 2015, 2015, 267985. [Google Scholar] [CrossRef]
- Bretti, C.; De Stefano, C.; Lando, G.; Sammartano, S. Thermodynamic Properties of Melamine (2,4,6-triamino-1,3,5-triazine) in Aqueous Solution. Effect of Ionic Medium, Ionic Strength and Temperature on ohe Solubility and Acid–Base Properties. Fluid Phase Equilibr. 2013, 355, 104–113. [Google Scholar] [CrossRef]
- Bretti, C.; Cigala, R.M.; De Stefano, C.; Lando, G.; Sammartano, S. Interaction of Phytate with Ag+, CH3Hg+, Mn2+, Fe2+, Co2+, and VO2+: Stability Constants and Sequestering Ability. J. Chem. Eng. Data 2012, 57, 2838–2847. [Google Scholar] [CrossRef]
- Foti, C.; Lando, G.; Millero, F.J.; Sammartano, S. Experimental Study and Modelling of Inorganic Cd2+ Speciation in Natural Waters. Environ. Chem. 2011, 8, 320–331. [Google Scholar] [CrossRef]
- Crea, F.; Milea, D.; Sammartano, S. Enhancement of Hydrolysis Through the Formation of Mixed Hetero-Metal Species. Talanta 2005, 65, 229–238. [Google Scholar] [CrossRef]
- Bazzicalupi, C.; Bianchi, A.; Giorgi, C.; Clares, M.P.; García-España, E. Addressing Selectivity Criteria in Binding Equilibria. Coord. Chem. Rev. 2012, 256, 13–27. [Google Scholar] [CrossRef]
- Gama, S.; Hermenau, R.; Frontauria, M.; Milea, D.; Sammartano, S.; Hertweck, C.; Plass, W. Iron Coordination Properties of Gramibactin as Model for the New Class of Diazeniumdiolate Based Siderophores. Chem. A Eur. J. 2021, 27, 2724–2733. [Google Scholar] [CrossRef]
- Martell, A.E.; Smith, R.M.; Motekaitis, R.J. NIST Standard Reference Database 46, Vers. 8; US Department of Commerce: Gaithersburg, MD, USA, 2004. [Google Scholar]
- Schwarzenbach, G.; Gut, R.; Anderegg, G. Komplexone XXV. Die polarographische Untersuchung von Austauschgleichgewichten. Neue Daten der Bildungskonstanten von Metallkomplexen der Äthylendiamin-tetraessigsäure und der 1,2-Diaminocyclohexan-tetraessigsäure. Helv. Chim. Acta 1954, 37, 937–957. [Google Scholar] [CrossRef]
- Harju, L. The Stability Constants of some Metal Chelates of Triethylenetetraminehexaacetic Acid (ttha). Anal. Chim. Acta 1970, 50, 475–489. [Google Scholar] [CrossRef]
- Majer, J.; Jokl, V.; Dvorakova, E.; Juracova, M. New Complexones. XIII. Potentiometric and Electrophoretic Study of Ethylenediamine-N,N’-Disuccinic Acid and its Metal Chelates. Chem. Zvesti 1968, 22, 415–423. [Google Scholar]
- Cucrowski, I.; Maseko, N. Solution Equilibria. A Unified Mathematical Treatment of Experimental Polarographic and Potentiometric Data from Acid-Base and Ligand Titrations. A Polarographic and Ion Selective Electrode Study of Cd(II) (N-(2-hydroxyethyl)iminodiacetic acid)OH system. Electroanalysis 2003, 15, 1377–1388. [Google Scholar] [CrossRef]
- Schwarzenbach, G.; Gut, R. Die Komplexe der Seltenen Erdkationen und die Gadoliniumecke. Helvetica Chim. Acta 1956, 39, 1589–1599. [Google Scholar] [CrossRef]
- Duffield, J.R.; May, P.M.; Williams, D.R. Computer Simulation of Metal Ion Equilibria in Biofluids. IV. Plutonium Speciation in Human Blood Plasma and Chelation Therapy using Polyaminopolycarboxylic Acids. J. Inorg. Biochem. 1984, 20, 199–214. [Google Scholar] [CrossRef]
- Anderegg, G. Komplexone XXXVI. Reakinsenthalpie und -entropie bei der Bildung der Metallkomplexe der höheren EDTA-Homologen. Helv. Chim. Acta 1964, 47, 1801–1814. [Google Scholar] [CrossRef]
- Hyvönen, H. Studies on Metal Complex Formation of environmentally Friendly Aminopolycarboxylate Chelating Agents. Ph.D. Thesis, University of Helsinki, Helsinki, Findland, 2008. [Google Scholar]


| Chemical | Formula | CAS n° | Purification | Assay (Mass) |
|---|---|---|---|---|
| Sodium chloride | NaCl | 7647-14-5 | NO | ≥99% |
| Potassium chloride | KCl | 7447-40-7 | NO | ≥99% |
| Tetraethylammonium iodide | (C2H5)4NI | 68-05-3 | [27] | 98% |
| Hydrochloric acid | HCl | 7647-01-0 | NO | ≥99% |
| Tetraethylammonium hydroxide | (C2H5)4NOH | 77-98-5 | NO | ~10% a |
| Sodium hydroxide | NaOH | 1310-73-2 | NO | ≥99% |
| Potassium phthalate monobasic | C8H5O4K | 877-24-7 | NO | ≥99.95% |
| Sodium carbonate | Na2CO3 | 497-19-8 | NO | 99.995% |
| Cadmium chloride hydrate | CdCl2 × H2O | 654054-66-7 | NO | ≥98% |
| L-glutamic acid N,N-diacetic acid tetrasodium salt (GLDA) | C9H10N1O8Na4 | 51981-21-6 | NO | >80% b |
| System | Medium | T/K | Ia | CHb | CLb | CMb | n.tit |
|---|---|---|---|---|---|---|---|
| H+/L | NaCl | 288.15 and 310.15 | 0.1 to 1.0 | 10 to 20 | 2.5 to 4 | 24 | |
| H+/L | KCl | 288.15 to 310.15 | 0.1 to 1.0 | 10 to 18 | 2.5 to 4 | 33 | |
| H+/L | (C2H5)4NI | 288.15 to 310.15 | 0.1 to 1.0 | 10 to 20 | 3.0 to 5 | 29 | |
| Cd2+/L | NaCl | 298.15 | 0.1 to 1.0 | 8.0 to 10 | 1.0 to 4.0 | 0.4 to 2.0 | 30 |
| Molar Concentration Scale | ||||||||||
| NaCl | KCl | (CH3)4NCl | (C2H5)4NI | |||||||
| i | z* a | Ci0 | Ci0 | Ci0 | Ci0 | |||||
| 1 | 10.560 | −11.6 ± 1.4 b | 8 | −0.03 ± 0.01 b | 8 ± 5 b | 0.46 ± 0.02 b | 0 ± 3 b | 0.55 ± 0.03 b | 1.07 ± 0.02 b | −4 ± 3 b |
| 2 | 5.324 | 2.0 ± 0.9 | 6 | 0.28 ± 0.01 | −20 ± 3 | 0.34 ± 0.02 | 2 ± 1 | 0.37 ± 0.02 | 0.82 ± 0.01 | 0 ± 2 |
| 3 | 3.071 | 3.0 ± 1.9 | 4 | 0.16 ± 0.02 | −13 ± 2 | 0.16 ± 0.02 | 1 ± 1 | 0.27 ± 0.02 | 0.63 ± 0.02 | 0 ± 1 |
| 4 | 1.897 | −7.0 ± 3.5 | 2 | 0.09 ± 0.02 | −6 ± 1 | 0.02 ± 0.09 | 0 ± 1 | 0.25 ± 0.01 | 0.55 ± 0.07 | 0 ± 1 |
| Molal Concentration Scale | ||||||||||
| NaCl | KCl | (CH3)4NCl | (C2H5)4NI | |||||||
| i | z* a | ∆εi0 | ∆εi0 | ∆εi0 | ∆εi0 | |||||
| 1 | 10.559 | −12.0 ± 1.4 b | 8 | −0.03 ± 0.01 b | 8 ± 5 b | 0.45 ± 0.02 b | 0 ± 3 b | 0.44 ± 0.03 b | 0.91 ± 0.02 b | −4 ± 3 b |
| 2 | 5.323 | 1.7 ± 0.9 | 6 | 0.27 ± 0.01 | −20 ± 3 | 0.33 ± 0.02 | 2 ± 1 | 0.29 ± 0.02 | 0.69 ± 0.01 | −1 ± 2 |
| 3 | 3.070 | 3.0 ± 1.9 | 4 | 0.15 ± 0.02 | −13 ± 2 | 0.15 ± 0.02 | 1 ± 1 | 0.19 ± 0.02 | 0.49 ± 0.02 | −1 ± 1 |
| 4 | 1.896 | −6.9 ± 3.5 | 2 | 0.08 ± 0.02 | −7 ± 1 | 0.01 ± 0.09 | 1 ± 1 | 0.16 ± 0.01 | 0.44 ± 0.07 | 0 ± 1 |
| NaCl | KCl | (C2H5)4NI | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T | I a | i | −∆G0 | ∆H0 | T∆S0 | −∆G0 | ∆H0 | T∆S0 | −∆G0 | ∆H0 | T∆S0 |
| 298.15 | 0.00 | 1 | 60.3 | −12 | 48 | 60.3 | −12 | 48 | 60.3 | −12 | 48 |
| 298.15 | 0.00 | 2 | 30.4 | 2 | 32 | 30.4 | 2 | 32 | 30.4 | 2 | 32 |
| 298.15 | 0.00 | 3 | 17.5 | 3 | 21 | 17.5 | 3 | 21 | 17.5 | 3 | 21 |
| 298.15 | 0.00 | 4 | 10.8 | −7 | 4 | 10.8 | −7 | 4 | 10.8 | −7 | 4 |
| 298.15 | 0.10 | 1 | 55.3 | −14 | 41 | 55.5 | −15 | 41 | 55.8 | −15 | 41 |
| 298.15 | 0.10 | 2 | 26.8 | −2 | 25 | 26.8 | 0 | 27 | 27.0 | 0 | 27 |
| 298.15 | 0.10 | 3 | 15.1 | 0 | 16 | 15.1 | 2 | 17 | 15.3 | 2 | 17 |
| 298.15 | 0.10 | 4 | 9.6 | −8 | 2 | 9.6 | −7 | 2 | 9.8 | −7 | 2 |
| 298.15 | 0.25 | 1 | 53.6 | −13 | 40 | 54.3 | −15 | 39 | 54.9 | −16 | 38 |
| 298.15 | 0.25 | 2 | 25.8 | −6 | 20 | 25.9 | 0 | 25 | 26.4 | −1 | 25 |
| 298.15 | 0.25 | 3 | 14.4 | −2 | 12 | 14.4 | 2 | 16 | 14.9 | 1 | 16 |
| 298.15 | 0.25 | 4 | 9.3 | −9 | 0 | 9.2 | −7 | 2 | 9.8 | −8 | 2 |
| 298.15 | 0.50 | 1 | 52.2 | −12 | 40 | 53.6 | −16 | 37 | 54.9 | −18 | 37 |
| 298.15 | 0.50 | 2 | 25.2 | −11 | 14 | 25.3 | 0 | 25 | 26.4 | −2 | 24 |
| 298.15 | 0.50 | 3 | 14.0 | −6 | 8 | 14.0 | 1 | 15 | 14.9 | 0 | 15 |
| 298.15 | 0.50 | 4 | 9.1 | −11 | −2 | 8.9 | −7 | 2 | 10.1 | −8 | 2 |
| 298.15 | 0.75 | 1 | 51.4 | −11 | 41 | 53.4 | −17 | 37 | 55.4 | −20 | 36 |
| 298.15 | 0.75 | 2 | 25.0 | −17 | 8 | 25.2 | 0 | 25 | 26.8 | −2 | 24 |
| 298.15 | 0.75 | 3 | 13.8 | −9 | 5 | 13.8 | 1 | 15 | 15.2 | 0 | 15 |
| 298.15 | 0.75 | 4 | 9.0 | −13 | −4 | 8.7 | −7 | 2 | 10.5 | −8 | 3 |
| 298.15 | 1.00 | 1 | 50.8 | −9 | 42 | 53.5 | −17 | 37 | 56.1 | −21 | 35 |
| 298.15 | 1.00 | 2 | 24.9 | −22 | 3 | 25.3 | 0 | 25 | 27.3 | −3 | 24 |
| 298.15 | 1.00 | 3 | 13.7 | −12 | 1 | 13.7 | 2 | 15 | 15.7 | 0 | 15 |
| 298.15 | 1.00 | 4 | 9.0 | −15 | −6 | 8.6 | −7 | 2 | 11.0 | −8 | 3 |
| Equilibrium | p* a | z* a | ||
|---|---|---|---|---|
| H+ + L4− = HL3− | 1 | 8 | 10.56 b | −0.0068 b |
| 2 H+ + L4− = H2L2− | 2 | 14 | 15.88 b | −0.0056 b |
| 3 H+ + L4− = H3L− | 3 | 18 | 18.96 b | −0.0039 b |
| 4 H+ + L4− = H4L0(aq) | 4 | 20 | 20.86 b | −0.008 b |
| Na+ + L4− = NaL3− | 1 | 8 | 2.50 ± 0.02 c | 0.017 ± 0.004 c |
| Na+ + H+ + L4− = NaHL2− | 2 | 14 | 12.25 ± 0.03 | 0.013 ± 0.004 |
| Na+ + 2 H+ + L4− = NaH2L− | 3 | 18 | 16.83 ± 0.03 | 0.007 ± 0.003 |
| Na+ + 3 H+ + L4− = NaH3L0(aq) | 4 | 20 | 19.08 ± 0.07 | 0.003 ± 0.007 |
| 2 Na+ + L4− = Na2L2− | 2 | 14 | 3.01 ± 0.10 | 0.018 ± 0.012 |
| K+ + L4− = KL3− | 1 | 8 | 2.20 ± 0.05 | 0.004 ± 0.005 |
| K+ + H+ + L4− = KHL2− | 2 | 14 | 12.12 ± 0.04 | −0.004 ± 0.004 |
| K+ + 2 H+ + L4− = KH2L− | 3 | 18 | 16.81 ± 0.03 | −0.004 ± 0.004 |
| K+ + 3 H+ + L4− = KH3L0(aq) | 4 | 20 | 19.11 ± 0.06 | −0.003 ± 0.007 |
| (CH3)4N+ + L4− = (CH3)4NL3− | 1 | 8 | 1.89 ± 0.08 | - |
| (CH3)4N+ + H+ + L4− = (CH3)4NHL2− | 2 | 14 | 11.82 ± 0.07 | - |
| (CH3)4N+ + 2 H+ + L4− = (CH3)4NH2L− | 3 | 18 | 16.45 ± 0.07 | - |
| (CH3)4N+ + 3 H+ + L4− = (CH3)4NH3L0(aq) | 4 | 20 | 18.59 ± 0.24 | - |
| Parameter | ||||
| c0 | 0.165 d | |||
| c1 | 0.200 ± 0.008 c | −0.0011 ± 0.0003 c |
| Equilibrium | z* a | Cij | ∆εij | Max (%) | pH | |
|---|---|---|---|---|---|---|
| Cd2+ + L4− = CdL2− | 16 | 12.68 ± 0.03 b | −0.32 ± 0.06 b | −0.31 c | 98 | 8.6 |
| Cd2+ + H+ + L4− = CdHL− | 20 | 17.61 ± 0.03 | 0.66 ± 0.06 | 0.65 | 50 | 4.2 |
| Cd2+ + 2 H+ + L4− = CdH2L0(aq) | 22 | 20.76 ± 0.05 | 1.81 ± 0.10 | 1.77 | 27 | 2.9 |
| 2 Cd2+ +L4− = Cd2L0(aq) | 24 | 17.52 ± 0.05 | 1.49 ± 0.07 | 1.46 | 5 | 4.7 |
| Cd2+ + H2O + L4− = Cd(OH)L3− + H+ | 10 | 1.77 ± 0.04 | −2.10 ± 0.14 | −2.05 | 18 | 10.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bretti, C.; Di Pietro, R.; Cardiano, P.; Gomez-Laserna, O.; Irto, A.; Lando, G.; De Stefano, C. Thermodynamic Solution Properties of a Biodegradable Chelant (L-glutamic-N,N-diacetic Acid, L-GLDA) and Its Sequestering Ability toward Cd2+. Molecules 2021, 26, 7087. https://doi.org/10.3390/molecules26237087
Bretti C, Di Pietro R, Cardiano P, Gomez-Laserna O, Irto A, Lando G, De Stefano C. Thermodynamic Solution Properties of a Biodegradable Chelant (L-glutamic-N,N-diacetic Acid, L-GLDA) and Its Sequestering Ability toward Cd2+. Molecules. 2021; 26(23):7087. https://doi.org/10.3390/molecules26237087
Chicago/Turabian StyleBretti, Clemente, Roberto Di Pietro, Paola Cardiano, Olivia Gomez-Laserna, Anna Irto, Gabriele Lando, and Concetta De Stefano. 2021. "Thermodynamic Solution Properties of a Biodegradable Chelant (L-glutamic-N,N-diacetic Acid, L-GLDA) and Its Sequestering Ability toward Cd2+" Molecules 26, no. 23: 7087. https://doi.org/10.3390/molecules26237087
APA StyleBretti, C., Di Pietro, R., Cardiano, P., Gomez-Laserna, O., Irto, A., Lando, G., & De Stefano, C. (2021). Thermodynamic Solution Properties of a Biodegradable Chelant (L-glutamic-N,N-diacetic Acid, L-GLDA) and Its Sequestering Ability toward Cd2+. Molecules, 26(23), 7087. https://doi.org/10.3390/molecules26237087







