Next Article in Journal
Mimotopes for Mycotoxins Diagnosis Based on Random Peptides or Recombinant Antibodies from Phage Library
Next Article in Special Issue
Undirected C-H Bond Activation in Aluminium Hydrido Enaminonates
Previous Article in Journal
Nanostructured Lipid Carriers Can Enhance Oral Absorption of Khellin, a Natural Pleiotropic Molecule
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 26
Issue 24
10.3390/molecules26247651
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

NH Stretching Frequencies of Intramolecularly Hydrogen-Bonded Systems: An Experimental and Theoretical Study

by
Poul Erik Hansen
1,*,
Mohammad Vakili
2,
Fadhil S. Kamounah
3 and
Jens Spanget-Larsen
1,*
1
Department of Science and Environment, Roskilde University, Universitetsvej 1, DK-4000 Roskilde, Denmark
2
Department of Chemistry, Faculty of Science, Ferdowsi University of Mashhad, Mashhad 91775-1436, Iran
3
Department of Chemistry, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen, Denmark
*
Authors to whom correspondence should be addressed.
Molecules 2021, 26(24), 7651; https://doi.org/10.3390/molecules26247651
Submission received: 12 November 2021 / Revised: 10 December 2021 / Accepted: 13 December 2021 / Published: 17 December 2021
(This article belongs to the Special Issue New Insights into Intramolecular Hydrogen Bonds)
Browse Figures
Review Reports Versions Notes

Abstract

:
The vibrational NH stretching transitions in secondary amines with intramolecular NH···O hydrogen bonds were investigated by experimental and theoretical methods, considering a large number of compounds and covering a wide range of stretching wavenumbers. The assignment of the NH stretching transitions in the experimental IR spectra was, in several instances, supported by measurement of the corresponding ND wavenumbers and by correlation with the observed NH proton chemical shifts. The observed wavenumbers were correlated with theoretical wavenumbers predicted with B3LYP density functional theory, using the basis sets 6-311++G(d,p) and 6-31G(d) and considering the harmonic as well as the anharmonic VPT2 approximation. Excellent correlations were established between observed wavenumbers and calculated harmonic values. However, the correlations were non-linear, in contrast to the results of previous investigations of the corresponding OH···O systems. The anharmonic VPT2 wavenumbers were found to be linearly related to the corresponding harmonic values. The results provide correlation equations for the prediction of NH stretching bands on the basis of standard B3LYP/6-311++G(d,p) and B3LYP/6-31G(d) harmonic analyses, with standard deviations close to 38 cm−1. This is significant because the full anharmonic VPT2 analysis tends to be impractical for large molecules, requiring orders of magnitude more computing time than the harmonic analysis.

1. Introduction

It is well known that hydrogen-bonded linkages play major roles in a variety of areas in chemistry and molecular biology, and the investigation of such linkages by spectroscopic procedures is a subject of current interest [1]. Historically, IR absorption spectroscopy has been the most important spectroscopic tool in the investigation of hydrogen-bonded systems, typically involving OH···O and NH···O linkages [2,3,4]. The corresponding OH and NH stretching frequencies are thus indicative of the hydrogen bond strength [5]. However, the assignment of these bands in the measured IR spectra is frequently difficult because of overlap with signals due to traces of water or CH stretching vibrations. In systems with strong hydrogen bonds, the situation is further complicated by the influence of anharmonic effects, leading to band broadening and distribution of the intensity associated with the OH or NH stretching motion over several vibrational modes. In many cases, a specific OH or NH stretching band may be difficult to identify in the experimental IR spectrum [6,7,8,9,10].
The possibility to predict the vibrational transitions of hydrogen-bonded systems by theoretical methods has been of interest for decades [11]. Today, advanced procedures such as coupled-cluster (CCSD(T)) calculations can predict vibrational wavenumbers for small molecules within 10 cm−1 of the experimental values [12]. However, this level of theory is not feasible for large molecules, and in general, approximate methods must be applied. Most calculations of vibrational frequencies are performed within the harmonic approximation [13,14]. Scott and Radom [14] and Wong [15] investigated the harmonic vibrational frequencies obtained by a variety of calculational procedures for a large test set of molecular vibrations. They found that density functional theories (DFT) [13,16] such as B3LYP [17,18] and B3PW91 [17,19] led to the most successful correlations between observed and calculated vibrational wavenumbers. With a modest basis set such as 6-31G(d) and using a semiempirical scale factor close to 0.96, the application of these procedures resulted in an overall root-mean-square (RMS) error equal to 34 cm−1 [14,15]. Harmonic wavenumbers calculated by DFT procedures (in particular B3LYP) have thus been used to support the vibrational assignments in numerous IR spectroscopic investigations.
However, as indicated above, the harmonic approximation tends to fail for strongly hydrogen-bonded systems. A study was performed some time ago of a series of OH···O systems including weak, strong, and very strong intramolecular hydrogen bonds, with OH stretching wavenumbers ranging from 3600 to 1900 cm−1 [20,21]. Standard B3LYP harmonic analyses with the usual scale factors led to the prediction of too large OH stretching wavenumbers for systems with strong and short hydrogen bonds, evidently due to lowering of the wavenumbers by anharmonic effects. On the other hand, application of the VPT2 anharmonic approximation developed by Barone et al. [22,23] overestimated the anharmonic lowering of the OH stretching wavenumbers, leading to predictions of much too low wavenumbers for strong hydrogen bonds, for example, almost 900 cm−1 too low for nitromalonamide enol with B3LYP/6-31G(d) and more than 1000 cm−1 too low for dibenzoylmethane enol with B3LYP/cc-pVDZ [20,21,24,25]. Fortunately, a satisfactory linear correlation was established between observed OH stretching wavenumbers and calculated harmonic values in the complete experimental range from 3600 to 1900 cm−1, thereby enabling a convenient prediction of effective OH stretching band centers from the results of a standard harmonic analysis [20,21].
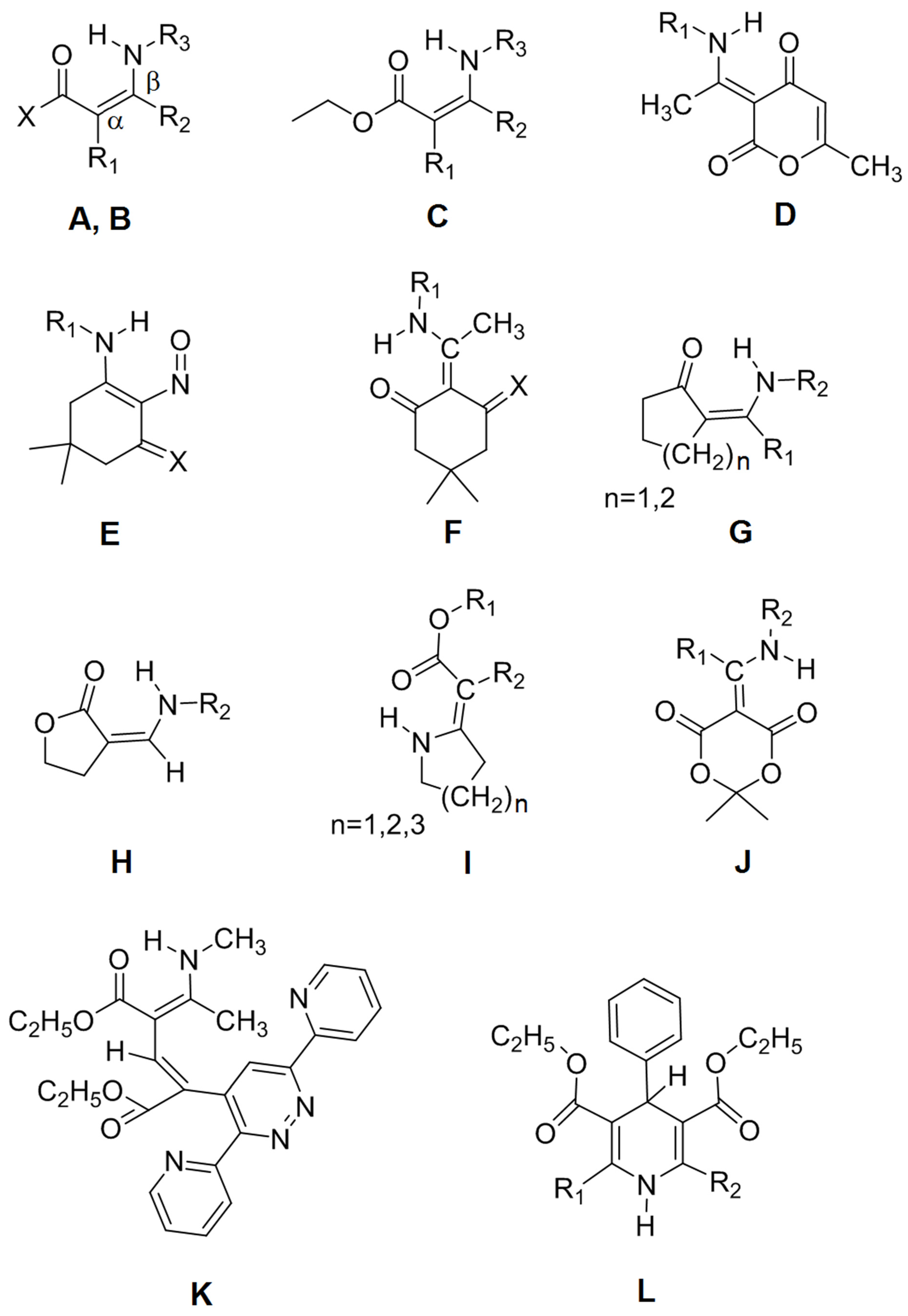
Molecules 26 07651 sch001 550
Scheme 1. General structures of the investigated compounds. For substituents and names, see Table 1.
Scheme 1. General structures of the investigated compounds. For substituents and names, see Table 1.
Molecules 26 07651 sch001
Table
Table 1. The compounds investigated in this study (for type, etc., see Scheme 1).
Table 1. The compounds investigated in this study (for type, etc., see Scheme 1).
No.TypeR1R2R3XName
1AHHt-ButylH(Z)-3-(tert-butylamino)acrylaldehyde
2AHHEthylCH3(Z)-4-(ethylamino)but-3-en-2-one
3AHHEthylCF3(Z)-4-(ethylamino)-1,1,1-trifluorobut-3-en-2-one
4ACH3HCH3CF3(Z)-1,1,1-trifluoro-3-methyl-4-(methylamino)but-3-en-2-one
5AHNO2CH3CH3(E)-4-methylamino-4-nitrobut-3-en-2-one
6BHCH3Ph (phenyl)CH3(Z)-4-(phenylamino)pent-3-en-2-one
7BHCH3p-ClPhPh(Z)-3-(4-chlorophenylamino)-1-phenylbut-2-en-1-one
8BHCH3o-CH3PhCH3(Z)-4-(o-tolylamino)pent-3-en-2-one
9BHCH3o-FPhCH3(Z)-4-(2-fluorophenylamino)pent-3-en-2-one
10BHCH3o-ClPhCH3(Z)-4-(2-chlorophenylamino)pent-3-en-2-one
11BHCH32,6-diCH3PhCH3(Z)-4-(2,6-dimethylphenylamino)pent-3-en-2-one
12BHCH3CH3CH3(Z)-4-(methylamino)pent-3-en-2-one
13BHPhIsopropylCF3(Z)-1,1,1-trifluoro-4-(isopropylamino)-4-phenylbut-3-en-2-one
14BCH3CH3CH3CH3(Z)-3-methyl-4-(methylamino)pent-3-en-2-one
15BCH3CH3p-OCH3PhCH3(Z)-4-(4-methoxyphenylamino)-3-methylpent-3-en-2-one
16CHCH3Ph-(Z)-ethyl 3-(phenylamino)but-2-enoate
17CHCH3CH3-(Z)-ethyl 3-(methylamino)but-2-enoate
18CCH3CH3Ph-(Z)-ethyl 2-methyl-3-(phenylamino)but-2-enoate
19CCH3CH3CH3-(Z)-ethyl 2-methyl-3-(methylamino)but-2-enoate
20CCH3CH3CH2Ph-(Z)-ethyl 3-(benzylamino)-2-methylbut-2-enoate
21CHCH3CH2Ph-(Z)-ethyl 3-(benzylamino)but-2-enoate
22DCH2CH2NH2---(E)-3-(1-(2-aminoethylamino)ethylidene)-6-methyl-2H-pyran-2,4(3H)-dione
23Dp-CH3OPh---(E)-3-(1-(4-methoxyphenylamino)ethylidene)-6-methyl-2H-pyran-2,4(3H)-dione
24Dp-ClPh---(E)-3-(1-(4-chlorophenylamino)ethylidene)-6-methyl-2H-pyran-2,4(3H)-dione
25Em-CH3OPh---5,5-dimethyl-3-(m-anisidino)-2-nitroso-2-cyclohexen-1-one
26EPh---5,5-dimethyl-3-anilino-2-nitroso-2-cyclohexen-1-one
27FCH3---5,5-dimethyl-2-(1-(methylamino)ethylidene)cyclohexane-1,3-dione
28FIso-propyl---2-(1-(isopropylamino)ethylidene)-5,5-dimethylcyclohexane-1,3-dione
29FPh---5,5-dimethyl-2-(1-(phenylamino)ethylidene)cyclohexane-1,3-dione
30GHCH3-n = 1(Z)-2-((methylamino)methylene)cyclopentanone
31GCH3CH3-n = 1(Z)-2-(1-(methylamino)ethylidene)cyclopentanone
32GHBu-n = 2(Z)-2-((butylamino)methylene)cyclohexanone
33HCH3---(E)-3-((methylamino)methylene)dihydrofuran-2(3H)-one
34HPh---(Z)-3-((phenylamino)methylene)dihydrofuran-2(3H)-one
35IEtCOOEt-n = 1diethyl 2-(pyrrolidin-2-ylidene)malonate
36IEtCOOEt-n = 2diethyl 2-(piperidin-2-ylidene)malonate
37IEtCOOEt-n = 3diethyl 2-(azepan-2-ylidene)malonate
38JCH3CH3--2,2-dimethyl-5-(1-(methylamino)ethylidene)-1,3-dioxane-4,6-dione
39JEtCH2COOEt--ethyl 2-(1-(2,2-dimethyl-4,6-dioxo-1,3-dioxan-5-ylidene)propylamino)acetate
40K----(2E,4Z)-diethyl 2-(3,6-di(pyridin-2-yl)pyridazin-4-yl)-4-(1-(methylamino)-ethylidene)pent-2-enedioate
41LCH2OCOCH3CH2OCOCH3--diethyl 2,6-bis(acetoxymethyl)-4-phenyl-1,4-dihydropyridine-3,5-dicarboxylate
42LCH3CH2OCOCH3--diethyl 2-(acetoxymethyl)-6-methyl-4-phenyl-1,4-dihydropyridine-3,5-dicarboxylate
43LCH3CH3--diethyl 2,6-dimethyl-4-phenyl-1,4-dihydropyridine-3,5-dicarboxylate
44BHCH3p-PhCOOEtCH3(Z)-ethyl 4-(4-oxopent-2-en-2-ylamino)benzoate
45BCH3CH3PhCH3(Z)-3-methyl-4-(phenylamino)pent-3-en-2-one
Table
Table 2. Theoretical NH stretching wavenumbers (cm−1; Harm = harmonic, Anh = VPT2 anharmonic) and NH bond lengths RNH (Å) computed with B3LYP. Observed or estimated wavenumbers νNH (cm−1) and observed NH proton chemical shifts δNH (ppm). Entries in italics indicate wavenumbers predicted by Equations (1) and (2).
Table 2. Theoretical NH stretching wavenumbers (cm−1; Harm = harmonic, Anh = VPT2 anharmonic) and NH bond lengths RNH (Å) computed with B3LYP. Observed or estimated wavenumbers νNH (cm−1) and observed NH proton chemical shifts δNH (ppm). Entries in italics indicate wavenumbers predicted by Equations (1) and (2).
Compound 16-31G(d)6-311++G(d,p)Observed
RNHHarmAnhP(Harm)2HarmP(Harm)3νNHδNHRef.
11.0236341032083247342432513195-[26]
21.0224340431763242340032323190-[27]
31.0238341132083248342232503222-[28]
41.022134323214326534413264320610.21[29]
51.0270334130793182336232003180-[30]
61.0303327429323101324430713031 4,512.48[31]
71.031532092909300132423068305613.07[32]
81.0305326629733090325330823058 512.34[33]
91.0307326829433093325830893063 512.25[33]
101.03063276-3104326030913047 512.42[33]
111.03113266-3090327431083058 511.95[33]
121.026333423052318333493188317110.70[9]
131.02723340-318133443183320511.11[34]
141.02653322-3161331131493041 511.86-
151.03223226-3030320530173004 4-[35]
161.0244338231473223338832233254 410.39[7]
171.01943432324732653469328332958.46[7]
181.02483363-320533603198---
191.01993442-32723439326332629.14-
201.02153425-32593422325032829.66 6[36]
211.02173427-3261344232653289 78.95[37]
221.037731382782286031022843287014.18[38]
231.042230592574265330222665261015.60[38]
241.044030272591255129782548260215.90[38]
251.0424305025742626304827282560 818.41[38]
261.0418304825842619303126872340 818.35[38]
271.033032082817299931812981-13.3[7]
281.0345317228142932314029132900 913.6[7]
291.038631242743282830772792276015.2[7]
301.02313420-325534403263-8.84[39]
311.02453367-320933743210-10.26[40,41]
321.0253338131213222339032243160-[27]
331.01183599-33593613336233026.60[42]
341.02163449-32773466328133149.05[42]
351.01943481-32993488329633179.52[42]
361.02363385-322633723209324210.08[42]
371.02223405-32433411324132808.83[43]
381.02623341-318233313170322411.32[44]
391.02923318-315733043142317211.60[44]
401.02173415-3251341432443270-[45]
411.01483558-33413559333634037.7[46]
421.01533541-33333551333233476.6[46]
431.00923631-33723636337133365.6[46]
441.03083266-3090323730623047 512.64[47]
451.03223226-3030320530172975 513.46[48]
1 See Table 1. 2 Wavenumbers predicted by Equation (2). 3 Wavenumbers predicted by Equation (1). 4 Not assigned as NH stretching in the referenced paper. 5 Estimated values (Table 3), not included in the correlation analyses. 6 NMR data from Ref. [36]. 7 Value varies slightly with solvent. 8 Not included in the correlation analyses, see Section 3.1. 9 Approximate.
Table
Table 3. NH and ND stretching wavenumbers, νNH and νND (cm−1), measured in CCl4 solution. Several νNH values are estimated on the basis of the νNH/νND ratio (footnote 2).
Table 3. NH and ND stretching wavenumbers, νNH and νND (cm−1), measured in CCl4 solution. Several νNH values are estimated on the basis of the νNH/νND ratio (footnote 2).
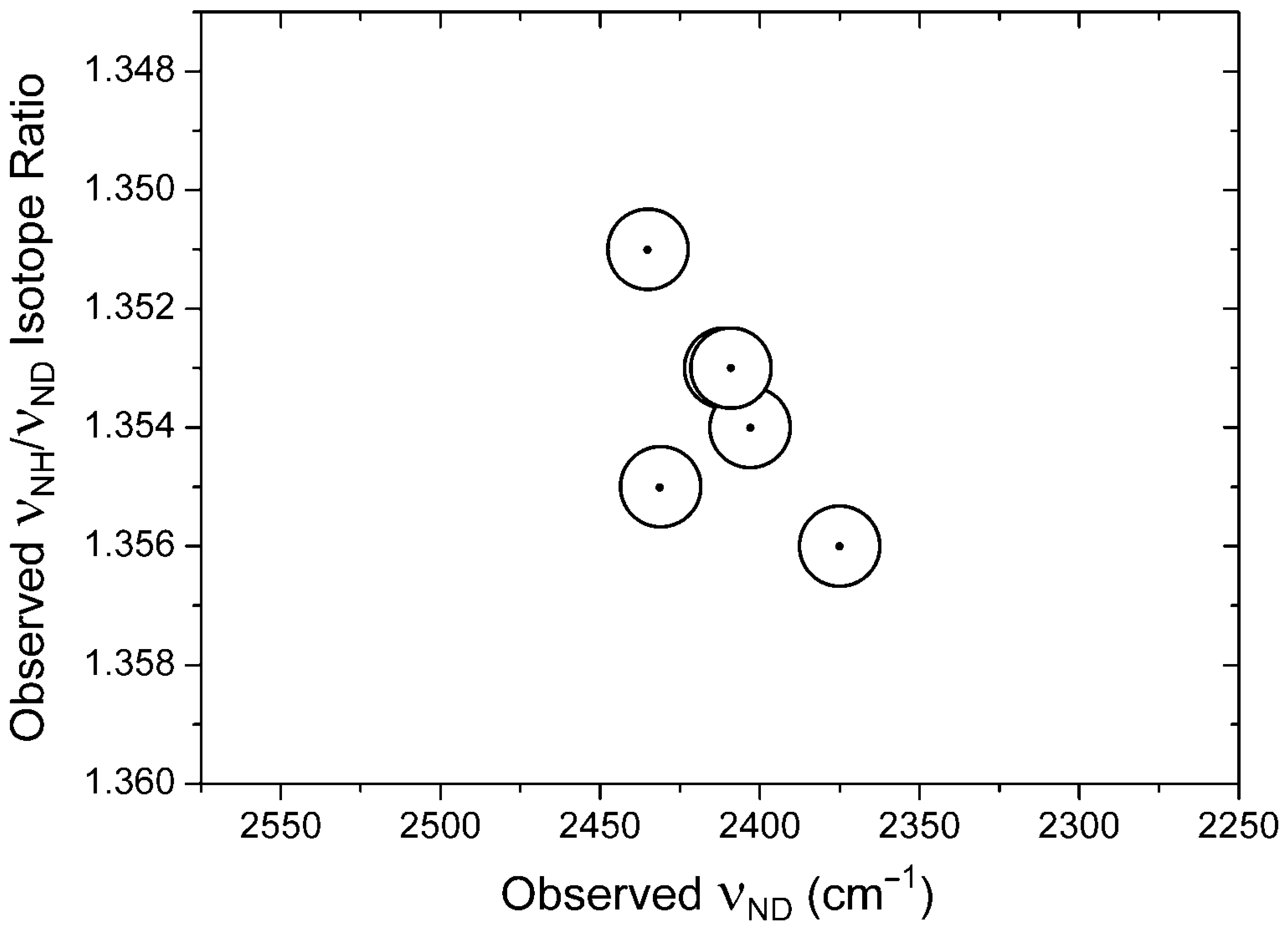
Compound 1νNHνND
63031 22262
83058 22280
93063 22286
103047 22274
113058 22282
143041 22270
163254, 3185 32403
1732952431
1932622411
2032592409
2132892435
443047 22274 4
452975 22220
1 See Table 1. 2 Estimated from the observed νND, assuming νNH/νND = 1.34 (see Section 4). 3 Two bands are observed [7]; the larger wavenumber is used in the correlation analyses. 4 Ref. [48].
In this publication we present the results of a similar investigation of a large number of secondary amines with intramolecular NH···O hydrogen-bonded linkages. This type of linkage has the advantage that a wide range of compounds can be investigated because, in general, systems of the type NH···O=C with an intervening double bond are not tautomeric, in contrast to the corresponding OH···O=C systems. In those cases where the compounds are tautomeric, the data are not included. The structures and names of the investigated compounds are listed in Scheme 1 and Table 1. The emphasis of our study is on the NH stretching bands of the NH···O linkages, covering wavenumbers in the range 3300–2600 cm−1. The aim is to develop simple correlation tools for the prediction of effective NH stretching wavenumbers for NH···O systems, to be useful in those cases where the NH stretching bands are not easily identified in the experimental spectra.
For the purpose of this investigation, a number of substances were synthesized and measured, but most spectroscopic data are quoted from the literature (Table 2). Vibrational assignments were in several cases supported by the investigation of deuterated compounds (NH hydrogen exchanged with deuterium). Further support was obtained by considering the correlation of NH stretching wavenumbers with 1H amine chemical shifts, following the original suggestion by Dudek [7]. Calculations of vibrational transitions were carried out with the B3LYP functional, using two different basis sets, and were performed both in the standard harmonic approximation and in the anharmonic VPT2 approximation. As we shall show, excellent correlations between observed and calculated NH stretching wavenumbers are obtained, but in contrast to the previous results for OH···O systems [20,21], the correlations are non-linear. Additional information is provided as Supplementary Materials, referred to in the ensuing text as Figures S1–S21.

2. Materials and Methods

2.1. Materials

The following substances were synthesized: 6, 14, 16, 17, 19, and 45. For details and characterization, see Figure S21. Deuterated compounds were prepared by dissolving the substances in CCl4 with a drop of trimethylamine [48]. After the addition of D2O (1 cm3), the mixture was stirred for 24 h, and the organic layer was separated and dried using Na2SO4.

2.2. Spectroscopy

The IR spectra of 6, 8, 9, 10, 11, 14, 16, 17, 19, 44, and 45 and of their deuterated analogs were recorded in the 4000–400 cm−1 region with a spectral resolution of 2 cm−1 by averaging the results of 10 scans on a PerkinElmer Spectrum 2000 FTIR spectrophotometer (Figures S1–S11). The compounds were measured in KBr tablets and when possible also in CCl4 solutions. The CCl4 solutions were dried with Na2SO4 to remove traces of water from the samples. An example of the recorded spectra is shown in Figure 1, which displays the absorbance curves for normal and deuterated (Z)-ethyl 3-(methylamino)but-2-enoate (17) in the range 3800 to 900 cm−1. NMR spectra were recorded on Bruker Ultrashield Plus 500 MHz and Bruker Avance 3 spectrometers using CDCl3 as a solvent. For details and spectra, see Figure S21.

2.3. Calculational Details

Quantum chemical calculations were performed with the Gaussian 09 [49] and the Gaussian 16 [50] software packages producing similar results. Geometry optimizations and standard harmonic analyses were carried out in the gas phase with B3LYP density functional theory (DFT) [17,18] using the basis sets 6-311++G(d,p) and 6-31G(d) [13,49,50]. Several calculations using 6-31G(d) were carried out also with the anharmonic VPT2 approximation [22,23] (freq = anharmonic). The computed NH stretching wavenumbers for the compounds 1–45 are listed in Table 2. Detailed listings of results for 17 are provided as Figure S20, considering fundamentals in the range 800–3500 cm−1. For a selection of compounds (1, 6, 16, 17, 23, 29, and 32) covering a broad range of NH stretching wavenumbers, additional calculations were performed by using the B3PW91 functional [17,19]. Hydrogen bond energies were estimated using the AIM 2000 software at the B3LYP/6-31G(d) level [51] (Figures S17 and S18).

3. Results

3.1. Experimental NH Stretching Wavenumbers

Measured or estimated NH stretching wavenumbers for the compounds 1–45 are listed in Table 2 and Table 3. A subset of these compounds, the enaminones, has been thoroughly investigated by Gilli et al. [38]. NH stretching wavenumbers for the compounds 6, 8, 9, 11, 14, 44, and 45 were estimated by measuring the IR spectra of the deuterated species and multiplying the observed ND stretching wavenumber with 1.34 (Table 3; see the discussion in Section 4). In these compounds, the NH stretching band appears to be overlapped by the CH stretching bands. The approximate wavenumbers derived in this manner are not included in the correlation analyses.
As a check of the assignments, the experimental NH stretching frequencies are correlated with the observed NH chemical shifts listed in Table 2. The available 26 data points are shown in Figure 2. A non-linear correlation is evident, in contrast to the linear relationships established in the literature, in particular by Dudek [7]. The points for the nitroso compounds 25 and 26 are outliers; they are not included in the correlation analysis (see Section 4). To a good approximation, the remaining 24 points follow an exponential function, leading to RMS standard deviation (SD) = 34.3 cm−1 (Figure 2). A similar fit of the data is obtained with a second-order polynomial function, but the exponential function is preferred because of a more satisfactory asymptotical behavior. The correlation equation in Figure 2 can be used to predict NH stretching wavenumbers from the observed chemical shifts.

3.2. Calculations

As pointed out in the Introduction Section, DFT calculations with the B3LYP functional are frequently used to support vibrational assignments in IR spectroscopic investigations. An example is given in Figure 3, which shows the scaling correlation of observed vibrational wavenumbers for the ester 17 and harmonic wavenumbers calculated with B3LYP/6-31++G(d,p), considering all fundamental wavenumbers in the range 800–3500 cm−1 (see Figures S19 and S20 for details). A good fit is obtained, even for the NH stretching vibration observed close to 3300 cm−1 (Figure 1, Table 2). The intramolecular hydrogen bond in 17 is weak (Figure S20) and particular anharmonic effects are apparently of minor significance. However, when systems with stronger NH···O hydrogen-bonding are considered, the importance of anharmonic effects increases. Mroginski et al. [52] studied compounds with strong NH···N hydrogen bonds and found that separate scaling of the calculated NH force constants was required in order to reproduce the observed IR bands. Figure 4 shows the correlation of observed NH stretching wavenumbers and calculated harmonic values for the present NH···O linkages, yielding a non-linear correlation that strongly deviates from the linear one in Figure 3. The exponential correlation equation obtained on the basis of the data listed in Table 2 is given in Equation (1):
B3LYP/6-311++G(d,p):
P(Harm) = 3509 − 6.310 × 106·exp(−Harm/338.8)
(32 points: R2 = 0.964, SD = 38.2 cm−1)
Harm is the calculated harmonic wavenumber, and P(Harm) is the value predicted with Equation (1). An SD close to 38 cm−1 seems quite acceptable, in view of the uncertainty of many of the experimental wavenumbers and the influence of different environmental effects. Results obtained with the much smaller basis set 6-31G(d) lead to a very similar correlation (Figure S12); the exponential correlation equation is given in Equation (2) as follows:
B3LYP/6-31G(d):
P(Harm) = 3470 − 6.714 × 107·exp(−Harm/270.3)
(32 points: R2 = 0.965, SD = 38.1 cm−1)
In fact, the wavenumbers obtained with B3LYP/6-31G(d) and B3LYP/6-311++G(d,p) are linearly related with R2 = 0.991, SD = 15 cm−1 (S13). For predictive purposes, the cheaper B3LYP/6-31G(d) procedure is just as efficient as B3LYP/6–311++G(d,p).
The non-linearity of the present correlations is unexpected in view of the previous results for OH···O systems where linear relationships between observed and calculated OH stretching wavenumbers were obtained [20,21]. We carried out VPT2 calculations [22,23] for a series of 21 NH···O species (Table 2), comprising weak as well as strong hydrogen-bonding. However, as shown in Figure S14, the anharmonic NH stretching wavenumbers are essentially linearly related to the harmonic ones (R2 = 0.986, SD = 27 cm−1) and do not explain the non-linearity of the present correlations. On the other hand, the VPT2 anharmonic wavenumbers are numerically much closer to the experimental values than the harmonic ones, particularly for compounds with strong hydrogen bonds. This is in contrast to the results for OH···O systems, in which the VPT2 approximation significantly underestimated the OH stretching wavenumbers for strongly hydrogen-bonded systems (see above) [20,21,24,25]. Additional calculations using the B3PW91 functional [17,19] were performed for the compounds 1, 6, 16, 17, 23, 29, and 32, covering a broad range of NH stretching wavenumbers. The computed harmonic wavenumbers are essentially linearly related to those obtained with B3LYP (R2 = 0.9999, SD = 2.6 cm−1).

3.3. Structures

The calculated molecular geometries evidently play important roles in the predicted NH stretching wavenumbers for the present NH···O linkages. An excellent linear correlation is observed for calculated wavenumbers and calculated NH bond lengths: R2 = 0.988, SD = 15 cm−1 (Figure S16). Much cruder correlations are found between wavenumbers and N····O and H···O distances. This is similar to the situation observed for OH···O systems [24].
Most of the investigated compounds have substituents with torsional degrees of freedom. In order to estimate the possible influence on the computed NH stretching wavenumber, calculations on several compounds were performed with consideration of different conformations. In general, the influence of the conformation is found to be of minor importance for the calculated wavenumber. For example, as shown in Figure S19, four conformational equilibrium geometries with different energies are located for 17, but the same NH stretching wavenumber was calculated for all four structures.
The N-phenyl groups present in several of the investigated compounds were calculated to be twisted out of the plane of the –NH···O– moieties, and substituents at the phenyl ring were expected to have a minor effect on the NH stretching frequency. This is in agreement with the predicted and observed wavenumbers, except in the case of the observed values for 25 and 26 (see Section 4). Some of the enaminones and enaminoesters may occur both as E and Z forms, and the ratio between the two may depend on the solvent [39]. These and other points are discussed in the following section.

4. Discussion

NH stretching bands in compounds with weak NH···O hydrogen bonds are generally easy to identify (e.g., Figure 1), but in compounds with stronger hydrogen bonds, the band may be overlapped by CH stretching or other absorption bands. In those cases, deuteration is frequently a good tool. Provided an adequate conversion factor is known, the NH stretching wavenumber (νNH) can be estimated from the observed ND band (νND). The isotope ratio νNH/νND was originally investigated by Novak [53] and more recently by Sobczyk et al. [54], showing a distinct dependence on the NH stretching frequency. However, in both cases, the majority of the data are from intermolecular hydrogen bonds. The intramolecular data reported by Sobczyk et al. [54] are for protonated dimethylaminonaphtalenes, DMANs, quite different from the compounds considered in this paper.
Figure 5 shows a plot of the measured νNH/νND ratios against νND for a series of C-type esters with relatively weak hydrogen bonds. These results do not necessarily follow the trends described by Novak [53] and by Sobczyk et al. [54]. The average values of νNH/νND and νND for these compounds are about 1.354 and 2400 cm−1, respectively. For the compounds of B type, such as 6, 8, 9, 10, 11, 14, 44, and 45, the observed values of νND are lower (Table 3), amounting to an average close to 2265 cm−1. This indicates stronger hydrogen bonding, and according to the direction suggested by Novak [53], we expect a smaller effective value of the νNH/νND ratio. We shall tentatively assume the value νNH/νND = 1.34 for these compounds, leading to the νNH wavenumbers listed in Table 3. The wavenumbers obtained in this manner are in the range 2975–3063 cm−1 (they are not included in the correlation analyses). This prediction supports the assumption that these NH stretching bands are overlapped by absorption due to CH stretching transitions. The predicted wavenumbers are consistent with the observed NH chemical shifts close to 12 ppm (Table 2), indicating wavenumbers around 3100 cm−1 according to the correlation in Figure 2. They are also in good agreement with the semiempirical P(Harm) predictions based on Equations (1) and (2) (Table 2).
In order to establish useful correlations between observed and theoretical NH stretching wavenumbers νNH, it is crucial to have reliable experimental assignments. Correlations between νNH and the NH proton chemical shift δNH have been demonstrated by Dudek [7] and by Gilli et al. [38]. A criterion for including data in the correlation analyses could therefore be that the experimental NH stretching wavenumbers should be consistent with the general correlation between experimental NH stretching frequencies and experimental NH chemical shifts. The plot of νNH wavenumbers vs. δNH chemical shifts is shown in Figure 2. The correlation is non-linear, in contrast to the linear relationship obtained for a range of related systems by Dudek [7]. Probably the extension of the range of compounds to include species of the types H, J, and L has led to the non-linear correlation. However, the points for 25 and 26 are striking outliers, and the wavenumbers for these compounds are not included in the correlation analyses. The δNH values reported [38] for these nitroso derivatives are exceptionally large (Table 2). The reason for the deviation from the correlation curve could be anisotropy effects, such contributions have recently been investigated in similar compounds [56]. Tautomerism could be another reason for a poor fit; deuterium isotope effects on 13C chemical shifts are good tests for tautomerism [57]. Derivatives of 4-amino-3-pentene-2-one (APO), linear and cyclic enaminones, and lactones have been shown to be non-tautomeric [39]. Some enaminones, esters, and lactones may exist both as E and Z forms; the assumed configurations of the investigated compounds are indicated in Table 1.
It is apparent that structure plays a great role in determining the NH stretching frequencies. The plot in Figure S16 shows a very tight correlation between νNH and the calculated NH bond length. In general, the NH stretching wavenumbers will depend on the strength of the hydrogen bond. The correlation of observed wavenumbers with the hydrogen bond strengths estimated by the Espinosa method [58] leads to SD = 64–76 cm−1, depending on the choice of fitting function (Figures S17 and S18).
In the following, we discuss a number of literature data using the established correlation equations relating observed and calculated NH stretching wavenumbers (Equations (1) and (2)). A characteristic example is 4-(methylamino)pent-3-en-2-one (12). For the observed NH stretching wavenumber, Dudek [7] reported 3100 cm−1, while Raissi et al. [9] reported 3171 cm−1, and Kidwai et al. [8] assigned a feature at 3263 cm−1. As indicated by the P(Harm) values listed in Table 2, Equations (1) and (2) predict 3188 and 3183 cm−1 for 12, pointing to the value 3171 cm−1 published by Raissi et al. [9].
Kidwai et al. [8] have published IR data for several β-enaminones. For (Z)-4-(phenylamino)pent-3-en-2-one (6) and (Z)-4-(p-nitrophenylamino)pent-3-en-2-one, they reported NH stretching wavenumbers equal to 3000 and 3362 cm−1, respectively. These assignments imply that the substitution of a nitro group in the para position of the N-phenyl ring of 6 shifts the NH stretching wavenumber by more than 300 cm−1. For the p-nitro derivative, we obtain with B3LYP/6-311++G(d,p) and B3LYP/6-31G(d) the harmonic wavenumbers 3229 and 3247 cm−1, respectively, leading to the P(Harm) predictions 3051 and 3063 cm−1. The present predictions indicate that the wavenumber 3362 cm−1 published by Kidwai et al. for (Z)-4-(p-nitrophenylamino)pent-3-en-2-one is much too large.
A number of other discrepancies are found in the literature. A large one is found for the compounds of D type (R = substituted phenyl), 23 and 24. Gilli et al. [38] report NH stretching frequencies close to 2600 cm−1, whereas Benkheira and Amari [59] report 3390 cm−1. Benkheira and Amari discussed the possibility of a tautomeric equilibrium and concluded that the NH form is dominant, as is also assumed by Gilli et al. The NH chemical shifts are 15.6–15.9 ppm. Hence, the NH stretching frequency 3390 cm−1 reported by Benkheira and Amari seems much too high; the correlation in Figure 2 suggests wavenumbers around 2600 cm−1. This prediction is consistent with the semiempirical P(Harm) values (Table 2). Hence, the solid-state value reported by Gilli et al. [38] close to 2600 cm−1 seems realistic.
As mentioned above, the experimental wavenumbers for 25 and 26 are not included in the correlation analyses. The latter compound differs from the former only in the substitution of a methoxy group in the meta position of the N-phenyl ring, which is twisted out of the plane. Very similar NH stretching wavenumbers were computed and predicted for the two compounds (Table 2). However, the reported wavenumber for 26 is 220 cm−1 lower than that of 25 [38], a difference that seems hard to explain. Unfortunately, the IR spectra of the two compounds were not published.
Kolev and Angelov [60] investigated 1,1,1-trichloro-3-(1-phenethylamino-ethylidene)-pentane-2,4-dione (Scheme 1, Type A: R1 = (C=O)CCl3, R2 = CH3, R3 = CH2CH2Ph, X = CH3). They assigned the observed IR spectrum to the E configuration and reported νNH = 3414 cm−1 in the solid state and δNH = 12.03 ppm. These values yield a point far from the correlation line in Figure 2. With δNH = 12.03 ppm, the correlation equation in Figure 2 predicts νNH = 3127 cm−1, indicating a relatively strong hydrogen bond. With B3LYP/6-311++G(d,p) and B3LYP/6-31G(d), we obtain harmonic NH stretching wavenumbers equal to 3272 and 3286 cm−1, respectively. With these values, Equations (1) and (2) predict 3106 and 3117 cm−1, consistent with the value indicated by correlation with the δNH value. Unfortunately, Kolev and Angelo [59] did not publish this region of the experimental spectrum.
An NH stretching frequency of 3317 cm−1 was recently reported for ethyl 2-(benzylamino)cyclopent-1-encarboxylate [36]. Our B3LYP/6-311++G(d,p) and B3LYP/6-31G(d) calculations yield 3451 and 3440 cm−1, respectively. This leads to P(Harm) values equal to 3271 and 3271 cm−1, in fair agreement with the experimental result.
The NH stretching wavenumbers for 27, 30, and 31 have apparently not been determined, but δNH values close to 13.3, 8.84, and 10.26 ppm have been published (Table 2) [7,39,40,41]. On the basis of the correlation in Figure 2, νNH values equal to 3007, 3295, and 3238 cm−1 can be estimated, respectively, in satisfactory consistency with the predicted P(Harm) values listed in Table 2.
In a number of papers [8,31,35,43,55], enaminones have been studied, but the NH stretching frequencies have not been assigned for all compounds. P(Harm) values predicted with Equations (1) and (2) may be of help in analyzing these spectra.

5. Conclusions

In this work, we considered NH stretching wavenumbers for a large number of species with intramolecular NH···O hydrogen bonding, ranging from weakly to strongly bonded systems. Additionally, a few systems with no intramolecular hydrogen bonding were included. The assignment of the NH stretching bands for a number of compounds was supported by measurements of the ND stretching wavenumbers of the deuterated species. The assignments were also supported by consideration of the correlation between observed NH stretching wavenumber and NH proton chemical shift. This correlation was well described by an exponential function (SD = 34 cm−1), in contrast to the linear relationships found in the literature for related systems.
Excellent exponential relationships were also established between observed NH stretching wavenumbers and harmonic wavenumbers predicted by B3LYP/6-31G(d) and B3LYP/6-311++G(d,p) calculations. With SD = 38 cm−1, these semiempirical correlation equations should be of considerable predictive value, as demonstrated in the Discussion Section of this article (Section 4). This result is significant because rigorous theoretical procedures exceeding the harmonic approximation, such as the VPT2 procedure, tend to be impractical for large molecules, requiring orders of magnitude more computing time than the harmonic analysis.
The non-linearity of these relationships is in contrast to previous results for OH···O systems, which were characterized by corresponding linear relationships. We have presently no obvious explanation for the apparent difference between NH···O and OH···O systems. NH stretching wavenumbers computed with the anharmonic VPT2 approximation are found to be linearly related to the corresponding harmonic values, offering no explanation of the non-linearity of the present correlations. It would seem that more advanced theoretical calculations, beyond the VPT2 approximation, are called for.

Supplementary Materials

The following are available online, Figures S1–S11: IR spectra; Figures S12–S18: Correlation analyses; Figures S19 and S20: Detailed results for (Z)-ethyl 3-(methylamino)but-2-enoate (17); Figure S21: Materials section with synthesis, characterization and NMR spectra.

Author Contributions

Conceptualization, methodology, investigation, formal analysis, writing—original draft preparation, writing—review and editing, P.E.H.; investigation, formal analysis, writing—review and editing, M.V.; investigation, writing—review and editing, F.S.K.; conceptualization, methodology, investigation, formal analysis, visualization, writing—original draft preparation, writing—review and editing, J.S.-L. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by Ferdowsi University of Mashhad, Iran, providing sabbatical time for Mohammad Vakili at Roskilde University, Denmark.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors wish to thank Eva Marie Karlsen for her help in recording IR spectra.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hansen, P.E. Review: A Spectroscopic Overview of Intramolecular Hydrogen Bonds of NH…O,S,N Type. Molecules 2021, 26, 2409. [Google Scholar] [CrossRef] [PubMed]
  2. Pimentel, G.C.; McClellan, A.L. The Hydrogen Bond; W.H. Freeman: San Francisco, CA, USA, 1960. [Google Scholar]
  3. Vinograd, S.N.; Linnell, R.H. Hydrogen Bonding; Van Nostrand Reinhold: New York, NY, USA, 1971. [Google Scholar]
  4. Joesten, M.D.; Schaad, L.J. Hydrogen Bonding; Marcel Dekker: New York, NY, USA, 1974. [Google Scholar]
  5. Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, V.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Definition of the hydrogen bond (IUPAC Recommendation 2011). Pure Appl. Chem. 2011, 83, 1537–1641. [Google Scholar] [CrossRef]
  6. Tayyari, S.F.; Zeegers-Hyuskens, T.; Wood, J.L. Spectroscopic study of hydrogen bonding in the enol form of β-diketones—II. Symmetry of the hydrogen bond. Spectrochim. Acta A 1979, 35, 1289–1295. [Google Scholar] [CrossRef]
  7. Dudek, G.O. Spectroscopic Studies of Keto—Enol Equilibria. VIII. Schiff Base Spectroscopic Correlations. J. Org. Chem. 1965, 30, 548–552. [Google Scholar] [CrossRef]
  8. Kidwai, M.; Bhardwaj, S.; Misshra, N.K.; Bansal, V.; Kumar, A.; Mozumdar, S. A novel method for the synthesis of β-enaminones using Cu-nanoparticles as catalyst. Catal. Commun. 2009, 10, 1514–1517. [Google Scholar] [CrossRef]
  9. Raissi, H.; Moshfeghi, E.; Farzad, F. Vibrational assignment, structure and intramolecular hydrogen bond of 4-methylamino-3-penten-2-one. Spectrochim. Acta A 2005, 62, 1004–1015. [Google Scholar] [CrossRef]
  10. Hansen, B.K.V.; Winther, M.; Spanget-Larsen, J. Intramolecular hydrogen bonding. Spectroscopic and theoretical studies of vibrational transitions in dibenzoylmethane enol. J. Mol. Struct. 2006, 790, 74–79. [Google Scholar] [CrossRef]
  11. Hadži, D. (Ed.) Theoretical Treatment of Hydrogen Bonding; Wiley: Chichester, UK, 1997. [Google Scholar]
  12. Ferrari, B.C.; Bennett, C.J. A Comparison of Medium-Sized Basis Sets for the Prediction of Geometries, Vibrational Frequencies, Infrared Intensities and Raman Activities for Water. J. Phys. Conf. Ser. 2019, 1290, 012013. [Google Scholar] [CrossRef]
  13. Foresman, J.B.; Frisch, A.E. Exploring Chemistry with Electronic Structure Methods, 3rd ed.; Gaussian, Inc.: Wallingford, CT, USA, 2015. [Google Scholar]
  14. Scott, A.P.; Radom, L. Harmonic Vibrational Frequencies: An Evaluation of Hartree-Fock, Møller-Plesset, Quadratic Configuration Interaction, Density Functional Theory, and Semiempirical Scale Factors. J. Phys. Chem. 1996, 100, 16502–16513. [Google Scholar] [CrossRef]
  15. Wong, M.W. Vibrational frequency prediction using density functional theory. Chem. Phys. Lett. 1996, 256, 391–399. [Google Scholar] [CrossRef]
  16. Becke, A.D. Perspective: Fifty years of density-functional theory in chemical physics. J. Chem. Phys. 2014, 140, 18A301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  17. Becke, A.D. Density functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
  18. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
  19. Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
  20. Spanget-Larsen, J.; Hansen, B.K.V.; Hansen, P.E. OH stretching frequencies in systems with intramolecular hydrogen bonds. Harmonic and anharmonic analyses. Chem. Phys. 2011, 389, 107–115. [Google Scholar] [CrossRef]
  21. Hansen, P.E.; Spanget-Larsen, J. Prediction of OH Stretching frequencies in systems with intramolecular hydrogen bonds. J. Mol. Struct. 2012, 1018, 8–13. [Google Scholar] [CrossRef]
  22. Barone, V. Anharmonic vibrational properties by a fully automated second order pertubative approach. J. Chem. Phys. 2005, 122, 14108. [Google Scholar] [CrossRef]
  23. Barone, V.; Biczysko, M.; Bloino, J. Fully anharmonic IR and Raman spectra of medium-size molecular systems: Accuracy and interpretation. Phys. Chem. Chem. Phys. 2014, 16, 1759–1787. [Google Scholar] [CrossRef] [PubMed]
  24. Hansen, P.E.; Spanget-Larsen, J. Review: NMR and IR Investigations of Strong Intramolecular Hydrogen Bonds. Molecules 2017, 22, 552. [Google Scholar] [CrossRef] [Green Version]
  25. Hansen, P.E.; Jezierska, A.; Panek, J.; Spanget-Larsen, J. Theoretical Calculations Are a Strong Tool in the Investigation of Strong Intramolecular Hydrogen Bonds. In Molecular Spectroscopy: A Quantum Chemistry Approach; Ozaki, Y., Wójcik, M.J., Popp, J., Eds.; Wiley-VCH: Weinheim, Germany, 2019; Volume 1, Chapter 8; pp. 215–251. [Google Scholar]
  26. Dabrowski, J. IR Spectra and Structure of substituted unsaturated Carbonyl compounds. X. β-alkylaminoacroleins. J. Mol. Struct. 1969, 3, 227–233. [Google Scholar] [CrossRef]
  27. Dabrowski, J.; Dabrowska, U. Infrarotspektren und Struktur substituierter ungesättigter Carbonylverbindungen, VII. Enaminoketone mit starrer s-cis- und s-trans-Konformation und sekundär Aminogruppe. Chem. Ber. 1968, 101, 2365–2374. [Google Scholar] [CrossRef]
  28. Vdovenko, S.I.; Gerus, I.I.; Pagacz-Kostrzewa, M.; Wierzejewska, M.; Zhuk, Y.I.; Kukhar, V.P. Special feature of kinetics of ZcE isomerisation of β-N-methylaminovinyl trifluoromethyl ketone in Ar matrix exposed to UV radiation and spontaneous E⇆Z isomerization of α-methyl-β-N-methylaminovinyl trifloromethyl ketone. Spectrochim. Acta A 2018, 199, 130–140. [Google Scholar] [CrossRef]
  29. Vdovenko, S.I.; Gerus, I.I.; Zhuk, Y.I.; Kukhar, V.P.; Pagacz-Kostrzewa, M.; Wierzejewska, M.; Daniluc, C.-G. The conformation analysis of push-pull enaminones using FTIR and NMR spectroscopy and quantum mechanical calculations.VI. 4-N-Methyl-aminovinyl trifluoromethyl ketone and 3-methyl-2-N-methylaminovinyl trifluoromethyl ketone. J. Mol. Struct. 2017, 1128, 741–753. [Google Scholar] [CrossRef]
  30. Chiara, J.L.; Gómez-Sánchez, A.; Bellanato, J. Spectral properties and isomerism of nitroenamines. Part 4. β-Amino-α-nitro-α,β-unsaturated ketones. J. Chem. Soc. Perkin Trans. 2 1998, 8, 1797–1806. [Google Scholar] [CrossRef] [Green Version]
  31. Das, B.; Venkateswarly, K.; Majhi, A.; Reddy, M.R.; Reddy, K.N.; Rao, Y.K.; Ravikumar, K.; Sridhar, B. Highly efficient, mild and chemo- and stereoselective synthesis of enaminones and enamino esters using silica supported perchloric acid under solvent-free conditions. J. Mol. Catal. A 2006, 246, 276–281. [Google Scholar] [CrossRef]
  32. Patil, S.A.; Gonzalez-Flores, D.; Medina, P.A.; Dever, S.; Stentzel, M.; Popp, J.; Pineda, L.W.; Montero, M.L.; Ziller, J.W.; Fahlman, B.D. Synthesis, Characterization and Crystal Structure of (Z)-3-(4-Chlorophenylamino)-1-Phenylbut-2-En-1-One. J. Chem. Crystallogr. 2012, 42, 543–548. [Google Scholar] [CrossRef]
  33. Zheglova, D.K.; Genov, D.G.; Bolvig, S.; Hansen, P.E. Deuterium Isotope Effects on 13C Chemical Shifts of Enaminones. Acta Chem. Scand. 1997, 51, 1016–1023. [Google Scholar] [CrossRef] [Green Version]
  34. Chipanina, N.N.; Oznobikhina, L.P.; Aksamentova, T.N.; Romanov, A.R.; Rulev, A.Y. Intramolecular hydrogen bond in the push-pull CF3-aminoenones: DFT and FTIR study, NBO analysis. Tetrahedron 2014, 70, 1207–1213. [Google Scholar] [CrossRef]
  35. Chen, X.; She, J.; Shang, Z.; Wu, J.; Wu, H.; Zhang, P. Synthesis of Pyrazoles, Diazepines, Enaminones, and Enamino Esters using 12-Tungstophosporic Acid as a Reusable Cata-lyst in Water. Synthesis 2008, 21, 3478–3486. [Google Scholar]
  36. Wang, D.; Zhang, L.; Luo, S. Visible Light Promoted β-C–H Alkylation of β-Ketocarbonyls via a β-Enaminyl Radical Intermediate. Chin. J. Chem. 2018, 36, 311–320. [Google Scholar] [CrossRef]
  37. Sánchez, A.G.; Valle, A.M.; Bellanato, J. Infrared Absorption and Isomerism of 3-Aminocrotonic Esters. Part I. 3-(Alkylamino)crotonic Esters. J. Chem. Soc. B: Phys. Org. 1971, 2330–2335. [Google Scholar] [CrossRef]
  38. Gilli, P.; Bertolasi, V.; Ferretti, V.; Gilli, G. Evidence for Intramolecular N-H···O Resonance-Assisted Hydrogen Bonding in β-Enaminones and Related Heterodienes. A Combined Crystal-Structural, IR and NMR Spectroscopic, and Quantum-Mechanical Investigation. J. Am. Chem. Soc. 2000, 122, 10405–10417. [Google Scholar] [CrossRef]
  39. Hansen, P.E.; Bolvig, S.; Duus, F.; Petrova, M.V.; Kawecki, R.; Krajewski, R.; Kozerski, L. Deuterium Isotope Effects on 13C Chemical Shifts of Intramolecular Hydrogen-Bonded Olefins. Magn. Reson. Chem. 1995, 33, 621–631. [Google Scholar] [CrossRef]
  40. Štefane, B.; Polanc, S. A new and a convenient route to enaminones and pyrazoles. New J. Chem. 2002, 26, 28–32. [Google Scholar] [CrossRef]
  41. Valduga, C.J.; Squizani, A.; Braibante, H.S.; Braibante, M.E.F. The Use of K-10/Ultrasound in the Selective Synthesis of Unsymmetrical β-Enamino Ketones. Synthesis 1998, 1019–1022. [Google Scholar] [CrossRef]
  42. Koduri, N.D.; Hileman, B.; Cox, J.D.; Scott, H.; Hoang, P.; Robbins, A.; Bowers, K.; Tsebaot, L.; Miao, K.; Castaned, M.; et al. Acceleration of the Eschenmoser coupling reaction by sonication: Efficient synthesis of enaminones. RSC Adv. 2013, 3, 181–188. [Google Scholar] [CrossRef]
  43. Célérier, J.-P.; Deloisy, E.; Hommet, G.L.; Maittte, P. Lactim Ether Chemistry. Cyclic β-Enamino Ester Synthesis. J. Org. Chem. 1979, 44, 3089. [Google Scholar] [CrossRef]
  44. Ullah, S.; Zhang, W.; Hansen, P.E. Deuterium Isotope Effects on 13C and 15N Chemical Shifts of Intramolecularly Hydrogen-Bonded β-Enamine Derivatives of Meldrum’s and Tetronic acid. J. Mol. Struct. 2010, 976, 377–391. [Google Scholar] [CrossRef]
  45. Balogh, M.; Laszlo, P.; Simon, K. Unusual Reactions between 1,4-Dihydropyridines and 1,2,4,5-Tetrazines in the Presence of K-10/Fe(III) Clay Catalyst. J. Org. Chem. 1987, 52, 2026–2029. [Google Scholar] [CrossRef]
  46. Petrova, M.; Muhamadejev, R.; Vigante, B.; Duburs, G.; Liepinsh, E. Intramolecular hydrogen bonds in 1,4-dihydropyridine derivatives. R. Soc. Open. Sci. 2018, 5, 180088. [Google Scholar] [CrossRef] [Green Version]
  47. Darugar, V.; Vakili, M.; Tayyari, S.F.; Hansen, P.E.; Kamounah, F.S. Molecular structure, intramolecular hydrogen bond strength, vibrational assignment, and spectroscopic insight of 4-phenylamino-3-penten-2-one and its derivatives: A theoretical and experimental study. J. Mol. Liq. 2021, 334, 116035. [Google Scholar] [CrossRef]
  48. Seyedkatouli, S.; Vakili, M.; Tayyari, S.F.; Hansen, P.E.; Kamounah, F.S. Molecular structure and intramolecular hydrogen bond strength of 3-methyl-4-amino-3-penten-2-one and its N-Me and N-Ph substitutions by experimental and theoretical methods. J. Mol. Struct. 2019, 1184, 233–245. [Google Scholar] [CrossRef]
  49. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
  50. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  51. Biegler-König, F.W.; Schönbohm, J.; Bayles, D. Software news and updates—AIM2000—A program to analyze and visualize atoms in molecules. J. Comp. Chem. 2001, 22, 545–559. [Google Scholar]
  52. Mroginski, M.-A.; Németh, K.; Bauschlicher, T.; Klotzbücher, W.; Goddard, R.; Heinemann, O.; Hildebrandt, P.; Mark, F. Calculation of Vibrational Spectra of Linear Tetrapyrroles. 3. Hydrogen-Bonded Hexamethylpyrromethene Dimers. J. Phys. Chem. A 2005, 109, 2139–2150. [Google Scholar] [CrossRef]
  53. Novak, A. Hydrogen Bonding in Solids, Correlation of Spectroscopic and Crystallographic Data. Struct. Bond. 1974, 18, 177–216. [Google Scholar]
  54. Sobczyk, L.; Obrzud, M.; Filarowski, A. H/D Isotope Effects in Hydrogen Bonded Systems. Molecules 2013, 18, 4467–4476. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  55. Rodríguez, M.; Santillan, R.; López, Y.; Farrán, N.; Barba, V.; Nakatani, K.; García-Baéz, E.V.; Padilla-Martínez, I.I. N–H·O Assisted Structural Changes Induced on Ketoenamine Systems. Supramol. Chem. 2007, 19, 641–653. [Google Scholar] [CrossRef]
  56. Hansen, P.E.; Koch, A.; Kleinpeter, E. Ring Current and Anisotropy Effects on OH Chemical Shifts. Tetrahedron Lett. 2018, 59, 22188–22192. [Google Scholar] [CrossRef]
  57. Hansen, P.E. Isotope Effects on Chemical Shifts of Hydrogen Bonded Systems. J. Label. Comp. Radiopharm. 2007, 50, 967–981. [Google Scholar] [CrossRef]
  58. Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
  59. Benkheira, F.Z.; Amari, M. Etude Spectroscopique de l’équilibre enaminone—Iminenol de la reaction de l’acide dehydroacetique avec les amines primaires. J. Mar. Chim. Heterocycl. 2016, 15, 85–91. [Google Scholar]
  60. Kolev, T.M.; Angelov, P. 1,1,1-Trichloro-3-(1-phenethylamino-ethylidene)-pentane-2,4-dione—Synthesis, spectroscopic, theoretical and structural elucidation. J. Phys. Org. Chem. 2007, 20, 1108–1113. [Google Scholar] [CrossRef]
Molecules 26 07651 g001 550
Figure 1. IR spectra of (Z)-ethyl 3-(methylamino)but-2-enoate (17) measured in CCl4 solution; 17-H and 17-D indicate the normal and the deuterated compound, respectively. Contributions of 17-H to the 17-D spectrum due to incomplete deuteration are removed by subtraction (Figure S15).
Figure 1. IR spectra of (Z)-ethyl 3-(methylamino)but-2-enoate (17) measured in CCl4 solution; 17-H and 17-D indicate the normal and the deuterated compound, respectively. Contributions of 17-H to the 17-D spectrum due to incomplete deuteration are removed by subtraction (Figure S15).
Molecules 26 07651 g001
Molecules 26 07651 g002 550
Figure 2. Correlation of observed NH stretching wavenumbers and observed NH chemical shifts. The points for the nitroso compounds 25 and 26 are not included in the correlation analysis.
Figure 2. Correlation of observed NH stretching wavenumbers and observed NH chemical shifts. The points for the nitroso compounds 25 and 26 are not included in the correlation analysis.
Molecules 26 07651 g002
Molecules 26 07651 g003 550
Figure 3. Scaling correlation of observed vibrational wavenumbers for (Z)-ethyl 3-(methylamino)but-2-enoate (17) and harmonic wavenumbers calculated with B3LYP/6-311++G(d,p) (see Figures S19 and S20 for details).
Figure 3. Scaling correlation of observed vibrational wavenumbers for (Z)-ethyl 3-(methylamino)but-2-enoate (17) and harmonic wavenumbers calculated with B3LYP/6-311++G(d,p) (see Figures S19 and S20 for details).
Molecules 26 07651 g003
Molecules 26 07651 g004 550
Figure 4. Correlation of observed NH stretching wavenumbers and harmonic wavenumbers calculated with B3LYP/6-311++G(d,p).
Figure 4. Correlation of observed NH stretching wavenumbers and harmonic wavenumbers calculated with B3LYP/6-311++G(d,p).
Molecules 26 07651 g004
Molecules 26 07651 g005 550
Figure 5. Observed isotope ratios νNH/νND against observed ND stretching wavenumbers νND (cm−1) for the esters 16, 17, 19, 20, and 21 (see Table 3). The data point (2375, 1.356) is from Ref. [55].
Figure 5. Observed isotope ratios νNH/νND against observed ND stretching wavenumbers νND (cm−1) for the esters 16, 17, 19, 20, and 21 (see Table 3). The data point (2375, 1.356) is from Ref. [55].
Molecules 26 07651 g005
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Hansen, P.E.; Vakili, M.; Kamounah, F.S.; Spanget-Larsen, J. NH Stretching Frequencies of Intramolecularly Hydrogen-Bonded Systems: An Experimental and Theoretical Study. Molecules 2021, 26, 7651. https://doi.org/10.3390/molecules26247651

AMA Style

Hansen PE, Vakili M, Kamounah FS, Spanget-Larsen J. NH Stretching Frequencies of Intramolecularly Hydrogen-Bonded Systems: An Experimental and Theoretical Study. Molecules. 2021; 26(24):7651. https://doi.org/10.3390/molecules26247651

Chicago/Turabian Style

Hansen, Poul Erik, Mohammad Vakili, Fadhil S. Kamounah, and Jens Spanget-Larsen. 2021. "NH Stretching Frequencies of Intramolecularly Hydrogen-Bonded Systems: An Experimental and Theoretical Study" Molecules 26, no. 24: 7651. https://doi.org/10.3390/molecules26247651

APA Style

Hansen, P. E., Vakili, M., Kamounah, F. S., & Spanget-Larsen, J. (2021). NH Stretching Frequencies of Intramolecularly Hydrogen-Bonded Systems: An Experimental and Theoretical Study. Molecules, 26(24), 7651. https://doi.org/10.3390/molecules26247651

Article Metrics

Back to TopTop