Next Article in Journal
The Pharmaceutical Industry in 2020. An Analysis of FDA Drug Approvals from the Perspective of Molecules
Next Article in Special Issue
Luminescent Ink Based on Upconversion of NaYF4:Er,Yb@MA Nanoparticles: Environmental Friendly Synthesis and Structural and Spectroscopic Assessment
Previous Article in Journal
Coupling of a Novel TIMP3 Peptide to Carboxypeptidase G2 for Pro-Drug Activation at the Tumour Site
Previous Article in Special Issue
Structural Aspects of the Ortho Chloro- and Fluoro- Substituted Benzoic Acids: Implications on Chemical Properties
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 26
Issue 3
10.3390/molecules26030626
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Structures, Molecular Orbital Properties and Vibrational Spectra of the Homo- and Heterodimers of Sulphur Dioxide and Ozone. An Ab Initio Study

by
Thomas A. Ford
School of Chemistry and Physics, University of KwaZulu-Natal, Westville Campus, Private Bag X54001, Durban 4000, South Africa
Molecules 2021, 26(3), 626; https://doi.org/10.3390/molecules26030626
Submission received: 1 January 2021 / Revised: 18 January 2021 / Accepted: 20 January 2021 / Published: 25 January 2021
(This article belongs to the Special Issue Molecular Spectroscopy and Molecular Structure: Commemorative Issue in Honor of Professor Austin J. Barnes on Occasion of his 75th Birthday)
Browse Figures
Versions Notes

Abstract

:
The structures of a number of dimers of sulphur dioxide and ozone were optimized by means of a series of ab initio calculations. The dimer species were classified as either genuine energy minima or transition states of first or higher order, and the most probable structures consistent with the experimental data were confirmed. The molecular orbitals engaged in the interactions resulting in adduct formation were identified and relations between the orbitals of the dimers of the valence isoelectronic monomer species were examined. The vibrational spectra of the most probable structures were computed and compared with those reported in the literature, particularly with spectra observed in cryogenic matrices. The calculations were extended to predict the properties of a number of possible heterodimers formed between sulphur dioxide and ozone.

1. Introduction

Among the family of non-covalent interactions [1], the chalcogen bond has enjoyed much prominence in recent years. The definition of a chalcogen bond is a “net attractive interaction between an electrophilic region associated with a chalcogen atom in a molecular entity and a nucleophilic region in another, or the same, molecular entity” [2]. Interest in non-covalent bonding in species containing oxygen and sulphur atoms has prompted us to revisit our theoretical study of the sulphur dioxide dimer [3], with particular emphasis on its vibrational spectrum, and to extend our computations to the dimer of the valence isoelectronic analogue ozone. The weakly-bound sulphur dioxide homodimer has been the subject of a number of theoretical investigations [3,4,5,6,7,8,9]; in most of these studies the authors considered a number of potential candidates for the global minimum structure, using a variety of medium-sized basis sets. Gas phase studies have been carried out on the dimer by microwave and radiofrequency spectroscopy [9,10,11,12], while the infrared spectrum of sulphur dioxide has been extensively investigated in cryogenic matrices [13,14,15,16,17,18,19,20,21,22,23]. In many of these vibrational studies the SO2 dimer has been specifically identified. Sulphur dioxide also forms binary complexes with a variety of atoms and other small molecules; theoretical studies have included those with H2S and HCN [5], H2O [5,11], Ar [6], BF3 [24], C2H2 [25], CHCl3 [26], NH3 and (CH3)3N [27], CO2, OCS, CS2 and N2O [28], NH3, H2O, HF, PH3, H2S and HCl [29], and CH3CN [30]. Many of these, and other, binary complexes have been observed in the gas phase, including those with H2O [11], BF3 [24], CH3CN [30], HF and HCN [31], C2H2 [32], C5H5N [33], (CH3)2O [34], CO2 [35], OCS [36], CS2 [37], N2O [38], and CHCl3 [39]. As was the case for the SO2 dimer, matrix isolation vibrational spectroscopy has also proved a fruitful source of data on binary complexes of sulphur dioxide. In this way, complexes of SO2 with CH3CN [30], Cl2, HBr, H2O, NH3 and C2H4 [40], NH3 and (CH3)3N [41], HF [42], H2O [43], C6H6 [44], and BF3 [45] in cryogenic matrices have been characterized.
Far less work has been reported on the analogous ozone dimer, indeed, only one theoretical study has apparently been carried out on this species [46]. The vibrational spectrum of ozone in cryogenic matrices has been investigated [16,47,48,49,50,51,52,53,54,55,56,57,58,59]. However, most of these studies have been more concerned with isotopic analysis [47,48,54,55], the geometry of the monomer [50], with fluorescence [53], or photochemical [55,56,57,58,59] reactions in the matrices. Only in one case was the ozone dimer mentioned [59], and in another example the appearance of additional absorptions was attributed to the existence of multiple trapping sites [51]. A number of binary complexes containing ozone have been observed in low-temperature matrices, including olefins [60], HBr, H2O, NH3, H2CO and C2H4 [61], PH3 [62,63], HF [42,64], H2O [65], H2O and SO2 [66], CH2F2 [67], CO [68], and O atoms [69]. In addition to the formation of binary complexes, ozone has been found to be a fairly reactive species in cryogenic matrices, and reactions between O3 and a range of small molecules and atoms have been analysed. These include reactions with CS2 and OCS [70], C2H4 [71], NO [72,73,74], NO2 [75], N2H4 [76], AsH3 [77], SbH3 [78], P2 and P4 [79,80,81], HCN [82], Cl2 and Br2 [83], Cl [84,85], and Ne atoms [86].
The SO2-O3 heterodimer has so far eluded investigation, either theoretically or experimentally.

2. Results and Discussion

2.1. Molecular Structures

A number of trial structures were investigated for each adduct. We used as a template the publication of Hargittai [87], which examined a set of seven likely structural models for the metal dihalides, which we considered candidates as potential structures for the sulphur dioxide dimer. This trial set included three cyclic, two “linear”, and two bifurcated models, most of which were also investigated by other workers [3,4,5,6,8,9]. Along with the seven Hargittai structures, we also included two species that involved a S…S interaction, with no expectation that they would be strong candidates for the preferred SO2 dimer structure, but simply for completeness. Our nine possible dimer structures are illustrated in Figure 1 and their symmetries, energies, and Hessian indices are given in Table 1. Figure 2 shows their relative energies, separated according to their classification as genuine minima or transition states. We conclude, in agreement with the previous works [3,4,5,6,9] and with most of the experimental data [9,10,12,13,15,19,20,22,23], that our dimer 5 is the global minimum and is a non-symmetric species of Cs symmetry. The centrosymmetric dimer 2 is also a genuine minimum, being less than 1 kJ mol−1 higher in energy. Dimer 2, however, being centrosymmetric, would not be observable by microwave spectroscopy, therefore, there is no possibility of identifying this structure in the gas phase. Table 2 reports the computed geometrical parameters of each dimer and their deviations from the corresponding monomer values. The perturbations of the bond lengths and bond angles from their monomer values are small (less than 0.3 pm and 0.6°, respectively), indicating a weak interaction in each case.
The corresponding set of nine potential dimer structures for ozone are illustrated in Figure 3 and their properties are collected in Table 3. Their relative energies are presented in Figure 4. Only one of our ozone dimers (dimer 2) was found to be a true minimum. This adduct corresponds with the second lowest energy sulphur dioxide dimer, while the counterpart of the Cs global minimum of (SO2)2 (ozone dimer 5) is about 5 kJ mol−1 higher in energy. Our result is in contrast to that of Slanina and Adamowicz [46], who found the Cs counterpart of our dimer 5 to be the global minimum species. Part of the difference may be attributed to the use of different basis sets, but it has long been realized that the ozone monomer presents particularly formidable challenges for computation [88,89], and this is even more apparent for its dimer. The parameters of our ozone dimer 2 species are shown in Table 4. Again, the perturbations are minimal (less than 0.25 pm and 0.2°).
Based on the genuine minimum structures we found for the sulphur dioxide and ozone homodimers, and the Cs first order transition state of (O3)2, we examined eight structures for the sulphur dioxide-ozone heterodimer, two each corresponding with dimers 2, 3, 5, and 7, with sulphur dioxide and ozone acting as electron donor or electron acceptor in turn (a or b). These eight structures are illustrated in Figure 5 and their properties in Table 5. Structures 2a, 2b, 3a, and 3b were found to be virtually identical; these four structures and complex 5b are all true minima. The relative energies are presented in Figure 6 and the bond lengths and angles and their changes in Table 6. Again, the pattern of very small perturbations is observed; only the free O2O6 bond of the ozone sub-unit in complex 2a shows a substantial increase on complexation.

2.2. Interaction Energies

The interaction energies of the five genuine minimum energy structures are given in Table 7, corrected in each case for BSSE [90] and for zero-point energy differences. Consistent with the relatively insignificant intramolecular structural perturbations discussed above, the interaction energies are all less than 10 kJ mol−1; the two SO2 dimers and the 2a heterodimer all have similar energies, while heterodimer 5b is barely bound at all.

2.3. Molecular Orbital Properties

The valence molecular orbitals of the sulphur dioxide and ozone monomers are illustrated in Figure 7 and Figure 8, and their descriptions are listed in Table 8 and Table 9. The energy ordering of the orbitals follows the conventional sequence, σ < lp(O) ≈ lp(S) < π < π* < σ*. One sulphur and four oxygen lone pairs are expected for the SO2 monomer, and four terminal and one central oxygen lone pair in the case of O3. For both SO2 and O3 the π orbitals separate into a bonding orbital delocalized over all three atoms, a non-bonding orbital involving only the out-of-plane p orbitals of the peripheral oxygen atoms, and an antibonding orbital with contributions from the p orbitals of all three atoms. The σ* orbitals, being more diffuse and involving more excited atomic orbitals, are less easy to visualize and to assign.
These monomer orbitals transform readily into those of the dimer and complex species, and the orbitals of the five genuine minima are shown in the Supplementary Material as Figures S1–S5. The corresponding descriptions of the orbitals of the adducts are given in Supplementary Material Tables S1–S5. The major changes in the characters of the orbitals on complexation are that some of the lone pair orbitals of the monomers transform into σ bonding orbitals associated with the intermolecular bonding interactions. Thus, for SO2 dimers 5 and 2, for example, four oxygen and one sulphur monomer lone pair orbitals go over into six oxygen and two sulphur lone pair orbitals, with two new σ(S…O) orbitals.
Further insights into the electronic rearrangements accompanying dimer or complex formation are provided by a consideration of the molecular electrostatic potential maps of the adducts. These plots are shown in Figure 9 for the five associated species. The diagrams indicate the regions of high electron density, shown in red, shading to more electropositive zones, shown in blue, with the peripheral oxygen atoms having the greatest negative potentials and the more positive potentials associated with the sulphur atoms and the central oxygen atoms of the ozone moieties. The potentials cover a range from about −240 to 240 kJ mol−1.

2.4. Vibrational Spectra

The computed wavenumbers of the five associated species, and their shifts relative to the uncomplexed monomers, are shown in Table 10. For the two sulphur dioxide dimers, the antisymmetric SO2 stretching modes tend to be displaced to the red and the symmetric stretching and the SO2 bending to the blue. These shifts are all less than 10 cm−1 in either direction, however, consistent with the very low interaction energies (see Table 7). The comparisons of our calculated intramolecular wavenumbers with experimental values derived from matrix isolation infrared spectroscopic studies [13,15,19,20,21,22,23] are given in Table 11. As a measure of the level of agreement between the calculated and experimental wavenumbers of SO2 dimer 5, the calculated/experimental ratios derived from the data in Table 11 are found to vary between 1.029 for ν1 (relative to ref. [23]) to 1.060 for ν5 (ref. [22]).
The vibrational data are all in agreement that the observed spectra are compatible with the Cs dimer 5 structure, except for the argon matrix results of Schriver-Mazzuoli et al. [21] and Ito and Hirabayashi [23], who proposed that the Ci isomer 2 more closely fits the experimental data. Indeed, Schriver-Mazzuoli and co-workers were able to assign only one band in each of the fundamental monomer regions with confidence, consistent with only one mode in each of the monomer regions being infrared-active [21]. There are some minor mismatches among the assignments of the stretching modes [20,23], but definitive assignments to the bands of the electron donor and acceptor based on the experimental spectra alone are difficult to achieve.
Table 10 includes the calculated data for ozone dimer 2. The shifts of the antisymmetric O3 stretching modes are spectacularly large, given the low interaction energy of this dimer, and are of opposite sign. This result must be viewed in the context of the computed wavenumbers of the ozone monomer, 1157.9, 741.5, and 2244.3 cm−1 for ν1, ν2, and ν3, respectively, which may be compared with the experimental values of 1134.9, 716.0, and 1089.2 cm−1, reported by Barbe et al. [91]. This assignment admits a most unusual ordering of the stretching vibrations, with ν1 > ν3, which has been confirmed by Lee et al. [88,89]. Slanina and Adamowicz [46] report values of 1135, 726, and 2391 cm−1 for the monomer wavenumbers, in much closer agreement with our results. The antisymmetric stretching mode shifts indicate a significant separation of the two (in-phase and out-of-phase) vibrations of 247.3 cm−1, compared with separations of only 3.4 cm−1 and 1.7 cm−1 for SO2 dimers 5 and 2, respectively, and of 17 cm−1 calculated for the Cs isomer of (O3)2 by Slanina and Adamowicz [46]. The anomalous position of the antisymmetric stretching wavenumber confirms the notoriously difficult task of accurately reproducing the experimental wavenumber of the ozone monomer theoretically [88,89,92,93]. These authors pointed out the multiconfigurational nature of the ground state of the ozone monomer, confirmed by a series of high-level computations, including at the CASSCF, MRCI, CCSD, and CCSD(T) levels of theory. In order to examine whether our treatment of the spectra of ozone and its dimer at the MP2/aug-cc-pVTZ level was sufficiently reliable, we repeated those calculations for the monomer at the CASSCF level. We selected the monomer for this test, since the experimental geometry [94] and vibrational spectrum [91] are well-established and are available for comparison. The comparisons of our geometrical parameters and vibrational wavenumbers at the MP2 and CASSCF levels with their experimental counterparts and with the parallel computations of Lee and Scuseria [89] are given in Table 12 and Table 13. While the computed bond length and angle are rather insensitive to the level of theory employed, and show fairly similar calculated and experimental differences (see Table 12), the estimation of the antisymmetric OO stretching mode exhibits a large scatter; only the theoretical treatment of Lee and Scuseria using CCSD/TZ+2Pf methodology [89] correctly reproduces the experimental ordering of the ν1 and ν3 vibrations (see Table 13). These uncertainties are responsible for the large, computed shifts associated with the monomer ν3 mode. Our shifts of the symmetric stretching and bending modes of the ozone dimer are much more in line with those of the SO2 dimers (less than 10 cm−1).
The computed wavenumber shifts of the SO2 moieties of SO2-O3 complexes 2a and 5b are quite consistent with those of the SO2 dimers (less than 5 cm−1, see Table 10). Similarly, the O3 shifts of heterodimer 5b are insignificant, but those of the symmetric and antisymmetric O3 stretching modes of complex 2a are quite substantial and of opposite sign, yielding a separation of 51.6 cm−1. While this separation is not as dramatic as the corresponding result for the Ci ozone dimer, it is quite apparent that the antisymmetric stretching vibrations of ozone molecules in these homo- and heterodimers are extremely sensitive to complexation.

3. Computational Methodology

The calculations were carried out using Gaussian-16 [95], at the second order level of the Møller–Plesset perturbation theory (MP2) [96] with Dunning’s augmented correlation-consistent polarized valence triple-zeta basis sets (aug-cc-pVTZ) [97,98]. Structures were optimized using the verytight keyword, where practicable, and stationary points were identified as genuine minima or transition states by vibrational analysis. The wavenumbers and infrared intensities of the resulting species were determined at the harmonic level. Interaction energies were computed and corrected for basis set superposition error (BSSE) [90], using the Boys–Bernardi full counterpoise procedure [99] and the counterpoise = 2 keyword and for zero-point energy differences. Molecular orbital properties and molecular electrostatic potentials were examined using the Gaussian input keywords pop = full, density = current, and cube(full,orbitals) [95]. The model chemistry employed here is consistent with those represented in a number of similar calculations [4,5,6,7,8] in terms of its ability to yield credible results.

4. Conclusions

A series of nine structures each of the sulphur dioxide and ozone homodimers and of eight of their heterodimers were investigated. Of these structures, two sulphur dioxide and one ozone dimer and two sulphur dioxide-ozone complexes were found to be genuine minima on their potential surfaces. These five species were all found to be very weakly bound (less than 10 kJ mol−1). These low interaction energies resulted in very small perturbations of the bond lengths and bond angles of the monomers (less than 0.36 and 1.39 pm for the SO and OO bond lengths and 0.29° and 0.58° for the OSO and OOO angles, respectively). The minimal perturbations of the intramolecular geometries are matched by the small, computed wavenumber shifts (less than 7 cm−1 for the SO2 dimers and the SO2 sub-units of the heterodimers, and less than 10 cm−1 for the symmetric stretching and bending of the O3 moieties of the ozone dimers and the heterodimers). The exceptions to this statement are ozone dimer 2, where the shifts of the antisymmetric O3 stretching mode are 175.0 and −72.3 cm−1, and SO2-O3 complex 2a, where the O3 stretching vibrations undergo shifts of 25.8 cm−1 to the blue (antisymmetric) and the red (symmetric). The ozone moiety appears to be much more sensitive than sulphur dioxide to perturbations of their vibrational spectra due to complexation, but the conclusions regarding the magnitudes of the shifts have to be tempered by recognition of the well-known susceptibility of ozone to the level of theoretical treatment [88,89,92,93]. Miliordos and Xantheas presented evidence that, while the bonding in SO2 consists of two σ and two π bonds, that in O3 is better described as a mixture of a closed shell structure featuring two O-O bonds having bond orders of 1.5 (a delocalized 3-centre-4-electron bond) (82%) and a diradical structure with two σ bonds, a lone pair on the central oxygen atom, and a single electron in a p orbital on each of the terminal atoms (18%) [92]. Takeshita et al. concurred with respect to the description of the SO2 bonding arrangement (recoupled pair bonds), and the fact that O3 “has significantly more diradical character than SO2” [93]. These fundamental differences are certainly partly responsible for the marked variations in the ability of sulphur dioxide and ozone to form stable dimers, and hence in the differences in the computed vibrational spectra of the dimers. Neither Miliordos and Xantheas [92] nor Takeshita and co-workers [93] offered any insights into the spectra of the monomers, nor into the properties of the dimers.
We acknowledge the limitations of our methodology as they apply to the ozone species, but in the interests of consistency with our other results, we stand by the conclusions presented in this work.

Supplementary Materials

The following are available online, Figures S1–S5 and Tables S1–S5: titles as indicated in Table of Contents.

Funding

This research was funded by the National Research Foundation of South Africa, grant number 2053648, and by the University of KwaZulu-Natal Research Fund.

Data Availability Statement

The data presented in this study are available from the author and in the Supplementary Material.

Acknowledgments

This material is based upon work supported by the National Research Foundation of South Africa. Any opinion, findings, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Research Foundation. The author acknowledges the Centre for High Performance Computing (South Africa) for the use of computing facilities, and Anton Lopis for invaluable technical assistance. The author is also grateful to a reviewer for bringing references 92 and 93 to his attention. He looks back with pleasure on a number of valuable detailed technical discussions and convivial social interactions with Austin Barnes in several countries over many years.

Conflicts of Interest

The author declares no conflict of interest.

Sample Availability

No physical samples of the compounds are available.

References

  1. Hobza, P.; Müller-Dethlefs, K. Non-Covalent Interactions. Theory and Experiment; RSC Publishing: Cambridge, UK, 2010. [Google Scholar]
  2. Aakeroy, C.B.; Bryce, D.L.; Desiraju, G.R.; Frontera, A.; Legon, A.C.; Nicotra, F.; Rissanen, K.; Terraneo, S.S.G.; Metrangolo, P.; Resnati, G. Definition of the chalcogen bond (IUPAC recommendations 2019). Pure Appl. Chem. 2019, 91, 1889–1892. [Google Scholar] [CrossRef]
  3. Nxumalo, L.M.; Ford, T.A. Ab initio calculations of the structural, energetic and vibrational properties of some hydrogen-bonded and van der Waals dimers. Part 2. Sulphur dioxide. Spectrochim. Acta Part A 1995, 51, 1847–1860. [Google Scholar] [CrossRef]
  4. Bone, R.G.A.; le Sueur, C.R.; Amos, R.D.; Stone, A.J. Stationary points on the potential energy surfaces of (SO2)2 and (SO2)3. J. Chem. Phys. 1992, 96, 8390–8410. [Google Scholar] [CrossRef]
  5. Plummer, P.L.M. Quantum mechanical studies of weakly-bound molecular clusters. J. Mol. Struct. (Theochem) 1994, 307, 119–133. [Google Scholar] [CrossRef]
  6. Bone, R.G.A.; Bader, R.F.W. Identifying and analyzing intermolecular bonding interactions in van der Waals molecules. J. Phys. Chem. 1996, 100, 10892–10911. [Google Scholar] [CrossRef]
  7. McKee, M.L. Computational study of the mono- and dianions of SO2, SO3, SO4, S2O3, S2O4, S2O6 and S2O8. J. Phys. Chem. 1996, 100, 3473–3481. [Google Scholar] [CrossRef]
  8. Groves, C.; Lewars, E. Dimers, trimers and oligomers of sulfur oxides: An ab initio and density functional study. J. Mol. Struct. (Theochem) 2000, 530, 265–279. [Google Scholar] [CrossRef]
  9. Ito, F. Gas phase infrared spectra of SO2 clusters and quantum chemical calculations of some stable isomers. Chem. Phys. Letters 2007, 436, 335–340. [Google Scholar] [CrossRef]
  10. Nelson, D.D.; Fraser, G.T.; Klemperer, W. The microwave and radiofrequency rotation-inversion spectrum of (SO2)2. J. Chem. Phys. 1985, 83, 945–949. [Google Scholar] [CrossRef]
  11. Matsumura, K.; Lovas, F.J.; Suenram, R.D. The microwave spectrum and structure of the H2O-SO2 complex. J. Chem. Phys. 1989, 91, 5887–5894. [Google Scholar] [CrossRef]
  12. Taleb-Bendiab, A.; Hillig, K.W., II; Kuczkowski, R.L. The microwave spectrum, structure and tunneling motion of the sulfur dioxide dimer. J. Chem. Phys. 1991, 94, 6956–6963. [Google Scholar] [CrossRef]
  13. Hastie, J.W.; Hauge, R.; Margrave, J.L. Infrared spectra and geometry of SO2 and SeO2 in rare gas matrices. J. Inorg. Nucl. Chem. 1969, 31, 281–289. [Google Scholar] [CrossRef]
  14. Allavena, M.; Rysnik, R.; White, D.; Calder, V.; Mann, D.E. Infrared spectra and geometry of SO2 isotopes in solid krypton matrices. J. Chem. Phys. 1969, 50, 3399–3409. [Google Scholar] [CrossRef]
  15. Fredin, L. An exploratory study of weak molecular complexes in low temperature matrices. Chem. Scripta 1973, 4, 97–102. [Google Scholar]
  16. Spoliti, M.; Grosso, V.; Nunziante-Cesaro, S. Infrared matrix isolation of, and bonding in, the oxides of group VIB elements: O3, SO2, SeO2 and TeO2. J. Mol. Struct. 1974, 21, 7–15. [Google Scholar] [CrossRef]
  17. Maillard, D.; Allavena, M.; Perchard, J.P. Spectres vibrationnels du dioxide de soufre dans une matrice d’argon, d’azote et de neon. Spectrochim. Acta Part A 1975, 31, 1523–1531. [Google Scholar] [CrossRef]
  18. Sodeau, J.R.; Lee, E.K.C. Photo-oxidation of sulfur dioxide in low temperature matrices. J. Phys. Chem. 1980, 84, 3358–3362. [Google Scholar] [CrossRef]
  19. Nord, L. On the sulphur dioxide dimer in solid nitrogen. J. Mol. Struct. 1982, 96, 19–25. [Google Scholar] [CrossRef]
  20. Wierzejewka-Hnat, M.; Schriver, A.; Schriver-Mazzuoli, L. FT infrared study of sulfur dioxide dimer. I. Nitrogen matrix. Chem. Phys. 1994, 183, 117–126. [Google Scholar] [CrossRef]
  21. Schriver-Mazzuoli, L.; Schriver, A.; Wierzejewka-Hnat, M. Fourier transform infrared study of sulfur dioxide dimer. II. Argon matrix. Chem. Phys. 1995, 199, 227–243. [Google Scholar] [CrossRef]
  22. Nxumalo, L.M.; Ford, T.A. The sulphur dioxide dimer. A matrix isolation infrared spectroscopic study. J. Mol. Struct. 1995, 347, 495–508. [Google Scholar] [CrossRef]
  23. Ito, F.; Hirabayashi, S. Infrared spectroscopy of SO2 clusters in rare gas matrices revisited. Assignment of species in Ar matrices. Chem. Phys. 2009, 358, 209–218. [Google Scholar] [CrossRef]
  24. Peebles, S.A.; Sun, L.; Kuczkowski, R.L.; Nxumalo, L.M.; Ford, T.A. The structure of the boron trifluoride-sulphur dioxide complex. J. Mol. Struct. 1998, 471, 235–242. [Google Scholar] [CrossRef]
  25. Rayon, V.M.; Sordo, J.A. Acetylene-sulfur dioxide van der Waals complexes. A theoretical study. Chem. Phys. Lett. 2001, 341, 575–584. [Google Scholar] [CrossRef]
  26. Hippler, M. Quantum chemical study of CHCl3-SO2 association. J. Chem. Phys. 2005, 123, 204311. [Google Scholar] [CrossRef]
  27. Steudel, R.; Steudel, Y. Charge-transfer complexes between the sulfur molecules SO2, S2O, S3, SONH and SOCl2 and the amine donors NH3 and NMe3—A theoretical study. Eur. J. Inorg. Chem. 2007, 2007, 4385–4392. [Google Scholar] [CrossRef]
  28. Venayagamoorthy, M.; Ford, T.A. Ab initio molecular orbital studies of the vibrational spectra of some van der Waals complexes. Part 4. Complexes of sulphur dioxide with carbon dioxide, carbonyl sulphide, carbon disulphide and nitrous oxide. S. Afr. J. Chem. 2009, 62, 149–155. [Google Scholar]
  29. Ford, T.A. Ab initio molecular orbital calculations of the structures and vibrational spectra of some molecular complexes containing sulphur dioxide. J. Mol. Struct. 2009, 924–926, 466–472. [Google Scholar] [CrossRef]
  30. Eigner, A.A.; Wrass, J.P.; Smith, E.L.; Knutson, C.C.; Phillips, J.A. Structural properties of CH3CN-SO2 in the gas phase and condensed-phase media via density functional theory and infrared spectroscopy. J. Mol. Struct. 2009, 919, 312–320. [Google Scholar] [CrossRef]
  31. Dayton, D.C.; Miller, R.E. Infrared spectroscopy of the sulfur dioxide-hydrogen fluoride and hydrogen cyanide-sulfur dioxide binary complexes. J. Phys. Chem. 1990, 94, 6641–6646. [Google Scholar] [CrossRef]
  32. Andrews, A.M.; Hillig, K.W., II; Kuczkowski, R.L.; Legon, A.C.; Howard, N.W. Microwave spectrum, structure, dipole moment and deuterium nuclear quadrupole coupling constants of the acetylene-sulfur dioxide van der Waals complex. J. Chem. Phys. 1991, 94, 6947–6955. [Google Scholar] [CrossRef] [Green Version]
  33. Oh, J.J.; Hillig, K.W.; Kuczkowski, R.L. Microwave spectrum and structure of the pyridine-sulfur dioxide complex. J. Am. Chem. Soc. 1991, 113, 7480–7484. [Google Scholar] [CrossRef]
  34. Oh, J.J.; Hillig, K.W.; Kuczkowski, R.L. Structure of the dimethyl ether-sulfur dioxide complex. Inorg. Chem. 1991, 30, 4583–4588. [Google Scholar] [CrossRef]
  35. Sun, L.; Ioannou, I.I.; Kuczkowski, R.L. The microwave spectrum and structure of the carbon dioxide-sulphur dioxide complex. Mol. Phys. 1996, 88, 255–268. [Google Scholar] [CrossRef]
  36. Peebles, S.A.; Sun, L.H.; Ioannou, I.I.; Kuczkowski, R.L. Rotational spectrum, structure and modeling of the SO2-OCS complex. J. Mol. Struct. 1999, 485–486, 211–223. [Google Scholar] [CrossRef]
  37. Peebles, S.A.; Sun, L.; Kuczkowski, R.L. Rotational spectrum, structure and modeling of the SO2-CS2 complex. J. Chem. Phys. 1999, 110, 6804–6811. [Google Scholar] [CrossRef] [Green Version]
  38. Peebles, R.A.; Kuczkowski, R.L. Microwave spectrum of the N2O-SO2 dimer: Evidence for tunneling and an asymmetric structure. J. Phys. Chem. A 2000, 104, 4968–4975. [Google Scholar] [CrossRef]
  39. Chung, S.; Hippler, M. Infrared spectroscopy of hydrogen-bonded CHCl3-SO2 in the gas phase. J. Chem. Phys. 2006, 124, 214316–214322. [Google Scholar] [CrossRef]
  40. Nord, L. Some sulphur dioxide complexes in solid nitrogen. J. Mol. Struct. 1982, 96, 27–35. [Google Scholar] [CrossRef]
  41. Sass, C.S.; Ault, B.S. Matrix isolation infrared spectroscopic study of sulfur dioxide-amine complexes. J. Phys. Chem. 1984, 88, 432–440. [Google Scholar] [CrossRef]
  42. Andrews, L.; Withnall, R.; Hunt, R.D. Infrared spectra of the ozone…hydrogen fluoride and sulfur dioxide…hydrogen fluoride complexes in solid argon. J. Phys. Chem. 1988, 92, 78–81. [Google Scholar] [CrossRef]
  43. Schriver, A.; Schriver, L.; Perchard, J.P. Infrared matrix isolation studies of complexes between water and sulfur dioxide: Identification and structures of the 1:1, 1:2 and 2:1 species. J. Mol. Spectrosc. 1988, 127, 125–142. [Google Scholar] [CrossRef]
  44. Ault, B.S. Infrared spectroscopic characterization of 1:1 molecular complexes of SO2 with benzene and related conjugated π electron donors in argon matrices. J. Mol. Struct. 1990, 238, 111–117. [Google Scholar] [CrossRef]
  45. Nxumalo, L.M.; Ford, T.A. The Fourier transform infrared spectrum of the boron trifluoride-sulphur dioxide van der Waals complex. J. Mol. Struct. 2003, 661–662, 153–159. [Google Scholar] [CrossRef]
  46. Slanina, Z.; Adamowicz, L. A computational study of the ozone dimer. J. Atmos. Chem. 1993, 16, 41–46. [Google Scholar] [CrossRef]
  47. Andrews, L.; Spiker, R.C. Argon matrix Raman and infrared spectrum and vibrational analysis of ozone and the oxygen-18 substituted ozone molecules. J. Phys. Chem. 1972, 76, 3208–3213. [Google Scholar] [CrossRef]
  48. Brewer, L.; Wang, J.L. Infrared absorption spectra of isotopic ozone isolated in rare-gas matrices. J. Chem. Phys. 1972, 56, 759–761. [Google Scholar] [CrossRef] [Green Version]
  49. Hopkins, A.G.; Brown, D.W. Raman spectrum of matrix isolated ozone. J. Chem. Phys. 1973, 58, 1776–1777. [Google Scholar] [CrossRef]
  50. Spoliti, M.; Nunziante-Cesaro, S.; Mariti, B. Infrared spectrum and geometry of ozone isolated in inert gas matrices at 20.4 K. J. Chem. Phys. 1973, 59, 985–986. [Google Scholar] [CrossRef]
  51. Brosset, P.; Dahoo, R.; Gauthier-Roy, B.; Abouaf-Marguin, L. Analysis of IR absorption spectrum of O3 in inert matrices: Spectroscopic evidence for two trapping sites. Chem. Phys. 1993, 172, 315–324. [Google Scholar] [CrossRef]
  52. Lakhlifi, A.; Girardet, C.; Dahoo, R.; Brosset, P.; Gauthier-Roy, B.; Abouaf-Marguin, L. Interpretation of the infrared spectrum of ozone trapped in inert matrices. Chem. Phys. 1993, 177, 31–44. [Google Scholar] [CrossRef]
  53. Jasmin, D.; Brosset, P.; Dahoo, R.; Raducu, V.; Gauthier-Roy, B.; Abouaf-Marguin, L. Laser-induced infrared fluorescence of O3 trapped in xenon matrices. J. Chem. Phys. 1994, 101, 7337–7341. [Google Scholar] [CrossRef]
  54. Schriver-Mazzuoli, L.; Schriver, A.; Lugez, C.; Perrin, A.; Camy-Peyret, C.; Flaud, J.M. Vibrational spectra of the 16O/17O/18O substituted ozone molecule isolated in matrices. J. Mol. Spectrosc. 1996, 176, 85–94. [Google Scholar] [CrossRef]
  55. Bahou, M.; Schriver-Mazzuoli, L.; Camy-Peyret, C.; Schriver, A. Photolysis of ozone at 693 nm in solid oxygen. Isotope effects in ozone reformation. Chem. Phys. Lett. 1997, 273, 31–36. [Google Scholar] [CrossRef]
  56. Bahou, M.; Schriver-Mazzuoli, L.; Camy-Peyretm, C.; Schriver, A. New information on the ozone monomer photochemistry at 266 nm in nitrogen matrices. J. Chem. Phys. 1998, 108, 6884–6891. [Google Scholar] [CrossRef]
  57. Flaud, J.M.; Bacis, R. The ozone molecule: Infrared and microwave spectroscopy. Spectrochim. Acta Part A 1998, 54, 3–16. [Google Scholar] [CrossRef]
  58. Bahou, M.; Schriver-Mazzuoli, L.; Schriver, A. Photolysis at 266 nm of argon matrix isolated ozone monomer. J. Chem. Phys. 1999, 110, 8636–8642. [Google Scholar] [CrossRef]
  59. Bahou, M.; Schriver-Mazzuoli, L.; Schriver, A. Infrared spectroscopy and photochemistry at 266 nm of the ozone dimer trapped in an argon matrix. J. Chem. Phys. 2001, 114, 4045–4052. [Google Scholar] [CrossRef]
  60. Nelander, B.; Nord, L. Do ozone-olefin complexes really exist? J. Am. Chem. Soc. 1979, 101, 3769–3770. [Google Scholar] [CrossRef]
  61. Nord, L. Ozone complexes in solid nitrogen. J. Mol. Struct. 1983, 96, 37–44. [Google Scholar] [CrossRef]
  62. Withnall, R.; Hawkins, M.; Andrews, L. Infrared spectrum of a symmetrical phosphine-ozone complex in solid argon. J. Phys. Chem. 1986, 90, 575–579. [Google Scholar] [CrossRef]
  63. Withnall, R.; Andrews, L. FTIR spectra of the photolysis products of the phosphine ozone complex in solid argon. J. Phys. Chem. 1987, 91, 784–797. [Google Scholar] [CrossRef]
  64. Andrews, L. FTIR spectra of base-HF complexes in noble gas matrices. J. Mol. Struct. 1988, 173, 103–110. [Google Scholar] [CrossRef]
  65. Schriver, L.; Barreau, C.; Schriver, A. Infrared spectroscopic and photochemical study of water-ozone complexes in solid argon. Chem. Phys. 1990, 140, 429–438. [Google Scholar] [CrossRef]
  66. Schriver, L.; Carrere, D.; Schriver, A.; Jaeger, K. Matrix isolation photolysis of SO2, O3 and H2O: Evidence for the H2O:SO3 complex. Chem. Phys. Lett. 1991, 181, 505–511. [Google Scholar] [CrossRef]
  67. Davis, S.R.; Liu, L. Matrix isolation IR spectroscopy, photochemistry and ab initio calculations of the difluoromethane-ozone complex. J. Phys. Chem. 1993, 97, 3690–3696. [Google Scholar] [CrossRef]
  68. Raducu, V.; Jasmin, D.; Dahoo, R.; Brosset, P.; Gauthier-Roy, B.; Abouaf-Marguin, L. Experimental study of the CO:O3 complex in argon matrices: Irradiation at 266 nm. J. Chem. Phys. 1994, 101, 1878–1884. [Google Scholar] [CrossRef]
  69. Schriver-Mazzuoli, L.; de Saxce, A.; Lugez, C.; Camy-Peyret, C.; Schriver, A. Ozone generation through photolysis of an oxygen matrix at 11 K: Fourier transform infrared spectroscopy identification of the O…O3 complex and isotopic studies. J. Chem. Phys. 1995, 102, 690–701. [Google Scholar] [CrossRef]
  70. Jones, P.R.; Taube, H. Photochemical studies on ozone with carbon disulfide and with carbonyl sulfide in low-temperature matrixes. J. Phys. Chem. 1973, 77, 1007–1011. [Google Scholar] [CrossRef]
  71. Nelander, B.; Nord, L. The reaction between ethylene and ozone. A matrix study. Tetrahedron Lett. 1977, 18, 2821–2822. [Google Scholar] [CrossRef]
  72. Lucas, D.; Pimentel, G.C. Reaction between nitric oxide and ozone in solid nitrogen. J. Phys. Chem. 1979, 83, 2311–2316. [Google Scholar] [CrossRef]
  73. Bhatia, S.C.; Hall, J.H., Jr. A matrix isolation infrared spectroscopic study of the reactions of nitric oxide with oxygen and ozone. J. Phys. Chem. 1980, 84, 3255–3259. [Google Scholar] [CrossRef]
  74. Frei, H.; Pimentel, G.C. Reaction of nitric oxide and ozone in cryogenic matrices: Quantum-mechanical tunneling and vibrational enhancement. J. Phys. Chem. 1981, 85, 3355–3360. [Google Scholar] [CrossRef]
  75. Morris, V.R.; Bhatia, S.C.; Hall, J.H. A study of the gas-phase reaction of nitrogen dioxide with ozone by matrix isolation infrared spectroscopy. J. Phys. Chem. 1987, 91, 3359–3361. [Google Scholar] [CrossRef]
  76. Lascola, R.; Withnall, R.; Andrews, L. Infrared spectra of hydrazine and products of its reactions with HF, F2 and O3 in solid argon. Inorg. Chem. 1988, 27, 642–648. [Google Scholar] [CrossRef]
  77. Andrews, L.; Withnall, R.; Moores, B.W. Infrared spectra of arsine-ozone complexes, reaction products and photolysis products in solid argon. J. Phys. Chem. 1989, 93, 1279–1285. [Google Scholar] [CrossRef]
  78. Andrews, L.; Moores, B.W.; Fonda, K.K. Matrix infrared spectra of reaction and photolysis products of stibine and ozone. Inorg. Chem. 1989, 28, 290–297. [Google Scholar] [CrossRef]
  79. Andrews, L.; McCluskey, M.; Mielke, Z.; Withnall, R. Matrix reactions of P4 and P2 with O3 molecules. J. Mol. Struct. 1990, 222, 95–108. [Google Scholar] [CrossRef]
  80. Mielke, Z.; McCluskey, M.; Andrews, L. Matrix reactions of P2 and O3 molecules. Chem. Phys. Lett. 1990, 165, 146–154. [Google Scholar] [CrossRef]
  81. Mielke, Z.; Andrews, L. Matrix infrared spectra of the products from photochemical reactions of P4 with O3 and decomposition of P4O6. Inorg. Chem. 1990, 29, 2773–2779. [Google Scholar] [CrossRef]
  82. Mielke, Z.; Andrews, L. Matrix infrared studies of the hydrogen cyanide + ozone and hydrogen cyanide + oxygen atom systems. J. Phys. Chem. 1990, 94, 3519–3525. [Google Scholar] [CrossRef]
  83. Schriver-Mazzuoli, L.; Abdeloui, O.; Lugez, C.; Schriver, A. Matrix reaction of ozone with Cl2 and Br2. FTIR identification of BrClO and ClBrO species. Chem. Phys. Lett. 1993, 214, 519–526. [Google Scholar] [CrossRef]
  84. Bhatia, S.C.; Hall, J.H., Jr. Matrix isolation infrared and laser Raman spectroscopic study of the gas-phase reactions of chlorine atoms and ozone. J. Phys. Chem. 1981, 85, 2055–2060. [Google Scholar] [CrossRef]
  85. Carter, R.O., III; Andrews, L. Matrix spectroscopic studies of chlorine atom-ozone reaction products. J. Phys. Chem. 1981, 85, 2351–2354. [Google Scholar] [CrossRef]
  86. Lugez, C.L.; Thompson, W.E.; Jacox, M.E. Matrix-isolated study of the interaction of excited neon atoms with O3: Infrared spectrum of O3- and evidence for the stabilization of O2…O4+. J. Chem. Phys. 1996, 105, 2153–2160. [Google Scholar] [CrossRef]
  87. Hargittai, M. Molecular structure of metal halides. Chem. Rev. 2000, 100, 2233–2302. [Google Scholar] [CrossRef]
  88. Lee, T.J.; Allen, W.D.; Schaefer, H.F., III. The analytical evaluation of energy first derivatives for two-configuration self-consistent-field configuration interaction (TCSCF-CI) wave functions. Application to ozone and ethylene. J. Chem. Phys. 1987, 87, 7062–7075. [Google Scholar] [CrossRef]
  89. Lee, T.J.; Scuseria, G.E. The vibrational frequencies of ozone. J. Chem. Phys. 1990, 93, 489–494. [Google Scholar] [CrossRef]
  90. Liu, B.; McLean, A.D. Accurate calculations of the attractive interactions of two ground state helium atoms. J. Chem. Phys. 1973, 59, 4557–4558. [Google Scholar] [CrossRef] [Green Version]
  91. Barbe, A.; Secroun, C.; Jouve, P. Infrared spectra of 16O3 and 18O3; Darling and Dennison resonance and anharmonic potential function of ozone. J. Mol. Spectrosc. 1974, 49, 171–182. [Google Scholar] [CrossRef]
  92. Miliordos, E.; Xantheas, S.S. On the bonding nature of ozone (O3) and its sulphur-substituted analogues SO2, OS2 and S3: Correlation between their diradical character and molecular properties. J. Am. Chem. Soc. 2014, 136, 2808–2817. [Google Scholar] [CrossRef]
  93. Takeshita, T.Y.; Lindquist, B.A.; Dunning, T.H., Jr. Insights into the electronic structure of ozone and sulphur dioxide from generalized valence bond theory: Bonding in O3 and SO2. J. Phys. Chem. A 2015, 119, 7683–7694. [Google Scholar] [CrossRef] [Green Version]
  94. Tanaka, T.; Morino, Y. Coriolis interaction and anharmonic potential function of ozone from the microwave spectra in the excited vibrational states. J. Mol. Spectrosc. 1970, 33, 538–551. [Google Scholar] [CrossRef]
  95. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  96. Møller, C.; Plesset, M.S. Notes on an approximation treatment for many-elextron systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef] [Green Version]
  97. Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
  98. Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wavefunctions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef] [Green Version]
  99. Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–556. [Google Scholar] [CrossRef]
Molecules 26 00626 g001 550
Figure 1. Optimized structures of some dimers of sulphur dioxide.
Figure 1. Optimized structures of some dimers of sulphur dioxide.
Molecules 26 00626 g001
Molecules 26 00626 g002 550
Figure 2. Relative energies of the sulphur dioxide dimers.
Figure 2. Relative energies of the sulphur dioxide dimers.
Molecules 26 00626 g002
Molecules 26 00626 g003 550
Figure 3. Optimized structures of some dimers of ozone.
Figure 3. Optimized structures of some dimers of ozone.
Molecules 26 00626 g003
Molecules 26 00626 g004 550
Figure 4. Relative energies of the ozone dimers.
Figure 4. Relative energies of the ozone dimers.
Molecules 26 00626 g004
Molecules 26 00626 g005 550
Figure 5. Optimized structures of some complexes of sulphur dioxide and ozone.
Figure 5. Optimized structures of some complexes of sulphur dioxide and ozone.
Molecules 26 00626 g005
Molecules 26 00626 g006 550
Figure 6. Relative energies of the sulphur dioxide-ozone complexes.
Figure 6. Relative energies of the sulphur dioxide-ozone complexes.
Molecules 26 00626 g006
Molecules 26 00626 g007 550
Figure 7. Valence molecular orbitals of the sulphur dioxide monomer.
Figure 7. Valence molecular orbitals of the sulphur dioxide monomer.
Molecules 26 00626 g007
Molecules 26 00626 g008 550
Figure 8. Valence molecular orbitals of the ozone monomer.
Figure 8. Valence molecular orbitals of the ozone monomer.
Molecules 26 00626 g008
Molecules 26 00626 g009 550
Figure 9. Molecular electrostatic potential plots of some dimers and complexes of sulphur dioxide and ozone. Units: hartree (1 H = 2625.346583 kJ mol−1).
Figure 9. Molecular electrostatic potential plots of some dimers and complexes of sulphur dioxide and ozone. Units: hartree (1 H = 2625.346583 kJ mol−1).
Molecules 26 00626 g009
Table
Table 1. Properties of some dimers of sulphur dioxide.
Table 1. Properties of some dimers of sulphur dioxide.
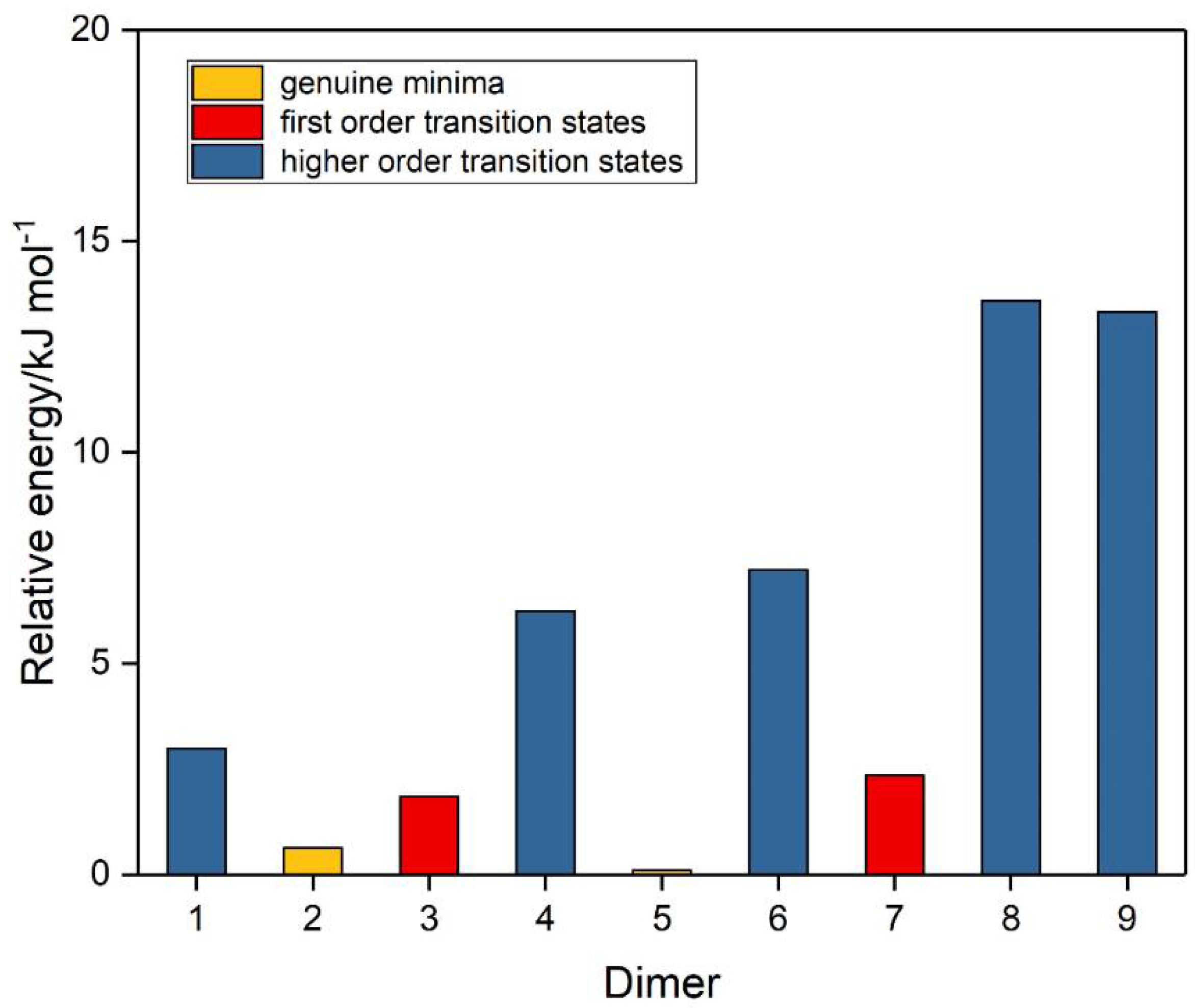
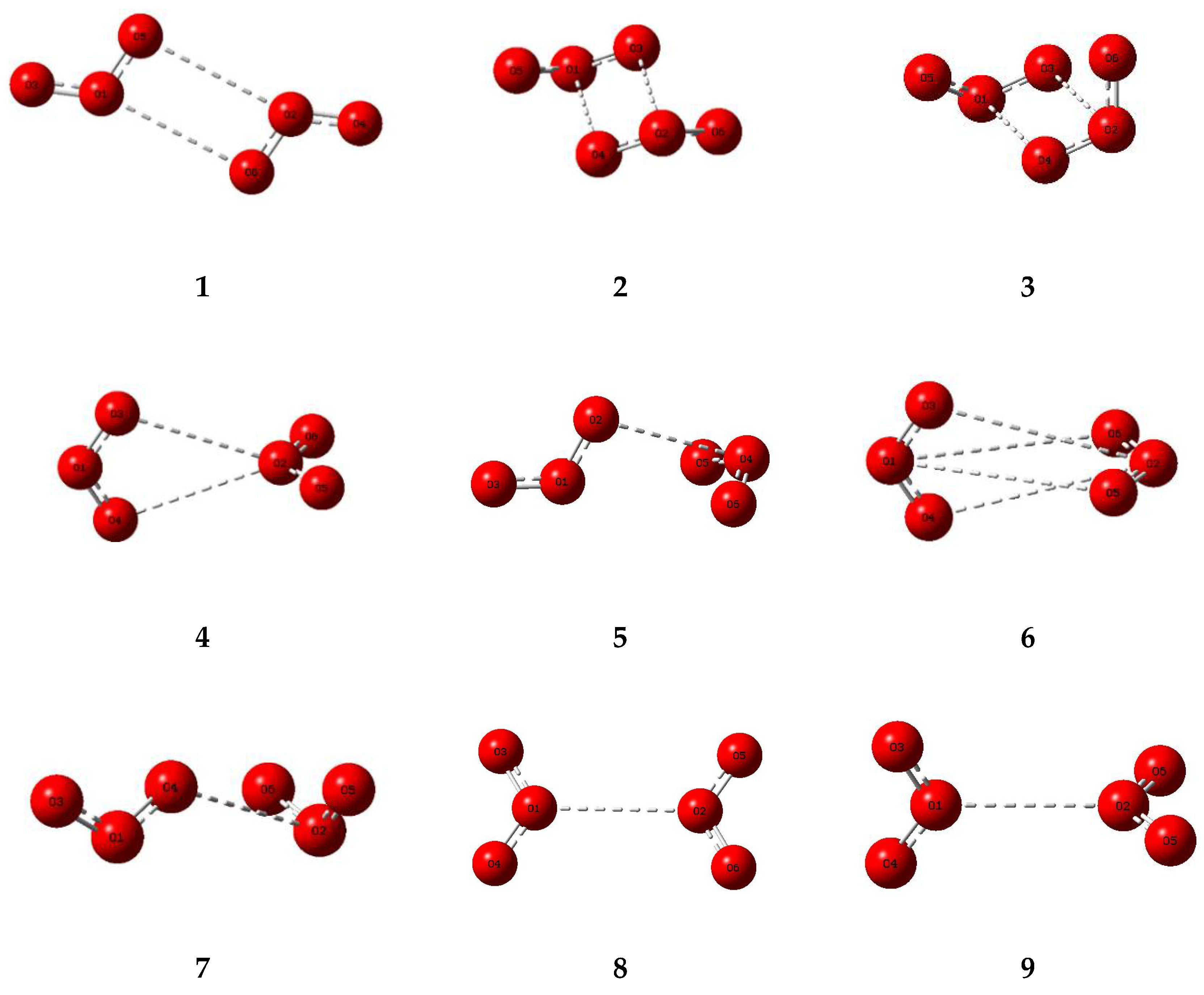
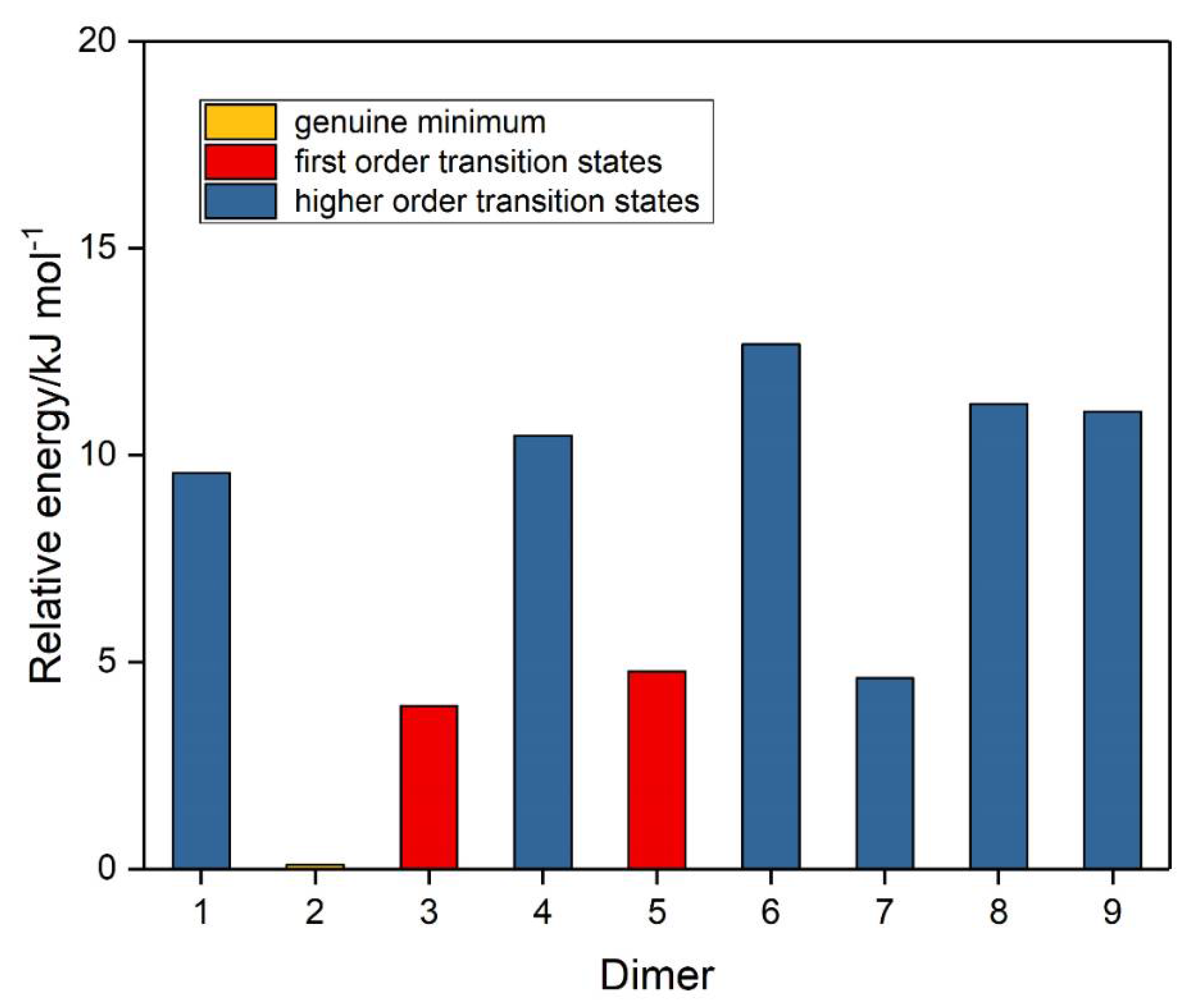
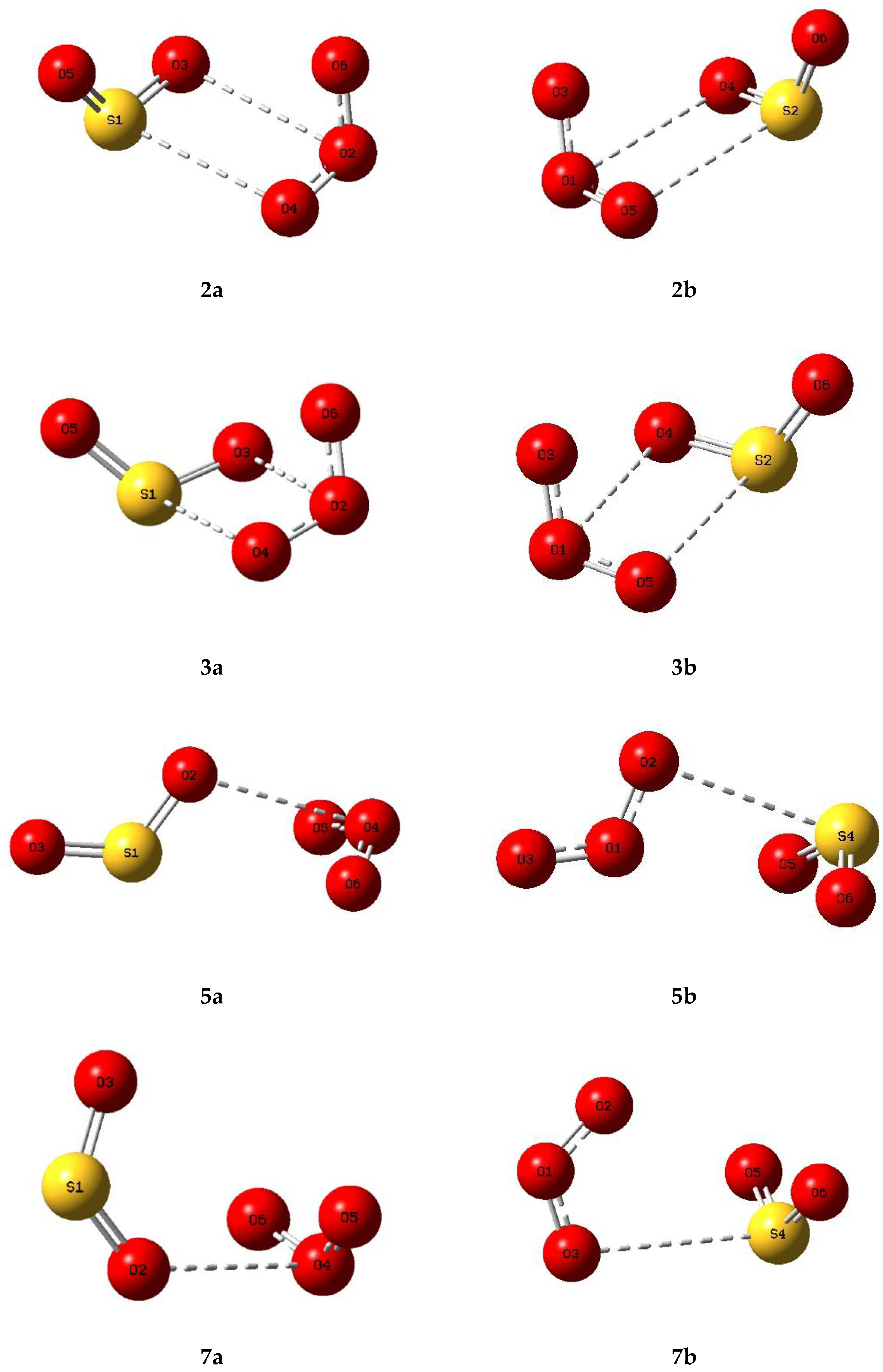
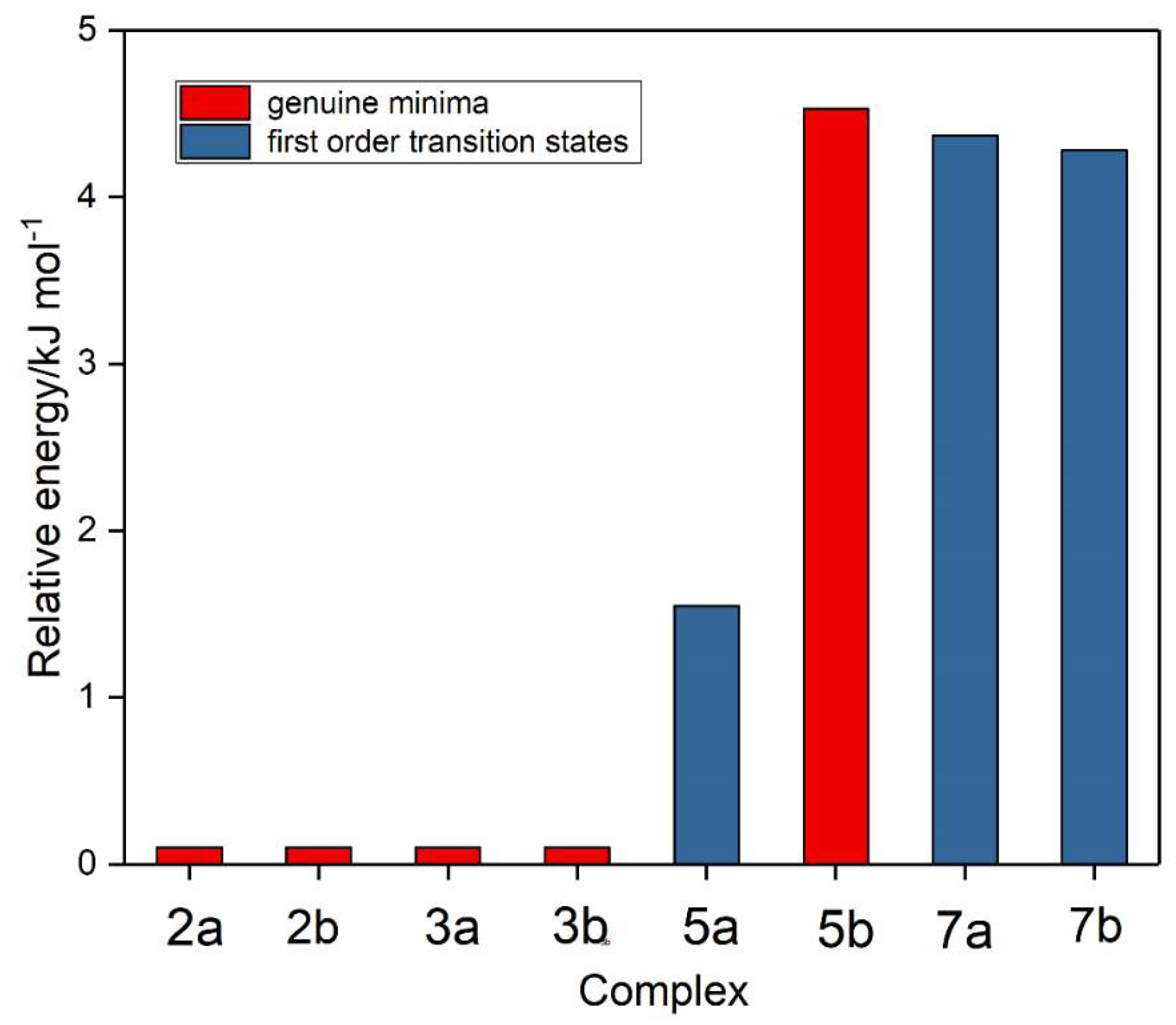
DimerSymmetryE/HHessian
Index		Relative Energy/
kJ mol−1
5Cs−1095.9350 3678 4100
2Ci−1095.9347 9649 5400.63
3C2−1095.9343 3272 0711.85
7Cs−1095.9341 4356 3212.35
1C2h−1095.9339 0229 8122.98
4C2v−1095.9326 6035 5526.24
6C2v−1095.9322 8723 0927.22
9D2d−1095.9300 0351 25213.32
8D2h−1095.9298 6160 93413.59
Table
Table 2. Optimized geometrical parameters of sulphur dioxide dimers 5 and 2, and their changes relative to the sulphur dioxide monomer. See Figure 1 for numbering of the atoms.
Table 2. Optimized geometrical parameters of sulphur dioxide dimers 5 and 2, and their changes relative to the sulphur dioxide monomer. See Figure 1 for numbering of the atoms.
Dimer 5Dimer 2
ParameterDimer ValueDifference from Monomer ValueParameterDimer ValueDifference from Monomer Value
r(S1O2)/pm146.570.21r(S1O3,S2O4)/pm146.510.15
r(S1O3)/pm146.32−0.03r(S1O5,S2O6)/pm146.30−0.05
r(S4O5,S4O6)/pm146.410.06∠O3S1O5,O4S2O6/deg118.40−0.39
∠O2S1O3/deg118.21−0.58r(S1…O4,S2…O3)/pm322.37-
∠O5S4O6/deg118.21−0.58∠O5S1…O4,O6S2…O3/deg83.85-
r(O2…S4)/pm318.79-∠S1O3…S2,S2O4…S1/deg106.60-
∠S1O2…S4/deg100.27-∠O5S1O3…S2/deg a 73.23-
∠O2…S4O5,O2…S4O6/deg79.37-∠O6S2O4…S1/deg a−73.23-
∠O5S4…O2S1/deg a−60.82-
∠O6S4…O2S1/deg a60.82-
a Dihedral angle.
Table
Table 3. Properties of some dimers of ozone.
Table 3. Properties of some dimers of ozone.
DimerSymmetryE/HHessian
Index		Relative Energy/
kJ mol−1
2Ci−450.2841 9179 49000
3C2−450.2826 9146 05113.94
7Cs−450.2824 3399 65424.61
5Cs−450.2823 7307 96514.77
1C2h−450.2805 4781 87229.57
4C2v−450.2802 0490 636410.47
9D2d−450.2799 8305 709411.05
8D2h−450.2799 1140 084511.24
6C2v−450.2793 6382 300212.68
Table
Table 4. Optimized geometrical parameters of ozone dimer 2 and their changes relative to the ozone monomer. See Figure 3 for numbering of the atoms.
Table 4. Optimized geometrical parameters of ozone dimer 2 and their changes relative to the ozone monomer. See Figure 3 for numbering of the atoms.
ParameterDimer ValueDifference from Monomer Value
r(O1O3,O2O4)/pm128.580.20
r(O1O5,O2O6)/pm128.530.15
∠O3O1O5,O4O2O6/deg116.49−0.17
r(O1…O4,O2…O3)/pm299.07-
∠O5O1…O4,O6…O2O3/deg65.08-
∠O1O3…O2,O2O4…O1/deg108.32-
∠O5O1…O4O2/deg a−43.17-
∠O6O2…O3O1/deg a43.17-
a Dihedral angle.
Table
Table 5. Properties of some complexes of sulphur dioxide and ozone.
Table 5. Properties of some complexes of sulphur dioxide and ozone.
ComplexSymmetryE/HHessian
Index		Relative Energy/
kJ mol−1
2aC1−773.1098 0096 46700
3aC1−773.1098 0095 88500
2bC1−773.1098 0095 75500
3bC1−773.1098 0095 16500
5aCs−773.1092 1061 63211.55
7bCs−773.1081 7161 05614.28
7aCs−773.1081 3721 83114.37
5bCs−773.1080 7683 40904.53
Table
Table 6. Optimized geometrical parameters of sulphur dioxide-ozone complexes 2a and 5b, and their changes relative to the sulphur dioxide and ozone monomers. See Figure 5 for numbering of the atoms.
Table 6. Optimized geometrical parameters of sulphur dioxide-ozone complexes 2a and 5b, and their changes relative to the sulphur dioxide and ozone monomers. See Figure 5 for numbering of the atoms.
Complex 2aComplex 5b
ParameterDimer ValueDifference from Monomer ValueParameterDimer ValueDifference from Monomer Value
r(S1O3)/pm146.720.36r(O1O2)/pm128.03−0.35
r(S1O5)/pm146.21−0.15r(O1O3)/pm128.690.31
r(O2O4)/pm127.85−0.53r(S4O5,S4O6)/pm146.370.02
r(O2O6)/pm129.761.39∠O2O1O3/deg116.50−0.16
∠O3S1O5/deg118.50−0.29∠O5S4O6/deg 118.51−0.28
∠O4O2O6/deg116.08−0.58r(O2…S4)/pm313.42-
r(S1…O4)/pm291.71-∠O1O2…S4/deg90.03-
r(O2…O3)/pm291.42-∠O2…S4O5,O2…S4O6/deg83.45-
∠O5S1…O4/deg113.06-∠O5S4…O2O1/deg a59.89-
∠O6O2…O3/deg66.12-∠O6S4…O2O1/deg a−59.89-
∠O5S1O3…O2/deg a107.94-
∠O6O2O4…S1/deg a55.56-
a Dihedral angle.
Table
Table 7. Interaction energies of some dimers and complexes of sulphur dioxide and ozone.
Table 7. Interaction energies of some dimers and complexes of sulphur dioxide and ozone.
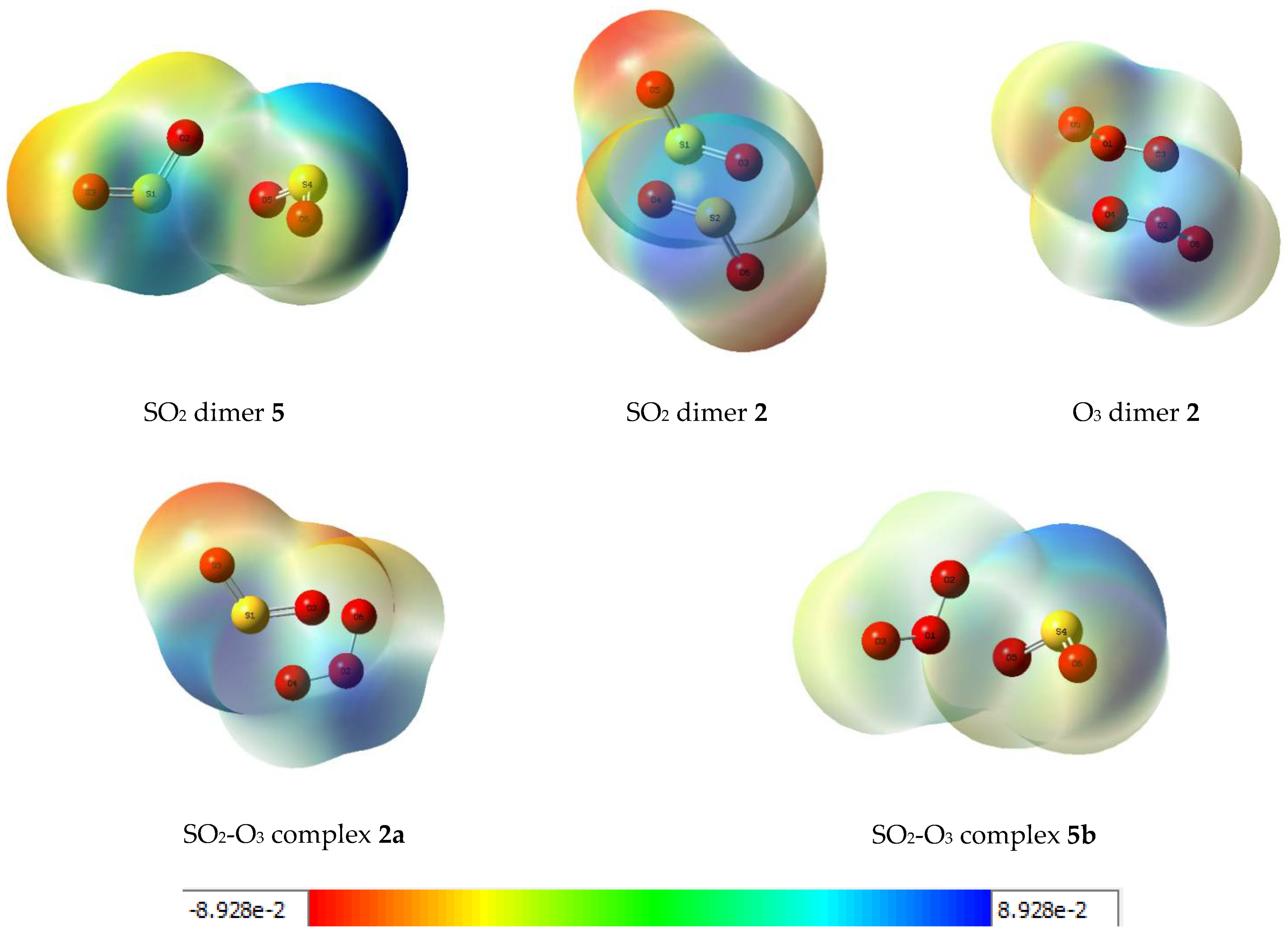
SpeciesInteraction Energy/kJ mol−1
RawBSSECorrectedΔEoNet
SO2 dimer 513.262.3810.881.938.95
SO2 dimer 212.592.2610.331.868.47
O3 dimer 214.393.1811.214.217.00
SO2-O3 complex 2a15.523.3412.183.678.51
SO2-O3 complex 5b9.872.177.701.915.79
Table
Table 8. Properties of the valence molecular orbitals of the sulphur dioxide monomer.
Table 8. Properties of the valence molecular orbitals of the sulphur dioxide monomer.
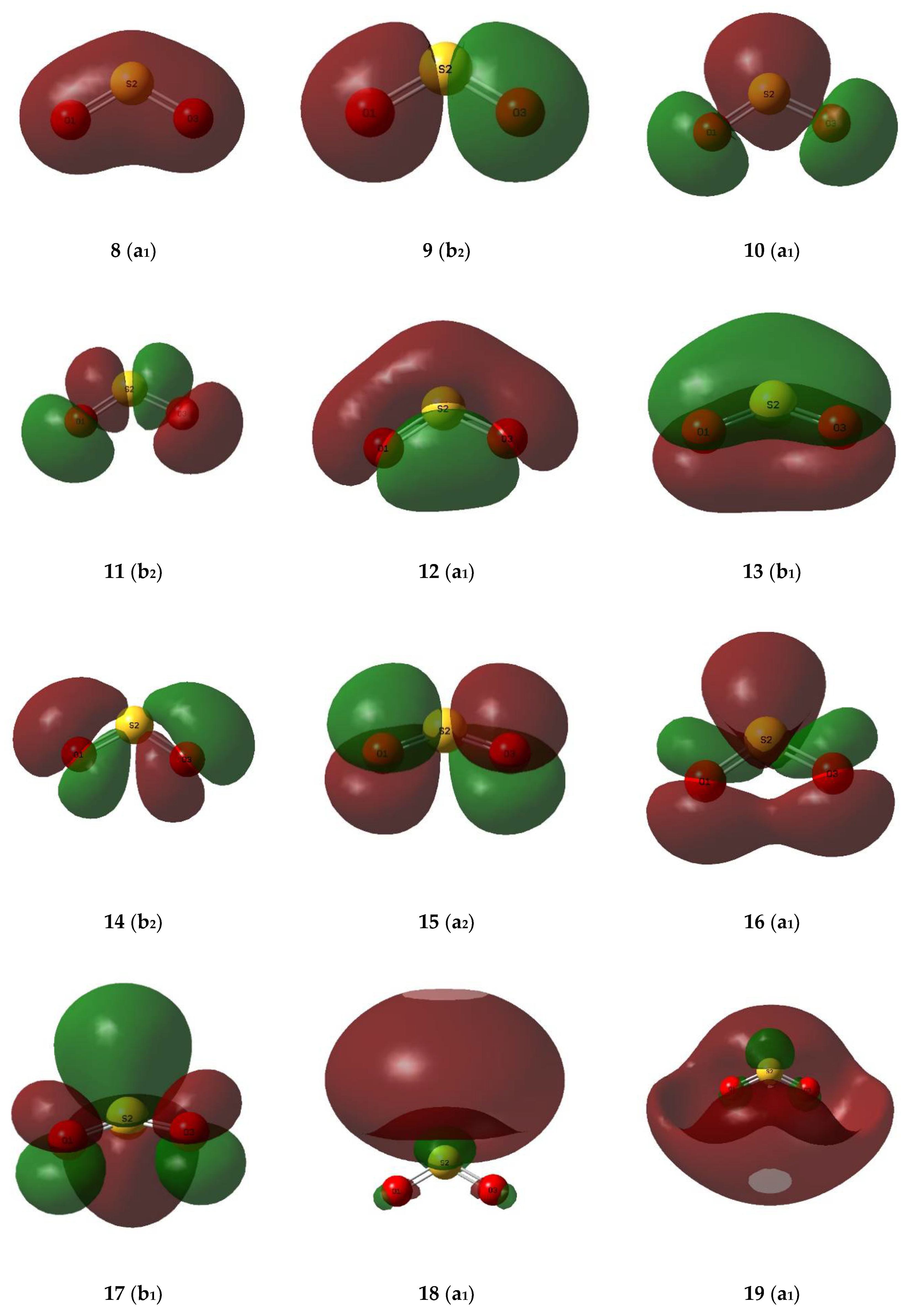
No.SymmetryEnergy/HApproximate Description a
1–7 core
8a1−1.48513σ(OSO)
9b2−1.38753σ(OSO)
10a1−0.88026lp(S)
11b2−0.69488lp(O)
12a1−0.68513lp(O)
13b1−0.65353π(OSO)
14b2−0.54142lp(O)
15a2−0.51405π(nb)(OSO)
16 (HOMO)a1−0.49779lp(O)
17 (LUMO)b1−0.00680π*(OSO)
18a10.06607σ*(OSO)
19a10.07129σ*(OSO)
a lp—lone pair; nb—non-bonding.
Table
Table 9. Properties of the valence molecular orbitals of the ozone monomer.
Table 9. Properties of the valence molecular orbitals of the ozone monomer.
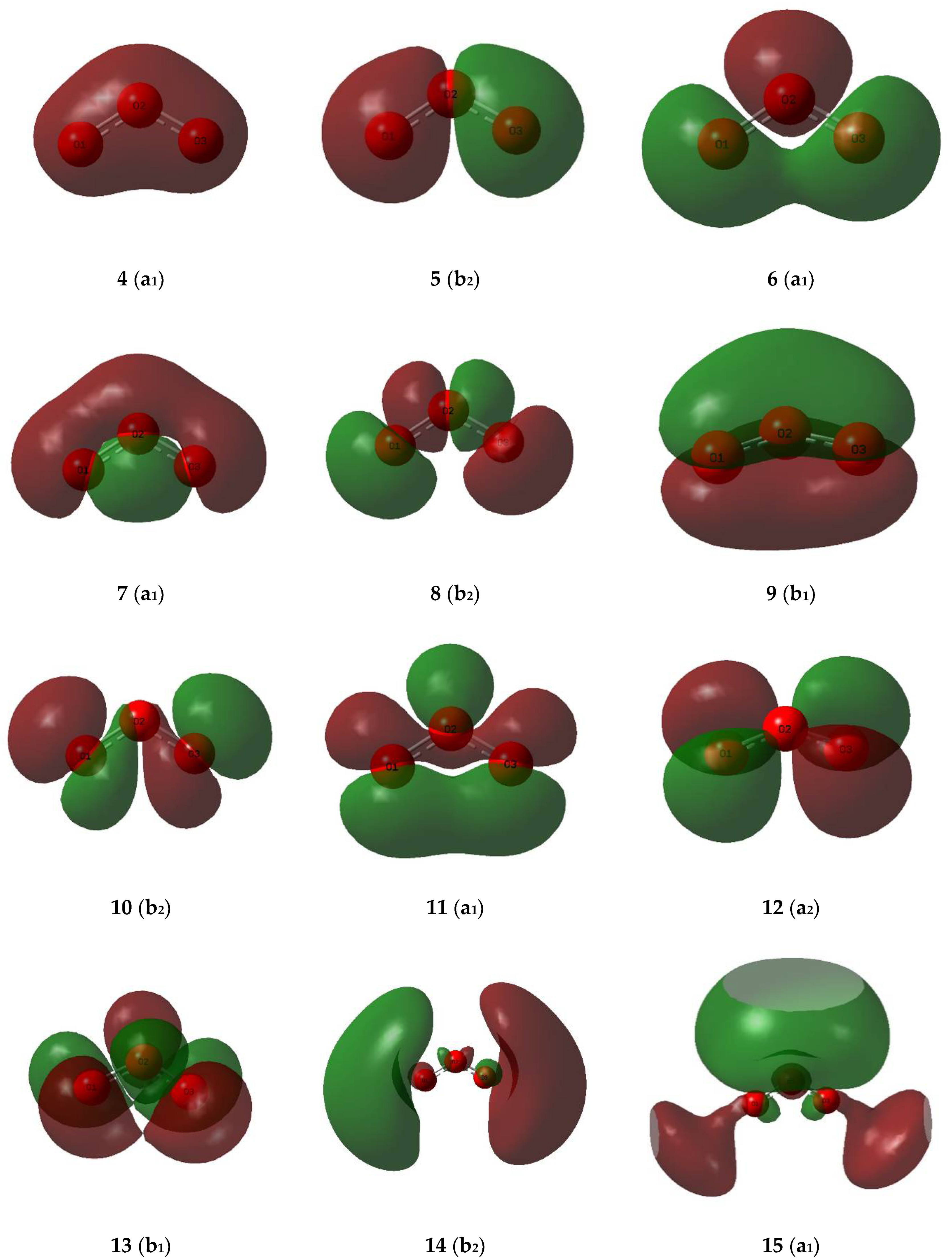
No.SymmetryEnergy/HApproximate Description a,b
1–3 core
4a1−1.74257σ(OOO)
5b2−1.42739σ(OOO)
6a1−1.09905lp(O2)
7a1−0.82911lp(O1) + lp(O3)
8b2−0.79824lp(O1) − lp(O3)
9b1−0.77653π(OOO)
10b2−0.56576lp(O1) − lp(O3)
11a1−0.55546lp(O1) + lp(O3)
12 (HOMO)a2−0.48829π(nb)(O1 − O3)
13 (LUMO)b1−0.05229π*(OOO)
14b20.10144σ*(OOO)
15a10.10566σ*(OOO)
a O1 and O3—terminal atoms; O2—central atom. b lp—lone pair; nb—non-bonding.
Table
Table 10. Wavenumbers and wavenumber shifts of some dimers and complexes of sulphur dioxide and ozone.
Table 10. Wavenumbers and wavenumber shifts of some dimers and complexes of sulphur dioxide and ozone.
SpeciesSO2O3
SymmetryMode aWavenumber
/cm−1		Shift
/cm−1		SymmetryModeWavenumber
/cm−1		Shift
/cm−1
SO2 dimer 5a′ν1 (ED)1300.5−5.0
ν2 (EA)1102.53.3
ν3 (ED)1099.1−0.1
ν4 (OP)500.06.7
ν5 (IP)494.61.3
a″ν9 (EA)1303.9−1.6
SO2 dimer 2agν1 (OP)1303.2−2.3
ν2 (IP)1101.42.2
ν3 (IP)494.91.6
auν7 (IP)1304.9−0.6
ν8 (OP)1101.52.3
ν9 (OP)495.82.5
O3 dimer 2 agν1 (OP)2419.3175.0
ν2 (IP)1150.2−7.7
ν3 (IP)743.11.6
auν7 (IP)2172.0−72.3
ν8 (OP)1151.6−6.3
ν9 (OP)742.81.3
SO2-O3 complex 2aaν2 1301.3−4.2aν1 2270.125.8
ν4 1096.5−2.7 ν3 1132.1−25.8
ν6 494.20.9 ν5740.4−1.1
SO2-O3 complex 5ba′ν31102.43.2a′ν12243.8−0.5
ν5 495.32.0 ν2 1159.21.3
a″ν9 1306.20.7 ν4 744.73.2
a ED—electron donor; EA—electron acceptor; IP—in-phase; OP—out-of-phase.
Table
Table 11. Calculated and experimental intramolecular wavenumbers of sulphur dioxide dimer 5.
Table 11. Calculated and experimental intramolecular wavenumbers of sulphur dioxide dimer 5.
ReferenceWavenumber/cm−1 a
ν1(a′)
νa(SO2)(ED)		ν2(a′)
νs(SO2)(EA)		ν3(a′)
νs(SO2)(ED)		ν4(a′)
δ(SO2)(OP)		ν5(a′)
δ(SO2)(IP)		ν9(a″)
νa(SO2)(EA)
This work b1300.51102.51099.1500.0494.61303.9
Ref. [13] c1343.1, 1345.2----1341.1
Ref. [15] d1348.21155.81153.7524.0521.71345.6
Ref. [19] d1349.21155.21153.9526.1524.01346.6
Ref. [20] d1346.61151.81154.2524.3522.41349.1
Ref. [21] c1341.31146.6-519.5--
Ref. [22] c1345.11155.41153.3527.2521.81341.1
Ref. [22] d1349.41156.11154.3526.5524.31346.5
Ref. [23] c1345.8, 1346.51154.8, 1155.51152.1, 1152.8 --1348.2, 1348.9
Ref. [23] e1344.4, 1345.21152.9, 1153.61149.9, 1150.5--1346.3, 1347.0
Ref. [23] f1338.8, 1339.61149.0, 1149.81145.7, 1146.3--1341.1, 1342.0
a EA—electron acceptor; ED—electron donor; OP—out-of-phase; IP—in-phase. b Calculated. c In argon. d In nitrogen. e In krypton. f In xenon.
Table
Table 12. Calculated and experimental bond length and bond angle of the ozone monomer.
Table 12. Calculated and experimental bond length and bond angle of the ozone monomer.
r(OO)/pm∠OOO/deg
Experimental (ref. [94])127.2116.8
MP2 (this work)128.38116.62
Difference1.18−0.18
CASSCF (this work)125.51115.82
Difference−1.69−0.98
CCSD/TZ+2Pf (ref. [89])125.2117.5
Difference−1.970.7
Table
Table 13. Calculated and experimental wavenumbers (cm−1) of the ozone monomer.
Table 13. Calculated and experimental wavenumbers (cm−1) of the ozone monomer.
ν1 (a1)ν2 (a1)ν3 (b2)
Experimental (ref. [91])11357161089
MP2 (this work)1157.9741.52244.3
Ratio1.021.042.06
CASSCF (this work)1092.3770.21358.4
Ratio0.961.081.25
CCSD/TZ+2Pf (ref. [89])12807581261
Ratio1.131.061.16
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Ford, T.A. The Structures, Molecular Orbital Properties and Vibrational Spectra of the Homo- and Heterodimers of Sulphur Dioxide and Ozone. An Ab Initio Study. Molecules 2021, 26, 626. https://doi.org/10.3390/molecules26030626

AMA Style

Ford TA. The Structures, Molecular Orbital Properties and Vibrational Spectra of the Homo- and Heterodimers of Sulphur Dioxide and Ozone. An Ab Initio Study. Molecules. 2021; 26(3):626. https://doi.org/10.3390/molecules26030626

Chicago/Turabian Style

Ford, Thomas A. 2021. "The Structures, Molecular Orbital Properties and Vibrational Spectra of the Homo- and Heterodimers of Sulphur Dioxide and Ozone. An Ab Initio Study" Molecules 26, no. 3: 626. https://doi.org/10.3390/molecules26030626

APA Style

Ford, T. A. (2021). The Structures, Molecular Orbital Properties and Vibrational Spectra of the Homo- and Heterodimers of Sulphur Dioxide and Ozone. An Ab Initio Study. Molecules, 26(3), 626. https://doi.org/10.3390/molecules26030626

Article Metrics

Back to TopTop