Organic Semiconductor Micro/Nanocrystals for Laser Applications
Abstract
:1. Introduction
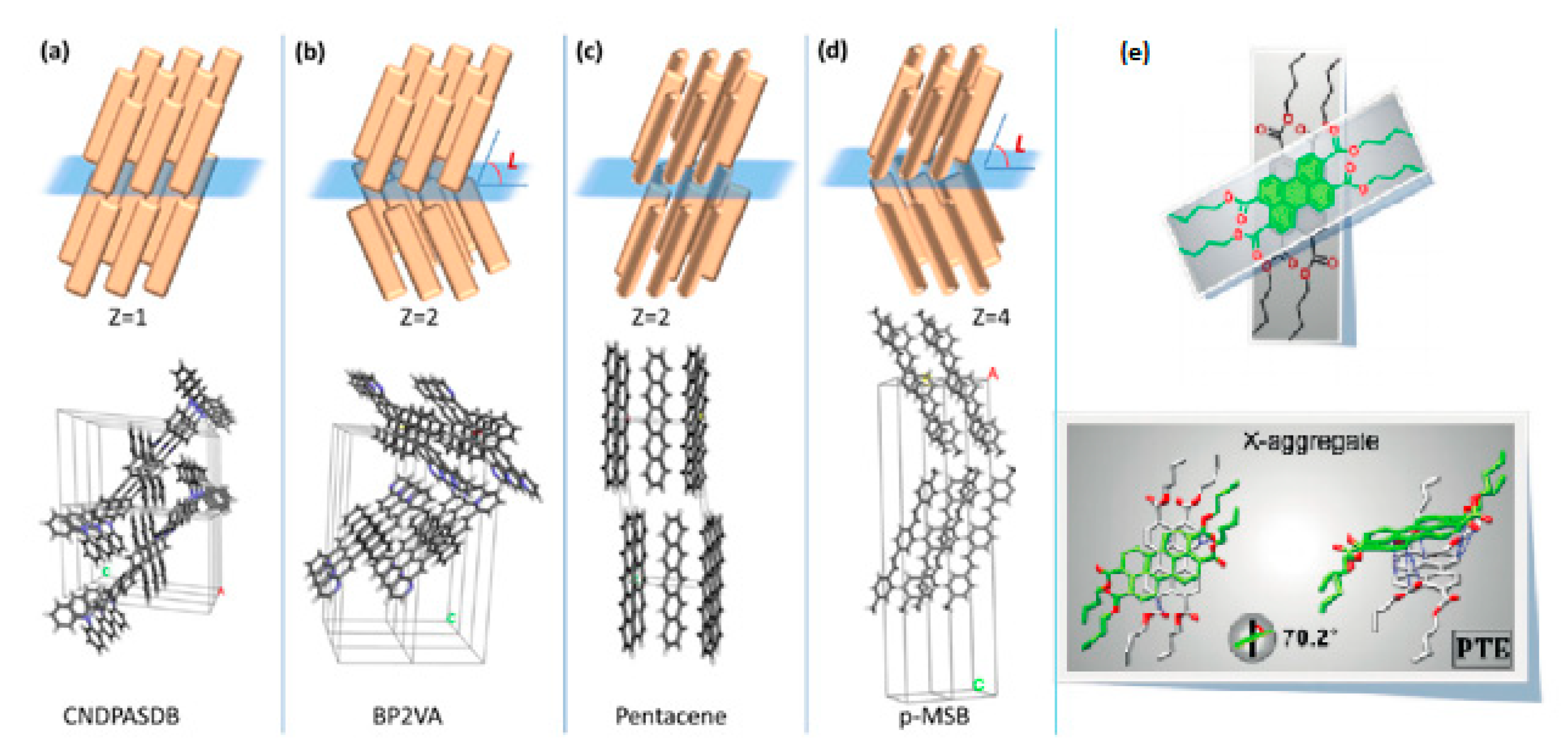
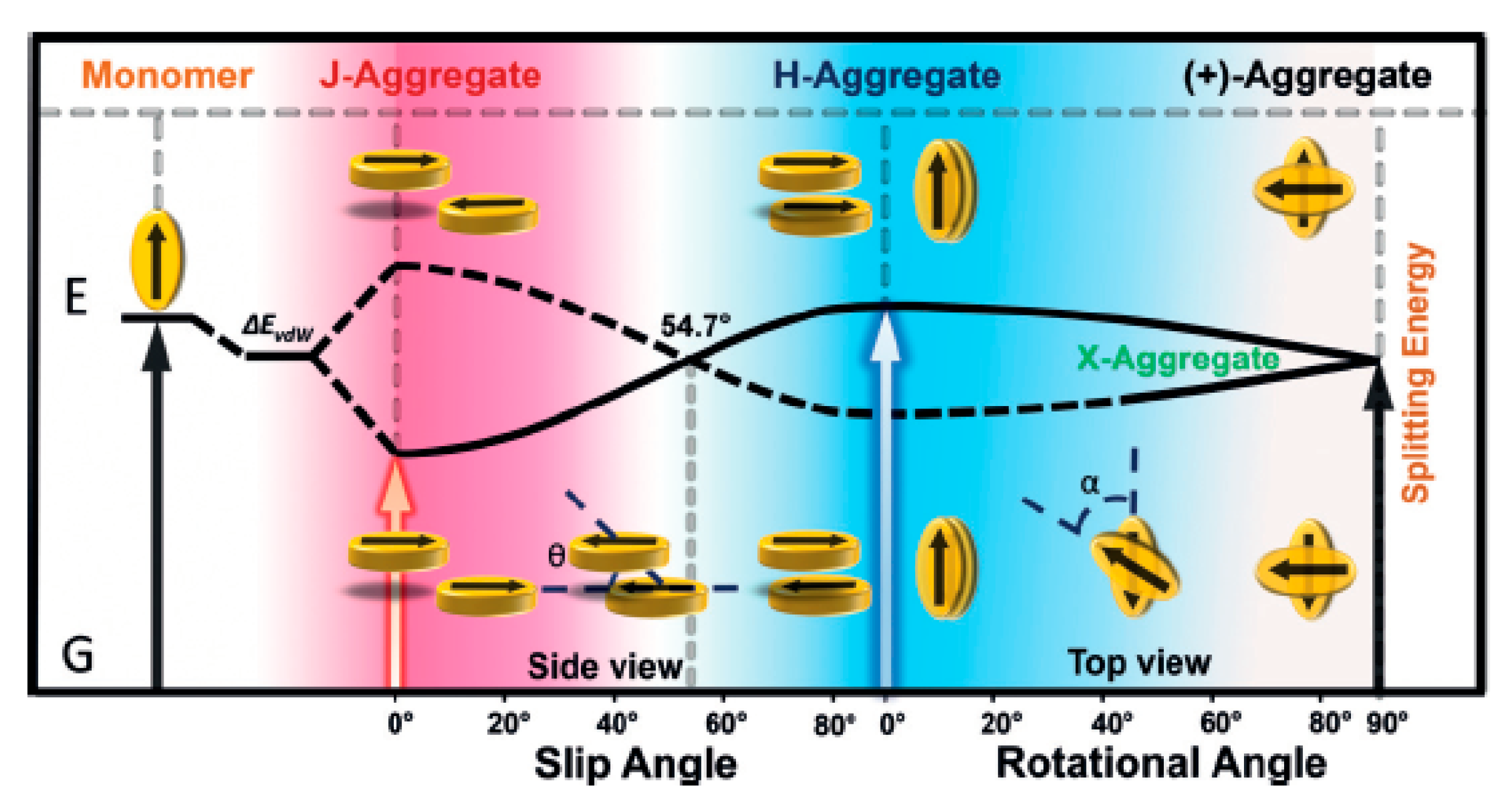
2. Molecular Packing in Crystals
3. The Growth Techniques for the Preparation of Organic Semiconductor Micro-/Nanocrystals
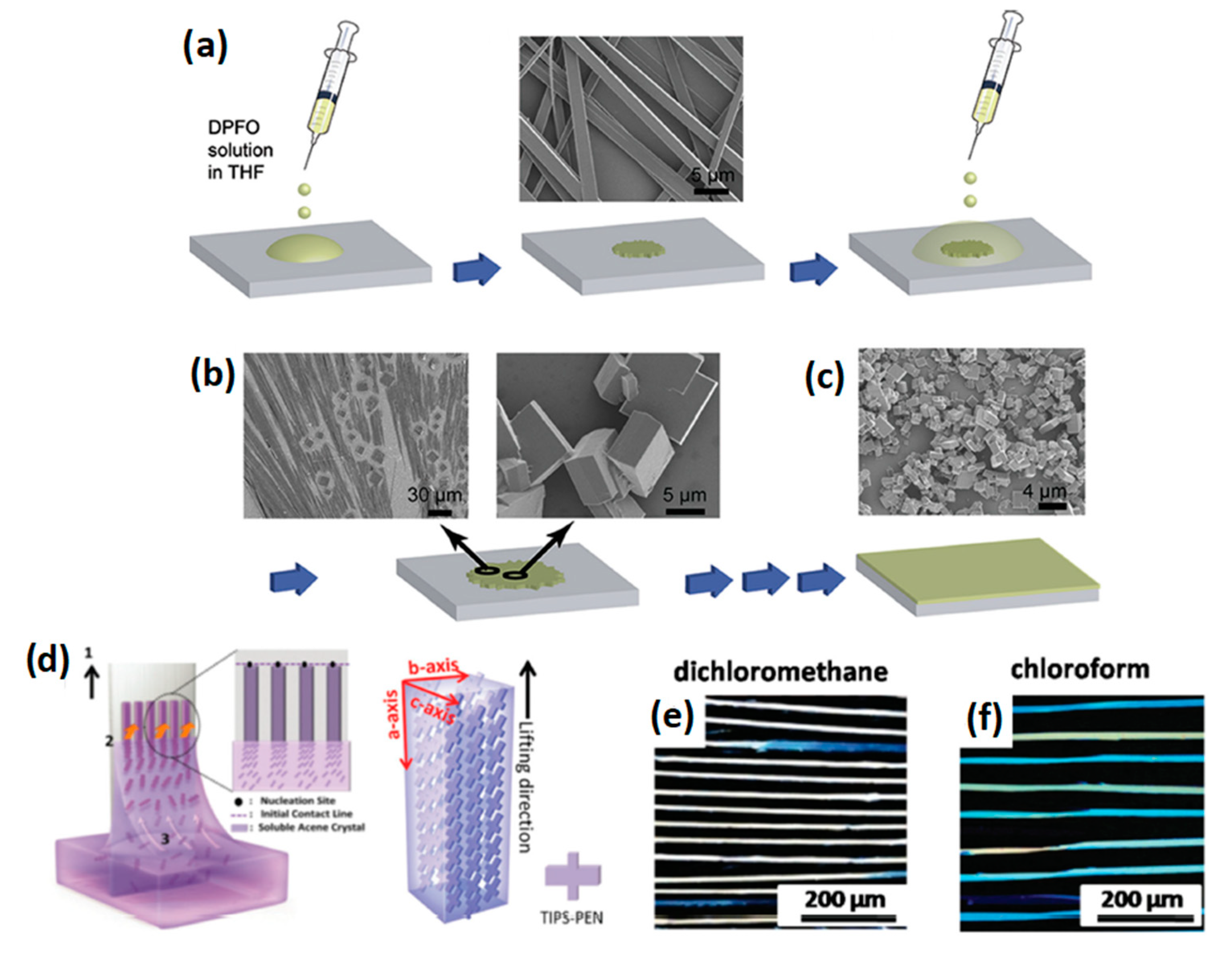
3.1. Solution-Processing Techniques
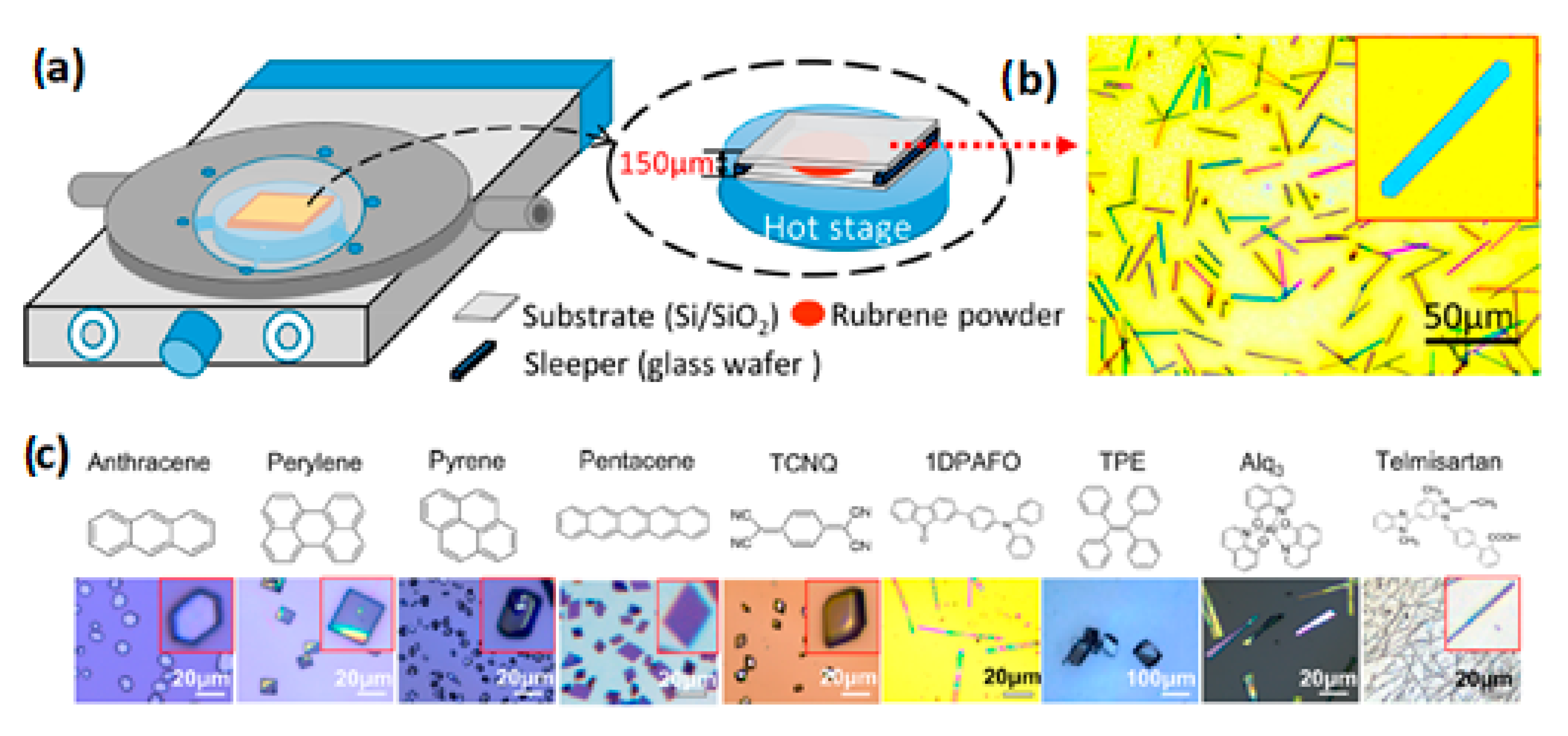
3.1.1. Drop-Casting
3.1.2. Dip-Coating
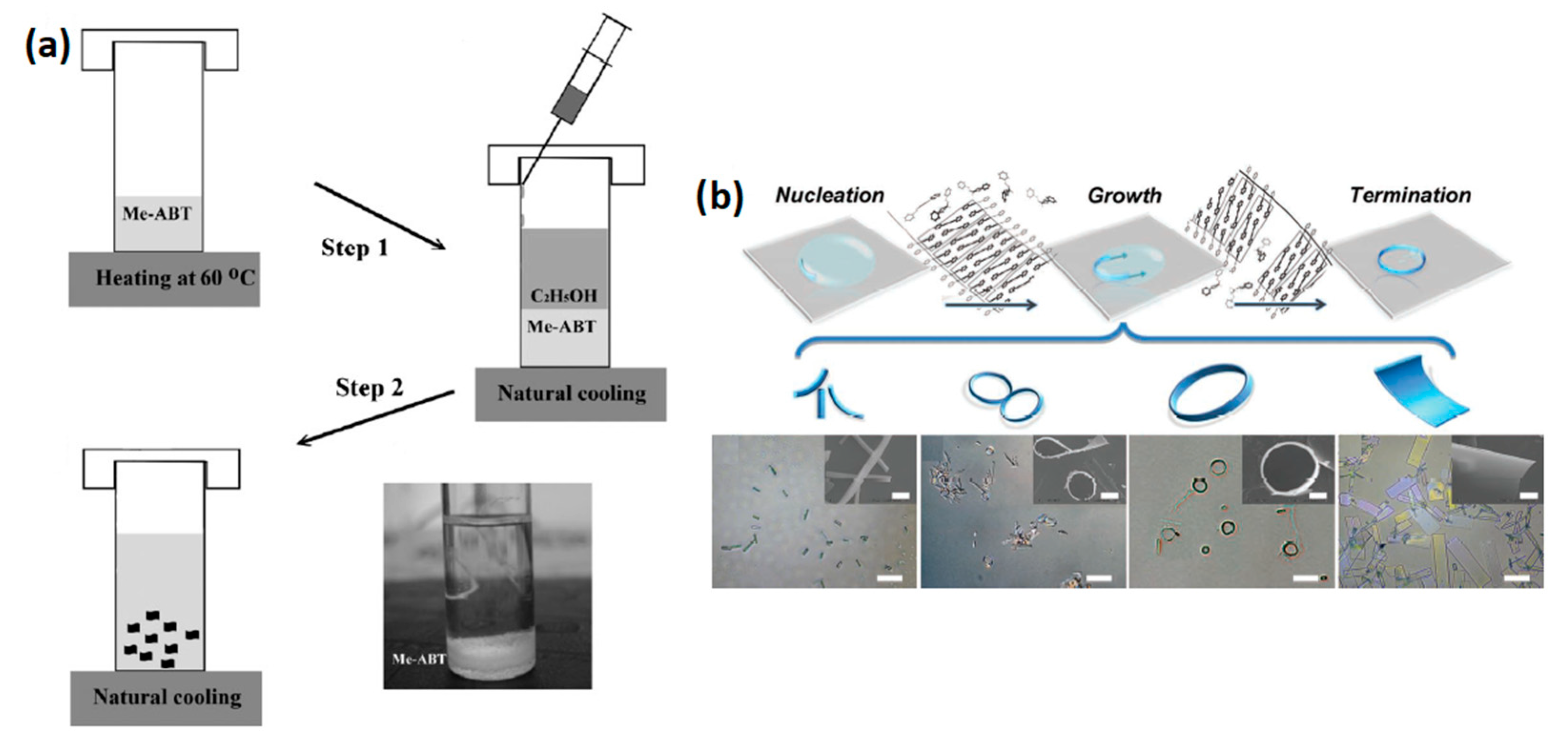
3.1.3. Solvent Exchange
3.1.4. Solvent Vapor Diffusion (SVD)
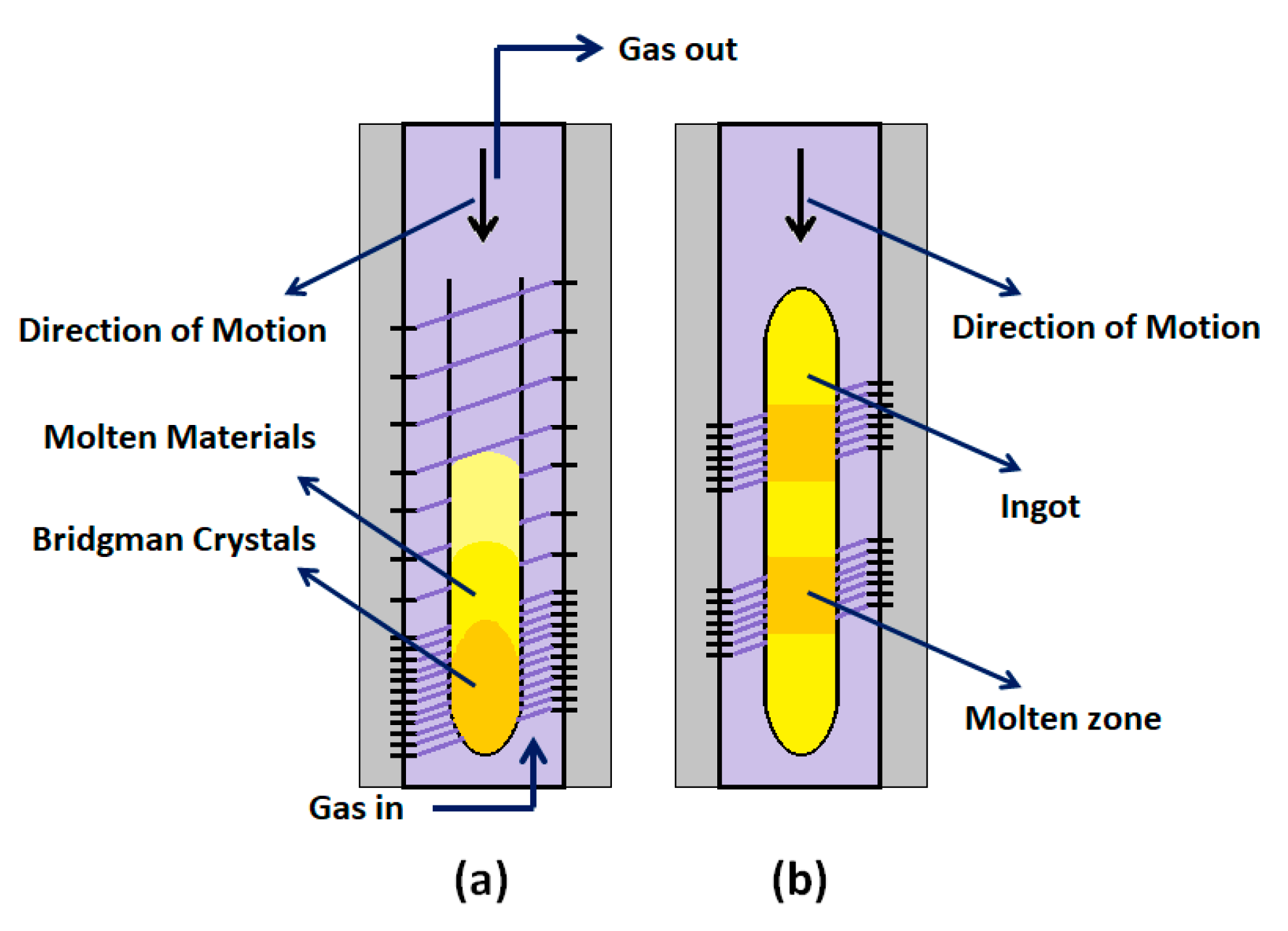
3.2. Melting Processed Crystals
3.3. Vapor Processed Crystals
3.3.1. Physical Vapor Transport (PVT)
3.3.2. Microspacing Sublimation
4. Organic Solid Lasers
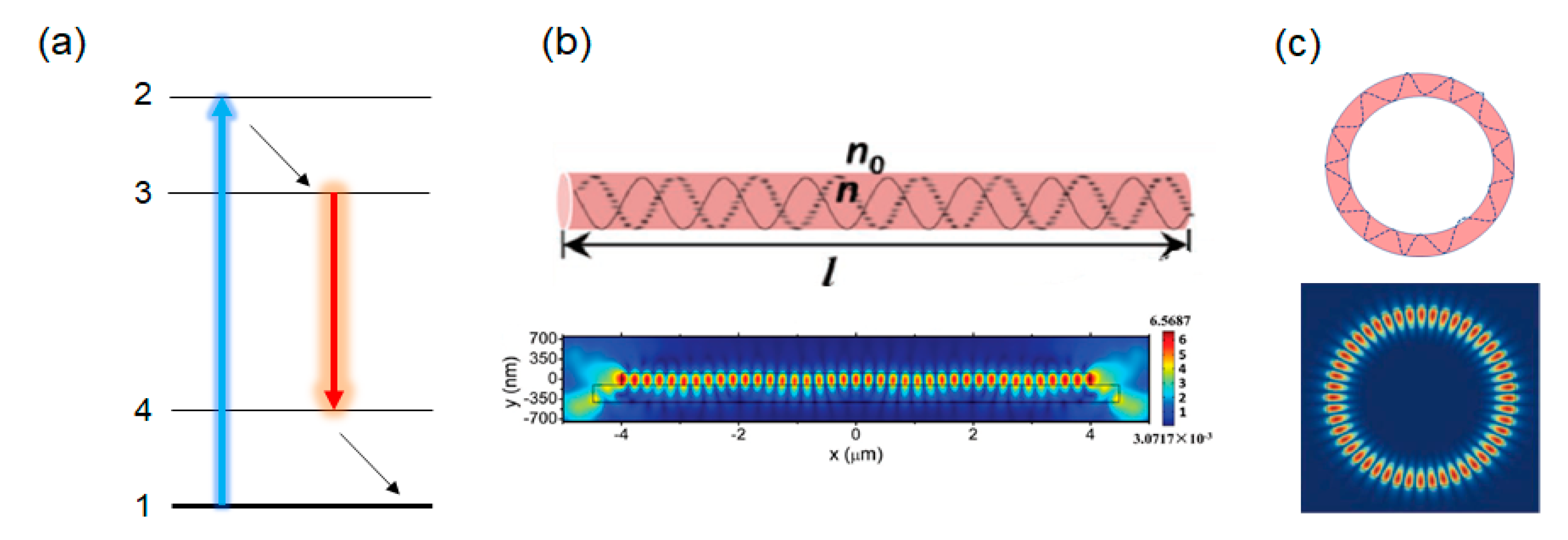
4.1. 1D Fabry-Perot Resonators
4.2. Whispering Gallery Mode Resonators
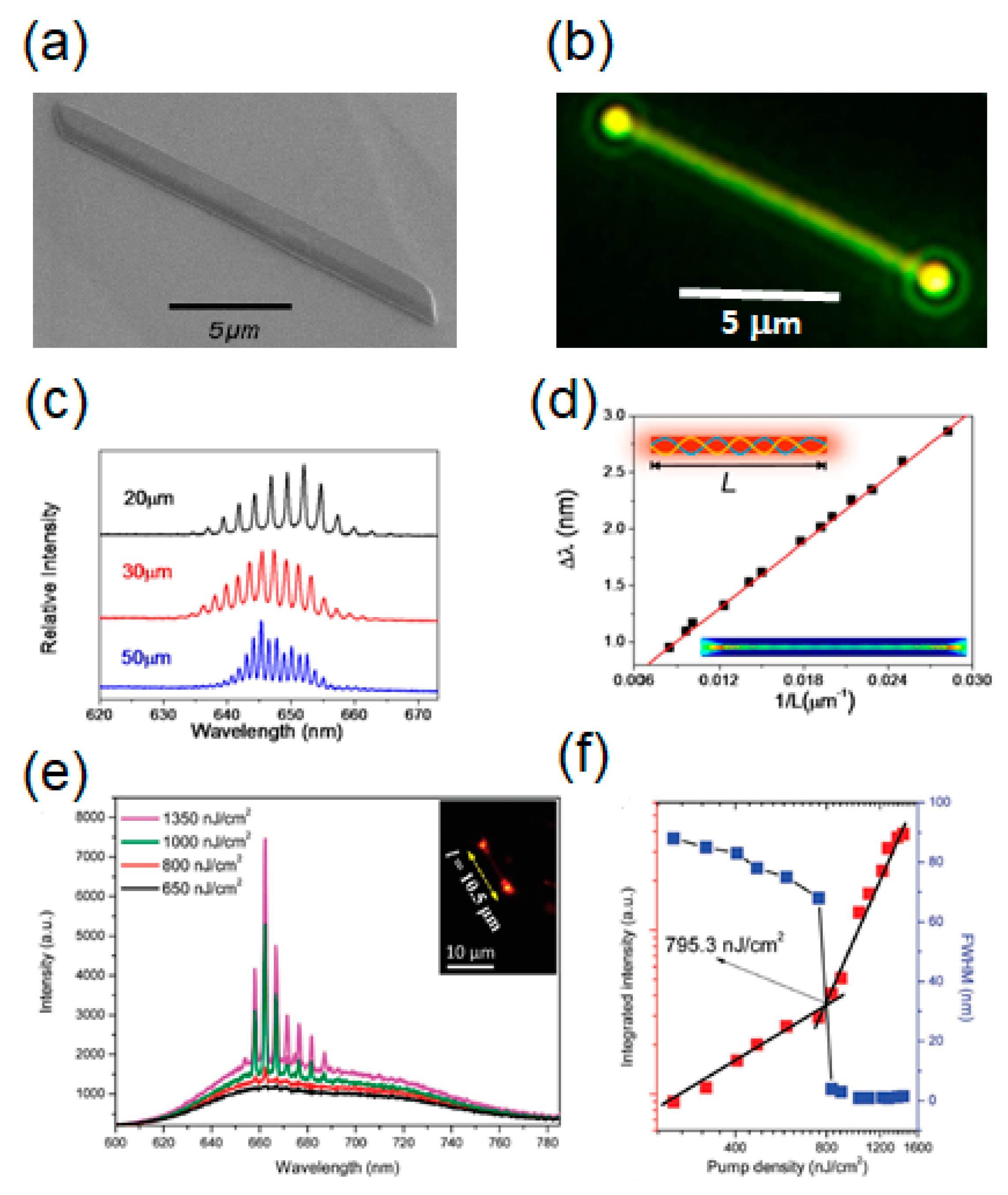
4.3. Lasers Based on 1D Fabry-Perot Resonators
4.4. Lasers Based on Whispering Gallery Mode Resonators
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deng, W.; Zhang, X.; Zhang, X.; Guo, J.; Jie, J. Ordered and Patterned Assembly of Organic Micro/Nanocrystals for Flexible Electronic and Optoelectronic Devices. Adv. Mater. Technol. 2017, 2, 1600280. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, L.; Wang, C.; Yang, F.; Ren, X.; Zhang, X.; Dong, H.; Hu, W. Organic Crystalline Materials in Flexible Electronics. Chem. Soc. Rev. 2019, 48, 1492–1530. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Dong, H.; Jiang, L.; Hu, W. Organic Semiconductor Crystals. Chem. Soc. Rev. 2018, 47, 422–500. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.J.; Jie, J.S.; Deng, W.; Shang, Q.X.; Wang, J.C.; Wang, H.; Chen, X.F.; Zhang, X.H. Alignment and Patterning of Ordered Small-Molecule Organic Semiconductor Micro-/Nanocrystals for Device Applications. Adv. Mater. 2016, 28, 2475–2503. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Hu, W.; Liu, Y.; Zhu, D. Micro- and Nanocrystals of Organic Semiconductors. Acc. Chem. Res. 2010, 43, 529–540. [Google Scholar] [CrossRef]
- Garcia-Frutos, E.M. Small Organic Single-Crystalline One-Dimensional Micro- and Nanostructures for Miniaturized Devices. J. Mater. Chem. C 2013, 1, 3633–3645. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.S.; Fu, H.; Peng, A.; Ma, Y.; Liao, Q.; Yao, J. Construction and Optoelectronic Properties of Organic One-Dimensional Nanostructures. Acc. Chem. Res. 2010, 43, 409–418. [Google Scholar] [CrossRef] [PubMed]
- Park, K.S.; Cho, B.; Baek, J.; Hwang, J.K.; Lee, H.; Sung, M.M. Single-Crystal Organic Nanowire Electronics by Direct Printing from Molecular Solutions. Adv. Funct. Mater. 2013, 23, 4776–4784. [Google Scholar] [CrossRef] [Green Version]
- Deng, W.; Zhang, X.; Gong, C.; Zhang, Q.; Xing, Y.; Wu, Y.; Zhang, X.; Jie, J. Aligned Nanowire Arrays on Thin Flexible Substrates for Organic Transistors with High Bending Stability. J. Mater. Chem. C 2014, 2, 1314–1320. [Google Scholar] [CrossRef]
- Yang, Y.S.; Yasuda, T.; Kakizoe, H.; Mieno, H.; Kino, H.; Tateyama, Y.; Adachi, C. High Performance Organic Field-Effect Transistors Based on Single-Crystal Microribbons and Microsheets of Solution-Processed Dithieno[3{,}2-b:2′{,}3′-d]Thiophene Derivatives. Chem. Commun. 2013, 49, 6483–6485. [Google Scholar] [CrossRef]
- Briseno, A.L.; Mannsfeld, S.C.B.; Jenekhe, S.A.; Bao, Z.; Xia, Y. Introducing Organic Nanowire Transistors. Mater. Today 2008, 11, 38–47. [Google Scholar] [CrossRef]
- Martín, C.; Kennes, K.; der Auweraer, M.; Hofkens, J.; de Miguel, G.; García-Frutos, E.M. Self-Assembling Azaindole Organogel for Organic Light-Emitting Devices (OLEDs). Adv. Funct. Mater. 2017, 27, 1702176. [Google Scholar] [CrossRef]
- Mei, J.; Hong, Y.; Lam, J.W.Y.; Qin, A.; Tang, Y.; Tang, B.Z. Aggregation-Induced Emission: The Whole Is More Brilliant than the Parts. Adv. Mater. 2014, 26, 5429–5479. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Yao, J.; Fu, H. Solvent-Assisted Self-Assembly of Fullerene into Single-Crystal Ultrathin Microribbons as Highly Sensitive UV–Visible Photodetectors. ACS Nano 2013, 7, 7573–7582. [Google Scholar] [CrossRef]
- Zhang, X.; Jie, J.; Zhang, W.; Zhang, C.; Luo, L.; He, Z.; Zhang, X.; Zhang, W.; Lee, C.; Lee, S. Photoconductivity of a Single Small-Molecule Organic Nanowire. Adv. Mater. 2008, 20, 2427–2432. [Google Scholar] [CrossRef]
- Zhao, F.; Liu, C.; Sun, Y.; Li, Q.; Zhao, J.; Li, Z.; Zhang, B.; Lu, C.; Li, Q.; Qiao, S.; et al. Controlled Self-Assembly of Triazatruxene Overlength Microwires for Optical Waveguide. Org. Electron. 2019, 74, 276–281. [Google Scholar] [CrossRef]
- Gierschner, J.; Varghese, S.; Park, S.Y. Organic Single Crystal Lasers: A Materials View. Adv. Opt. Mater. 2016, 4, 348–364. [Google Scholar] [CrossRef]
- Hayashi, S.; Koizumi, T.; Kamiya, N. 2,5-Dimethoxybenzene-1,4-Dicarboxaldehyde: An Emissive Organic Crystal and Highly Efficient Fluorescent Waveguide. Chempluschem 2019, 84, 247–251. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, J.; Zhao, Y.S. Organic Micro/Nanoscale Lasers. Acc. Chem. Res. 2016, 49, 1691–1700. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, Y.-Y.; Liu, X.; Lin, H.; Gao, K.; Lai, W.-Y.; Huang, W. Organic Solid-State Lasers: A Materials View and Future Development. Chem. Soc. Rev. 2020, 49, 5885–5944. [Google Scholar] [CrossRef] [PubMed]
- Briseno, A.L.; Tseng, R.J.; Ling, M.-M.; Falcao, E.H.L.; Yang, Y.; Wudl, F.; Bao, Z. High-Performance Organic Single-Crystal Transistors on Flexible Substrates. Adv. Mater. 2006, 18, 2320–2324. [Google Scholar] [CrossRef]
- Yu, P.; Zhen, Y.; Dong, H.; Hu, W. Crystal Engineering of Organic Optoelectronic Materials. Chem 2019, 5, 2814–2853. [Google Scholar] [CrossRef]
- Mikhnenko, O.V.; Blom, P.W.M.; Nguyen, T.-Q. Exciton Diffusion in Organic Semiconductors. Energy Environ. Sci. 2015, 8, 1867–1888. [Google Scholar] [CrossRef]
- Lunt, R.R.; Benziger, J.B.; Forrest, S.R. Relationship between Crystalline Order and Exciton Diffusion Length in Molecular Organic Semiconductors. Adv. Mater. 2010, 22, 1233–1236. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hasegawa, T. 18-Advances in Device Fabrication Scale-up Methods. In Handbook of Organic Materials for Electronic and Photonic Devices (Second Edition); Ostroverkhova, O., Ed.; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publishing: Sawston, UK; Cambridge, UK, 2019; pp. 579–597. [Google Scholar] [CrossRef]
- Wang, W.; Wang, L.; Dai, G.; Deng, W.; Zhang, X.; Jie, J.; Zhang, X. Controlled Growth of Large-Area Aligned Single-Crystalline Organic Nanoribbon Arrays for Transistors and Light-Emitting Diodes Driving. Nano-Micro Lett. 2017, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Gierschner, J.; Park, S.Y. Luminescent Distyrylbenzenes: Tailoring Molecular Structure and Crystalline Morphology. J. Mater. Chem. C 2013, 1, 5818–5832. [Google Scholar] [CrossRef]
- Gierschner, J.; Huang, Y.S.; Van Averbeke, B.; Cornil, J.; Friend, R.H.; Beljonne, D. Excitonic versus Electronic Couplings in Molecular Assemblies: The Importance of Non-Nearest Neighbor Interactions. J. Chem. Phys. 2009, 130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gierschner, J.; Lüer, L.; Milián-Medina, B.; Oelkrug, D.; Egelhaaf, H.J. Highly Emissive H-Aggregates or Aggregation-Induced Emission Quenching? The Photophysics of All-Trans Para-Distyrylbenzene. J. Phys. Chem. Lett. 2013, 4, 2686–2697. [Google Scholar] [CrossRef]
- Coropceanu, V.; Cornil, J.; da Silva Filho, D.A.; Olivier, Y.; Silbey, R.; Brédas, J.L. Charge Transport in Organic Semiconductors. Chem. Rev. 2007, 107, 926–952. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Wang, L.; Bai, F.; Jiang, Y.; Guo, J.; Xu, B.; Tian, W. Polymorphism Dependent Charge Transport Property of 9,10-Bis((E)-2-(Pyrid-2-Yl)Vinyl)Anthracene: A Theoretical Study. RSC Adv. 2015, 5, 18875–18880. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, H.; Hu, W. Organic Semiconductor Single Crystals for Electronics and Photonics. Adv. Mater. 2018, 30, 1–34. [Google Scholar] [CrossRef]
- Kaufmann, C.; Bialas, D.; Stolte, M.; Würthner, F. Discrete Ï€-Stacks of Perylene Bisimide Dyes within Folda-Dimers: Insight into Long- and Short-Range Exciton Coupling. J. Am. Chem. Soc. 2018, 140, 9986–9995. [Google Scholar] [CrossRef]
- Curtis, M.D.; Cao, J.; Kampf, J.W. Solid-State Packing of Conjugated Oligomers: From π-Stacks to the Herringbone Structure. J. Am. Chem. Soc. 2004, 126, 4318–4328. [Google Scholar] [CrossRef] [PubMed]
- Cornil, J.; Beljonne, D.; Calbert, J.P.; Brédas, J.L. Interchain Interactions in Organic $π$-Conjugated Materials: Impact on Electronic Structure, Optical Response, and Charge Transport. Adv. Mater. 2001, 13, 1053–1067. [Google Scholar] [CrossRef]
- Spano, F.C. The Spectral Signatures of Frenkel Polarons in H- And J-Aggregates. Acc. Chem. Res. 2010, 43, 429–439. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, W.; Jiang, X.F.; Wang, C.; Zhou, X.; Xu, B.; Liu, L.; Xie, Z.; Ma, Y. Magic-Angle Stacking and Strong Intermolecular $π$-$π$ Interaction in a Perylene Bisimide Crystal: An Approach for Efficient Near-Infrared (NIR) Emission and High Electron Mobility. J. Phys. Chem. Lett. 2018, 9, 596–600. [Google Scholar] [CrossRef]
- Hestand, N.J.; Spano, F.C. Interference between Coulombic and CT-Mediated Couplings in Molecular Aggregates: H- to J-Aggregate Transformation in Perylene-Based $π$-Stacks. J. Chem. Phys. 2015, 143. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Shen, F.; Wang, H.; He, F.; Xie, Z.; Zhang, H.; Wang, Z.; Liu, L.; Li, F.; Hanif, M.; et al. Supramolecular Network Conducting the Formation of Uniaxially Oriented Molecular Crystal of Cyano Substituted Oligo(p-Phenylene Vinylene) and Its Amplified Spontaneous Emission (ASE) Behavior. Chem. Mater. 2008, 20, 7312–7318. [Google Scholar] [CrossRef]
- Li, C.; Hanif, M.; Li, X.; Zhang, S.; Xie, Z.; Liu, L.; Yang, B.; Su, S.; Ma, Y. Effect of Cyano-Substitution in Distyrylbenzene Derivatives on Their Fluorescence and Electroluminescence Properties. J. Mater. Chem. C 2016, 4, 7478–7484. [Google Scholar] [CrossRef]
- Fang, H.-H.; Chen, Q.-D.; Yang, J.; Xia, H.; Ma, Y.-G.; Wang, H.-Y.; Sun, H.-B. Two-Photon Excited Highly Polarized and Directional Upconversion Emission from Slab Organic Crystals. Opt. Lett. 2010, 35. [Google Scholar] [CrossRef]
- Mattheus, C.C.; Dros, A.B.; Baas, J.; Meetsma, A.; De Boer, J.L.; Palstra, T.T.M. Polymorphism in Pentacene. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 2001, 57, 939–941. [Google Scholar] [CrossRef] [Green Version]
- Cao, M.; Zhang, C.; Cai, Z.; Xiao, C.; Chen, X.; Yi, K.; Yang, Y.; Lu, Y.; Wei, D. Enhanced Photoelectrical Response of Thermodynamically Epitaxial Organic Crystals at the Two-Dimensional Limit. Nat. Commun. 2019, 10, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Guerrini, M.; Calzolari, A.; Corni, S. Solid-State Effects on the Optical Excitation of Push-Pull Molecular J-Aggregates by First-Principles Simulations. ACS Omega 2018, 3, 10481–10486. [Google Scholar] [CrossRef]
- Liu, J.; Meng, L.; Zhu, W.; Zhang, C.; Zhang, H.; Yao, Y.; Wang, Z.; He, P.; Zhang, X.; Wang, Y.; et al. A Cross-Dipole Stacking Molecule of an Anthracene Derivative: Integrating Optical and Electrical Properties. J. Mater. Chem. C 2015, 3, 3068–3071. [Google Scholar] [CrossRef]
- Ramakrishnan, R.; Niyas, M.A.; Lijina, M.P.; Hariharan, M. Distinct Crystalline Aromatic Structural Motifs: Identification, Classification, and Implications. Acc. Chem. Res. 2019, 52, 3075–3086. [Google Scholar] [CrossRef] [PubMed]
- Ge, Y.; Wen, Y.; Liu, H.; Lu, T.; Yu, Y.; Zhang, X.; Li, B.; Zhang, S.T.; Li, W.; Yang, B. A Key Stacking Factor for the Effective Formation of Pyrene Excimer in Crystals: Degree of $π$-$π$ Overlap. J. Mater. Chem. C 2020, 8, 11830–11838. [Google Scholar] [CrossRef]
- Sebastian, E.; Philip, A.M.; Benny, A.; Hariharan, M. Null Exciton Splitting in Chromophoric Greek Cross (+) Aggregate. Angew. Chemie-Int. Ed. 2018, 57, 15696–15701. [Google Scholar] [CrossRef]
- Dong, Y.; Xu, B.; Zhang, J.; Tan, X.; Wang, L.; Chen, J.; Lv, H.; Wen, S.; Li, B.; Ye, L.; et al. Piezochromic Luminescence Based on the Molecular Aggregation of 9,10-Bis((E)-2-(Pyrid-2-Yl)Vinyl)Anthracene. Angew. Chemie-Int. Ed. 2012, 51, 10782–10785. [Google Scholar] [CrossRef] [PubMed]
- Fang, H.H.; Yang, J.; Feng, J.; Yamao, T.; Hotta, S.; Sun, H.B. Functional Organic Single Crystals for Solid-State Laser Applications. Laser Photonics Rev. 2014, 8, 687–715. [Google Scholar] [CrossRef]
- Kabe, R.; Nakanotani, H.; Sakanoue, T.; Yahiro, M.; Adachi, C. Effect of Molecular Morphology on Amplified Spontaneous Emission of Bis-Styrylbenzene Derivatives. Adv. Mater. 2009, 21, 4034–4038. [Google Scholar] [CrossRef]
- Rhodes, S.; Liang, W.; Wang, X.; Reddy, N.R.; Fang, J. Transition from H-Aggregate Nanotubes to J-Aggregate Nanoribbons. J. Phys. Chem. C 2020, 124, 11722–11729. [Google Scholar] [CrossRef]
- Li, J.; Zhou, K.; Liu, J.; Zhen, Y.; Liu, L.; Zhang, J.; Dong, H.; Zhang, X.; Jiang, L.; Hu, W. Aromatic Extension at 2,6-Positions of Anthracene toward an Elegant Strategy for Organic Semiconductors with Efficient Charge Transport and Strong Solid State Emission. J. Am. Chem. Soc. 2017, 139, 17261–17264. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhang, H.; Dong, H.; Meng, L.; Jiang, L.; Jiang, L.; Wang, Y.; Yu, J.; Sun, Y.; Hu, W.; et al. High Mobility Emissive Organic Semiconductor. Nat. Commun. 2015, 6, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.Z.; Liao, L.S.; Wang, X.D. Controllable Synthesis of Organic Microcrystals with Tunable Emission Color and Morphology Based on Molecular Packing Mode. Small 2018, 14, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.; Zhou, K.; Hu, M.; Li, Q.; Liu, Y.; Zhang, H.; Jing, J.; Dong, H.; Xu, B.; Hu, W.; et al. Integrating Efficient Optical Gain in High-Mobility Organic Semiconductors for Multifunctional Optoelectronic Applications. Adv. Funct. Mater. 2018, 28, 1–8. [Google Scholar] [CrossRef]
- Kloc, C.; Siegrist, T.; Pflaum, J. Growth of Single-Crystal Organic Semiconductors. In Springer Handbook of Crystal Growth; Dhanaraj, G., Byrappa, K., Prasad, V., Dudley, M., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2010; pp. 845–867. [Google Scholar]
- Dunitz, J.D.; Gavezzotti, A. How Molecules Stick Together in Organic Crystals: Weak Intermolecular Interactions. Chem. Soc. Rev. 2009, 38, 2622–2633. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Dong, H.; Meng, Q.; Li, H.; He, M.; Wei, Z.; He, Y.; Hu, W. Millimeter-Sized Molecular Monolayer Two-Dimensional Crystals. Adv. Mater. 2011, 23, 2059–2063. [Google Scholar] [CrossRef] [PubMed]
- Ito, F.; Fujimori, J.I. Fluorescence Visualization of the Molecular Assembly Processes during Solvent Evaporation via Aggregation-Induced Emission in a Cyanostilbene Derivative. CrystEngComm 2014, 16, 9779–9782. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Liang, Z.; Liu, Y.; Wang, X.; Zhao, N.; Miao, Q.; Hu, W.; Xu, J. Single Crystal N-Channel Field Effect Transistors from Solution-Processed Silylethynylated Tetraazapentacene. J. Mater. Chem. 2011, 21, 15201–15204. [Google Scholar] [CrossRef]
- Liu, D.; Li, C.; Niu, S.; Li, Y.; Hu, M.; Li, Q.; Zhu, W.; Zhang, X.; Dong, H.; Hu, W. A Case Study of Tuning the Crystal Polymorphs of Organic Semiconductors towards Simultaneously Improved Light Emission and Field-Effect Properties. J. Mater. Chem. C 2019, 7, 5925–5930. [Google Scholar] [CrossRef]
- Inada, Y.; Yamao, T.; Inada, M.; Itami, T.; Hotta, S. Giant Organic Single-Crystals of a Thiophene/Phenylene Co-Oligomer toward Device Applications. Synth. Met. 2011, 161, 1869–1877. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Y.; Wei, Z.; Li, H.; Xu, W.; Hu, W. Biphase Micro/Nanometer Sized Single Crystals of Organic Semiconductors: Control Synthesis and Their Strong Phase Dependent Optoelectronic Properties. Appl. Phys. Lett. 2010, 96, 94–97. [Google Scholar] [CrossRef]
- Xu, J.; Semin, S.; Cremers, J.; Wang, L.; Savoini, M.; Fron, E.; Coutino, E.; Chervy, T.; Wang, C.; Li, Y.; et al. Controlling Microsized Polymorphic Architectures with Distinct Linear and Nonlinear Optical Properties. Adv. Opt. Mater. 2015, 3, 948–956. [Google Scholar] [CrossRef]
- Wakahara, T.; D’Angelo, P.; Miyazawa, K.; Nemoto, Y.; Ito, O.; Tanigaki, N.; Bradley, D.D.C.; Anthopoulos, T.D. Fullerene/Cobalt Porphyrin Hybrid Nanosheets with Ambipolar Charge Transporting Characteristics. J. Am. Chem. Soc. 2012, 134, 7204–7206. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.; Chae, S.H.; Hoang, M.H.; Kim, K.H.; Huh, J.A.; Kim, Y.; Kim, S.J.; Choi, D.H.; Lee, S.J. An Unsymmetrically $π$-Extended Porphyrin-Based Single-Crystal Field-Effect Transistor and Its Anisotropic Carrier-Transport Behavior. Chem.-A Eur. J. 2013, 19, 2247–2251. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Song, X.; Wang, S.; Li, F.; Zhang, H.; Ye, K.; Wang, Y. Two-Dimensional Organic Single Crystals with Scale Regulated, Phase-Switchable, Polymorphism-Dependent, and Amplified Spontaneous Emission Properties. J. Phys. Chem. Lett. 2016, 7, 1697–1702. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Du, C.; Yu, C.; Di, C.A.; Jiang, S.; Xi, H.; Zheng, J.; Yan, S.; Yu, C.; Hu, W.; et al. High-Performance Phototransistors Based on Organic Microribbons Prepared by a Solution Self-Assembly Process. Adv. Funct. Mater. 2010, 20, 1019–1024. [Google Scholar] [CrossRef]
- Zhou, C.; Worku, M.; Neu, J.; Lin, H.; Tian, Y.; Lee, S.; Zhou, Y.; Han, D.; Chen, S.; Hao, A.; et al. Facile Preparation of Light Emitting Organic Metal Halide Crystals with Near-Unity Quantum Efficiency. Chem. Mater. 2018, 30, 2374–2378. [Google Scholar] [CrossRef]
- Wang, S.; Lai, Z.; Tran, T.H.; Han, F.; Su, D.; Wang, R.; Zhang, H.; Wang, H.; Chen, H. Solvent Exchange as a Synthetic Handle for Controlling Molecular Crystals. Carbon, N.Y. 2020, 160, 188–195. [Google Scholar] [CrossRef]
- Zhang, C.; Zou, C.L.; Yan, Y.; Wei, C.; Cui, J.M.; Sun, F.W.; Yao, J.; Zhao, Y.S. Self-Assembled Organic Crystalline Microrings as Active Whispering-Gallery-Mode Optical Resonators. Adv. Opt. Mater. 2013, 1, 357–361. [Google Scholar] [CrossRef]
- Wang, S.; Dössel, L.; Mavrinskiy, A.; Gao, P.; Feng, X.; Pisula, W.; Müllen, K. Self-Assembly and Microstructural Control of a Hexa-Peri-Hexabenzocoronene- Perylene Diimide Dyad by Solvent Vapor Diffusion. Small 2011, 7, 2841–2846. [Google Scholar] [CrossRef]
- Wang, C.; Fang, Y.; Wen, L.; Zhou, M.; Xu, Y.; Zhao, H.; De Cola, L.; Hu, W.; Lei, Y. Vectorial Diffusion for Facile Solution-Processed Self-Assembly of Insoluble Semiconductors: A Case Study on Metal Phthalocyanines. Chem.-A Eur. J. 2014, 20, 10990–10995. [Google Scholar] [CrossRef] [PubMed]
- Shi, D.; Qin, X.; Li, Y.; He, Y.; Zhong, C.; Pan, J.; Dong, H.; Xu, W.; Li, T.; Hu, W.; et al. Spiro-OMeTAD Single Crystals: Remarkably Enhanced Charge-Carrier Transport via Mesoscale Ordering. Sci. Adv. 2016, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lv, A.; Puniredd, S.R.; Zhang, J.; Li, Z.; Zhu, H.; Jiang, W.; Dong, H.; He, Y.; Jiang, L.; Li, Y.; et al. High Mobility, Air Stable, Organic Single Crystal Transistors of an n-Type Diperylene Bisimide. Adv. Mater. 2012, 24, 2626–2630. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Kloc, C. Single-Crystal Growth of Organic Semiconductors. MRS Bull. 2013, 38, 28–33. [Google Scholar] [CrossRef]
- Schweicher, G.; Paquay, N.; Amato, C.; Resel, R.; Koini, M.; Talvy, S.; Lemaur, V.; Cornil, J.; Geerts, Y.; Gbabode, G. Toward Single Crystal Thin Films of Terthiophene by Directional Crystallization Using a Thermal Gradient. Cryst. Growth Des. 2011, 11, 3663–3672. [Google Scholar] [CrossRef]
- Tavazzi, S.; Miozzo, L.; Silvestri, L.; Mora, S.; Spearman, P.; Moret, M.; Rizzato, S.; Braga, D.; Diagne Diaw, A.K.; Gningue-Sall, D.; et al. Crystal Structure and Optical Properties of N-Pyrrole End-Capped Thiophene/Phenyl Co-Oligomer: Strong h-Type Excitonic Coupling and Emission Self-Waveguiding. Cryst. Growth Des. 2010, 10, 2342–2349. [Google Scholar] [CrossRef]
- Kloc, C.; Simpkins, P.G.; Siegrist, T.; Laudise, R.A. Physical Vapor Growth of Centimeter-Sized Crystals of $α$-Hexathiophene. J. Cryst. Growth 1997, 182, 416–427. [Google Scholar] [CrossRef]
- Laudise, R.A.; Kloc, C.; Simpkins, P.G.; Siegrist, T. Physical Vapor Growth of Organic Semiconductors. J. Cryst. Growth 1998, 187, 449–454. [Google Scholar] [CrossRef]
- Yong, B.; Zhao, S.; Fu, H.; Hu, F.; Peng, A.; Yang, W.; Yao, J. Tunable Emission from Binary Organic One-Dimensional Nanomaterials: An Alternative Approach to White-Light Emission. Adv. Mater. 2008, 20, 79–83. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, R.; Zhou, S. Gas Phase-Based Growth of Highly Sensitive Single-Crystal Rectangular Micro- and Nanotubes. J. Mater. Chem. 2012, 22, 883–888. [Google Scholar] [CrossRef]
- Roberson, L.B.; Kowalik, J.; Tolbert, L.M.; Kloc, C.; Zeis, R.; Chi, X.; Fleming, R.; Wilkins, C. Pentacene Disproportionation during Sublimation for Field-Effect Transistors. J. Am. Chem. Soc. 2005, 127, 3069–3075. [Google Scholar] [CrossRef]
- Ding, R.; Feng, J.; Dong, F.X.; Zhou, W.; Liu, Y.; Zhang, X.L.; Wang, X.P.; Fang, H.H.; Xu, B.; Li, X.B.; et al. Highly Efficient Three Primary Color Organic Single-Crystal Light-Emitting Devices with Balanced Carrier Injection and Transport. Adv. Funct. Mater. 2017, 27. [Google Scholar] [CrossRef]
- Ye, X.; Liu, Y.; Han, Q.; Ge, C.; Cui, S.; Zhang, L.; Zheng, X.; Liu, G.; Liu, J.; Liu, D.; et al. Microspacing In-Air Sublimation Growth of Organic Crystals. Chem. Mater. 2018, 30, 412–420. [Google Scholar] [CrossRef]
- Ye, X.; Liu, Y.; Guo, Q.; Han, Q.; Ge, C.; Cui, S.; Zhang, L.; Tao, X. 1D versus 2D Cocrystals Growth via Microspacing In-Air Sublimation. Nat. Commun. 2019, 10. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Ye, X.; Lin, Q.; Han, Q.; Ge, C.; Zheng, X.; Zhang, L.; Cui, S.; Wu, Y.; Li, C.; et al. Micro-Spacing In-Air Sublimation Growth of Ultrathin Organic Single Crystals. Chem. Mater. 2020, 32, 7618–7629. [Google Scholar] [CrossRef]
- Qian, Y.; Wei, Q.; Del Pozo, G.; Mróz, M.M.; Lüer, L.; Casado, S.; Cabanillas-Gonzalez, J.; Zhang, Q.; Xie, L.; Xia, R.; et al. H-Shaped Oligofluorenes for Highly Air-Stable and Low-Threshold Non-Doped Deep Blue Lasing. Adv. Mater. 2014, 26, 2937–2942. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Y.; Lian, S.; Gao, J.; Zhang, S.; Hai, G.; Sun, C.; Li, X.; Xia, R.; Cabanillas-Gonzalez, J.; et al. Simultaneously Enhancing Photoluminescence Quantum Efficiency and Optical Gain of Polyfluorene via Backbone Intercalation of 2,5-Dimethyl-1,4-Phenylene. Adv. Opt. Mater. 2020, 8. [Google Scholar] [CrossRef]
- Bai, K.; Wang, S.; Zhao, L.; Ding, J.; Wang, L. Efficient Blue, Green, and Red Electroluminescence from Carbazole-Functionalized Poly(Spirobifluorene)S. Macromolecules 2017, 50, 6945–6953. [Google Scholar] [CrossRef]
- Wang, J.; Song, C.; Zhong, Z.; Hu, Z.; Han, S.; Xu, W.; Peng, J.; Ying, L.; Wang, J.; Cao, Y. In Situ Patterning of Microgrooves via Inkjet Etching for a Solution-Processed OLED Display. J. Mater. Chem. C 2017, 5, 5005–5009. [Google Scholar] [CrossRef]
- Smirnov, J.R.C.; Zhang, Q.; Wannemacher, R.; Wu, L.; Casado, S.; Xia, R.; Rodriguez, I.; Cabanillas-González, J. Flexible All-Polymer Waveguide for Low Threshold Amplified Spontaneous Emission. Sci. Rep. 2016, 6, 34565. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, J.; Wei, Q.; Guo, X.; Xu, Y.; Xia, R.; Xie, L.; Qian, Y.; Sun, C.; Lüer, L.; et al. Host Exciton Confinement for Enhanced Förster-Transfer-Blend Gain Media Yielding Highly Efficient Yellow-Green Lasers. Adv. Funct. Mater. 2018, 28, 1705824. [Google Scholar] [CrossRef] [Green Version]
- Cabanillas-Gonzalez, J.; Sciascia, C.; Lanzani, G.; Toffanin, S.; Capelli, R.; Ramon, M.C.; Muccini, M.; Gierschner, J.; Hwu, T.-Y.; Wong, K.-T. Molecular Packing Effects on the Optical Spectra and Triplet Dynamics in Oligofluorene Films. J. Phys. Chem. B 2008, 112, 11605–11609. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; Wei, Y.; Zhang, W.; Wei, C.; Zhang, C.; Yao, J.; Zhao, Y.S. Broadband Tunable Microlasers Based on Controlled Intramolecular Charge-Transfer Process in Organic Supramolecular Microcrystals. J. Am. Chem. Soc. 2016, 138, 1118–1121. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Wang, M.; Usman, R.; Sun, H.; Du, M.; Xu, C. Molecular Marriage via Charge Transfer Interaction in Organic Charge Transfer Co-Crystals toward Solid-State Fluorescence Modulation. Cryst. Growth Des. 2017, 17, 1251–1257. [Google Scholar] [CrossRef]
- Yan, D.; Delori, A.; Lloyd, G.O.; Friščić, T.; Day, G.M.; Jones, W.; Lu, J.; Wei, M.; Evans, D.G.; Duan, X. A Cocrystal Strategy to Tune the Luminescent Properties of Stilbene-Type Organic Solid-State Materials. Angew. Chemie Int. Ed. 2011, 50, 12483–12486. [Google Scholar] [CrossRef]
- Park, S.K.; Kim, J.H.; Ohto, T.; Yamada, R.; Jones, A.O.F.; Whang, D.R.; Cho, I.; Oh, S.; Hong, S.H.; Kwon, J.E.; et al. Highly Luminescent 2D-Type Slab Crystals Based on a Molecular Charge-Transfer Complex as Promising Organic Light-Emitting Transistor Materials. Adv. Mater. 2017, 29, 1701346. [Google Scholar] [CrossRef]
- He, D.; Qiao, J.; Zhang, L.; Wang, J.; Lan, T.; Qian, J.; Li, Y.; Shi, Y.; Chai, Y.; Lan, W.; et al. Ultrahigh Mobility and Efficient Charge Injection in Monolayer Organic Thin-Film Transistors on Boron Nitride. Sci. Adv. 2017, 3, e1701186. [Google Scholar] [CrossRef] [Green Version]
- Ullah, M.; Wawrzinek, R.; Nagiri, R.C.R.; Lo, S.-C.; Namdas, E.B. UV–Deep Blue–Visible Light-Emitting Organic Field Effect Transistors with High Charge Carrier Mobilities. Adv. Opt. Mater. 2017, 5, 1600973. [Google Scholar] [CrossRef]
- Sandanayaka, A.S.D.; Matsushima, T.; Bencheikh, F.; Terakawa, S.; Potscavage, W.J.; Qin, C.; Fujihara, T.; Goushi, K.; Ribierre, J.-C.; Adachi, C. Indication of Current-Injection Lasing from an Organic Semiconductor. Appl. Phys. Express 2019, 12, 61010. [Google Scholar] [CrossRef] [Green Version]
- Stagira, S.; Zavelani-Rossi, M.; Nisoli, M.; DeSilvestri, S.; Lanzani, G.; Zenz, C.; Mataloni, P.; Leising, G. Single-Mode Picosecond Blue Laser Emission from a Solid Conjugated Polymer. Appl. Phys. Lett. 1998, 73, 2860–2862. [Google Scholar] [CrossRef]
- Canazza, G.; Scotognella, F.; Lanzani, G.; De Silvestri, S.; Zavelani-Rossi, M.; Comoretto, D. Lasing from All-Polymer Microcavities. Laser Phys. Lett. 2014, 11. [Google Scholar] [CrossRef]
- Navarro-Fuster, V.; Calzado, E.M.; Boj, P.G.; Quintana, J.A.; Villalvilla, J.M.; Díaz-García, M.A.; Trabadelo, V.; Juarros, A.; Retolaza, A.; Merino, S. Highly Photostable Organic Distributed Feedback Laser Emitting at 573 Nm. Appl. Phys. Lett. 2010, 97, 171104. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Hai, G.; Xu, H.; Zhang, H.; Zuo, Z.; Zhang, Q.; Xia, R.; Sun, C.; Castro-Smirnov, J.; Sousaraei, A.; et al. Efficient Optical Gain from Near-Infrared Polymer Lasers Based on Poly[N-9′-Heptadecanyl-2,7-Carbazole-Alt-5,5-(4′,7′-Di-2-Thienyl-2′,1′,3′-Benzothiadiazole)]. Adv. Opt. Mater. 2018, 6, 1800263. [Google Scholar] [CrossRef]
- Milanese, S.; De Giorgi, M.L.; Anni, M. Determination of the Best Empiric Method to Quantify the Amplified Spontaneous Emission Threshold in Polymeric Active Waveguides. Molecules 2020, 25, 2992. [Google Scholar] [CrossRef]
- Muñoz-Mármol, R.; Bonal, V.; Paternò, G.M.; Ross, A.M.; Boj, P.G.; Villalvilla, J.M.; Quintana, J.A.; Scotognella, F.; D’Andrea, C.; Sardar, S.; et al. Dual Amplified Spontaneous Emission and Lasing from Nanographene Films. Nanomaterials 2020, 10, 1525. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Mróz, M.M.; Castro Smirnov, J.R.; Lüer, L.; Hermida-Merino, D.; Zhao, C.; Takeuchi, M.; Sugiyasu, K.; Cabanillas-González, J. Amplified Spontaneous Emission in Insulated Polythiophenes. J. Mater. Chem. C 2018, 6, 6591–6596. [Google Scholar] [CrossRef]
- Calzado, E.M.; Villalvilla, J.M.; Boj, P.G.; Quintana, J.A.; Díaz-García, M.A. Concentration Dependence of Amplified Spontaneous Emission in Organic-Based Waveguides. Org. Electron. 2006, 7, 319–329. [Google Scholar] [CrossRef]
- Illarramendi, M.A.; Arrue, J.; Ayesta, I.; Jiménez, F.; Zubia, J.; Bikandi, I.; Tagaya, A.; Koike, Y. Amplified Spontaneous Emission in Graded-Index Polymer Optical Fibers: Theory and Experiment. Opt. Express 2013, 21, 24254–24266. [Google Scholar] [CrossRef]
- Zhang, Q.; Wei, Q.; Guo, X.; Hai, G.; Sun, H.; Li, J.; Xia, R.; Qian, Y.; Casado, S.; Castro-Smirnov, J.R.; et al. Concurrent Optical Gain Optimization and Electrical Tuning in Novel Oligomer:Polymer Blends with Yellow-Green Laser Emission. Adv. Sci. 2019, 6, 1801455. [Google Scholar] [CrossRef]
- Huang, R.; Wang, C.; Wang, Y.; Zhang, H. Elastic Self-Doping Organic Single Crystals Exhibiting Flexible Optical Waveguide and Amplified Spontaneous Emission. Adv. Mater. 2018, 30, 1800814. [Google Scholar] [CrossRef] [PubMed]
- Fang, H.-H.; Ding, R.; Lu, S.-Y.; Yang, J.; Zhang, X.-L.; Yang, R.; Feng, J.; Chen, Q.-D.; Song, J.-F.; Sun, H.-B. Distributed Feedback Lasers Based on Thiophene/Phenylene Co-Oligomer Single Crystals. Adv. Funct. Mater. 2012, 22, 33–38. [Google Scholar] [CrossRef]
- Zhu, W.-S.; Han, Y.-M.; An, X.; Weng, J.-N.; Yu, M.-N.; Bai, L.-B.; Wei, C.-X.; Lin, J.-Y.; Liu, W.; Ou, C.-J.; et al. Highly Emissive Hierarchical Uniform Dialkylfluorene-Based Dimer Microcrystals for Ultraviolet Organic Laser. J. Phys. Chem. C 2019, 123, 28881–28886. [Google Scholar] [CrossRef]
- Ou, C.-J.; Ding, X.-H.; Li, Y.-X.; Zhu, C.; Yu, M.-N.; Xie, L.-H.; Lin, J.-Y.; Xu, C.-X.; Huang, W. Conformational Effect of Polymorphic Terfluorene on Photophysics, Crystal Morphologies, and Lasing Behaviors. J. Phys. Chem. C 2017, 121, 14803–14810. [Google Scholar] [CrossRef]
- Varghese, S.; Park, S.K.; Casado, S.; Fischer, R.C.; Resel, R.; Milián-Medina, B.; Wannemacher, R.; Park, S.Y.; Gierschner, J. Stimulated Emission Properties of Sterically Modified Distyrylbenzene-Based H-Aggregate Single Crystals. J. Phys. Chem. Lett. 2013, 4, 1597–1602. [Google Scholar] [CrossRef]
- Xu, Z.; Liao, Q.; Shi, Q.; Zhang, H.; Yao, J.; Fu, H. Low-Threshold Nanolasers Based on Slab-Nanocrystals of H-Aggregated Organic Semiconductors. Adv. Mater. 2012, 24, OP216–OP220. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Li, Z.-Z.; Zhuo, M.-P.; Wu, Y.; Chen, S.; Yao, J.; Fu, H. Tunable Near-Infrared Organic Nanowire Nanolasers. Adv. Funct. Mater. 2017, 27, 1703470. [Google Scholar] [CrossRef]
- Duong Ta, V.; Chen, R.; Ma, L.; Jun Ying, Y.; Dong Sun, H. Whispering Gallery Mode Microlasers and Refractive Index Sensing Based on Single Polymer Fiber. Laser Photon. Rev. 2013, 7, 133–139. [Google Scholar] [CrossRef]
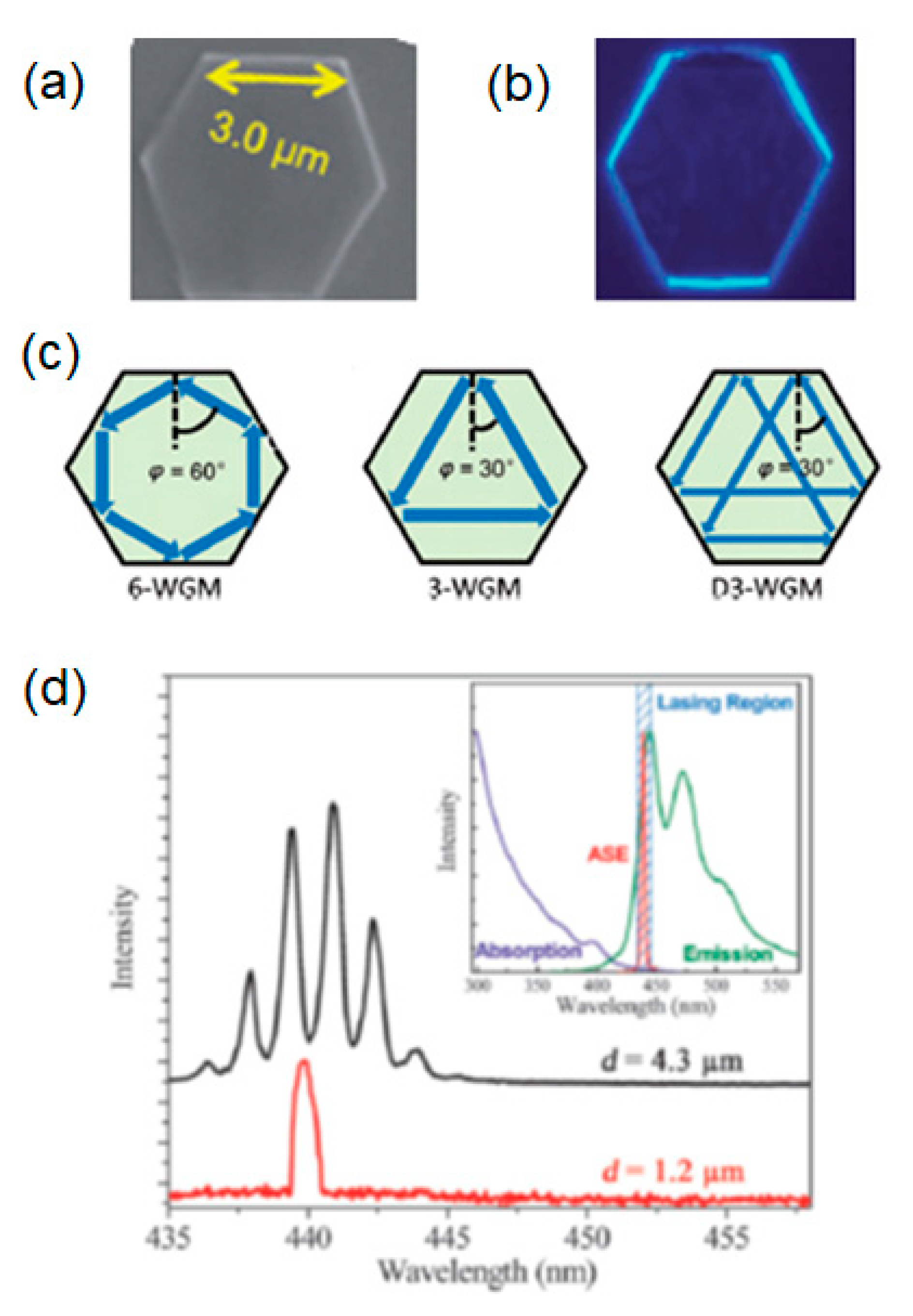
- Fang, H.H.; Ding, R.; Lu, S.Y.; De Yang, Y.; Chen, Q.D.; Feng, J.; Huang, Y.Z.; Sun, H.B. Whispering-Gallery Mode Lasing from Patterned Molecular Single-Crystalline Microcavity Array. Laser Photonics Rev. 2013, 7, 281–288. [Google Scholar] [CrossRef]
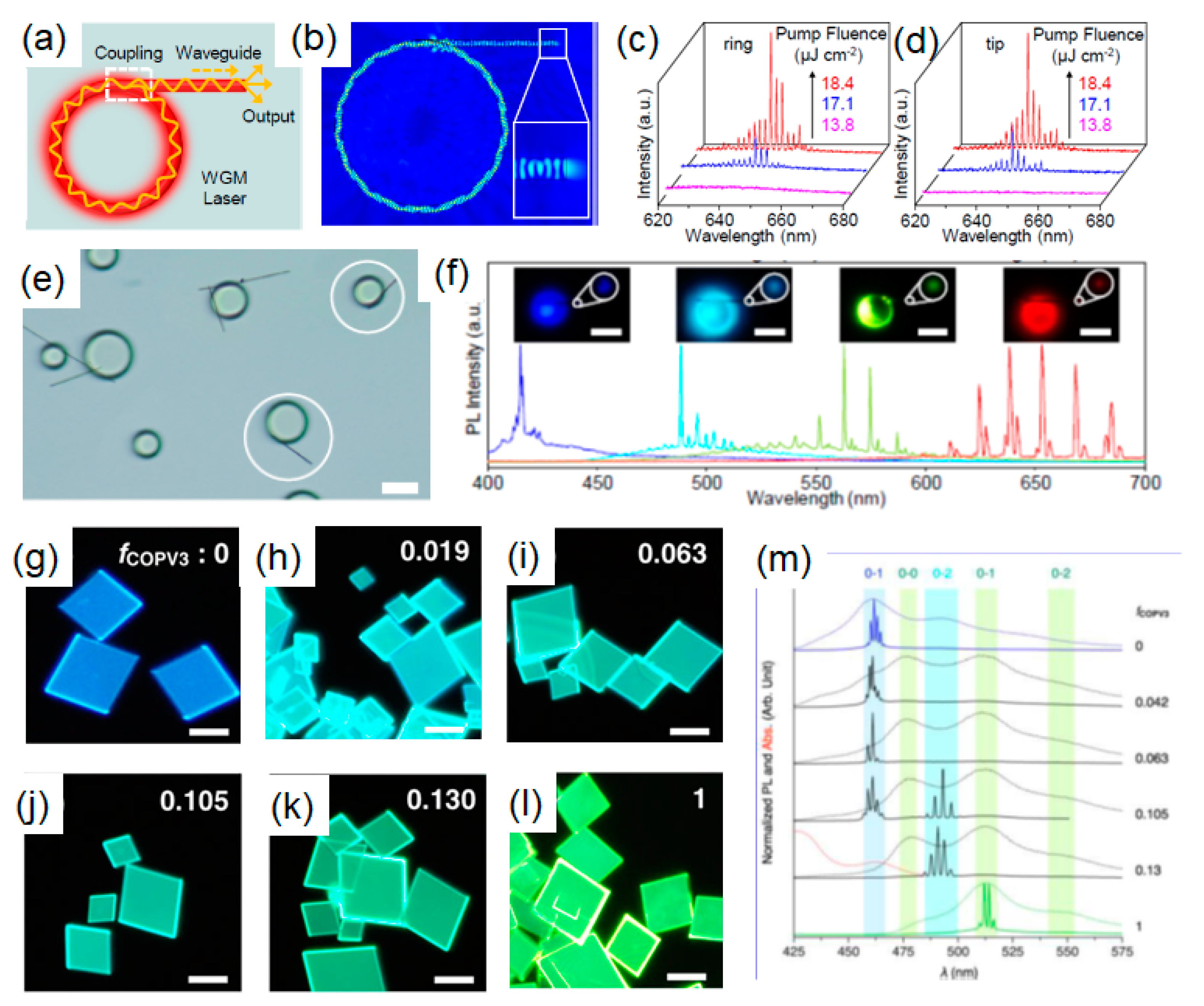
- Lv, Y.; Xiong, X.; Liu, Y.; Yao, J.; Li, Y.J.; Zhao, Y.S. Controlled Outcoupling of Whispering-Gallery-Mode Lasers Based on Self-Assembled Organic Single-Crystalline Microrings. Nano Lett. 2019, 19, 1098–1103. [Google Scholar] [CrossRef]
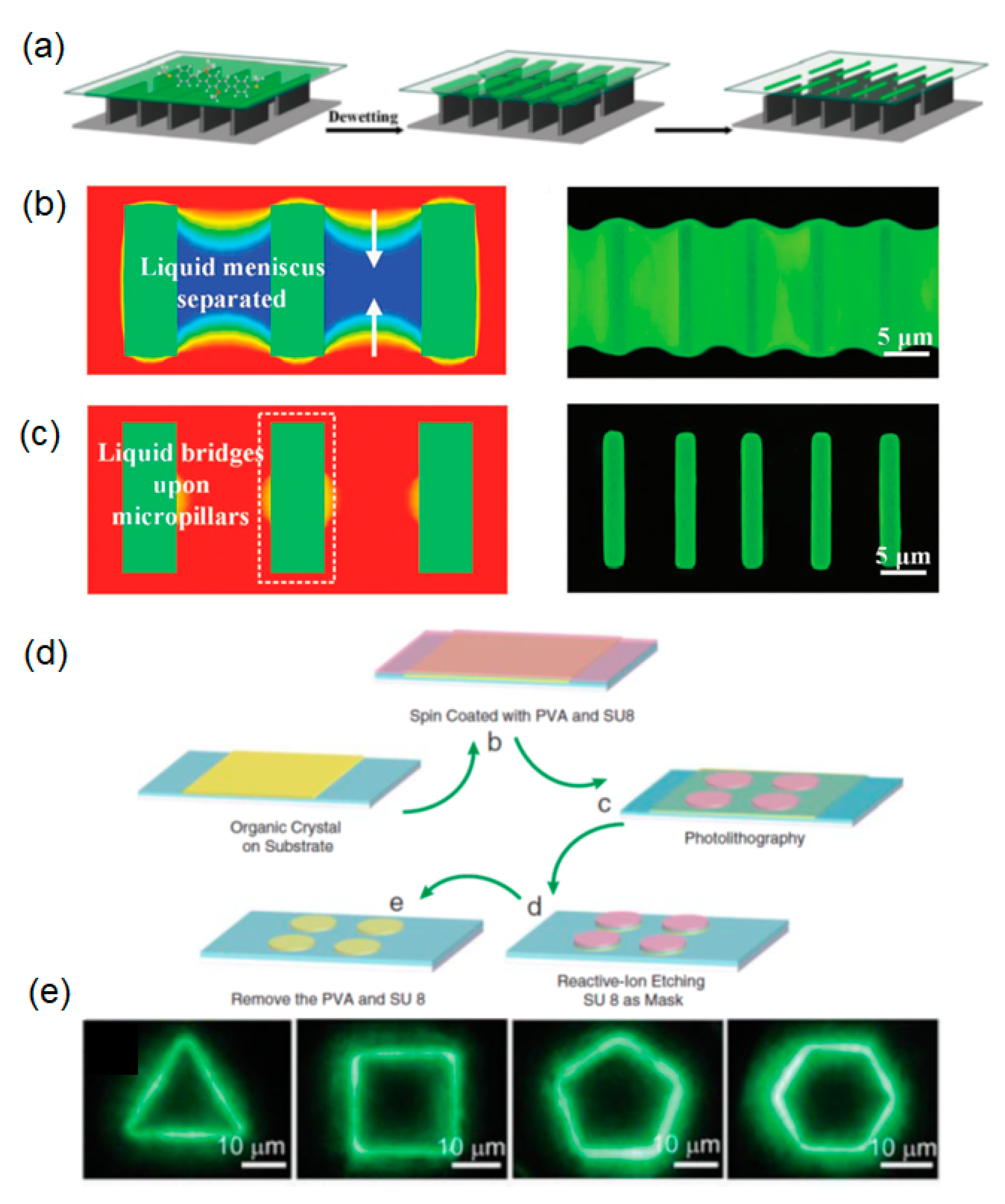
- Feng, J.; Jiang, X.; Yan, X.; Wu, Y.; Su, B.; Fu, H.; Yao, J.; Jiang, L. “Capillary-Bridge Lithography” for Patterning Organic Crystals toward Mode-Tunable Microlaser Arrays. Adv. Mater. 2017, 29, 1603652. [Google Scholar] [CrossRef]
- Xu, Z.; Liao, Q.; Wang, X.; Fu, H. Whispering Gallery Mode Laser Based on a Self-Assembled Organic Octahedron Microcrystal Microresonator. Adv. Opt. Mater. 2014, 2, 1160–1166. [Google Scholar] [CrossRef]
- Varghese, S.; Yoon, S.-J.; Casado, S.; Fischer, R.C.; Wannemacher, R.; Park, S.Y.; Gierschner, J. Orthogonal Resonator Modes and Low Lasing Threshold in Highly Emissive Distyrylbenzene-Based Molecular Crystals. Adv. Opt. Mater. 2014, 2, 542–548. [Google Scholar] [CrossRef]
- Wang, X.; Liao, Q.; Kong, Q.; Zhang, Y.; Xu, Z.; Lu, X.; Fu, H. Whispering-Gallery-Mode Microlaser Based on Self-Assembled Organic Single-Crystalline Hexagonal Microdisks. Angew. Chemie Int. Ed. 2014, 53, 5863–5867. [Google Scholar] [CrossRef] [PubMed]
- O’Carroll, D.; Lieberwirth, I.; Redmond, G. Microcavity Effects and Optically Pumped Lasing in Single Conjugated Polymer Nanowires. Nat. Nanotechnol. 2007, 2, 180–184. [Google Scholar] [CrossRef] [PubMed]
- Wei, G.-Q.; Wang, X.-D.; Liao, L.-S. Recent Advances in Organic Whispering-Gallery Mode Lasers. Laser Photon. Rev. 2020, 14, 2000257. [Google Scholar] [CrossRef]
- Zhang, C.; Zou, C.-L.; Dong, H.; Yan, Y.; Yao, J.; Zhao, Y.S. Dual-Color Single-Mode Lasing in Axially Coupled Organic Nanowire Resonators. Sci. Adv. 2017, 3, e1700225. [Google Scholar] [CrossRef] [Green Version]
- Kushida, S.; Okada, D.; Sasaki, F.; Lin, Z.-H.; Huang, J.-S.; Yamamoto, Y. Lasers: Low-Threshold Whispering Gallery Mode Lasing from Self-Assembled Microspheres of Single-Sort Conjugated Polymers. Adv. Opt. Mater. 2017, 5, 1700123. [Google Scholar] [CrossRef]
- Foreman, M.R.; Swaim, J.D.; Vollmer, F. Whispering Gallery Mode Sensors. Adv. Opt. Photonics 2015, 7, 168–240. [Google Scholar] [CrossRef]
- Wun, A.W.; Snee, P.T.; Chan, Y.; Bawendi, M.G.; Nocera, D.G. Non-Linear Transduction Strategies for Chemo/Biosensing on Small Length Scales. J. Mater. Chem. 2005, 15, 2697–2706. [Google Scholar] [CrossRef]
- Humar, M.; Hyun Yun, S. Intracellular Microlasers. Nat. Photonics 2015, 9, 572–576. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.-L.; Wang, X.-D. 1D Organic Micro/Nanostructures for Photonics. Adv. Funct. Mater. 2020, 2008149. [Google Scholar] [CrossRef]
- Torii, K.; Higuchi, T.; Mizuno, K.; Bando, K.; Yamashita, K.; Sasaki, F.; Yanagi, H. Organic Nanowire Lasers with Epitaxially Grown Crystals of Semiconducting Oligomers. ChemNanoMat 2017, 3, 625–631. [Google Scholar] [CrossRef]
- Yu, Z.; Wu, Y.; Xiao, L.; Chen, J.; Liao, Q.; Yao, J.; Fu, H. Organic Phosphorescence Nanowire Lasers. J. Am. Chem. Soc. 2017, 139, 6376–6381. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.-J.; Gao, H.; Lai, R.; Zhuo, M.-P.; Feng, J.; Wang, X.-D.; Wu, Y.; Liao, L.-S.; Jiang, L. Near-Infrared Organic Single-Crystal Nanolaser Arrays Activated by Excited-State Intramolecular Proton Transfer. Matter 2020, 2, 1233–1243. [Google Scholar] [CrossRef] [Green Version]
- Liao, Q.; Jin, X.; Zhang, H.; Xu, Z.; Yao, J.; Fu, H. An Organic Microlaser Array Based on a Lateral Microcavity of a Single J-Aggregation Microbelt. Angew. Chemie Int. Ed. 2015, 54, 7037–7041. [Google Scholar] [CrossRef]
- Wang, X.; Liao, Q.; Lu, X.; Li, H.; Xu, Z.; Fu, H. Shape-Engineering of Self-Assembled Organic Single Microcrystal as Optical Microresonator for Laser Applications. Sci. Rep. 2014, 4, 7011. [Google Scholar] [CrossRef]
- Okada, D.; Azzini, S.; Nishioka, H.; Ichimura, A.; Tsuji, H.; Nakamura, E.; Sasaki, F.; Genet, C.; Ebbesen, T.W.; Yamamoto, Y. π-Electronic Co-Crystal Microcavities with Selective Vibronic-Mode Light Amplification: Toward Förster Resonance Energy Transfer Lasing. Nano Lett. 2018, 18, 4396–4402. [Google Scholar] [CrossRef]
- Lv, Y.; Li, Y.J.; Li, J.; Yan, Y.; Yao, J.; Zhao, Y.S. All-Color Subwavelength Output of Organic Flexible Microlasers. J. Am. Chem. Soc. 2017, 139, 11329–11332. [Google Scholar] [CrossRef]




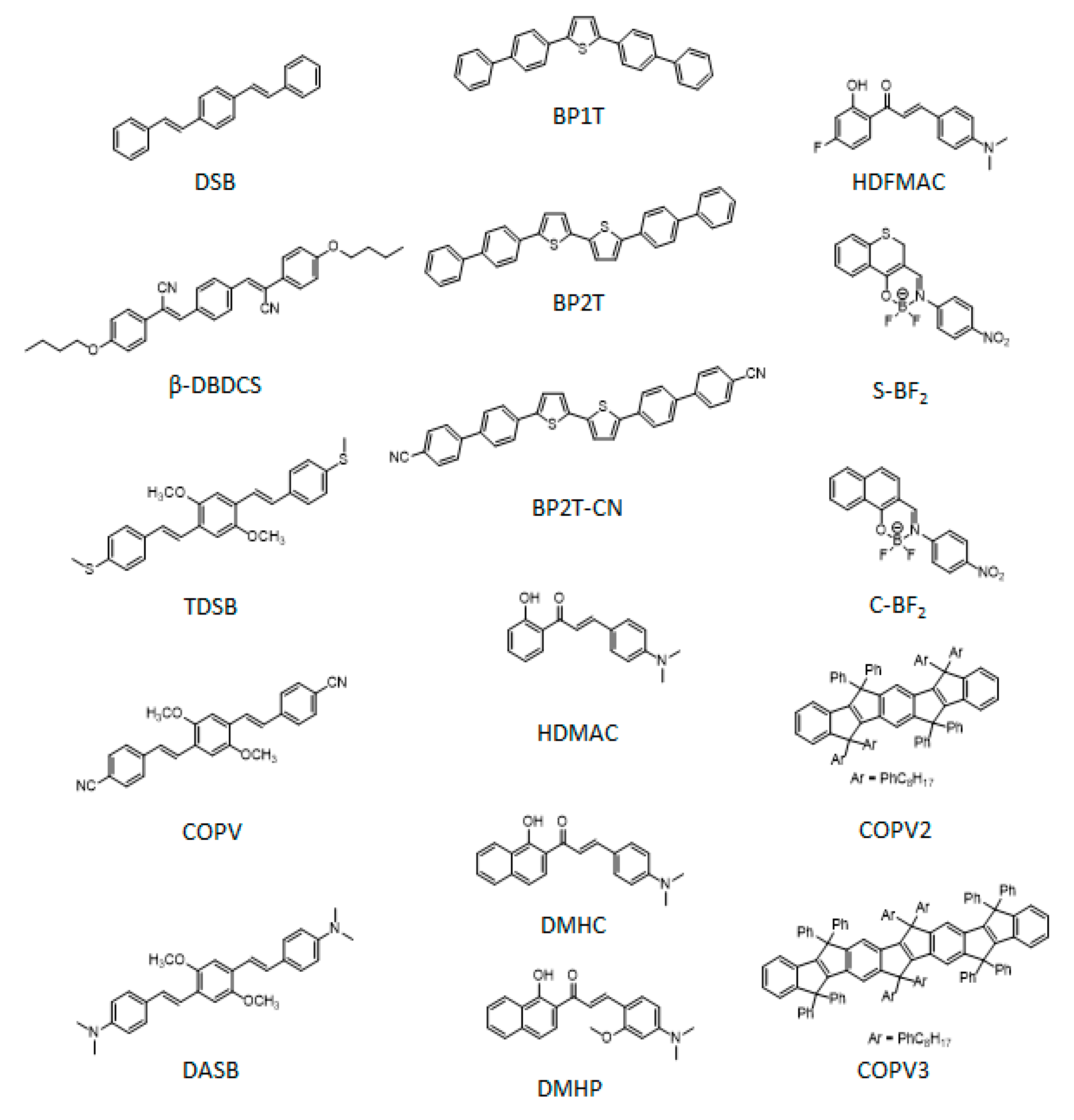
| Molecule | Crystal Structure | Type of Cavity | Dimensions (W × L) | Lasing Threshold (μJ cm−2) | Q-factor | Lasing Wavelength (nm) | PLQE (%) | Ref |
|---|---|---|---|---|---|---|---|---|
| TDSB | H-aggregates monoclinic, space group of P 2 1/c | wires, slab FP | 0.5–2μm (rectangular section) × 10–30 μm | 0.1 | 1000 | 500 | 81 | [118] |
| DMHP | orthorhombic, space group of Pca21 | wires, FP | 0.05–0.25 μm × 5–100 μm | 1.4 | - | 660–720 | 30 | [119] |
| TDSB | H.aggregates, monoclinic, space group of P 2 1 / c | patterned wires, FP | 0.5 μm (square section) × 10–30 μm | 0.4 | - | 500 | - | [123] |
| S-BF2 | monoclinic | wires, FP | 2 μm × 20–100 μm | 12.8 | 850 | 645 | 10 | [136] |
| COPV | J-aggregates, monoclinic | microbelts, slab FP | 0.3–0.6 μm × 1–10 μm | 1.09 | 868 | 525 | 58 | [138] |
| DMHC | Anhortic, space group P-1 | patterned wires, FP | 0.3 μm × 1 μm | 9.9 | 2340 | 775 | 2 | [137] |
| BP2T (BP2T-CN) | monoclinic P21/c (P21) | microbelts, FP | 1 μm × 5–100 μm | 11 | 354 (377) | 535 | - | [138] |
| HDMAC | monoclinic | wires FP; square microdisks WGM* | 500 x 10–30 μm; 2–10 μm, 600 nm height | 1.05; 0.43 | ~ 7500 in microdisks | 650 | 30 | [139] |
| DASB | Monoclinic P21/c | octahedron crystals WGM | > 1 μm side of lateral faces | 6.9 | > 1500 | 531 | 30 | [124] |
| DSB | H-aggregates herringbone, orthorhombic | hexagonal microdisks WGM | 1–5 μm edge | 0.79 | 210 | 440 | 65 | [126] |
| BP1T, (BP2T) | - | patterned multishape microdisks WGM | Variable circular radii/ polygonal > 1 μm edge | 88 nJ | 2030 | 500, (525) | 36, (59) | [121] |
| HDFMAC | micro-rings WGM | 10–30 μm diameter, 250 nm width, 2.5 μm height | 14.2 | 2000–4000 | 647 | 23 | [122] | |
| COPV2, (COPV3) | monoclinic P21/n | rhombic microdisks quasi-WGM | 4 × 35 μm Edge | 18 | 3400 | 460, 490, 510 | 65–76 | [140] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Álvarez-Conde, J.; García-Frutos, E.M.; Cabanillas-Gonzalez, J. Organic Semiconductor Micro/Nanocrystals for Laser Applications. Molecules 2021, 26, 958. https://doi.org/10.3390/molecules26040958
Álvarez-Conde J, García-Frutos EM, Cabanillas-Gonzalez J. Organic Semiconductor Micro/Nanocrystals for Laser Applications. Molecules. 2021; 26(4):958. https://doi.org/10.3390/molecules26040958
Chicago/Turabian StyleÁlvarez-Conde, Javier, Eva M. García-Frutos, and Juan Cabanillas-Gonzalez. 2021. "Organic Semiconductor Micro/Nanocrystals for Laser Applications" Molecules 26, no. 4: 958. https://doi.org/10.3390/molecules26040958
APA StyleÁlvarez-Conde, J., García-Frutos, E. M., & Cabanillas-Gonzalez, J. (2021). Organic Semiconductor Micro/Nanocrystals for Laser Applications. Molecules, 26(4), 958. https://doi.org/10.3390/molecules26040958






