Phase-Transition Thermal Charging of a Channel-Shape Thermal Energy Storage Unit: Taguchi Optimization Approach and Copper Foam Inserts
Abstract
:1. Introduction
2. Mathematical Model
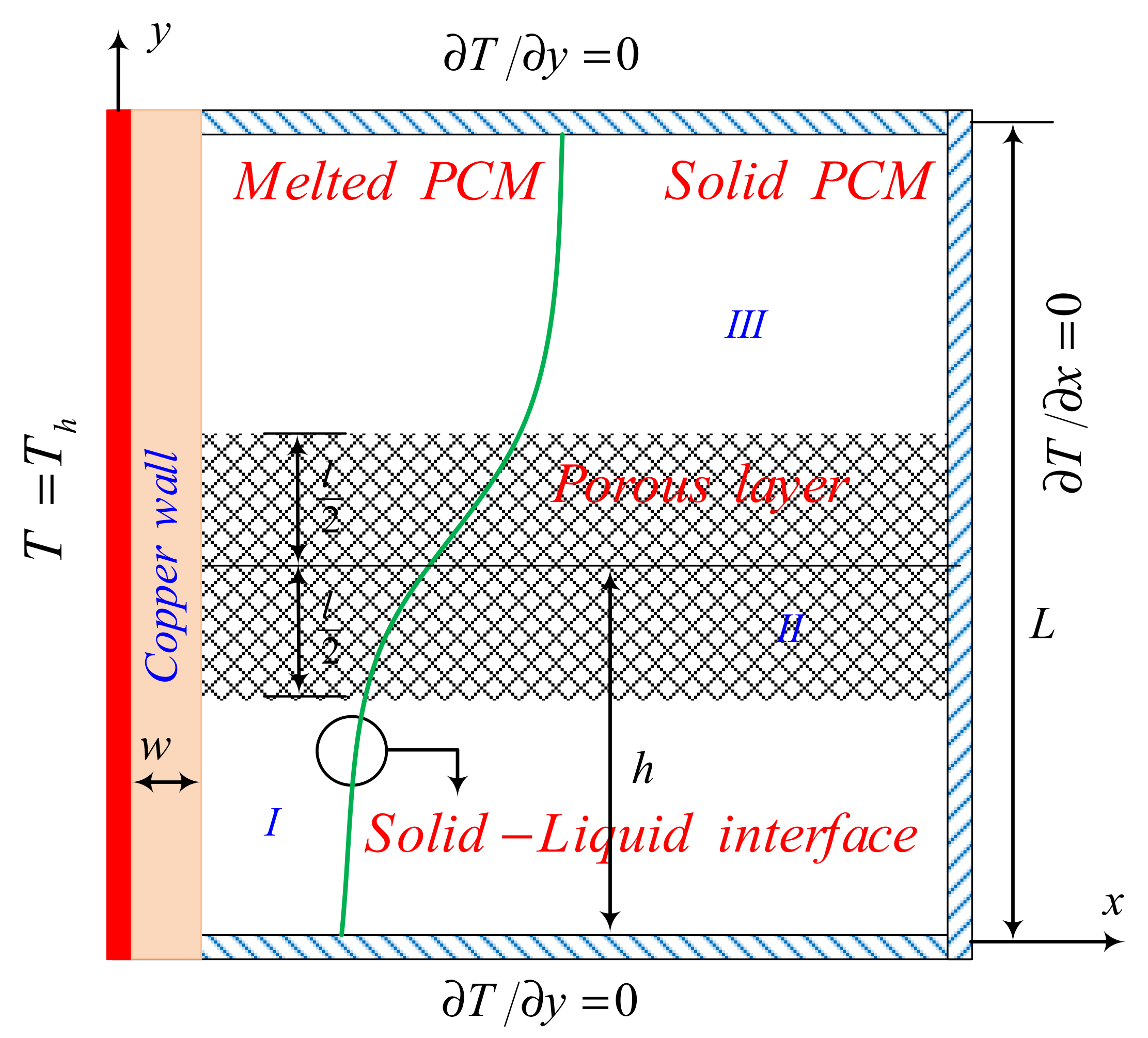
2.1. Model Description
2.2. Physical Model and Governing Equations
2.3. Characteristic Parameters
3. Solution Approach and Validation
3.1. Numerical Method
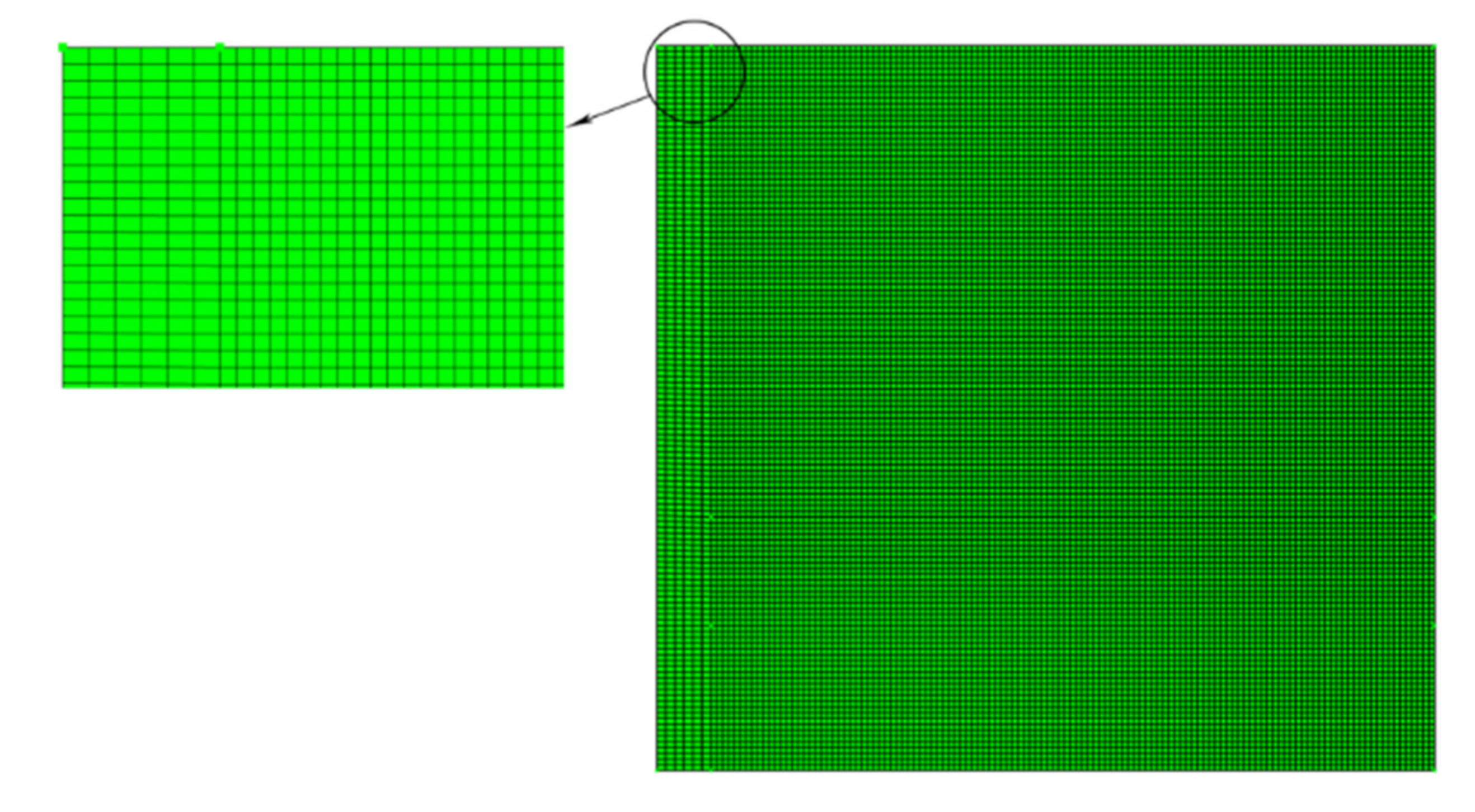
3.2. Impact of Mesh Size
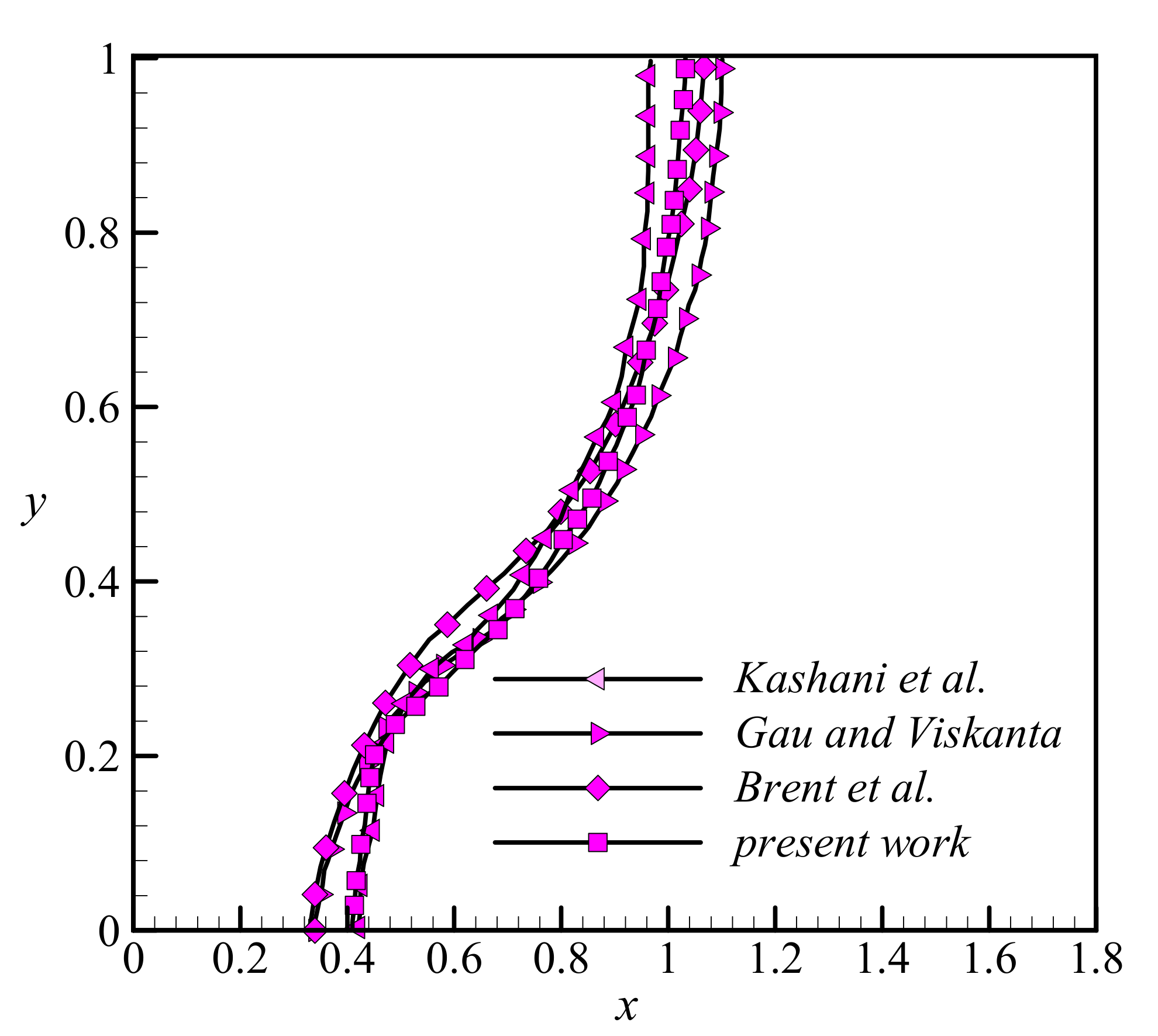
3.3. Validation
4. Results and Discussion
5. Conclusions
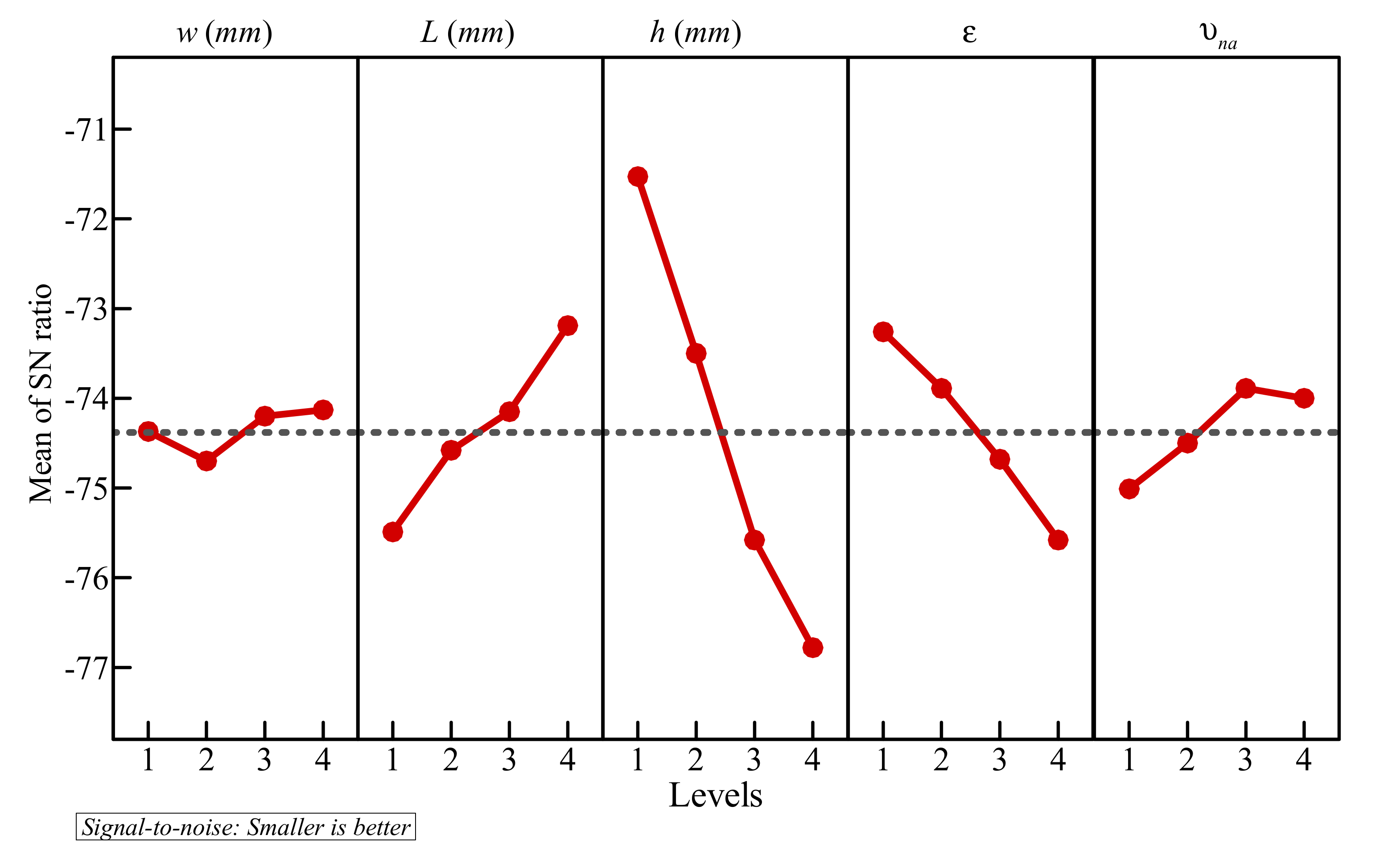
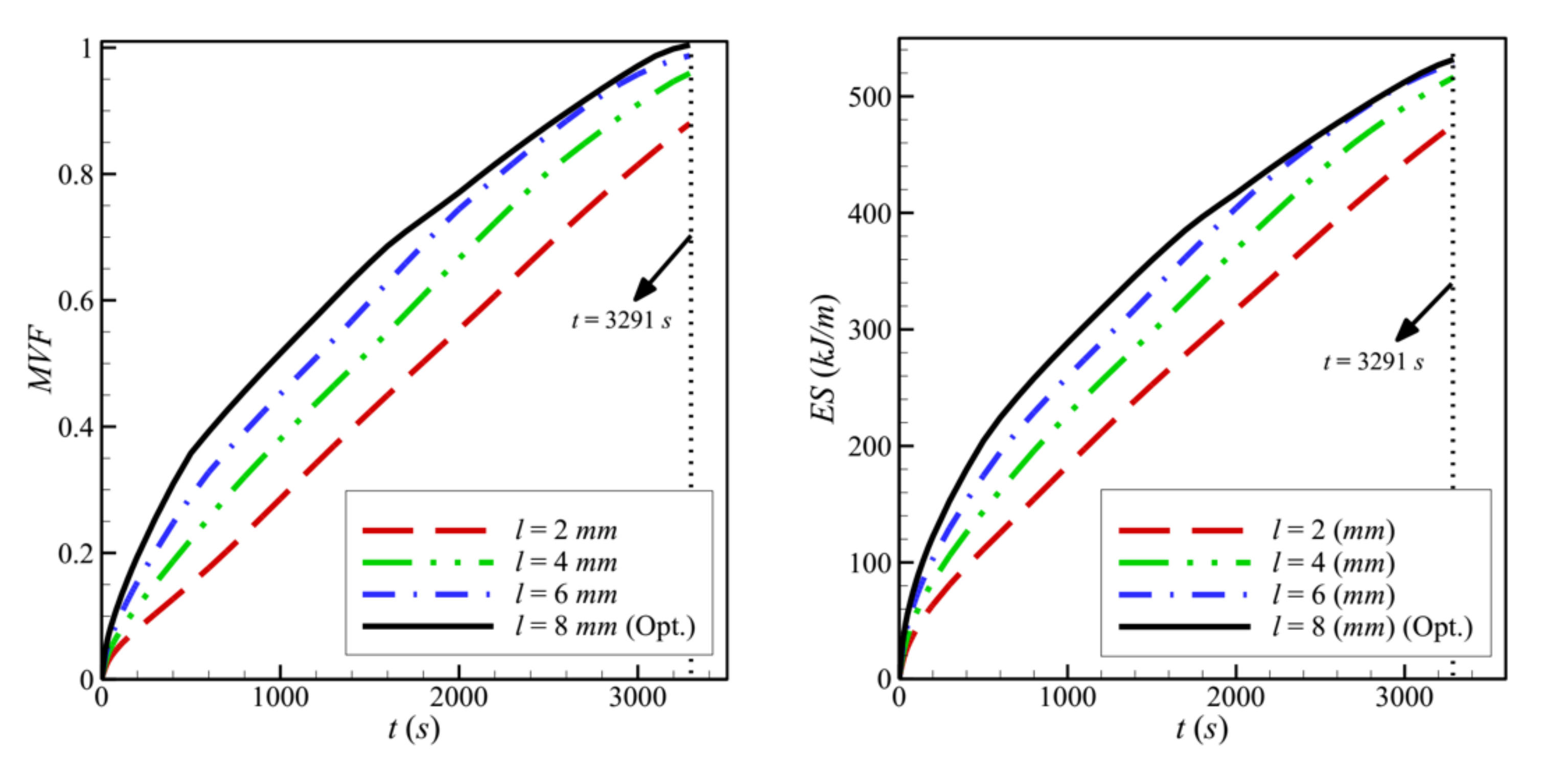
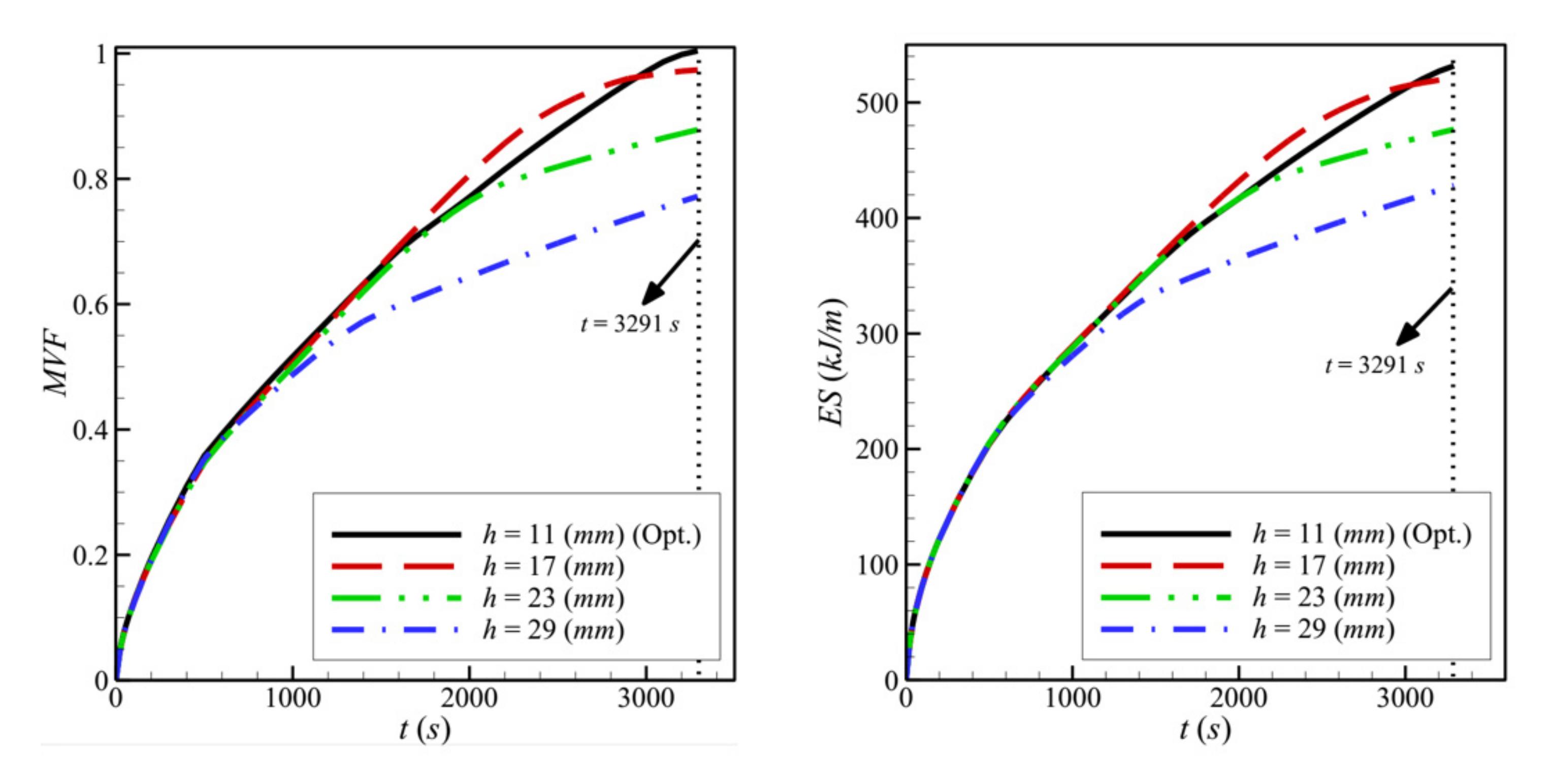
- In a cavity with side length, L = 40 mm, the optimal values obtained for the control factors are the following: w = 4 mm, l = 8 mm, h = 11 mm, ε = 0.8, and υna = 0.04. By their decreasing order of influence, the control factors are ranked as: h > ε > l > υna > w. The variation of the design parameters could induce a 58% variation in the melting time.
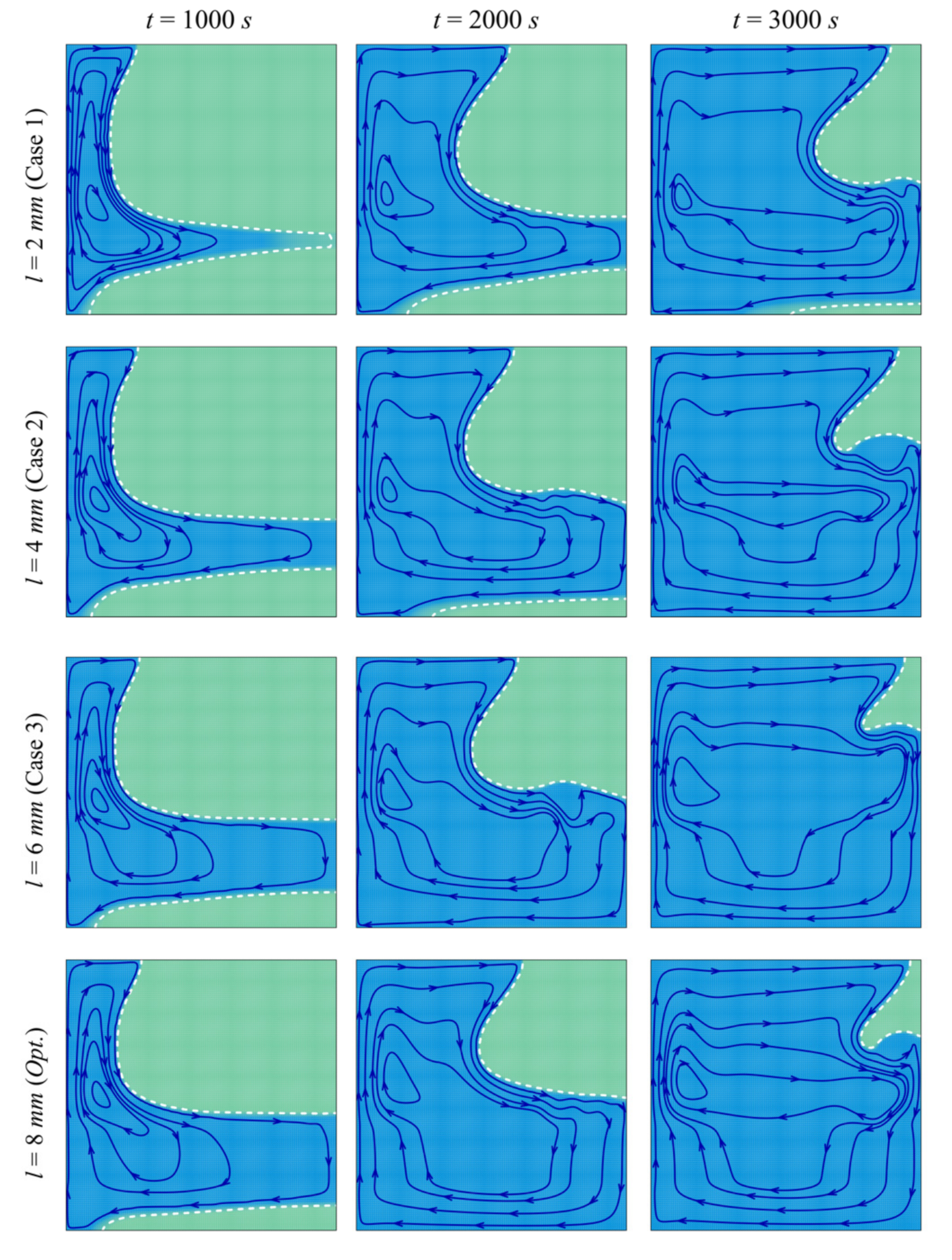
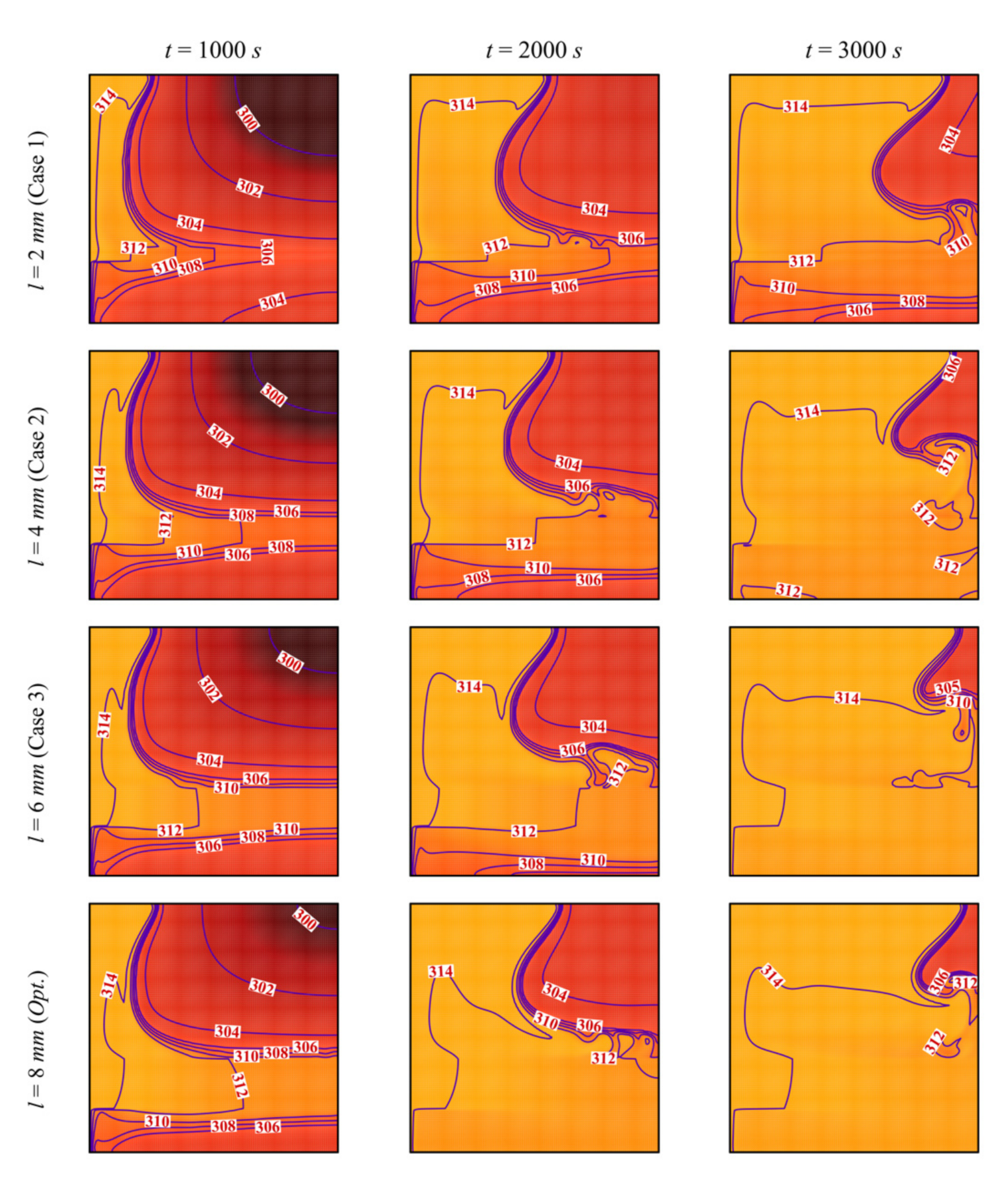
- When the left wall is heated, PCM starts melting, and convective flow takes place. The presence of the porous layer in the cavity improves heat transfer and contributes to PCM melting.
- The size and location of the porous layer affect the thermal behavior of the PCM. Increasing the layer size, l, enhances and accelerates heat transfer. The charging power increases with l. Just shifting the porous layer from 2 mm to 6 mm increased the melting rate by 8.8%.
- Moving the porous layer upwards (increasing h) hinders the convective effects in the bottom part of the cavity and lowers the contribution of the porous layer to PCM melting. The charging power decreases when h is raised.
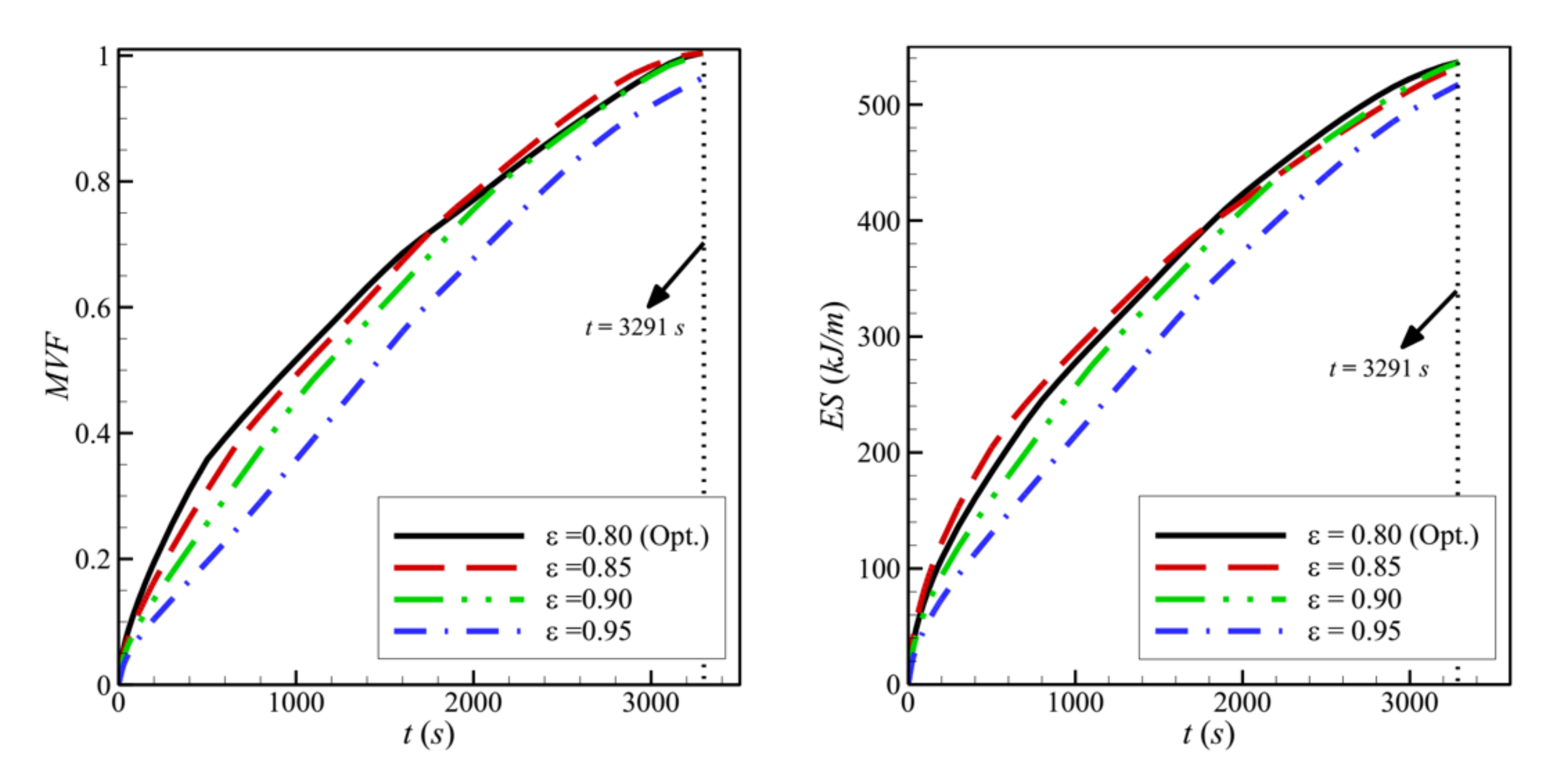
- Reducing the porosity of the porous layer, ε, which is equivalent to a higher presence of the solid matrix and, consequently, a higher thermal conductivity, enhances heat transfer and PCM melting. The charging power increases as ε decreases.
- The width of the heated copper wall, w, has a very limited effect on the charging power.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Voronin, D.V.; Ivanov, E.; Gushchin, P.; Fakhrullin, R.; Vinokurov, V. Clay Composites for Thermal Energy Storage: A Review. Molecules 2020, 25, 1504. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Chuck, W.; Zhang, G. Study on heat-transfer mechanism of wallboards containing active phase change material and parameter optimization with ventilation. Appl. Therm. Eng. 2018, 144, 1091–1108. [Google Scholar] [CrossRef]
- Jouhara, H.; Żabnieńska-Góra, A.; Khordehgah, N.; Ahmad, D.; Lipinski, T. Latent thermal energy storage technologies and applications: A review. Int. J. Therm. 2020, 5, 100039. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S.; Liu, Z.; Wen, T.; Ding, Z.; Yan, J.; Zhang, G. Passive and active phase change materials integrated building energy systems with advanced machine-learning based climate-adaptive designs, intelligent operations, uncertainty-based analysis and optimisations: A state-of-the-art review. Renew. Sustain. Energy Rev. 2020, 130, 109889. [Google Scholar] [CrossRef]
- Faraj, K.; Khaled, M.; Faraj, J.; Hachem, F.; Castelain, C. Phase change material thermal energy storage systems for cooling applications in buildings: A review. Renew. Sustain. Energy Rev. 2020, 119, 109579. [Google Scholar] [CrossRef]
- Keshteli, A.N.; Sheikholeslami, M. Nanoparticle enhanced PCM applications for intensification of thermal performance in building: A review. J. Mol. Liq. 2019, 274, 516–533. [Google Scholar] [CrossRef]
- Suresh, C.; Saini, R.P. Review on solar thermal energy storage technologies and their geometrical configurations. Int. J. Energy Res. 2020, 44, 4163–4195. [Google Scholar] [CrossRef]
- Kazemi, M.; Hosseini, M.; Ranjbar, A.; Bahrampoury, R. Improvement of longitudinal fins configuration in latent heat storage systems. Renew. Energy 2018, 116, 447–457. [Google Scholar] [CrossRef]
- Yang, G.; Yim, Y.-J.; Lee, J.W.; Heo, Y.-J.; Park, S.-J. Carbon-filled organic phase-change materials for thermal energy storage: A review. Molecules 2019, 24, 2055. [Google Scholar] [CrossRef] [Green Version]
- Sardari, P.T.; Grant, D.; Giddings, D.; Walker, G.S.; Gillott, M. Composite metal foam/PCM energy store design for dwelling space air heating. Energy Convers. Manag. 2019, 201, 112151. [Google Scholar] [CrossRef]
- Alsabery, A.; Armaghani, T.; Chamkha, A.; Hashim, I. Conjugate heat transfer of Al 2 O 3–water nanofluid in a square cavity heated by a triangular thick wall using Buongiorno’s two-phase model. J. Therm. Anal. Calorim. 2019, 135, 161–176. [Google Scholar] [CrossRef]
- Alsabery, A.; Yazdi, M.; Altawallbeh, A.; Hashim, I. Effects of nonhomogeneous nanofluid model on convective heat transfer in partially heated square cavity with conducting solid block. J. Therm. Anal. Calorim. 2019, 136, 1489–1514. [Google Scholar] [CrossRef]
- Alsabery, A.; Sheremet, M.; Chamkha, A.; Hashim, I. Conjugate natural convection of Al2O3–water nanofluid in a square cavity with a concentric solid insert using Buongiorno’s two-phase model. Int. J. Mech. Sci. 2018, 136, 200–219. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S.; Zhang, G. Artificial neural network based multivariable optimization of a hybrid system integrated with phase change materials, active cooling and hybrid ventilations. Energy Convers. Manag. 2019, 197, 111859. [Google Scholar] [CrossRef]
- Tang, L.; Zhou, Y.; Zheng, S.; Zhang, G. Exergy-based optimisation of a phase change materials integrated hybrid renewable system for active cooling applications using supervised machine learning method. Sol. Energy 2020, 195, 514–526. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S.; Zhang, G. Multivariable optimisation of a new PCMs integrated hybrid renewable system with active cooling and hybrid ventilations. J. Build. Eng. 2019, 26, 100845. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S.; Zhang, G. Study on the energy performance enhancement of a new PCMs integrated hybrid system with the active cooling and hybrid ventilations. Energy 2019, 179, 111–128. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S. Multi-level uncertainty optimisation on phase change materials integrated renewable systems with hybrid ventilations and active cooling. Energy 2020, 202, 117747. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S.; Zhang, G. Machine learning-based optimal design of a phase change material integrated renewable system with on-site PV, radiative cooling and hybrid ventilations—study of modelling and application in five climatic regions. Energy 2020, 192, 116608. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S.; Zhang, G. Machine-learning based study on the on-site renewable electrical performance of an optimal hybrid PCMs integrated renewable system with high-level parameters’ uncertainties. Renew. Energy 2020, 151, 403–418. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S.; Zhang, G. A review on cooling performance enhancement for phase change materials integrated systems—flexible design and smart control with machine learning applications. Build. Environ. 2020, 174, 106786. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S.; Zhang, G. A state-of-the-art-review on phase change materials integrated cooling systems for deterministic parametrical analysis, stochastic uncertainty-based design, single and multi-objective optimisations with machine learning applications. Energy Build. 2020, 220, 110013. [Google Scholar] [CrossRef]
- Yagci, O.K.; Avci, M.; Aydin, O. Melting and solidification of PCM in a tube-in-shell unit: Effect of fin edge lengths’ ratio. J. Energy Storage 2019, 24, 100802. [Google Scholar] [CrossRef]
- Gürtürk, M.; Kok, B. A new approach in the design of heat transfer fin for melting and solidification of PCM. Int. J. Heat Mass Transf. 2020, 153, 119671. [Google Scholar] [CrossRef]
- Aly, K.A.; El-Lathy, A.R.; Fouad, M.A. Enhancement of solidification rate of latent heat thermal energy storage using corrugated fins. J. Energy Storage 2019, 24, 100785. [Google Scholar] [CrossRef]
- Abdi, A.; Martin, V.; Chiu, J.N. Numerical investigation of melting in a cavity with vertically oriented fins. Appl. Energy 2019, 235, 1027–1040. [Google Scholar] [CrossRef]
- Li, F.; Muhammad, N.; Abohamzeh, E.; Hakeem, A.A.; Hajizadeh, M.R.; Li, Z.; Bach, Q.-V. Finned unit solidification with use of nanoparticles improved PCM. J. Mol. Liq. 2020, 314, 113659. [Google Scholar] [CrossRef]
- Kadhim, H.T.; Jabbar, F.A.; Rona, A. Cu-Al2O3 hybrid nanofluid natural convection in an inclined enclosure with wavy walls partially layered by porous medium. Int. J. Mech. Sci. 2020, 186, 105889. [Google Scholar] [CrossRef]
- Babazadeh, H.; Zeeshan, A.; Jacob, K.; Hajizadeh, A.; Bhatti, M. Numerical modelling for nanoparticle thermal migration with effects of shape of particles and magnetic field inside a porous enclosure. Iran. J. Sci. Technol. Trans. Mech. Eng. 2020, 1–11. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Sheremet, M.A.; Shafee, A.; Li, Z. CVFEM approach for EHD flow of nanofluid through porous medium within a wavy chamber under the impacts of radiation and moving walls. J. Therm. Anal. Calorim. 2019, 138, 573–581. [Google Scholar] [CrossRef]
- Ferfera, R.S.; Madani, B. Thermal characterization of a heat exchanger equipped with a combined material of phase change material and metallic foams. Int. J. Heat Mass Transf. 2020, 148, 119162. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, J.; Lei, D.; Liu, H.; Li, J.; Wu, Z. Experimental study on latent thermal energy storage system with gradient porosity copper foam for mid-temperature solar energy application. Appl. Energy 2020, 261, 114472. [Google Scholar] [CrossRef]
- Mohammed, H.I.; Talebizadehsardari, P.; Mahdi, J.M.; Arshad, A.; Sciacovelli, A.; Giddings, D. Improved melting of latent heat storage via porous medium and uniform Joule heat generation. J. Energy Storage 2020, 31, 101747. [Google Scholar] [CrossRef]
- Zhao, C.; Opolot, M.; Liu, M.; Bruno, F.; Mancin, S.; Hooman, K. Numerical study of melting performance enhancement for PCM in an annular enclosure with internal-external fins and metal foams. Int. J. Heat Mass Transf. 2020, 150, 119348. [Google Scholar] [CrossRef]
- Joshi, V.; Rathod, M.K. Thermal performance augmentation of metal foam infused phase change material using a partial filling strategy: An evaluation for fill height ratio and porosity. Appl. Energy 2019, 253, 113621. [Google Scholar] [CrossRef]
- Sardari, P.T.; Mohammed, H.I.; Giddings, D.; Gillott, M.; Grant, D. Numerical study of a multiple-segment metal foam-PCM latent heat storage unit: Effect of porosity, pore density and location of heat source. Energy 2019, 189, 116108. [Google Scholar] [CrossRef]
- Li, W.; Wan, H.; Lou, H.; Fu, Y.; Qin, F.; He, G. Enhanced thermal management with microencapsulated phase change material particles infiltrated in cellular metal foam. Energy 2017, 127, 671–679. [Google Scholar] [CrossRef]
- Li, W.; Zhang, D.; Jing, T.; Gao, M.; Liu, P.; He, G.; Qin, F. Nano-encapsulated phase change material slurry (Nano-PCMS) saturated in metal foam: A new stable and efficient strategy for passive thermal management. Energy 2018, 165, 743–751. [Google Scholar] [CrossRef]
- Al-Jethelah, M.; Ebadi, S.; Venkateshwar, K.; Tasnim, S.; Mahmud, S.; Dutta, A. Charging nanoparticle enhanced bio-based PCM in open cell metallic foams: An experimental investigation. Appl. Therm. Eng. 2019, 148, 1029–1042. [Google Scholar] [CrossRef]
- Tasnim, S.H.; Hossain, R.; Mahmud, S.; Dutta, A. Convection effect on the melting process of nano-PCM inside porous enclosure. Int. J. Heat Mass Transf. 2015, 85, 206–220. [Google Scholar] [CrossRef]
- Hussanan, A.; Salleh, M.Z.; Khan, I.; Shafie, S. Convection heat transfer in micropolar nanofluids with oxide nanoparticles in water, kerosene and engine oil. J. Mol. Liq. 2017, 229, 482–488. [Google Scholar] [CrossRef] [Green Version]
- Kant, K.; Shukla, A.; Sharma, A.; Biwole, P.H. Heat transfer study of phase change materials with graphene nano particle for thermal energy storage. Sol. Energy 2017, 146, 453–463. [Google Scholar] [CrossRef]
- Mahdi, J.M.; Mohammed, H.I.; Hashim, E.T.; Talebizadehsardari, P.; Nsofor, E.C. Solidification enhancement with multiple PCMs, cascaded metal foam and nanoparticles in the shell-and-tube energy storage system. Appl. Energy 2020, 257, 113993. [Google Scholar] [CrossRef]
- Ranut, P. On the effective thermal conductivity of aluminum metal foams: Review and improvement of the available empirical and analytical models. Appl. Therm. Eng. 2016, 101, 496–524. [Google Scholar] [CrossRef]
- Mesalhy, O.; Lafdi, K.; Elgafy, A.; Bowman, K. Numerical study for enhancing the thermal conductivity of phase change material (PCM) storage using high thermal conductivity porous matrix. Energy Convers. Manag. 2005, 46, 847–867. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, C.; Liu, Q.; Tian, Z.; Fan, X. Thermal performance of copper foam/paraffin composite phase change material. Energy Convers. Manag. 2018, 157, 372–381. [Google Scholar] [CrossRef]
- Ali, A.R.I.; Salam, B. A review on nanofluid: Preparation, stability, thermophysical properties, heat transfer characteristics and application. SN Appl. Sci. 2020, 2, 1–17. [Google Scholar] [CrossRef]
- Reddy, J.N.; Gartling, D.K. The Finite Element Method in Heat Transfer and Fluid Dynamics; CRC Press: New York, NY, USA, 2010. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Nithiarasu, P. The Finite Element Method for Fluid Dynamics, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- De Los Reyes, J.C.; González Andrade, S. A combined BDF-semismooth Newton approach for time-dependent Bingham flow. Numer. Methods Part. Differ. Equ. 2012, 28, 834–860. [Google Scholar] [CrossRef]
- Schenk, O.; Gärtner, K. Solving unsymmetric sparse systems of linear equations with PARDISO. Future Gener. Comput. Syst. 2004, 20, 475–487. [Google Scholar] [CrossRef]
- Wriggers, P. Nonlinear Finite Element Methods; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Verbosio, F.; De Coninck, A.; Kourounis, D.; Schenk, O. Enhancing the scalability of selected inversion factorization algorithms in genomic prediction. J. Comput. Sci. 2017, 22, 99–108. [Google Scholar] [CrossRef]
- Bertrand, O.; Binet, B.; Combeau, H.; Couturier, S.; Delannoy, Y.; Gobin, D.; Lacroix, M.; Le Quéré, P.; Médale, M.; Mencinger, J.; et al. Melting driven by natural convection A comparison exercise: First results. Int. J. Therm. Sci. 1999, 38, 5–26. [Google Scholar] [CrossRef]
- Gau, C.; Viskanta, R. Melting and solidification of a pure metal on a vertical wall. J. Heat Transfer. 1986, 1, 174–181. [Google Scholar] [CrossRef]
- Kashani, S.; Ranjbar, A.; Abdollahzadeh, M.; Sebti, S. Solidification of nano-enhanced phase change material (NEPCM) in a wavy cavity. Heat Mass Transf. 2012, 48, 1155–1166. [Google Scholar] [CrossRef]








| Properties | Capric Acid | Copper |
|---|---|---|
| Density (kg m−3) | Solid: 1018 Liquid: 888 | 8933 |
| Kinematic viscosity (m2 s−1) | 3 × 10−6 | N/A |
| Thermal expansion coefficient (K−1) | 1 × 10−3 | 1.67 × 10−5 |
| Thermal conductivity (Wm−1 K−1) | Solid: 0.372 Liquid: 0.153 | 401 |
| Latent heat (kJ kg−1) | 152.7 | N/A |
| Phase change temperature (°C) | 32 | N/A |
| Specific heat (kJ kg−1 K−1) | Solid: 1.9 Liquid: 2.4 | 0.385 |
| Cases | Mesh Size in Wall | Mesh Size in PCM | Computational Time | |
|---|---|---|---|---|
| Case I | 4 × 75 | 75 × 75 | 0.7281 | 14 h 19 min 15 s |
| Case II | 5 × 100 | 100 × 100 | 0.7273 | 9 h 45 min 20 s |
| * Case III | 6 × 125 | 125 × 125 | 0.7327 | 10 h 13 min 36 s |
| Case IV | 7 × 150 | 150 × 150 | 0.7369 | 10 h 14 min 17 s |
| Case V | 8 × 175 | 175 × 175 | 0.7401 | 12 h 33 min 11 s |
| Factors | Description | Level 1 | Level 2 | Level 3 | Level 4 |
|---|---|---|---|---|---|
| A | w / mm (Copper wall thickness) | 1 | 2 | 3 | 4 |
| B | l / mm (Porous layer thickness) | 2 | 4 | 6 | 8 |
| C | h / mm (Porous layer height) | 11 | 17 | 23 | 29 |
| D | ε (Porosity) | 0.80 | 0.85 | 0.90 | 0.95 |
| E | υna (Nanoparticles volume fraction) | 0.00 | 0.02 | 0.04 | 0.06 |
| Case No. | Control Parameters | MVF = 1 | ||||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | t|MVF=1 / s | * CP / J m−1 s−1 | S/N Ratio | |
| w / mm | l / mm | h / mm | ε | υna | ||||
| 1 | 1 | 2 | 11 | 0.8 | 0 | 4100 | 131.5572 | −72.2557 |
| 2 | 1 | 4 | 17 | 0.85 | 0.02 | 4700 | 113.2655 | −73.4420 |
| 3 | 1 | 6 | 23 | 0.90 | 0.04 | 5800 | 91.0539 | −75.2686 |
| 4 | 1 | 8 | 29 | 0.95 | 0.06 | 6700 | 78.6821 | −76.5215 |
| 5 | 2 | 2 | 17 | 0.90 | 0.06 | 5600 | 93.6736 | −74.9638 |
| 6 | 2 | 4 | 11 | 0.95 | 0.04 | 4400 | 122.7105 | −72.8691 |
| 7 | 2 | 6 | 29 | 0.8 | 0.02 | 6300 | 80.5411 | −75.9868 |
| 8 | 2 | 8 | 23 | 0.85 | 0 | 5600 | 95.4117 | −74.9638 |
| 9 | 3 | 2 | 23 | 0.95 | 0.02 | 7900 | 68.6977 | −77.9525 |
| 10 | 3 | 4 | 29 | 0.90 | 0 | 7800 | 68.6409 | −77.8419 |
| 11 | 3 | 6 | 11 | 0.85 | 0.06 | 3300 | 159.8793 | −70.3703 |
| 12 | 3 | 8 | 17 | 0.8 | 0.04 | 3400 | 153.9024 | −70.6296 |
| 13 | 4 | 2 | 29 | 0.85 | 0.04 | 6900 | 73.5752 | −76.7770 |
| 14 | 4 | 4 | 23 | 0.8 | 0.06 | 5100 | 98.5855 | −74.1514 |
| 15 | 4 | 6 | 17 | 0.95 | 0 | 5600 | 98.7377 | −74.9638 |
| 16 | 4 | 8 | 11 | 0.90 | 0.02 | 3400 | 159.6877 | −70.6296 |
| Optimum Factors | Optimum Melting Time at MVF = 1 | |||||
|---|---|---|---|---|---|---|
| W | L | H | ε | υna | Taguchi Prediction | Tested Case |
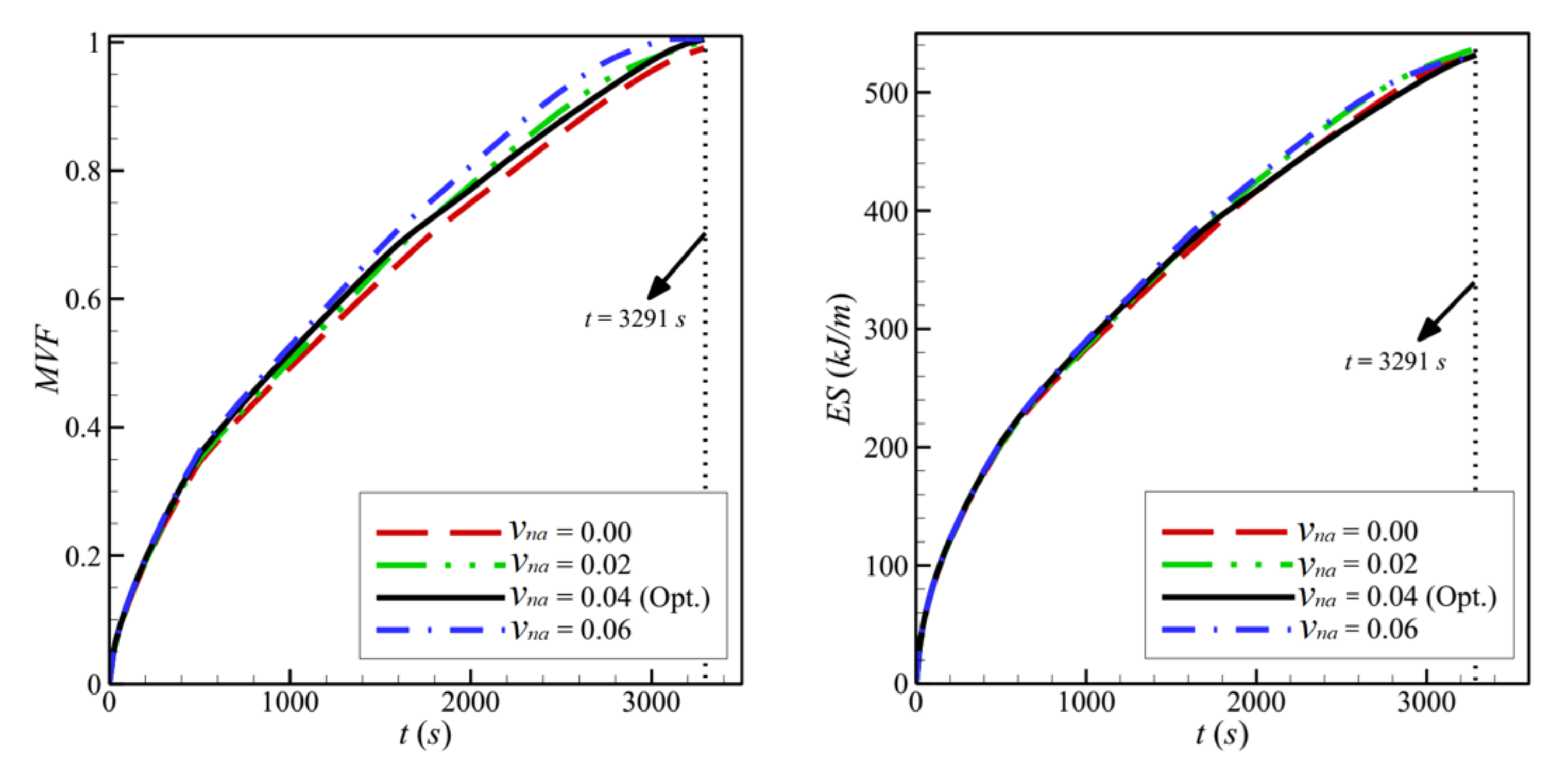
| 4 mm | 8 mm | 11 mm | 0.80 | 0.04 | 2025s | 3291.6 |
| w / mm | l / mm | h / mm | ε | υna | |
|---|---|---|---|---|---|
| Level 1 | −74.37 | −75.49 | −71.53 | −73.26 | −75.01 |
| Level 2 | −74.70 | −74.58 | −73.50 | −73.89 | −74.50 |
| Level 3 | −74.20 | −74.15 | −75.58 | −74.68 | −73.89 |
| Level 4 | −74.13 | −73.19 | −76.78 | −75.58 | −74.00 |
| δ | 0.57 | 2.30 | 5.25 | 2.32 | 1.12 |
| Rank | 5 | 3 | 1 | 2 | 4 |
| Case No. | Parameter | Control Parameters | at t = 3291.6 s | |||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | MVF | *CP / J m−1 s−1 | ||
| w / mm | l / mm | h / mm | ε | υna | ||||
| 1 | l | 4 | 2 | 11 | 0.80 | 0.04 | 0.9171 | 144.6119 |
| 2 | 4 | 4 | 11 | 0.80 | 0.04 | 0.9845 | 156.9111 | |
| 3 | 4 | 6 | 11 | 0.80 | 0.04 | 0.9976 | 160.5965 | |
| 4 | h | 4 | 8 | 17 | 0.80 | 0.04 | 0.9998 | 158.3983 |
| 5 | 4 | 8 | 23 | 0.80 | 0.04 | 0.9317 | 144.8368 | |
| 6 | 4 | 8 | 29 | 0.80 | 0.04 | 0.8469 | 130.0390 | |
| 7 | ε | 4 | 8 | 11 | 0.85 | 0.04 | 1.0000 | 163.0727 |
| 8 | 4 | 8 | 11 | 0.9 | 0.04 | 0.9982 | 162.9335 | |
| 9 | 4 | 8 | 11 | 0.95 | 0.04 | 0.9635 | 157.2007 | |
| 10 | υna | 4 | 8 | 11 | 0.80 | 0.0 | 0.9856 | 163.2366 |
| 11 | 4 | 8 | 11 | 0.80 | 0.02 | 0.9961 | 163.2134 | |
| 12 | 4 | 8 | 11 | 0.80 | 0.06 | 1.0000 | 160.8724 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghalambaz, M.; Mehryan, S.A.M.; Hajjar, A.; Younis, O.; Sheremet, M.A.; Pour, M.S.; Hulme-Smith, C. Phase-Transition Thermal Charging of a Channel-Shape Thermal Energy Storage Unit: Taguchi Optimization Approach and Copper Foam Inserts. Molecules 2021, 26, 1235. https://doi.org/10.3390/molecules26051235
Ghalambaz M, Mehryan SAM, Hajjar A, Younis O, Sheremet MA, Pour MS, Hulme-Smith C. Phase-Transition Thermal Charging of a Channel-Shape Thermal Energy Storage Unit: Taguchi Optimization Approach and Copper Foam Inserts. Molecules. 2021; 26(5):1235. https://doi.org/10.3390/molecules26051235
Chicago/Turabian StyleGhalambaz, Mohammad, Seyed Abdollah Mansouri Mehryan, Ahmad Hajjar, Obai Younis, Mikhail A. Sheremet, Mohsen Saffari Pour, and Christopher Hulme-Smith. 2021. "Phase-Transition Thermal Charging of a Channel-Shape Thermal Energy Storage Unit: Taguchi Optimization Approach and Copper Foam Inserts" Molecules 26, no. 5: 1235. https://doi.org/10.3390/molecules26051235
APA StyleGhalambaz, M., Mehryan, S. A. M., Hajjar, A., Younis, O., Sheremet, M. A., Pour, M. S., & Hulme-Smith, C. (2021). Phase-Transition Thermal Charging of a Channel-Shape Thermal Energy Storage Unit: Taguchi Optimization Approach and Copper Foam Inserts. Molecules, 26(5), 1235. https://doi.org/10.3390/molecules26051235








