Unusual Spin Exchanges Mediated by the Molecular Anion P₂S₆⁴⁻: Theoretical Analyses of the Magnetic Ground States, Magnetic Anisotropy and Spin Exchanges of MPS₃ (M = Mn, Fe, Co, Ni)

Abstract

We examined the magnetic ground states, the preferred spin orientations and the spin exchanges of four layered phases MPS₃ (M = Mn, Fe, Co, Ni) by first principles density functional theory plus onsite repulsion (DFT + U) calculations. The magnetic ground states predicted for MPS₃ by DFT + U calculations using their optimized crystal structures are in agreement with experiment for M = Mn, Co and Ni, but not for FePS₃. DFT + U calculations including spin-orbit coupling correctly predict the observed spin orientations for FePS₃, CoPS₃ and NiPS₃, but not for MnPS₃. Further analyses suggest that the ||z spin direction observed for the Mn²⁺ ions of MnPS₃ is caused by the magnetic dipole–dipole interaction in its magnetic ground state. Noting that the spin exchanges are determined by the ligand p-orbital tails of magnetic orbitals, we formulated qualitative rules governing spin exchanges as the guidelines for discussing and estimating the spin exchanges of magnetic solids. Use of these rules allowed us to recognize several unusual exchanges of MPS₃, which are mediated by the symmetry-adapted group orbitals of P₂S₆⁴⁻ and exhibit unusual features unknown from other types of spin exchanges.

1. Introduction

In an extended solid, transition-metal magnetic cations M are surrounded by main-group ligands L to form ML_n (typically, n = 3–6) polyhedra, and the unpaired spins of M are accommodated in the singly occupied d-states (i.e., the magnetic orbitals) of ML_n. Each d-state has the metal d-orbital combined out-of-phase with the p-orbitals of the surrounding ligands L. The tendency for two adjacent magnetic ions to have a ferromagnetic (FM) or an antiferromagnetic (AFM) spin alignment is determined by the spin exchange between them, which takes place through the M-L-M or M-L…L-M exchange path [1,2,3,4]. Whereas the characteristics (e.g., the angular and distance dependence) of the M-L-M exchanges is conceptually well understood [5,6,7,8], the properties of the M-L…L-M exchanges involving several main-group ligands have only come into focus in the last two decades [1,2,3,4]. Furthermore, the character of a M-L…L-M exchange can be modified if the L…L contact is bridged by a d⁰ metal cation A to form a L…A…L bridge [1,2,3,4]. What has not been well understood so far is the M-L…L-M exchange in which the L…L contact is an integral part of the covalent framework of a molecular anion made up of main group elements (e.g., the P₂S₆⁴⁻ anion in MPS₃, where M = Mn, Fe, Co, Ni), which might be termed the M-(L-L)-M exchange to emphasize its difference from the M-L-M, M-L…L-M and M-L…A…L-M exchanges.

In the present work we examine the M-(L-L)-M spin exchanges in the layered phases MPS₃ (M = Mn [9,10,11], Fe [9,10,11], Co [10,11], Ni [10,11]), which crystallize with a monoclinic structure (space group C2/m, no. 12). Each layer of MPS₃ is made up of the molecular anions P₂S₆⁴⁻ possessing the structure of staggered ethane (i.e., a trigonal antiprism structure) (Figure 1a,b). The molecular anions P₂S₆⁴⁻ form a trigonal layer (Figure 1c) with the P-P bonds perpendicular to the layer, and a high-spin M²⁺ cation occupies every S₆ octahedral site (deviations from a trigonal symmetry caused by the monoclinic distortions are less than 1°). Thus, each MPS₃ layer consists of a honeycomb arrangement of M²⁺ cations. With the c*-direction of the MPS₃ taken as the z-direction, the P-P bond of each P₂S₆⁴⁻ is parallel to the z-direction (||z), and each MS₆ octahedron is arranged with one of its three-fold rotational axes along the ||z-direction.

To a first approximation, it may be assumed that each MPS₃ layer has a trigonal symmetry (see below for further discussion), so there are three types of spin exchanges to consider, i.e., the first nearest-neighbor (NN) spin exchange J₁₂, the second NN spin exchange J₁₃, and the third NN exchange J₁₄ (Figure 1d). J₁₂ is a spin exchange of the M-L-M type, in which the two metal ions share a common ligand, while J₁₃ and J₁₄ are nominally spin exchanges of the M-L…L-M type, in which the two metal ions do not share a common ligand. In describing the magnetic properties of MPS₃ in terms of the spin exchanges J₁₂, J₁₃ and J₁₄, an interesting conceptual problem arises. Each P₂S₆⁴⁻ anion is coordinated to the six surrounding M²⁺ cations simultaneously (Figure 1c,d), so one P₂S₆⁴⁻ anion participates in all three different types of spin exchanges simultaneously with the surrounding six M²⁺ ions. Furthermore, the lone-pair orbitals of the S atoms of P₂S₆⁴⁻, responsible for the coordination with M²⁺ ions, form symmetry-adapted group orbitals, in which all six S atoms participate (for example, see Figure 1e). Consequently, there is no qualitative argument with which to even guess the possible differences in J₁₂, J₁₃, and J₁₄. Over the past two decades, it became almost routine to quantitatively determine any spin exchanges of a magnetic solid by performing an energy-mapping analysis based on first principles DFT calculations. From a conceptual point of view, it would be very useful to have qualitative rules with which to judge whether the spin exchange paths involving complex intermediates are usual or unusual.

A number of experimental studies examined the magnetic properties of MPS₃ (M = Mn [9,11,12,13,14], Fe [9,11,15,16,17,18], Co [11,19], Ni [11,20]). The magnetic properties of MPS₃ (M = Mn, Fe, Co, Ni) monolayers were examined by DFT calculations to find their potential use as single-layer materials possessing magnetic order [21]. The present work is focused on the magnetic properties of bulk MPS₃. For the ordered AFM states of MPS₃, the neutron diffraction studies reported that the layers of MnPS₃ exhibits a honeycomb-type AFM spin arrangement, AF1 (Figure 2a), but those of FePS₃, CoPS₃ and NiPS₃ a zigzag-chain spin array, AF2 (Figure 2b), in which the FM chains running along the a-direction are antiferromagnetically coupled (hereafter, the ||a-chain arrangement). An alternative AFM arrangement, AF3 (Figure 2c), in which the FM zigzag chains running along the (a + b)-direction are antiferromagnetically coupled (hereafter, the ||(a + b)-chain arrangement), is quite similar in nature to the ||a-chain arrangement.

At present, it is unclear why the spin arrangement of MnPS₃ differs from those of FePS₃, CoPS₃ and NiPS₃ and why FePS₃, CoPS₃ and NiPS₃ all adopt the ||a-chain arrangement rather than the ||(a + b)-chain arrangement. To explore these questions, it is necessary to examine the relative stabilities of a number of possible ordered spin arrangements of MPS₃ (M = Mn, Fe, Co, Ni) by electronic structure calculations and analyze the spin exchanges of their spin lattices.

Other quantities of importance for the magnetic ions M of an extended solid are the preferred orientations of their magnetic moments with respect to the local coordinates of the ML_n polyhedra. These quantities, i.e., the magnetic anisotropy energies, are also readily determined by DFT calculations including spin orbit coupling (SOC). For the purpose of interpreting the results of these calculations, the selection rules for the preferred spin orientation of ML_n were formulated [2,3,22,23,24] based on the SOC-induced interactions between the highest-occupied molecular orbital (HOMO) and lowest-unoccupied molecular orbital (LUMO) of ML_n. With the local z-axis of ML_n taken along its n-fold rotational axis (n = 3, 4), the quantity needed for the selection rules is the minimum difference, |ΔL_z|, in the magnetic quantum numbers L_z of the d-states describing the angular behaviors of the HOMO and LUMO. It is of interest to analyze the preferred spin orientations of the M²⁺ ions in MPS₃ (M = Mn, Fe, Co, Ni) from the viewpoint of the selection rules.

Our work is organized as follows: Section 2 describes simple qualitative rules governing spin exchanges. The details of our DFT calculations are presented in Section 3.1. The magnetic ground states of MPS₃ (M = Mn, Fe, Co, Ni) are discussed in Section 3.2, the preferred spin orientations of M²⁺ ions of MPS₃ in Section 3.3, and the quantitative values of the spin exchanges determined for MPS₃ in Section 3.4. We analyze the unusual features of the calculated spin exchanges via the P₂S₆⁴⁻ anion in Section 3.5, and investigate in Section 3.6 the consequences of the simplifying assumption that the honeycomb spin lattice has a trigonal symmetry rather than a slight monoclinic distortion found experimentally. Our concluding remarks are summarized in Section 4.

2. Qualitative Rules Governing Spin Exchanges

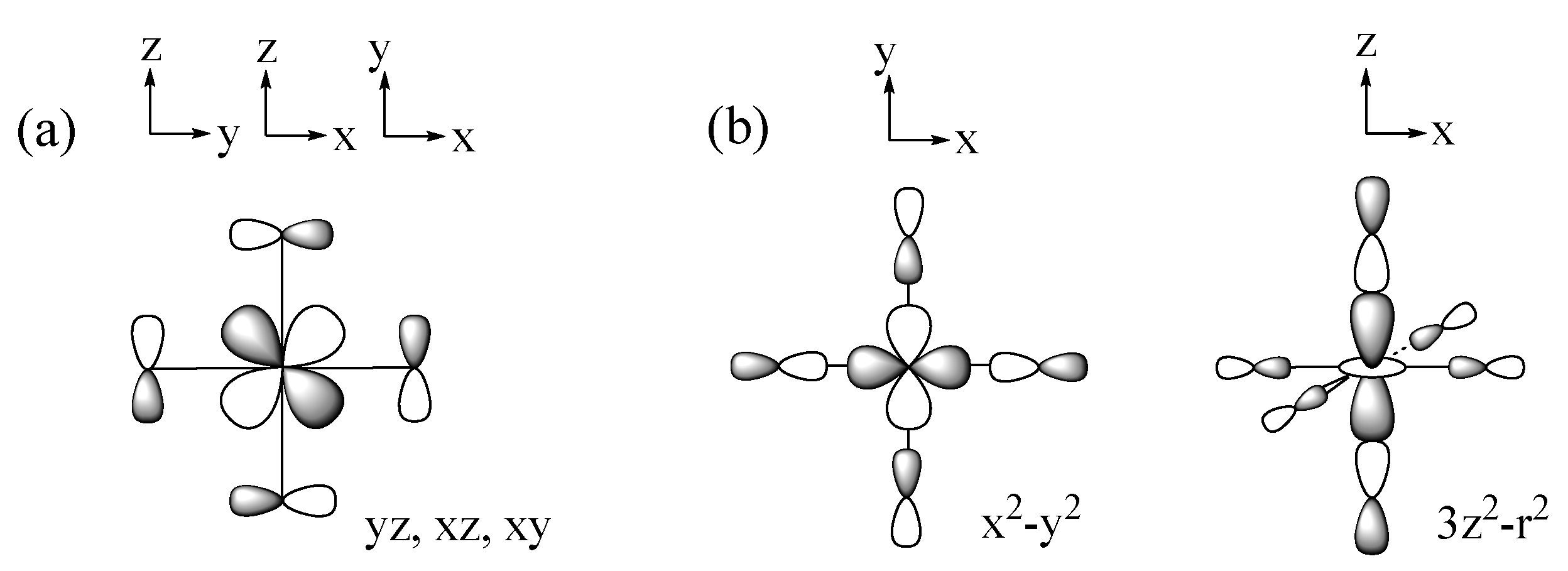
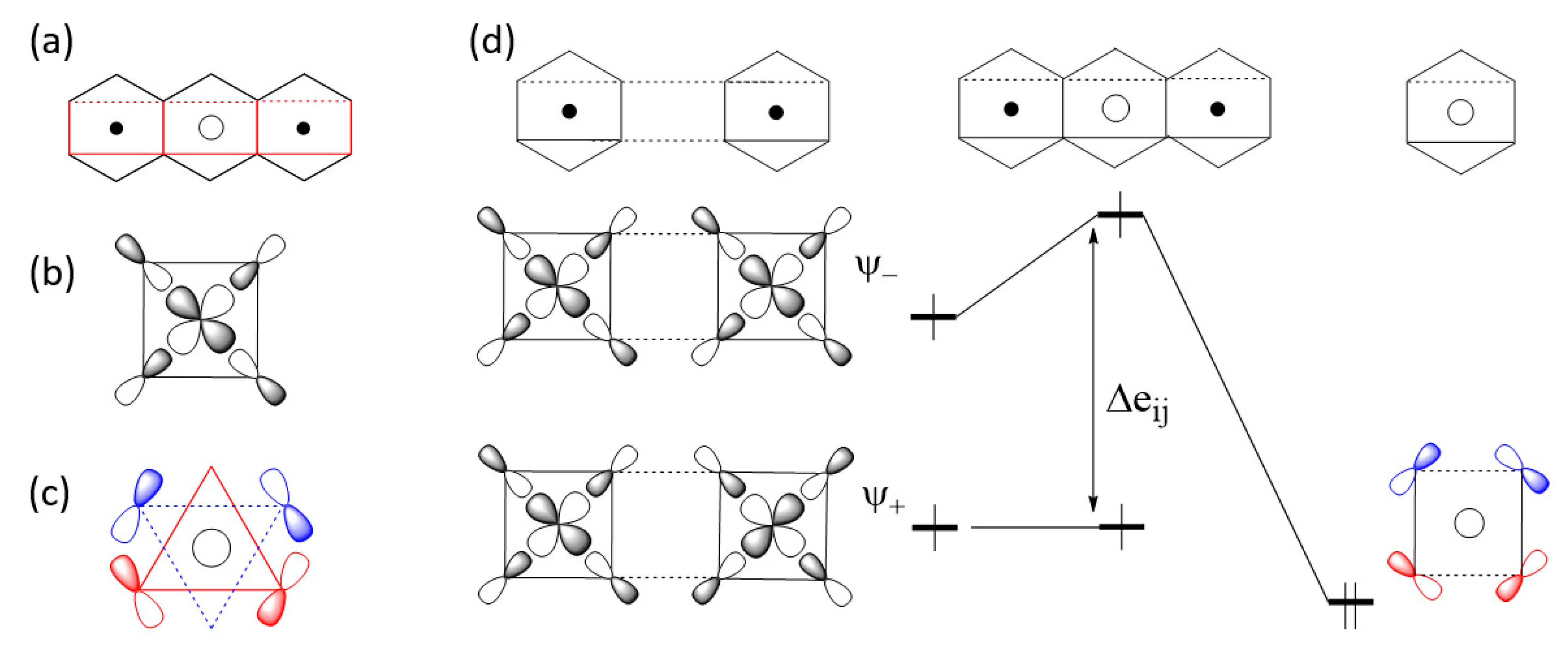
2.1. Spin Exchange between Magnetic Orbitals

For clarity, we use the notation $({\mathsf{\phi }}_{\mathrm{i}},{\mathsf{\phi }}_{\mathrm{j}})$ to represent the spin exchange arising from the magnetic orbitals ${\mathsf{\phi }}_{\mathrm{i}}$ and ${\mathsf{\phi }}_{\mathrm{j}}$ at the magnetic ion sites A and B, respectively. It is well known that $({\mathsf{\phi }}_{\mathrm{i}},{\mathsf{\phi }}_{\mathrm{j}})$ consists of two competing terms [1,2,3,4,25]

$$({\mathsf{\phi }}_{\mathrm{i}},{\mathsf{\phi }}_{\mathrm{j}})={\mathrm{J}}_{\mathrm{F}}+{\mathrm{J}}_{\mathrm{A}\mathrm{F}}$$

(1)

The FM component ${\mathrm{J}}_{\mathrm{F}}$ (>0) is proportional to the exchange repulsion,

$${\mathrm{J}}_{\mathrm{F}}\propto {\mathrm{K}}_{\mathrm{i}\mathrm{j}}$$

(2)

which increases with increasing the overlap electron density ${\mathsf{\rho }}_{\mathrm{i}\mathrm{j}}={\mathsf{\phi }}_{\mathrm{i}}{\mathsf{\phi }}_{\mathrm{j}}$. In case when the magnetic orbitals ${\mathsf{\phi }}_{\mathrm{i}}$ and ${\mathsf{\phi }}_{\mathrm{j}}$ are degenerate (e.g., between the t_2g states or between e_g states of the magnetic ions at octahedral sites), the AFM component J_AF (<0) is proportional to the square of the energy split $\Delta {\mathrm{e}}_{\mathrm{i}\mathrm{j}}$ between ${\mathsf{\phi }}_{\mathrm{i}}$ and ${\mathsf{\phi }}_{\mathrm{j}}$ induced by the interaction between them,

$${\mathrm{J}}_{\mathrm{A}\mathrm{F}}\propto -{(\Delta {\mathrm{e}}_{\mathrm{i}\mathrm{j}})}^2\propto -{({\mathrm{S}}_{\mathrm{i}\mathrm{j}})}^2$$

(3)

The energy split $\Delta {\mathrm{e}}_{\mathrm{i}\mathrm{j}}$ is proportional to the overlap integral ${\mathrm{S}}_{\mathrm{i}\mathrm{j}}$ = 〈${\mathsf{\phi }}_{\mathrm{i}}$|${\mathsf{\phi }}_{\mathrm{j}}$〉, so that the magnitude of the AFM component ${\mathrm{J}}_{\mathrm{A}\mathrm{F}}$ increases with increasing that of ${({\mathrm{S}}_{\mathrm{i}\mathrm{j}})}^2$. If ${\mathsf{\phi }}_{\mathrm{i}}$ and ${\mathsf{\phi }}_{\mathrm{j}}$ are not degenerate (e.g., between the t_2g and e_g states of the magnetic ions), the magnitude of ${\mathrm{J}}_{\mathrm{A}\mathrm{F}}$ is approximately proportional to $-{({\mathrm{S}}_{\mathrm{i}\mathrm{j}})}^2$.

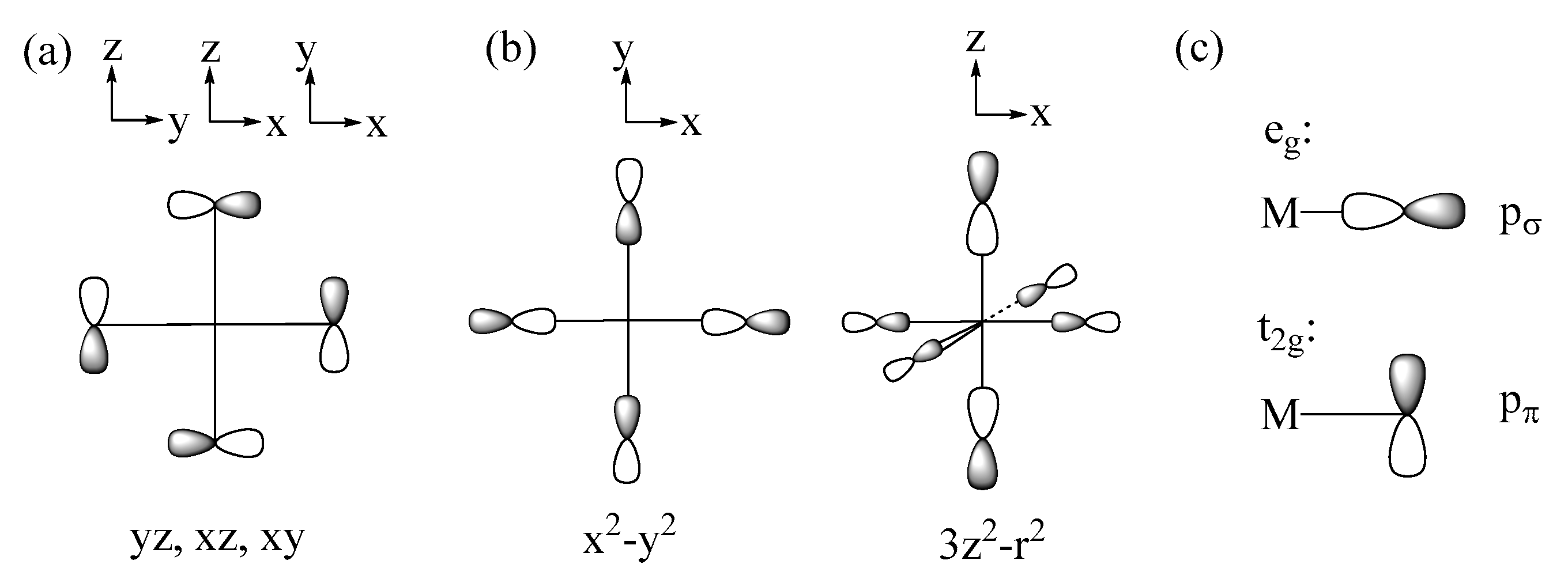
2.2. p-Orbital Tails of Magnetic Orbitals

The spin exchanges between adjacent transition-metal cations M are determined by the interactions between their magnetic orbitals, which in turn are governed largely by the overlap and the overlap electron density that are generated by the p-orbitals of the ligands present in the magnetic orbitals (the p-orbital tails, for short) [1,2,3,4]. Suppose that the metal ions M are surrounded by main-group ligands L to form ML₆ octahedra. In the t_2g and e_g states of an ML₆ octahedron (Figure 3a,b), the d-orbitals of M make σ and π antibonding combinations with the p-orbitals of the ligands L. Thus, the p-orbital tails of the t_2g and e_g states are represented as in Figure 4a,b, respectively, so that each M-L bond has the p_π and p_σ tails in the t_2g and e_g states, respectively, as depicted in Figure 4c. The triple-degeneracy of the t_2g and the double-degeneracy of the e_g states are lifted in a ML₅ square pyramid and a ML₄ square plane, both of which have a four-fold rotational symmetry; the t_2g states (xz, yz, xy) are split into (xz, yz) and xy, and the e_g states (3z² − r², x² − y²) into 3z² − r² and x² − y². Nevertheless, the description of the ligand p-orbital tails of the d-states depicted in Figure 4c remains valid.

2.3. Spin Exchanges in Terms of the p-Orbital Tails

In this section, we generalize the qualitative rules of spin exchanges formulated for the magnetic solids of Cu²⁺ ions [4]. Each Cu²⁺ ion has only one magnetic orbital, i.e., the x²−y² state in which each Cu-L bond has a p_σ tail. The d-electron configuration of the magnetic ion is (t_2g↑)³(e_g↑)²(t_2g↓)⁰(e_g↓)⁰ in MnPS₃, (t_2g↑)³(e_g↑)²(t_2g↓)¹(e_g↓)⁰ in FePS₃, (t_2g↑)³(e_g↑)²(t_2g↓)²(e_g↓)⁰ in CoPS₃, and (t_2g↑)³(e_g↑)²(t_2g↓)³(e_g↓)⁰ in NiPS₃. Thus, the Mn²⁺, Fe²⁺, Co²⁺, and Ni²⁺ ions possess 5, 4, 3, and 2 magnetic orbitals, respectively. For magnetic ions with several magnetic orbitals, the spin exchange J_AB between two such ions located at sites A and B is given by the sum of all possible individual exchanges $({\mathsf{\phi }}_{\mathrm{i}},{\mathsf{\phi }}_{\mathrm{j}})$,

$${\mathrm{J}}_{\mathrm{A}\mathrm{B}}=\frac{2}{{\mathrm{n}}_{\mathrm{A}}{\mathrm{n}}_{\mathrm{B}}}{\displaystyle \sum _{\mathrm{i}\in \mathrm{A}}{\displaystyle \sum _{\mathrm{j}\in \mathrm{B}}}}({\mathsf{\phi }}_{\mathrm{i}},{\mathsf{\phi }}_{\mathrm{j}})\propto {\displaystyle \sum _{\mathrm{i}\in \mathrm{A}}{\displaystyle \sum _{\mathrm{j}\in \mathrm{B}}}}({\mathsf{\phi }}_{\mathrm{i}},{\mathsf{\phi }}_{\mathrm{j}})$$

(4)

where ${\mathrm{n}}_{\mathrm{A}}$ and ${\mathrm{n}}_{\mathrm{B}}$ are the number of magnetic orbitals at the sites A and B, respectively. Each individual exchange $({\mathsf{\phi }}_{\mathrm{i}},{\mathsf{\phi }}_{\mathrm{j}})$ can be FM or AFM depending on which term, J_F or J_AF, dominates. Whether J_AB is FM or AFM depends on the sum of all individual $({\mathsf{\phi }}_{\mathrm{i}},{\mathsf{\phi }}_{\mathrm{j}})$ contributions.

2.3.1. M-L-M Exchange

As shown in Figure 5, there occur three types of M-L-M exchanges between the magnetic orbitals of t_2g and e_g states.

If the M-L-M bond angle θ is 90° for the (e_g, e_g) and (t_2g, t_2g) exchanges, and also when θ is 180° for the (e_g, t_2g) exchange, the two p-orbital tails have an orthogonal arrangement so that 〈${\mathsf{\phi }}_{\mathrm{i}}$|${\mathsf{\phi }}_{\mathrm{j}}$〉 = 0 (i.e., ${\mathrm{J}}_{\mathrm{A}\mathrm{F}}$ = 0). However, the overlap electron density ${\mathsf{\phi }}_{\mathrm{i}}{\mathsf{\phi }}_{\mathrm{j}}$ is nonzero (i.e., ${\mathrm{J}}_{\mathrm{F}}$ ≠ 0), hence predicting these spin exchanges to be FM. When the θ angles of the (e_g, e_g) and (t_2g, t_2g) exchanges increase from 90° toward 180°, and also when the angle θ of the (e_g, t_2g) exchange decreases from 180° toward 90°, both ${\mathrm{J}}_{\mathrm{A}\mathrm{F}}$ and ${\mathrm{J}}_{\mathrm{F}}$ are nonzero so that the balance between the two determines if the overall exchange $({\mathsf{\phi }}_{\mathrm{i}},{\mathsf{\phi }}_{\mathrm{j}})$ becomes FM or AFM. These trends are what the Goodenough–Kanamori rules [5,6,7,8] predict.

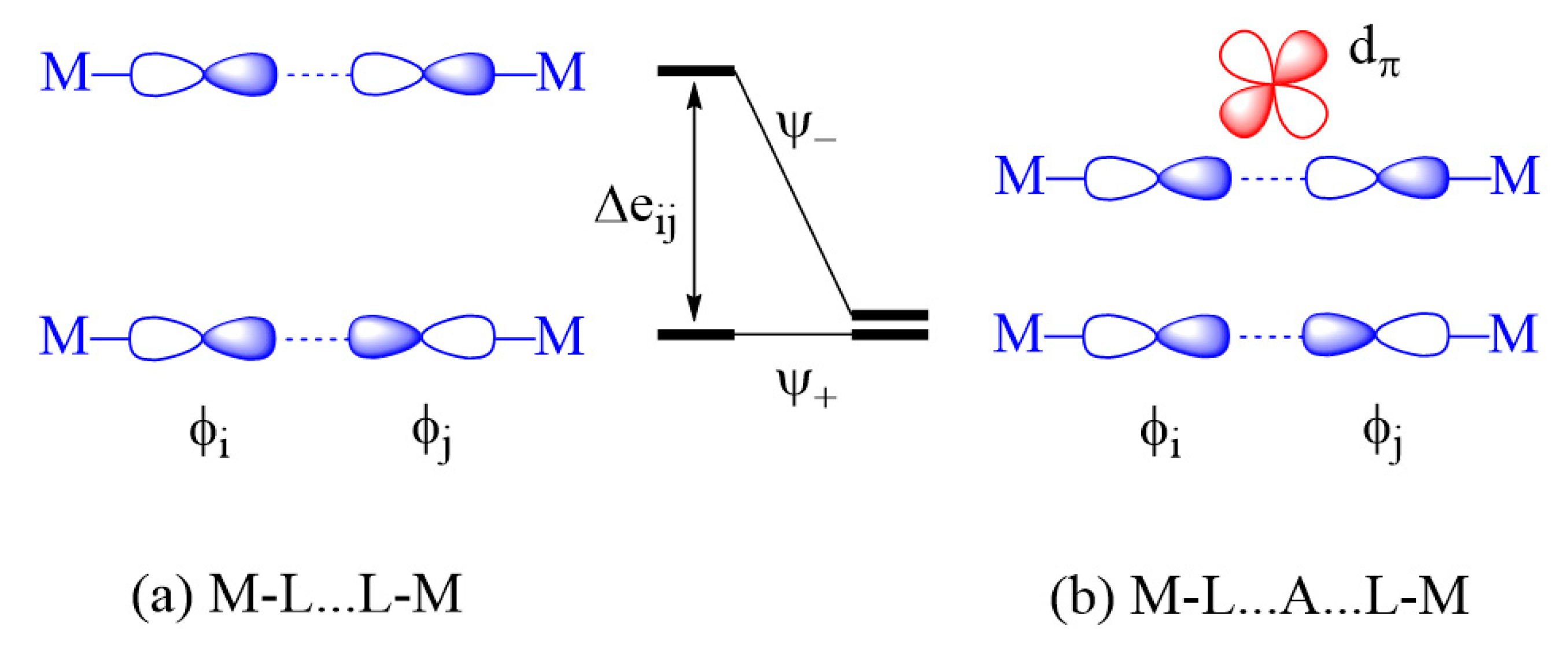
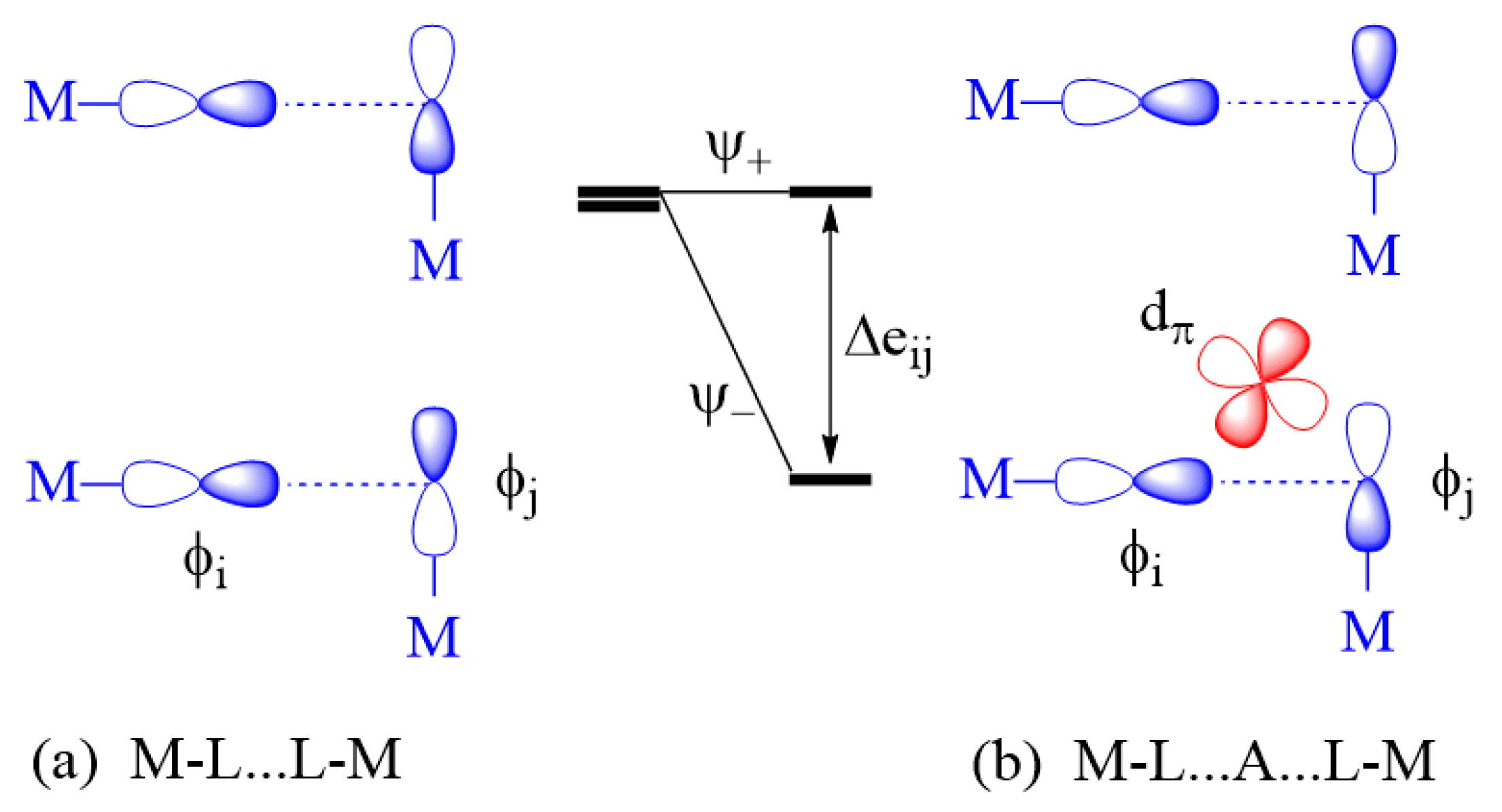
2.3.2. M-L…L-M Exchange

There are two extreme cases of M-L…L-M exchange. When the p_σ-orbital tails are pointing toward each other (Figure 6a), the overlap integral, 〈${\mathsf{\phi }}_{\mathrm{i}}$|${\mathsf{\phi }}_{\mathrm{j}}$〉, can be substantial if the contact distance L…L lies in the vicinity of the van der Waals distance. However, the overlap electron density ${\mathsf{\rho }}_{\mathrm{i}\mathrm{j}}={\mathsf{\phi }}_{\mathrm{i}}{\mathsf{\phi }}_{\mathrm{j}}$ is practically zero because ${\mathsf{\phi }}_{\mathrm{i}}$ and ${\mathsf{\phi }}_{\mathrm{j}}$ do not have an overlapping region. Consequently, the in-phase and out-of-phase states Ψ₊ and Ψ_- are split in energy with a large separation $\Delta {\mathrm{e}}_{\mathrm{i}\mathrm{j}}$. Thus, it is predicted that the M-L…L-M type exchange can only be AFM [1,2,3,4]. When the L…L linkage is bridged by a d⁰ cation such as V⁵⁺ or W⁶⁺, for example, only the out-of-phase state Ψ_- is lowered in energy by the d_π orbital of the cation A, reducing the $\Delta {\mathrm{e}}_{\mathrm{i}\mathrm{j}}$ so that the M-L…A…L-M exchange becomes weak (Figure 6b). Conversely, when the p-orbital tails of the M-L…L-M exchange path have an orthogonal arrangement (Figure 7a), the overlap integral, 〈${\mathsf{\phi }}_{\mathrm{i}}$|${\mathsf{\phi }}_{\mathrm{j}}$〉, is zero, making the M-L…L-M exchange weak. If the L…L linkage of such an exchange path is bridged by a d⁰ cation, the out-of-phase state Ψ_- level is lowered in energy enlarging $\Delta {\mathrm{e}}_{\mathrm{i}\mathrm{j}}$ so that the M-L…A…L-M becomes strongly AFM (Figure 7b) [2,3,4].

In the M-L…A…L-M exchange of Figure 7, the vanishingly small $\Delta {\mathrm{e}}_{\mathrm{i}\mathrm{j}}$ of the M-L…L-M exchange results because the two p_σ tails have an orthogonal arrangement. A very small $\Delta {\mathrm{e}}_{\mathrm{i}\mathrm{j}}$ for the M-L…L-M exchange occurs even if the two M-L bonds are pointing to each other as in Figure 6 when one M-L bond has a p_σ tail and the other has a p_π tail, and also when both M-L bonds have p_π tails. Such M-L…L-M spin exchanges become strong in the corresponding M-L…A…L-M exchanges.

2.3.3. Qualitative Rules Governing Spin Exchanges

The above discussions are based on the observation that the nature of a spin exchange, be it the M-L-M, M-L…L-M or M-L…A…L-M type, is governed by the ligand p-orbital tails present in the magnetic orbitals of the spin exchange path. The essential points of our discussions can be summarized as follows:

• For an individual $({\mathsf{\phi }}_{\mathrm{i}},{\mathsf{\phi }}_{\mathrm{j}})$ exchange of a M-L-M type, the (t_2g, t_2g) and (e_g, e_g) exchanges are FM if the bond angle θ is 90°, and so is the (t_2g, e_g) exchange if the bond angle θ is 180°. These exchanges become AFM when the bond angles θ deviate considerably from these values.
• An individual $({\mathsf{\phi }}_{\mathrm{i}},{\mathsf{\phi }}_{\mathrm{j}})$ exchange of a M-L…L-M or M-L…A…L-M type can only be AFM if not weak.
• A strong individual $({\mathsf{\phi }}_{\mathrm{i}},{\mathsf{\phi }}_{\mathrm{j}})$ exchange of a M-L…L-M is weakened by the d⁰ metal cation A in the M-L…A…L-M exchange, but a weak individual $({\mathsf{\phi }}_{\mathrm{i}},{\mathsf{\phi }}_{\mathrm{j}})$ exchange of a M-L…L-M is strengthened by the presence of a d⁰ metal cation A in the M-L…A…L-M exchange.
• When a magnetic ion has several unpaired spins, the spin exchange between two magnetic ions is given by the sum of all possible individual $({\mathsf{\phi }}_{\mathrm{i}},{\mathsf{\phi }}_{\mathrm{j}})$ exchanges.

These qualitative rules governing spin exchanges can serve as guidelines for exploring how the calculated spin exchanges are related to the structures of the exchange paths and also for ensuring that important exchange paths are included the set of spin exchanges to evaluate by the energy-mapping analysis.

3. Results and Discussion

3.1. Details of Calculations

We performed spin-polarized DFT calculations using the Vienna ab initio Simulation Package (VASP) [26,27], the projector augmented wave (PAW) method, and the PBE exchange-correlation functionals [28]. The electron correlation associated with the 3d states of M (M = Mn, Fe, Co, Ni) was taken into consideration by performing the DFT+U calculations [29] with the effective on-site repulsion U_eff = U − J = 4 eV on the magnetic ions. Our DFT + U calculations carried out for numerous magnetic solids of transition-metal ions showed that use of the U_eff values in the range of 3 − 5 eV correctly reproduce their magnetic properties (see the original papers cited in the review articles [1,2,3,22,24]). The primary purpose of using DFT + U calculations is to produce magnetic insulating states for magnetic solids. Use of U_eff = 3 − 5 eV in DFT + U calculations leads to magnetic insulating states for magnetic solids of Mn²⁺, Fe²⁺, Co²⁺, and Ni²⁺ ions. The present work employed the representative U_eff value of 4 eV. We carried out DFT + U calculations (with U_eff = 4 eV) to optimize the structures of MPS₃ (M = Mn, Fe, Co, Ni) in their FM states by relaxing only the ion positions while keeping the cell parameters fixed and using a set of (4 × 2 × 6) k-points and the criterion of 5 × 10⁻³ eV/Å for the ionic relaxation. All our DFT + U calculations for extracting the spin-exchange parameters employed a (2a, 2b, c) supercell, the plane wave cutoff energy of 450 eV, the threshold of 10⁻⁶ eV for self-consistent-field energy convergence, and a set of (4 × 2 × 6) k-points. The preferred spin direction of the cation M²⁺ (M = Mn, Fe, Co, Ni) cation was determined by DFT + U + SOC calculations [30], employing a set of (4 × 2 × 6) k-points and the threshold of 10⁻⁶ eV for self-consistent-field energy convergence.

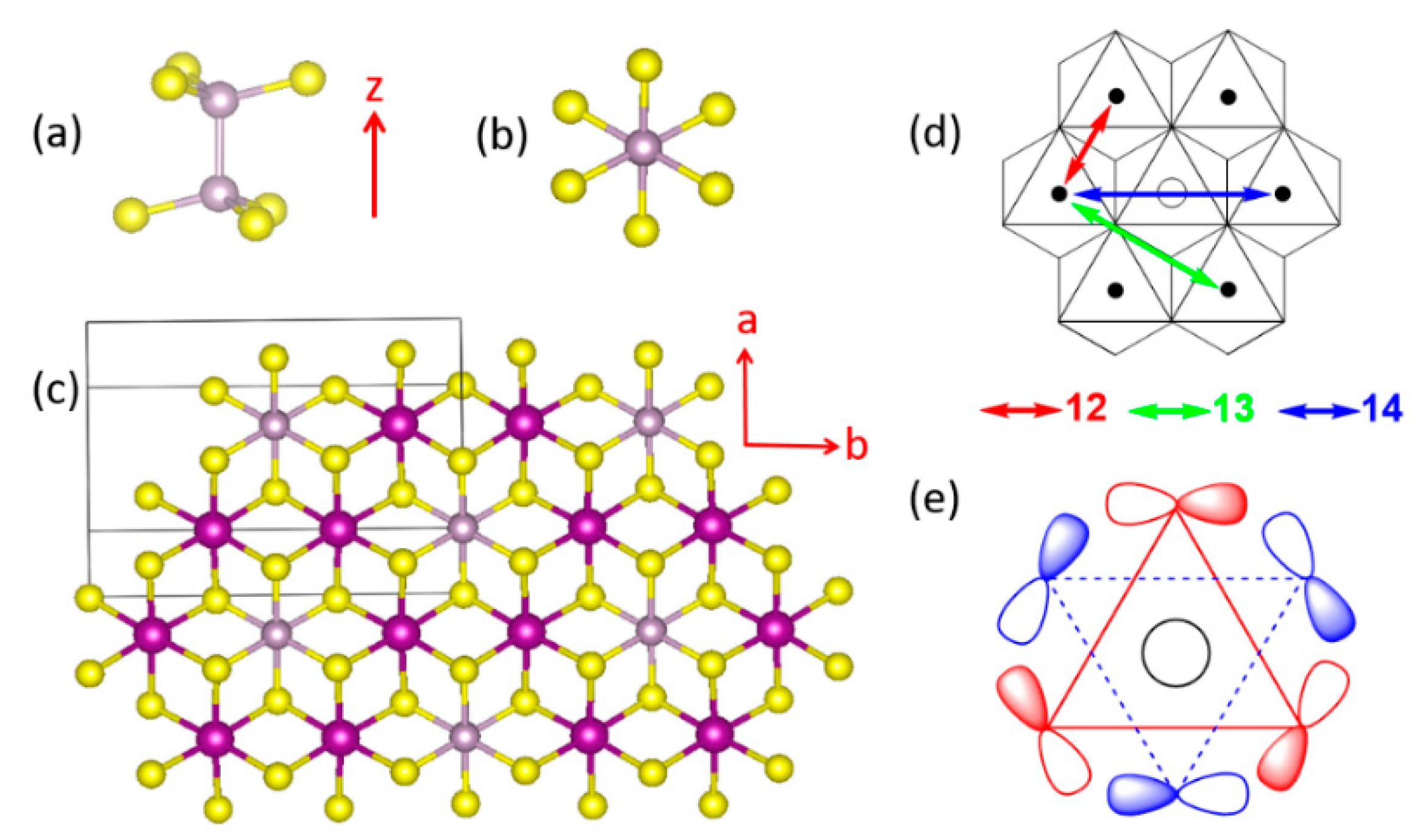
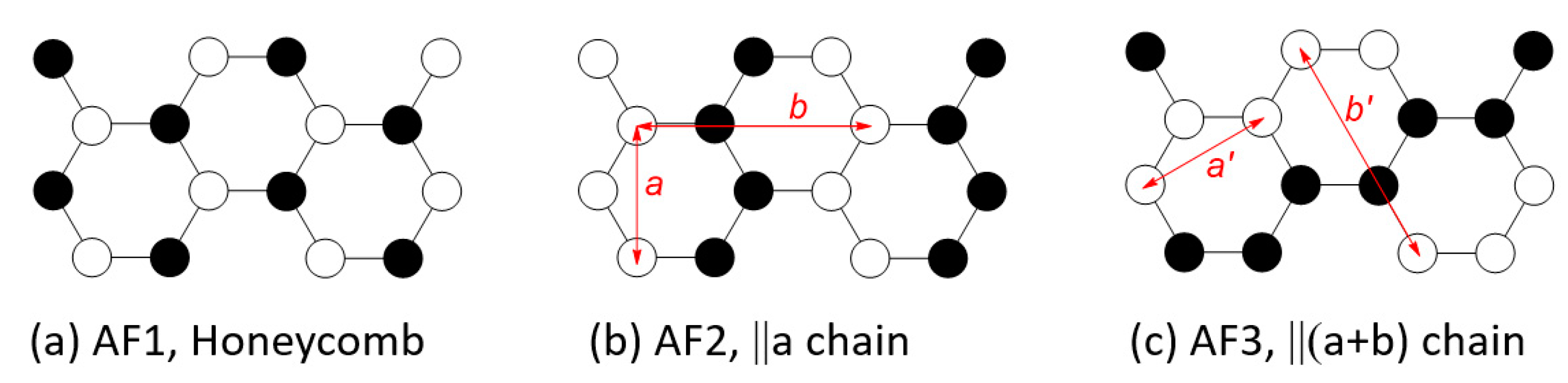
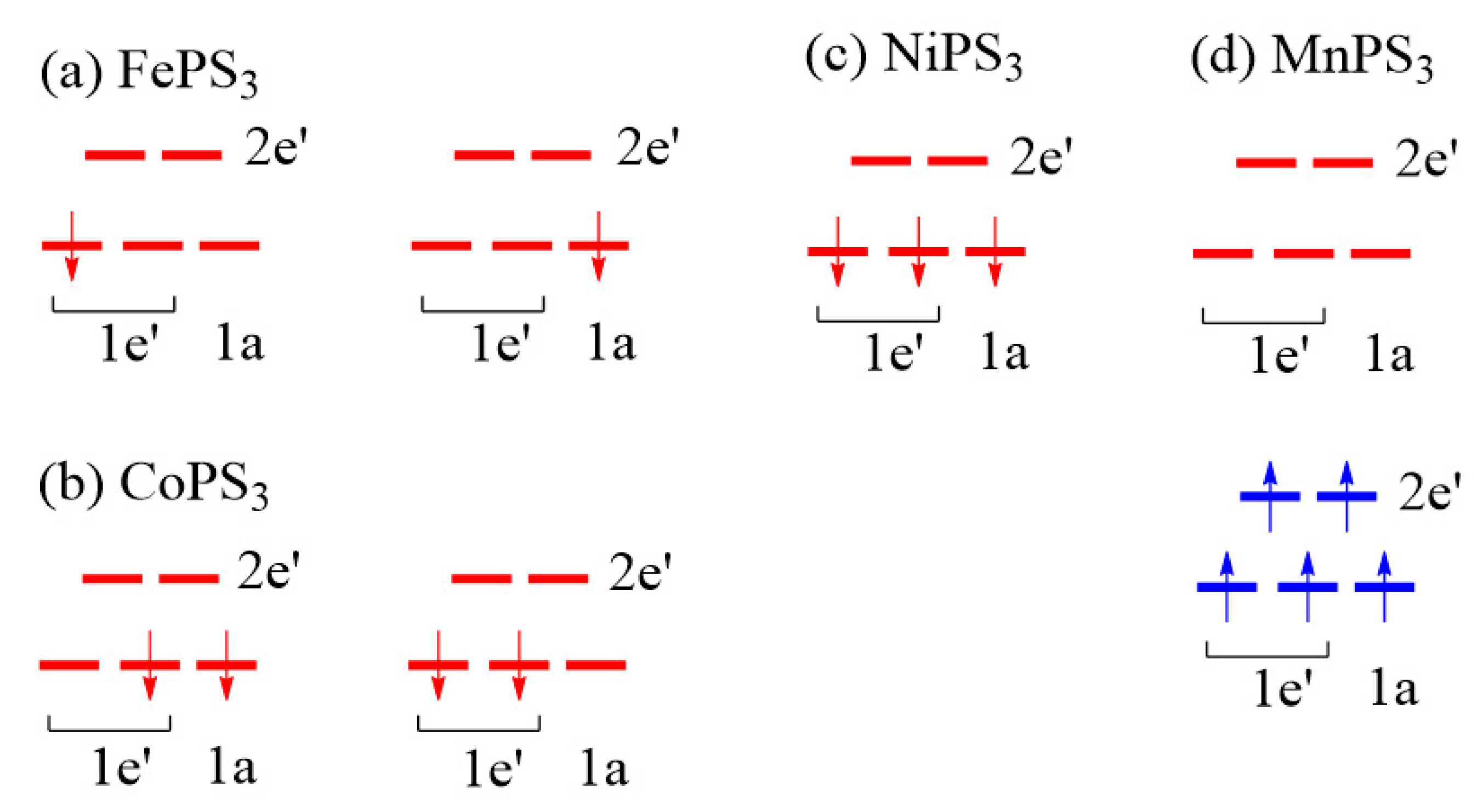
3.2. Magnetic Ground States of MPS₃

We probed the magnetic ground states of the MPS₃ phases by evaluating the relative energies, on the basis of DFT + U calculations, of the AF1, AF2 and AF3 spin configurations shown in Figure 2 as well as the FM, AF4, AF5, and AF6 states depicted in Supplementary Materials Figure S1. As summarized in

Table 1. Relative energies (in meV/formula unit) obtained for the seven ordered spin states of MPS₃ (M = Mn, Fe, Co, Ni) from DFT + U calculations with U_eff = 4 eV. The numbers without parentheses are obtained by using the experimental structures, and those in parentheses by using the structures optimized by DFT + U calculations.

	Mn	Fe	Co	Ni
FM	33.77 (33.36)	31.25 (25.10)	71.46 (55.00)	45.00 (42.04)
AF1	0 (0)	12.24 (5.16)	0 (5.70)	6.50 (7.11)
AF2	15.54 (15.50)	12.92 (7.93)	45.05 (0)	0 (0)
AF3	14.25 (14.21)	0 (0)	34.02 (24.99)	0.35 (0.34)
AF4	14.72 (14.45)	20.85 (18.57)	22.16 (26.00)	52.40 (49.53)
AF5	12.77 (12.58)	15.79 (12.95)	157.25 (158.33)	33.62 (31.98)
AF6	17.24 (17.07)	10.57 (6.33)	140.58 (143.05)	16.43 (15.21)

, our calculations using the experimental structures of MPS₃ show that the magnetic ground states of MnPS₃ and NiPS₃ adopt the honeycomb state AF1 and the ||a-chain state AF2, respectively, in agreement with experiment. In disagreement with experiment, however, the magnetic ground state is predicted to be the ||(a + b)-chain state AF3 for FePS₃, and the honeycomb state AF1 for CoPS₃. Since the energy differences between different spin ordered states are small, it is reasonable to speculate if they may be affected by small structural (monoclinic) distortion. Thus, we optimize the crystal structures of MPS₃ (M = Mn, Fe, Co, Ni) by performing DFT + U calculations to obtain the structures presented in the supporting material. Then, we redetermined the relative stabilities of the FM and AF1–AF6 states using these optimized structures. Results of these calculations are also summarized in Table 1. The optimized structures predict that the magnetic ground states of MnPS₃, CoPS₃ and NiPS₃ are the same as those observed experimentally, but that of FePS₃ is still the ||(a+b)-chain state AF3 rather than the ||a-chain state AF2 reported experimentally. This result is not a consequence of using the specific value of U_eff = 4 eV, because our DFT + U calculations for FePS₃ with U_eff = 3.5 and 4.5 eV lead to the same conclusion.

To resolve the discrepancy between theory and experiment on the magnetic ground state of FePS₃, we note that the magnetic peak positions in the neutron diffraction profiles are determined by the repeat distances of the rectangular magnetic structures, namely, a and b for the AF2 state (Figure 2b), and a’ and b’ for the AF3 state (Figure 2c). In both the experimental and the optimized structures of FePS₃, it was found that a = a’ = 5.947 Å and b = b’ = 10.300 Å. Thus, for the neutron diffraction refinement of the magnetic structure for FePS₃, the AF2 and AF3 states provide an equally good model. In view of our computational results, we conclude that the AF3 state is the correct magnetic ground state for FePS₃.

The experimental and optimized structures of MPS₃ (M = Mn, Fe, Co, Ni) are very similar, as expected. The important differences between them affecting the magnetic ground state would be the M-S distances of the MS₆ octahedra, because the d-state splitting of the MS₆ octahedra is sensitively affected by them. The M-S distances of the MS₆ octahedra taken from the experimental and optimized crystal structures of MPS₃ are summarized in

Table 2. The M-S bond distances (in Å) of the MS₆ octahedra in MPS₃ (M = Mn, Fe, Co, Ni) obtained from the experimental and the optimized crystal structures, which are shown without and with parentheses, respectively.

Mn	Fe	Co	Ni
2.627 (2.632)	2.546 (2.525)	2.485 (2.492)	2.457 (2.453)
2.627 (2.632)	2.546 (2.526)	2.485 (2.492)	2.457 (2.453)
2.625 (2.635)	2.547 (2.571)	2.504 (2.525)	2.462 (2.457)
2.625 (2.635)	2.547 (2.572)	2.504 (2.525)	2.462 (2.457)
2.634 (2.639)	2.549 (2.572)	2.491 (2.537)	2.465 (2.461)
2.634 (2.639)	2.549 (2.573)	2.491 (2.537)	2.465 (2.461)

, and their arrangements in the honeycomb layer are schematically presented in Figure 8. All Mn-S bonds of MnS₆ in MnPS₃ are nearly equal in length, as expected for a high-spin d⁵ ion (Mn²⁺) environment. The Fe-S bonds of FeS₆ in the optimized structure of FePS₃ are grouped into two short and four long Fe-S bonds. This distinction is less clear in the experimental structure. The Co-S bonds of CoS₆ in the experimental and optimized structures of CoPS₃ are grouped into two short, two medium and two long Co-S bonds. However, the sequence of the medium and long Co-S bonds is switched between the two structures. In the experimental and optimized structures of NiPS₃, the Ni-S bonds of NiS₆ are grouped into two short, two medium and two long Ni-S bonds. This distinction is less clear in the experimental structure. Thus, between the experimental and optimized structures of MPS₃, the sequence of the two short, two medium and two long M-S bonds do not switch for M = Fe and Ni whereas it does for M = Co. The latter might be the cause for why the relative stabilities of the AF1 and AF2 states in CoPS₃ switches between the experimental and optimized structures.

3.3. Preferred Spin Orientation of MPS₃

3.3.1. Quantitative Evaluation

We determine the preferred spin orientations of the M²⁺ ions in MPS₃ (M = Mn, Fe, Co, Ni) phases by performing DFT + U + SOC calculations using their FM states with the ||z and ⊥z spin orientations. For the ⊥z direction we selected the ||a-direction. As summarized in

Table 3. Relative energies (in K per formula unit) of the ||z and ⊥z spin orientations of the M²⁺ ions in the FM states of MPS₃ (M = Mn, Fe, Co, Ni) obtained by DFT + U + SOC calculations. The results calculated by using the optimized (experimental) structures are presented without (with) the parentheses.

	MnPS3 a	FePS3 b	CoPS3	NiPS3
⊥z	0 (0)	20.0 (21.8)	0 (0)	0 (0)
||z	0.3 (0.3)	0 (0)	3.8 (5.2)	0.8 (0.7)

^a The same result is obtained by using the AF1 state, which is the magnetic ground state of MnPS₃. ^b The same results are obtained from our DFT+U calculations with U_eff = 3.5 and 4.5 eV.

, these calculations predict the preferred spin orientation to be the ||z direction for FePS₃, and the ||x direction for MnPS₃, CoPS₃ and NiPS₃. These predictions are in agreement with experiment for FePS₃ [9,18], CoPS₃ [19], and NiPS₃ [20], while this is not the case for MnPS₃ [9,12,14,31]. Our DFT + U + SOC calculations for the AF1 state of MnPS₃ show that the ||x spin orientation is still favored over the ||z orientation just as found from the calculations using the FM state of MnPS₃. The Mn²⁺ spins of MnPS₃ were reported to have the ||z orientation in the early studies [9,12], but were found to be slightly tilted away from the z-axis (by 8°) [14,31]. In our further discussion (see below), this small deviation is neglected.

3.3.2. Qualitative Picture

Selection Rules of Spin Orientation and Implications

With the local z-axis of a ML₆ octahedron along its three-fold rotational axis (Figure 1a), the t_2g set is described by {1a, 1e’}, and the e_g set by {2e’}[22,23,24], where

$$\begin{array}{l}1\mathrm{a}=3{\mathrm{z}}^2-{\mathrm{r}}^2\\ \left\{1{\mathrm{e}}^{\prime }\right\}=\left\{\sqrt{\frac{2}{3}}\mathrm{x}\mathrm{y}-\sqrt{\frac{1}{3}}\mathrm{x}\mathrm{z},\sqrt{\frac{2}{3}}({\mathrm{x}}^2-{\mathrm{y}}^2)-\sqrt{\frac{1}{3}}\mathrm{y}\mathrm{z}\right\}\\ \left\{2{\mathrm{e}}^{\prime }\right\}=\left\{\sqrt{\frac{1}{3}}\mathrm{x}\mathrm{y}+\sqrt{\frac{2}{3}}\mathrm{x}\mathrm{z},\sqrt{\frac{1}{3}}({\mathrm{x}}^2-{\mathrm{y}}^2)+\sqrt{\frac{2}{3}}\mathrm{y}\mathrm{z}\right\}\end{array}$$

(5)

Using these d-states, the electron configurations expected for the M²⁺ ions of MPS₃ (M = Mn, Fe, Co, Ni) are presented in Figure 9. In the spin polarized description of a magnetic ion, the up-spin d-states lie lower in energy than the down-spin states so that the HOMO and LUMO occur in the down-spin d-states for the M²⁺ ions with more than the d⁵ electron count, so only the down-spin states are shown for FePS₃, CoPS₃, and NiPS₃ in Figure 9a–c. For MnPS₃ with d⁵ Mn²⁺ ion, the HOMO is represented by the up-spin 1e’, and the LUMO by the down-spin 1a and 2e’ (Figure 9d).

In terms of the d-orbital angular states |L, L_z〉 (L = 2, L_z = −2, −1, 0, 1, 2), the 1e’ state consists of the |2, ±2〉 and |2, ±1〉 sets in the weight ratio of 2:1, and the 2e’ state in the weight ratio of 1:2 ratio. Consequently, the major component of the 1e’ set is the |2, ±2〉 set, while that of the 2e’ set is the |2, ±1〉 set.

The selection rules of the spin orientation are based on the |ΔL_z| value between the HOMO and LUMO of ML_n. If the HOMO and LUMO both occur in the up-spin state or in down-spin states (Figure 9a–c), the ||z spin orientation is predicted if |ΔL_z| = 0, and the ⊥z spin orientation if |ΔL_z| = 1. When |ΔL_z| > 1, the HOMO and LUMO do not interact under SOC and hence do not affect the spin orientation. Between the 1a, 1e’ and 2e’ states, we note the following cases of values:

$$\left|\Delta L_{\mathrm{z}}\right|=0\{\begin{array}{c}\mathrm{between} \mathrm{the} \mathrm{major} \mathrm{components} \mathrm{of} \mathrm{the} 1{\mathrm{e}}^{\prime } \mathrm{set}\\ \mathrm{between} \mathrm{the} \mathrm{major} \mathrm{components} \mathrm{of} \mathrm{the} 2{\mathrm{e}}^{\prime } \mathrm{set}\end{array}$$

(6)

$$\left|\Delta L_{\mathrm{z}}\right|=1\{\begin{array}{c}\mathrm{between} \mathrm{1a} \mathrm{and} \mathrm{the} \mathrm{minor} \mathrm{component} \mathrm{of} 1{\mathrm{e}}^{\prime }\\ \mathrm{between} \mathrm{1a} \mathrm{and} \mathrm{the} \mathrm{major} \mathrm{component} \mathrm{of} 2{\mathrm{e}}^{\prime }\\ \mathrm{between} \mathrm{the} \mathrm{major} \mathrm{components} \mathrm{of} 1{\mathrm{e}}^{\prime } \mathrm{and} 2{\mathrm{e}}^{\prime }\end{array}$$

(7)

We now examine the preferred spin orientations of MPS₃ from the viewpoint of the selection rules and their electron configurations (Figure 9). The d-electron configuration of FePS₃ can be either (d↑)⁵(1e’↓)¹ or (d↑)⁵(1a↓)¹ (Figure 9a), where the notation (d↑)⁵ indicates that all up-spin d-states are occupied. The (d↑)⁵(1e’↓)¹ configuration, for which |ΔL_z| = 0, predicts the ||z spin orientation, while the (d↑)⁵(1a↓)¹ configuration, for which |ΔL_z| = 1, predicts the ⊥z spin orientation. Thus, the (d↑)⁵(1a↓)¹ configuration is correct for the Fe²⁺ ion of FePS₃. Since this configuration has the degenerate level 1e’ unevenly occupied, it should possess uniaxial magnetism [2,3,22,23,24] and hence a large magnetic anisotropy energy. This is in support of the experimental finding of the Ising character of the spin lattice of FePS₃ [16] or the single-ion anisotropic character of the Fe²⁺ ion [17,18]. The d-electron configuration of CoPS₃ can be either (d↑)⁵(1e’↓)² or (d↑)⁵(1a↓)¹(1e’↓)¹ (Figure 9b). The (d↑)⁵(1e’↓)² configuration, for which |ΔL_z| = 1, predicts the ⊥z spin orientation, while the (d↑)⁵(1a↓)¹(1e’↓)¹ configuration, for which |ΔL_z| = 0, predicts the ||z spin orientation. Thus, the (d↑)⁵(1e’↓)² configuration is correct for the Co²⁺ ion of CoPS₃. Since this configuration has the degenerate level 1e’ evenly occupied, it does not possess uniaxial magnetism [2,3,22,23,24] and hence a small magnetic anisotropy energy. The d-electron configuration of NiPS₃ is given by (d↑)⁵(1a)¹(1e’↓)² (Figure 9c), for which |ΔL_z| = 1, so the ⊥z spin orientation is predicted in agreement with experiment.

Let us now consider the spin orientation of the Mn²⁺ ion of MnPS₃. First, it should be noted that, if the HOMO and LUMO occur in different spin states as in MnPS₃ (Figure 9d), the selection rules predict the opposite to those found for the case when the HOMO and LUMO occur all in up-spin states or all in down-spin states [2,3,22,23,24]. Namely, the preferred spin orientation is the ||z spin orientation if |ΔL_z| = 1, but the ⊥z spin orientation if |ΔL_z| = 0 [2,3,22,23,24]. According to Equation (7), |ΔL_z| = 1 for the Mn²⁺ ion of MnPS₃, which predicts the ⊥z orientation as the preferred spin direction in agreement with the quantitative estimate of the magnetic anisotropy energy obtained from the DFT + U + SOC calculations, although this is in disagreement with experiment [5,8,9,10]. It has been suggested that the ||z spin orientation is caused by the magnetic dipole–dipole (MDD) interactions [13]. This subject will be probed in the following.

Magnetic Dipole–Dipole Interactions

Being of the order of 0.01 meV for two spin-1/2 ions separated by 2 Å, the MDD interaction is generally weak. For two spins located at sites i and j with the distance r_ij and the unit vector e_ij along the distance, the MDD interaction is defined as [32]

$$\left(\frac{{\mathrm{g}}^2{\mathsf{\mu }}_{\mathrm{B}}^2}{{\mathrm{a}}_0^3}\right){\left(\frac{{\mathrm{a}}_0}{{\mathrm{r}}_{\mathrm{i}\mathrm{j}}}\right)}^3\left[-3({\overrightarrow{\mathrm{S}}}_{\mathrm{i}}\cdot {\overrightarrow{\mathrm{e}}}_{\mathrm{i}\mathrm{j}})({\overrightarrow{\mathrm{S}}}_{\mathrm{j}}\cdot {\overrightarrow{\mathrm{e}}}_{\mathrm{i}\mathrm{j}}) +({\overrightarrow{\mathrm{S}}}_{\mathrm{i}}\cdot {\overrightarrow{\mathrm{S}}}_{\mathrm{j}})\right]$$

(8)

where a₀ is the Bohr radius (0.529177 Å), and (gμ_B)²/(a₀)³ = 0.725 meV. The MDD effect on the preferred spin orientation of a given magnetic solid can be examined by comparing the MDD interaction energies calculated for a number of ordered spin arrangements. In summing the MDD interactions between various pairs of spin sites, it is necessary to employ the Ewald summation method [33,34,35].

Table 4. Relative energies (in K per formula unit) of the ||x and ||z spin orientations calculated by MDD calculations for the M²⁺ ions of MPS₃ (M = Mn, Fe, Co, Ni) in the AF1, AF2 and AF3 states using the optimized crystal structures.

	MnPS3		FePS3		CoPS3		NiPS3
	||x	||z	||x	||z	||x	||z	||x	||z
AF1	0.48	0.17	0.36	0.12	0.21	0.07	0.09	0.03
AF2	0.00	0.35	0.00	0.26	0.00	0.15	0.00	0.07
AF3	0.55	0.38	0.38	0.27	0.22	0.15	0.10	0.07

summarizes the MDD interaction energies calculated, by using the optimized structures of MPS₃ (M = Mn, Fe, Co, Ni), for the ||z and ||x spin directions in the AF1, AF2 and AF3 states. The corresponding results obtained by using the experimental structures of MPS₃ are summarized in Table S1.

These results can be summarized as follows: for the ||z spin orientation, the AF1 state is more stable than the AF2 and AF3 states. For the ||x spin orientation, the AF2 state is more stable than the AF1 and AF3 states. The ||x spin direction of the AF2 state is more stable than the ||z spin direction of the AF1 state. However, none of these results can reverse the relative stabilities of the ||z and ||x spin directions determined for FePS₃, CoPS₃, and NiPS₃ from the DFT + U + SOC calculations (Table 3). The situation is slightly different for MnPS₃, which adopts the AF1 state as the magnetic ground state. For MnPS₃ in this state, the MDD calculations predict that the ||z spin orientation is more stable than the ||x spin orientation by 0.3 K per formula unit (Table 4). Note that this prediction is the exact opposite to what the DFT + U + SOC calculations predict for MnPS₃ in the AF1 state (Table 3). Thus, the balance between these two opposing energy contributions will determine whether the ||z spin orientation is more stable than the ⊥z spin orientation in agreement with the experimental observation. Consequently, for MnPS₃ the MDD interaction dominates over the SOC effect which is plausible because of the half-filled shell electronic configuration. This is because the AF1 magnetic structure is forced on MnPS₃; in terms of purely MDD interactions alone, the ⊥z spin orientation in the AF2 state is most stable.

3.4. Quantitative Evaluations of Spin Exchanges

Due to the monoclinic crystal structure that MPS₃ adopts, each of the exchanges J₁₂, J₁₃ and J₁₄ (Figure 10a) are expected to split into two slightly different spin exchanges (Figure 10b) so that there are six spin exchanges J₁–J₆ to consider. To extract the values of the six spin exchanges J₁–J₆ (Figure 3), we employ the spin Hamiltonian expressed as:

$${\mathrm{H}}_{\mathrm{s}\mathrm{p}\mathrm{i}\mathrm{n}}=-{\displaystyle {\sum }_{\mathrm{i}>\mathrm{j}}}{\mathrm{J}}_{\mathrm{i}\mathrm{j}}{\widehat{\mathrm{S}}}_{\mathrm{i}}\cdot {\widehat{\mathrm{S}}}_{\mathrm{j}}$$

(9)

Then, the energies of the FM and AF1–AF6 states of MPS₃ (M = Mn, Fe, Co, Ni) per 2 × 2 × 1 supercell are written as:

E_FM = (–16J₁ − 8J₂ − 16J₃ − 32J₄ − 16J₅ − 8J₆)S²
     E_AF1 = (+16J₁ + 8J₂ − 16J₃ − 32J₄ + 16J₅ + 8J₆)S²
     E_AF2 = (−16J₁ + 8J₂ − 16J₃ + 32J₄ + 16J₅ + 8J₆)S²
E_AF3 = (−8J₂ + 16J₃ + 16J₅ + 8J₆)S²      
     E_AF4 = (+16J₁ − 8J₂ − 16J₃ + 32J₄ − 16J₅ − 8J₆)S²
E_AF5 = (+8J₂ + 16J₃ − 16J₅ + 8J₆)S²      
E_AF6 = (−8J₂ + 16J₃ + 16J₅ − 8J₆)S²      

where S is the spin on each M²⁺ ion (i.e., S = 5/2, 2, 3/2 and 1 for M = Mn, Fe, Co, and Ni, respectively). By mapping the relative energies of the FM and AF1–AF6 states determined in terms of the spin exchange J₁–J₆ onto the corresponding relative energies obtained from the DFT + U calculations (Table 1), we find the values of J₁–J₆ listed in

Table 5. Spin exchanges J₁–J₆ obtained (for the optimized structures of MPS₃ (M = Mn, Fe, Co, Ni) from DFT + U calculations with U_eff = 4 eV) by simulating the relative energies of the FM and AF1–AF6 states with the six spin exchanges.

	Mn	Fe	Co	Ni
J1	1.00	0.37	0.05	−0.25
J2	0.87	−0.32	−0.91	−0.14
J3	0.06	0.36	−0.55	0.04
J4	0.05	0.07	0.04	−0.01
J5	0.34	0.86	0.11	0.99
J6	0.33	1.00	1.00	1.00
	J1 = −16.0 K	J6 = −18.4 K	J6 = −608.7 K	J6 = −172.4 K

. (The spin exchanges of MPS₃ determined by using their experimental crystal structures are summarized in Table S2)

With the sign convention adopted in Eq. 1, AFM exchanges are represented by J_ij < 0, and FM exchanges by J_ij > 0. From Table 5, the following can be observed:

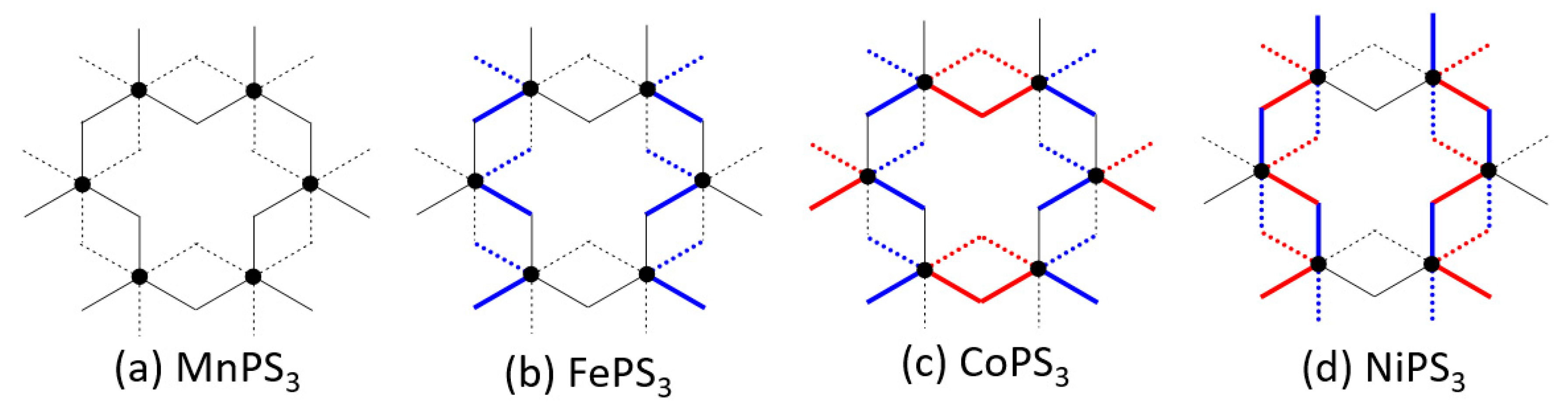
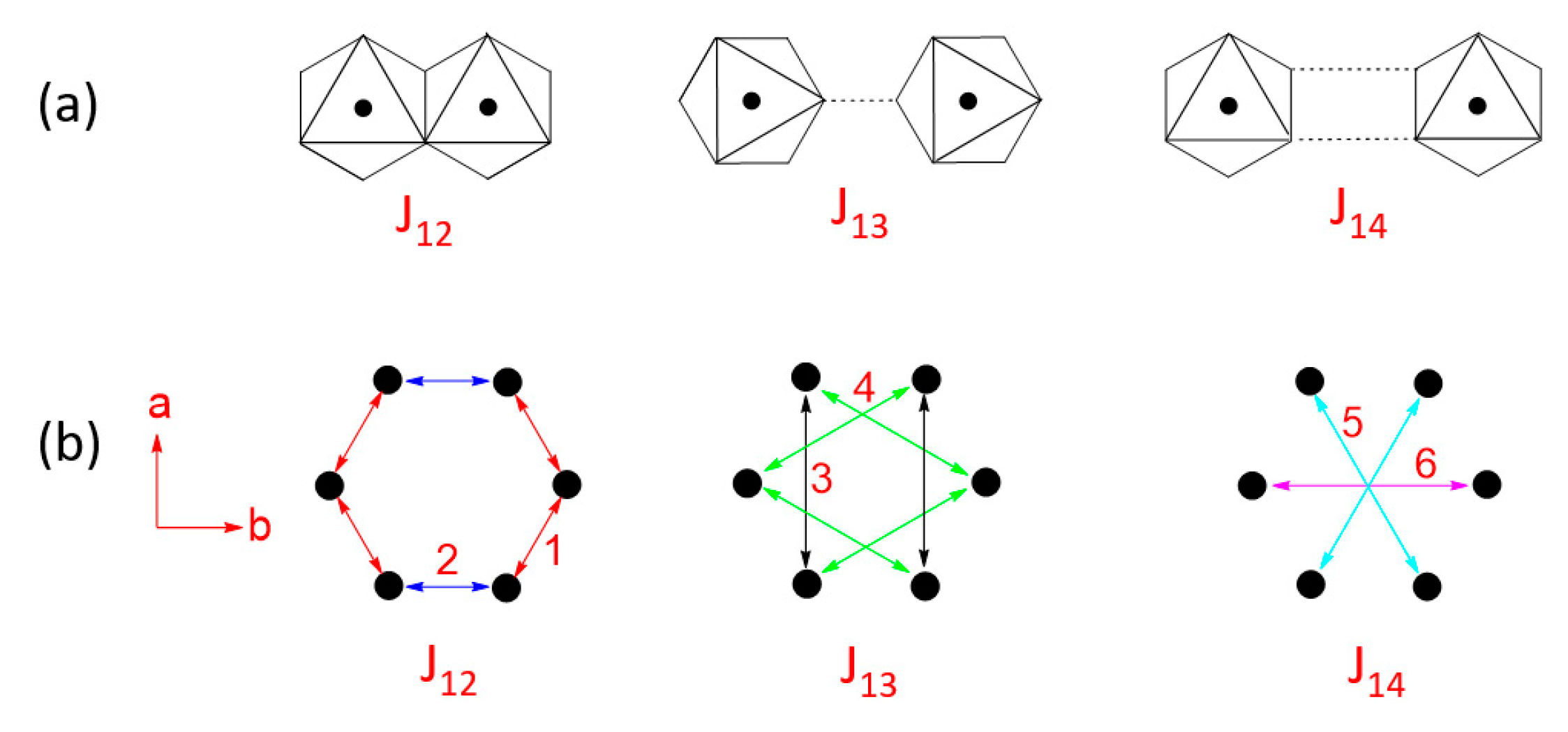
• In all MPS₃ (M = Mn, Fe, Co, Ni), J₁ ≠ J₂, J₃ ≠ J₄, and J₅ ≠ J₆, reflecting that the exchange paths are different between J₁ and J₂, between J₃ and J₄, and between J₅ and J₆ (Figure 10).
• J₁ ≈ J₂ < 0, J₃ ≈ J₄ ≈ 0, and J₅ ≈ J₆ < 0 for MnPS₃ while J₁ ≈ J₂ > 0, J₃ ≈ J₄ ≈ 0, and J₅ ≈ J₆ < 0 NiPS₃. To a first approximation, the electron configurations of MnPS₃ and NiPS₃ can be described by (t_2g)³(e_g)² and (t_2g)⁶(e_g)², respectively. That is, they do not possess an unevenly occupied degenerate state t_2g.
• In FePS₃ and CoPS₃, J₁ and J₂ are quite different, and so are J₃ and J₄. While J₅ and J₆ are comparable in FePS₃, they are quite different in CoPS₃. The electron configurations of FePS₃ and NiPS₃ can be approximated by (t_2g)⁴(e_g)² and (t_2g)⁵(e_g)², respectively. Namely, they possess an unevenly occupied degenerate state t_2g.
• The strongest exchange is J₁ in MnPS₃, but J₆ in other MPS₃ (M = Fe, Co, Ni).
• The second NN exchange J₃ is strongly FM in CoPS₃, while the third NN exchange J₆ is very strongly AFM in CoPS₃ and NiPS₃.

From the viewpoints of the expected trends in spin exchanges, the observation (e) is quite unusual. This will be discussed in the next section.

3.5. Unusual Features of the M-L…L-M Spin Exchanges

3.5.1. Second Nearest-Neighbor Exchange

As pointed out in the previous section, the second NN exchange J₃ of CoPS₃ is strongly FM despite that it is a M-L…L-M exchange to a first approximation. This implies that the J_F component in some $({\mathsf{\phi }}_{\mathrm{i}},{\mathsf{\phi }}_{\mathrm{j}})$ exchanges is nonzero, namely, the overlap electron density associated with those exchanges is nonzero. This implies that the p-orbital tails of the two magnetic orbitals are hybridized with the group orbitals of the P₂S₆⁴⁻ anion, i.e., they become delocalized into the whole P₂S₆⁴⁻ anion. Each MS₆ octahedron has three mutually orthogonal “MS₄ square planes” containing the yz, xz and xy states (Figure 11a). At the four corners of these three square planes, the p-orbital tails of the d-states are present (Figure 3a).

The lone-pair orbitals of the S atoms are important for the formation of each MS₆ octahedron. Due to the bonding requirement of the P₂S₆⁴⁻ anion, such lone pair orbitals become symmetry-adapted. An example in which the p-orbitals of all the S atoms are present is shown in Figure 1e.

With the (t_2g)⁵(e_g)² configuration, the Co²⁺ ion of CoPS₃ has five electrons in the t_2g level, namely, it has only one t_2g magnetic orbital. This magnetic orbital is contained in one of the three CoS₄ square planes presented in Figure 11b–d. When the S p-orbital at one corner of the P₂S₆⁴⁻ anion interacts with a d-orbital of M, the S p-orbitals at the remaining corners are also mixed in. Thus, when P₂S₆⁴⁻ anion shares corners with both MS₄ square planes of the J₃ exchange path, a nonzero overlap electron density is generated, thereby making the spin exchange FM. For convenience, we assume that the magnetic t_2g orbital of the Co²⁺ ion is the xy state. Then, there will be not only the (xy, xy) exchange, but also the (xy, x²−y²) and (x²−y², xy) exchanges between the two Co²⁺ ions of the J₃ path. All these individual exchanges lead to nonzero overlap electron densities by the delocalization of the p-orbital tails with the group orbitals of the molecular anion P₂S₆⁴⁻. In other words, the spin exchange J₃ in CoPS₃ is nominally a M-L…L-M, which is expected to be AFM by the qualitative rule, but it is strongly FM. It is clear that, if the L…L linkage is a part of the covalent framework of a molecular anion such as P₂S₆⁴⁻, a nominal M-L…L-M exchange can become FM for a certain combination of the d-electron count of the metal M and the geometries of the exchange path.

3.5.2. Third Nearest-Neighbor Exchange

Unlike in MnPS₃ and FePS₃, the M-S…S-M exchange J₆ is unusually strong in CoPS₃ and NiPS₃ (Section 3.3). This is so despite that the S…S contact distances are longer in CoPS₃ and NiPS₃ than in MnPS₃ and FePS₃ (i.e., the S…S contact distance of the J₆ path in MPS₃ is 3.409, 3.416, 3.421 and 3.450 Å for M = Mn, Fe, Co and Ni, respectively). We note that a strong M-L…L-M exchange (i.e., a spin exchange leading to a large energy split $\Delta {\mathrm{e}}_{\mathrm{i}\mathrm{j}}$) becomes weak, when the L…L contact is bridged by a d⁰ cation like, e. g., V⁵⁺ and W⁶⁺ to form the M-L…A…L-M exchange path (Figure 6b), because the out-of-phase combination ${\mathsf{\psi }}_{-}$ is lowered in energy by interacting with the unoccupied d_π orbital of the cation A. Conversely, then, one may ask if the strength of a M-L…L-M spin exchange can be enhanced by raising the ${\mathsf{\psi }}_{-}$ level. The latter can be achieved if the L…L path provides an occupied level of π-symmetry that can interact with ${\mathsf{\psi }}_{-}$. As depicted in Figure 12a, the J₆ path has the two MS₄ square planes containing the x²-y² magnetic orbitals (Figure 12b). The lone-pair group orbital of the S₄ rectangular plane (Figure 12c) of the P₂S₆⁴⁻ anion has the correct symmetry to interact with ${\mathsf{\psi }}_{-}$, so that the ${\mathsf{\psi }}_{-}$ level is raised in energy thereby enlarging the energy split between ${\mathsf{\psi }}_{+}$ and ${\mathsf{\psi }}_{-}$ and strengthening the J₆ exchange (Figure 12d). Although this reasoning applies equally to MnPS₃ and FePS₃, the latter do not have a strong J₆ exchange. This can be understood by considering Equation (1), which shows that a magnetic ion with several magnetic orbitals leads to several individual spin exchanges that can lead to FM contributions.

In view of the above discussion, which highlights the unusual nature of the second and third NN spin exchanges mediated by a molecular anion such as P₂S₆⁴⁻, we propose to use the notation M-(L-L)-M to distinguish it from M-L-M. M-L…L-M and M-L…A…L-M type exchanges. The notation (L-L) indicates two different ligand sites of a multidentate molecular anion, each with lone pairs for the coordination with a cation M. Such M-(L-L)-M exchanges can be strongly FM or strongly AFM, as discussed above. Currently, there are no qualitative rules with which to predict whether they will be FM or AFM. A similar situation was found, for example, for the mineral Azurite Cu₃(CO₃)₂(OH)₂, in which every molecular anion CO₃²⁻ participates in three different Cu-(O-O)-Cu exchanges. DFT + U calculations show that one of these three is substantially AFM, but the remaining two are negligible. So far, this observation has not been understood in terms of qualitative reasoning.

3.6. Description Using Three Exchanges

Experimentally, the magnetic properties of MPS₃ have been interpreted in terms of three exchange parameters, namely, by assuming that J₁ = J₂ (≡ J₁₂), J₃ = J₄ (≡ J₁₃), and J₅ = J₆ (≡ J₁₄). To investigate whether this simplified description is justified, we simulate the relative energies of the seven ordered spin states of MPS₃ by using the three exchanges J₁₂, J₁₃ and J₁₄ as parameters in terms of the least-square fitting analysis. Our results, summarized in

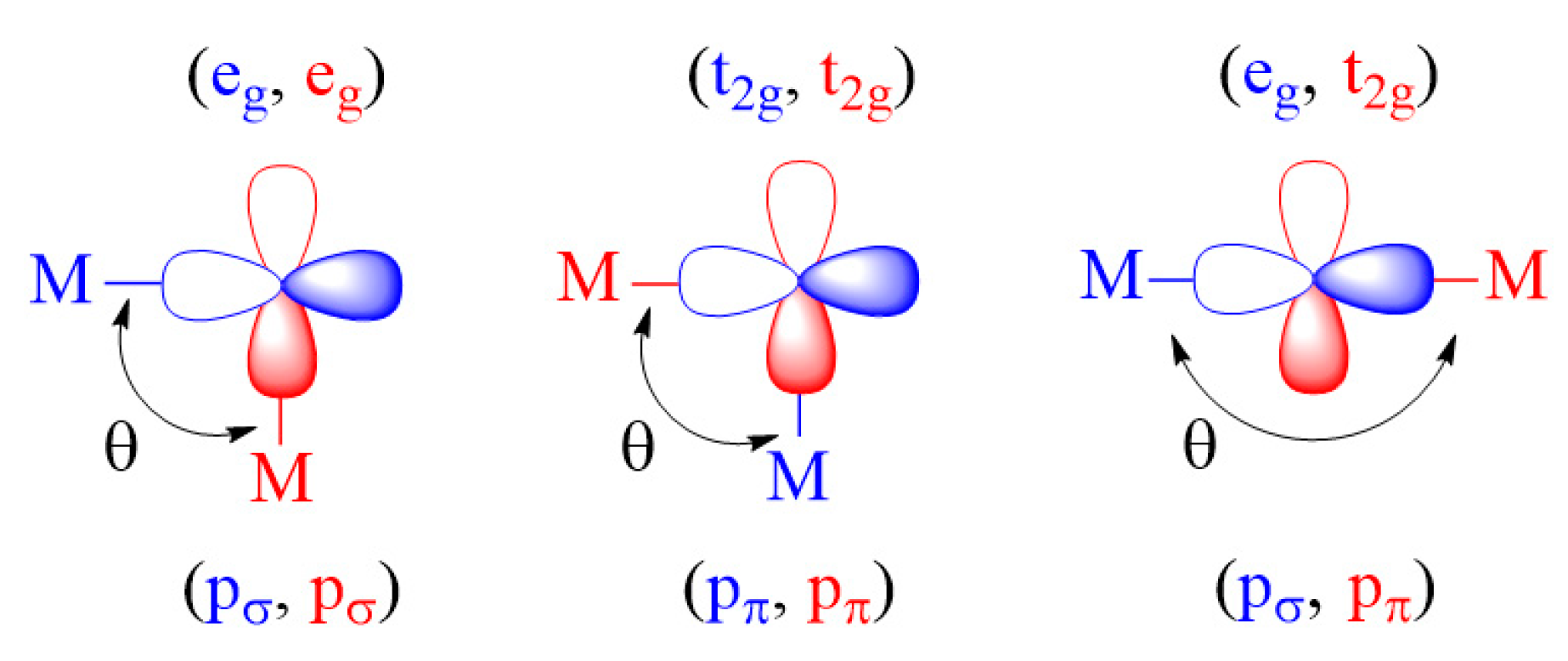
Table 6. Spin exchanges J₁₂, J₁₃ and J₁₄ in K obtained (for the optimized structures of MPS₃ (M = Mn, Fe, Co, Ni) from DFT + U calculations with U_eff = 4 eV) by simulating the relative energies of the FM and AF1–AF6 states with the three spin exchanges.

	Mn	Fe	Co	Ni
J12	−15.5 ± 0.4	2.0 ± 7.7	−61.4 ± 119.0	36.3 ± 4.3
J13	−0.9 ± 0.2	−7.7 ± 3.9	60.7 ± 55.3	0.0 ± 2.0
J14	−5.3 ± 0.3	−20.9 ± 4.5	−59.1 ± 95.6	−186.0 ± 3.4

, show that the standard deviations of J₁₂, J₁₃ and J₁₄ are small for MnPS₃ and NiPS₃, moderate in FePS₃, but extremely large in CoPS₃ (for details, see Figures S2–S5). The exchanges experimentally deduced for FePS₃ are J₁₂ = −17 K, J₁₃ = −0.5 K, and J₁₄ = 7 K from neutron inelastic scattering measurements [17], −17 K ≤ J₁₂ ≤ −5.6 K, −7.2 K ≤ J₁₃ ≤ 2.8 K, and 0 ≤ J₁₄ ≤ 10 K from powder susceptibility measurements [9], and J₁₂ = −19.6 K, J₁₃ = 10.3 K, and J₁₄ = −2.2 K from high field measurements [17]. These experimental estimates are dominated by J₁₂, but the theoretical estimates of Table 6 by J₁₄. One might note from Table 6 that the magnetic properties of MnPS₃, FePS₃ and NiPS₃ can be reasonably well approximated by two exchanges, that is, by J₁₂ and J₁₄ for MnPS₃, by J₁₄ and J₁₂ for NiPS₃, and by J₁₄ and J₁₃ for FePS₃. However, this three-parameter description leads to erroneous predictions for the magnetic ground states of MPS₃; it predicts the AF1 state to be the ground state for both MnPS₃ and CoPS₃. This prediction is correct for MnPS₃, but incorrect for CoPS₃. In addition, it predicts that the AF2 and AF3 states possess the same stability for all MPS₃ (M = Mn, Fe, Co, Ni), and are the ground states for FePS₃ and NiPS₃. These two predictions are both incorrect.

4. Concluding Remarks

Our DFT + U calculations for the optimized structures of MPS₃ (M = Mn, Fe, Co, Ni) reveal that, in agreement with experiment, the magnetic ground state of MnPS₃ is the AF1 state while those of CoPS₃ and NiPS₃ are the AF2 state. In disagreement with experiment, however, our calculations predict the AF2 state to be the magnetic ground state for FePS₃. Our DFT + U + SOC calculations show that, in agreement with experiment, the preferred spin orientation of FePS₃ is the ||z direction while those of CoPS₃ and NiPS₃ are the ⊥z direction, and the Fe²⁺ ion of FePS₃ exhibits uniaxial anisotropy. In disagreement with experiment, these calculations predict the preferred spin orientation for MnPS₃ to be the ⊥z direction. Our analyses suggest that the ||z spin direction experimentally observed for the Mn²⁺ ions arises from the magnetic dipole–dipole interactions in the AF1 magnetic state. We presented simple qualitative rules governing spin exchanges to be used as guidelines for gauging the nature of various spin exchanges. These rules allowed us to recognize several unusual exchanges of MPS₃; the second NN exchange J₃ of CoPS₃ is strongly FM while the third NN exchanges J₆ of CoPS₃ and NiPS₃ are very strongly AFM. These observations reflect the fact that the lone-pair orbitals of the P₂S₆⁴⁻ ion, mediating the spin exchanges in MPS₃ are symmetry-adapted group orbitals, so the effect of coordinating one S atom to one M²⁺ ion is felt by all the remaining five S atoms of P₂S₆⁴⁻. The spin exchanges mediated by molecular anions, termed the M-(L-L)-M type exchanges, differ in nature from the M-L-M, M-L…L-M and M-L…A…L-M type exchanges. To find qualitative trends in the M-(L-L)-M type exchanges, it is necessary to further study the spin exchanges involving various other molecular anions.