Unusual Spin Exchanges Mediated by the Molecular Anion P2S64−: Theoretical Analyses of the Magnetic Ground States, Magnetic Anisotropy and Spin Exchanges of MPS3 (M = Mn, Fe, Co, Ni)
Abstract
:1. Introduction
2. Qualitative Rules Governing Spin Exchanges
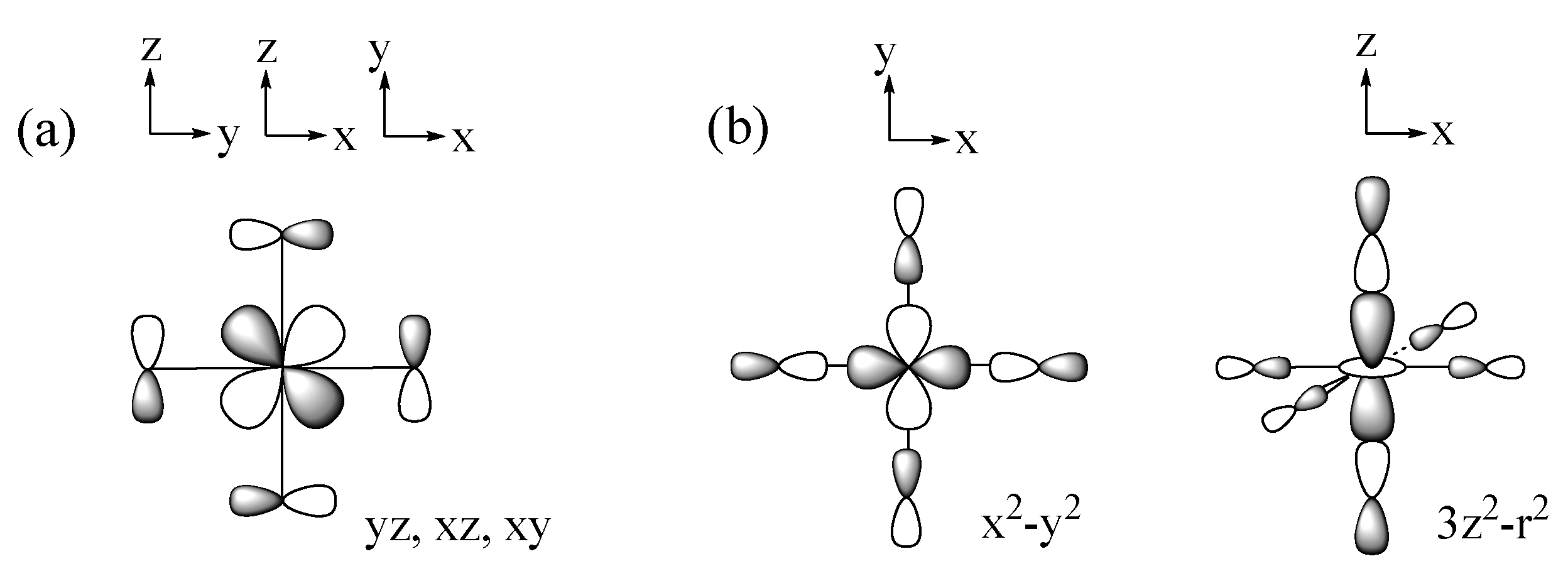
2.1. Spin Exchange between Magnetic Orbitals
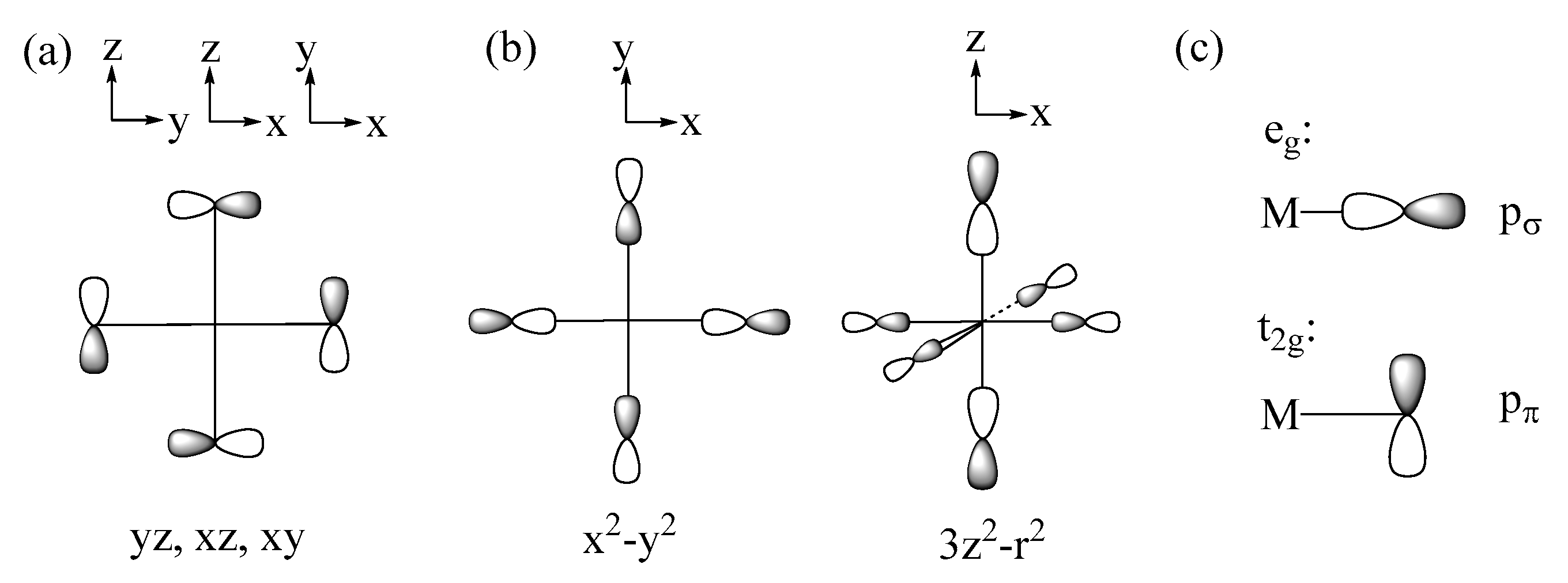
2.2. p-Orbital Tails of Magnetic Orbitals
2.3. Spin Exchanges in Terms of the p-Orbital Tails
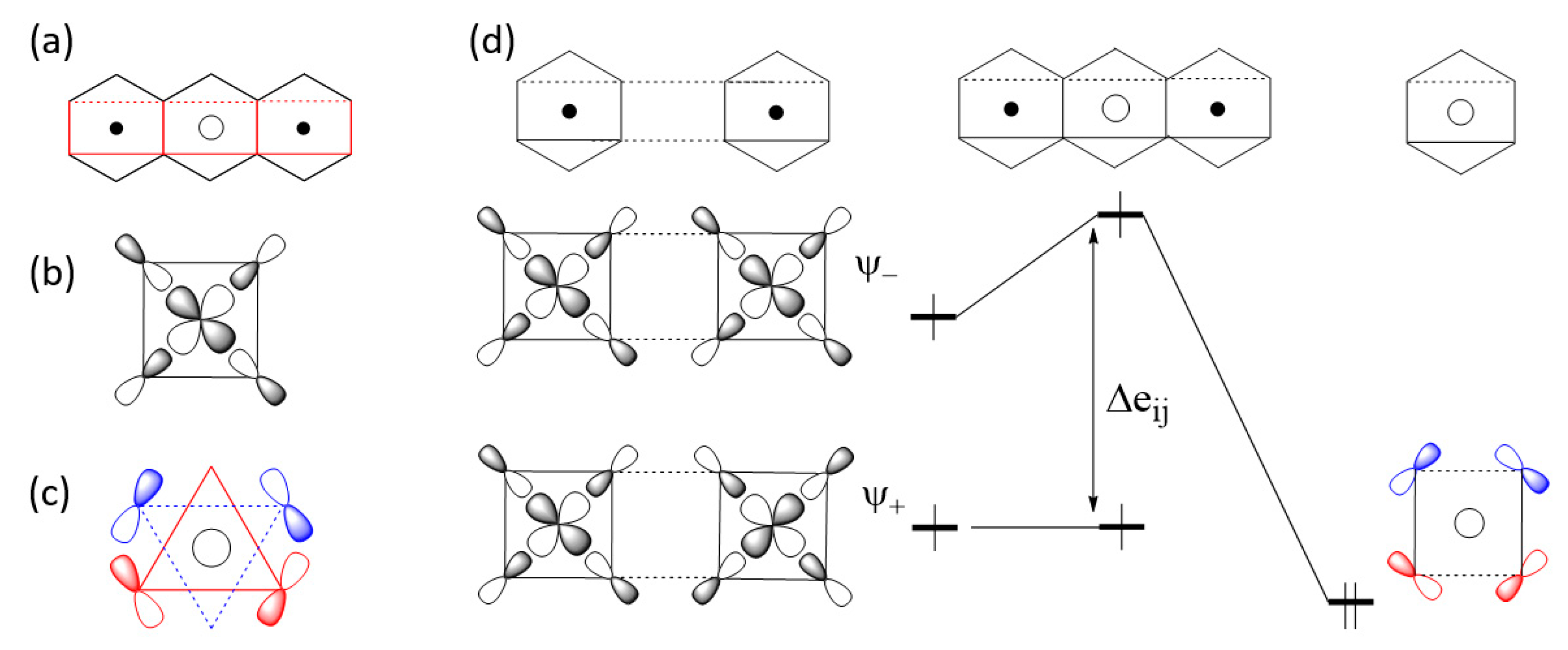
2.3.1. M-L-M Exchange
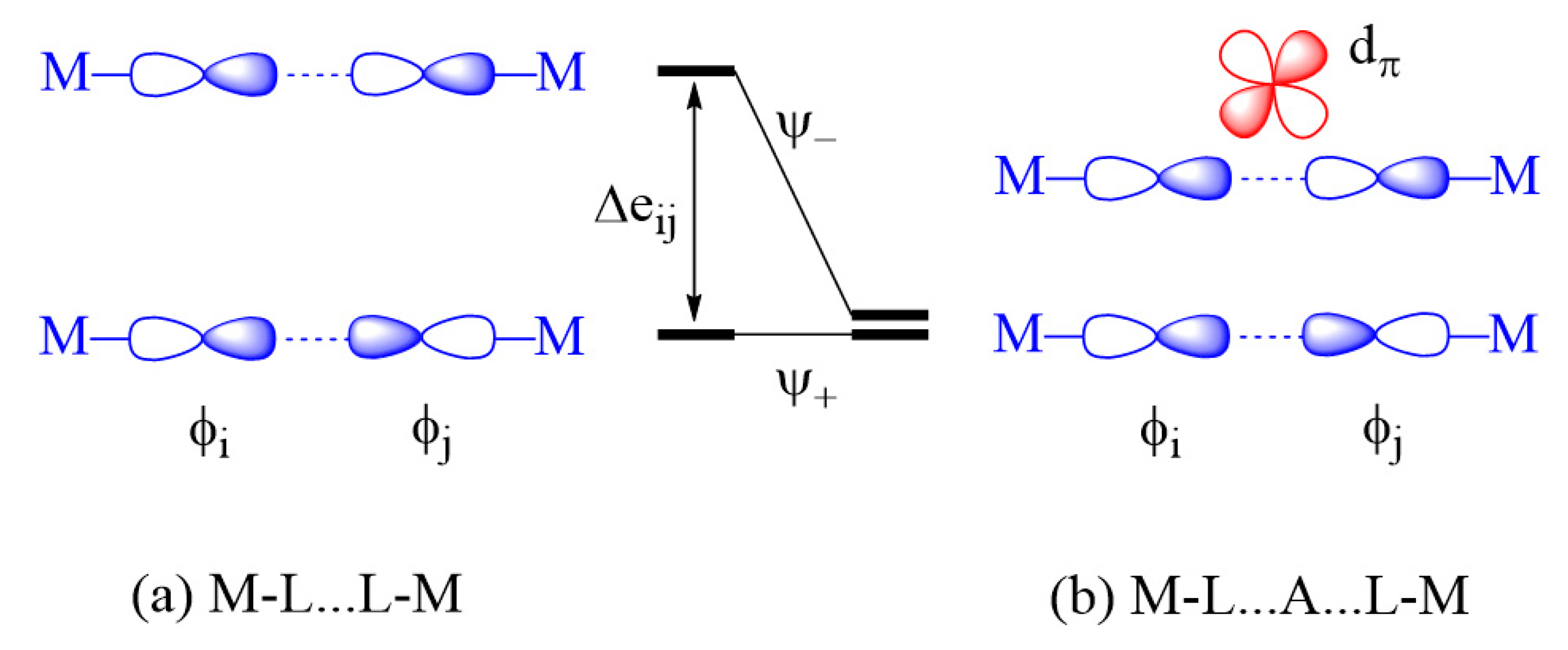
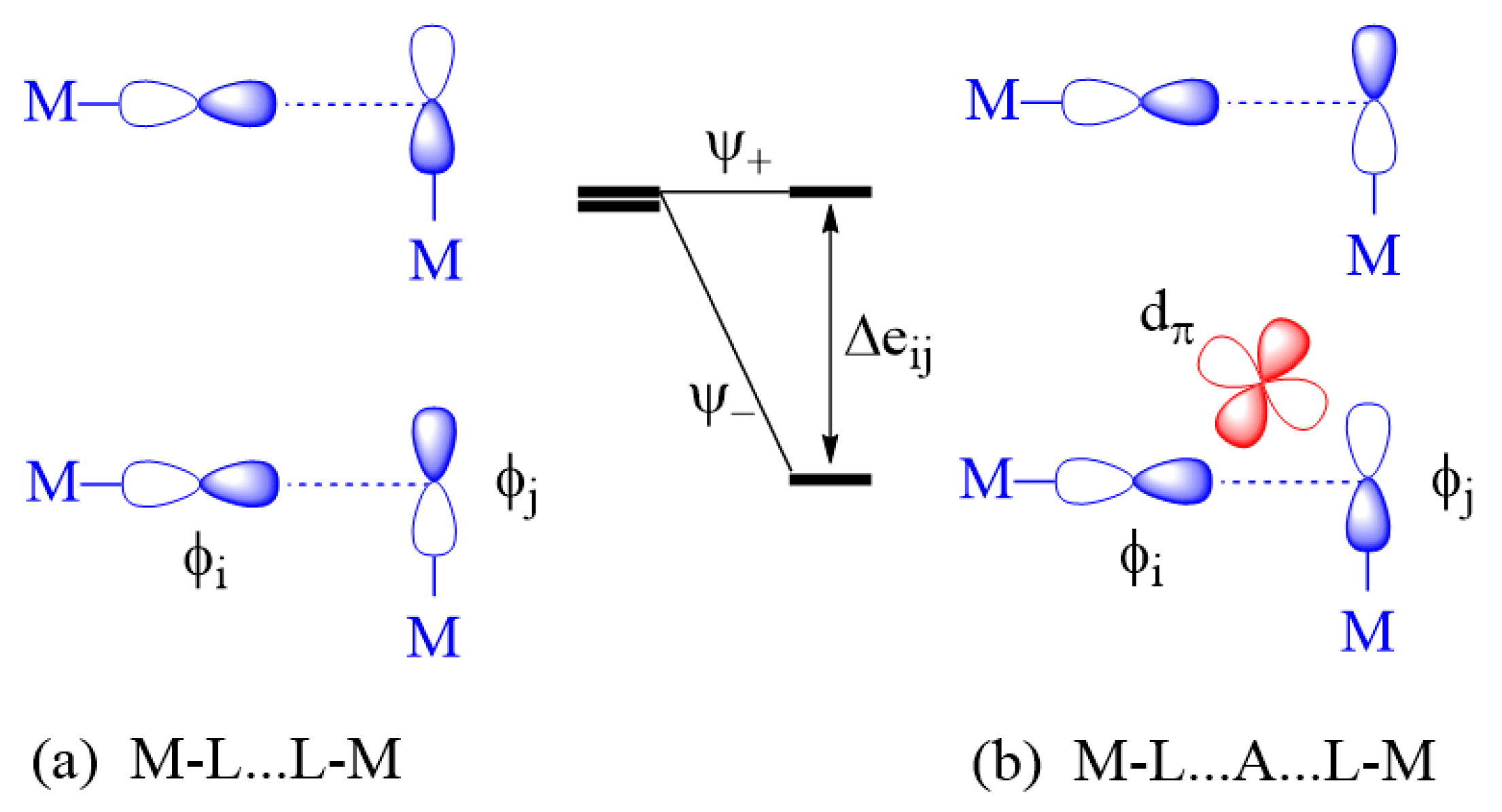
2.3.2. M-L…L-M Exchange
2.3.3. Qualitative Rules Governing Spin Exchanges
- For an individual exchange of a M-L-M type, the (t2g, t2g) and (eg, eg) exchanges are FM if the bond angle θ is 90°, and so is the (t2g, eg) exchange if the bond angle θ is 180°. These exchanges become AFM when the bond angles θ deviate considerably from these values.
- An individual exchange of a M-L…L-M or M-L…A…L-M type can only be AFM if not weak.
- A strong individual exchange of a M-L…L-M is weakened by the d0 metal cation A in the M-L…A…L-M exchange, but a weak individual exchange of a M-L…L-M is strengthened by the presence of a d0 metal cation A in the M-L…A…L-M exchange.
- When a magnetic ion has several unpaired spins, the spin exchange between two magnetic ions is given by the sum of all possible individual exchanges.
3. Results and Discussion
3.1. Details of Calculations
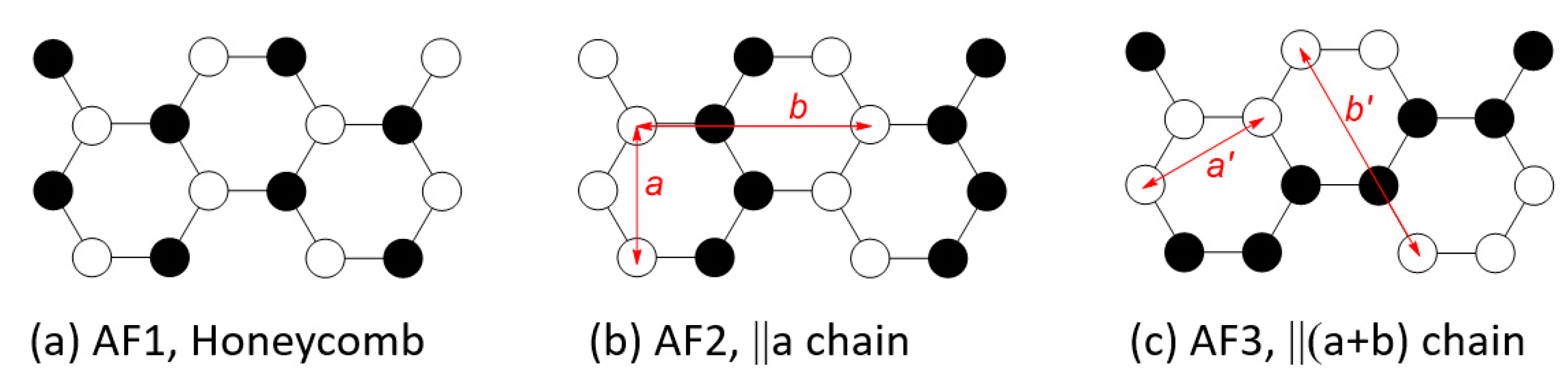
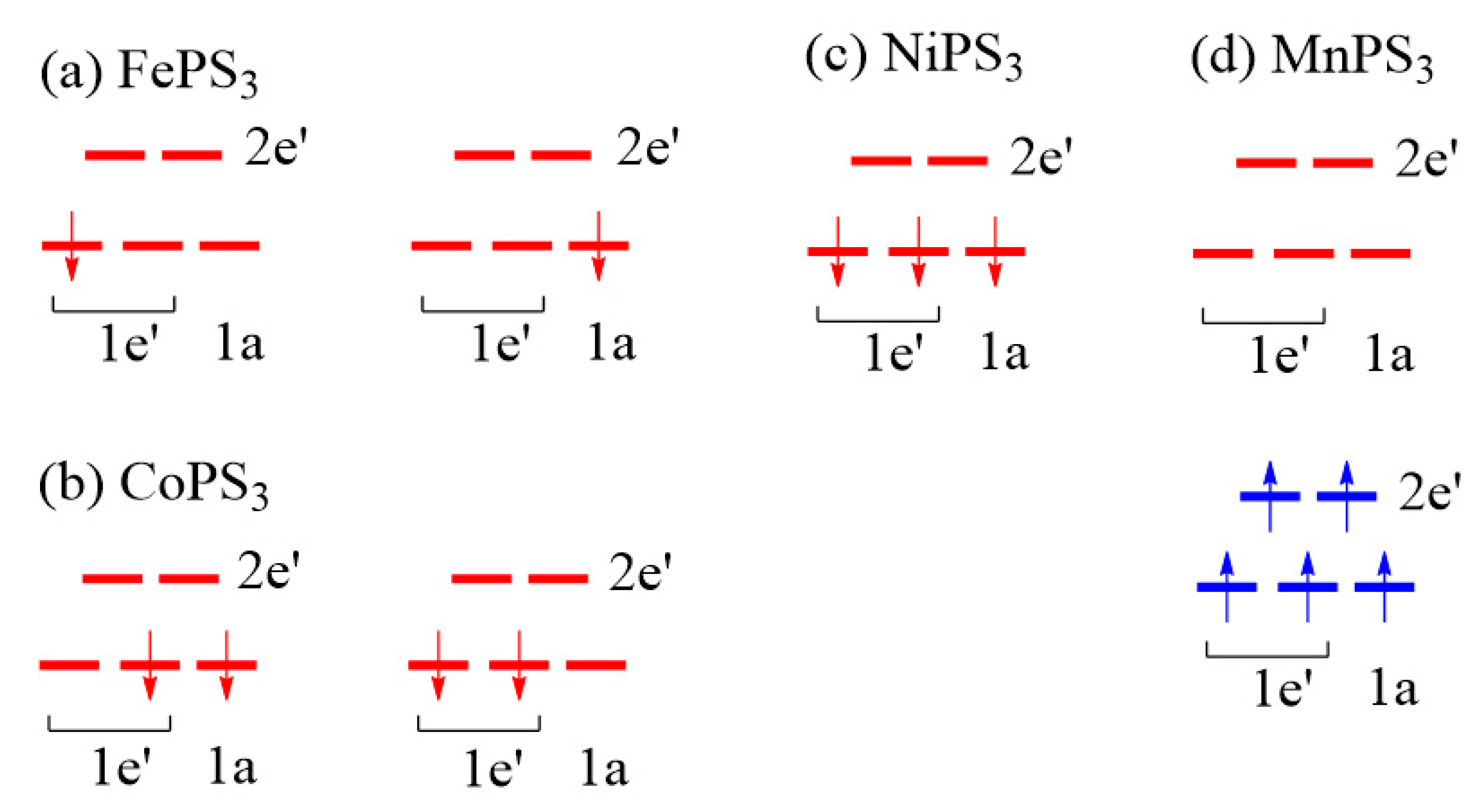
3.2. Magnetic Ground States of MPS3
3.3. Preferred Spin Orientation of MPS3
3.3.1. Quantitative Evaluation
3.3.2. Qualitative Picture
Selection Rules of Spin Orientation and Implications
Magnetic Dipole–Dipole Interactions
3.4. Quantitative Evaluations of Spin Exchanges
EAF1 = (+16J1 + 8J2 − 16J3 − 32J4 + 16J5 + 8J6)S2
EAF2 = (−16J1 + 8J2 − 16J3 + 32J4 + 16J5 + 8J6)S2
EAF3 = (−8J2 + 16J3 + 16J5 + 8J6)S2
EAF4 = (+16J1 − 8J2 − 16J3 + 32J4 − 16J5 − 8J6)S2
EAF5 = (+8J2 + 16J3 − 16J5 + 8J6)S2
EAF6 = (−8J2 + 16J3 + 16J5 − 8J6)S2
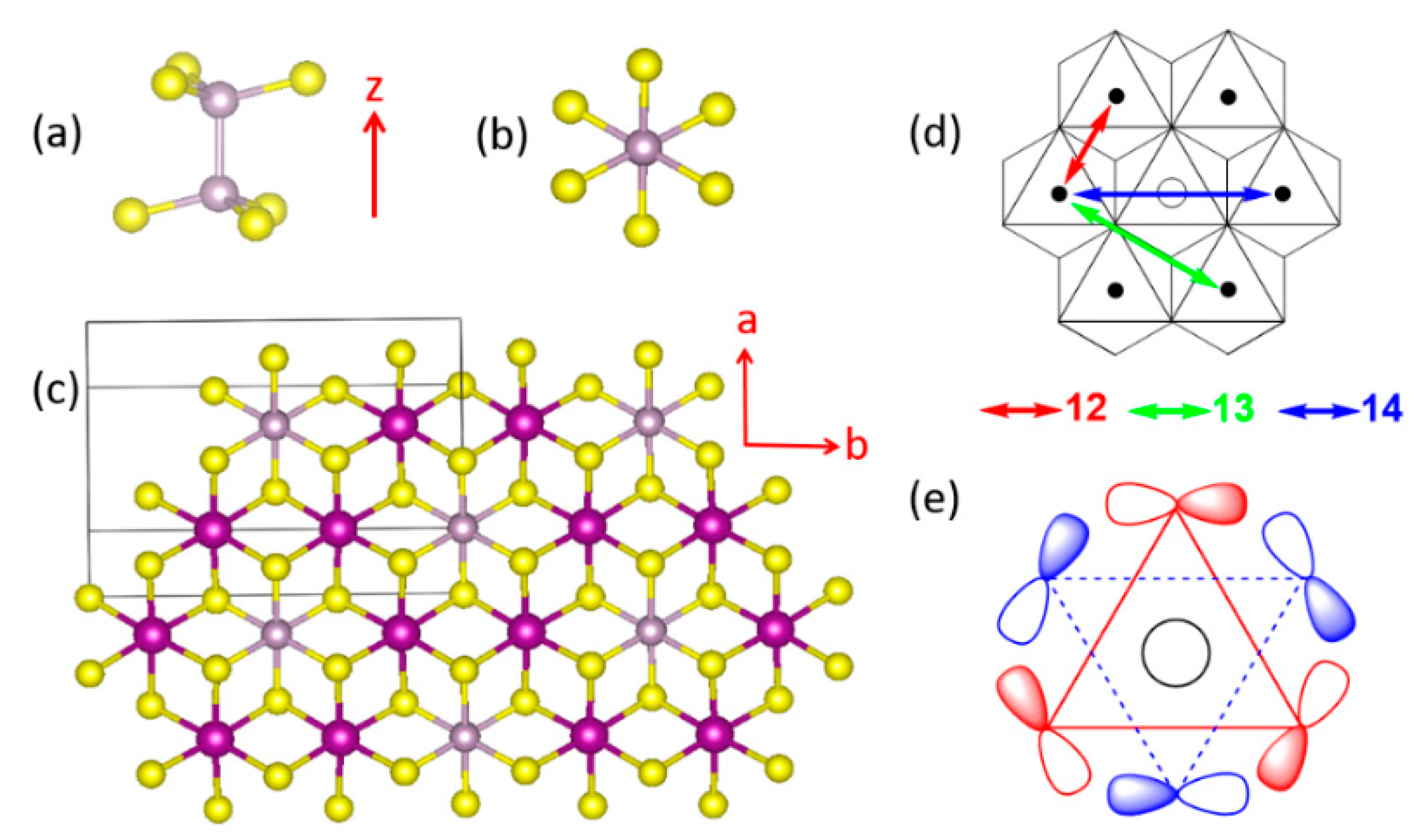
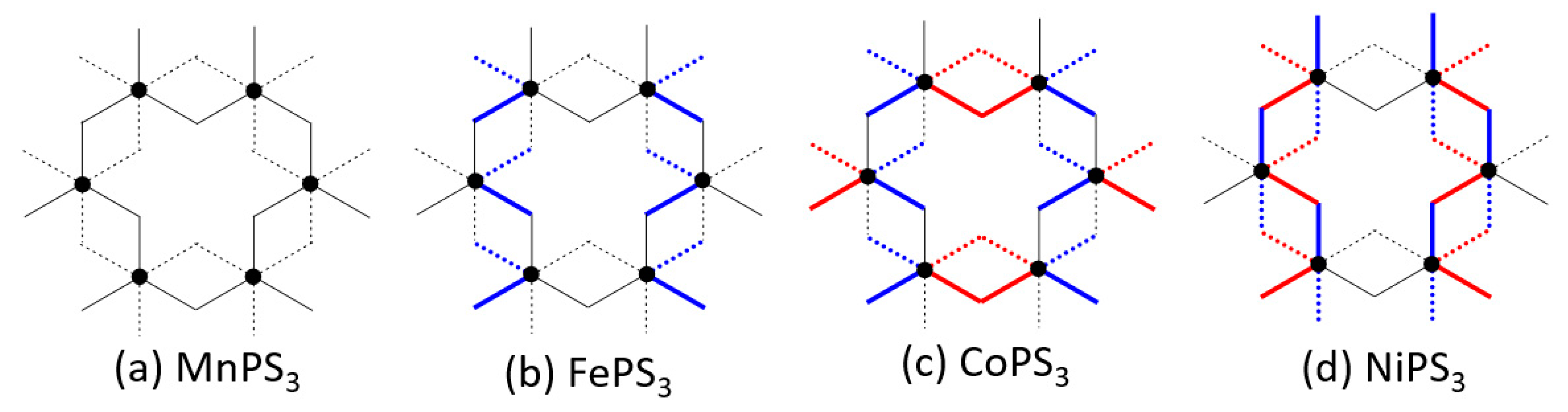
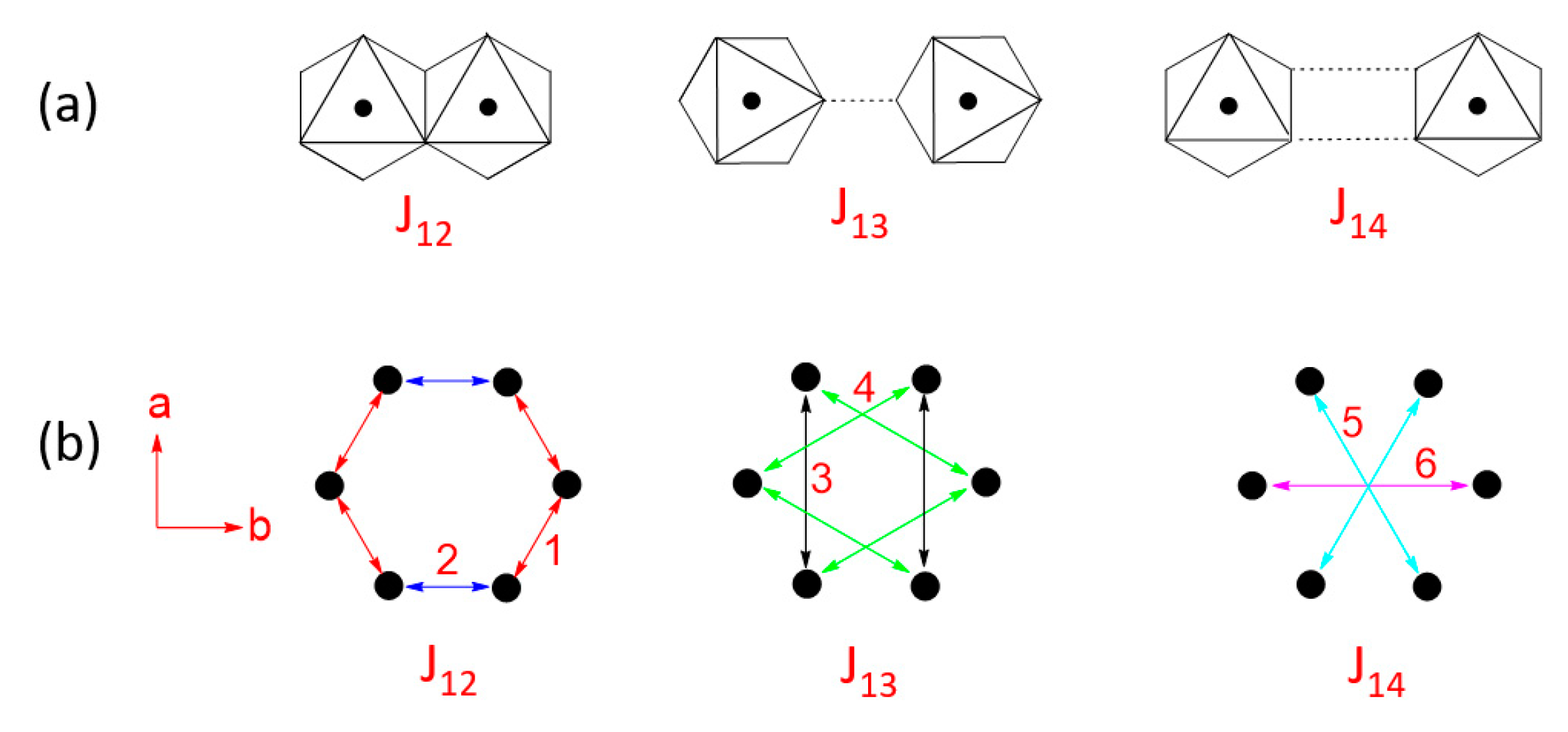
- In all MPS3 (M = Mn, Fe, Co, Ni), J1 ≠ J2, J3 ≠ J4, and J5 ≠ J6, reflecting that the exchange paths are different between J1 and J2, between J3 and J4, and between J5 and J6 (Figure 10).
- J1 ≈ J2 < 0, J3 ≈ J4 ≈ 0, and J5 ≈ J6 < 0 for MnPS3 while J1 ≈ J2 > 0, J3 ≈ J4 ≈ 0, and J5 ≈ J6 < 0 NiPS3. To a first approximation, the electron configurations of MnPS3 and NiPS3 can be described by (t2g)3(eg)2 and (t2g)6(eg)2, respectively. That is, they do not possess an unevenly occupied degenerate state t2g.
- In FePS3 and CoPS3, J1 and J2 are quite different, and so are J3 and J4. While J5 and J6 are comparable in FePS3, they are quite different in CoPS3. The electron configurations of FePS3 and NiPS3 can be approximated by (t2g)4(eg)2 and (t2g)5(eg)2, respectively. Namely, they possess an unevenly occupied degenerate state t2g.
- The strongest exchange is J1 in MnPS3, but J6 in other MPS3 (M = Fe, Co, Ni).
- The second NN exchange J3 is strongly FM in CoPS3, while the third NN exchange J6 is very strongly AFM in CoPS3 and NiPS3.
3.5. Unusual Features of the M-L…L-M Spin Exchanges
3.5.1. Second Nearest-Neighbor Exchange
3.5.2. Third Nearest-Neighbor Exchange
3.6. Description Using Three Exchanges
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Whangbo, M.-H.; Koo, H.-J.; Dai, D. Spin exchange interactions and magnetic structures of extended magnetic solids with localized spins: Theoretical descriptions on formal, quantitative and qualitative levels. J. Solid State Chem. 2003, 176, 417–481. [Google Scholar] [CrossRef]
- Xiang, H.J.; Lee, C.; Koo, H.-J.; Gong, X.; Whangbo, M.-H. Magnetic properties and energy-mapping analysis. Dalton Trans. 2013, 42, 823–853. [Google Scholar] [CrossRef]
- Whangbo, M.-H.; Xiang, H.J. Magnetic Properties from the Perspectives of Electronic Hamiltonian: Spin Exchange Parameters, Spin Orientation and Spin-Half Misconception. In Handbook in Solid State Chemistry, Volume 5: Theoretical Descriptions; Wiley: New York, NY, USA, 2017; pp. 285–343. [Google Scholar]
- Whangbo, M.-H.; Koo, H.-J.; Kremer, R.K. Spin Exchanges Between Transition-Metal Ions Governed by the Ligand p-Orbitals in Their Magnetic Orbitals. Molecules 2021, 26, 531. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Loeb, A.L. Theory of ionic ordering, crystal distortion, and magnetic exchange due to covalent forces in spinels. Phys. Rev. 1955, 98, 391–408. [Google Scholar] [CrossRef]
- Goodenough, J.B. Theory of the role of covalence in the perovskite-type manganites [La, M(II)]MnO3. Phys. Rev. 1955, 100, 564–573. [Google Scholar] [CrossRef] [Green Version]
- Kanamori, J. Superexchange interaction and symmetry properties of electron orbitals. J. Phys. Chem. Solids 1959, 10, 87–98. [Google Scholar] [CrossRef]
- Goodenough, J.B. Magnetism and the Chemical Bond; Interscience; Wiley: New York, NY, USA, 1963. [Google Scholar]
- Kurosawa, K.; Saito, S.; Yamaguchi, Y. Neutron diffraction study on MnPS3 and FePS3. J. Phys. Soc. Jpn. 1983, 52, 3919–3926. [Google Scholar] [CrossRef]
- Ouvrard, G.; Brec, R.; and Rouxel, J. Structural determination of some MPS3 phases (M = Mn, Fe, Co, Ni and Cd). Mater. Res. Bull. 1985, 20, 1181–1189. [Google Scholar] [CrossRef]
- Brec, R. Review on structural and chemical properties of transition metal phosphorus trisulfides MPS3. Solid State Ionics 1986, 22, 3–30. [Google Scholar] [CrossRef]
- Kuroda, K.; Kurosawa, K.; Shozo, S.; Honda, M.; Zhihong, Y.; Date, M. Magnetic-properties of layered compound MnPS3. J. Phys. Soc. Jpn. 1986, 55, 4456–4463. [Google Scholar]
- Hicks, T.J.; Keller, T.; Wildes, A.R. Magnetic dipole splitting of magnon bands in a two-dimensional antiferromagnet. J. Magn. Magn. Mater. 2019, 474, 512–516. [Google Scholar] [CrossRef]
- Ressouche, E.; Loire, M.; Simonet, V.; Ballou, L.; Stunault, A.; Wildes, A. Magnetoelectric MnPS3 as a candidate for ferrotoroicity. Phys. Rev. B 2010, 82, 100408(R). [Google Scholar] [CrossRef] [Green Version]
- Okuda, K.; Kurosawa, K.; Saito, S. High field magnetization process in FePS3. In High Field Magnetism; Date, M., Ed.; Elsevier: North Holland, Amsterdam, The Netherlands, 1983; pp. 55–58. [Google Scholar]
- Rule, K.C.; McIntyre, G.J.; Kennedy, S.J.; Hicks, T.J. Single-crystal and powder neutron diffraction experiments on FePS3: Search for the magnetic structure. Phys. Rev. B 2007, 76, 134402. [Google Scholar] [CrossRef]
- Wildes, A.R.; Rule, K.C.; Bewley, R.I.; Enderle, M.; Hicks, T.J. The magnon dynamics and spin exchange parameters of FePS3. J. Phys. Condens. Matter 2012, 24, 416004. [Google Scholar] [CrossRef]
- Lançon, D.; Walker, H.C.; Ressouche, E.; Ouladiaf, B.; Rule, K.C.; McIntyre, G.J.; Hicks, T.J.; Rønnow, H.M.; Wildes, A.R. Magnetic structure and magnon dynamics of the quasi0two-dimensional antiferromagnet FePS3. Phys. Rev. B 2016, 94, 214407. [Google Scholar] [CrossRef]
- Wildes, A.R.; Simonet, V.; Ressouche, E.; Ballou, R.; McIntyre, G.J. The magnetic properties and structure of the quasi-two-dimensional antiferromagnet CoPS3. J. Phys. Condes. Matter 2017, 29, 455801. [Google Scholar] [CrossRef] [Green Version]
- Wildes, A.R.; Simonet, V.; Ressouche, E.; McIntyre, G.J.; Avdeev, M.; Suard, E.; Kimber, S.A.J.; Lançon, D.; Pepe, G.; Moubaraki, B.; et al. Magnetic structure of the quasi-two-dimensional antiferromagnet NiPS3. Phys. Rev. B 2015, 92, 224408. [Google Scholar] [CrossRef]
- Chittari, B.L.; Park, Y.J.; Lee, D.K.; Han, M.S.; MacDonal, A.H.; Hwang, E.H.; Jung, J.I. Electronic and magnetic properties of single-layer MPX3 metal phosphorous trichalcogenides. Phys. Rev. B 2016, 94, 184428. [Google Scholar] [CrossRef] [Green Version]
- Whangbo, M.-H.; Gordon, E.E.; Xiang, H.J.; Koo, H.-J.; Lee, C. Prediction of spin orientations in terms of HOMO-LUMO interactions using spin-orbit coupling as perturbation. Acc. Chem. Res. 2015, 48, 3080–3087. [Google Scholar] [CrossRef] [Green Version]
- Gordon, E.E.; Xiang, H.J.; Köhler, J.; Whangbo, M.-H. Spin orientations of the spin-half Ir4+ ions in Sr3NiIrO6, Sr2IrO4 and Na2IrO3: Density functional, perturbation theory and Madelung potential analyses. J. Chem. Phys. 2016, 144, 114706. [Google Scholar] [CrossRef] [Green Version]
- Whangbo, M.-H.; Xiang, H.J.; Koo, H.-J.; Gordon, E.E.; Whitten, J.L. Electronic and Structural Factors Controlling the Spin Orientations of Magnetic Ions. Inorg. Chem. 2019, 58, 11854–11874. [Google Scholar] [CrossRef]
- Hay, P.J.; Thibeault, J.C.; Hoffmann, R. Orbital interactions in metal dimer complexes. J. Am. Chem. Soc. 1975, 97, 4884–4899. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505. [Google Scholar] [CrossRef]
- Kuneš, K.; Novák, P.; Schmid, R.; Blaha, P.; Schwarz, K. Electronic structure of fcc Th: Spin-orbit calculation with 6p1/2 local orbital extension. Phys. Rev. Lett. 2001, 64, 153102. [Google Scholar]
- Vaclavkova, D.; Delhomme, A.; Faugeras, C.; Potemski, M.; Bogucki, A.; Suffczyński, J.; Kossacki, P.; Wildes, A.R.; Grémaud, B.; Saúl, A. Magnetoelastic interaction in the two-dimensional magnetic material MnPS3 studied by first principles calculations and Raman experiments. 2D Mater. 2020, 7, 035030. [Google Scholar] [CrossRef]
- Koo, H.-J.; Xiang, H.J.; Lee, C.; Whangbo, M.-H. Effect of Magnetic Dipole-Dipole Interactions on the Spin Orientation and Magnetic Ordering of the Spin-Ladder Compound Sr3Fe2O5. Inorg. Chem. 2009, 48, 9051. [Google Scholar] [CrossRef]
- Ewald, P.P. Die Berechnung Optischer und Elektroststischer Gitterpotentiale. Ann. Phys. 1921, 64, 253. [Google Scholar] [CrossRef] [Green Version]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Dommert, F.; Holm, C. Optimizing working parameters of the smooth particle mesh Ewald algorithm in terms of accuracy and efficiency. J. Chem. Phys. 2010, 133, 034117. [Google Scholar] [CrossRef] [PubMed]
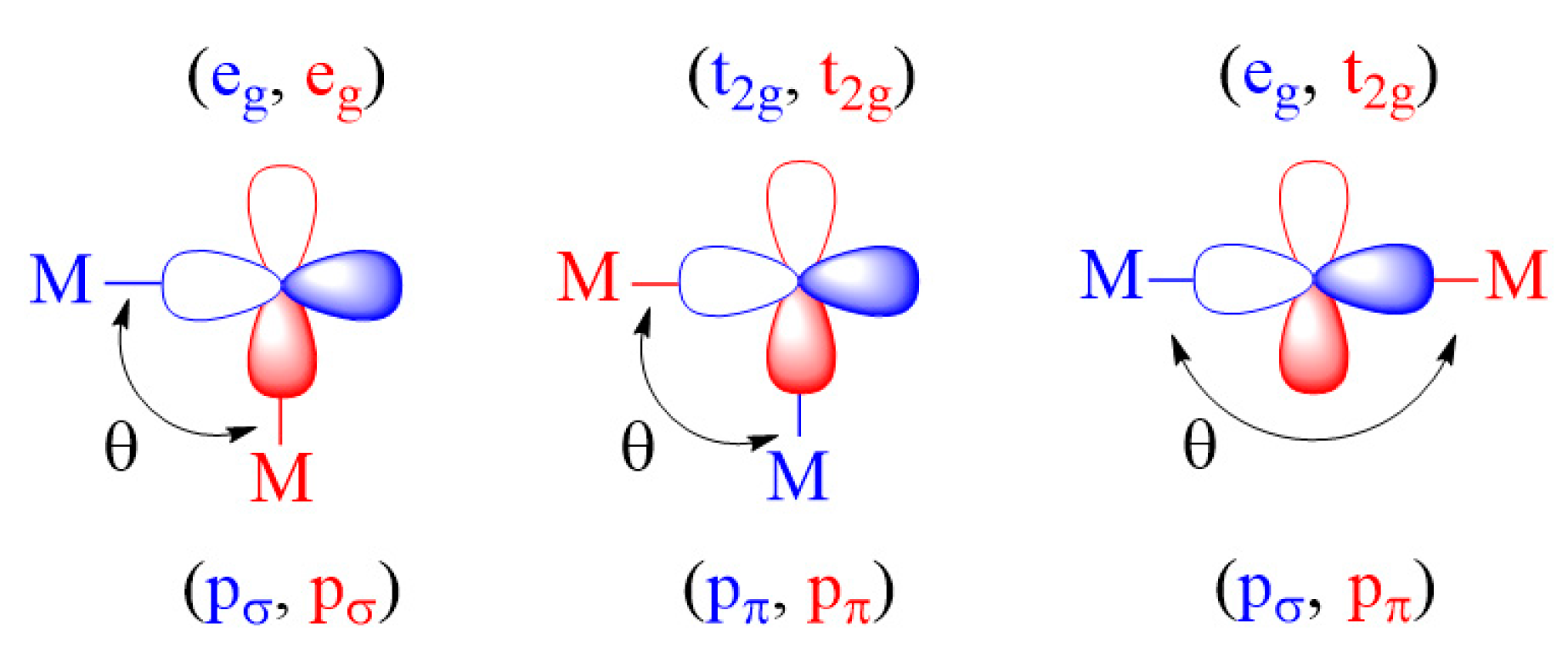

| Mn | Fe | Co | Ni | |
|---|---|---|---|---|
| FM | 33.77 (33.36) | 31.25 (25.10) | 71.46 (55.00) | 45.00 (42.04) |
| AF1 | 0 (0) | 12.24 (5.16) | 0 (5.70) | 6.50 (7.11) |
| AF2 | 15.54 (15.50) | 12.92 (7.93) | 45.05 (0) | 0 (0) |
| AF3 | 14.25 (14.21) | 0 (0) | 34.02 (24.99) | 0.35 (0.34) |
| AF4 | 14.72 (14.45) | 20.85 (18.57) | 22.16 (26.00) | 52.40 (49.53) |
| AF5 | 12.77 (12.58) | 15.79 (12.95) | 157.25 (158.33) | 33.62 (31.98) |
| AF6 | 17.24 (17.07) | 10.57 (6.33) | 140.58 (143.05) | 16.43 (15.21) |
| Mn | Fe | Co | Ni |
|---|---|---|---|
| 2.627 (2.632) | 2.546 (2.525) | 2.485 (2.492) | 2.457 (2.453) |
| 2.627 (2.632) | 2.546 (2.526) | 2.485 (2.492) | 2.457 (2.453) |
| 2.625 (2.635) | 2.547 (2.571) | 2.504 (2.525) | 2.462 (2.457) |
| 2.625 (2.635) | 2.547 (2.572) | 2.504 (2.525) | 2.462 (2.457) |
| 2.634 (2.639) | 2.549 (2.572) | 2.491 (2.537) | 2.465 (2.461) |
| 2.634 (2.639) | 2.549 (2.573) | 2.491 (2.537) | 2.465 (2.461) |
| MnPS3 a | FePS3 b | CoPS3 | NiPS3 | |
|---|---|---|---|---|
| ⊥z | 0 (0) | 20.0 (21.8) | 0 (0) | 0 (0) |
| ||z | 0.3 (0.3) | 0 (0) | 3.8 (5.2) | 0.8 (0.7) |
| MnPS3 | FePS3 | CoPS3 | NiPS3 | |||||
|---|---|---|---|---|---|---|---|---|
| ||x | ||z | ||x | ||z | ||x | ||z | ||x | ||z | |
| AF1 | 0.48 | 0.17 | 0.36 | 0.12 | 0.21 | 0.07 | 0.09 | 0.03 |
| AF2 | 0.00 | 0.35 | 0.00 | 0.26 | 0.00 | 0.15 | 0.00 | 0.07 |
| AF3 | 0.55 | 0.38 | 0.38 | 0.27 | 0.22 | 0.15 | 0.10 | 0.07 |
| Mn | Fe | Co | Ni | |
|---|---|---|---|---|
| J1 | 1.00 | 0.37 | 0.05 | −0.25 |
| J2 | 0.87 | −0.32 | −0.91 | −0.14 |
| J3 | 0.06 | 0.36 | −0.55 | 0.04 |
| J4 | 0.05 | 0.07 | 0.04 | −0.01 |
| J5 | 0.34 | 0.86 | 0.11 | 0.99 |
| J6 | 0.33 | 1.00 | 1.00 | 1.00 |
| J1 = −16.0 K | J6 = −18.4 K | J6 = −608.7 K | J6 = −172.4 K |
| Mn | Fe | Co | Ni | |
|---|---|---|---|---|
| J12 | −15.5 ± 0.4 | 2.0 ± 7.7 | −61.4 ± 119.0 | 36.3 ± 4.3 |
| J13 | −0.9 ± 0.2 | −7.7 ± 3.9 | 60.7 ± 55.3 | 0.0 ± 2.0 |
| J14 | −5.3 ± 0.3 | −20.9 ± 4.5 | −59.1 ± 95.6 | −186.0 ± 3.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koo, H.-J.; Kremer, R.; Whangbo, M.-H. Unusual Spin Exchanges Mediated by the Molecular Anion P2S64−: Theoretical Analyses of the Magnetic Ground States, Magnetic Anisotropy and Spin Exchanges of MPS3 (M = Mn, Fe, Co, Ni). Molecules 2021, 26, 1410. https://doi.org/10.3390/molecules26051410
Koo H-J, Kremer R, Whangbo M-H. Unusual Spin Exchanges Mediated by the Molecular Anion P2S64−: Theoretical Analyses of the Magnetic Ground States, Magnetic Anisotropy and Spin Exchanges of MPS3 (M = Mn, Fe, Co, Ni). Molecules. 2021; 26(5):1410. https://doi.org/10.3390/molecules26051410
Chicago/Turabian StyleKoo, Hyun-Joo, Reinhard Kremer, and Myung-Hwan Whangbo. 2021. "Unusual Spin Exchanges Mediated by the Molecular Anion P2S64−: Theoretical Analyses of the Magnetic Ground States, Magnetic Anisotropy and Spin Exchanges of MPS3 (M = Mn, Fe, Co, Ni)" Molecules 26, no. 5: 1410. https://doi.org/10.3390/molecules26051410
APA StyleKoo, H.-J., Kremer, R., & Whangbo, M.-H. (2021). Unusual Spin Exchanges Mediated by the Molecular Anion P2S64−: Theoretical Analyses of the Magnetic Ground States, Magnetic Anisotropy and Spin Exchanges of MPS3 (M = Mn, Fe, Co, Ni). Molecules, 26(5), 1410. https://doi.org/10.3390/molecules26051410








