The Fascinating World of Low-Dimensional Quantum Spin Systems: Ab Initio Modeling
Abstract
:1. Introduction
2. Theoretical Framework
3. Selected Inorganic Quantum Spin Systems
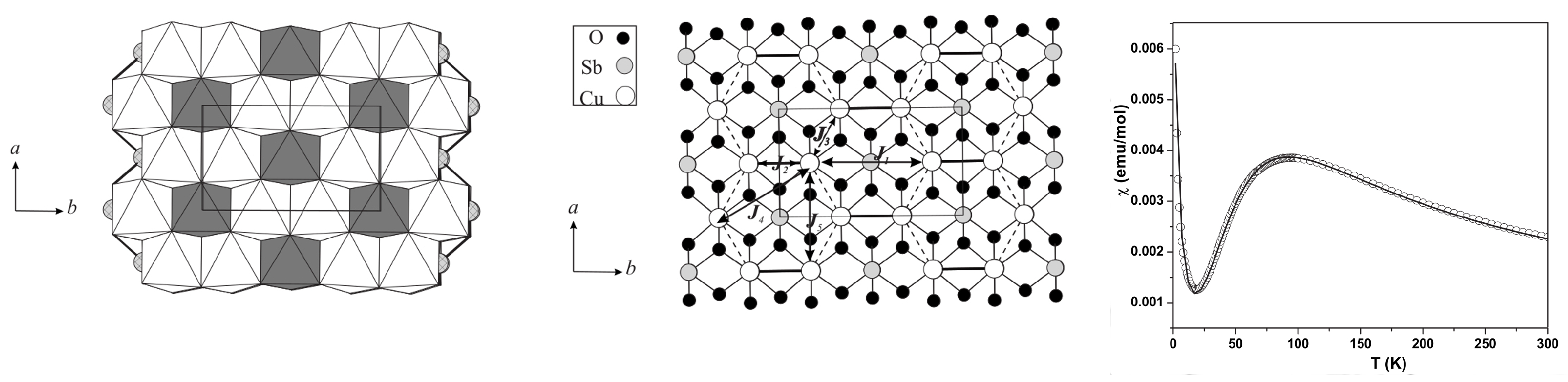
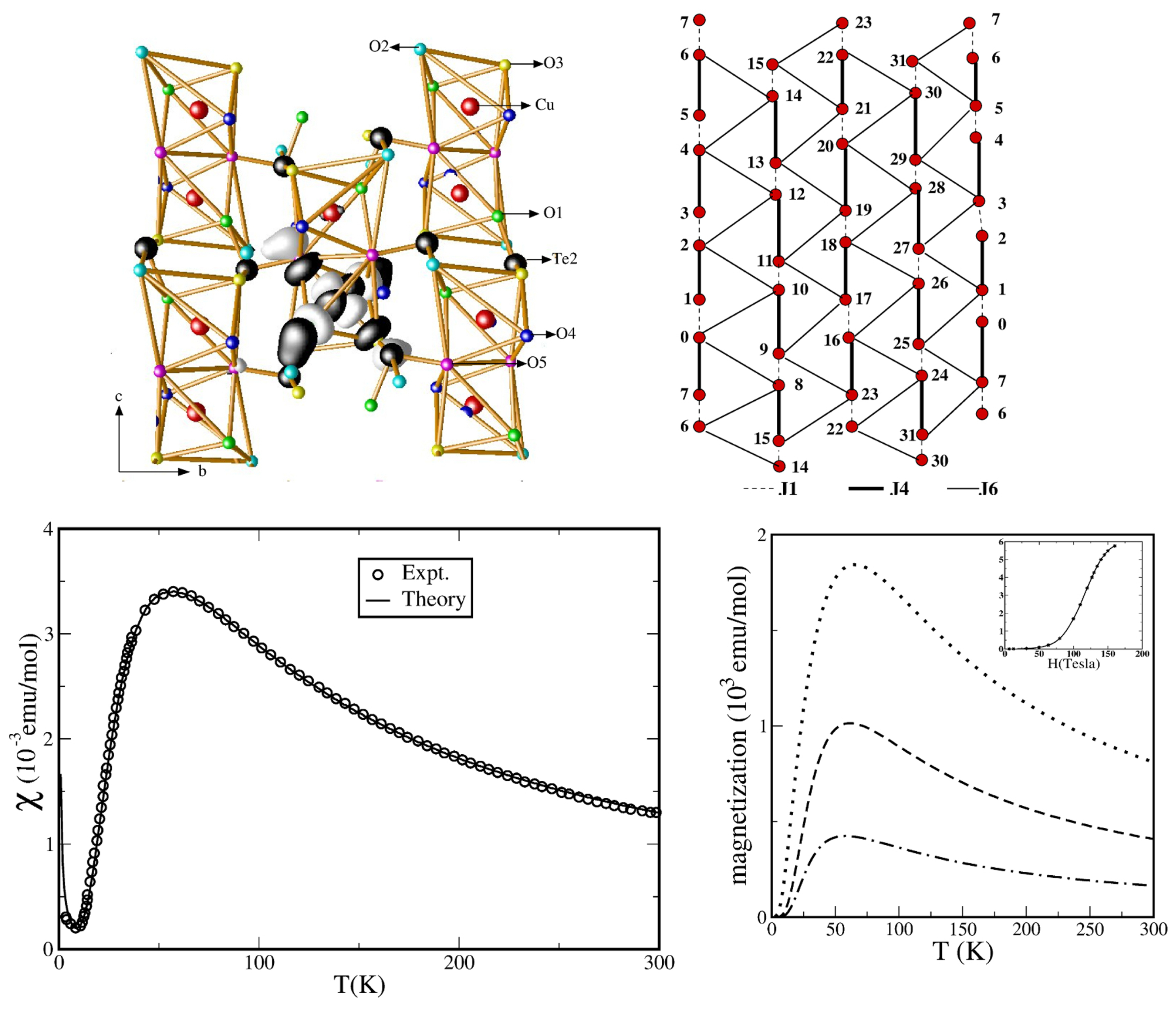
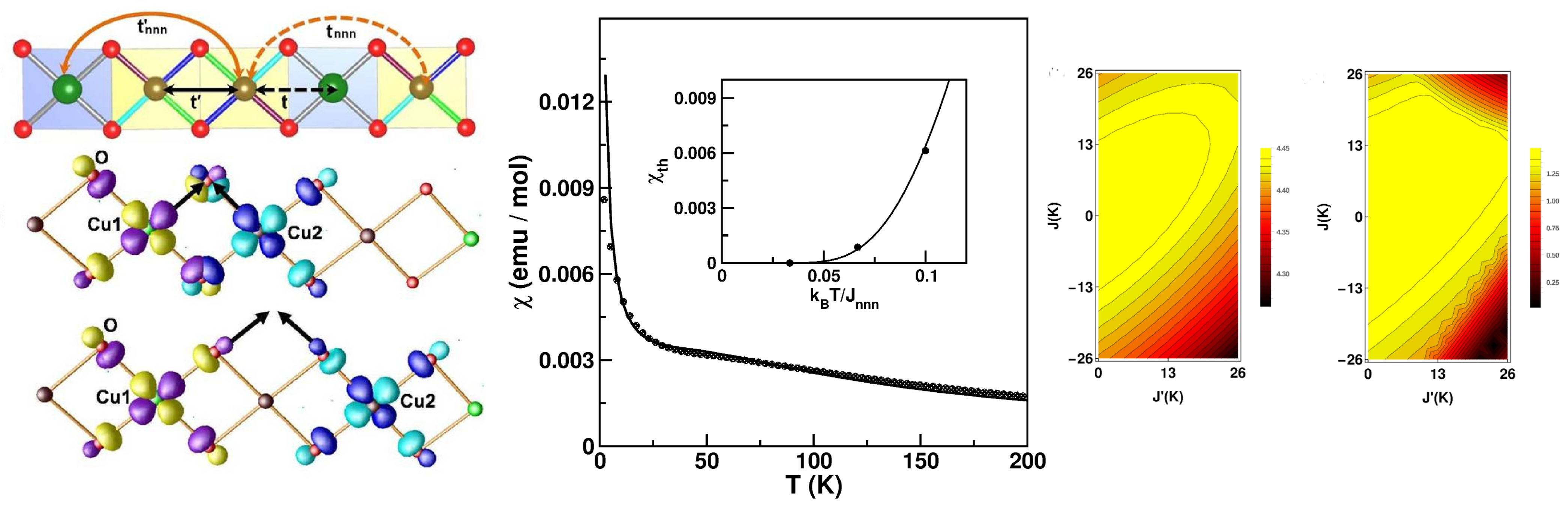
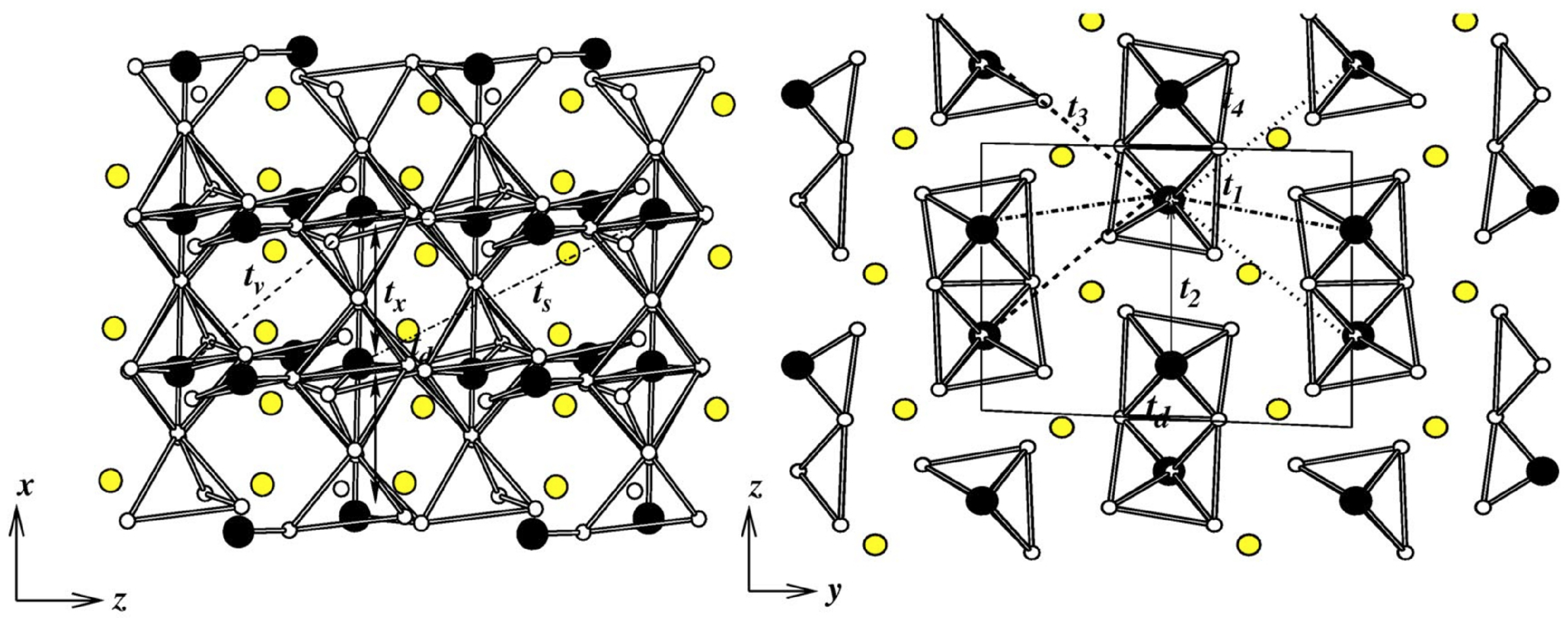
3.1. Cuprates
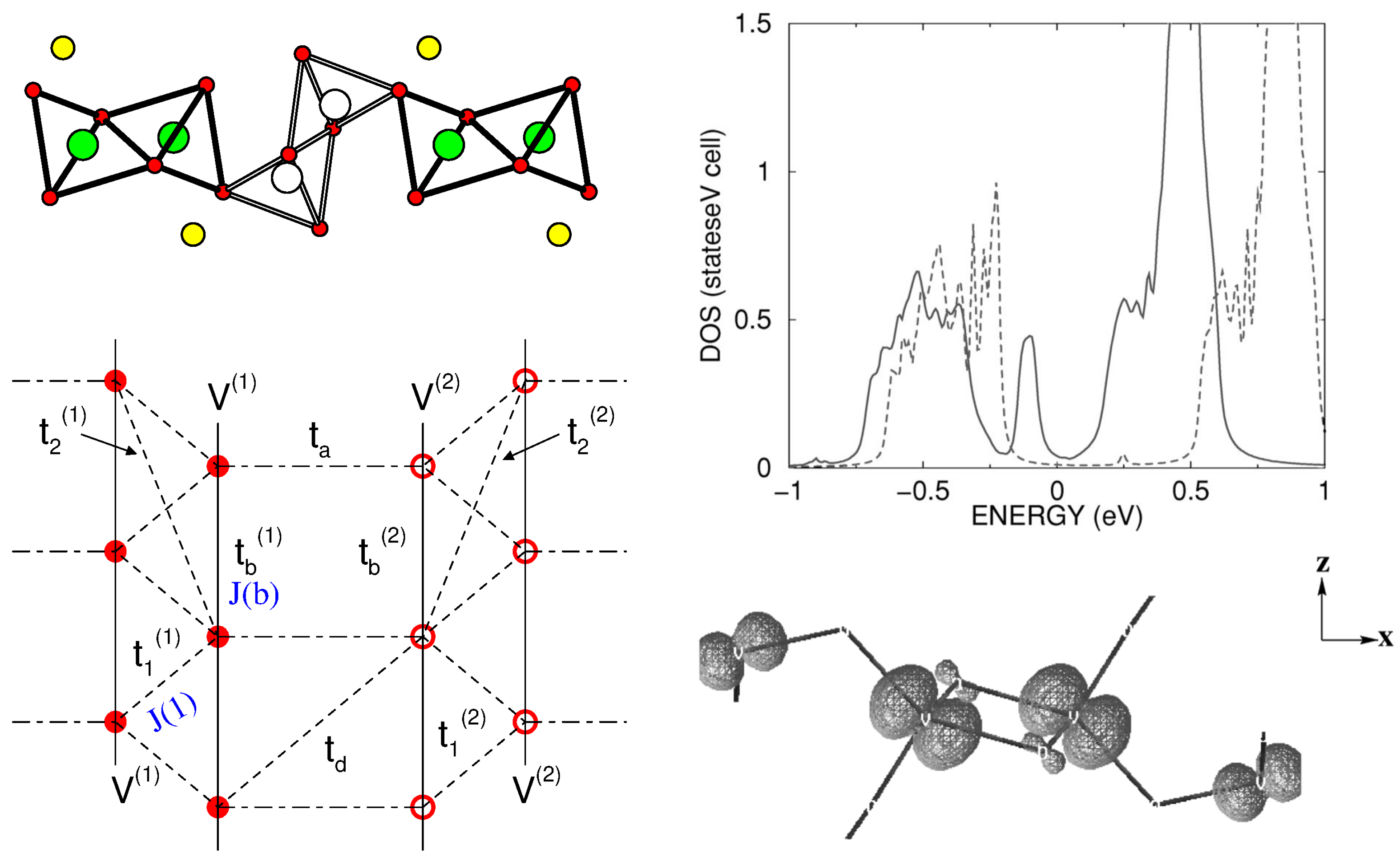
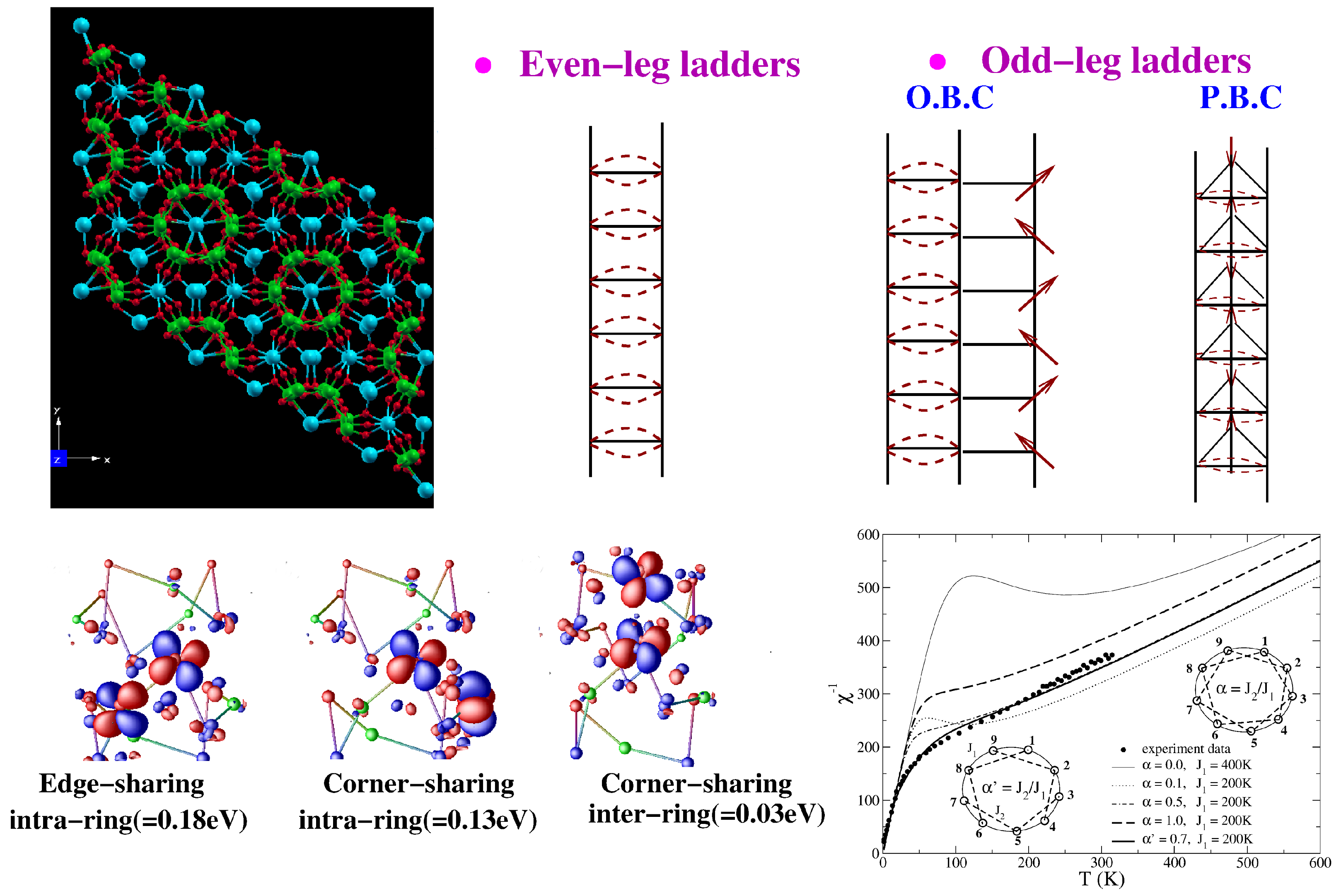
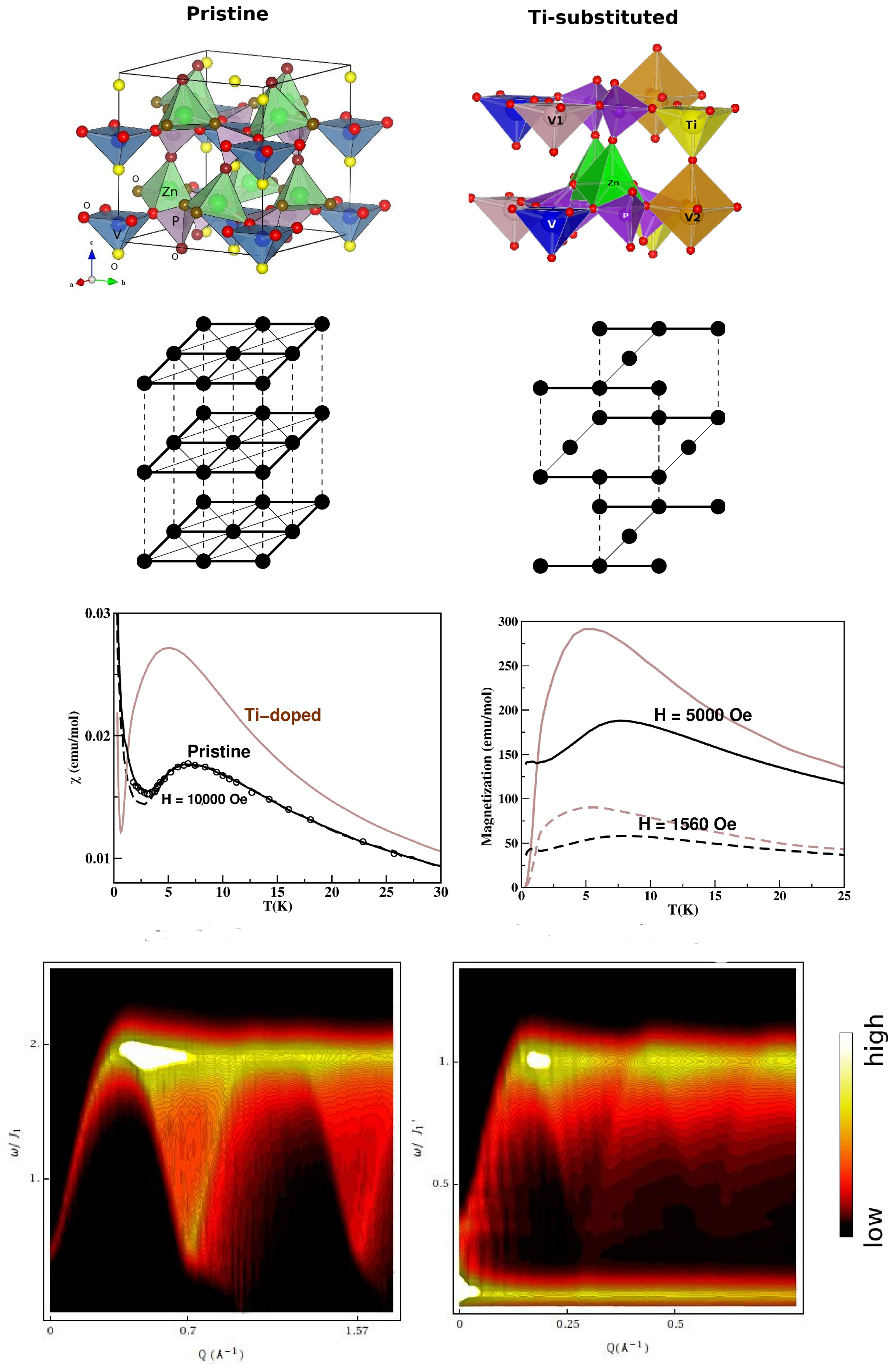
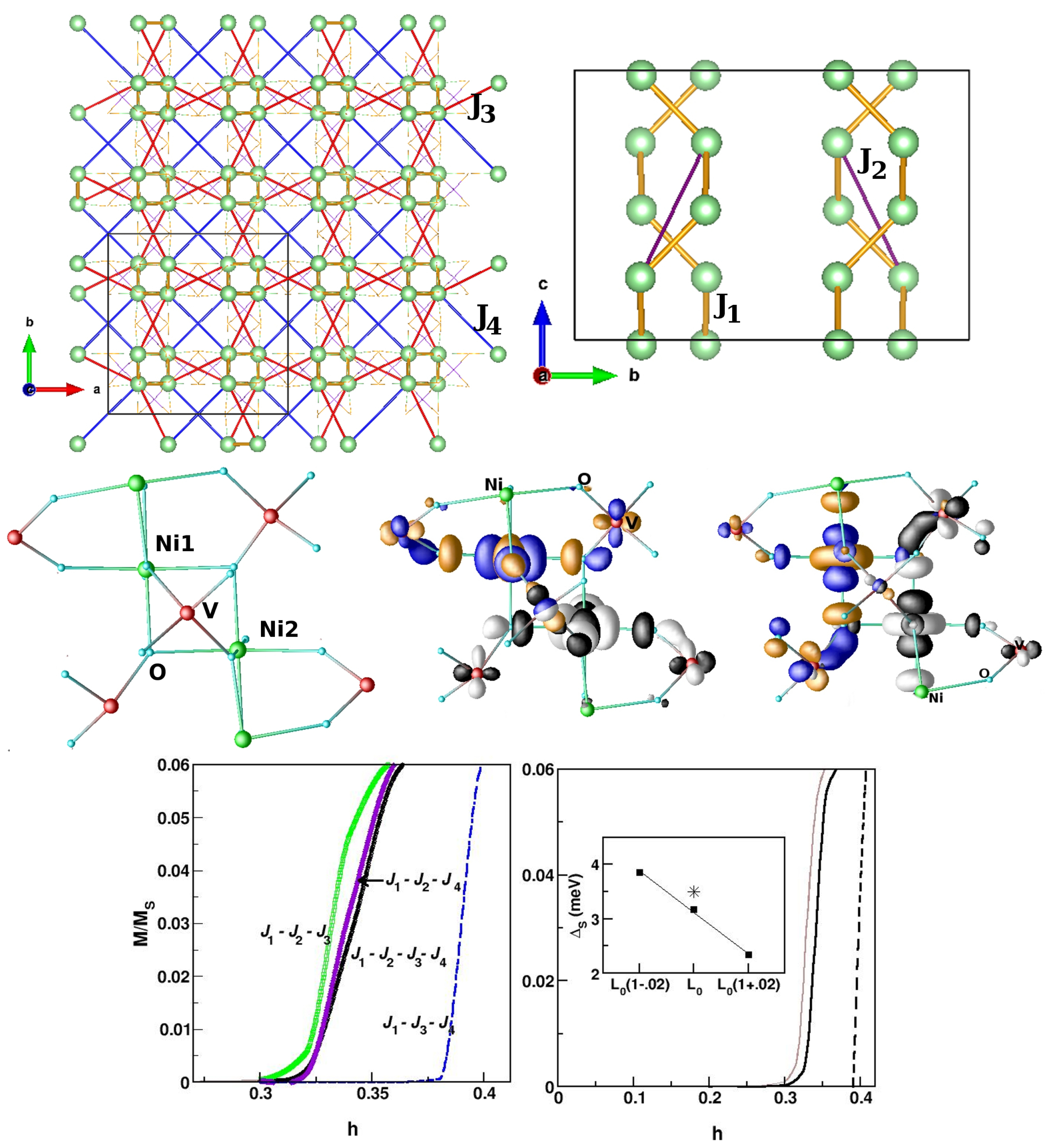
3.2. Vanadates
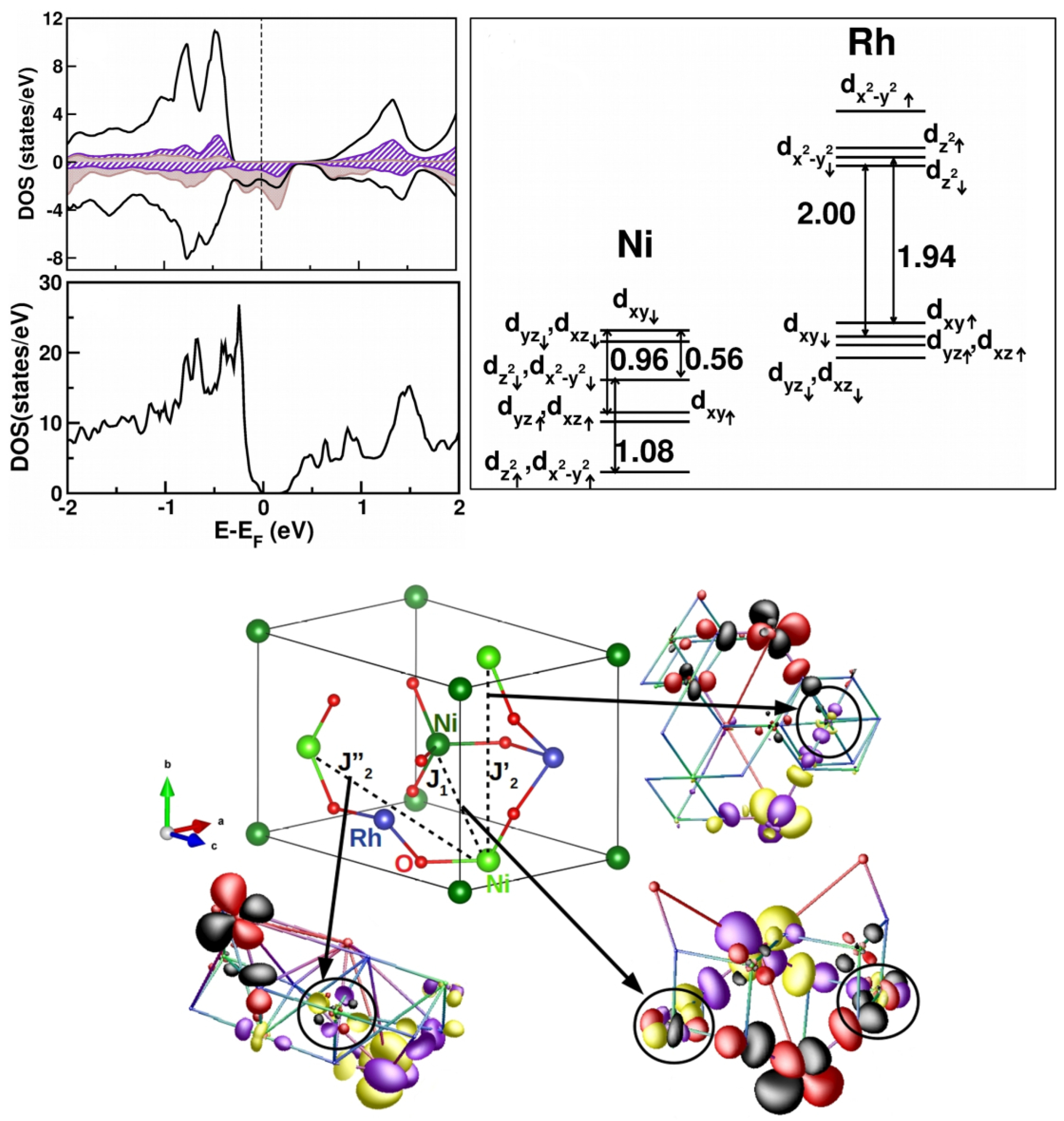
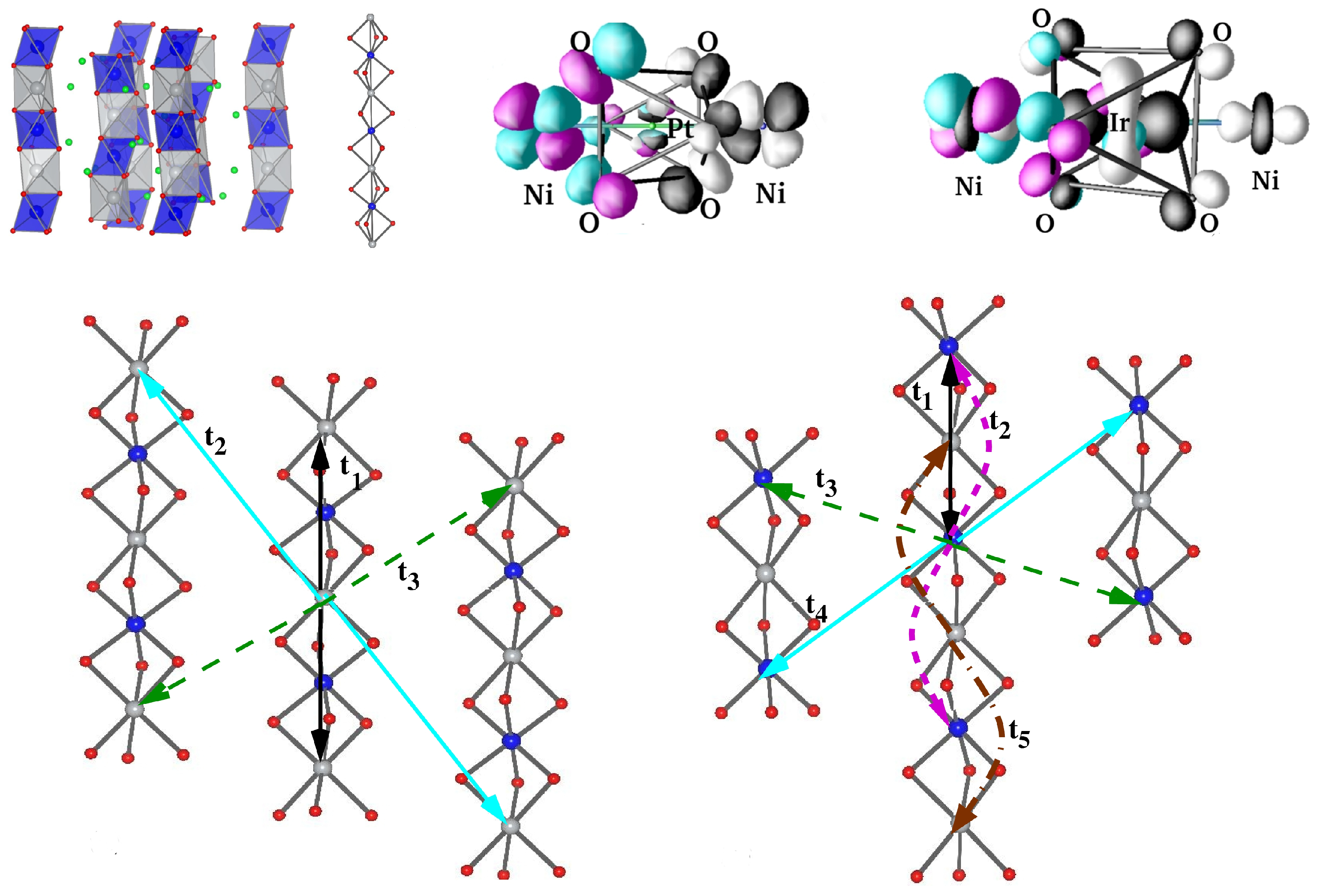
3.3. Nickelates
4. Summary and Outlook
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183. [Google Scholar] [CrossRef]
- Eftekhari, A. Tungsten dichalcogenides (WS2, WSe2, and WTe2): Materials chemistry and applications. J. Mater. Chem. A. 2017, 5, 18299. [Google Scholar] [CrossRef]
- Chakraborty, I.; Pradeep, T. Atomically Precise Clusters of Noble Metals: Emerging Link between Atoms and Nanoparticles. Chem. Rev. 2017, 117, 8208. [Google Scholar] [CrossRef]
- Boston, R.; Schnepp, Z.; Nemoto, Y.; Sakka, Y.; Hall, S.R. In Situ TEM Observation of a Microcrucible Mechanism of Nanowire Growth. Science 2014, 344, 623. [Google Scholar] [CrossRef]
- Ising, E. Beitrag zur Theorie des Ferromagnetismus. Z. Phys. 1925, 31, 253. [Google Scholar] [CrossRef]
- Heisenberg, W. Zur Theorie des Ferromagnetismus. Z. Phys. 1928, 49, 619. [Google Scholar] [CrossRef]
- Onsager, L. Crystal Statistics. I. A Two-Dimensional Model with an Order-Disorder Transition. Phys. Rev. 1944, 65, 117. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys. Rev. Lett. 1966, 17, 1133. [Google Scholar] [CrossRef]
- Berezinskii, V.L. Destruction of Long-range Order in One-dimensional and Two-dimensional Systems Possessing a Continuous Symmetry Group. II. Quantum Systems. Sov. Phys. JETP 1972, 34, 610. [Google Scholar]
- Kosterlitz, J.M.; Thouless, D.J. Long range order and metastability in two dimensional solids and superfluids. (Application of dislocation theory). J. Phys. C Solid State Phys. 1972, 5, L124. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Continuum dynamics of the 1-D Heisenberg antiferromagnet: Identification with the O(3) nonlinear sigma model. Phys. Lett. A 1983, 93, 464. [Google Scholar] [CrossRef]
- Dagotto, E.; Rice, T.M. Surprises on the Way from 1D to 2D Quantum Magnets: The Novel Ladder Materials. Science 1996, 271, 618. [Google Scholar] [CrossRef] [Green Version]
- Fazekas, P. Lecture Notes on Electron Correlation and Magnetism; World Scientific: Singapore, 1999. [Google Scholar]
- Lemmens, P.; Gúntherodtb, G.; Gros, C. Magnetic light scattering in low-dimensional quantum spin systems. Phys. Rep. 2003, 375, 1. [Google Scholar] [CrossRef] [Green Version]
- Bednorz, J.G.; Mueller, K.A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. B. 1986, 64, 189. [Google Scholar] [CrossRef]
- Shastry, B.S.; Sutherland, B. Exact ground state of a quantum mechanical antiferromagnet. Phys. B 1981, 108, 1069. [Google Scholar] [CrossRef]
- Shores, M.P.; Nytko, E.A.; Bartlett, B.M.; Nocera, D.G. A structurally perfect S= 1/2 kagome antiferromagnet. J. Am. Chem. Soc. 2005, 127, 13462. [Google Scholar] [CrossRef]
- Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 2006, 321, 2. [Google Scholar] [CrossRef] [Green Version]
- Goodenough, J.B. Theory of the Role of Covalence in the Perovskite-Type Manganites [La, M(II)]MnO3. Phys. Rev. 1955, 100, 564. [Google Scholar] [CrossRef] [Green Version]
- Kanamori, J. Superexchange interaction and symmetry properties of electron orbitals. J. Phys. Chem. Solids 1959, 10, 87. [Google Scholar] [CrossRef]
- Hoffmann, R.; Lipscomb, W.N. Theory of Polyhedral Molecules. I. Physical Factorizations of the Secular Equation. J. Chem. Phys. 1962, 36, 2179. [Google Scholar] [CrossRef]
- Whangbo, M.-H.; Koo, H.-J.; Kremer, R.K. Spin Exchanges Between Transition Metal Ions Governed by the Ligand p-Orbitals in Their Magnetic Orbitals. Molecules 2021, 26, 531. [Google Scholar] [CrossRef] [PubMed]
- Kaul, E.E.; Rosner, H.; Yushankhai, V.; Sichelschmidt, J.; Shpanchenko, R.V.; Geibel, C. Sr2V3O9 and Ba2V3O9: Quasi-one-dimensional spin-systems with an anomalous low temperature susceptibility. Phys. Rev. B 2003, 67, 174417. [Google Scholar] [CrossRef] [Green Version]
- Tocchio, L.; Feldner, H.; Becca, F.; Valentí, R.; Gros, C. Spin-liquid versus spiral-order phases in the anisotropic triangular lattice. Phys. Rev. B 2013, 87, 035143. [Google Scholar] [CrossRef] [Green Version]
- Danilovich, I.L.; Karpova, E.V.; Morozov, I.V.; Ushakov, A.V.; Streltsov, S.V.; Shakin, A.A.; Volkova, O.S.; Zvereva, E.A.; Vasiliev, A.N. Spin-singlet Quantum Ground State in Zigzag Spin Ladder Cu(CF3COO)2. Chem. Phys. Chem. 2017, 18, 2482. [Google Scholar] [CrossRef] [PubMed]
- Weickert, F.; Aczel, A.A.; Stone, M.B.; Garlea, V.O.; Dong, C.; Kohama, Y.; Movshovich, R.; Demuer, A.; Harrison, N.; Gamża, M.N.; et al. Field-induced double dome and Bose-Einstein condensation in the crossing quantum spin chain system AgVOAsO4. Phys. Rev. B 2019, 100, 104422. [Google Scholar] [CrossRef] [Green Version]
- Hallberg, K. New trends in density matrix renormalization. Adv. Phys. 2006, 55, 477. [Google Scholar] [CrossRef] [Green Version]
- Hubbard, J. Electron Correlations in Narrow Energy Bands. Proc. R. Soc. Lond. 1963, 276, 238. [Google Scholar]
- Spałek, J. t-J Model Then and Now: A Personal Perspective from the Pioneering Times. Acta Phys. Pol. A 2007, 111, 409. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B. 1992, 45, 13244. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Andersen, O.K.; Saha-Dasgupta, T. Muffin-tin orbitals of arbitrary order. Phys. Rev. B 2000, 62, R16219. [Google Scholar] [CrossRef] [Green Version]
- Andersen, O.K.; Jepsen, O. Explicit, First-Principles Tight-Binding Theory. Phys. Rev. Lett. 1984, 53, 2571. [Google Scholar] [CrossRef]
- Saha-Dasgupta, T.; Andersen, O.K.; Nuss, J.; Poteryaev, A.I.; Georges, A.; Lichtenstein, A.I. Electronic structure of V2O3: Wannier orbitals from LDA-NMTO calculations. arXiv 2009, arXiv:0907.2841. [Google Scholar]
- Andersen, O.K.; Saha-Dasgupta, T.; Ezhov, S.; Tsetseris, L.; Jepsen, O.; Tank, R.W.; Arcangeli, C.; Krier, G. Third-generation MTOs. Psi-k Newsl. 2001, 45, 86. [Google Scholar]
- Anderson, P.W. Antiferromagnetism. Theory of Superexchange Interaction. Phys. Rev. 1950, 79, 350. [Google Scholar] [CrossRef]
- Lichtenstein, A.I.; Zaanen, J.; Anisimov, V.I. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 1995, 52, R5467. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sandvik, A.W. Stochastic series expansion method with operator-loop update. Phys. Rev. B 1999, 59, R14157. [Google Scholar] [CrossRef] [Green Version]
- Dorneich, A.; Troyer, M. Accessing the dynamics of large many-particle systems using the stochastic series expansion. Phys. Rev. E 2001, 64, 066701. [Google Scholar] [CrossRef] [Green Version]
- Louis, K.; Gros, C. Stochastic cluster series expansion for quantum spin systems. Phys. Rev. B 2004, 70, 100410. [Google Scholar] [CrossRef] [Green Version]
- McCarron, E.M.; Subramanian, M.A.; Calabrese, J.C.; Harlow, R.L. The incommensurate structure of (Sr14−xCax)Cu24O41 (0 < x ∼ 8) a superconductor byproduct. Mater. Res. Bull. 1988, 23, 1355. [Google Scholar]
- Siegrist, T.; Schneemeyer, L.F.; Sunshine, S.A.; Waszczak, J.V. A new layered cuprate structure-type, (A1−xA′x)14Cu24O41. Mater. Res. Bull. 1988, 23, 1429. [Google Scholar] [CrossRef]
- Motoyama, N.; Osafune, T.; Kakeshita, T.; Eisaki, H.; Uchida, S. Effect of Ca substitution and pressure on the transport and magnetic properties of Sr14Cu24O41 with doped two-leg Cu-O ladders. Phys. Rev. B 1997, 55, R3386. [Google Scholar] [CrossRef]
- Müller, T.A.; Anisimov, V.; Rice, T.M.; Dasgupta, I.; Saha-Dasgupta, T. Electronic structure of ladder cuprates. Phys. Rev. B 1998, 57, R12655. [Google Scholar] [CrossRef] [Green Version]
- Osafune, T.; Motoyama, N.; Eisaki, H.; Uchida, S. Optical Study of the Sr14−xCaxCu24O41 System: Evidence for Hole-Doped Cu2O3 Ladders. Phys. Rev. Lett. 1997, 78, 1980. [Google Scholar] [CrossRef]
- Behruzi, M.; Breuer, K.-H.; Eysel, W. Copper (II) silicates and germanates with chain structures. Z. Kristallogr. 1986, 176, 205. [Google Scholar] [CrossRef]
- Sasago, Y.; Hase, M.; Uchinokura, K.; Tokunaga, M.; Miura, N. Discovery of a spin-singlet ground state with an energy gap in CaCuGe2O6. Phys. Rev. B 1995, 52, 3533. [Google Scholar] [CrossRef]
- Hase, M.; Terasaki, I.; Uchinokura, K. Observation of the spin-Peierls transition in linear Cu2+ (spin-1/2) chains in an inorganic compound CuGeO3. Phys. Rev. Lett. 1993, 70, 3651. [Google Scholar] [CrossRef] [PubMed]
- Zheludev, A.; Shirane, G.; Sasago, Y.; Hase, M.; Uchinokura, K. Dimerized ground state and magnetic excitations in CaCuGe2O6. Phys. Rev. B 1996, 53, 11642. [Google Scholar] [CrossRef] [PubMed]
- Valentí, R.; Saha-Dasgupta, T.; Gros, C. Nature of the spin-singlet ground state in CaCuGe2O. Phys. Rev. B 2002, 66, 054426. [Google Scholar] [CrossRef] [Green Version]
- Johnsson, M.; Törnroos, K.W.; Mila, F.; Millet, P. Tetrahedral Clusters of Copper(II): Crystal Structures and Magnetic Properties of Cu2Te2O5X2. (X = Cl, Br). Chem. Mater. 2000, 12, 2853. [Google Scholar] [CrossRef]
- Lemmens, P.; Choi, K.-Y.; Kaul, E.E.; Geibel, C.; Becker, K.; Brenig, K.; Valenti, R.; Gros, C.; Johnsson, M.; Millet, P.; et al. Evidence for an Unconventional Magnetic Instability in the Spin-Tetrahedra System Cu2Te2O5Br2. Phys. Rev. Lett. 2001, 87, 227201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Valenti, R.; Saha-Dasgupta, T.; Gros, C.; Rosner, H. Halogen-mediated exchange in the coupled-tetrahedra quantum spin systems Cu2Te2O5X2(X=Br,Cl). Phys. Rev. B 2003, 67, 245110. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Assoud, A.; Soheinia, N.; Derakhshan, S.; Cuthbert, H.L.; Greedan, J.; Whangbo, M.H.; Kleinke, H. Synthesis, Structure, and Magnetic Properties of the Layered Copper(II) Oxide Na2Cu2TeO6. Inorg. Chem. 2005, 44, 5042. [Google Scholar] [CrossRef]
- Miura, Y.; Hirai, R.; Kobayashi, Y.; Sato, M. Spin-Gap Behavior of Na3Cu2SbO6 with Distorted Honeycomb Structure. J. Phys. Soc. Jpn. 2006, 75, 847071. [Google Scholar] [CrossRef]
- Derakhshan, S.; Cuthbert, L.H.; Greedan, J.E.; Rahaman, B.; Saha-Dasgupta, T. Electronic structures and low-dimensional magnetic properties of the ordered rocksalt oxides Na3Cu2SbO6 and Na2Cu2TeO6. Phys. Rev. B 2007, 76, 104403. [Google Scholar] [CrossRef]
- Deisenhofer, J.; Eremina, R.M.; Pimenov, A.; Gavrilova, T.; Berger, H.; Johnsson, M.; Lemmens, P.; Krug von Nidda, H.-A.; Loidl, A.; Lee, K.-S.; et al. Structural and magnetic dimers in the spin-gapped system CuTe2O5. Phys. Rev. B 2006, 74, 174421. [Google Scholar] [CrossRef] [Green Version]
- Hanke, K.; Kupcik, V.; Lindqvist, O. The crystal structure of CuTe2O5. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1973, 29, 963. [Google Scholar] [CrossRef]
- Das, H.; Saha-Dasgupta, T.; Gros, C.; Valentí, R. Proposed low-energy model Hamiltonian for the spin-gapped system CuTe2O5. Phys. Rev. B 2008, 77, 224437. [Google Scholar] [CrossRef] [Green Version]
- Diederix, K.M.; Groen, J.P.; Klaassen, T.O.; Poulis, N.J. Spin Dynamics in an Alternating Linear-Chain Heisenberg Antiferromagnet. Phys. Rev. Lett. 1978, 41, 1520. [Google Scholar] [CrossRef]
- Majumdar, C.K.; Ghosh, D.K. On Next-Nearest-Neighbor Interaction in Linear Chain. II. J. Math. Phys. 1969, 10, 1388. [Google Scholar] [CrossRef]
- Shvanskaya, L.; Yakubovich, O.; Massa, W.; Vasiliev, A. Two-dimensional zeolite-like network in the new caesium copper aluminate Cs2CuAl4O8. Acta Crystallogr. Sect. B 2015, 71, 498. [Google Scholar] [CrossRef]
- Rahaman, B.; Kar, S.; Vasiliev, A.; Saha-Dasgupta, T. Interplay of alternation and further neighbor interaction in S=12 spin chains: A case study of Cs2CuAl4O8. Phys. Rev. B 2018, 98, 144412. [Google Scholar] [CrossRef]
- Ueda, Y. Vanadate Family as Spin-Gap Systems. Chem. Mater. 1998, 10, 2653. [Google Scholar] [CrossRef]
- Onoda, M.; Nishiguchi, N. Crystal Structure and Spin Gap State of CaV2O5. J. Solid State Chem. 1996, 127, 359. [Google Scholar] [CrossRef]
- Millet, P.; Satto, C.; Bonvoisin, J.; Normand, B.; Penc, K.; Albrecht, M.; Mila, F. Magnetic properties of the coupled ladder system MgV2O5. Phys. Rev. B 1998, 57, 5005. [Google Scholar] [CrossRef] [Green Version]
- Smolinski, H.; Gros, C.; Weber, W.; Peuchert, U.; Roth, G.; Weiden, M.; Geibel, C. NaV2O5 as a Quarter-Filled Ladder Compound. Phys. Rev. Lett. 1998, 80, 5164. [Google Scholar] [CrossRef] [Green Version]
- Takeo, Y.; Yosihama, T.; Nishi, M.; Nakajima, K.; Kakurai, K.; Isobe, M.; Ueda, Y. Inelastic neutron scattering study of LiV2O5. J. Phys. Chem. Solids 1999, 60, 1145. [Google Scholar] [CrossRef]
- Isobe, M.; Ueda, Y. Magnetic Susceptibilities of AV2O5 ( A=Li and Cs) with Square Pyramidal V(IV)O5. J. Phys. Soc. Jpn. 1996, 65, 3142. [Google Scholar] [CrossRef]
- Galy, J.; Hardy, A. Structure cristalline du bronze de vanadium–lithium LiV2O5. Acta Crystallogr. 1955, 19, 432. [Google Scholar] [CrossRef]
- Anderson, D.N.; Willett, R.D. Refinement of the structure of LiV2O5. Acta Crystallogr. B 1971, 27, 1476. [Google Scholar] [CrossRef]
- Nakao, H.; Ohwada, K.; Takesue, N.; Fujii, Y.; Isobe, M.; Ueda, Y.; Zimmermann, M.V.; Hill, J.P.; Gibbs, D.; Woicik, J.C.; et al. X-ray Anomalous Scattering Study of a Charge-Ordered State in NaV2O5. Phys. Rev. Lett. 2000, 85, 4349. [Google Scholar] [CrossRef] [Green Version]
- Presura, C.; van der Marel, D.; Damascelli, A.; Kremer, R.K. Low-temperature ellipsometry of α′-NaV2O5. Phys. Rev. B 2000, 61, 15762. [Google Scholar] [CrossRef] [Green Version]
- Mazurenko, V.V.; Lichtenstein, A.I.; Katsnelson, M.I.; Dasgupta, I.; Saha-Dasgupta, T.; Anisimov, V.I. Nature of insulating state in NaV2O5 above charge-ordering transition: A cluster dynamical mean-field study. Phys. Rev. B 2002, 66, 081104. [Google Scholar] [CrossRef] [Green Version]
- Lichtenstein, A.I.; Katsnelson, M.I. Antiferromagnetism and d-wave superconductivity in cuprates: A cluster dynamical mean-field theory. Phys. Rev. B 2000, 62, R9283. [Google Scholar] [CrossRef] [Green Version]
- Valentí, R.; Saha-Dasgupta, T.; Alvarez, J.V.; Pozgajcic, K.; Gros, C. Modeling the Electronic Behavior of γ-LiV2O5: A Microscopic Study. Phys. Rev. Lett. 2001, 86, 5381. [Google Scholar] [CrossRef] [Green Version]
- Waltersson, K.; Forslund, B. A refinement of the crystal structure of CsV2O5. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1977, 33, 789. [Google Scholar] [CrossRef]
- Garrett, A.W.; Nagler, S.E.; Tennant, D.A.; Sales, B.C.; Barnes, T. Magnetic Excitations in the S=1/2 Alternating Chain Compound (VO)2P2O7. Phys. Rev. Lett. 1997, 79, 745. [Google Scholar] [CrossRef] [Green Version]
- Oosawa, A.; Kato, T.; Tanaka, H.; Kakurai, K.; Müller, M.; Mikeska, H.-J. Magnetic excitations in the spin-gap system TlCuCl3. Phys. Rev. B 2002, 65, 094426. [Google Scholar] [CrossRef] [Green Version]
- Valentí, R.; Saha-Dasgupta, T. Electronic and magnetic structure of CsV2O5. Phys. Rev. B 2002, 65, 144445. [Google Scholar] [CrossRef] [Green Version]
- Mila, F. Ladders in a magnetic field: A strong coupling approach. Eur. Phys. J. B 1998, 6, 201. [Google Scholar] [CrossRef] [Green Version]
- Trombe, J.-C.; Gleizes, A.; Galy, J.; Renard, J.-P.; Journaux, Y.; Verdaguer, M. Structure and magnetic properties of vanadyl chains: Crystal structure of VOSeO3 and comparative study of VOSeO3 and VOSe2O5. New J. Chem. 1987, 11, 321. [Google Scholar]
- Valentí, R.; Saha-Dasgupta, T.; Mila, F. Ab initio investigation of VOSeO3: A spin gap system with coupled spin dimers. Phys. Rev. B 2003, 68, 024411. [Google Scholar] [CrossRef] [Green Version]
- Millet, P.; Henry, J.Y.; Mila, F.; Galy, J. Vanadium(IV)–Oxide Nanotubes: Crystal Structure of the Low-Dimensional Quantum Magnet Na2V3O7. J. Solid State Chem. 1999, 147, 676. [Google Scholar] [CrossRef]
- Whangbo, M.-H.; Koo, H.-J. Investigation of the spin exchange interactions in the nanotube system Na2V3O7 by spin dimer analysis. Solid State Commun. 2000, 115, 675. [Google Scholar] [CrossRef]
- Gavilano, J.; Rau, D.; Mushkolaj, S.; Ott, H.R.; Millet, P.; Mila, F. Low-Dimensional Spin S=1/2 System at the Quantum Critical Limit: Na2V3O7. Phys. Rev. Lett. 2003, 90, 167202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Subrahmanyam, V. Effective chiral-spin Hamiltonian for odd-numbered coupled Heisenberg chains. Phys. Rev. B 1994, 50, 16109. [Google Scholar] [CrossRef] [Green Version]
- Saha-Dasgupta, T.; Valentí, R.; Capraro, F.; Gros, C. Na2V3O7: A Frustrated Nanotubular System with Spin-1/2 Diamond Ring Geometry. Phys. Rev. Lett. 2005, 95, 107201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taniguchi, S.; Nishikawa, Y.; Yasui, Y.; Kobayashi, Y.; Sato, M.; Nishikawa, T.; Kontani, M.; Sano, K. Spin Gap Behavior of S=1/2 Quasi-Two-Dimensional System CaV4O9. J. Phys. Soc. Jpn. 1995, 64, 2758. [Google Scholar] [CrossRef]
- Kanungo, S.; Kar, S.; Saha-Dasgupta, T. Tuning of magnetic ground state of the spin-12 square-lattice compound Zn2VO(PO4)2 through chemical substitution. Phys. Rev. B 2013, 87, 054431. [Google Scholar] [CrossRef]
- Lii, K.H.; Tsai, H.J. Synthesis and crystal structure of Zn2VO(PO4)2, a vanadyl(IV) orthophosphate containing a dimer of edge-sharing ZnO5 square pyramids. J. Solid State Chem. 1991, 90, 291. [Google Scholar] [CrossRef]
- Yusuf, S.M.; Bera, A.K.; Kini, N.S.; Mirebeau, I.; Petit, S. Two- and three-dimensional magnetic correlations in the spin-12 square-lattice system Zn2VO(PO4)2. Phys. Rev. B 2010, 82, 094412. [Google Scholar] [CrossRef] [Green Version]
- Kini, N.S.; Kaul, E.E.; Geibel, C. Zn2VO(PO4)2: An S = 1/2 Heisenberg antiferromagnetic square lattice system. J. Phys. Condens. Matter 2006, 18, 1303. [Google Scholar] [CrossRef]
- Kar, S.; Saha-Dasgupta, T. Quasi-2D J1–J2 antiferromagnet Zn2VO(PO4)2 and its Ti-substituted derivative: A spin-wave analysis. Physica B 2014, 432, 71. [Google Scholar] [CrossRef] [Green Version]
- Adhikary, P.; Bandyopadhyay, S.; Das, T.; Dasgupta, I.; Saha-Dasgupta, T. Orbital-selective. Phys. Rev. B 2020, 102, 100501. [Google Scholar] [CrossRef]
- Nakua, A.M.; Greedan, J.E. Structural and Magnetic Properties of Transition Metal Arsenates, AAs2O6, A = Mn, Co, and Ni. J. Solid State Chem. 1995, 118, 402. [Google Scholar] [CrossRef]
- Orosel, D.; Jansen, M. PdAs2O6, das erste paramagnetische Palladiumoxid. Z. Anorg. Allg. Chem. 2006, 632, 1131. [Google Scholar] [CrossRef]
- Reehuis, M.; Saha-Dasgupta, T.; Orosel, D.; Nuss, J.; Rahaman, B.; Keimer, B.; Andersen, O.K.; Jansen, M. Magnetic properties of PdAs2O6: A dilute spin system with an unusually high Néel temperature. Phys. Rev. B 2012, 85, 115118. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Nahum, A.; Senthil, T. Topological paramagnetism in frustrated spin-1 Mott insulators. Phys. Rev. B 2015, 91, 195131. [Google Scholar] [CrossRef] [Green Version]
- Affleck, I.; Kennedy, T.; Lieb, E.H.; Tasaki, H. Rigorous results on valence-bond ground states in antiferromagnets. Phys. Rev. Lett. 1987, 59, 799. [Google Scholar] [CrossRef]
- Fritsch, V.; Hemberger, J.; Büttgen, N.; Scheidt, E.-W.; Krug von Nidda, H.-A.; Loidl, A.; Tsurkan, V. Spin and Orbital Frustration in MnSc2S4 and FeSc2S4. Phys. Rev. Lett. 2004, 92, 116401. [Google Scholar] [CrossRef] [Green Version]
- Tristan, N.; Hemberger, J.; Krimmel, A.; Krug von Nidda, H.-A.; Tsurkan, V.; Loidl, A. Geometric frustration in the cubic spinels MAl2O4 (M=Co, Fe, and Mn). Phys. Rev. B 2005, 72, 174404. [Google Scholar] [CrossRef]
- Chamorro, J.R.; Ge, L.; Flynn, J.; Subramanian, M.A.; Mourigal, M.; McQueen, T.M. Frustrated spin one on a diamond lattice in NiRh2O4. Phys. Rev. Mater. 2018, 2, 034404. [Google Scholar] [CrossRef]
- Das, S.; Nafday, D.; Saha-Dasgupta, T.; Paramekanti, A. NiRh2O4: A spin-orbit entangled diamond-lattice paramagnet. Phys. Rev. B 2019, 100, 140408. [Google Scholar] [CrossRef] [Green Version]
- Vishwanath, A.; Senthil, T. Physics of Three-Dimensional Bosonic Topological Insulators: Surface-Deconfined Criticality and Quantized Magnetoelectric Effect. Phys. Rev. X 2013, 3, 011016. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Haverkort, M.W.; Hu, Z.; Khomskii, D.I.; Tjeng, L.H. Nature of Magnetism in Ca3Co2O6. Phys. Rev. Lett. 2005, 95, 186401. [Google Scholar] [CrossRef] [Green Version]
- Sarkar, S.; Kanungo, S.; Saha-Dasgupta, T. Ab initio study of low-dimensional quantum spin systems Sr3NiPtO6, Sr3CuPtO6, and Sr3NiIrO6. Phys. Rev. B 2010, 82, 235122. [Google Scholar] [CrossRef]
- Flahaut, D.; Hebert, S.; Amignan, A.; Hardy, V.; Martin, C.; Hervieu, M.; Costes, M.; Raquet, B.; Broto, J.M. A magnetic study of the one dimensional Sr3 NiIrO6 compound. Eur. Phys. J. B 2003, 35, 317–323. [Google Scholar] [CrossRef]
- Rice, T.M. To Condense or Not to Condense. Science 2002, 298, 760. [Google Scholar] [CrossRef] [PubMed]
- Sakai, T.; Takahashi, M. Effect of the Haldane gap on quasi-one-dimensional systems. Phys. Rev. B 1990, 42, 4537. [Google Scholar] [CrossRef] [PubMed]
- Wichmann, R.; Müller-Buschbaum, H. SrNi2V2O8: Ein neuer Strukturtyp der Erdalkali-Oxometallate. Rev. Chim. Miner. 1986, 23, 1. [Google Scholar]
- Samanta, K.; Kar, S.; Saha-Dasgupta, T. Magnetic modeling and effect of biaxial strain on the Haldane chain compound SrNi2V2O8. Phys. Rev. B 2016, 93, 224404. [Google Scholar] [CrossRef]
- Winter, S.M.; Li, Y.; Jeschke, H.O.; Valentí, R. Challenges in design of Kitaev materials: Magnetic interactions from competing energy scales. Phys. Rev. B 2016, 93, 214431. [Google Scholar] [CrossRef] [Green Version]
Sample Availability: Not applicable. |
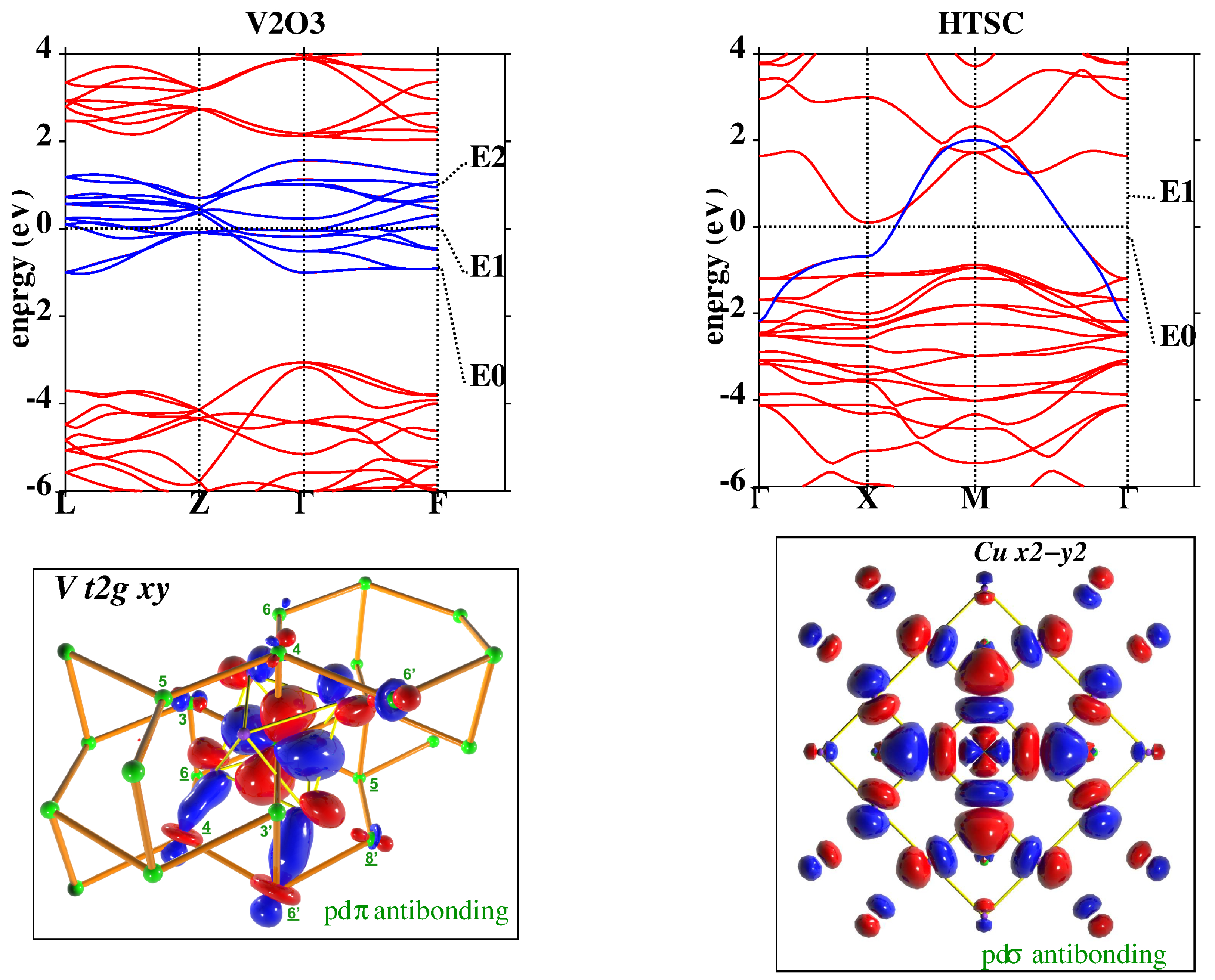
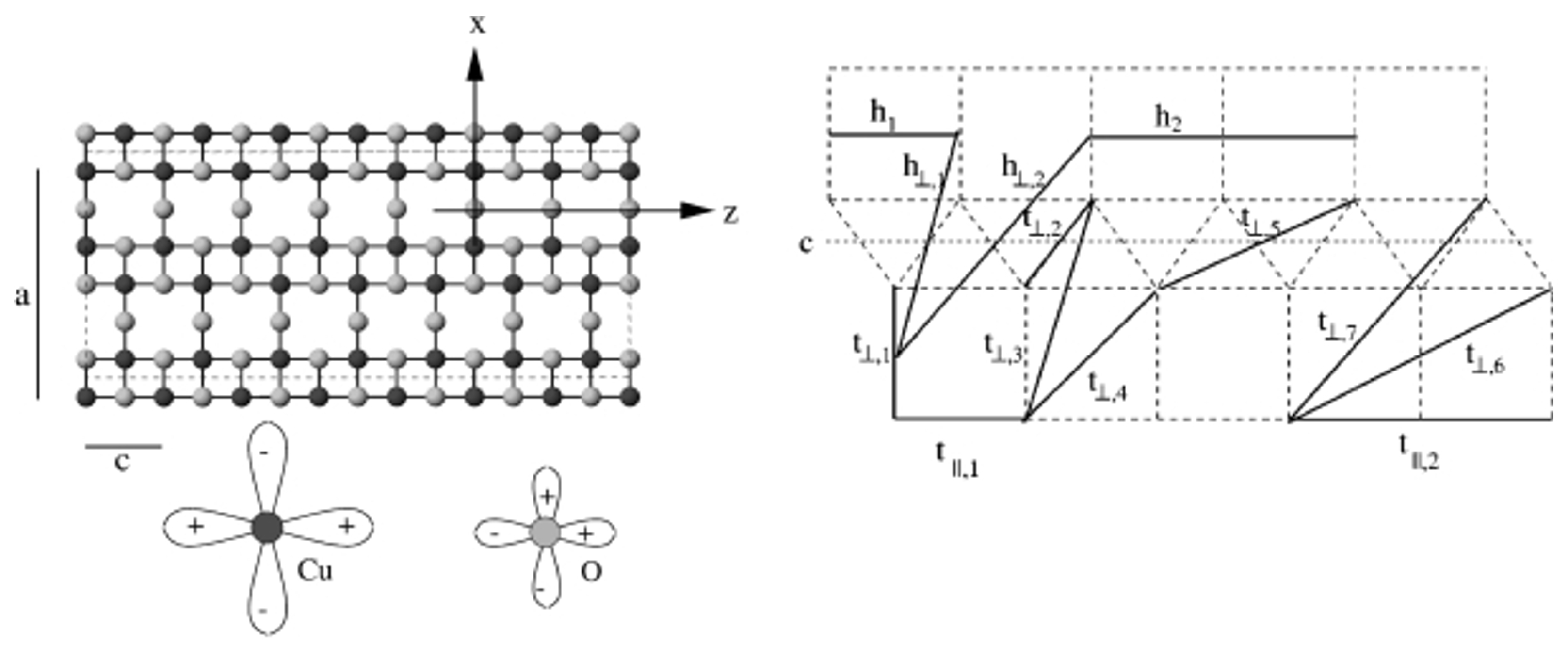
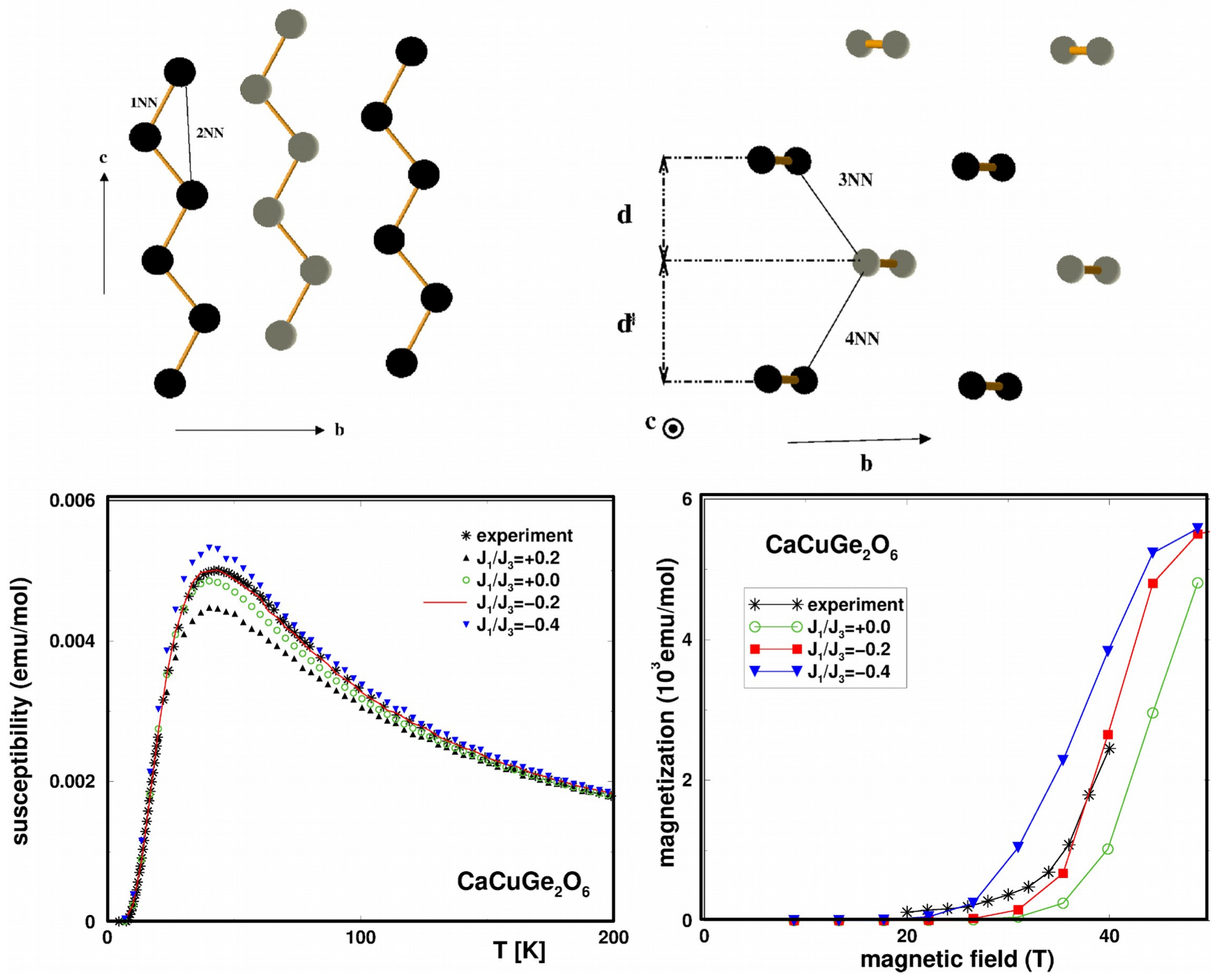
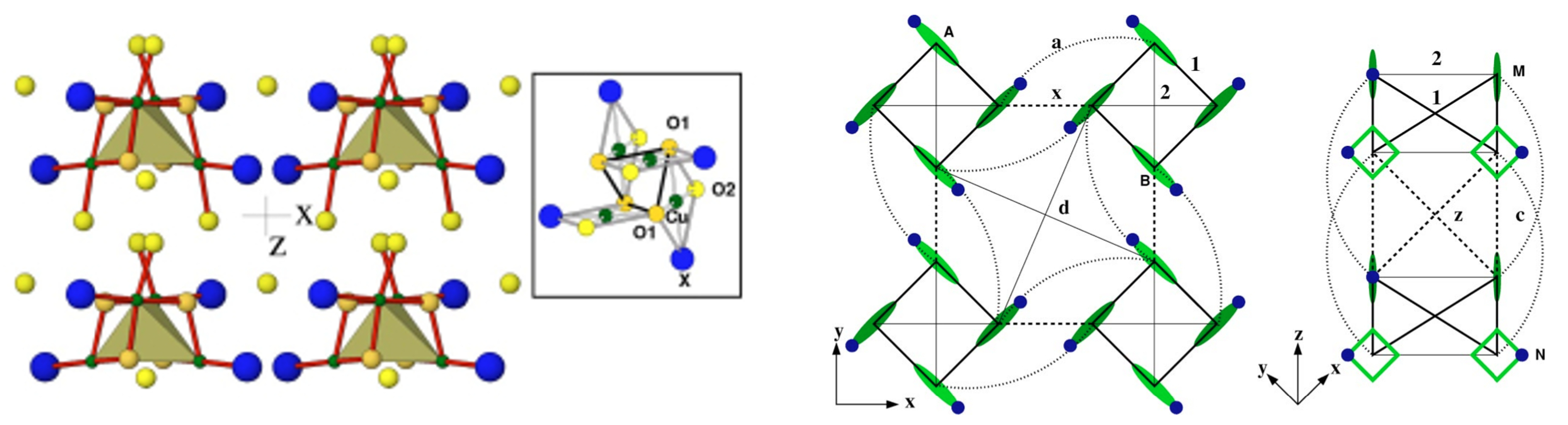


| Compound Name | Magnetic Ion | Occupancy | Spin |
|---|---|---|---|
| SrCuO | Cu | S = 1/2 | |
| CaCuGeO | Cu | S = 1/2 | |
| CuTeOX (X=Cl/Br) | Cu | S = 1/2 | |
| NaCuTe(Sb)O | Cu | S = 1/2 | |
| CuTeO | Cu | S = 1/2 | |
| CsCuAlO | Cu | S = 1/2 | |
| -LiVO | V | S = 1/2 | |
| -NaVO | V | S = 1/2 | |
| CsVO | V | S = 1/2 | |
| VOSeO | V | S = 1/2 | |
| NaVO | V | S = 1/2 | |
| ZnVO(PO) | V | S = 1/2 | |
| Ti-ZnVO(PO) | Ti/V | / | S = 1/2 |
| NiAsO | Ni | S = 1 | |
| NiRhO | Ni | S = 1 | |
| SrNiPt(Ir)O | Ni | S = 1 | |
| SrNiVO | Ni | S = 1 |
| Compound Name | Proposed Spin Model | Ref. |
|---|---|---|
| SrCuO | Two-leg ladder | Ref. [45] |
| CaCuGeO | Coupled dimer | Ref. [51] |
| CuTeOX (X=Cl/Br) | Interacting spin cluster | Ref. [54] |
| NaCuTe(Sb)O | AF-AF chain | Ref. [57] |
| CuTeO | 2-d coupled dimer | Ref. [60] |
| CsCuAlO | 1-d AF-F chain with NN–NNN interaction | Ref. [64] |
| -LiVO | Asymmetric spin ladder | Ref. [77] |
| -NaVO | Spin ladder | Ref. [75] |
| CsVO | 2-d coupled spin dimer | Ref. [81] |
| VOSeO | Alternating spin chain | Ref. [84] |
| NaVO | Partially frustrated spin tube | Ref. [89] |
| ZnVO(PO) | 2-d AF spin model | Ref. [91] |
| Ti-ZnVO(PO) | Coupled AF chain | Ref. [91] |
| NiAsO | 2-d spin lattice formed by third-NN interactions | Ref. [99] |
| NiRhO | Spin–orbit entangled singlet | Ref. [105] |
| SrNiPt(Ir)O | Interacting spin chain | Ref. [108] |
| SrNiVO | Coupled Haldane chain | Ref. [113] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha-Dasgupta, T. The Fascinating World of Low-Dimensional Quantum Spin Systems: Ab Initio Modeling. Molecules 2021, 26, 1522. https://doi.org/10.3390/molecules26061522
Saha-Dasgupta T. The Fascinating World of Low-Dimensional Quantum Spin Systems: Ab Initio Modeling. Molecules. 2021; 26(6):1522. https://doi.org/10.3390/molecules26061522
Chicago/Turabian StyleSaha-Dasgupta, Tanusri. 2021. "The Fascinating World of Low-Dimensional Quantum Spin Systems: Ab Initio Modeling" Molecules 26, no. 6: 1522. https://doi.org/10.3390/molecules26061522
APA StyleSaha-Dasgupta, T. (2021). The Fascinating World of Low-Dimensional Quantum Spin Systems: Ab Initio Modeling. Molecules, 26(6), 1522. https://doi.org/10.3390/molecules26061522






