Thermal Degradation Kinetics and Modeling Study of Ultra High Molecular Weight Polyethylene (UHMWP)/Graphene Nanocomposite
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Fabrication of UHMWPE/Graphene Nanocomposites
2.3. Morphological Characterization
2.4. Thermal Assessment
2.5. Analytical Methods
3. Results and Discussion
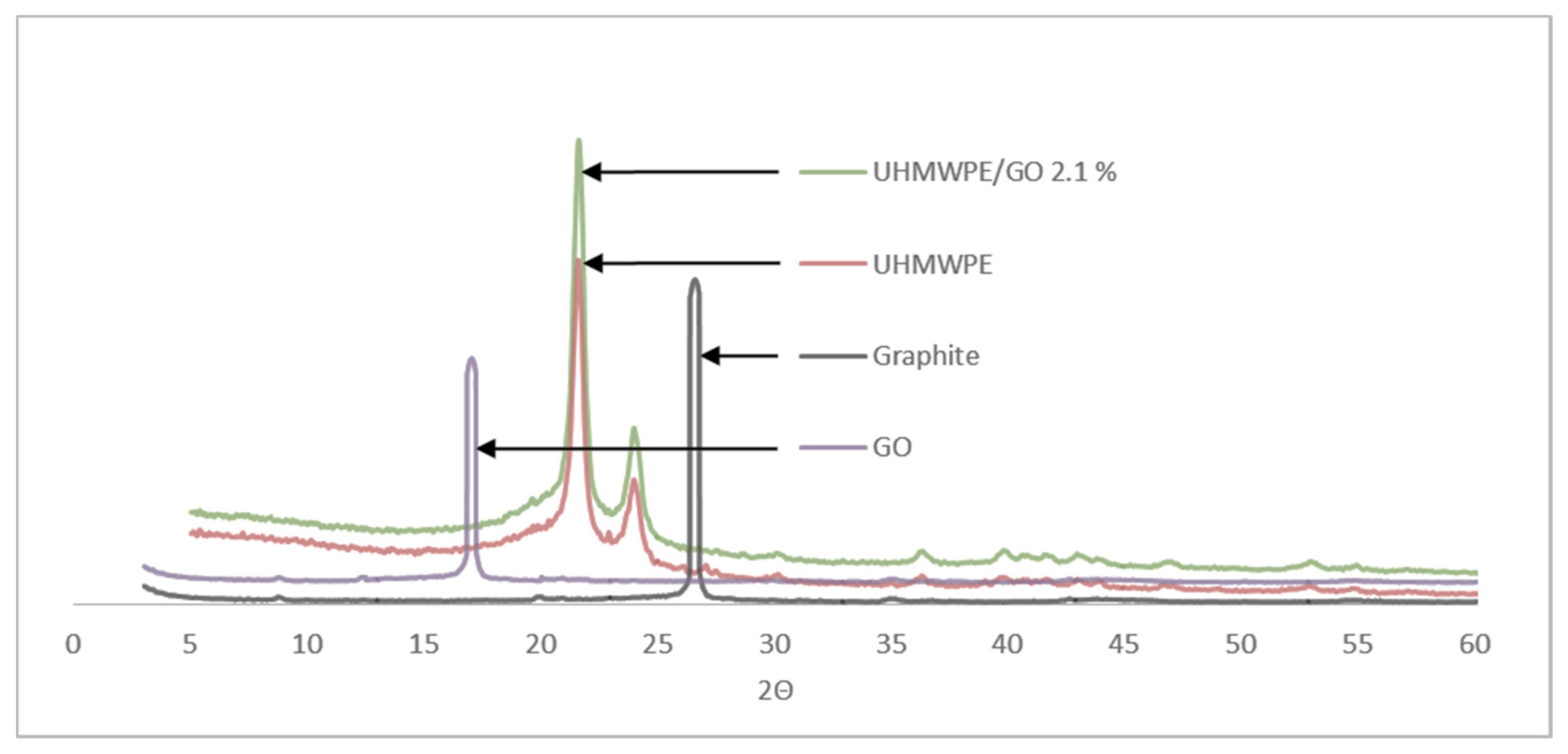
3.1. Morphology

3.2. Differential Scanning Calorimetry (DSC)
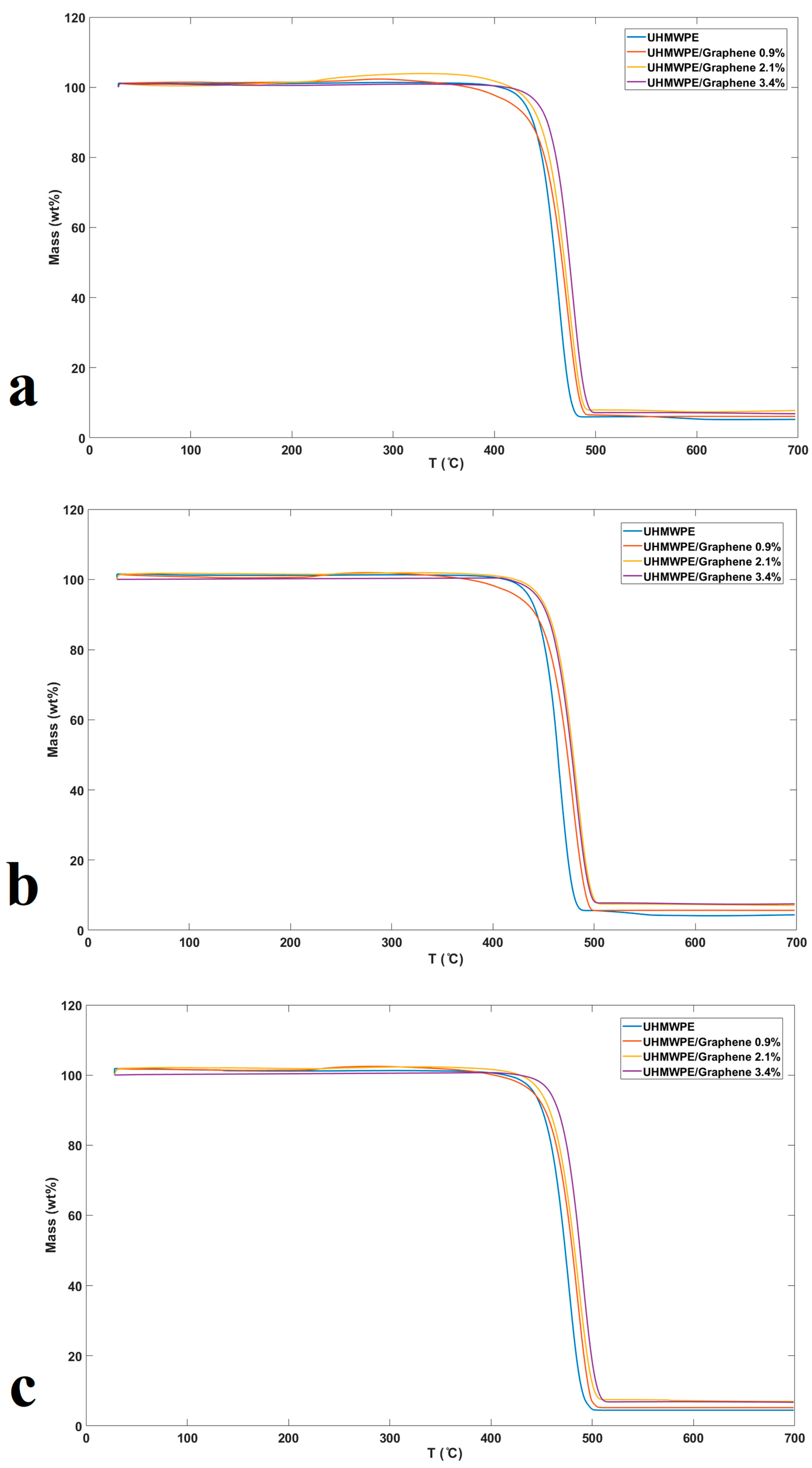
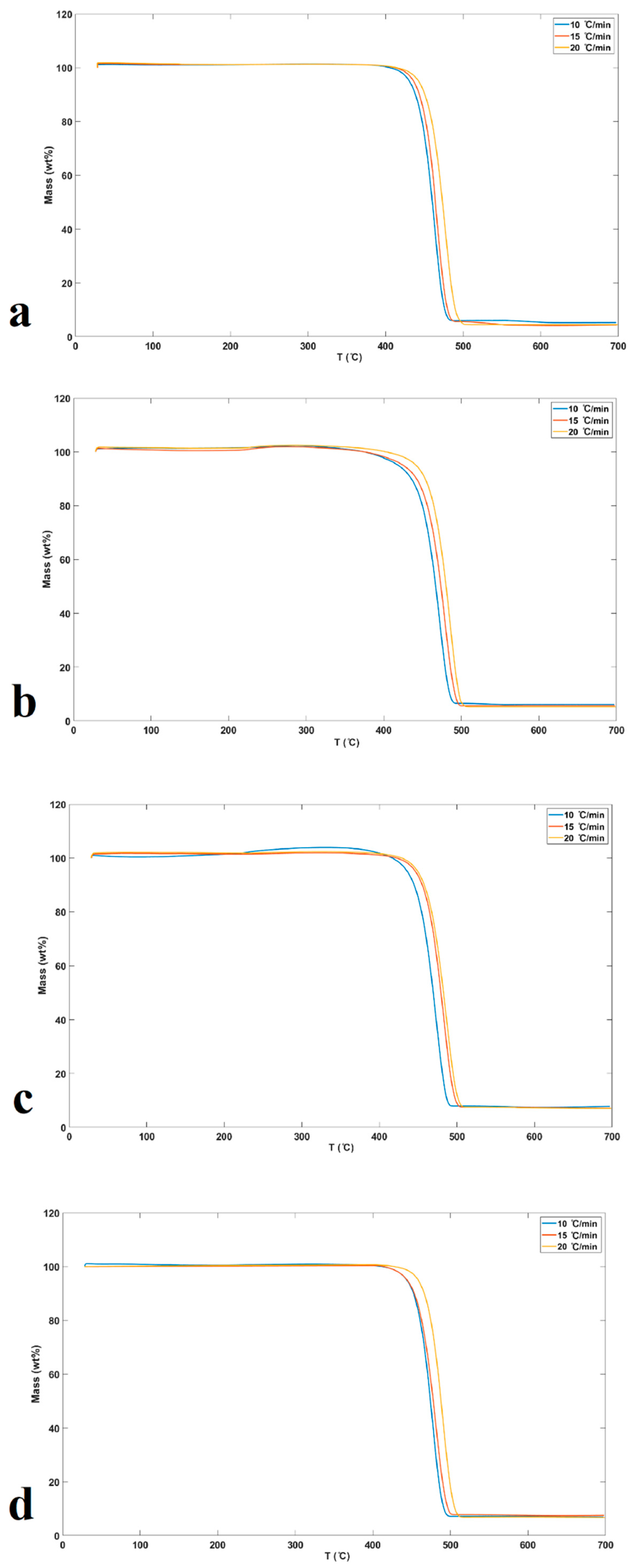
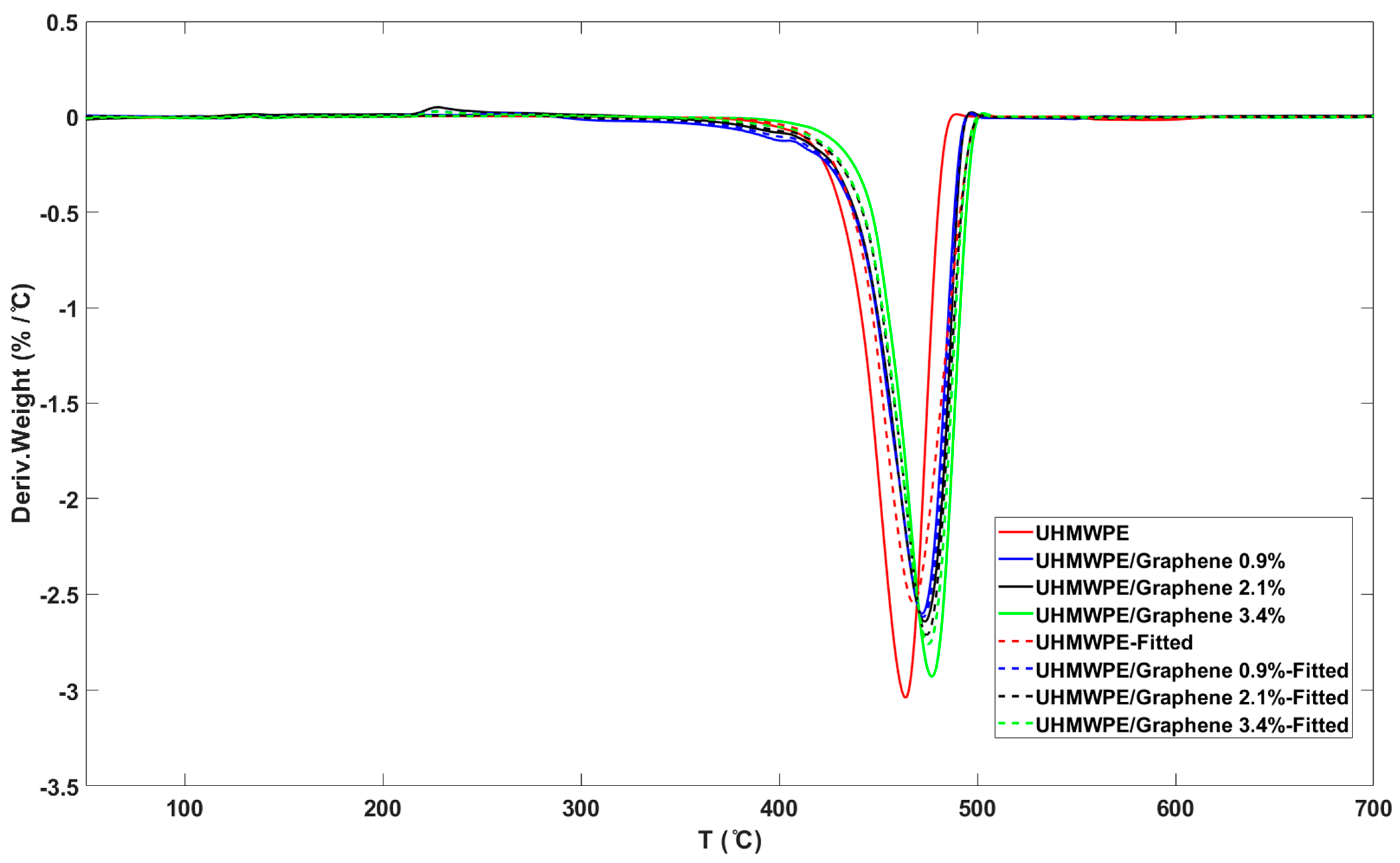
3.3. Thermal Degradation Studies
3.4. Model-Fitting Method
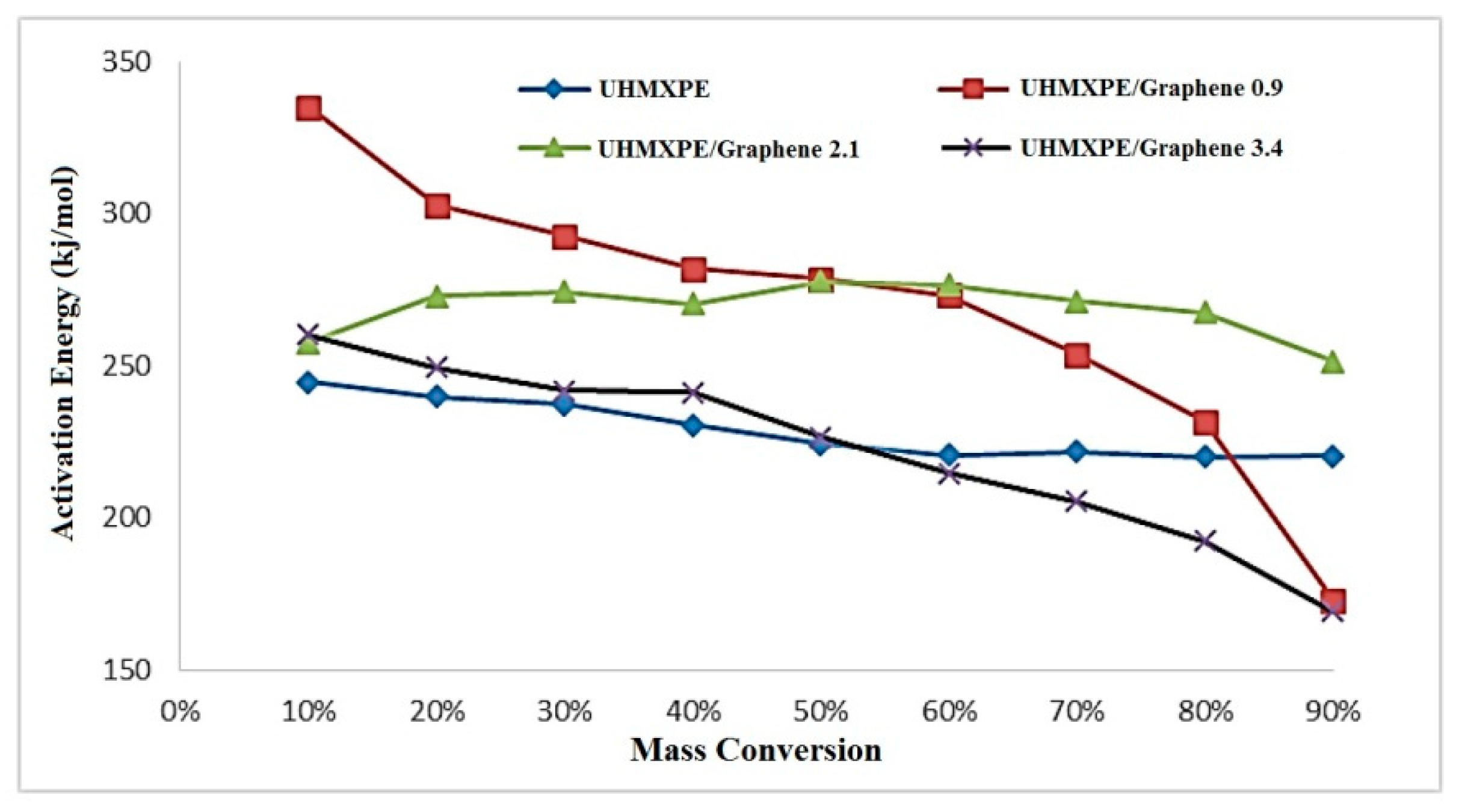
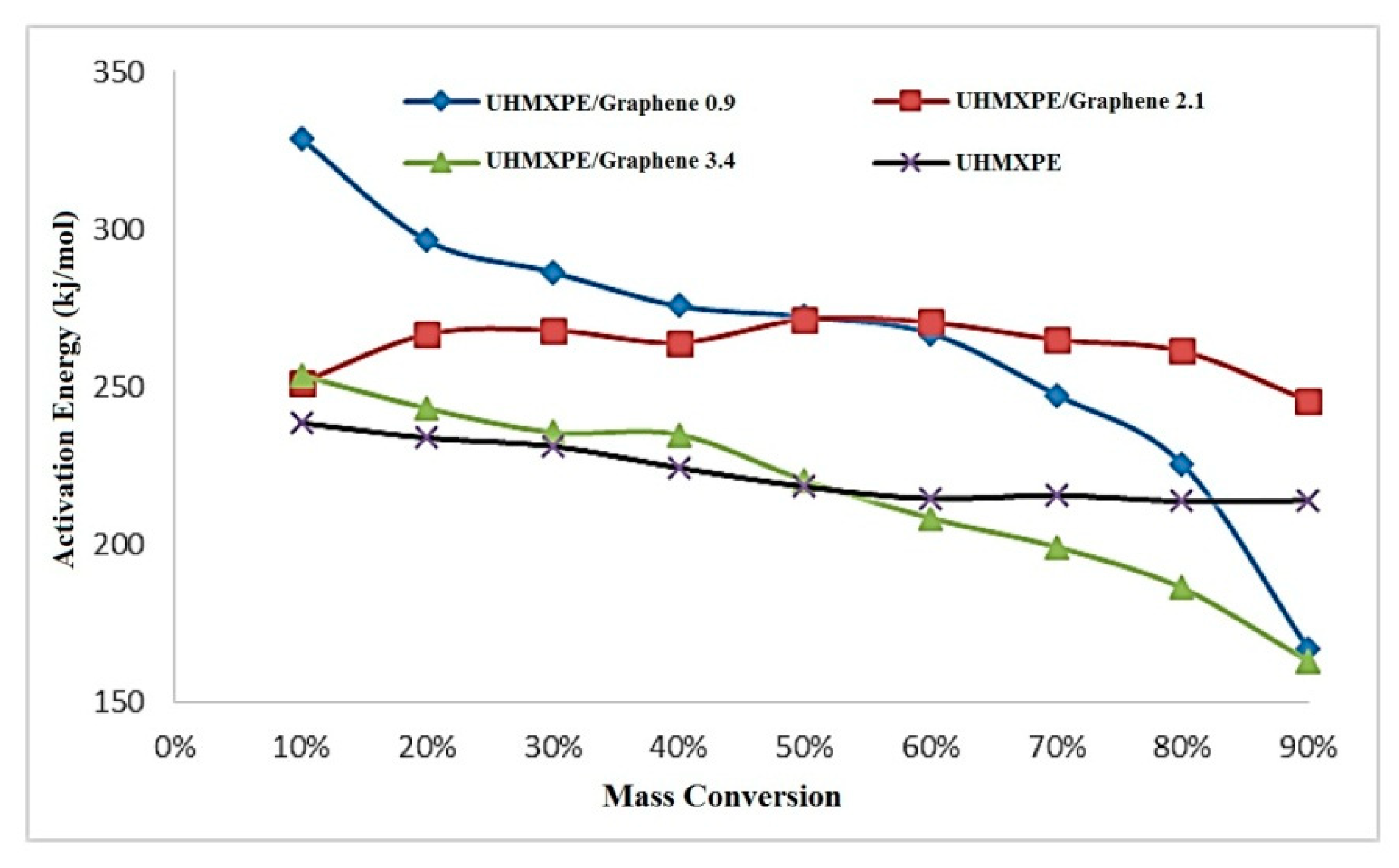
3.5. Isoconversional Analysis
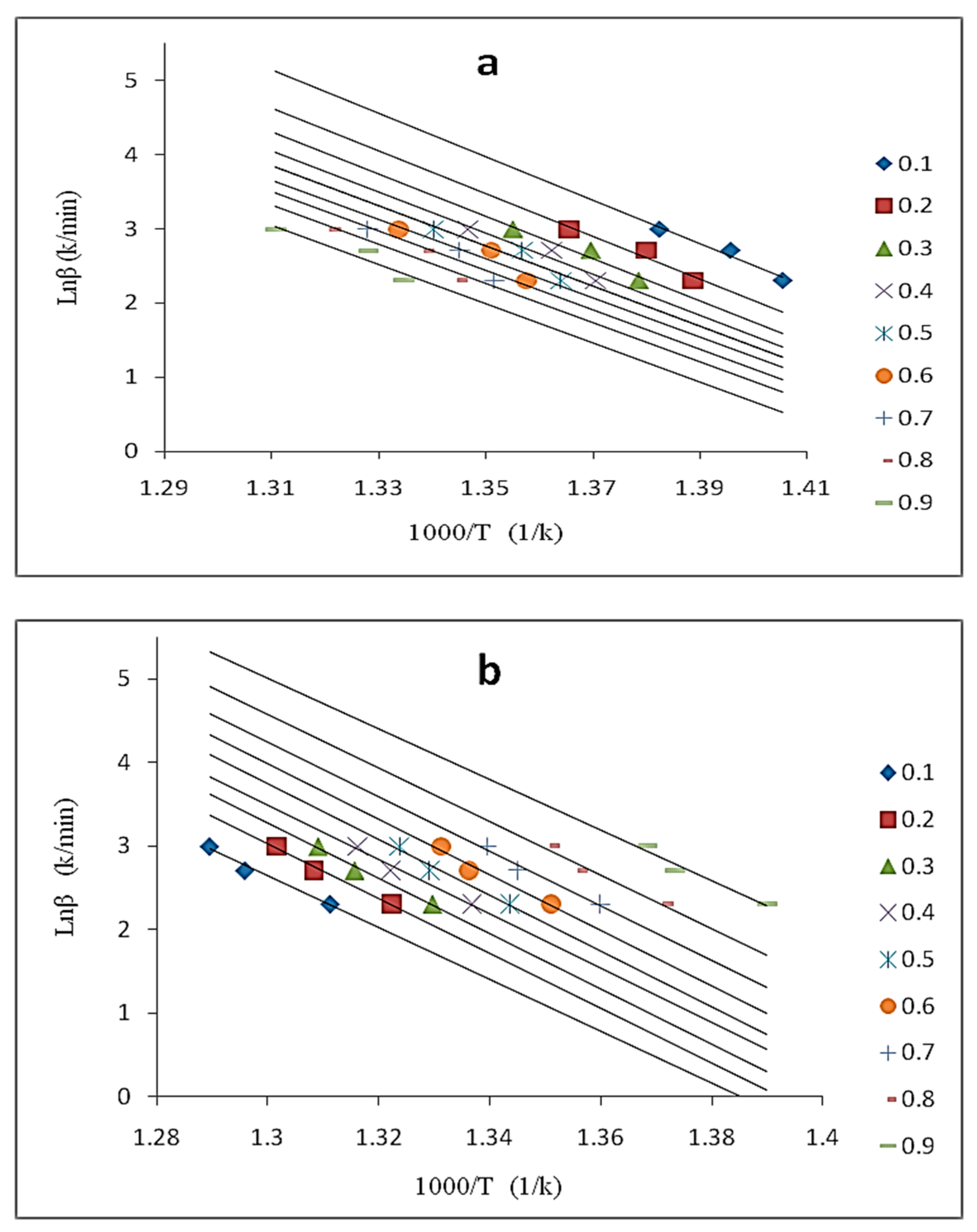
3.5.1. Ozawa–Flynn–Wall (OFW) Method
3.5.2. Friedman Method
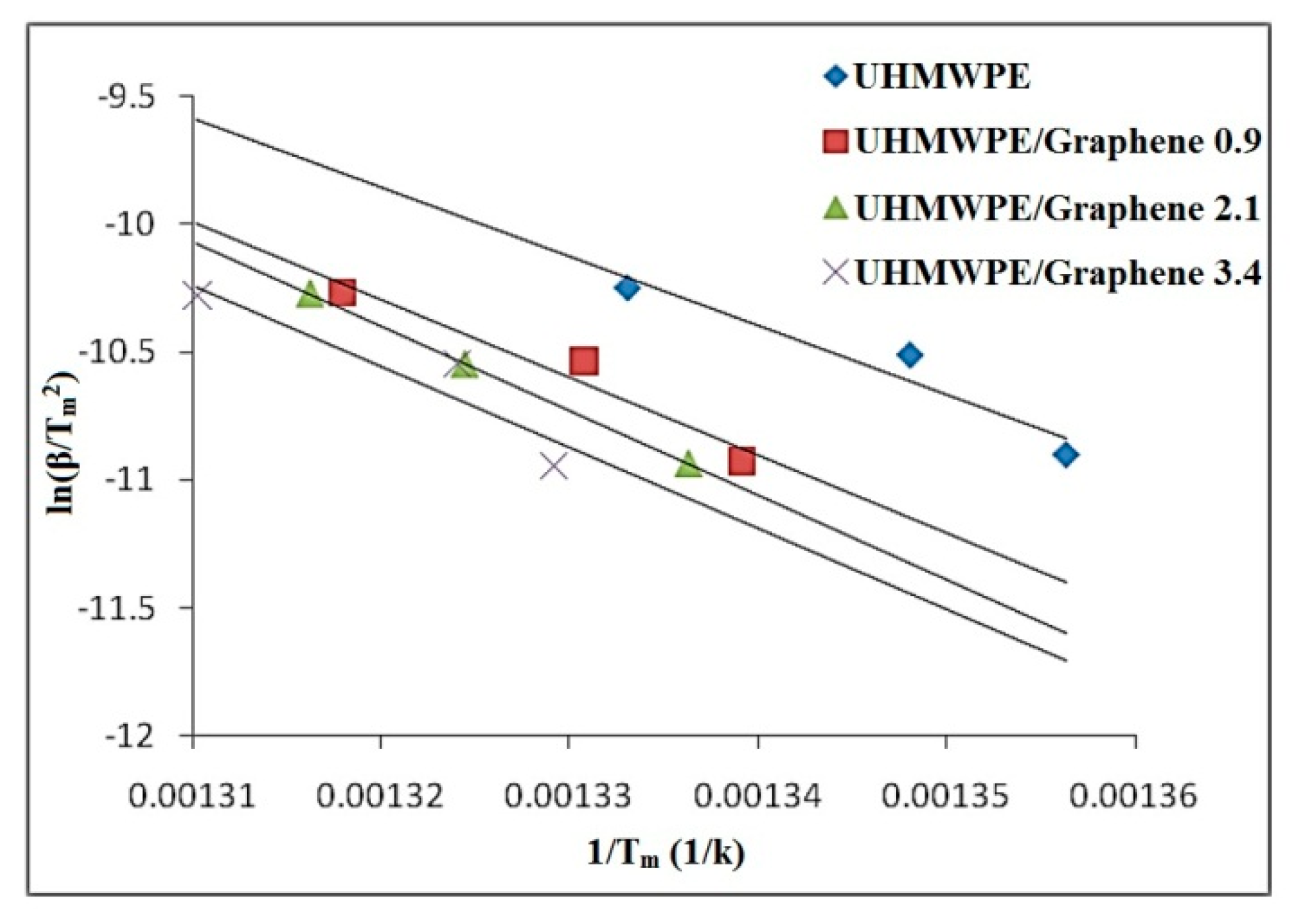
3.5.3. Kissinger Method
3.5.4. Augis and Bennett Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lomakin, S.M.; Novokshonova, L.A.; Brevnov, P.N.; Shchegolikhin, A.N. Thermal properties of polyethylene/montmorillonite nanocomposites prepared by intercalative polymerization. J. Mater. Sci. 2008, 43, 1340–1353. [Google Scholar] [CrossRef]
- Stürzel, M.; Kempe, F.; Thomann, Y.; Mark, S.; Enders, M.; Mülhaupt, R. Novel Graphene UHMWPE Nanocomposites Prepared by Polymerization Filling Using Single-Site Catalysts Supported on Functionalized Graphene Nanosheet Dispersions. Macromolecules 2012, 45, 6878–6887. [Google Scholar] [CrossRef]
- Ramazani, A.; Saremi, M.G.; Amoli, B.N.; Izadi, H. Production and characterization of UHMWPE/fumed silica nanocomposites. Polym. Compos. 2012, 33, 1858–1864. [Google Scholar] [CrossRef]
- Das, O.; Neisiany, R.E.; Capezza, A.J.; Hedenqvist, M.S.; Försth, M.; Xu, Q.; Jiang, L.; Ji, D.; Ramakrishna, S. The need for fully bio-based facemasks to counter coronavirus outbreaks: A perspective. Sci. Total Environ. 2020, 736, 139611. [Google Scholar] [CrossRef] [PubMed]
- Yousef, S.; Visco, A.; Galtieri, G.; Nocita, D.; Espro, C. Wear behaviour of UHMWPE reinforced by carbon nanofiller and paraffin oil for joint replacement. Mater. Sci. Eng. C 2017, 73, 234–244. [Google Scholar] [CrossRef]
- Alam, F.; Choosri, M.; Gupta, T.K.; Varadarajan, K.M.; Choi, D.; Kumar, S. Electrical, mechanical and thermal properties of graphene nanoplatelets reinforced UHMWPE nanocomposites. Mater. Sci. Eng. B 2019, 241, 82–91. [Google Scholar] [CrossRef]
- Martínez-Morlanes, M.J.; Pascual, F.J.; Guerin, G.; Puértolas, J.A. Influence of processing conditions on microstructural, mechanical and tribological properties of graphene nanoplatelet reinforced UHMWPE. J. Mech. Behav. Biomed. Mater. 2021, 115, 104248. [Google Scholar] [CrossRef] [PubMed]
- Grinev, V.G.; Krasheninnikov, V.G.; Zabolotnov, A.S.; Ladygina, T.A.; Brevnov, P.N.; Novokshonova, L.A.; Berlin, A.A. The Effect of Filler Type on the Mechanical Properties of Composite Materials Based on Ultra-High-Molecular-Weight Polyethylene. Polym. Sci. Ser. D 2018, 11, 202–208. [Google Scholar] [CrossRef]
- Wang, B.; Li, H.; Li, L.; Chen, P.; Wang, Z.; Gu, Q. Electrostatic adsorption method for preparing electrically conducting ultrahigh molecular weight polyethylene/graphene nanosheets composites with a segregated network. Compos. Sci. Technol. 2013, 89, 180–185. [Google Scholar] [CrossRef]
- Rezvani Ghomi, E.; Esmaeely Neisiany, R.; Nouri Khorasani, S.; Dinari, M.; Ataei, S.; Koochaki, M.S.; Ramakrishna, S. Development of an epoxy self-healing coating through the incorporation of acrylic acid-co-acrylamide copolymeric gel. Prog. Org. Coat. 2020, 149, 105948. [Google Scholar] [CrossRef]
- Ghomi, E.R.; Khorasani, S.N.; Kichi, M.K.; Dinari, M.; Ataei, S.; Enayati, M.H.; Koochaki, M.S.; Neisiany, R.E. Synthesis and characterization of TiO2/acrylic acid-co-2-acrylamido-2-methyl propane sulfonic acid nanogel composite and investigation its self-healing performance in the epoxy coatings. Colloid Polym. Sci. 2020, 298, 213–223. [Google Scholar] [CrossRef]
- Kaminsky, W.; Funck, A.; Klinke, C. In-situ Polymerization of Olefins on Nanoparticles or Fibers by Metallocene Catalysts. Top. Catal. 2008, 48, 84. [Google Scholar] [CrossRef]
- Kaminsky, W.; Funck, A.; Wiemann, K. Nanocomposites by In Situ Polymerization of Olefins with Metallocene Catalysts. Macromol. Symp. 2006, 239, 1–6. [Google Scholar] [CrossRef]
- Thongruang, W.; Balik, C.M.; Spontak, R.J. Volume-exclusion effects in polyethylene blends filled with carbon black, graphite, or carbon fiber. J. Polym. Sci. Part B Polym. Phys. 2002, 40, 1013–1025. [Google Scholar] [CrossRef]
- Zhu, Y.; Murali, S.; Cai, W.; Li, X.; Suk, J.W.; Potts, J.R.; Ruoff, R.S. Graphene and Graphene Oxide: Synthesis, Properties, and Applications. Adv. Mater. 2010, 22, 3906–3924. [Google Scholar] [CrossRef]
- Hu, W.; Zhan, J.; Wang, X.; Hong, N.; Wang, B.; Song, L.; Stec, A.A.; Hull, T.R.; Wang, J.; Hu, Y. Effect of Functionalized Graphene Oxide with Hyper-Branched Flame Retardant on Flammability and Thermal Stability of Cross-Linked Polyethylene. Ind. Eng. Chem. Res. 2014, 53, 3073–3083. [Google Scholar] [CrossRef]
- Khosravi, F.; Nouri Khorasani, S.; Khalili, S.; Esmaeely Neisiany, R.; Rezvani Ghomi, E.; Ejeian, F.; Das, O.; Nasr-Esfahani, M.H. Development of a Highly Proliferated Bilayer Coating on 316L Stainless Steel Implants. Polymers 2020, 12, 1022. [Google Scholar] [CrossRef] [PubMed]
- Das, O.; Hedenqvist, M.S.; Johansson, E.; Olsson, R.T.; Loho, T.A.; Capezza, A.J.; Singh Raman, R.K.; Holder, S. An all-gluten biocomposite: Comparisons with carbon black and pine char composites. Compos. Part A Appl. Sci. Manuf. 2019, 120, 42–48. [Google Scholar] [CrossRef]
- Das, O.; Loho, T.A.; Capezza, A.J.; Lemrhari, I.; Hedenqvist, M.S. A Novel Way of Adhering PET onto Protein (Wheat Gluten) Plastics to Impart Water Resistance. Coatings 2018, 8, 388. [Google Scholar] [CrossRef] [Green Version]
- Khosravi, F.; Nouri Khorasani, S.; Rezvani Ghomi, E.; Kichi, M.K.; Zilouei, H.; Farhadian, M.; Esmaeely Neisiany, R. A bilayer GO/nanofibrous biocomposite coating to enhance 316L stainless steel corrosion performance. Mater. Res. Express 2019, 6, 086470. [Google Scholar] [CrossRef]
- Shariati, J.; Saadatabadi, A.R.; Khorasheh, F. Thermal Degradation Behavior and Kinetic Analysis of Ultra High Molecular Weight Polyethylene Based Multi-Walled Carbon Nanotube Nanocomposites Prepared Via in-situ Polymerization. J. Macromol. Sci. Part A 2012, 49, 749–757. [Google Scholar] [CrossRef]
- Kuilla, T.; Bhadra, S.; Yao, D.; Kim, N.H.; Bose, S.; Lee, J.H. Recent advances in graphene based polymer composites. Prog. Polym. Sci. 2010, 35, 1350–1375. [Google Scholar] [CrossRef]
- Quan, H.; Zhang, B.-q.; Zhao, Q.; Yuen, R.K.K.; Li, R.K.Y. Facile preparation and thermal degradation studies of graphite nanoplatelets (GNPs) filled thermoplastic polyurethane (TPU) nanocomposites. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1506–1513. [Google Scholar] [CrossRef]
- Vadukumpully, S.; Paul, J.; Mahanta, N.; Valiyaveettil, S. Flexible conductive graphene/poly(vinyl chloride) composite thin films with high mechanical strength and thermal stability. Carbon 2011, 49, 198–205. [Google Scholar] [CrossRef]
- Rezvani Ghomi, E.; Khosravi, F.; Mossayebi, Z.; Saedi Ardahaei, A.; Morshedi Dehaghi, F.; Khorasani, M.; Neisiany, R.E.; Das, O.; Marani, A.; Mensah, R.A.; et al. The Flame Retardancy of Polyethylene Composites: From Fundamental Concepts to Nanocomposites. Molecules 2020, 25, 5157. [Google Scholar] [CrossRef]
- Shakiba, M.; Kakoei, A.; Jafari, I.; Rezvani Ghomi, E.; Kalaee, M.; Zarei, D.; Abdouss, M.; Shafiei-Navid, S.; Khosravi, F.; Ramakrishna, S. Kinetic Modeling and Degradation Study of Liquid Polysulfide Resin-Clay Nanocomposite. Molecules 2021, 26, 635. [Google Scholar] [CrossRef]
- Kim, J.Y.; Park, H.S.; Kim, S.H. Multiwall-carbon-nanotube-reinforced poly(ethylene terephthalate) nanocomposites by melt compounding. J. Appl. Polym. Sci. 2007, 103, 1450–1457. [Google Scholar] [CrossRef]
- Stürzel, M.; Thomann, Y.; Enders, M.; Mülhaupt, R. Graphene-Supported Dual-Site Catalysts for Preparing Self-Reinforcing Polyethylene Reactor Blends Containing UHMWPE Nanoplatelets and in Situ UHMWPE Shish-Kebab Nanofibers. Macromolecules 2014, 47, 4979–4986. [Google Scholar] [CrossRef]
- Nikkhah, S.J.; Ramazani, S.A.; Baniasadi, H.; Tavakolzadeh, F. Investigation of properties of polyethylene/clay nanocomposites prepared by new in situ Ziegler–Natta catalyst. Mater. Des. 2009, 30, 2309–2315. [Google Scholar] [CrossRef]
- Chrissafis, K.; Bikiaris, D. Can nanoparticles really enhance thermal stability of polymers? Part I: An overview on thermal decomposition of addition polymers. Thermochim. Acta 2011, 523, 1–24. [Google Scholar] [CrossRef]
- Shafiee, M.; Ramazani, S.A. Preparation and Characterization of UHMWPE/Graphene Nanocomposites Using Bi-Supported Ziegler-Natta Polymerization. Int. J. Polym. Mater. Polym. Biomater. 2014, 63, 815–819. [Google Scholar] [CrossRef]
- Shakiba, M.; Nabavi, S.R.; Emadi, H.; Faraji, M. Development of a superhydrophilic nanofiber membrane for oil/water emulsion separation via modification of polyacrylonitrile/polyaniline composite. Polym. Adv. Technol. 2021, 32, 1301–1316. [Google Scholar] [CrossRef]
- Zaaba, N.I.; Foo, K.L.; Hashim, U.; Tan, S.J.; Liu, W.-W.; Voon, C.H. Synthesis of Graphene Oxide using Modified Hummers Method: Solvent Influence. Procedia Eng. 2017, 184, 469–477. [Google Scholar] [CrossRef]
- Chrissafis, K.; Paraskevopoulos, K.M.; Tsiaoussis, I.; Bikiaris, D. Comparative study of the effect of different nanoparticles on the mechanical properties, permeability, and thermal degradation mechanism of HDPE. J. Appl. Polym. Sci. 2009, 114, 1606–1618. [Google Scholar] [CrossRef]
- Chrissafis, K. Kinetics of thermal degradation of polymers. J. Therm. Anal. Calorim. 2009, 95, 273–283. [Google Scholar] [CrossRef]
- Mittal, V.; Luckachan, G.E.; Matsko, N.B. PE/Chlorinated-PE Blends and PE/Chlorinated-PE/Graphene Oxide Nanocomposites: Morphology, Phase Miscibility, and Interfacial Interactions. Macromol. Chem. Phys. 2014, 215, 255–268. [Google Scholar] [CrossRef]
- Haddadi, S.A.; Saadatabadi, A.R.; Kheradmand, A.; Amini, M.; Ramezanzadeh, M. SiO2-covered graphene oxide nanohybrids for in situ preparation of UHMWPE/GO(SiO2) nanocomposites with superior mechanical and tribological properties. J. Appl. Polym. Sci. 2019, 136, 47796. [Google Scholar] [CrossRef]
- Das, O.; Kim, N.K.; Hedenqvist, M.S.; Lin, R.J.T.; Sarmah, A.K.; Bhattacharyya, D. An Attempt to Find a Suitable Biomass for Biochar-Based Polypropylene Biocomposites. Environ. Manag. 2018, 62, 403–413. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, K.; Liu, M.; Song, C.; Shen, L.; Chen, P.; Xu, S. Surface-conductive UHMWPE fibres via in situ reduction and deposition of graphene oxide. Mater. Des. 2018, 148, 167–176. [Google Scholar] [CrossRef]
- Sun, T.; Luo, W.; Luo, Y.; Wang, Y.; Zhou, S.; Liang, M.; Chen, Y.; Zou, H. Self-Reinforced Polypropylene/Graphene Composite with Segregated Structures To Achieve Balanced Electrical and Mechanical Properties. Ind. Eng. Chem. Res. 2020, 59, 11206–11218. [Google Scholar] [CrossRef]
- Das, O.; Sarmah, A.K. Value added liquid products from waste biomass pyrolysis using pretreatments. Sci. Total Environ. 2015, 538, 145–151. [Google Scholar] [CrossRef]
- Chrissafis, K.; Paraskevopoulos, K.M.; Pavlidou, E.; Bikiaris, D. Thermal degradation mechanism of HDPE nanocomposites containing fumed silica nanoparticles. Thermochim. Acta 2009, 485, 65–71. [Google Scholar] [CrossRef]
- Lomakin, S.M.; Dubnikova, I.L.; Shchegolikhin, A.N.; Zaikov, G.E.; Kozlowski, R.; Kim, G.M.; Michler, G.H. Thermal degradation and combustion behavior of the polyethylene/clay nanocomposite prepared by melt intercalation. J. Therm. Anal. Calorim. 2008, 94, 719–726. [Google Scholar] [CrossRef]
- Tan, L.; Xu, J.; Zhang, X.; Hang, Z.; Jia, Y.; Wang, S. Synthesis of g-C3N4/CeO2 nanocomposites with improved catalytic activity on the thermal decomposition of ammonium perchlorate. Appl. Surf. Sci. 2015, 356, 447–453. [Google Scholar] [CrossRef]
- Farjas, J.; Roura, P. Isoconversional analysis of solid state transformations. J. Therm. Anal. Calorim. J. Anal. Calorim 2011, 105, 757–766. [Google Scholar] [CrossRef]
- Antoniadis, G.; Paraskevopoulos, K.M.; Bikiaris, D.; Chrissafis, K. Melt-crystallization mechanism of poly(ethylene terephthalate)/multi-walled carbon nanotubes prepared by in situ polymerization. J. Polym. Sci. Part B Polym. Phys. 2009, 47, 1452–1466. [Google Scholar] [CrossRef]
- Ozawa, T. Thermal analysis—review and prospect. Thermochim. Acta 2000, 355, 35–42. [Google Scholar] [CrossRef]
- Doyle, C.D. Kinetic analysis of thermogravimetric data. J. Appl. Polym. Sci. 1961, 5, 285–292. [Google Scholar] [CrossRef]
- Opfermann, J.R.; Kaisersberger, E.; Flammersheim, H.J. Model-free analysis of thermoanalytical data-advantages and limitations. Thermochim. Acta 2002, 391, 119–127. [Google Scholar] [CrossRef]
- Król-Morkisz, K.; Pielichowska, K. 13-Thermal Decomposition of Polymer Nanocomposites With Functionalized Nanoparticles. In Polymer Composites with Functionalized Nanoparticles; Pielichowski, K., Majka, T.M., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 405–435. [Google Scholar]
- Friedman, H.L. New methods for evaluating kinetic parameters from thermal analysis data. J. Polym. Sci. Part B Polym. Lett. 1969, 7, 41–46. [Google Scholar] [CrossRef]
- Fernandez, A.; Mazza, G.; Rodriguez, R. Thermal decomposition under oxidative atmosphere of lignocellulosic wastes: Different kinetic methods application. J. Environ. Chem. Eng. 2018, 6, 404–415. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction Kinetics in Differential Thermal Analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Starink, M.J. The determination of activation energy from linear heating rate experiments: A comparison of the accuracy of isoconversion methods. Thermochim. Acta 2003, 404, 163–176. [Google Scholar] [CrossRef] [Green Version]
- Boswell, P.G. On the calculation of activation energies using a modified Kissinger method. J. Therm. Anal. Calorim. 1980, 18, 353–358. [Google Scholar] [CrossRef]
- Ray, S.; Cooney, R.P. Chapter 9—Thermal Degradation of Polymer and Polymer Composites. In Handbook of Environmental Degradation of Materials (Third Edition); Kutz, M., Ed.; William Andrew Publishing: Amsterdam, The Netherlands, 2018; pp. 185–206. [Google Scholar]
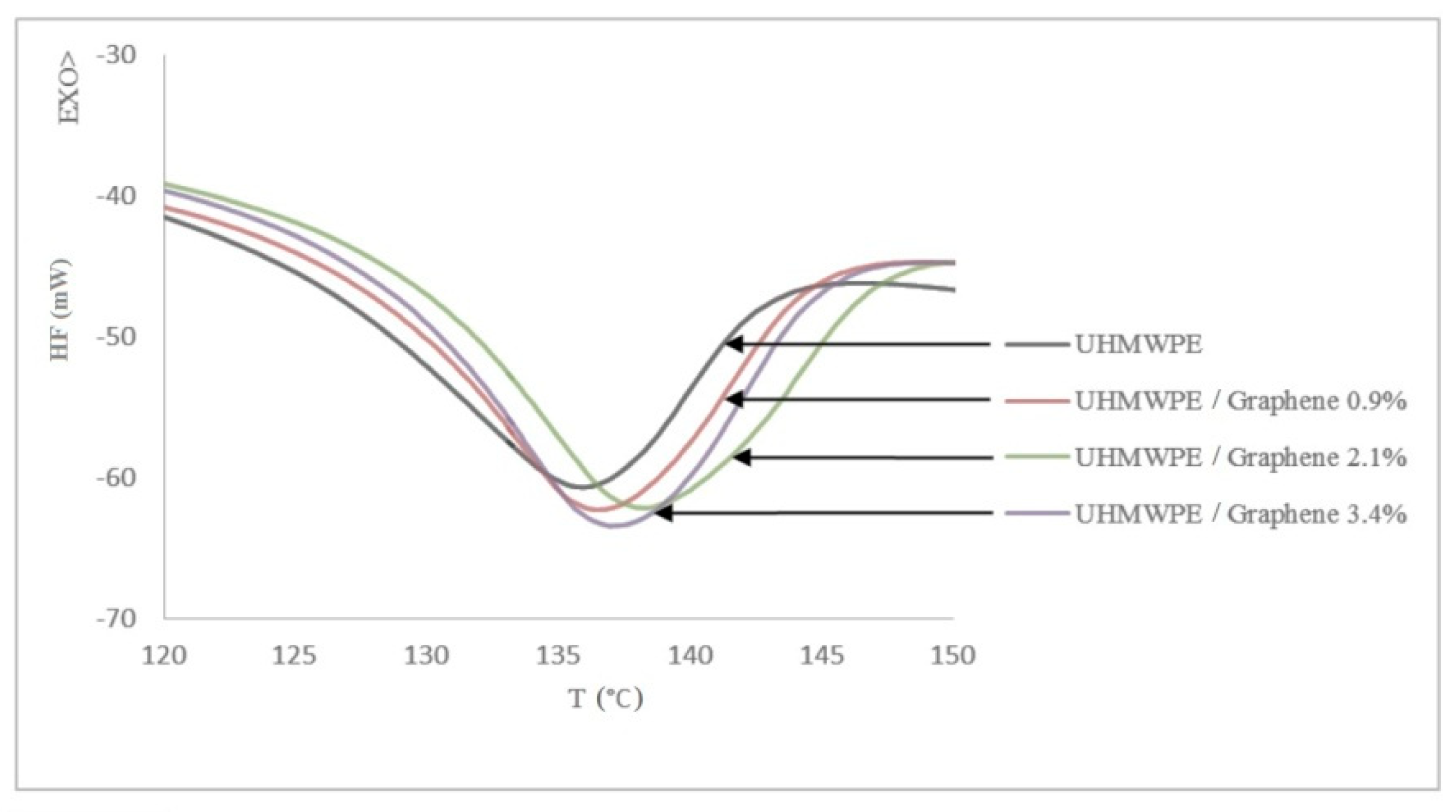

| Sample | DHf (J/g) | Tm (°C) |
|---|---|---|
| UHMWPE | 123.06 (± 0.30) | 137 (± 0.33) |
| UHMWPE/graphene 0.9 wt% | 152.31 (± 0.35) | 140 (± 0.32) |
| UHMWPE/graphene 2.1 wt% | 156.95 (± 0.38) | 142 (± 0.46) |
| UHMWPE/graphene 3.4 wt% | 153.03 (± 0.51) | 140 (± 0.38) |
| Sample | T0.1 (˚C) | T0.5 (˚C) | Tm (˚C) | Ash Content (%) |
|---|---|---|---|---|
| UHMWPE | 438.3 (± 1.16) | 459.9 (± 1.10) | 464.1 (± 1.11) | 0.6 (± 0.001) |
| UHMWPE/graphene 0.9 wt% | 437.4 (± 1.00) | 468.8 (± 1.08) | 473.6 (± 1.09) | 2.7 (± 0.006) |
| UHMWPE/graphene 2.1 wt% | 446.3 (± 0.80) | 471.1 (± 0.85) | 475.2 (± 0.86) | 3.5 (± 0.006) |
| UHMWPE/graphene 3.4 wt% | 453.8 (± 0.27) | 475.7 (± 0.28) | 479.2 (± 0.29) | 4.6 (± 0.002) |
| Sample | LogA | LogKcat | N | E (kJ/mol) |
|---|---|---|---|---|
| UHMWPE | 13.98 | 0.74 | 1.63 | 221.2 |
| UHMWPE/graphene 0.9 wt% | 14.23 | 0.82 | 1.82 | 249.3 |
| UHMWPE/graphene 2.1 wt% | 14.68 | 0.63 | 1.73 | 271.4 |
| UHMWPE/graphene 3.4 wt% | 14.43 | 0.31 | 1.75 | 262.7 |
| Friedman | OFW | Kissinger | A and B | |
|---|---|---|---|---|
| Sample | Ea (kJ/mol) | Ea (kJ/mol) | Ea (kJ/mol) | Ea (kJ/mol) |
| UHMWPE | 222.7 | 228.8 | 224.4 | 218.3 |
| UHMWPE/graphene 0.9 wt.% | 262.9 | 269.1 | 252.5 | 248.6 |
| UHMWPE/graphene 2.1 wt.% | 262.7 | 268.9 | 274.6 | 269.2 |
| UHMWPE/graphene 3.4 wt.% | 216.1 | 222.7 | 264.5 | 256.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jafari, I.; Shakiba, M.; Khosravi, F.; Ramakrishna, S.; Abasi, E.; Teo, Y.S.; Kalaee, M.; Abdouss, M.; Ramazani S. A, A.; Moradi, O.; et al. Thermal Degradation Kinetics and Modeling Study of Ultra High Molecular Weight Polyethylene (UHMWP)/Graphene Nanocomposite. Molecules 2021, 26, 1597. https://doi.org/10.3390/molecules26061597
Jafari I, Shakiba M, Khosravi F, Ramakrishna S, Abasi E, Teo YS, Kalaee M, Abdouss M, Ramazani S. A A, Moradi O, et al. Thermal Degradation Kinetics and Modeling Study of Ultra High Molecular Weight Polyethylene (UHMWP)/Graphene Nanocomposite. Molecules. 2021; 26(6):1597. https://doi.org/10.3390/molecules26061597
Chicago/Turabian StyleJafari, Iman, Mohamadreza Shakiba, Fatemeh Khosravi, Seeram Ramakrishna, Ehsan Abasi, Ying Shen Teo, Mohammadreza Kalaee, Majid Abdouss, Ahmad Ramazani S. A, Omid Moradi, and et al. 2021. "Thermal Degradation Kinetics and Modeling Study of Ultra High Molecular Weight Polyethylene (UHMWP)/Graphene Nanocomposite" Molecules 26, no. 6: 1597. https://doi.org/10.3390/molecules26061597
APA StyleJafari, I., Shakiba, M., Khosravi, F., Ramakrishna, S., Abasi, E., Teo, Y. S., Kalaee, M., Abdouss, M., Ramazani S. A, A., Moradi, O., & Rezvani Ghomi, E. (2021). Thermal Degradation Kinetics and Modeling Study of Ultra High Molecular Weight Polyethylene (UHMWP)/Graphene Nanocomposite. Molecules, 26(6), 1597. https://doi.org/10.3390/molecules26061597









