Isomorph Invariance of Higher-Order Structural Measures in Four Lennard–Jones Systems
Abstract
1. Introduction
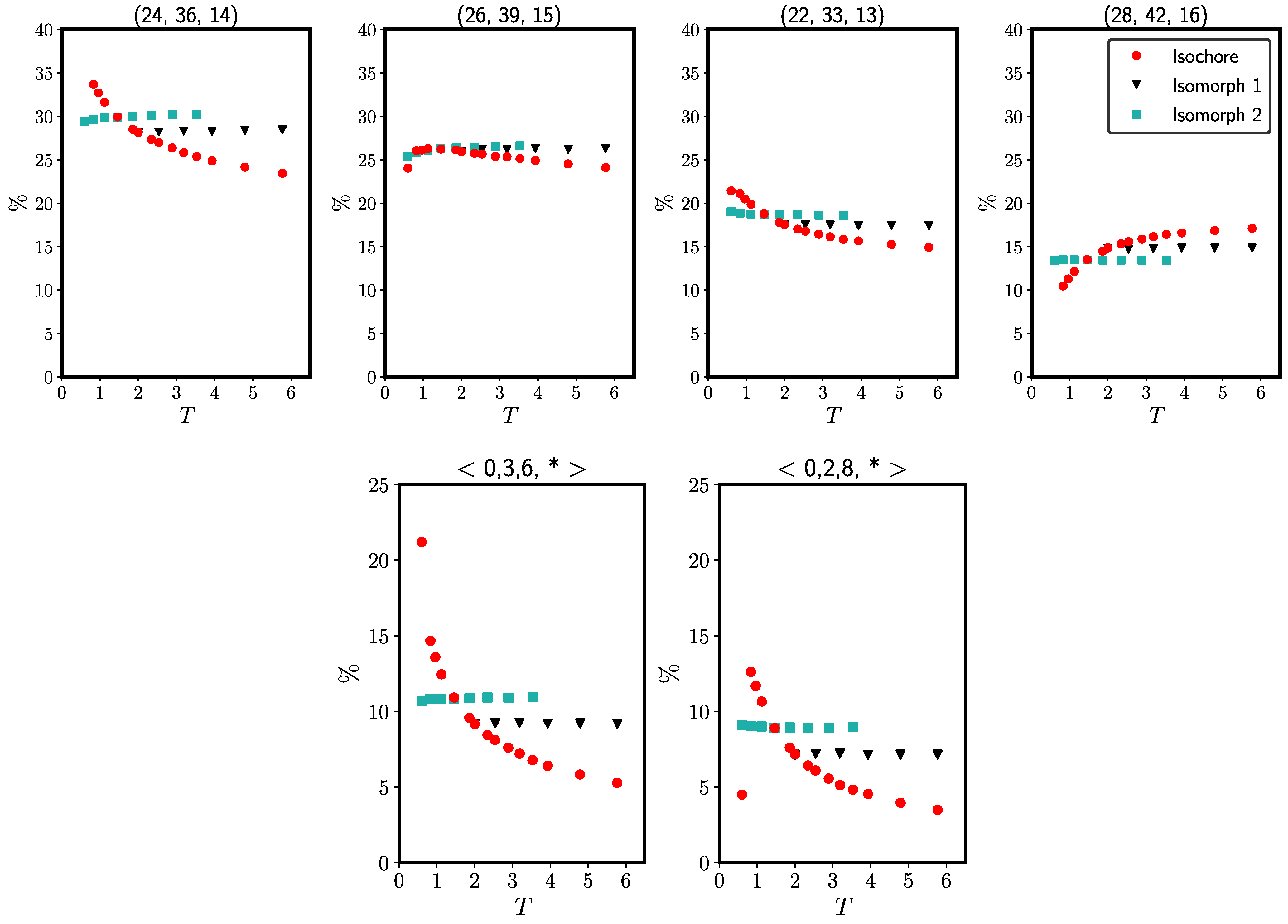
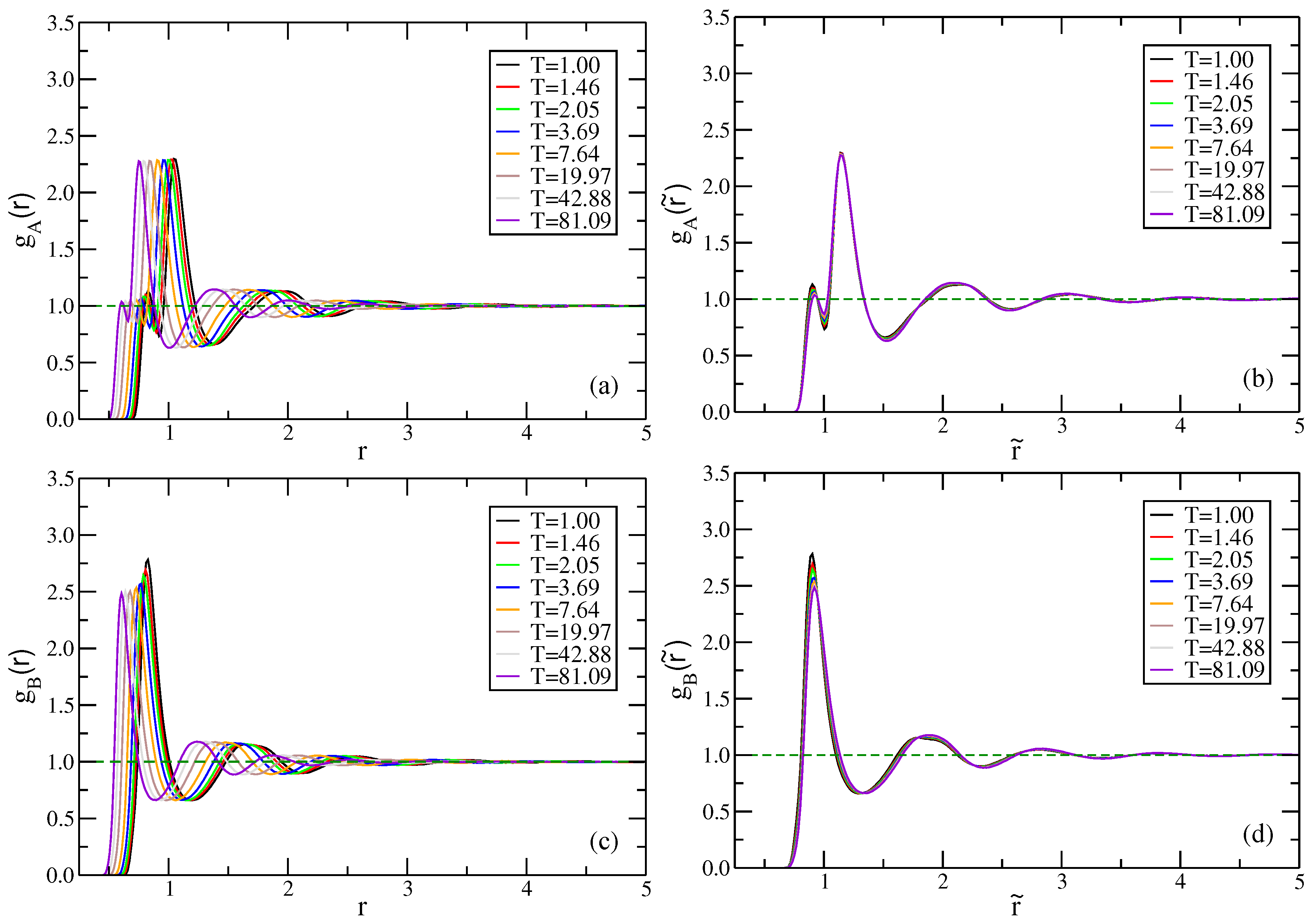
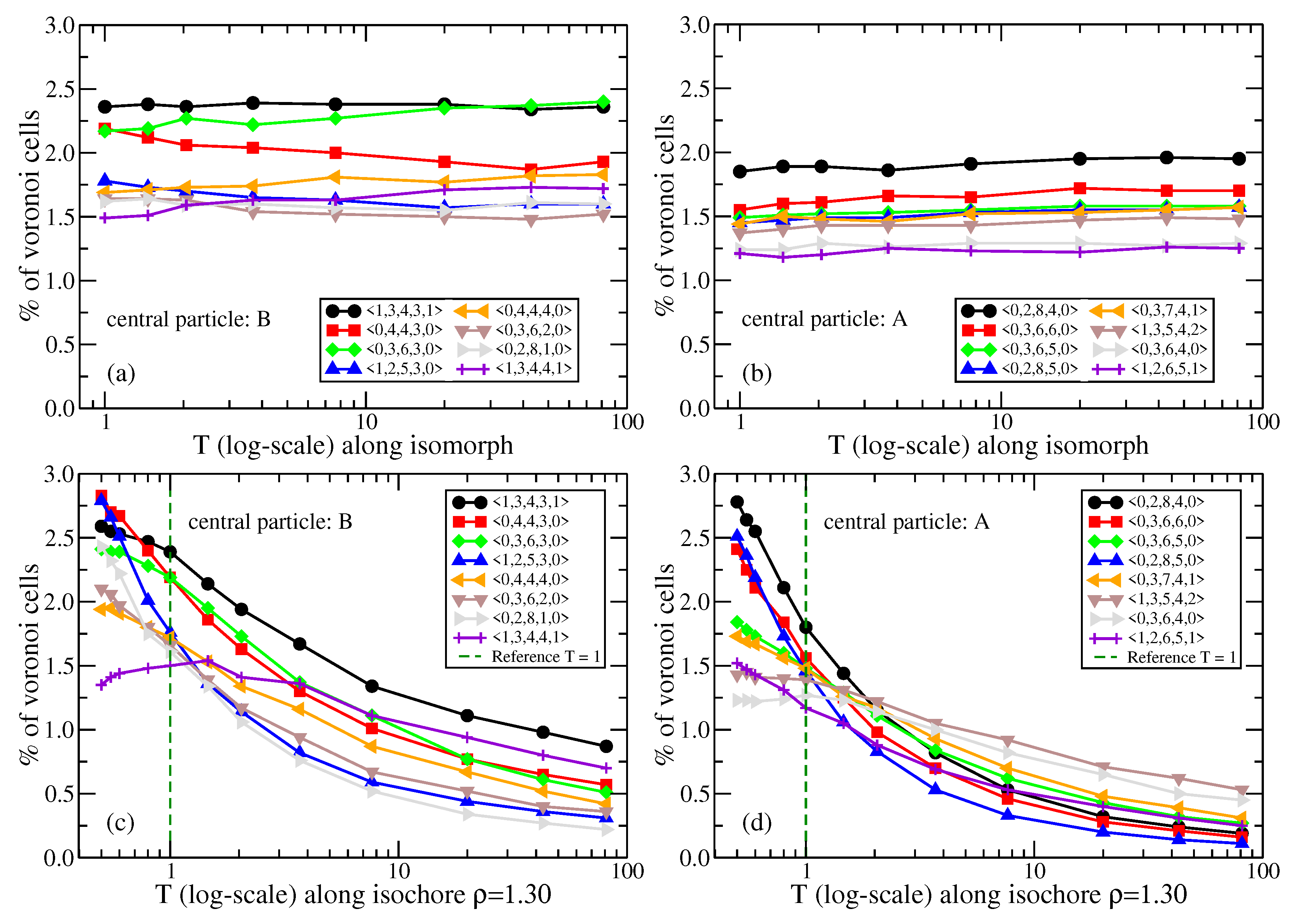
2. Results and Discussion
2.1. Standard Lennard–Jones System
2.2. Binary Lennard–Jones Mixtures
2.2.1. Wahnström Mixture
2.2.2. Kob–Andersen Mixture
2.2.3. Mixture
3. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Isomorph State-Point Data
| T | R | ||
|---|---|---|---|
| 1.000 | 2.000 | 0.994 | 5.021 |
| 1.050 | 2.545 | 0.995 | 4.881 |
| 1.100 | 3.186 | 0.997 | 4.768 |
| 1.150 | 3.930 | 0.997 | 4.676 |
| 1.200 | 4.788 | 0.998 | 4.608 |
| 1.250 | 5.772 | 0.998 | 4.544 |
| 0.850 | 0.600 | 0.956 | 5.895 |
| 0.900 | 0.832 | 0.979 | 5.564 |
| 0.950 | 1.116 | 0.987 | 5.293 |
| 1.000 | 1.458 | 0.993 | 5.114 |
| 1.050 | 1.864 | 0.995 | 4.957 |
| 1.100 | 2.340 | 0.996 | 4.827 |
| 1.150 | 2.894 | 0.997 | 4.733 |
| 1.200 | 3.534 | 0.998 | 4.653 |
| T | R | ||
|---|---|---|---|
| 0.75 | 0.646 | 0.982 | 5.050 |
| 0.80 | 0.893 | 0.990 | 4.911 |
| 0.85 | 1.200 | 0.994 | 4.785 |
| 0.90 | 1.572 | 0.996 | 4.681 |
| 0.95 | 2.018 | 0.997 | 4.596 |
| 1.00 | 2.549 | 0.998 | 4.525 |
| 1.50 | 14.738 | 0.999 | 4.205 |
| 2.00 | 48.610 | 0.999 | 4.110 |
| 0.65 | 0.493 | 0.936 | 5.600 |
| 0.70 | 0.748 | 0.977 | 5.364 |
| 0.75 | 1.076 | 0.988 | 5.106 |
| 0.80 | 1.489 | 0.993 | 4.912 |
| 0.85 | 2.000 | 0.995 | 4.772 |
| 0.90 | 2.620 | 0.997 | 4.659 |
| 0.95 | 3.364 | 0.998 | 4.573 |
| 1.00 | 4.248 | 0.998 | 4.505 |
| 1.50 | 24.564 | 0.999 | 4.197 |
| 2.00 | 81.016 | 0.999 | 4.105 |
| 2.50 | 201.615 | 0.999 | 4.066 |
| T | R | ||
|---|---|---|---|
| 1.200 | 0.500 | 0.939 | 5.158 |
| 1.403 | 1.091 | 0.983 | 4.784 |
| 1.607 | 2.058 | 0.993 | 4.568 |
| 1.810 | 3.520 | 0.997 | 4.424 |
| 2.001 | 5.461 | 0.998 | 4.339 |
| 1.200 | 0.750 | 0.958 | 5.149 |
| 1.400 | 1.601 | 0.988 | 4.774 |
| 1.600 | 2.966 | 0.995 | 4.552 |
| 1.800 | 5.009 | 0.997 | 4.415 |
| 2.000 | 7.916 | 0.999 | 4.324 |
| 1.200 | 1.000 | 0.968 | 5.111 |
| 1.400 | 2.126 | 0.990 | 4.743 |
| 1.600 | 3.929 | 0.996 | 4.530 |
| 1.800 | 6.625 | 0.998 | 4.399 |
| 2.000 | 10.459 | 0.999 | 4.311 |
| 1.200 | 1.200 | 0.973 | 5.081 |
| 1.400 | 2.542 | 0.992 | 4.721 |
| 1.600 | 4.689 | 0.996 | 4.514 |
| 1.800 | 7.897 | 0.998 | 4.387 |
| 2.000 | 12.459 | 0.999 | 4.303 |
References
- Bernal, J.D. The Bakerian Lecture, 1962. The Structure of Liquids. Proc. R. Soc. Lond. Ser. A 1964, 280, 299–322. [Google Scholar]
- Wong, J.; Angell, C.A. Glass Structure by Spectroscopy; Marcel Dekker: New York, NY, USA, 1976. [Google Scholar]
- Elliott, S.R. Medium-range structural order in covalent amorphous solids. Nature 1991, 354, 445–452. [Google Scholar] [CrossRef]
- Gutzow, I.; Schmelzer, J. The Vitreous State: Thermodynamics, Structure, Rheology, and Crystallization; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Debenedetti, P.G. Structure, Dynamics and Thermodynamics in Complex Systems: Theoretical Challenges and Opportunities. AICHE J. 2005, 51, 2391–2395. [Google Scholar] [CrossRef]
- Cheng, Y.Q.; Ma, E. Atomic-level structure and structure—Property relationship in metallic glasses. Prog. Mater. Sci. 2011, 56, 379–473. [Google Scholar] [CrossRef]
- Coslovich, D. Locally preferred structures and many-body static correlations in viscous liquids. Phys. Rev. E 2011, 83, 051505. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, A.; Sengupta, S.; Sastry, S.; Bhattacharyya, S.M. Role of Structure and Entropy in Determining Differences in Dynamics for Glass Formers with Different Interaction Potentials. Phys. Rev. Lett. 2014, 113, 225701. [Google Scholar] [CrossRef]
- Böhmer, R.; Gainaru, C.; Richert, R. Structure and dynamics of monohydroxy alcohols—Milestones towards their microscopic understanding, 100 years after Debye. Phys. Rep. 2014, 545, 125–195. [Google Scholar] [CrossRef]
- Royall, C.P.; Williams, S.R. The role of local structure in dynamical arrest. Phys. Rep. 2015, 560, 1–75. [Google Scholar] [CrossRef]
- Cubuk, E.D.; Ivancic, R.J.S.; Schoenholz, S.S.; Strickland, D.J.; Basu, A.; Davidson, Z.S.; Fontaine, J.; Hor, J.L.; Huang, Y.R.; Jiang, Y.; et al. Structure-property relationships from universal signatures of plasticity in disordered solids. Science 2017, 358, 1033–1037. [Google Scholar] [CrossRef] [PubMed]
- Gangopadhyay, A.; Kelton, K. Recent progress in understanding high temperature dynamical properties and fragility in metallic liquids, and their connection with atomic structure. J. Mater. Res. 2017, 32, 2638–2657. [Google Scholar] [CrossRef]
- Wei, D.; Yang, J.; Jiang, M.Q.; Dai, L.H.; Wang, Y.J.; Dyre, J.C.; Douglass, I.; Harrowell, P. Assessing the utility of structure in amorphous materials. J. Chem. Phys. 2019, 150, 114502. [Google Scholar] [CrossRef]
- Dyre, J.C. The Glass Transition and Elastic Models of Glass-Forming Liquids. Rev. Mod. Phys. 2006, 78, 953–972. [Google Scholar] [CrossRef]
- Dyre, J.C. Master-equation approach to the glass transition. Phys. Rev. Lett. 1987, 58, 792–795. [Google Scholar] [CrossRef] [PubMed]
- Schrøder, T.B.; Dyre, J.C. Simplicity of condensed matter at its core: Generic definition of a Roskilde-simple system. J. Chem. Phys. 2014, 141, 204502. [Google Scholar] [CrossRef]
- Dyre, J.C. Simple liquids’ quasiuniversality and the hard-sphere paradigm. J. Phys. Condens. Matter 2016, 28, 323001. [Google Scholar] [CrossRef] [PubMed]
- Dyre, J.C. Perspective: Excess-entropy scaling. J. Chem. Phys. 2018, 149, 210901. [Google Scholar] [CrossRef]
- Dyre, J.C. Isomorph theory beyond thermal equilibrium. J. Chem. Phys. 2020, 153, 134502. [Google Scholar] [CrossRef]
- Gnan, N.; Schrøder, T.B.; Pedersen, U.R.; Bailey, N.P.; Dyre, J.C. Pressure-energy correlations in liquids. IV. “Isomorphs” in liquid phase diagrams. J. Chem. Phys. 2009, 131, 234504. [Google Scholar] [CrossRef] [PubMed]
- Ingebrigtsen, T.S.; Schrøder, T.B.; Dyre, J.C. Isomorphs in Model Molecular Liquids. J. Phys. Chem. B 2012, 116, 1018–1034. [Google Scholar] [CrossRef]
- Dyre, J.C. Hidden scale envariance in condensed matter. J. Phys. Chem. B 2014, 118, 10007–10024. [Google Scholar] [CrossRef]
- Hummel, F.; Kresse, G.; Dyre, J.C.; Pedersen, U.R. Hidden scale invariance of metals. Phys. Rev. B 2015, 92, 174116. [Google Scholar] [CrossRef]
- Costigliola, L.; Pedersen, U.R.; Heyes, D.; Schrøder, T.B.; Dyre, J.C. Communication: Simple liquids’ high-density viscosity. J. Chem. Phys. 2018, 148, 081101. [Google Scholar] [CrossRef]
- Rosenfeld, Y. Relation between the transport coefficients and the internal entropy of simple systems. Phys. Rev. A 1977, 15, 2545–2549. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford Science Publications: Oxford, UK, 1987. [Google Scholar]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids: With Applications to Soft Matter, 4th ed.; Academic Press: New York, NY, USA, 2013. [Google Scholar]
- Bailey, N.P.; Pedersen, U.R.; Gnan, N.; Schrøder, T.B.; Dyre, J.C. Pressure-energy correlations in liquids. I. Results from computer simulations. J. Chem. Phys. 2008, 129, 184507. [Google Scholar] [CrossRef] [PubMed]
- Ingebrigtsen, T.S.; Schrøder, T.B.; Dyre, J.C. What is a simple liquid? Phys. Rev. X 2012, 2, 011011. [Google Scholar] [CrossRef]
- Schrøder, T.B.; Gnan, N.; Pedersen, U.R.; Bailey, N.P.; Dyre, J.C. Pressure-energy correlations in liquids. V. Isomorphs in generalized Lennard–Jones systems. J. Chem. Phys. 2011, 134, 164505. [Google Scholar] [CrossRef] [PubMed]
- Albrechtsen, D.E.; Olsen, A.E.; Pedersen, U.R.; Schrøder, T.B.; Dyre, J.C. Isomorph Invariance of the Structure and Dynamics of Classical Crystals. Phys. Rev. B 2014, 90, 094106. [Google Scholar] [CrossRef]
- Costigliola, L.; Schrøder, T.B.; Dyre, J.C. Freezing and melting line invariants of the Lennard–Jones system. Phys. Chem. Chem. Phys. 2016, 18, 14678–14690. [Google Scholar] [CrossRef]
- Bacher, A.K.; Schrøder, T.B.; Dyre, J.C. The EXP pair-potential system. II. Fluid phase isomorphs. J. Chem. Phys. 2018, 149, 114502. [Google Scholar] [CrossRef]
- Friedeheim, L.; Dyre, J.C.; Bailey, N.P. Hidden scale invariance at high pressures in gold and five other face-centered-cubic metal crystals. Phys. Rev. E 2019, 99, 022142. [Google Scholar] [CrossRef]
- Pedersen, U.R.; Bacher, A.K.; Schrøder, T.B.; Dyre, J.C. The EXP pair-potential system. III. Thermodynamic phase diagram. J. Chem. Phys. 2019, 150, 174501. [Google Scholar] [CrossRef]
- Tolias, P.; Castello, F.L. Isomorph-based empirically modified hypernetted-chain approach for strongly coupled Yukawa one-component plasmas. Phys. Plasmas 2019, 26, 043703. [Google Scholar] [CrossRef]
- Saw, S.; Dyre, J.C. Structure of the Lennard–Jones liquid estimated from a single simulation. Phys. Rev. E 2021, 103, 012110. [Google Scholar] [CrossRef] [PubMed]
- Ingebrigtsen, T.S.; Tanaka, H. Effect of size polydispersity on the nature of Lennard–Jones liquids. J. Phys. Chem. B 2015, 119, 11052–11062. [Google Scholar] [CrossRef]
- Ingebrigtsen, T.S.; Tanaka, H. Effect of energy polydispersity on the nature of Lennard–Jones liquids. J. Phys. Chem. B 2016, 120, 7704–7713. [Google Scholar] [CrossRef] [PubMed]
- Malins, A.; Eggers, J.; Royall, C.P. Investigating Isomorphs with the Topological Cluster Classification. J. Chem. Phys. 2013, 139, 234505. [Google Scholar] [CrossRef]
- Kob, W.; Andersen, H.C. Testing mode-coupling theory for a supercooled binary Lennard–Jones mixture I: The van Hove correlation function. Phys. Rev. E 1995, 51, 4626–4641. [Google Scholar] [CrossRef]
- Lennard–Jones, J.E. On the determination of molecular fields. I. From the variation of the viscosity of a gas with temperature. Proc. R. Soc. Lond. A 1924, 106, 441–462. [Google Scholar]
- Bailey, N.P.; Ingebrigtsen, T.S.; Hansen, J.S.; Veldhorst, A.A.; Bøhling, L.; Lemarchand, C.A.; Olsen, A.E.; Bacher, A.K.; Costigliola, L.; Pedersen, U.R.; et al. RUMD: A general purpose molecular dynamics package optimized to utilize GPU hardware down to a few thousand particles. Scipost Phys. 2017, 3, 038. [Google Scholar] [CrossRef]
- Rycroft, C.H.; Grest, G.S.; Landry, J.; Bazant, M.Z. Analysis of granular flow in a pebble-bed nuclear reactor. Phys. Rev. E 2006, 74, 021306. [Google Scholar] [CrossRef]
- Rycroft, C.H. Voro++: A three-dimensional Voronoi cell library in C++. Chaos 2009, 19, 041111. [Google Scholar] [CrossRef] [PubMed]
- Wahnström, G. Molecular-dynamics study of a supercooled two-component Lennard–Jones system. Phys. Rev. A 1991, 44, 3752. [Google Scholar] [CrossRef] [PubMed]
- Bøhling, L.; Ingebrigtsen, T.S.; Grzybowski, A.; Paluch, M.; Dyre, J.C.; Schrøder, T.B. Scaling of viscous dynamics in simple liquids: Theory, simulation and experiment. New J. Phys. 2012, 14, 113035. [Google Scholar] [CrossRef]
- Ingebrigtsen, T.S.; Bøhling, L.; Schrøder, T.B.; Dyre, J.C. Thermodynamics of Condensed Matter with Strong Pressure-Energy Correlations. J. Chem. Phys. 2012, 136, 061102. [Google Scholar] [CrossRef]
- Costigliola, L.; Heyes, D.M.; Schrøder, T.B.; Dyre, J.C. Revisiting the Stokes–Einstein relation without a hydrodynamic diameter. J. Chem. Phys. 2019, 150, 021101. [Google Scholar] [CrossRef]
- Frank, F.C.; Kasper, J.S. Complex alloy structures regarded as sphere packings. I. Definitions and basic principles. Acta Crystallograph. 1958, 11, 184–190. [Google Scholar] [CrossRef]
- Frank, F.C. Supercooling of Liquids. Proc. R. Soc. Lond. A 1952, 215, 43–46. [Google Scholar]
- Pedersen, U.R.; Schrøder, T.B.; Dyre, J.C.; Harrowell, P. Geometry of slow structural fluctuations in a supercooled binary alloy. Phys. Rev. Lett. 2010, 104, 105701. [Google Scholar] [CrossRef]
- Pedersen, U.R.; Douglass, I.; Harrowell, P. How a supercooled liquid borrows structure from the crystal. J. Chem. Phys. 2021, 154, 054503. [Google Scholar] [CrossRef]
- Rahman, A. Liquid Structure and Self-Diffusion. J. Chem. Phys. 1966, 45, 2585–2592. [Google Scholar] [CrossRef]
- Tanemura, M.; Hiwatari, Y.; Matsuda, H.; Ogawa, T.; Ogita, N.; Ueda, A. Geometrical Analysis of Crystallization of the Soft-Core Model. Prog. Theor. Phys. 1977, 58, 1079–1095. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Nelson, D.R.; Ronchetti, M. Bond-orientational order in liquids and glasses. Phys. Rev. B 1983, 28, 784–805. [Google Scholar] [CrossRef]
- Valle, R.G.D.; Gazzillo, D.; Frattini, R.; Pastore, G. Microstructural analysis of simulated Ni33Y67 glass. Phys. Rev. B 1994, 49, 12625–12632. [Google Scholar] [CrossRef]
- Coslovich, D.; Pastore, G. Understanding fragility in supercooled Lennard–Jones mixtures. II. Potential energy surface. J. Chem. Phys. 2007, 127, 124505. [Google Scholar] [CrossRef] [PubMed]
- Toxvaerd, S.; Dyre, J.C. Communication: Shifted forces in molecular dynamics. J. Chem. Phys. 2011, 134, 081102. [Google Scholar] [CrossRef] [PubMed]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.; Carter, B.M.G.D.; Saw, S.; Douglass, I.M.; Costigliola, L.; Ingebrigtsen, T.S.; Schrøder, T.B.; Pedersen, U.R.; Dyre, J.C. Isomorph Invariance of Higher-Order Structural Measures in Four Lennard–Jones Systems. Molecules 2021, 26, 1746. https://doi.org/10.3390/molecules26061746
Rahman M, Carter BMGD, Saw S, Douglass IM, Costigliola L, Ingebrigtsen TS, Schrøder TB, Pedersen UR, Dyre JC. Isomorph Invariance of Higher-Order Structural Measures in Four Lennard–Jones Systems. Molecules. 2021; 26(6):1746. https://doi.org/10.3390/molecules26061746
Chicago/Turabian StyleRahman, Mahajabin, Benjamin M. G. D. Carter, Shibu Saw, Ian M. Douglass, Lorenzo Costigliola, Trond S. Ingebrigtsen, Thomas B. Schrøder, Ulf R. Pedersen, and Jeppe C. Dyre. 2021. "Isomorph Invariance of Higher-Order Structural Measures in Four Lennard–Jones Systems" Molecules 26, no. 6: 1746. https://doi.org/10.3390/molecules26061746
APA StyleRahman, M., Carter, B. M. G. D., Saw, S., Douglass, I. M., Costigliola, L., Ingebrigtsen, T. S., Schrøder, T. B., Pedersen, U. R., & Dyre, J. C. (2021). Isomorph Invariance of Higher-Order Structural Measures in Four Lennard–Jones Systems. Molecules, 26(6), 1746. https://doi.org/10.3390/molecules26061746







