Stochastic Modelling of 13C NMR Spin Relaxation Experiments in Oligosaccharides
Abstract
:1. Introduction
2. Methods
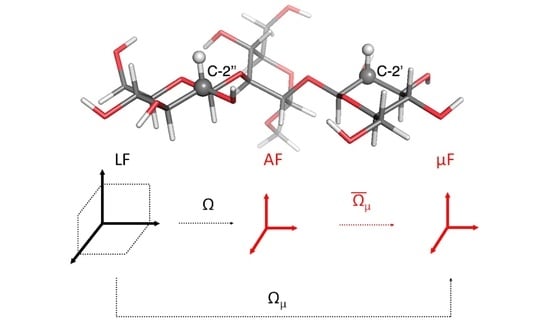
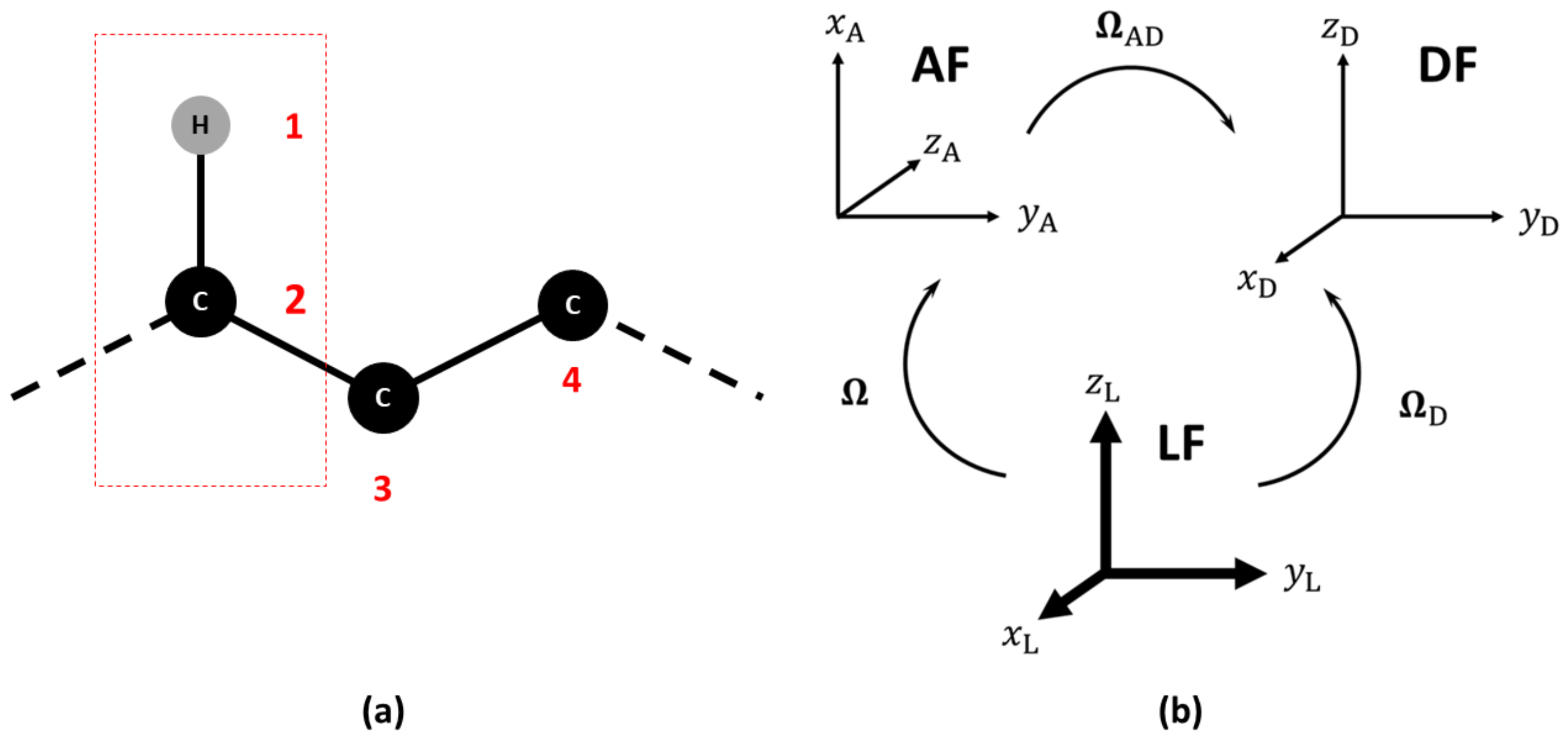
2.1. Observable and Geometric Setup
2.2. Dynamic Model
2.3. Parameterization and Implementation
3. Results
4. Discussion
Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of Relaxation Observables: An Example
References
- Cavanagh, J.; Fairbrother, W.J.; Palmer, I.A.G.; Skelton, N.J.; Rance, M. Protein NMR Spectroscopy: Principles and Practice; Elsevier Science: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Loth, K.; Pelupessy, P.; Bodenhausen, G. Chemical shift anisotropy tensors of carbonyl, nitrogen, and amide proton nuclei in proteins through cross-correlated relaxation in NMR spectroscopy. J. Am. Chem. Soc. 2005, 127, 6062–6068. [Google Scholar] [CrossRef]
- Sheppard, D.; Li, D.W.; Godoy-Ruiz, R.; Brueschweiler, R.; Tugarinov, V. Variation in Quadrupole Couplings of a Deuterons in Ubiquitin Suggests the Presence of C-alpha-H-alpha center dot center dot center dot O=C Hydrogen Bonds. J. Am. Chem. Soc. 2010, 132, 7709–7719. [Google Scholar] [CrossRef] [PubMed]
- Bucci, E.; Steiner, R.F. Anisotropy Decay of Fluorescence as an Experimental Approach to Protein Dynamics. Biophys. Chem. 1988, 30, 199–224. [Google Scholar] [CrossRef]
- Vergani, B.; Kintrup, M.; Hillen, W.; Lami, H.; Piemont, E.; Bombarda, E.; Alberti, P.; Doglia, S.M.; Chabbert, M. Backbone dynamics of Tet repressor alpha 8 boolean AND alpha 9 loop. Biochemistry 2000, 39, 2759–2768. [Google Scholar] [CrossRef] [PubMed]
- Hubbell, W.L.; Mchaourab, H.S.; Altenbach, C.; Lietzow, M.A. Watching proteins move using site-directed spin labeling. Structure 1996, 4, 779–783. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Fleissner, M.R.; Tipikin, D.S.; Liang, Z.; Moscicki, J.K.; Earle, K.A.; Hubbell, W.L.; Freed, J.H. Multifrequency Electron Spin Resonance Study of the Dynamics of Spin Labeled T4 Lysozyme. J. Phys. Chem. B 2010, 114, 5503–5521. [Google Scholar] [CrossRef] [Green Version]
- Hofmann, H.; Hillger, F.; Pfeil, S.H.; Hoffmann, A.; Streich, D.; Haenni, D.; Nettels, D.; Lipman, E.A.; Schuler, B. Single-molecule spectroscopy of protein folding in a chaperonin cage. Proc. Natl. Acad. Sci. USA 2010, 107, 11793–11798. [Google Scholar] [CrossRef] [Green Version]
- Hamon, L.; Pastre, D.; Dupaigne, P.; Breton, C.L.; Cam, E.L.; Pietrement, O. High-resolution AFM imaging of single-stranded DNA-binding (SSB) protein-DNA complexes. Nucleic Acids Res. 2007, 35, e58. [Google Scholar] [CrossRef] [Green Version]
- Kowalewski, J.; Maler, L. Nuclear Spin Relaxation in Liquids: Theory, Experiments, and Applications; Taylor & Francis: Abingdon, UK, 2006. [Google Scholar]
- Lipari, G.; Szabo, A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 1982, 104, 4546–4559. [Google Scholar] [CrossRef]
- Lipari, G.; Szabo, A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 2. Analysis of experimental results. J. Am. Chem. Soc. 1982, 104, 4559–4570. [Google Scholar] [CrossRef]
- Shapiro, Y.E.; Kahana, E.; Tugarinov, V.; Liang, Z.C.; Freed, J.H.; Meirovitch, E. Domain flexibility in ligand-free and inhibitor-bound Escherichia coli adenylate kinase based on a mode-coupling analysis of N-15 spin relaxation. Biochemistry 2002, 41, 6271–6281. [Google Scholar] [CrossRef] [Green Version]
- Meirovitch, E.; Shapiro, Y.E.; Polimeno, A.; Freed, J.H. An improved picture of methyl dynamics in proteins from slowly relaxing local structure analysis of H-2 spin relaxation. J. Phys. Chem. B 2007, 111, 12865–12875. [Google Scholar] [CrossRef] [Green Version]
- Abergel, D.; Bodenhausen, G. Predicting internal protein dynamics from structures using coupled networks of hindered rotators. J. Chem. Phys. 2005, 123, 204901. [Google Scholar] [CrossRef]
- Dhulesia, A.; Bodenhausen, G.; Abergel, D. Predicting conformational entropy of bond vectors in proteins by networks of coupled rotators. J. Chem. Phys. 2008, 129, 095107. [Google Scholar] [CrossRef] [Green Version]
- Calandrini, V.; Abergel, D.; Kneller, G.R. Fractional protein dynamics seen by nuclear magnetic resonance spectroscopy: Relating molecular dynamics simulation and experiment. J. Chem. Phys. 2010, 133, 145101. [Google Scholar] [CrossRef]
- Polimeno, A.; Zerbetto, M.; Abergel, D. Stochastic modelling of macromolecules in solution. I. Relaxation processes. J. Chem. Phys. 2019, 150, 184107. [Google Scholar] [CrossRef]
- Polimeno, A.; Zerbetto, M.; Abergel, D. Stochastic modelling of macromolecules in solution. II. Spectral densities. J. Chem. Phys. 2019, 150, 184108. [Google Scholar] [CrossRef]
- Abragam, A. The Principles of Nuclear Magnetism; Clarendon Press: Oxford, UK, 1961. [Google Scholar]
- Peng, J.W.; Wagner, G. Investigation of Protein Motions via Relaxation Measurements; Methods in Enzymology; Academic Press: Cambridge, MA, USA, 1994; pp. 563–595. [Google Scholar]
- Zare, R. Angular Momentum: Understanding Spatial Aspects in Chemistry and Physics; Wiley: Hoboken, NJ, USA, 1988. [Google Scholar]
- Moro, G.J. A stochastic model for crankshaft transitions. J. Phys. Chem. 1996, 100, 16419–16422. [Google Scholar] [CrossRef]
- Nigro, B.; Moro, G.J. A stochastic model for crankshaft transitions. II. Analysis of transition dynamics. J. Phys. Chem. B 2002, 106, 7365–7375. [Google Scholar] [CrossRef]
- Risken, H. The Fokker-Planck Equation: Methods of Solution and Applications; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Barone, V.; Zerbetto, M.; Polimeno, A. Hydrodynamic Modeling of Diffusion Tensor Properties of Flexible Molecules. J. Comput. Chem. 2009, 30, 2–13. [Google Scholar] [CrossRef]
- Rackers, J.A.; Wang, Z.; Lu, C.; Laury, M.L.; Lagardère, L.; Schnieders, M.J.; Piquemal, J.P.; Ren, P.; Ponder, J.W. Tinker 8: Software Tools for Molecular Design. J. Chem. Theory Comput. 2018, 14, 5273–5289. [Google Scholar] [CrossRef]
- Pendrill, R.; Engstrom, O.; Volpato, A.; Zerbetto, M.; Polimeno, A.; Widmalm, G. Flexibility at a glycosidic linkage revealed by molecular dynamics, stochastic modelling, and 13C NMR spin relaxation: Conformational preferences of α-l-Rhap-α-(1 → 2)-α-l-Rhap-OMe in water and dimethyl sulfoxide solutions. Phys. Chem. Chem. Phys. 2016, 18, 3086–3096. [Google Scholar] [CrossRef] [Green Version]
- Zerbetto, M.; Polimeno, A.; Kotsyubynskyy, D.; Ghalebani, L.; Kowalewski, J.; Meirovitch, E.; Olsson, U.; Widmalm, G. An integrated approach to NMR spin relaxation in flexible biomolecules: Application to β-D-glucopyranosyl-(1→6)-α-D-mannopyranosyl-OMe. J. Chem. Phys. 2009, 131, 234501. [Google Scholar] [CrossRef]
- Zerbetto, M.; Angles d’Ortoli, T.; Polimeno, A.; Widmalm, G. Differential Dynamics at Glycosidic Linkages of an Oligosaccharide as Revealed by 13C NMR Spin Relaxation and Stochastic Modeling. J. Phys. Chem. B 2018, 122, 2287–2294. [Google Scholar] [CrossRef] [Green Version]
- Kotsyubynskyy, D.; Zerbetto, M.; Soltesova, M.; Engström, O.; Pendrill, R.; Kowalewski, J.; Widmalm, G.; Polimeno, A. Stochastic Modeling of Flexible Biomolecules Applied to NMR Relaxation. 2. Interpretation of Complex Dynamics in Linear Oligosaccharides. J. Phys. Chem. B 2012, 116, 14541–14555. [Google Scholar] [CrossRef]
- Zerbetto, M.; Kotsyubynskyy, D.; Kowalewski, J.; Widmalm, G.; Polimeno, A. Stochastic Modeling of Flexible Biomolecules Applied to NMR Relaxation. I. Internal Dynamics of Cyclodextrins: γ-Cyclodextrin as a Case Study. J. Phys. Chem. B 2012, 116, 13159–13171. [Google Scholar] [CrossRef] [PubMed]
- Allinger, N.L.; Yuh, Y.H.; Lii, J.H. Molecular mechanics. The MM3 force field for hydrocarbons. 1. J. Am. Chem. Soc. 1989, 111, 8551–8566. [Google Scholar] [CrossRef]
- Lii, J.H.; Allinger, N.L. Molecular mechanics. The MM3 force field for hydrocarbons. 2. Vibrational frequencies and thermodynamics. J. Am. Chem. Soc. 1989, 111, 8566–8575. [Google Scholar] [CrossRef]
- Lii, J.H.; Allinger, N.L. Molecular mechanics. The MM3 force field for hydrocarbons. 3. The van der Waals’ potentials and crystal data for aliphatic and aromatic hydrocarbons. J. Am. Chem. Soc. 1989, 111, 8576–8582. [Google Scholar] [CrossRef]
- Stroylov, V.; Panova, M.; Toukach, P. Comparison of Methods for Bulk Automated Simulation of Glycosidic Bond Conformations. Int. J. Mol. Sci. 2020, 21, 7626. [Google Scholar] [CrossRef] [PubMed]
- Foley, B.L.; Tessier, M.B.; Woods, R.J. Carbohydrate force fields. WIREs Comput. Mol. Sci. 2012, 2, 652–697. [Google Scholar] [CrossRef] [PubMed]
- Zerbetto, M.; Polimeno, A.; Widmalm, G. Glycosidic linkage flexibility: The Ψ torsion angle has a bimodal distribution in α-L-Rhap-(1→2)-α-L-Rhap-OMe as deduced from 13C NMR spin relaxation. J. Chem. Phys. 2020, 152, 035103. [Google Scholar] [CrossRef]
- Kuprov, I.; Morris, L.C.; Glushka, J.N.; Prestegard, J.H. Using molecular dynamics trajectories to predict nuclear spin relaxation behaviour in large spin systems. J. Magn. Res. 2021, 323, 106891. [Google Scholar] [CrossRef] [PubMed]
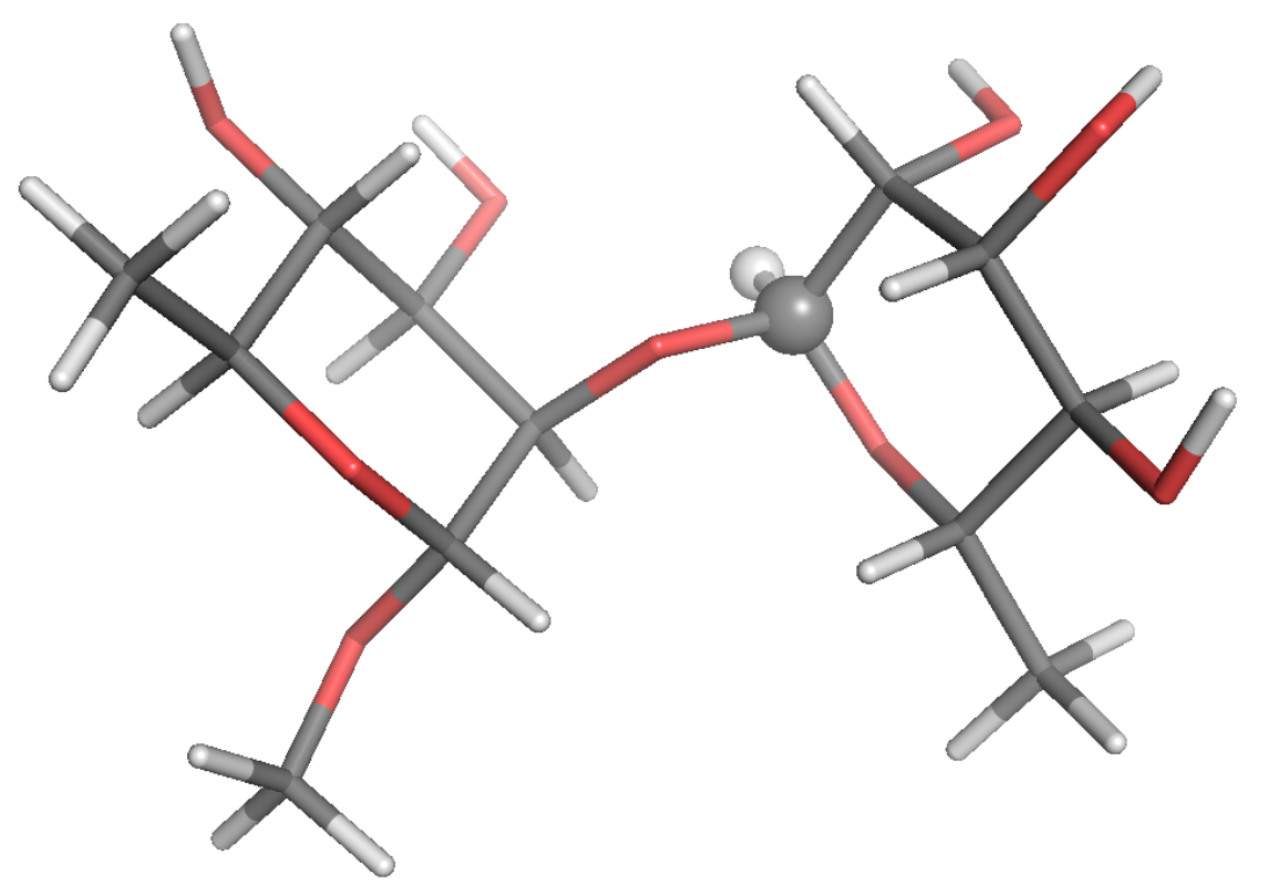
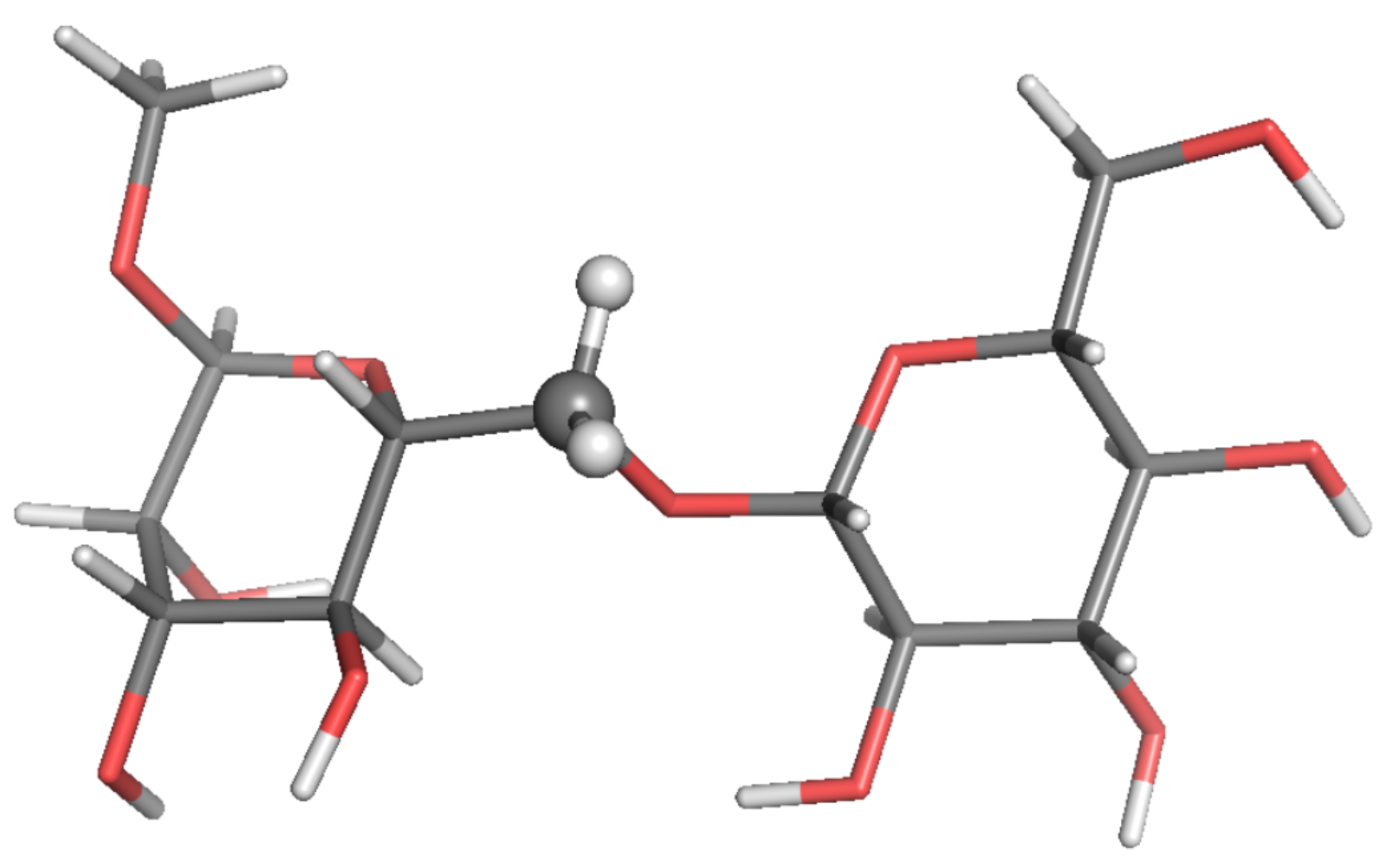

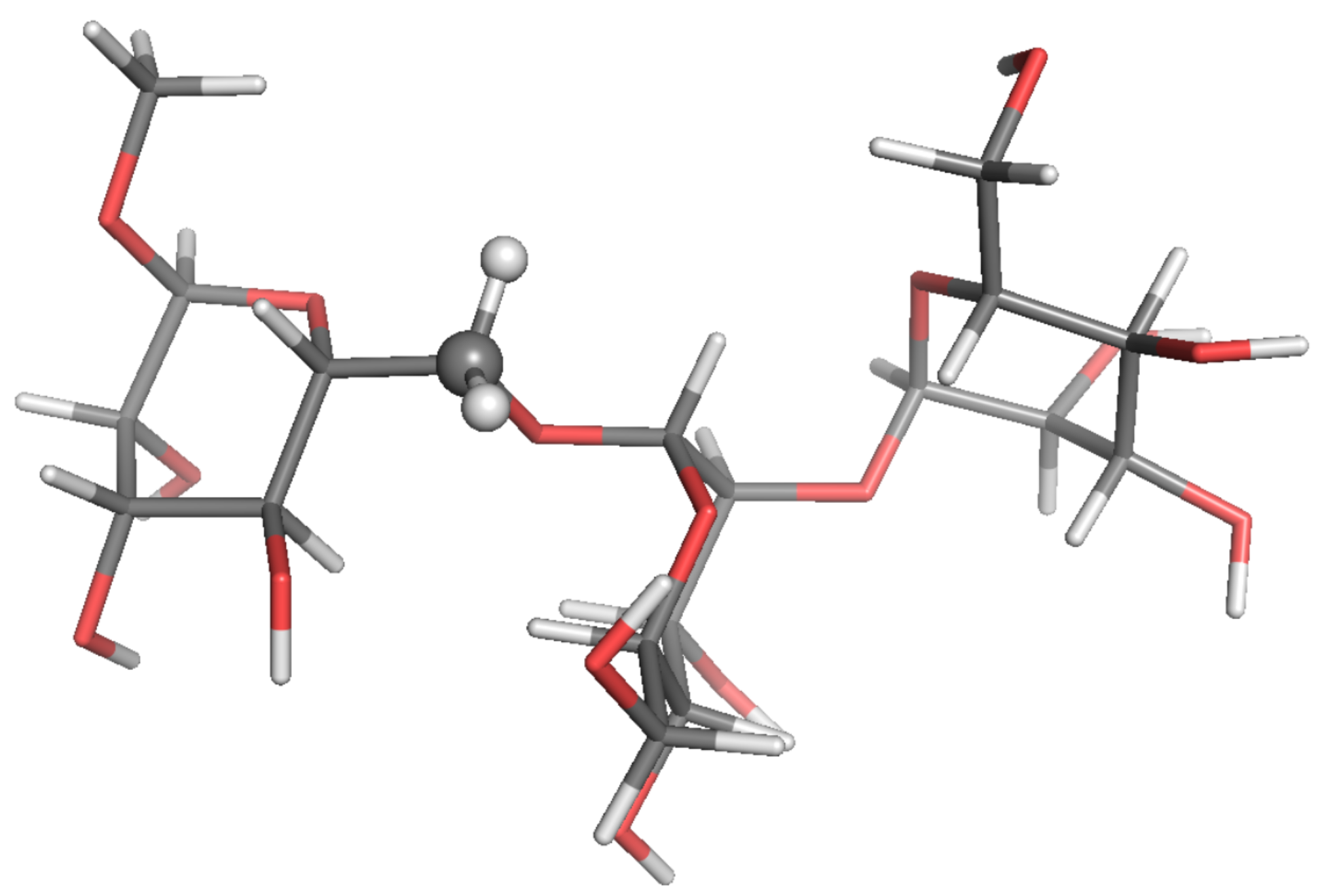
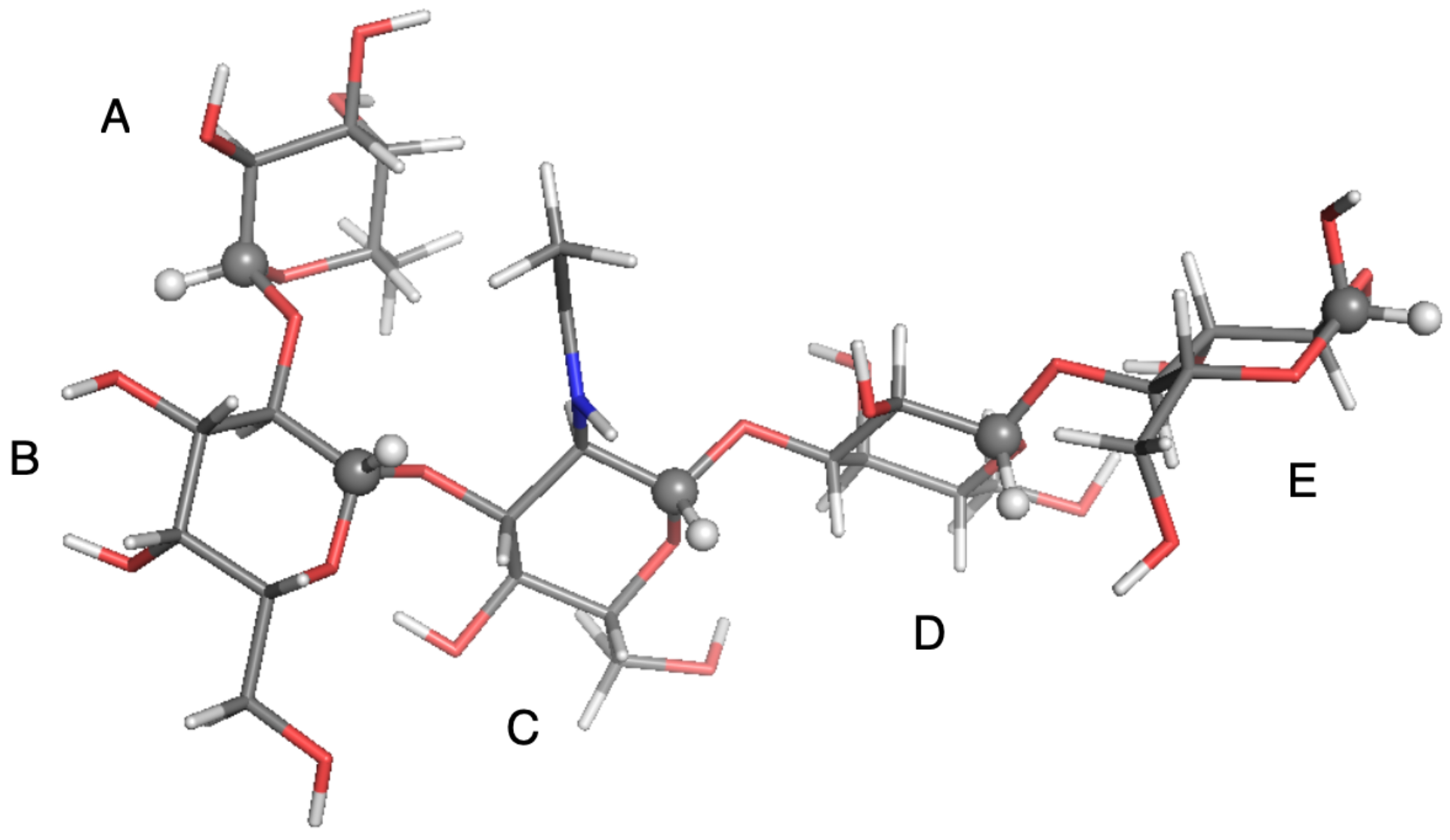
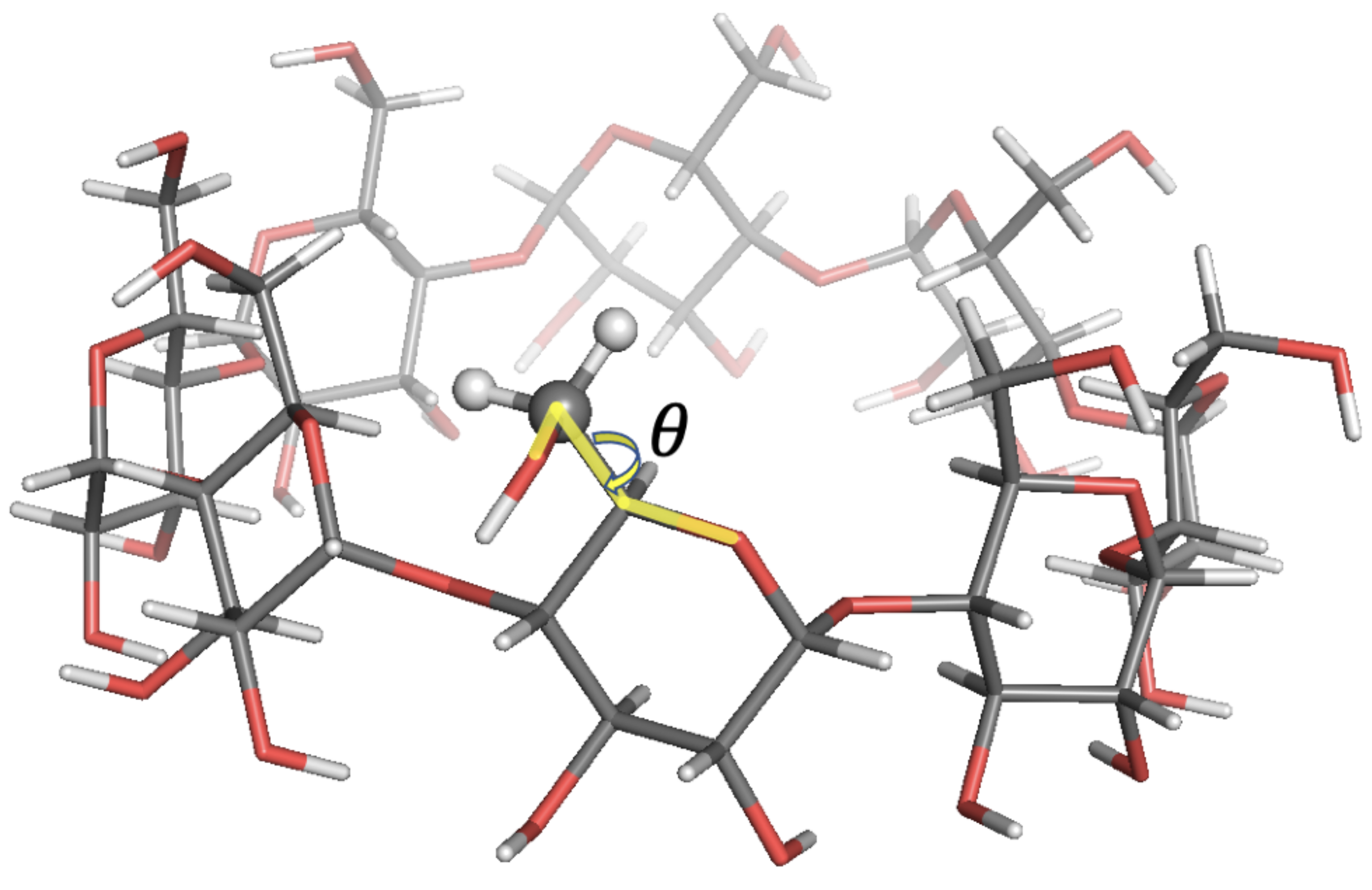
| Probe: CH, Solvent: DMSO-d,T/K: 298.2, Visc./(Pa s): 2.19 × 10 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Freq./MHz | /ms | /ms | NOE | e () | e () | e (NOE) | ||
| 600.1 | exp. | 440.0 | 402.6 | 2.361 | ||||
| calc. | 449.9 | 420.5 | 2.308 | 1.6 | 2.3 | 4.4 | 2.3 | |
| 700.0 | exp. | 475.6 | 432.9 | 2.215 | ||||
| calc. | 497.5 | 456.1 | 2.150 | 1.6 | 4.6 | 5.4 | 2.9 | |
| Probe: CH, Solvent: DMSO-d/DO 7:3 Molar Ratio,T/K: 253, Visc./(Pa s): 2.82 × 10 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Freq./MHz | /ms | /ms | NOE | e () | e () | e (NOE) | ||
| 400 | exp. | 150 | 32.5 | 1.03 | ||||
| calc. | 177 | 31.4 | 1.22 | 1.8 | 17.8 | 3.2 | 18.5 | |
| 600 | exp. | 284 | 30.1 | 1.08 | ||||
| calc. | 344 | 33.1 | 1.21 | 1.8 | 21.1 | 10.1 | 12.2 | |
| /K: 263, Visc./(Pa s): 1.42 × 10 | ||||||||
| Freq./MHz | /ms | /ms | NOE | e () | e () | e (NOE) | ||
| 400 | exp. | 117 | 48.0 | 1.19 | ||||
| calc. | 121 | 53.7 | 1.26 | 1.8 | 3.6 | 11.8 | 5.9 | |
| 600 | exp. | 205 | 55.0 | 1.10 | ||||
| calc. | 219 | 61.0 | 1.23 | 1.8 | 6.9 | 10.9 | 12.1 | |
| /K: 293, Visc./(Pa s): 4.30 × 10 | ||||||||
| Freq./MHz | /ms | /ms | NOE | e () | e () | e (NOE) | ||
| 400 | exp. | 127 | 106 | 1.86 | ||||
| calc. | 124 | 107 | 1.78 | 1.8 | 2.0 | 1.0 | 4.5 | |
| 600 | exp. | 166 | 128 | 1.58 | ||||
| calc. | 170 | 133 | 1.51 | 1.8 | 2.6 | 3.8 | 4.5 | |
| 900 | exp. | 219 | 152 | 1.45 | ||||
| calc. | 249 | 153 | 1.33 | 1.8 | 13.6 | 0.6 | 8.3 | |
| Solvent: DO,T/K: 298.6, Visc./(Pa s): 1.09 × 10, Probe:CH on C-2′ | ||||||||
|---|---|---|---|---|---|---|---|---|
| Freq./MHz | /ms | /ms | NOE | e () | e () | e (NOE) | ||
| 600.13 | exp. | 456.2 | 416.6 | 2.398 | ||||
| calc. | 453.2 | 425.7 | 2.299 | 1.8 | 0.7 | 2.2 | 4.1 | |
| 699.87 | exp. | 491.1 | 447.4 | 2.267 | ||||
| calc. | 503.8 | 463.6 | 2.148 | 1.8 | 2.6 | 3.6 | 5.3 | |
| Probe:CH on C-2′ | ||||||||
| Freq./MHz | /ms | /ms | NOE | e () | e () | e (NOE) | ||
| 600.13 | exp. | 491.6 | 450.2 | 2.466 | ||||
| calc. | 470.0 | 444.6 | 2.358 | 1.8 | 4.4 | 1.2 | 4.4 | |
| 699.87 | exp. | 524.5 | 483.9 | 2.346 | ||||
| calc. | 521.5 | 483.6 | 2.203 | 1.8 | 0.6 | 0.1 | 6.1 | |
| Probe: CH, Solvent: DMSO-d/DO 7:3 Molar Ratio,T/K: 298, Visc./(Pa s): 3.66 × 10 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Freq./MHz | /ms | /ms | NOE | e () | e () | e (NOE) | ||
| 500 | exp. | 144.79 | 111.57 | 1.670 | ||||
| calc. | 143.60 | 108.21 | 1.481 | 2.2 | 0.8 | 3.0 | 11.3 | |
| 600 | exp. | 167.59 | 117.67 | 1.460 | ||||
| calc. | 169.40 | 118.20 | 1.422 | 2.2 | 1.1 | 0.4 | 2.6 | |
| 700 | exp. | 188.36 | 124.55 | 1.320 | ||||
| calc. | 197.78 | 127.06 | 1.385 | 2.2 | 5.0 | 2.0 | 4.9 | |
| Solvent: DMSO-d/D2O 7:3 Molar Ratio,T/K: 303, Visc./(Pa s): 1.40 × 10, Probe:13CH on C-1 (A Residue) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Freq./MHz | /ms | /ms | NOE | e () | e () | e (NOE) | ||
| 600 | exp. | 305.0 | 222.0 | 1.460 | ||||
| calc. | 349.5 | 213.0 | 1.489 | 3.2 | 14.6 | 4.1 | 2.0 | |
| 700 | exp. | 354.0 | 244.0 | 1.420 | ||||
| calc. | 418.6 | 227.9 | 1.451 | 3.2 | 18.2 | 6.6 | 2.2 | |
| Probe:CH on C-1 (B residue) | ||||||||
| Freq./MHz | /ms | /ms | NOE | e () | e () | e (NOE) | ||
| 600 | exp. | 319.0 | 241.0 | 1.600 | ||||
| calc. | 336.3 | 214.4 | 1.423 | 3.2 | 5.4 | 11.0 | 11.0 | |
| 700 | exp. | 366.0 | 264.0 | 1.530 | ||||
| calc. | 400.3 | 229.9 | 1.386 | 3.2 | 9.4 | 12.9 | 9.4 | |
| Probe:CH on C-1 (C residue) | ||||||||
| Freq./MHz | /ms | /ms | NOE | e () | e () | e (NOE) | ||
| 600 | exp. | 318.0 | 225.0 | 1.630 | ||||
| calc. | 336.6 | 235.9 | 1.438 | 3.2 | 5.9 | 4.8 | 11.8 | |
| 700 | exp. | 360.0 | 240.0 | 1.560 | ||||
| calc. | 395.9 | 254.1 | 1.392 | 3.2 | 10.0 | 6.9 | 10.7 | |
| Probe:CH on C-1 (D residue) | ||||||||
| Freq./MHz | /ms | /ms | NOE | e () | e () | e (NOE) | ||
| 600 | exp. | 372.0 | 286.0 | 1.740 | ||||
| calc. | 365.8 | 275.2 | 1.525 | 3.2 | 1.7 | 3.8 | 12.3 | |
| 700 | exp. | 404.0 | 302.0 | 1.690 | ||||
| calc. | 421.2 | 296.7 | 1.469 | 3.2 | 4.3 | 1.7 | 13.1 | |
| Probe:CH on C-1 (E residue) | ||||||||
| Freq./MHz | /ms | /ms | NOE | e () | e () | e (NOE) | ||
| 600 | exp. | 325.0 | 259.0 | 1.490 | ||||
| calc. | 390.1 | 270.1 | 1.728 | 3.2 | 20.0 | 4.3 | 15.6 | |
| 700 | exp. | 374.0 | 262.0 | 1.500 | ||||
| calc. | 455.5 | 289.9 | 1.677 | 3.2 | 21.8 | 10.6 | 11.8 | |
| Probe: CH, Solvent: DMSO-d/DO 7:3 Molar Ratio,T/K: 323, Visc./(Pa s): 2.90 × 10 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Freq./MHz | /ms | /ms | NOE | e () | e () | e (NOE) | ||
| 400 | exp. | 123.5 | 75.00 | 1.430 | ||||
| calc. | 130.7 | 81.59 | 1.458 | 1.8 | 5.9 | 8.8 | 1.9 | |
| 600 | exp. | 187.0 | 85.00 | 1.330 | ||||
| calc. | 213.3 | 96.58 | 1.400 | 1.8 | 14.1 | 13.6 | 5.3 | |
| 900 | exp. | 314.5 | 110.9 | 1.250 | ||||
| calc. | 370.3 | 109.4 | 1.384 | 1.8 | 17.7 | 1.3 | 10.7 | |
| /K: 343, Visc./(Pa s): 2.30 × 10 | ||||||||
| Freq./MHz | /ms | /ms | NOE | e () | e () | e (NOE) | ||
| 400 | exp. | 134.1 | 107.2 | 1.630 | ||||
| calc. | 132.5 | 96.8 | 1.498 | 1.8 | 1.1 | 9.7 | 8.1 | |
| 600 | exp. | 183.8 | 130.1 | 1.510 | ||||
| calc. | 203.6 | 117.3 | 1.405 | 1.8 | 10.8 | 9.9 | 6.9 | |
| 900 | exp. | 274.0 | 154.8 | 1.330 | ||||
| calc. | 335.3 | 137.0 | 1.366 | 1.8 | 22.4 | 11.5 | 2.7 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rampino, S.; Zerbetto, M.; Polimeno, A. Stochastic Modelling of 13C NMR Spin Relaxation Experiments in Oligosaccharides. Molecules 2021, 26, 2418. https://doi.org/10.3390/molecules26092418
Rampino S, Zerbetto M, Polimeno A. Stochastic Modelling of 13C NMR Spin Relaxation Experiments in Oligosaccharides. Molecules. 2021; 26(9):2418. https://doi.org/10.3390/molecules26092418
Chicago/Turabian StyleRampino, Sergio, Mirco Zerbetto, and Antonino Polimeno. 2021. "Stochastic Modelling of 13C NMR Spin Relaxation Experiments in Oligosaccharides" Molecules 26, no. 9: 2418. https://doi.org/10.3390/molecules26092418
APA StyleRampino, S., Zerbetto, M., & Polimeno, A. (2021). Stochastic Modelling of 13C NMR Spin Relaxation Experiments in Oligosaccharides. Molecules, 26(9), 2418. https://doi.org/10.3390/molecules26092418