Computational NMR of Carbohydrates: Theoretical Background, Applications, and Perspectives
Abstract
:1. Introduction
2. Theoretical Background
2.1. Levels of Theory
2.1.1. Non-Empirical Level
2.1.2. DFT Level
- Pople’s 6-31G and 6-311G family of functionals with or without diffuse functions and different sets of polarization functions;
- Dunning’s cc-pVnZ (n = D, T, Q, 5) correlation-consistent basis sets and their augmented (diffuse) versions (aug-cc-pVnZ);
- Dunning’s cc-pCVnZ (n = D, T, Q, 5) correlation-consistent core-valence basis sets and their augmented versions (aug-cc-pCVnZ);
- Sauer’s augmented correlation-consistent basis sets aug-cc-pVTZ-J;
- Sauer’s correlation-consistent 6-31G-J and 6-311G-J basis sets;
- Jensen’s polarized-consistent basis sets (pc-n, n = 0−4) and their augmented versions (aug-pc-n);
- Jensen’s pc-n-based basis sets (pcS-n and pcJ-n) and their augmented versions (aug-pcS-n and aug-pcJ-n) used accordingly for the calculations of NMR chemical shifts and, on the other hand, spin-spin coupling constants;
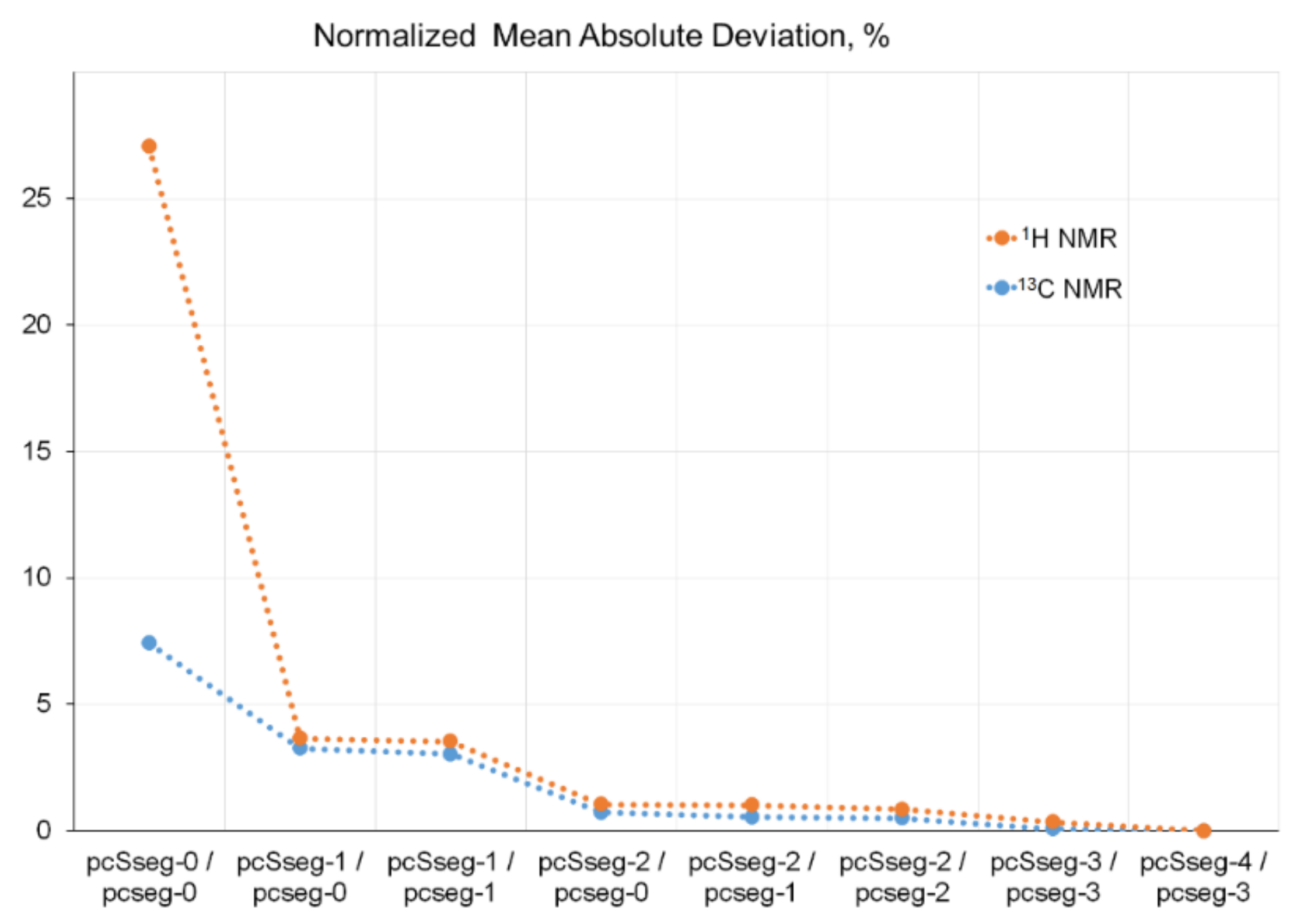
- Jensen’s segment contracted pcS-n basis sets (pcSseg-n, n = 0, 4) and their augmented versions (aug-pcSseg-n) used for the calculations of NMR chemical shifts;
- Four different groups of “relativistic” Dyall’s basis sets of double-, triple- and quadruple-zeta quality, namely, valence (dyall.vXz), core-valence (dyall.cvXz), diffuse valence (dyall.avXz) and diffuse core-valence (dyall.acvXz), X = 2, 3 and 4.
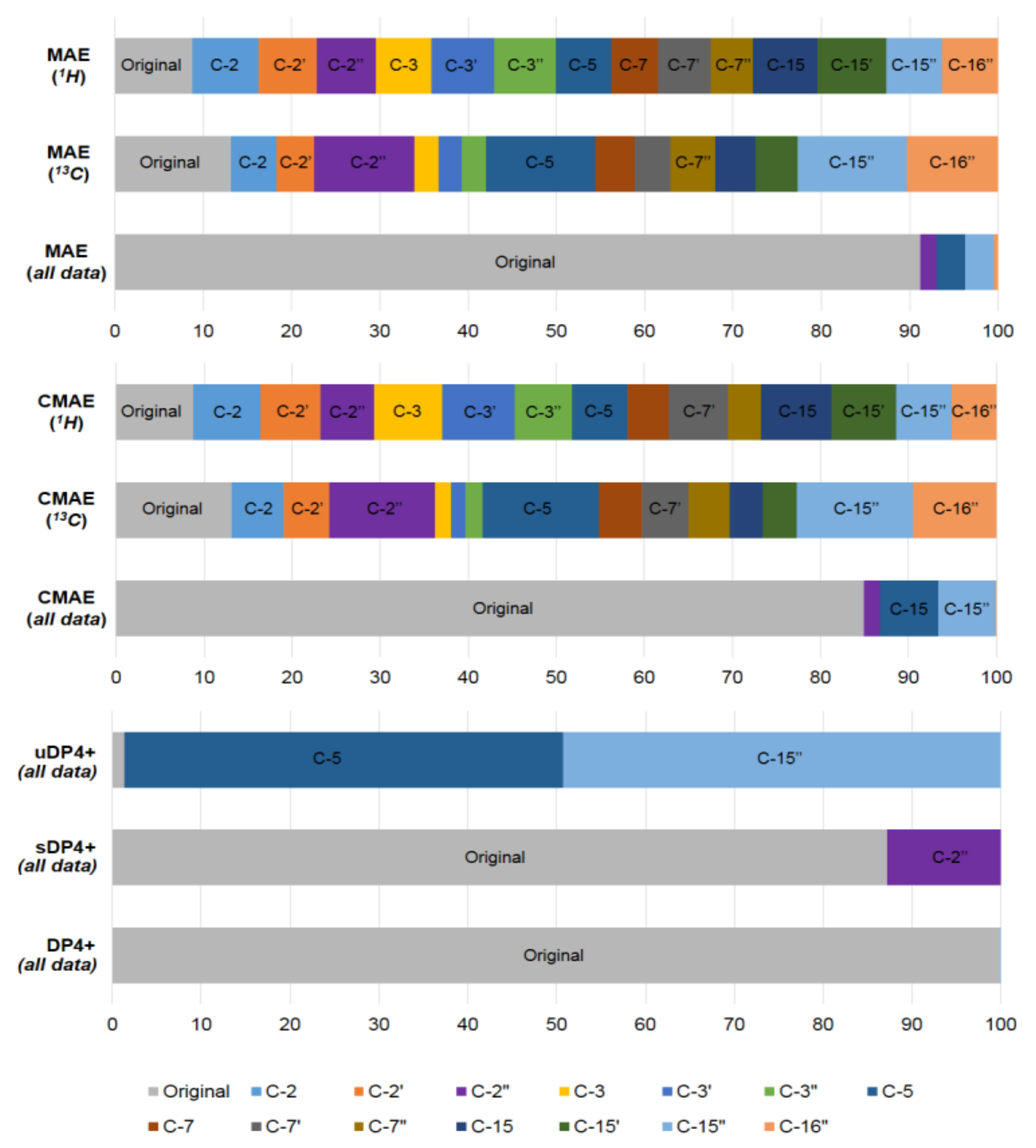
2.1.3. DP4 Analysis
2.1.4. Locally Dense Basis Set Scheme
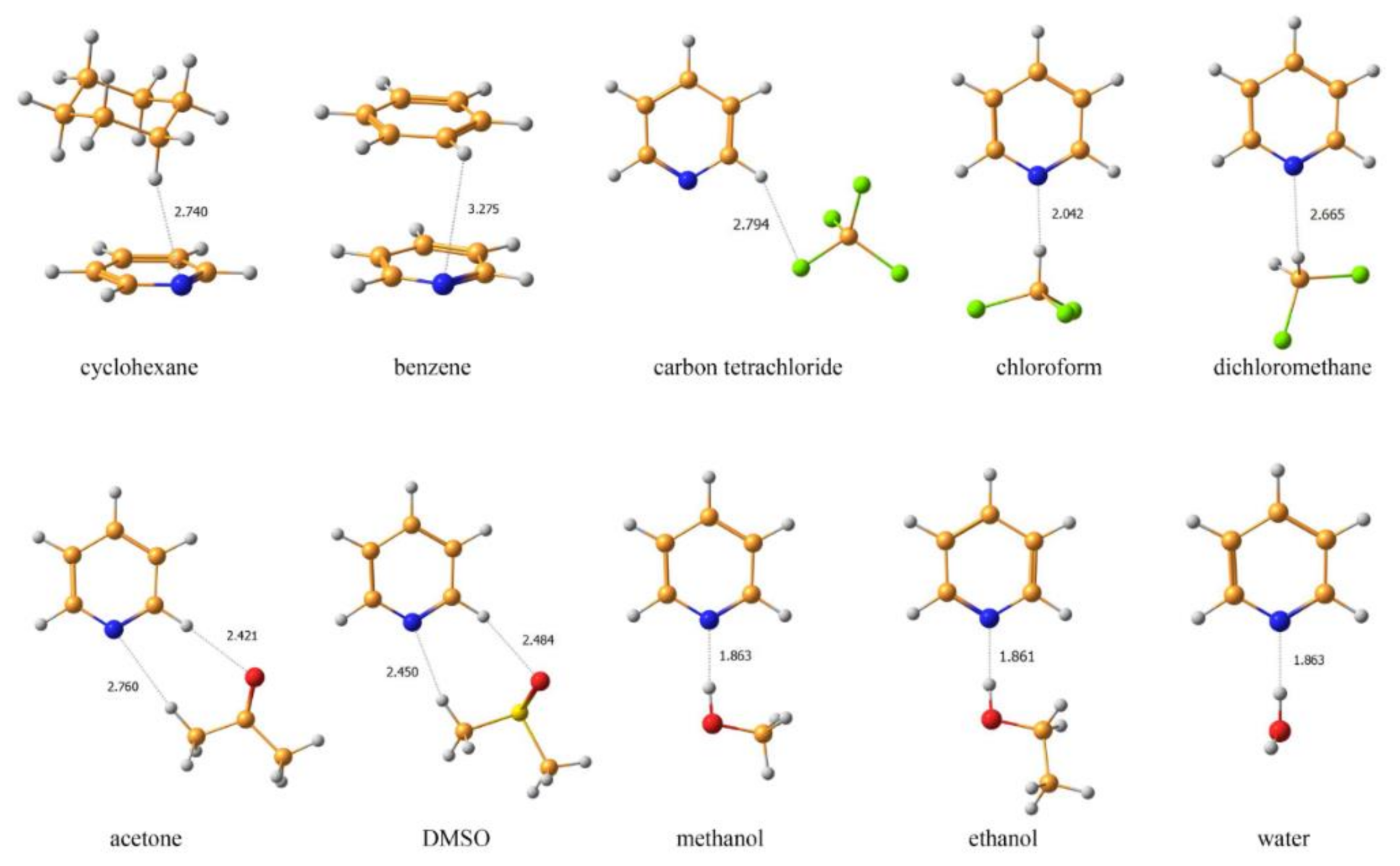
2.1.5. Solvent Effects
2.1.6. Vibrational Corrections
2.1.7. Relativistic Effects
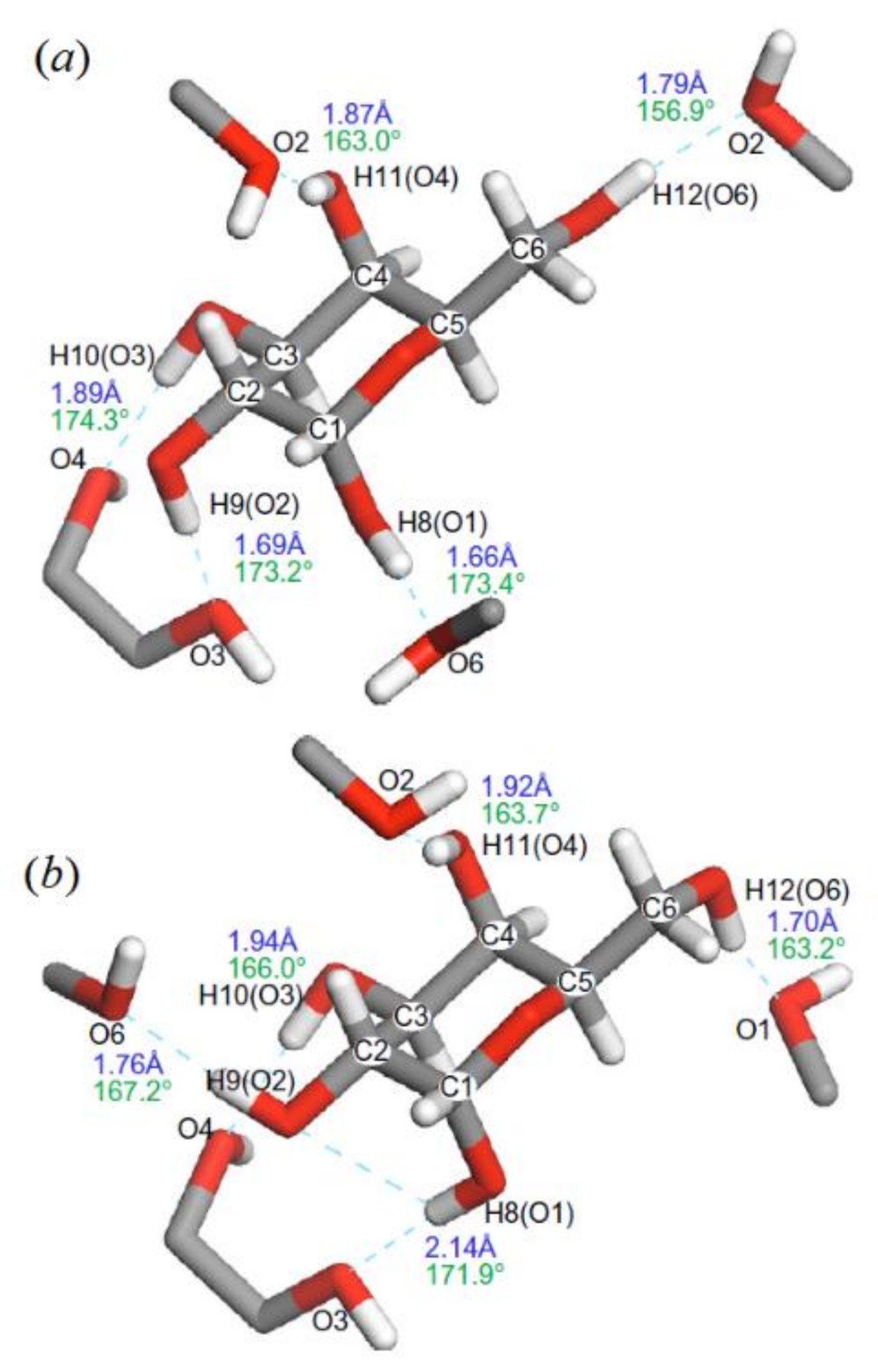
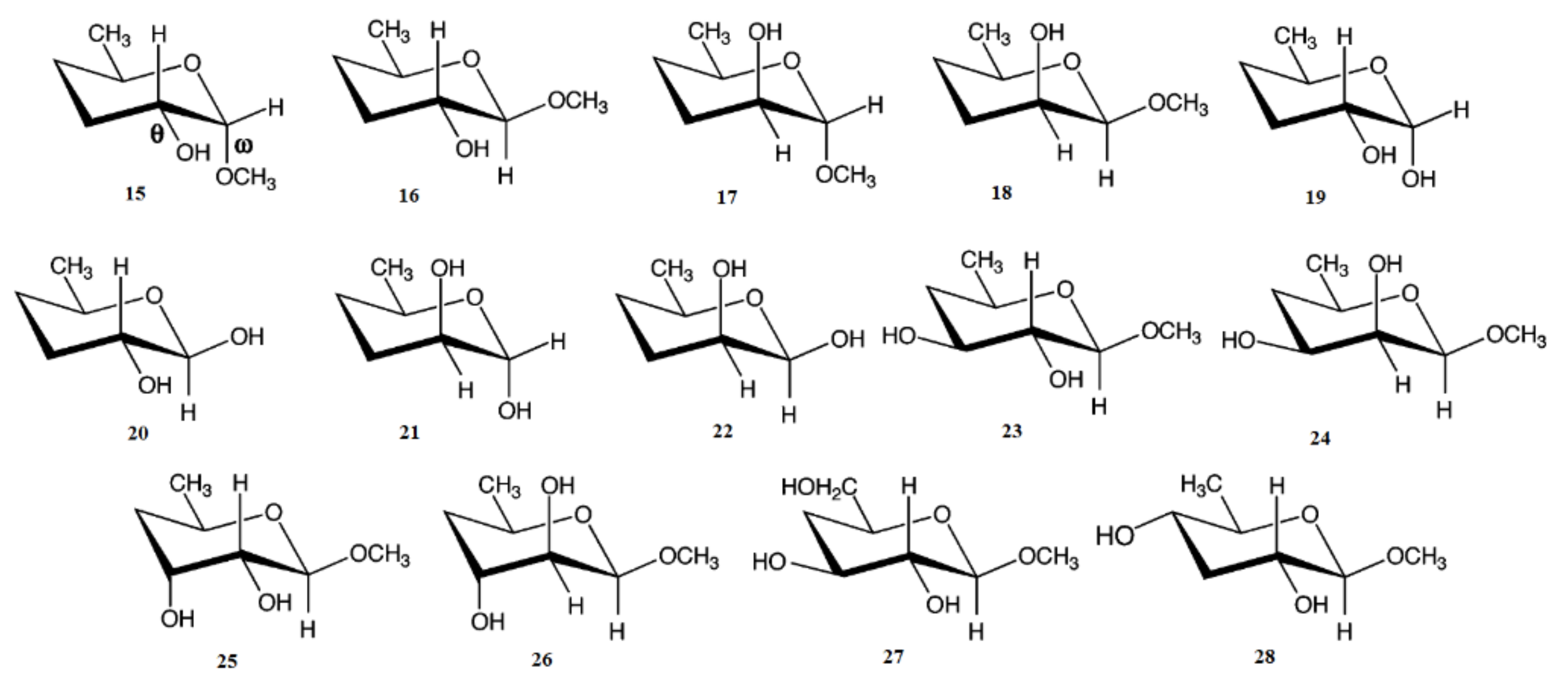
3. Monosaccharides

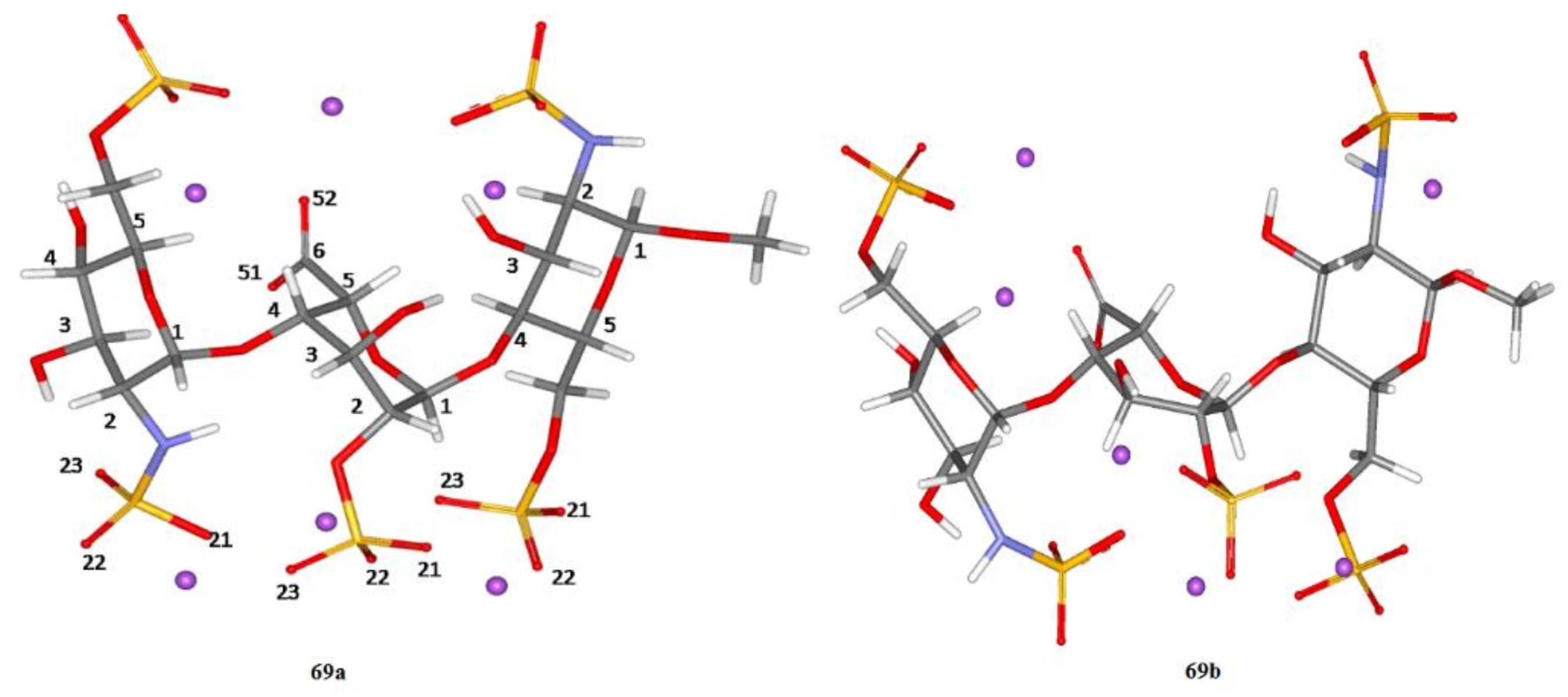
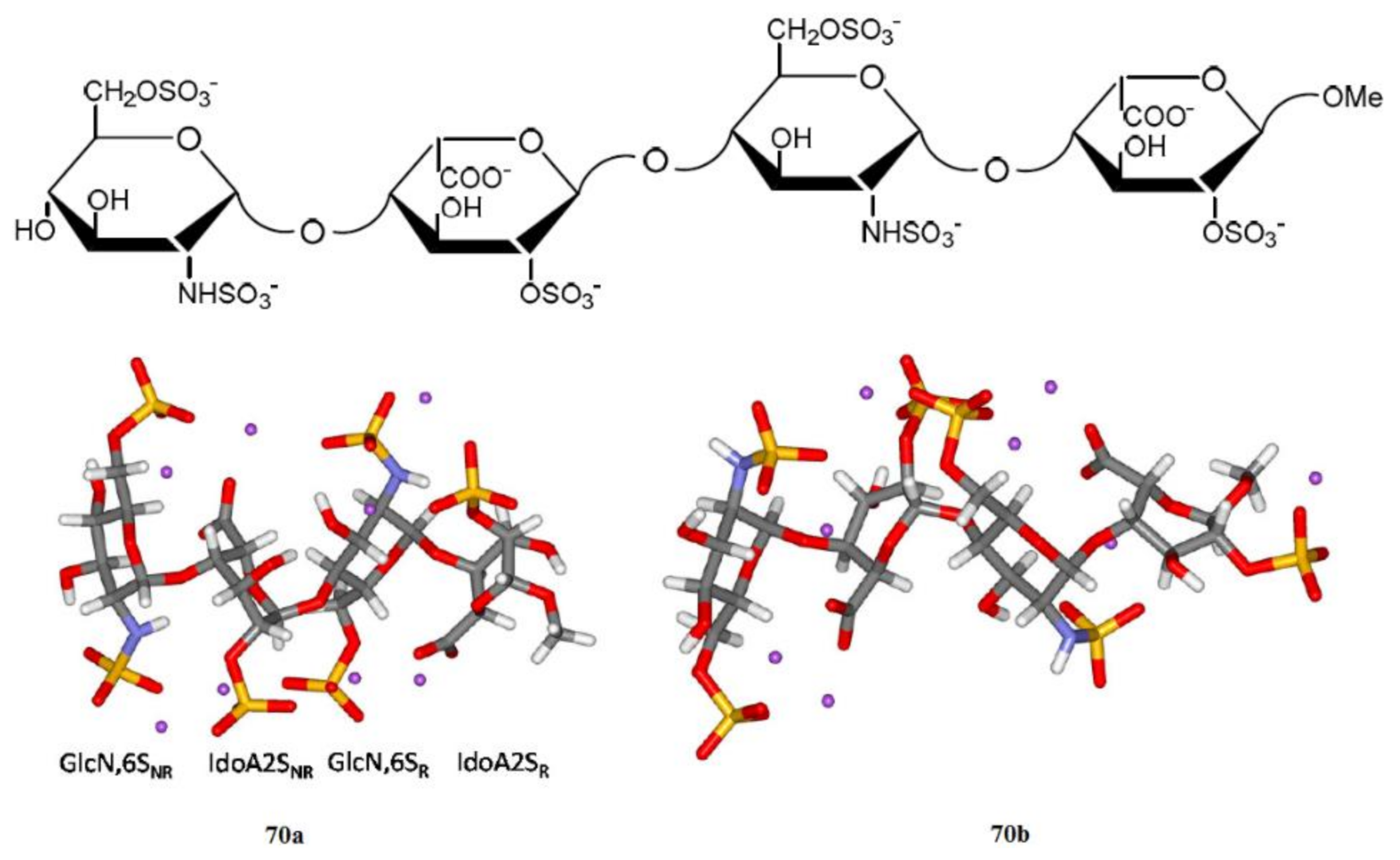
4. Di- and Polysaccharides
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
Abbreviations
| AM1 | Austin Model 1 |
| B3 | Three-parameter hybrid functional of Becke |
| BH | Becke’s “half and half” HF/DFT hybrid exchange functional |
| CBS | Complete Basis Set |
| CC3 | Coupled Cluster Iterative Triples (model) |
| CCSD | Coupled Cluster Singles and Doubles |
| CCSD(T) | Coupled Cluster Singles and Doubles with Perturbative Triples Corrections |
| CCSDT | Coupled Cluster Single-Double and Triple corrections |
| CMAE | Corrected Mean Absolute Error |
| CPCM | Conductor-like Polarizable Continuum Model |
| CP/MAS | Cross-Polarization/Magic-Angle Spinning |
| DFT | Density Functional Theory |
| EFG | Electic Field Gradient |
| Fuc | Fucose |
| Gal | Galactose |
| GlcNAc | N-acetyl glucosime |
| GIAO | Gauge including atomic orbitals |
| GIPAW | Gauge Including Projector Augmented Waves |
| HRPA(D) | Highest Random Phase Approximation Doubles (model) |
| IEF-PCM: | Integral Equation Formalism Polarizable Continuum Model |
| KT2 | Generalized gradient exchange-correlation functional of Keal and Tozer |
| KT3 | Generalized gradient exchange-correlation functional of Keal and Tozer with the gradient-corected exchange and correlation terms |
| LDBS | Locally Dense Basis Set |
| LYP | Lee, Yang, and Parr (correlation functional) |
| MAD | Mean Absolute Deviations |
| MAE | Mean Absolute Error |
| MAS | Magic-Angle Spinning |
| MD | Molecular Dynamics |
| MM | Molecular Mechanics |
| MP2 | Møller-Plesset perturbation theory (second-order) |
| Neu5Ac | N-acetyl neuramic acid |
| NMR | Nuclear Magnetic Resonance |
| OLYP | Handy and Cohen’s hybrid functional in combination with Lee, Yang and Parr’s correlation functional |
| OPBE | Handy and Cohen’s hybrid functional in combination with the generalized gradient functional of Perdew, Burke and Ernzerhof |
| OPTX | Handy and Cohen’s hybrid functional |
| OPW91 | Handy and Cohen’s hybrid functional in combination with the generalized gradient functional of Perdew and Wang |
| PBE0 | the generalized gradient functional of Perdew, Burke and Ernzerhof with a predetermined amount of exact exchange |
| PBEc | Perdew, Burke and Ernzerhof correlation functional |
| PW91 | Generalized gradient functional of Perdew and Wang |
| QM/MM | Quantum Mechanics/Molecular Mechanics (approach) |
| RPA | Random Phase Approximation |
| RPA(D) | Random Phase Approximation Doubles (model) |
| RHF | Restricted Hartree-Fock |
| SOPPA(CC2) | Second-Order Polarization Propagator Approach in combination with the second-order approximate Coupled Cluster to second order |
| SOPPA(CCSD) | Second-Order Polarization Propagator Approach in combination with Coupled Cluster Singles and Doubles |
| SOPPA(MP2) | Second-Order Polarization Propagator Approach within the second-order Møller-Plesset perturbation theory |
| SSM | Supermolecular Solvation Model |
| ZPVC | Zero-Point Vibrational Correction |
References
- Klepach, T.; Zhao, H.; Hu, X.; Zhang, W.; Stenutz, R.; Hadad, M.J.; Carmichael, I.; Serianni, A.S. Informing Saccharide Structural NMR Studies with Density Functional Theory Calculations. In Glycoinformatics, Methods in Molecular Biology; Lütteke, T., Frank, M., Eds.; Springer Science+Business Media: New York, NY, USA, 2015; pp. 289–331. [Google Scholar]
- Hadad, M.J.; Zhang, W.; Turney, T.; Sernau, L.; Wang, X.; Woods, R.J.; Incandela, A.; Surjancev, I.; Wang, A.; Yoon, M.-K.; et al. NMR Spin-Couplings in Saccharides: Relationships Between Structure, Conformation and the Magnitudes of JHH, JCH and JCC Values. In NMR in Glycoscience and Glycotechnology; Kato, K., Peters, T., Eds.; Royal Soc. Chem.: London, UK, 2017; pp. 20–100. [Google Scholar]
- Serianni, A.S.; Barker, R. Synthetic Approaches to Carbohydrates Enriched with Stable Isotopes of Carbon, Hydrogen and Oxygen, Isotopes in the Physical and Biomedical Sciences, Vol. I, Labelled Compounds (Part, A); Buncel, E., Jones, J.R., Eds.; Elsevier: London, UK, 1987; pp. 211–236. [Google Scholar]
- Serianni, A.S. Nuclear Magnetic Resonance Approaches to Oligosaccharide Structure Elucidation, Glycoconjugates: Composition, Structure and Function; Allen, H.J., Kisailus, E.C., Eds.; Marcel Dekker: New York, NY, USA, 1992; pp. 71–102. [Google Scholar]
- Serianni, A.S. Stable Isotope Labeled Carbohydrates and Nucleosides: Synthesis and Applications in Chemistry and Biology, Stable Isotope Applications in Biomolecular Structure and Mechanisms; Trewhella, J., Cross, T.A., Unkefer, C.J., Eds.; Los Alamos National Laboratory: Washington, DC, USA, 1994; pp. 209–245. [Google Scholar]
- Serianni, A.S. Carbohydrate Structure, Conformation and Reactivity: NMR Studies with Stable Isotopes, Bio-Organic Chemistry: Carbohydrates; Hecht, S.M., Ed.; Oxford University Press: Oxford, UK, 1999; pp. 244–312. [Google Scholar]
- Toukach, F.V.; Ananikov, V.P. Recent advances in computational predictions of NMR parameters for the structure elucidation of carbohydrates: Methods and limitations. Chem. Soc. Rev. 2013, 42, 8376–8415. [Google Scholar] [CrossRef] [PubMed]
- Sauer, S.P.A. Molecular Electromagnetism. In A Computational Chemistry Approach; University Press: Oxford, UK, 2012; 322p. [Google Scholar]
- Krivdin, L.B. Computational 1H-NMR: Part 1. Theoretical background. Magn. Reson. Chem. 2019, 57, 897–914. [Google Scholar] [CrossRef] [PubMed]
- Krivdin, L.B. Computational 1H-NMR: Part 2. Chemical applications. Magn. Reson. Chem. 2020, 58, 5–14. [Google Scholar] [CrossRef]
- Krivdin, L.B. Computational 1H-NMR: Part 3. Biochemical studies. Magn. Reson. Chem. 2020, 58, 15–30. [Google Scholar] [CrossRef] [PubMed]
- Krivdin, L.B. Computational protocols for calculating 13C-NMR chemical shifts. Prog. NMR Spectrosc. 2019, 112–113, 103–156. [Google Scholar] [CrossRef] [PubMed]
- Krivdin, L.B. Theoretical calculations of carbon-hydrogen spin-spin coupling constants. Prog. NMR Spectrosc. 2018, 108, 17–73. [Google Scholar] [CrossRef] [PubMed]
- Krivdin, L.B. Carbon-carbon spin-spin coupling constants: Practical applications of theoretical calculations. Prog. NMR Spectrosc. 2018, 105, 54–99. [Google Scholar] [CrossRef]
- Helgaker, T.; Jaszuński, M.; Ruud, K. Ab initio methods for the calculation of NMR shielding and indirect spin-spin coupling constants. Chem. Rev. 1999, 99, 293–352. [Google Scholar] [CrossRef]
- Helgaker, T.; Jaszuński, M.; Pecul, M. The quantum-chemical calculation of NMR indirect spin-spin coupling constants. Prog. NMR Spectrosc. 2008, 53, 249–268. [Google Scholar] [CrossRef]
- Helgaker, T.; Coriani, S.; Jørgensen, P.; Kristensen, K.; Olsen, J.; Ruud, K. Recent advances in wave function-based methods of molecular-property calculations. Chem. Rev. 2012, 112, 543–631. [Google Scholar] [CrossRef]
- Cremer, D.; Grafenstein, J. Calculation and analysis of NMR spin-spin coupling constants. Phys. Chem. Chem. Phys. 2007, 9, 2791–2816. [Google Scholar] [CrossRef]
- Vaara, J. Theory and computation of nuclear magnetic resonance parameters. Phys. Chem. Chem. Phys. 2007, 9, 5399–5418. [Google Scholar] [CrossRef] [PubMed]
- Aucar, G.A.; Romero, R.H.; Maldonado, A.F. Polarization propagators: A powerful theoretical tool for a deeper understanding of NMR spectroscopic parameters. Int. Rev. Phys. Chem. 2010, 29, 1–64. [Google Scholar] [CrossRef]
- Bühl, M.; van Mourik, T. NMR spectroscopy: Quantum-chemical calculations. WIREs Comput. Mol. Sci. 2011, 1, 634–647. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Krivdin, L.B. Modern quantum chemical methods for calculating spin-spin coupling constants: Theoretical basis and structural applications in chemistry. Russ. Chem. Rev. 2013, 82, 99–130. [Google Scholar] [CrossRef]
- Rusakova, I.L.; Rusakov, Y.Y.; Krivdin, L.B. Theoretical grounds of relativistic methods for calculation of spin-spin coupling constants in nuclear magnetic resonance spectra. Russ. Chem. Rev. 2016, 85, 356–426. [Google Scholar] [CrossRef] [Green Version]
- Mulder, F.A.A.; Filatov, M. NMR chemical shift data and ab initio shielding calculations: Emerging tools for protein structure determination. Chem. Soc. Rev. 2010, 39, 578–590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krivdin, L.B.; Contreras, R.H. Recent advances in theoretical calculations of indirect spin-spin coupling constants. Ann. Rep. NMR Spectrosc. 2007, 61, 133–245. [Google Scholar]
- Navarro-Vázquez, A. State of the art and perspectives in the application of quantum chemical prediction of 1H and 13C chemical shifts and scalar couplings for structural elucidation of organic compounds. Magn. Reson. Chem. 2017, 55, 29–32. [Google Scholar] [CrossRef] [PubMed]
- Krivdin, L.B. Calculation of 15N-NMR chemical shifts: Recent advances and perspectives. Prog. NMR Spectrosc. 2017, 102–103, 98–119. [Google Scholar] [CrossRef]
- Krivdin, L.B. Computational aspects of 19F-NMR. Russ. Chem. Rev. 2020, 89, 1040–1073. [Google Scholar] [CrossRef]
- Krivdin, L.B. Computational liquid-phase and solid-state 29Si-NMR. Russ. Chem. Rev. 2020, 89, 449–468. [Google Scholar] [CrossRef]
- Krivdin, L.B. Recent advances in computational 31P-NMR: Part 1. Chemical shifts. Magn. Reson. Chem. 2020, 58, 478–499. [Google Scholar] [CrossRef]
- Krivdin, L.B. Recent advances in computational 31P-NMR: Part 2. Spin-spin coupling constants. Magn. Reson. Chem. 2020, 58, 500–511. [Google Scholar] [CrossRef] [PubMed]
- Krivdin, L.B.; Rusakov, Y.Y. Structural and stereochemical applications of computational NMR using 29Si-1H and 77Se-1H indirect spin-spin coupling constants. Enc. Magn. Reson. 2014, 3, 87–110. [Google Scholar]
- Krivdin, L.B. Recent advances in computational liquid-phase 77Se-NMR. Russ. Chem. Rev. 2020, 89, 265–279. [Google Scholar] [CrossRef]
- Rusakova, I.L.; Rusakov, Y.Y. Quantum chemical calculations of 77Se and 125Te nuclear magnetic resonance spectral parameters and their structural applications. Magn. Reson. Chem. 2021, 59, 359–407. [Google Scholar] [CrossRef] [PubMed]
- Rusakova, I.L.; Krivdin, L.B. Relativistic effects in the NMR spectra of compounds containing heavy chalcogens. Mendeleev Commun. 2018, 28, 1–13. [Google Scholar] [CrossRef]
- Krivdin, L.B. Computational NMR of heavy nuclei involving 109Ag, 113Cd, 119Sn, 125Te, 195Pt, 199Hg, 205Tl, and 207Pb. Russ. Chem. Rev. 2020, 89. in press. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B. GAUSSIAN 09, Revision, C.01; Gaussian, Inc.: Wallingford, CT, USA, 2009; Available online: http://www.gaussian.com (accessed on 1 April 2021).
- Auer, A.A.; Gauss, J. Triple excitation effects in coupled-cluster calculations of indirect spin-spin coupling constants. J. Chem. Phys. 2001, 115, 1619–1622. [Google Scholar] [CrossRef]
- Faber, R.; Sauer, S.P.A.; Gauss, J. The importance of triples contributions to NMR spin-spin coupling constants computed at the CC3 and CCSDT levels. J. Chem. Theory Comp. 2016, 13, 696–709. [Google Scholar] [CrossRef] [Green Version]
- Sauer, S.P.A. Second order polarization propagator approximation with coupled cluster singles and doubles amplitudes—SOPPA(CCSD): The polarizability and hyperpolarizability of Li-. J. Phys. B At. Mol. Opt. Phys. 1997, 30, 3773–3780. [Google Scholar] [CrossRef]
- Enevoldsen, T.; Oddershede, J.; Sauer, S.P.A. Correlated calculations of indirect nuclear spin-spin coupling constants using second order polarization propagator approximations: SOPPA and SOPPA(CCSD). Theor. Chem. Acc. 1998, 100, 275–284. [Google Scholar] [CrossRef]
- Kjær, H.; Sauer, S.P.A.; Kongsted, J. Benchmarking NMR indirect nuclear spin-spin coupling constants: SOPPA, SOPPA(CC2) and SOPPA(CCSD) versus CCSD. J. Chem. Phys. 2010, 133, 144106. [Google Scholar] [CrossRef] [PubMed]
- Kjær, H.; Sauer, S.P.A.; Kongsted, J.; Rusakov, Y.Y.; Krivdin, L.B. Benchmarking SOPPA(CC2) for the calculation of indirect nuclear spin-spin coupling constants: Carbocycles. Chem. Phys. 2011, 381, 35–43. [Google Scholar] [CrossRef]
- Schnack-Petersen, A.C.; Haase, P.A.B.; Faber, R.; Provasi, P.F.; Sauer, S.P.A. RPA(D) and HRPA(D): Two new models for calculations of NMR indirect nuclear spin-spin coupling constants. J. Comp. Chem. 2018, 39, 2647–2666. [Google Scholar] [CrossRef] [PubMed]
- Møller, C.H.S.; Sauer, S.P.A. RPA(D) and HRPA(D): Calculation of carbon-carbon spin-spin coupling constants for saturated cycloalkanes. Mol. Phys. 2020, 118, e1757773. [Google Scholar] [CrossRef]
- Becke, A.D. Density functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar]
- Becke, A.D. A new mixing of Hartree-Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Handy, N.C.; Cohen, A.J. Left-right correlation energy. Mol. Phys. 2001, 99, 403–412. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Burke, K.; Perdew, J.P.; Wang, Y. Derivation of a Generalized Gradient Approximation: The PW91 Density Functional. In Electronic Density Functional Theory; Dobson, J.F., Ed.; Springer: New York, NY, USA, 1998; p. 81. [Google Scholar]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Keal, T.W.; Tozer, D.J. The exchange-correlation potential in Kohn–Sham nuclear magnetic resonance shielding calculations. J. Chem. Phys. 2003, 119, 3015–3024. [Google Scholar]
- Keal, T.W.; Tozer, D.J. A semiempirical generalized gradient approximation exchange-correlation functional. J. Chem. Phys. 2004, 121, 5654–5660. [Google Scholar]
- Basis Set Exchange Database. Available online: https://www.basissetexchange.org/ (accessed on 1 April 2021).
- Iron, M.A. Evaluation of the factors impacting the accuracy of 13C-NMR chemical shift predictions using density functional theory—the advantage of long-range corrected functionals. J. Chem. Theory Comp. 2017, 13, 5798–5819. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.G.; Goodman, J.M. Assigning stereochemistry to single diastereoisomers by GIAO NMR calculation: The DP4 Probability. J. Am. Chem. Soc. 2010, 132, 12946–12959. [Google Scholar] [CrossRef]
- Grimblat, N.; Zanardi, M.M.; Sarotti, A.M. Beyond DP4: An improved probability for the stereochemical assignment of isomeric compounds using quantum chemical calculations of NMR shifts. J. Org. Chem. 2015, 80, 12526–12534. [Google Scholar] [CrossRef]
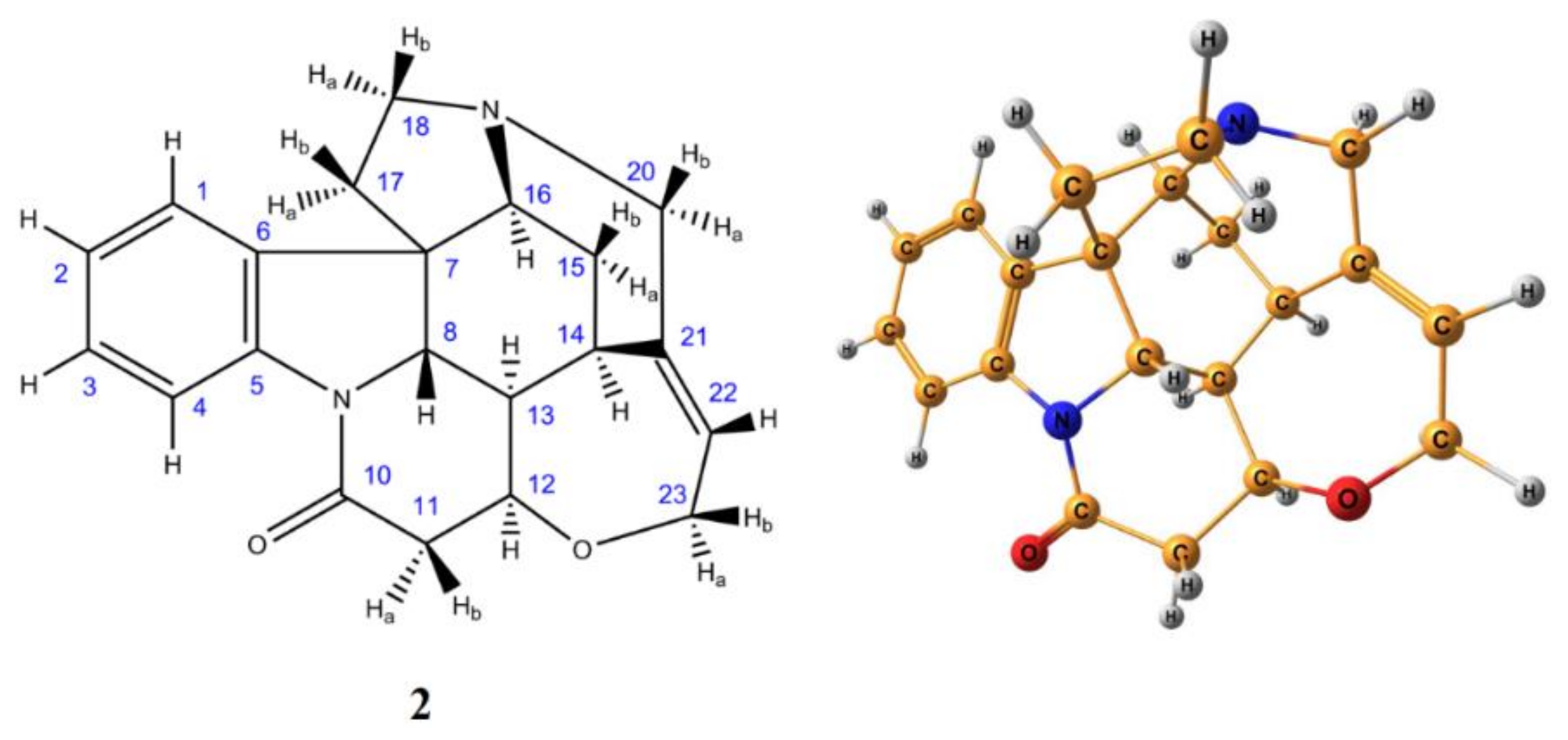
- Semenov, V.A.; Krivdin, L.B. Computational 1H and 13C-NMR of the trimeric monoterpenoid indole alkaloid strychnohexamine: Selected spectral updates. Magn. Reson. Chem. 2021, 59. [Google Scholar] [CrossRef]
- Chesnut, D.B.; Moore, K.D. Locally dense basis sets for chemical shift calculations. J. Comp. Chem. 1989, 10, 648–659. [Google Scholar] [CrossRef]
- Chesnut, D.B.; Rusiloski, B.E.; Moore, K.D.; Egolf, D.A. Use of locally dense basis sets for nuclear magnetic resonance shielding calculations. J. Comp. Chem. 1993, 14, 1364–1375. [Google Scholar] [CrossRef]
- Chesnut, D.B.; Byrd, E.F.C. The use of locally dense basis sets in correlated NMR chemical shielding calculations. Chem. Phys. 1996, 213, 153–158. [Google Scholar] [CrossRef]
- Provasi, P.F.; Aucar, G.A.; Sauer, S.P.A. The use of locally dense basis sets in the calculation of indirect nuclear spin-spin coupling constants: The vicinal coupling constants in H3C-CH2X (X. = H., F., Cl, Br, I). J. Chem. Phys. 2000, 112, 6201–6208. [Google Scholar] [CrossRef] [Green Version]
- Sanchez, M.; Provasi, P.F.; Aucar, G.A.; Sauer, S.P.A. On the usage of locally dense basis sets in the calculation of nmr indirect nuclear spin-spin coupling constants: Vicinal fluorine-fluorine couplings. Adv. Quantum Chem. 2005, 48, 161–183. [Google Scholar]
- Kirby, R.A.; Hansen, A.E. Study of locally dense and locally saturated basis sets in localized molecular orbital calculations of nuclear shielding: Ab initio LORG calculations for 13C and 17O in norbornenone. Int. J. Quantum Chem. 1996, 57, 199–205. [Google Scholar] [CrossRef]
- Chesnut, D.B.; Phung, C.G. Ab initio determination of chemical shielding in a model dipeptide. Chem. Phys. Lett. 1991, 183, 505–509. [Google Scholar] [CrossRef]
- Semenov, V.A.; Krivdin, L.B. DFT computational schemes for 1H and 13C-NMR chemical shifts of natural products, exemplified by strychnine. Magn. Reson. Chem. 2020, 58, 56–64. [Google Scholar] [CrossRef] [PubMed]
- Rusakov, Y.Y.; Krivdin, L.B. One-bond 29Si-1H spin-spin coupling constants in the series of halosilanes: Benchmark SOPPA and DFT calculations, relativistic effects, and vibrational corrections. Magn. Reson. Chem. 2013, 51, 557–561. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Krivdin, L.B.; Osterstrom, F.F.; Sauer, S.P.A.; Potapov, V.A.; Amosova, S.V. First example of a high-level correlated calculation of the indirect spin-spin coupling constants involving tellurium: Tellurophene and divinyl telluride. Phys. Chem. Chem. Phys. 2013, 15, 13101–13107. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Krivdin, L.B.; Nosova, V.M.; Kisin, A.V.; Lakhtin, V.G. Structural trends of 29Si-1H spin-spin coupling constants across double bond. Magn. Reson. Chem. 2012, 50, 665–671. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Krivdin, L.B.; Penzik, M.V.; Potapov, V.A.; Amosova, S.V. Open-chain unsaturated selanyl sulfides: Stereochemical structure and stereochemical behavior of their 77Se-1H spin-spin coupling constants. Magn. Reson. Chem. 2012, 50, 653–658. [Google Scholar] [CrossRef] [PubMed]
- Rusakov, Y.Y.; Krivdin, L.B. Stereochemical behavior of 2J(Se,H) and 3J(Se,H) spin-spin coupling constants across sp3 carbons: A theoretical scrutiny. Magn. Reson. Chem. 2012, 50, 557–562. [Google Scholar] [CrossRef] [PubMed]
- Rusakov, Y.Y.; Krivdin, L.B.; Kumar, A.A.; Szilagyi, L.; Kover, K.E. Resonance assignments of diastereotopic CH2 protons in the anomeric side-chain of selenoglycosides by means of 2J(Se,H) spin-spin coupling constants. Magn. Reson. Chem. 2012, 50, 488–495. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Krivdin, L.B.; Nosova, V.M.; Kisin, A.V. Benchmark calculations of 29Si-1H spin-spin coupling constants across double bond. Magn. Reson. Chem. 2012, 50, 278–283. [Google Scholar] [CrossRef] [PubMed]
- Rusakov, Y.Y.; Krivdin, L.B.; Papernaya, L.K.; Shatrova, A.A. Stereochemical behavior of 77Se-1H spin-spincoupling constants in pyrazolyl-1,3-diselenanes and 1,2-diselenolane. Magn. Reson. Chem. 2012, 50, 169–173. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Krivdin, L.B.; Orlov, N.V.; Ananikov, V.P. Stereochemical study of the sterically crowded phenylselanylalkenes by means of 77Se-1H spin-spin coupling constants. Magn. Reson. Chem. 2011, 49, 570–574. [Google Scholar] [CrossRef] [PubMed]
- Rusakov, Y.Y.; Krivdin, L.B.; Potapov, V.A.; Penzik, M.V.; Amosova, S.V. Conformational analysis and diastereotopic assignments in the series of seleniumcontaining heterocycles by means of 77Se-1H spin-spin coupling constants: A combined theoretical and experimental study. Magn. Reson. Chem. 2011, 49, 389–396. [Google Scholar] [CrossRef] [PubMed]
- Rusakov, Y.Y.; Krivdin, L.B.; Sauer, S.P.A.; Levanova, E.P.; Levkovskaya, G.G. Structural trends of 77Se-1H spin-spin coupling constants and conformational behavior of 2-substituted selenophenes. Magn. Reson. Chem. 2010, 48, 44–52. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Krivdin, L.B.; Istomina, N.V.; Potapov, V.M.; Amosova, S.V. Divinyl selenide: Conformational study and stereochemical behavior of its 77Se-1H spin-spin coupling constants. Magn. Reson. Chem. 2008, 46, 979–985. [Google Scholar] [CrossRef]
- Semenov, V.A.; Samultsev, D.O.; Krivdin, L.B. The 1H and 13C-NMR chemical shifts of Strychnos alkaloids revisited at the DFT level. Magn. Reson. Chem. 2020, 58, 532–539. [Google Scholar] [CrossRef]
- Semenov, V.A.; Samultsev, D.O.; Krivdin, L.B. 1H and 13C-NMR spectra of Strychnos alkaloids: Selected NMR updates. Int. J. Quant. Chem. 2020, 120, e26348. [Google Scholar] [CrossRef]
- Semenov, V.A.; Samultsev, D.O.; Krivdin, L.B. DFT computational schemes for 15N-NMR chemical shifts of the condensed nitrogen—Containing heterocycles. Magn. Reson. Chem. 2019, 57, 346–358. [Google Scholar] [CrossRef] [PubMed]
- Semenov, V.A.; Samultsev, D.O.; Krivdin, L.B. Substitution effects in the 15N-NMR chemical shifts of heterocyclic azines evaluated at the GIAO—DFT level. Magn. Reson. Chem. 2018, 56, 767–774. [Google Scholar] [CrossRef] [PubMed]
- Semenov, V.A.; Samultsev, D.O.; Krivdin, L.B. GIAO—DFT calculation of 15N-NMR chemical shifts of Schiff bases: Accuracy factors and protonation effects. Magn. Reson. Chem. 2018, 56, 727–739. [Google Scholar] [CrossRef]
- Samultsev, D.O.; Semenov, V.A.; Krivdin, L.B. On the accuracy factors and computational cost of the GIAO–DFT calculation of 15N-NMR chemical shifts of amides. Magn. Reson. Chem. 2017, 55, 1015–1021. [Google Scholar] [CrossRef] [PubMed]
- Mennucci, B.; Tomasi, J. Continuum solvation models: A new approach to the problem of solute’s charge distribution and cavity boundaries. J. Chem. Phys. 1997, 106, 5151–5158. [Google Scholar] [CrossRef]
- Cancès, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Mennucci, B.; Cancès, E.; Tomasi, J. Evaluation of solvent effects in isotropic and anisotropic dielectrics and in ionic solutions with a unified integral equation method: theoretical bases, computational implementation, and numerical applications. J. Phys. Chem. B 1997, 101, 10506–10517. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cancès, E. The IEF version of the PCM solvation method: An overview of a new method addressed to study molecular solutes at the QM ab initio level. THEOCHEM 1999, 464, 211–226. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef]
- Klamt, A.; Schüürmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 2 1993, 5, 799–805. [Google Scholar] [CrossRef]
- Andzelm, J.; Kölmel, C.; Klamt, A. Incorporation of solvent effects into density functional calculations of molecular energies and geometries. J. Chem. Phys. 1995, 103, 9312–9320. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Takano, Y.; Houk, K.N. Benchmarking the conductor-like polarizable continuum model (CPCM) for aqueous solvation free energies of neutral and ionic organic molecules. J. Chem. Theory Comput. 2005, 1, 70–77. [Google Scholar] [CrossRef]
- Semenov, V.A.; Samultsev, D.O.; Krivdin, L.B. Solvent effects in the GIAO-DFT calculations of the 15N-NMR chemical shifts of azoles and azines. Magn. Reson. Chem. 2014, 52, 686–693. [Google Scholar] [CrossRef] [PubMed]
- Caputo, M.C.; Provasi, P.F.; Sauer, S.P.A. The role of explicit solvent molecules in the calculation of NMR chemical shifts of glycine in water. Theor. Chem. Acc. 2018, 137, 88. [Google Scholar] [CrossRef] [Green Version]
- Lacerda, E.G., Jr.; Kamounah, F.S.; Coutinho, K.; Sauer, S.P.A.; Hansen, P.E.; Hammerich, O. Computational Prediction of 1H and 13C-NMR Chemical Shifts for Protonated Alkylpyrroles: Electron Correlation and Not Solvation is the Salvation. ChemPhysChem 2019, 20, 78–91. [Google Scholar] [PubMed] [Green Version]
- Møgelhøj, A.; Aidas, K.; Mikkelsen, K.V.; Sauer, S.P.A.; Kongsted, J. Prediction of spin-spin coupling constants in solution based on combined density functional theory/molecular mechanics. J. Chem. Phys. 2009, 130, 134508. [Google Scholar] [CrossRef]
- Ruden, T.A.; Lutnæs, O.B.; Helgaker, T.; Ruud, K. Vibrational corrections to indirect nuclear spin-spin coupling constants calculated by density-functional theory. J. Chem. Phys. 2003, 118, 9572–9581. [Google Scholar] [CrossRef]
- Lutnæs, O.B.; Ruden, T.A.; Helgaker, T. The performance of hybrid density functional theory for the calculation of indirect nuclear spin-spin coupling constants in substituted hydrocarbons. Magn. Reson. Chem. 2004, 42, S117–S127. [Google Scholar] [CrossRef] [Green Version]
- Barone, V. Anharmonic vibrational properties by a fully automated second-order perturbative approach. J. Chem. Phys. 2005, 122, 014108. [Google Scholar] [CrossRef] [PubMed]
- Irikura, K.K. Experimental vibrational zero-point energies: Diatomic molecules. J. Phys. Chem. Ref. Data 2007, 36, 389–397. [Google Scholar] [CrossRef] [Green Version]
- Faber, R.; Buczek, A.; Kupka, T.; Sauer, S.P.A. On the convergence of zero-point vibrational corrections to nuclear shieldings and shielding anisotropies towards the complete basis set limit in water. Mol. Phys. 2016, 115, 144–160. [Google Scholar] [CrossRef]
- Kupka, T.; Buczek, A.; Broda, M.A.; Stachów, M.; Tarnowski, P. DFT studies on the structural and vibrational properties of polyenes. J. Mol. Model. 2016, 22, 101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ruden, T.A.; Ruud, K. Calculation of NMR and EPR Parameters: Theory and Applications; Kaupp, M., Malkin, V.G., Buehl, M., Eds.; Wiley-VCH: Weinheim, Germany, 2004; Chapter 10; p. 153. [Google Scholar]
- Faber, R.; Kaminsky, J.; Sauer, S.P.A. Rovibrational and temperature effects in theoretical studies of NMR parameters. In Gas Phase NMR.; Jackowski, K., Jaszuński, M., Eds.; Royal Society of Chemistry: London, UK, 2016; Chapter 7; pp. 218–266. [Google Scholar]
- Autschbach, J. Relativistic effects on NMR parameters. In High Resolution NMR Spectroscopy: Understanding Molecules and Their Electronic Structures; Contreras, R.H., Ed.; Elsevier: Amsterdam, The Netherlands, 2013; Volume 3, pp. 69–117. [Google Scholar]
- Xiao, Y.; Liu, W.; Autschbach, J. Relativistic theories of NMR shielding. In Handbook of Relativistic Quantum Chemistry; Liu, W., Ed.; Springer: Berlin, Germany, 2017; pp. 657–692. [Google Scholar]
- Zhu, Y.; Zajicek, J.; Serianni, A.S. Acyclic forms of [1-13C]aldohexoses in aqueous solution: quantitation by 13C-NMR and deuterium isotope effects on tautomeric equilibria. J. Org. Chem. 2001, 66, 6244–6251. [Google Scholar] [CrossRef]
- Roslund, M.U.; Tähtinen, P.; Niemitz, M.; Sjöholm, R. Complete assignments of the 1H and 13C chemical shifts and JH,H coupling constants in NMR spectra of D-glucopyranose and all D-glucopyranosyl-D-glucopyranosides. Carbohydr. Res. 2008, 343, 101–112. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, C.O.; Mennucci, B.; Vreven, T. Density functional study of the optical rotation of glucose in aqueous solution. J. Org. Chem. 2004, 69, 8161–8164. [Google Scholar] [CrossRef] [PubMed]
- Zrelov, O.Y.; Syroeshkin, A.V.; Uspenskaya, E.V.; Titorovich, O.V.; Pleteneva, T.V. Effect of water isotopic composition on galactose mutarotation kinetics. Pharm. Chem. J. 2015, 49, 413–416. [Google Scholar] [CrossRef]
- Bagno, A.; Rastrelli, F.; Saielli, G. Prediction of the 1H and 13C-NMR spectra of α-D-glucose in water by DFT methods and MD simulations. J. Org. Chem. 2007, 72, 7373–7381. [Google Scholar] [CrossRef] [PubMed]
- Saielli, G.; Bagno, A. Preferential solvation of glucose and talose in water-acetonitrile mixtures: A molecular dynamics simulation study. Phys. Chem. Chem. Phys. 2010, 12, 2981–2988. [Google Scholar] [CrossRef] [PubMed]
- Kibalchenko, M.; Lee, D.; Shao, L.; Payne, M.C.; Titman, J.J.; Yates, J.R. Distinguishing hydrogen bonding networks in α-D-galactose using NMR experiments and first principles calculations. Chem. Phys. Lett. 2010, 498, 270–276. [Google Scholar] [CrossRef]
- Pickard, C.J.; Mauri, F. All-electron magnetic response with pseudopotentials: NMR chemical shifts. Phys. Rev. B 2001, 63, 245101. [Google Scholar] [CrossRef] [Green Version]
- Szeleszczuk, Ł.; Gubica, T.; Zimniak, A.; Pisklak, D.M.; Dạbrowska, K.; Cyrański, M.K.; Kańska, M. The potential for the indirect crystal structure verification of methyl glycosides based on acetates’ parent structures: GIPAW and solid-state NMR approaches. Chem. Phys. Lett. 2017, 686, 7–11. [Google Scholar] [CrossRef]
- Kaseman, D.C.; McKenney, M. Quadrupolar Coupling. 2020. Available online: https://chem.libretexts.org/@go/page/1827 (accessed on 18 April 2021).
- Haasnoot, C.A.G.; de Leeuw, F.A.A.M.; Altona, C. The relationship between proton-proton NMR coupling constants and substituent electronegativities—I: An empirical generalization of the Karplus equation. Tetrahedron 1980, 36, 2783–2792. [Google Scholar] [CrossRef]
- Altona, C.; Ippel, J.H.; Hoekzema, A.J.A.W.; Erkelens, C.; Groesbeek, M.; Donders, L.A. Relationship between proton-proton NMR coupling constants and substituent electronegativities. V—Empirical substituent constants deduced from ethanes and propanes. Magn. Reson. Chem. 1989, 27, 564–576. [Google Scholar] [CrossRef]
- Altona, C.; Francke, R.; de Haan, R.; Ippel, J.H.; Daalmans, G.J.; Hoekzema, A.J.A.W.; van Wijk, J. Empirical group electronegativities for vicinal NMR proton-proton couplings along a C-C bond: Solvent effects and reparameterization of the Haasnoot equation. Magn. Reson. Chem. 1994, 32, 670–678. [Google Scholar] [CrossRef]
- Barfield, M.; Dean, A.M.; Fallick, C.J.; Spear, R.J.; Sternhell, S.; Westerman, P.W. Conformational dependence and mechanisms for long-range hydrogen-hydrogen coupling constants over four bonds. J. Am. Chem. Soc. 1975, 97, 1482–1492. [Google Scholar] [CrossRef]
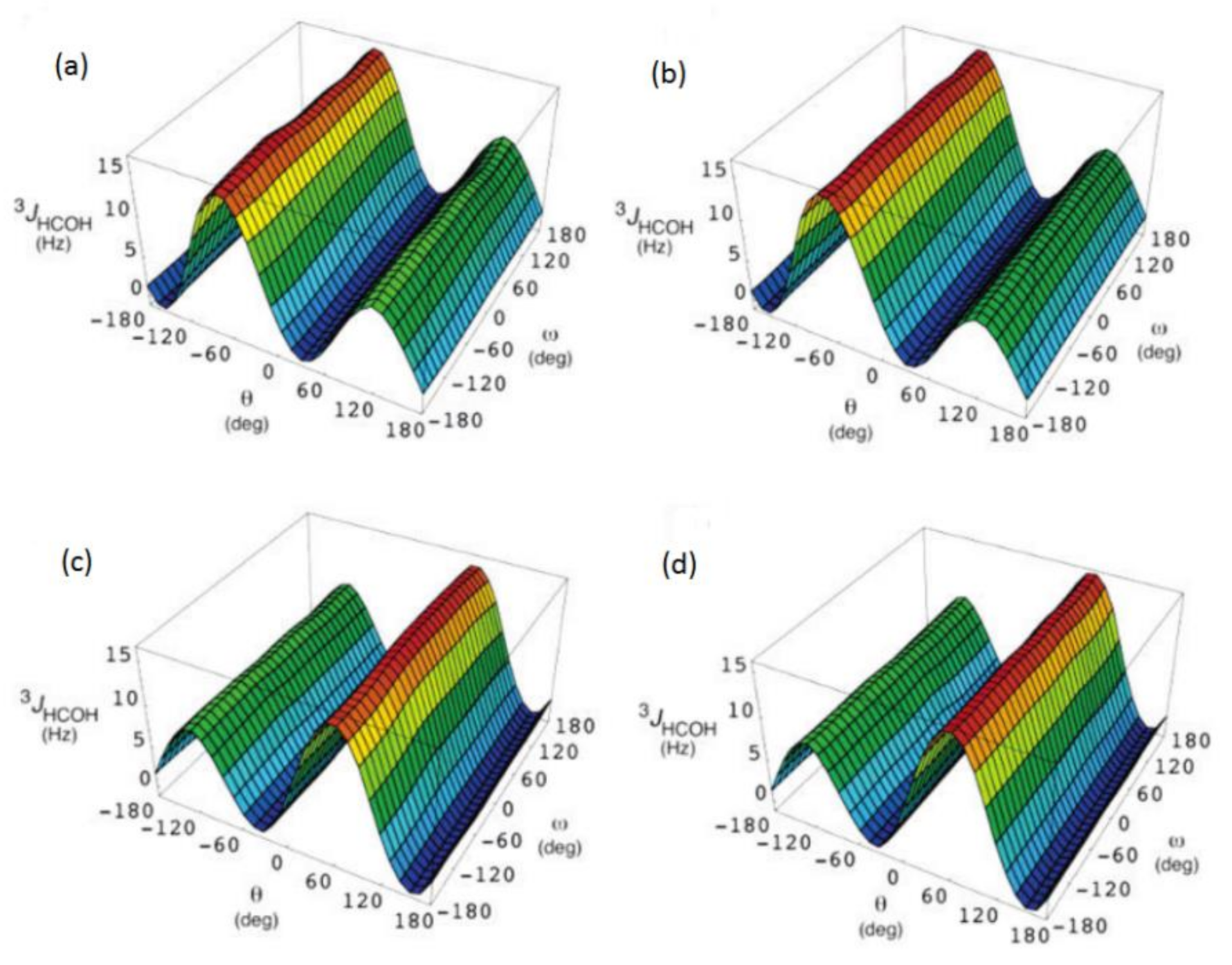
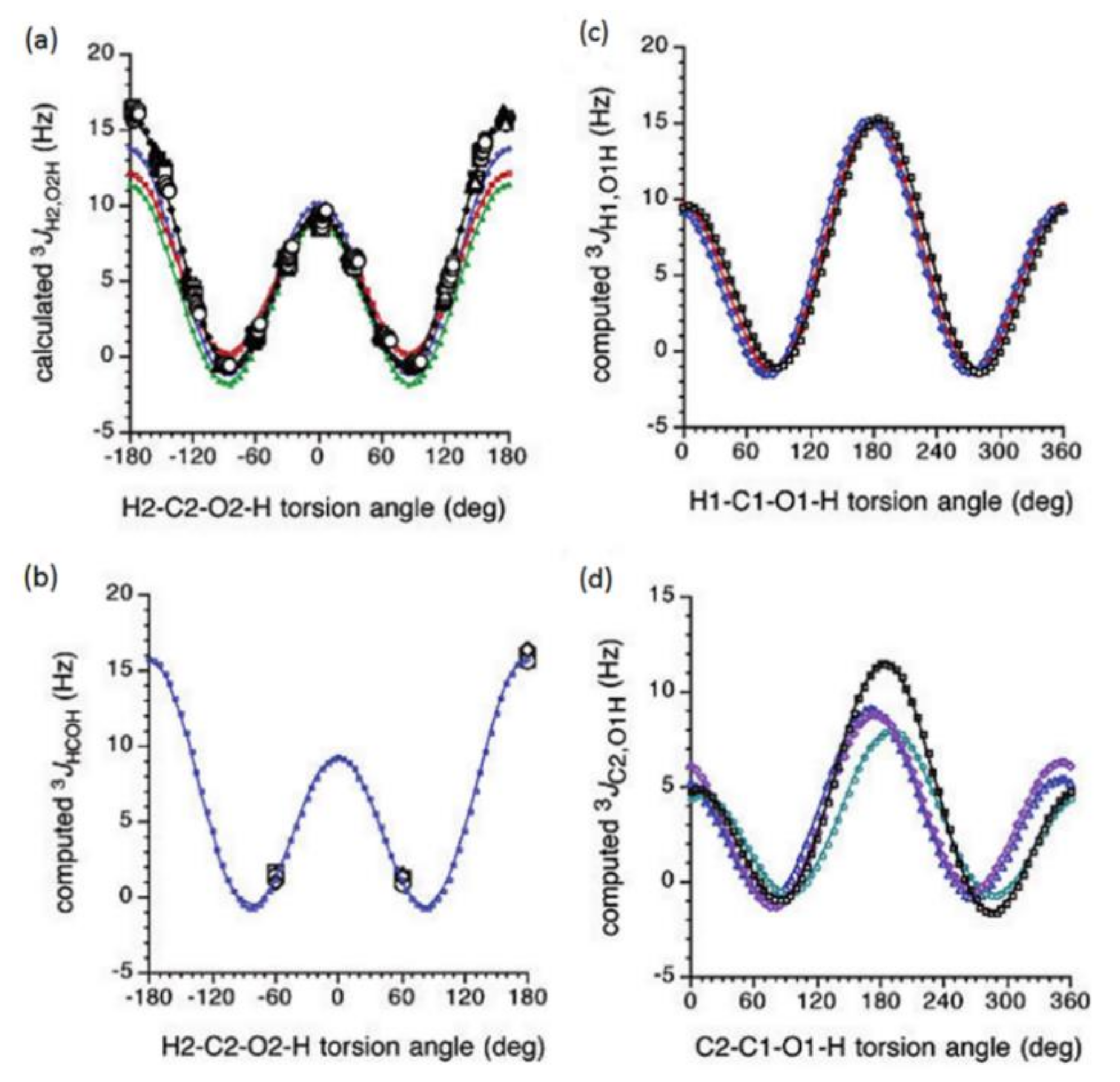
- Zhao, H.; Pan, Q.; Zhang, W.; Carmichael, I.; Serianni, A.S. DFT and NMR studies of 2JCOH, 3JHCOH, and 3JCCOH spin-couplings in saccharides: C−O torsional bias and H-bonding in aqueous solution. J. Org. Chem. 2007, 72, 7071–7082. [Google Scholar] [CrossRef]
- Serianni, A.S.; Wu, J.; Carmichael, I. One-bond 13C-1H spin-coupling constants in aldofuranosyl rings: Effect of conformation on coupling magnitude. J. Am. Chem. Soc. 1995, 117, 8645–8650. [Google Scholar] [CrossRef]
- Podlasek, C.A.; Wu, J.; Stripe, W.A.; Bondo, P.B.; Serianni, A.S. [13C]-Enriched methyl aldopyranosides: Structural interpretations of 13C–1H spin-coupling constants and 1H chemical shifts. J. Am. Chem. Soc. 1995, 117, 8635–8644. [Google Scholar] [CrossRef]
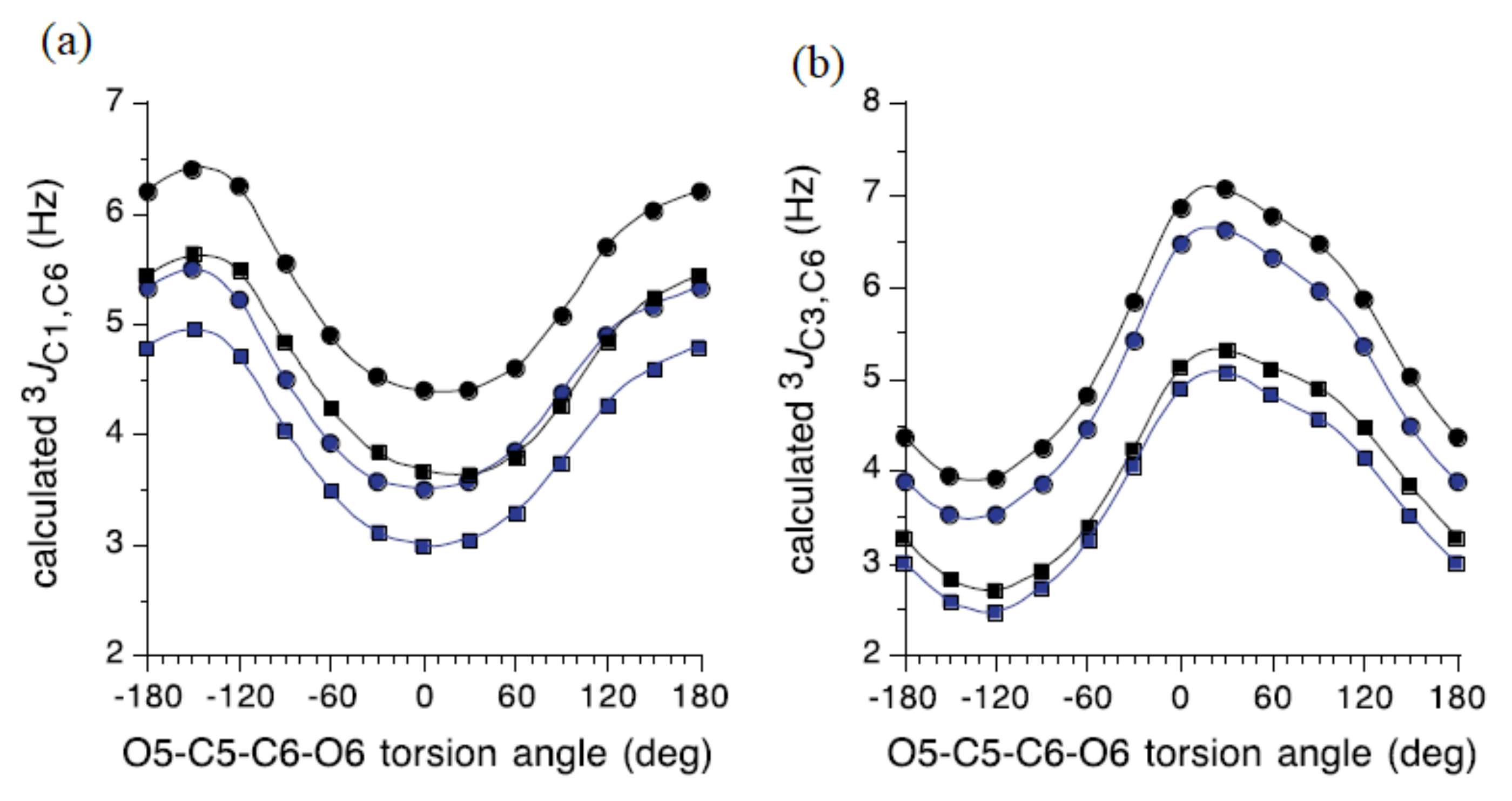
- Thibaudeau, C.; Stenutz, R.; Hertz, B.; Klepach, T.; Zhao, S.; Wu, Q.; Carmichael, I.; Serianni, A.S. Correlated C−C and C−O bond conformations in saccharide hydroxymethyl groups: parametrization and application of redundant 1H−1H, 13C−1H, and 13C−13C-NMR J.-couplings. J. Am. Chem. Soc. 2004, 126, 15668–15685. [Google Scholar] [CrossRef]
- Klepach, T.; Carmichael, I.; Serianni, A.S. Geminal 2JCCH spin−spin coupling constants as probes of the φ glycosidic torsion angle in oligosaccharides. J. Am. Chem. Soc. 2005, 127, 9781–9793. [Google Scholar] [CrossRef]
- Tafazzoli, M.; Ghiasi, M. New Karplus equations for 2JHH, 3JHH, 2JCH, 3JCH, 3JCOCH, 3JCSCH, and 3JCCCH in some aldohexopyranoside derivatives as determined using NMR spectroscopy and density functional theory calculations. Carbohydr. Res. 2007, 342, 2086–2096. [Google Scholar] [CrossRef]
- Carmichael, I.; Chipman, D.M.; Podlasek, C.A.; Serianni, A.S. Torsional effects on the one-bond 13C-13C spin coupling constant in ethylene glycol: Insights into the behavior of 1JCC in carbohydrates. J. Am. Chem. Soc. 1993, 115, 10863–10870. [Google Scholar] [CrossRef]
- Church, T.; Carmichael, I.; Serianni, A.S. Two-bond 13C-13C spin-coupling constants in carbohydrates: Effect of structure on coupling magnitude and sign. Carbohydr. Res. 1996, 280, 177–186. [Google Scholar] [CrossRef]
- Serianni, A.S.; Bondo, P.B.; Zajicek, J. Verification of the projection resultant method for two-bond 13C-13C coupling sign determinations in carbohydrates. J. Magn. Reson. Ser. B 1996, 112, 69–74. [Google Scholar] [CrossRef]
- Zhao, H.; Carmichael, I.; Serianni, A.S. Oligosaccharide trans-glycoside 3JCOCC Karplus curves are not equivalent: Effect of internal electronegative substituents. J. Org. Chem. 2008, 73, 3255–3257. [Google Scholar] [CrossRef] [PubMed]
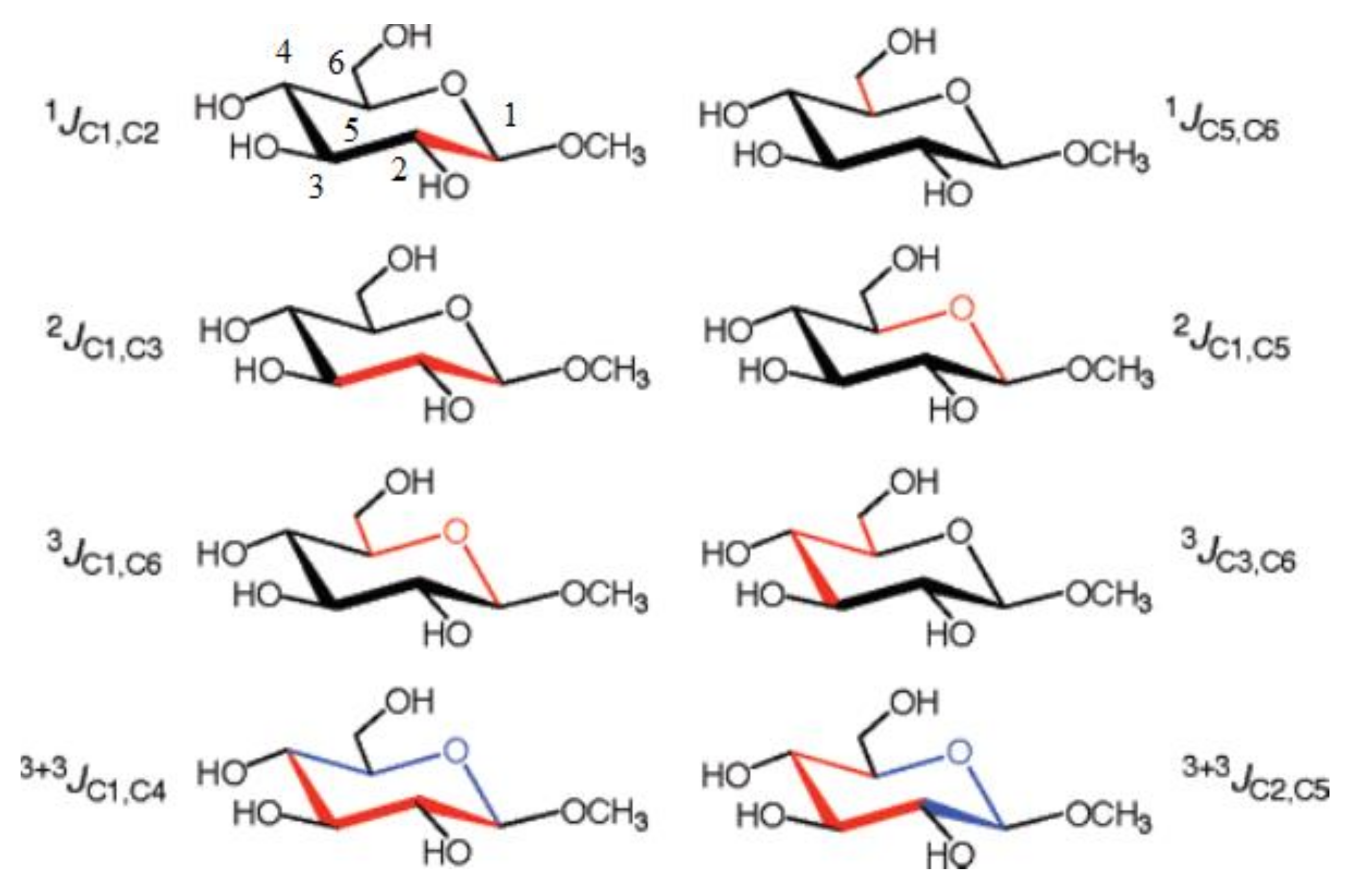
- Bose-Basu, B.; Klepach, T.; Bondo, G.; Bondo, P.B.; Zhang, W.; Carmichael, I.; Serianni, A.S. 13C−13C-NMR spin-spin coupling constants in saccharides: Structural correlations involving all carbons in aldohexopyranosyl rings. J. Org. Chem. 2007, 72, 7511–7522. [Google Scholar] [CrossRef] [PubMed]
- Stenutz, R.; Carmichael, I.; Widmalm, G.; Serianni, A.S. Hydroxymethyl group conformation in saccharides: Structural dependencies of 2JHH, 3JHH, and 1JCH spin-spin coupling constants. J. Org. Chem. 2002, 67, 949–958. [Google Scholar] [CrossRef]
- Danilova, V.A. Stereochemical Dependences of 13C-13C Spin-Spin Coupling Constants of Carbohydrates. Ph.D. Thesis, Irkutsk Institute of Chemistry of the Russian Academy of Sciences, Irkutsk, Russia, 2003. [Google Scholar]
- Danilova, V.A.; Krivdin, L.B. 13C-13C Coupling constants in structural studies: XXXIII. Stereochemical study of the pyranose ring. Russ. J. Org. Chem. 2003, 39, 663–671. [Google Scholar] [CrossRef]
- Danilova, V.A.; Krivdin, L.B. 13C-13C Spin-spin coupling constants in structural studies: XXXV. Stereochemical study of the furanose ring. Russ. J. Org. Chem. 2003, 39, 1764–1771. [Google Scholar] [CrossRef]
- Danilova, V.A.; Krivdin, L.B. 13C-13C Spin-spin coupling constants in structural studies: XXXVI. Stereochemical study of the septanose ring. Russ. J. Org. Chem. 2004, 40, 57–62. [Google Scholar] [CrossRef]
- Danilova, V.A.; Istomina, N.V.; Krivdin, L.B. 13C-13C Spin-spin coupling constants in structural studies: XXXVII. Rotational conformations of hydroxy groups in pyranose, furanose, and septanose rings. Russ. J. Org. Chem. 2004, 40, 1194–1199. [Google Scholar] [CrossRef]
- Taurian, O.E.; Contreras, R.H.; de Kowalewski, D.G.; Pérez, J.E.; Tormena, C.F. Lone-pair orientation effect of an α-oxygen atom on 1JCC NMR spin-spin coupling constants in o-substituted phenols. Experimental and DFT study. J. Chem. Theory Comput. 2007, 3, 1284–1294. [Google Scholar] [CrossRef] [PubMed]
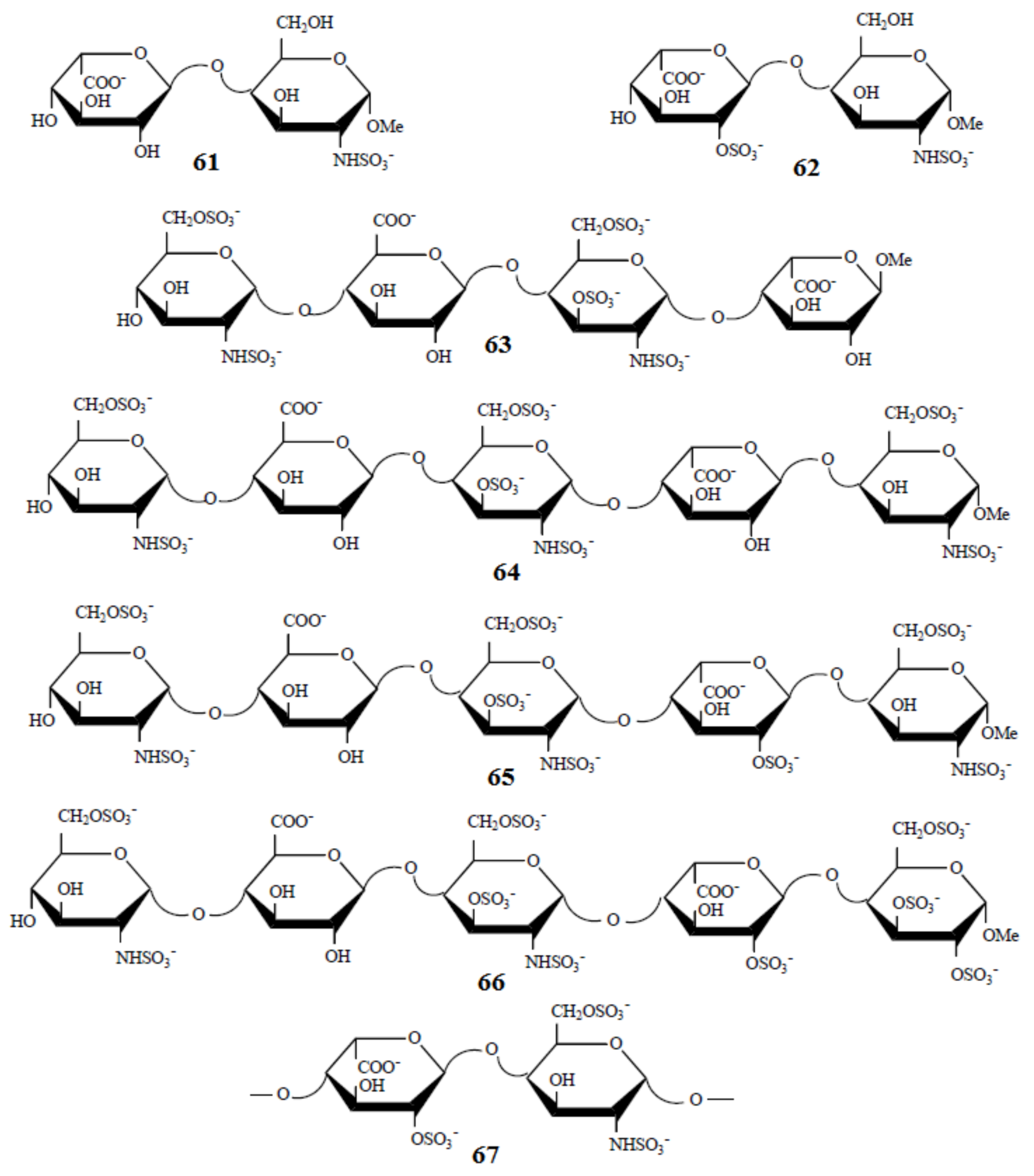
- Guerrini, M.; Hricovíni, M.; Torri, G. Interaction of heparins with fibroblast growth factors: Conformational aspects. Curr. Pharm. Des. 2007, 13, 2045–2056. [Google Scholar] [CrossRef] [PubMed]
- Hricovíni, M.; Scholtzová, E.; Bízik, F. B3LYP/6-311++G** study of structure and spin-spin coupling constant in heparin disaccharide. Carbohydr. Res. 2007, 342, 1350–1356. [Google Scholar] [CrossRef]
- Hricovíni, M. Effect of solvent and counterions upon structure and nmr spin-spin coupling constants in heparin disaccharide. J. Phys. Chem. B 2011, 115, 1503–1511. [Google Scholar] [CrossRef]
- Hricovíni, M.; Driguez, P.-A.; Malkina, O.L. NMR and DFT analysis of trisaccharide from heparin repeating sequence. J. Phys. Chem. B 2014, 118, 11931–11942. [Google Scholar] [CrossRef]
- Rudd, T.R.; Yates, E.A.; Hricovíni, M. Spectroscopic and theoretical approaches for the determination of heparin saccharide structure and the study of protein-glycosaminoglycan complexes in solution. Curr. Med. Chem. 2009, 16, 4750–4766. [Google Scholar] [CrossRef] [PubMed]
- Hricovíni, M.; Hricovíni, M. Solution conformation of heparin tetrasaccharide. DFT analysis of structure and spin-spin coupling constants. Molecules 2018, 23, 3042. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hricovini, M. The solution structure of heparin pentasaccharide: NMR and DFT analysis. J. Phys. Chem. B 2015, 119, 12397–12409. [Google Scholar] [CrossRef]
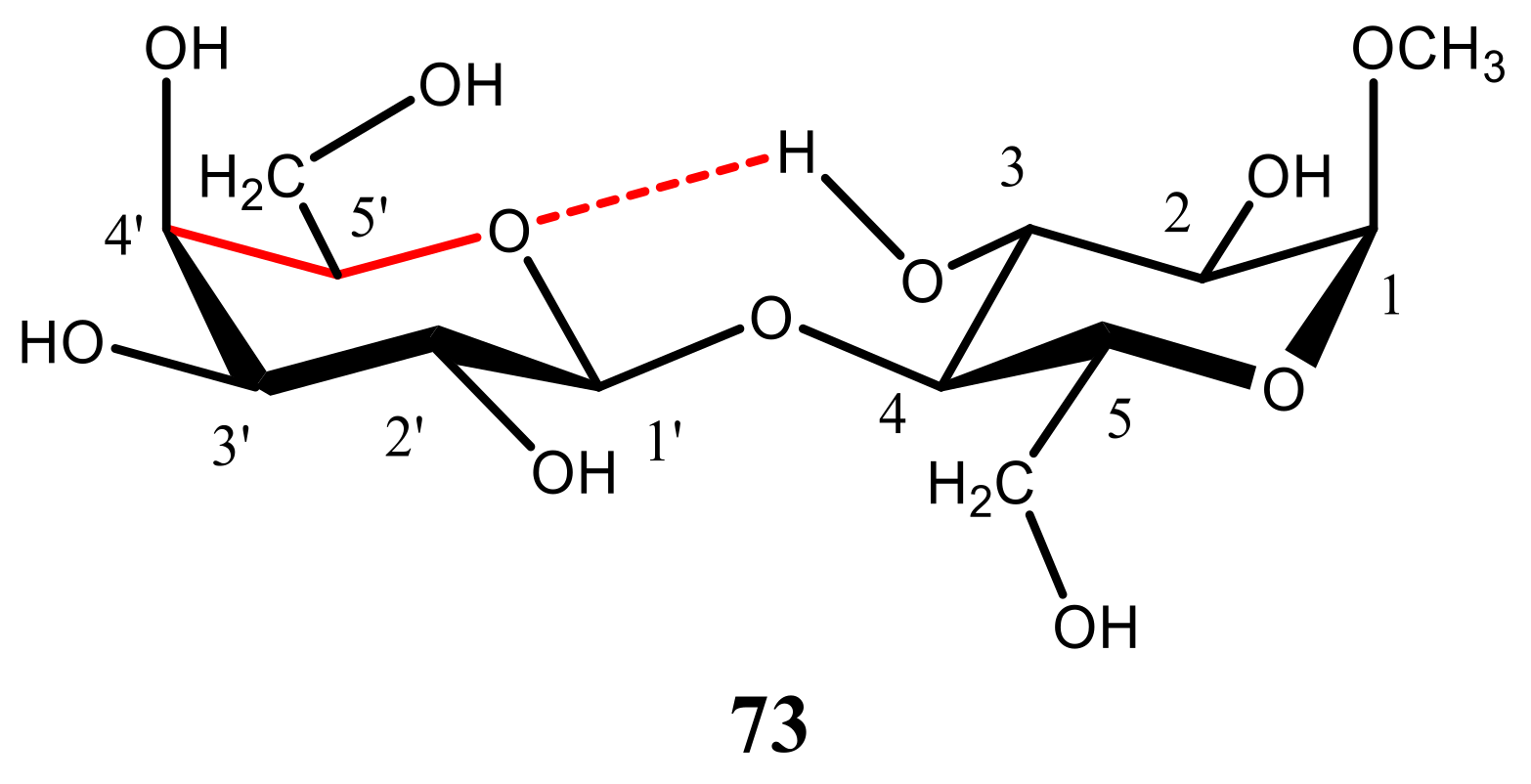
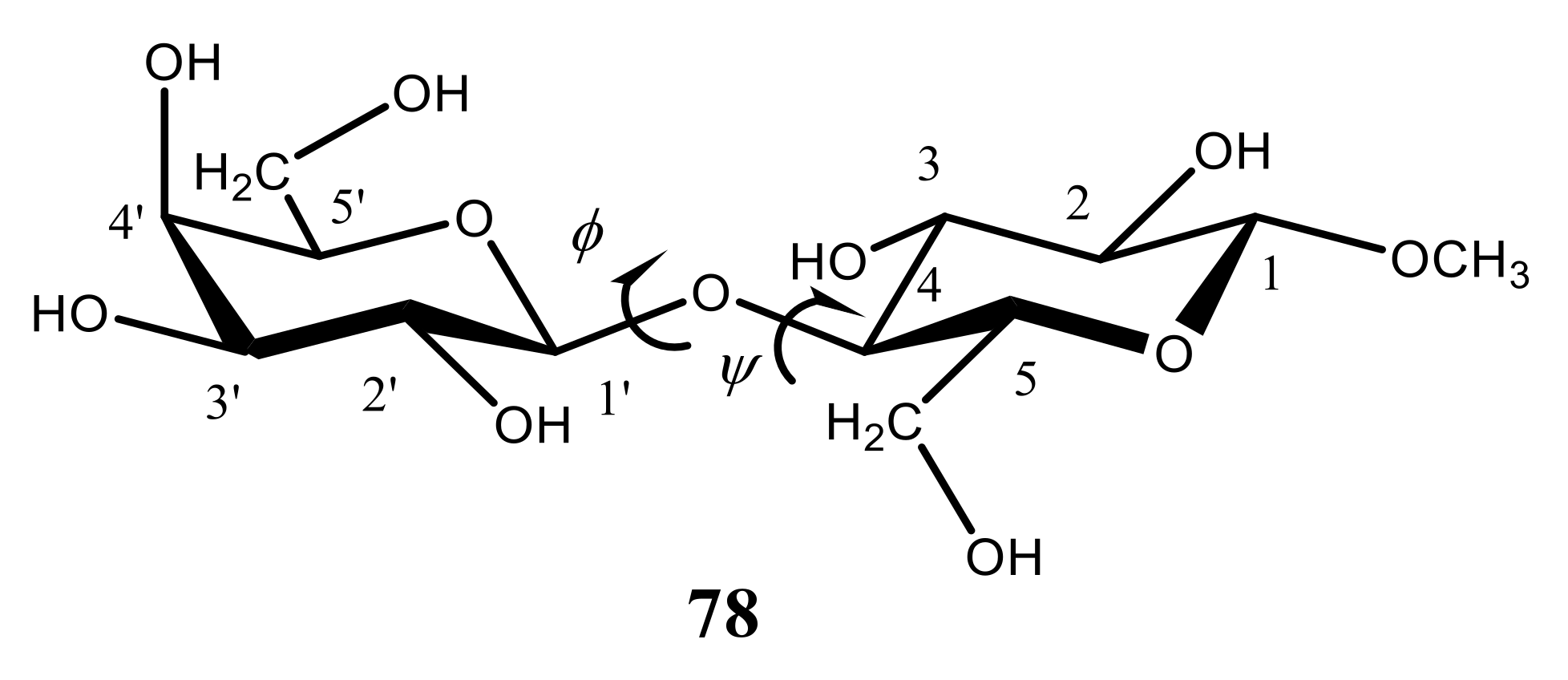
- Zhang, W.; Zhao, H.; Carmichael, I.; Serianni, A.S. An NMR investigation of putative interresidue H-bonding in methyl α-cellobioside in solution. Carbohydr. Res. 2009, 344, 1582–1587. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Turney, T.; Meredith, R.; Pan, Q.; Sernau, L.; Wang, X.; Hu, X.; Woods, R.J.; Carmichael, I.; Serianni, A.S. Conformational populations of β-(1→4) O-glycosidic linkages using redundant NMR J.-couplings and circular statistics. J. Phys. Chem. B 2017, 121, 3042–3058. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sefzik, T.H.; Turco, D.; Iuliucci, R.J.; Facelli, J.C. Modeling NMR chemical shift: A survey of density functional theory approaches for calculating tensor properties. J. Phys. Chem. A 2005, 109, 1180–1187. [Google Scholar] [CrossRef] [PubMed]
- Sergeyev, I.; Moyna, G. Determination of the three-dimensional structure of oligosaccharides in the solid state from experimental 13C-NMR data and ab initio chemical shift surfaces. Carbohydr. Res. 2005, 340, 1165–1174. [Google Scholar] [CrossRef]
- Kapla, J.; Engström, O.; Stevensson, B.; Wohlert, J.; Widmalm, G.; Maliniak, K. Molecular dynamics simulations and NMR spectroscopy studies of trehalose-lipid bilayer systems. Phys. Chem. Chem. Phys. 2015, 17, 22438–22447. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, J.; Zhang, H.; Wu, J.; Zhang, J.; He, J.; Xiang, J. NMR spectroscopic studies of cellobiose solvation in EmimAc aimed to understand the dissolution mechanism of cellulose in ionic liquids. Phys. Chem. Chem. Phys. 2010, 12, 1941–1947. [Google Scholar] [CrossRef] [PubMed]
- Esrafili, M.D.; Elmi, F.; Hadipour, N.L. Density functional theory investigation of hydrogen bonding effects on the oxygen, nitrogen and hydrogen electric field gradient and chemical shielding tensors of anhydrous chitosan crystalline structure. J. Phys. Chem. A 2007, 111, 963–970. [Google Scholar] [CrossRef]
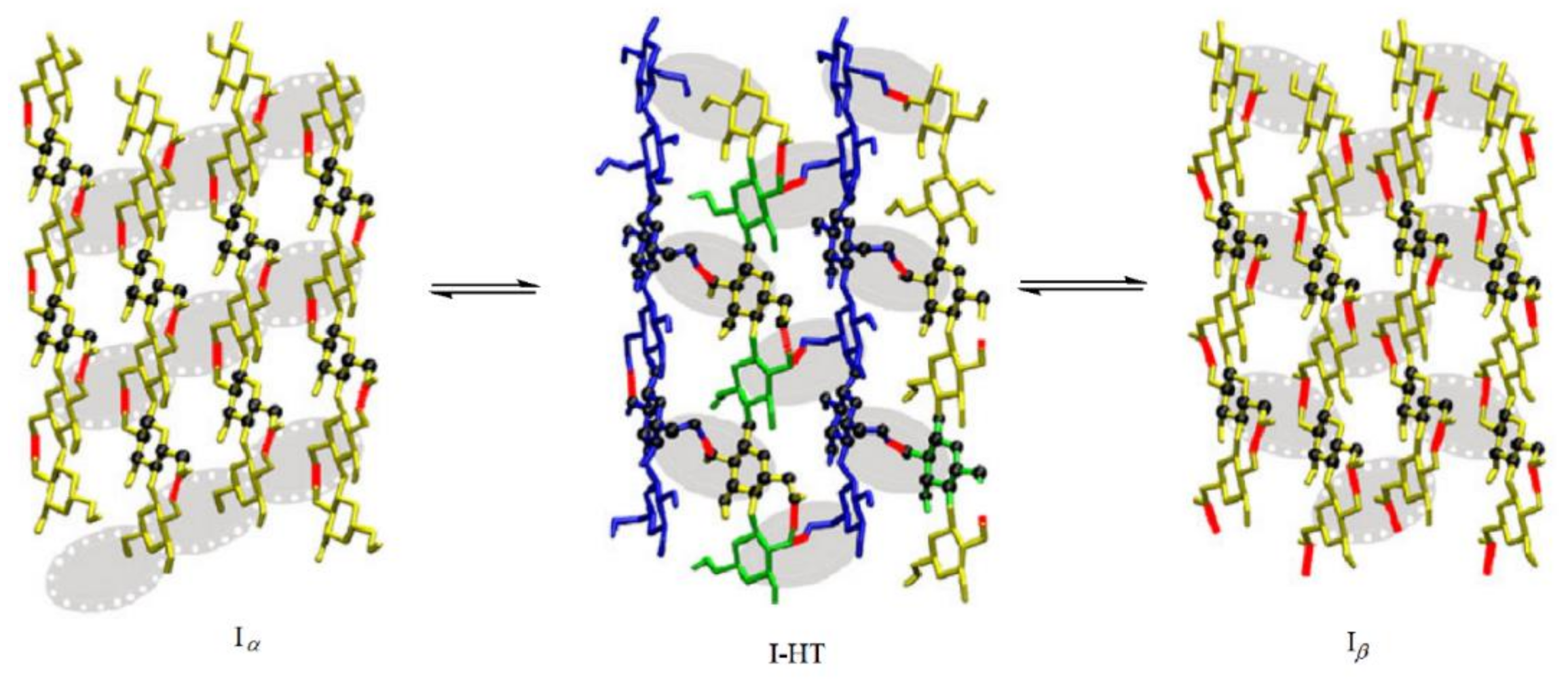
- Matthews, J.F.; Himmel, M.E.; Crowley, M.F. Conversion of cellulose Iα to Iβ via a high temperature intermediate (I-HT) and other cellulose phase transformations. Cellulose 2012, 19, 297–306. [Google Scholar] [CrossRef] [Green Version]
- Kasat, R.B.; Wang, N.-H.L.; Franses, E.I. Effects of backbone and side chain on the molecular environments of chiral cavities in polysaccharide-based biopolymers. Biomacromolecules 2007, 8, 1676–1685. [Google Scholar] [CrossRef]
- Lefort, R.; Bordat, P.; Attilio Cesaro, A.; Descamps, M. Exploring conformational energy landscape of glassy disaccharides by cross polarization magic angle spinning 13C-NMR and numerical simulations. I. Methodological aspects. J. Chem. Phys. 2007, 126, 014510. [Google Scholar]
- Shao, L.; Yates, J.R.; Titman, J.J. Carbon-13 chemical shift tensors of disaccharides: Measurement, computation and assignment. J. Phys. Chem. A 2007, 111, 13126–13132. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar] [CrossRef] [Green Version]
- Navarro, D.A.; Stortz, C.A. DFT/MM modeling of the five-membered ring in 3,6-anhydrogalactose derivatives and its influence on disaccharide adiabatic maps. Carbohyd. Res. 2008, 343, 2292–2298. [Google Scholar] [CrossRef]
- Suzuki, S.; Horii, F.; Kurosu, H. Theoretical investigations of 13C chemical shifts in glucose, cellobiose, and native cellulose by quantum chemistry calculations. J. Mol. Struct. 2009, 921, 219–226. [Google Scholar] [CrossRef]
- Klemm, D.; Heublein, B.; Fink, H.-P.; Bohn, A. Cellulose: Fascinating biopolymer and sustainable raw material. Angew. Chem. Int. Ed. 2005, 44, 3358–3393. [Google Scholar] [CrossRef]
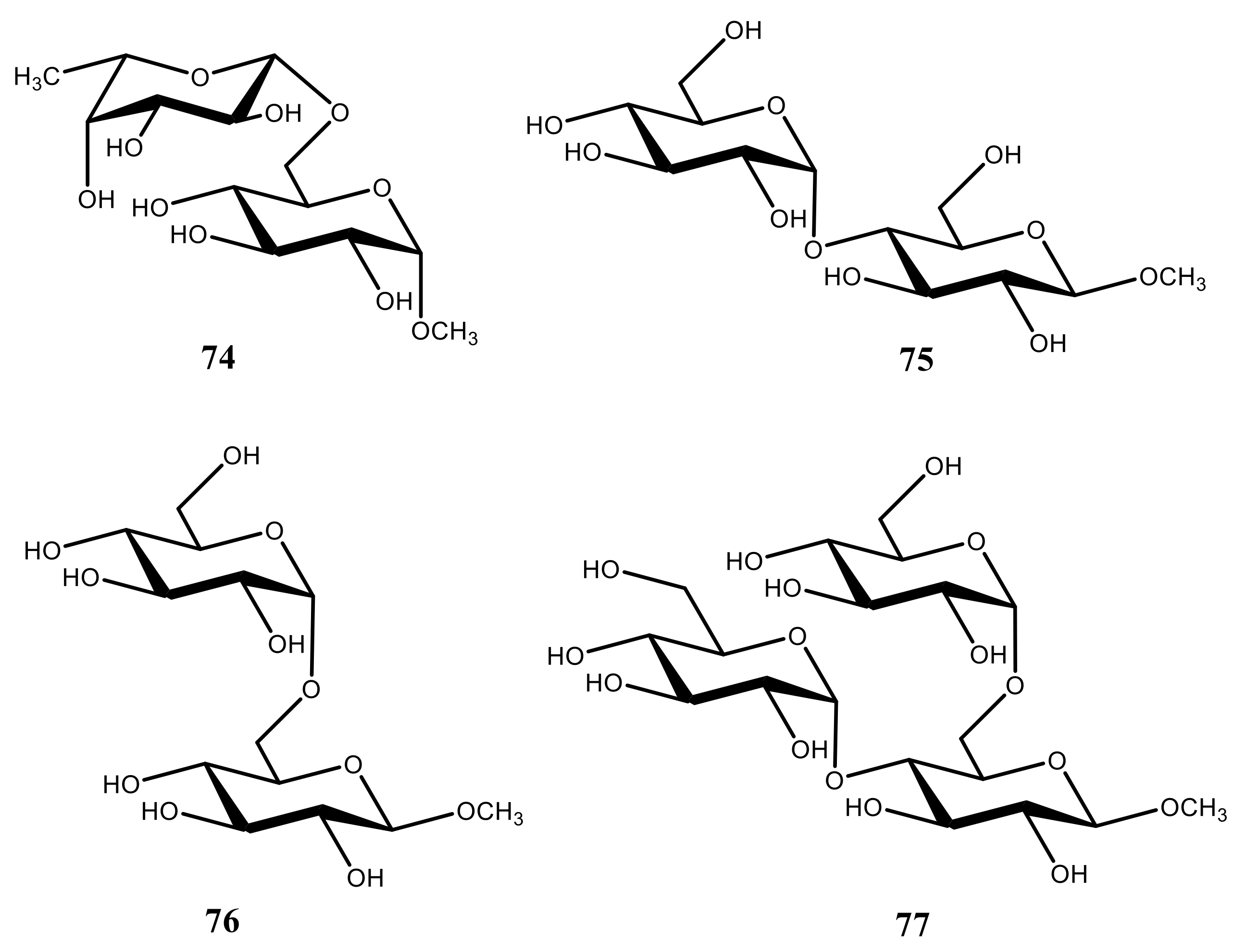
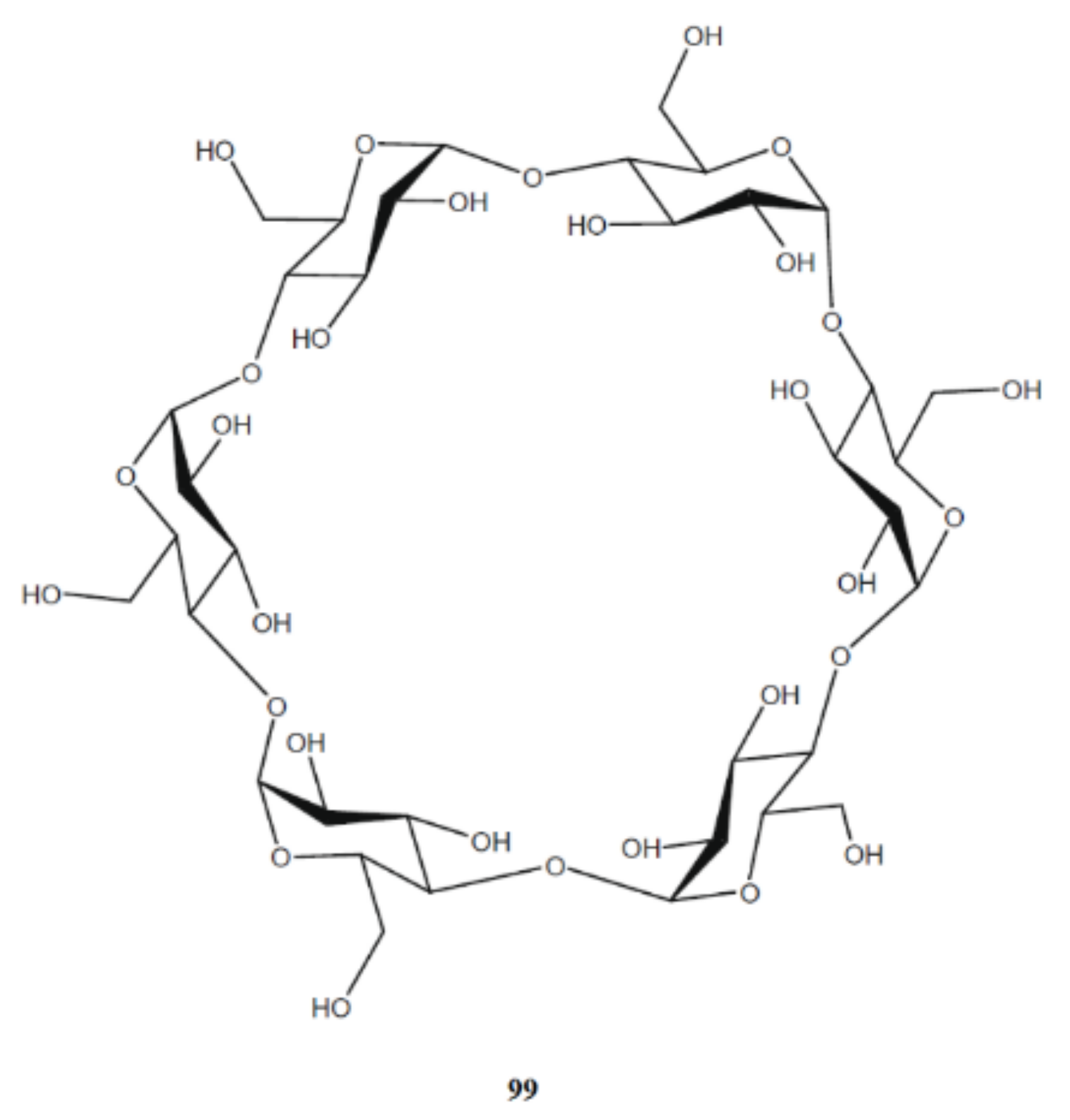
- Tafazzoli, M.; Ghiasi, M. Structure and conformation of α-, β- and γ-cyclodextrin in solution: Theoretical approaches and experimental validation. Carbohydr. Pol. 2009, 78, 10–15. [Google Scholar] [CrossRef]
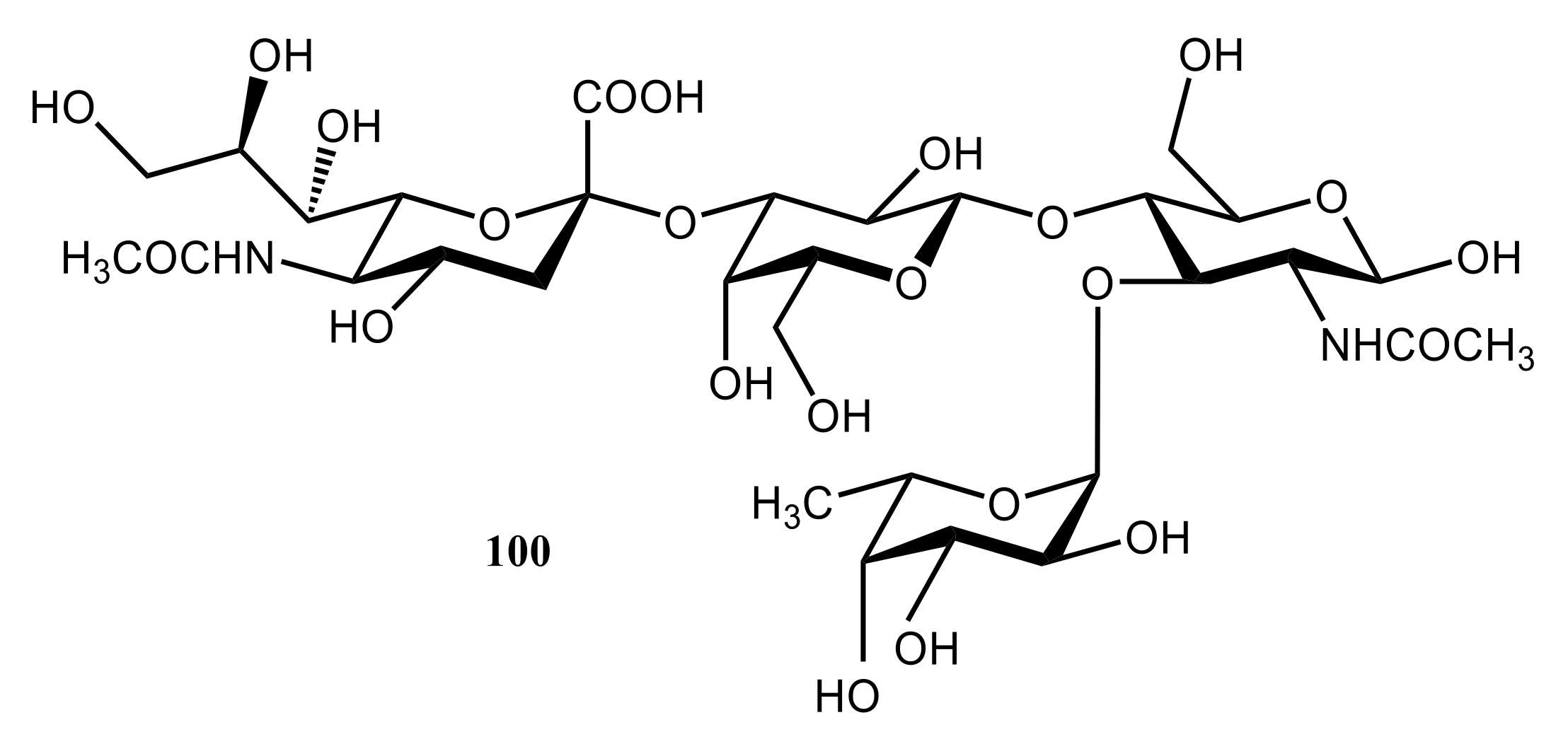
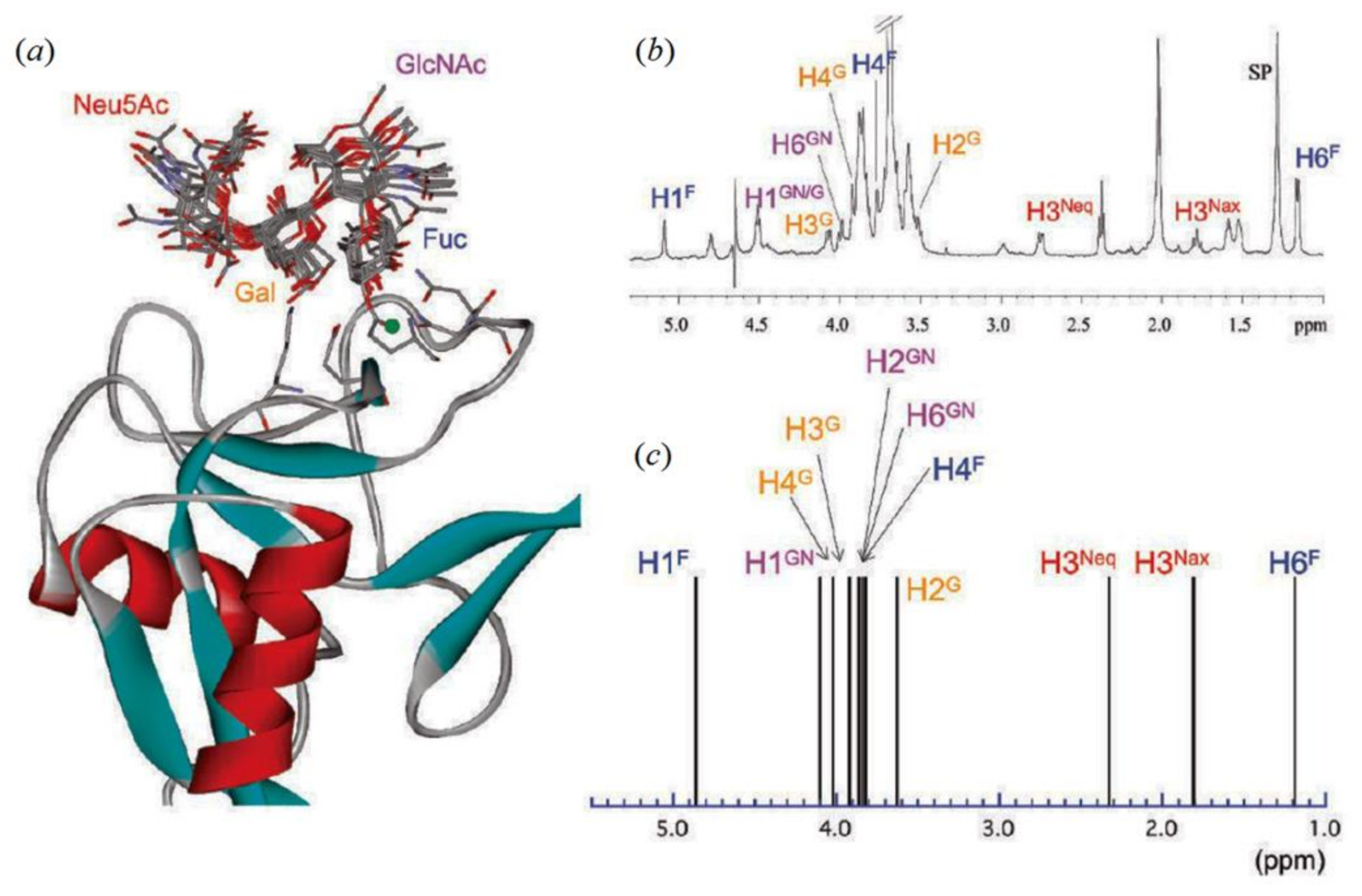
- Ishida, T. Computational modeling of carbohydrate-recognition process in E-selectin complex: Structural mapping of Sialyl Lewis X onto ab initio QM/MM free energy surface. J. Phys. Chem. B 2010, 114, 3950–3964. [Google Scholar] [CrossRef] [PubMed]





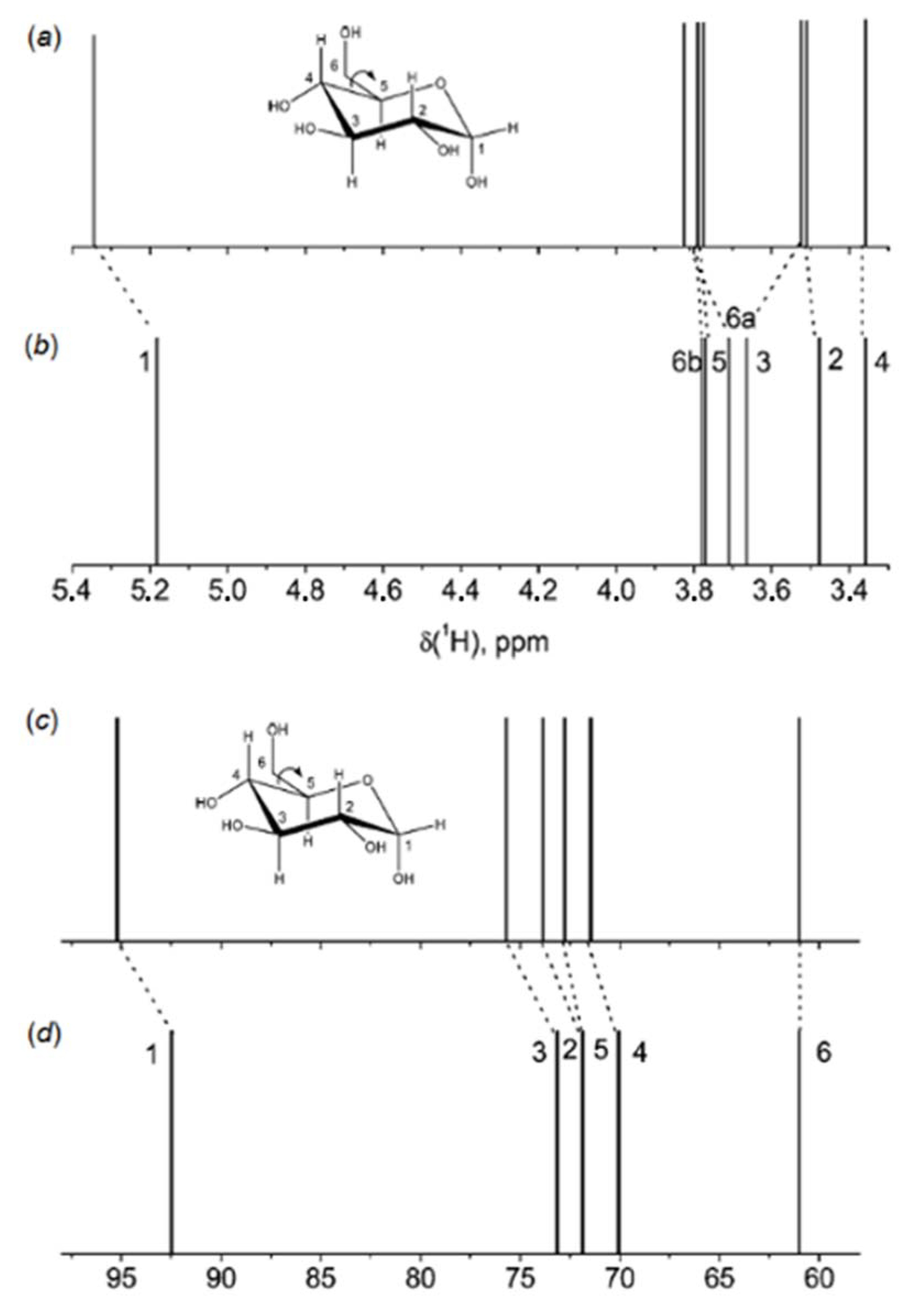

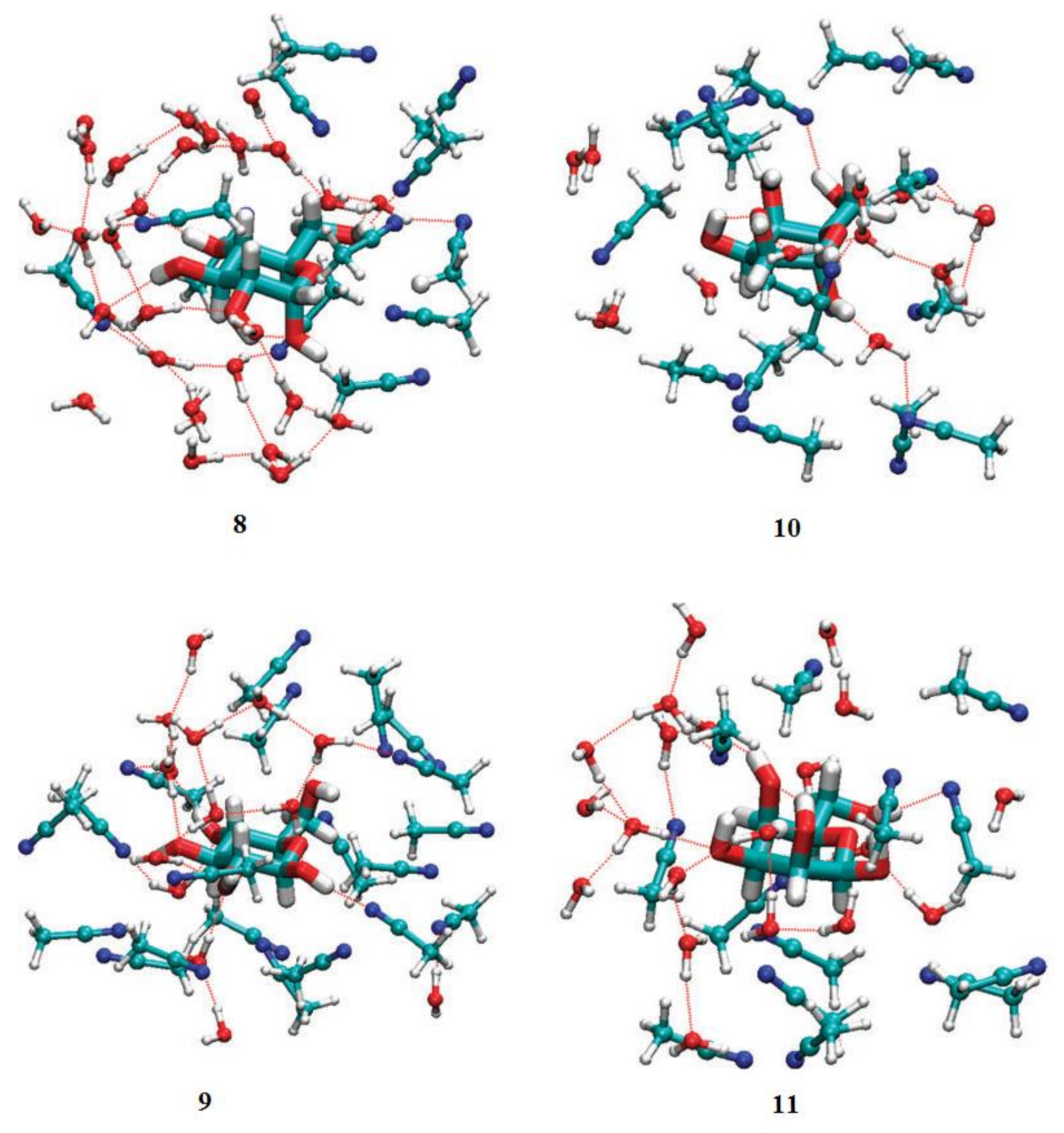
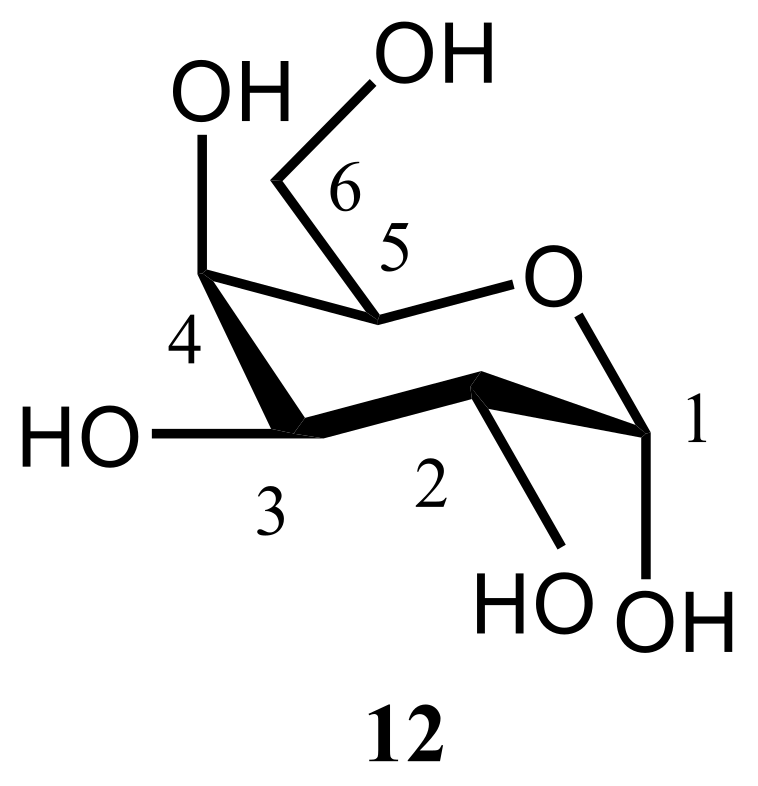
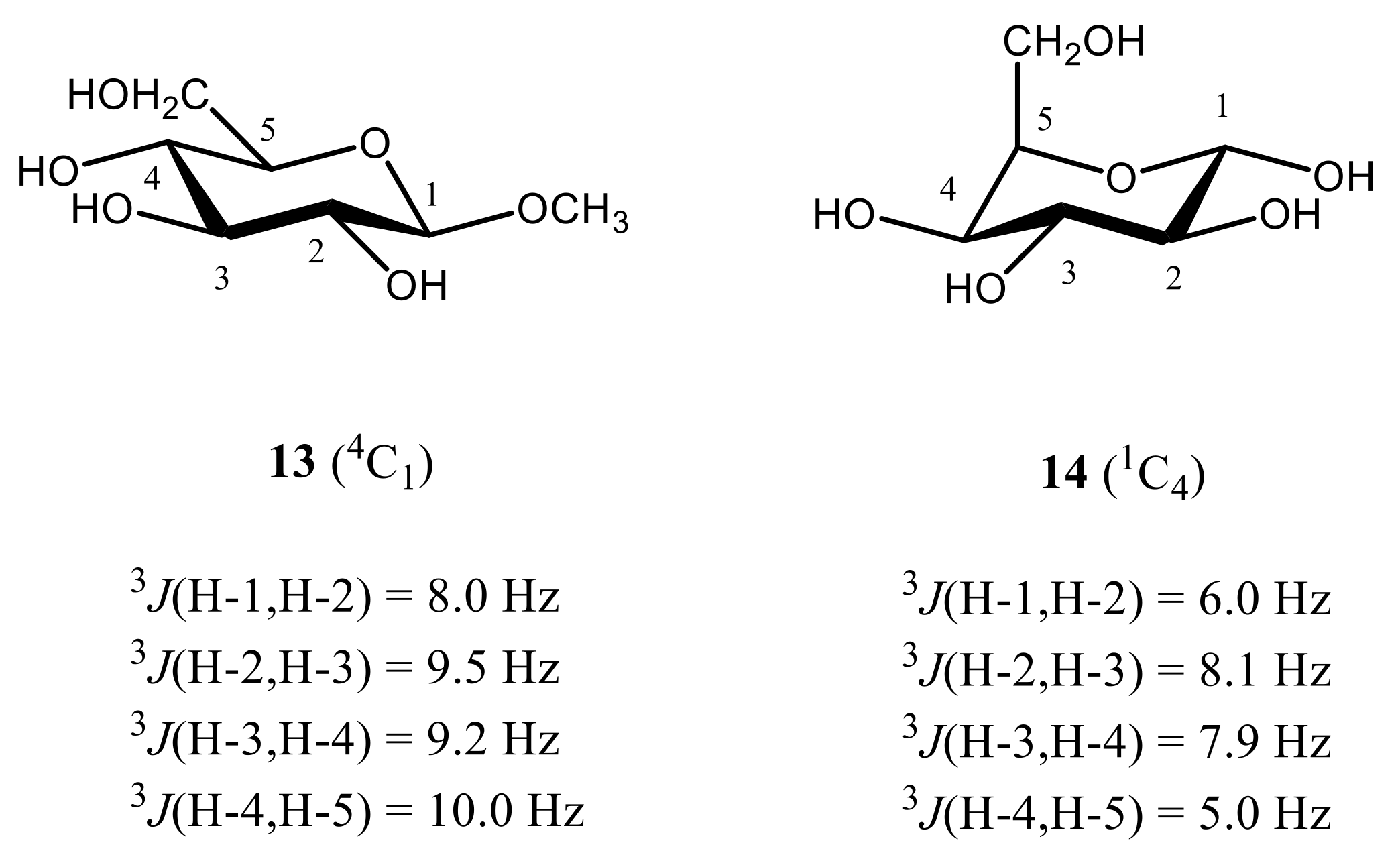














| NMR Parameter | α-D-Glucopyranose | β-D-Glucopyranose | ||
|---|---|---|---|---|
| Calc. | Exp. | Calc. | Exp. | |
| H-1 | 5.301 | 5.214 | 4.586 | 4.627 |
| H-2 | 3.273 | 3.516 | 3.152 | 3.226 |
| H-3 | 3.653 | 3.696 | 3.478 | 3.469 |
| H-4 | 3.589 | 3.393 | 3.614 | 3.385 |
| H-5 | 3.907 | 3.817 | 3.422 | 3.447 |
| H-6a | 3.913 | 3.823 | 3.966 | 3.879 |
| H-6b | 3.768 | 3.745 | 3.753 | 3.704 |
| MAD | 0.110 | 0.073 | ||
| C-1 | 104.74 | 92.77 | 108.59 | 96.59 |
| C-2 | 82.14 | 72.15 | 85.01 | 74.81 |
| C-3 | 83.96 | 73.43 | 86.00 | 76.43 |
| C-4 | 79.55 | 70.32 | 79.23 | 70.27 |
| C-5 | 81.89 | 72.10 | 86.58 | 76.61 |
| C-6 | 70.10 | 61.27 | 70.18 | 61.42 |
| MAD | 10.06 | 9.91 | ||
| 3J(H-1,H-2) | 4.59 | 3.80 | 7.75 | 7.97 |
| 4J(H-1,H-3) | −0.45 | −0.39 | 0.00 | |
| 4J(H-1,H-5) | -0.80 | −0.53 | −0.01 | |
| 3J(H-2,H-3) | 9.83 | 9.84 | 9.58 | 9.46 |
| 3J(H-3,H-4) | 9.26 | 9.17 | 9.11 | 9.17 |
| 3J(H-4,H-5) | 10.06 | 9.99 | 9.74 | 9.92 |
| 3J(H-5,H-6a) | 4.00 | 2.31 | 3.84 | 2.27 |
| 3J(H-5,H-6b) | 6.23 | 5.40 | 7.49 | 5.95 |
| 3J(H-6a,H-6b) | −13.01 | −12.37 | −12.99 | −12.30 |
| MAD | 0.49 | 0.62 | ||
| Atom | PBE | KT3 | Exp. | ||
|---|---|---|---|---|---|
| Model A | Model B | Model A | Model B | ||
| C-1 | 95.0 | 96.5 | 94.5 | 96.1 | 92.4 |
| C-2 | 70.3 | 69.2 | 69.9 | 68.9 | 70.4 |
| C-3 | 70.0 | 69.5 | 69.9 | 69.2 | 70.6 |
| C-4 | 70.4 | 70.0 | 71.2 | 71.0 | 70.1 |
| C-5 | 68.8 | 68.9 | 68.1 | 69.0 | 68.8 |
| C-6 | 57.6 | 56.9 | 57.7 | 57.0 | 58.8 |
| MAE | 0.9 | 1.4 | 1.0 | 1.6 | |
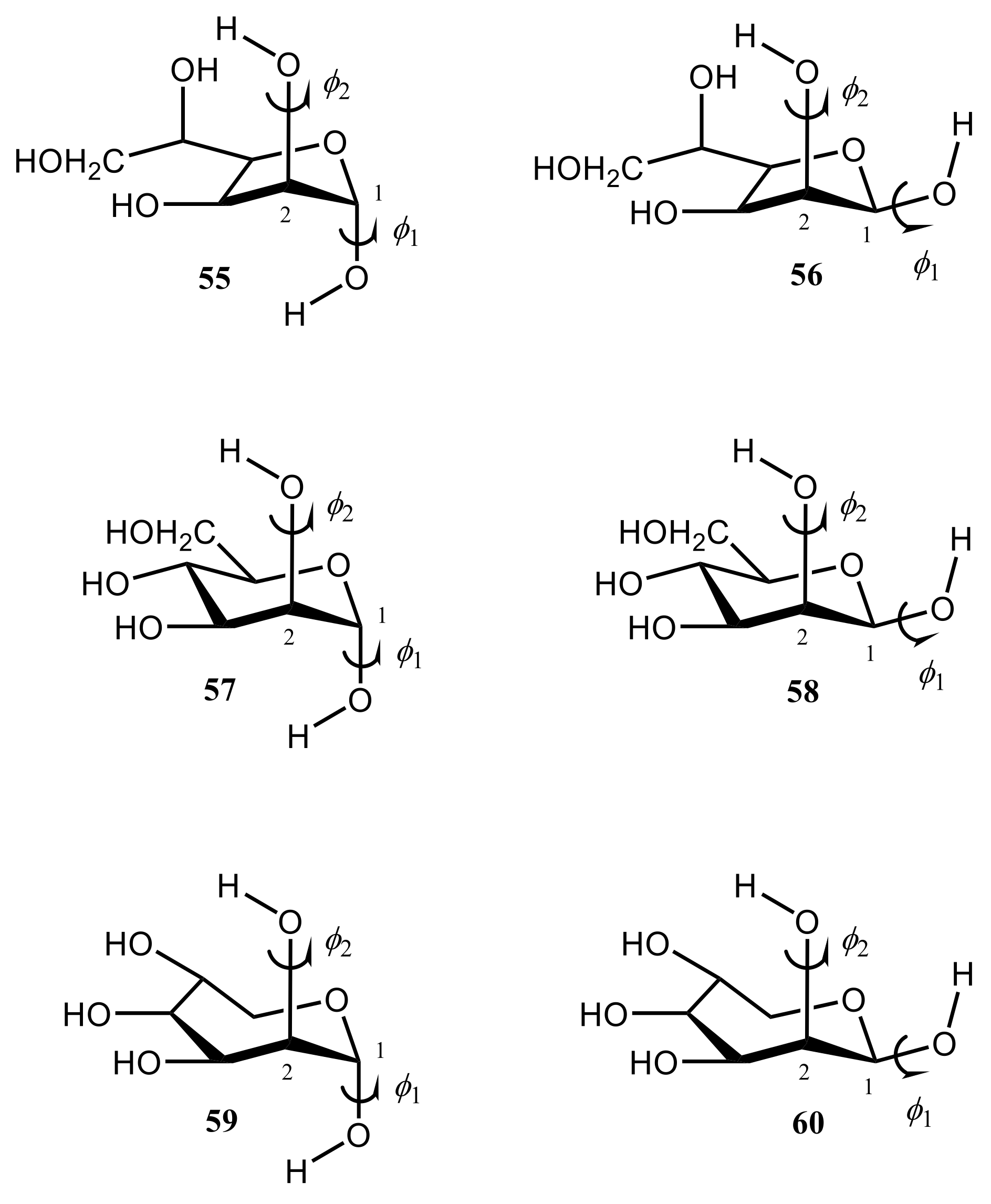
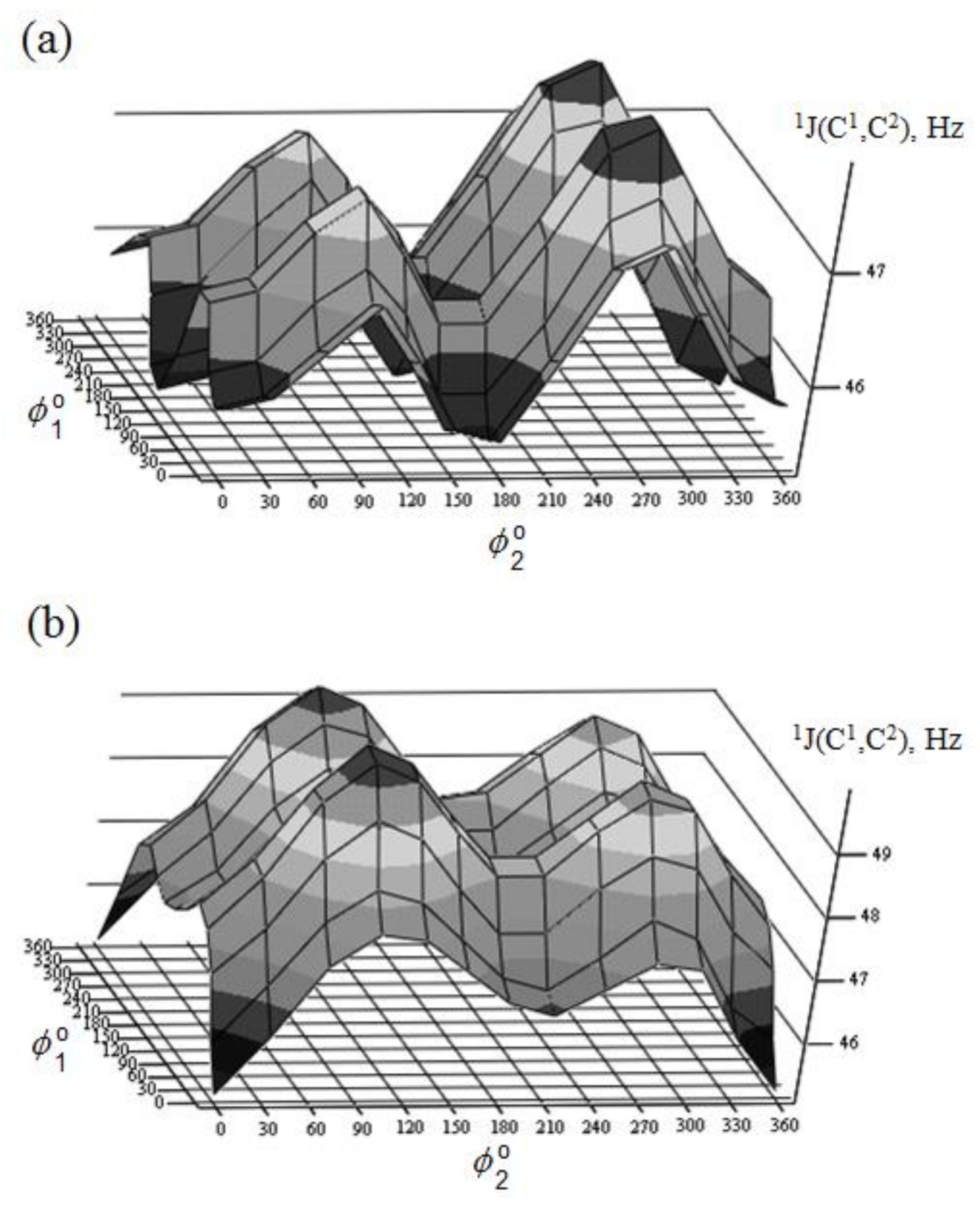
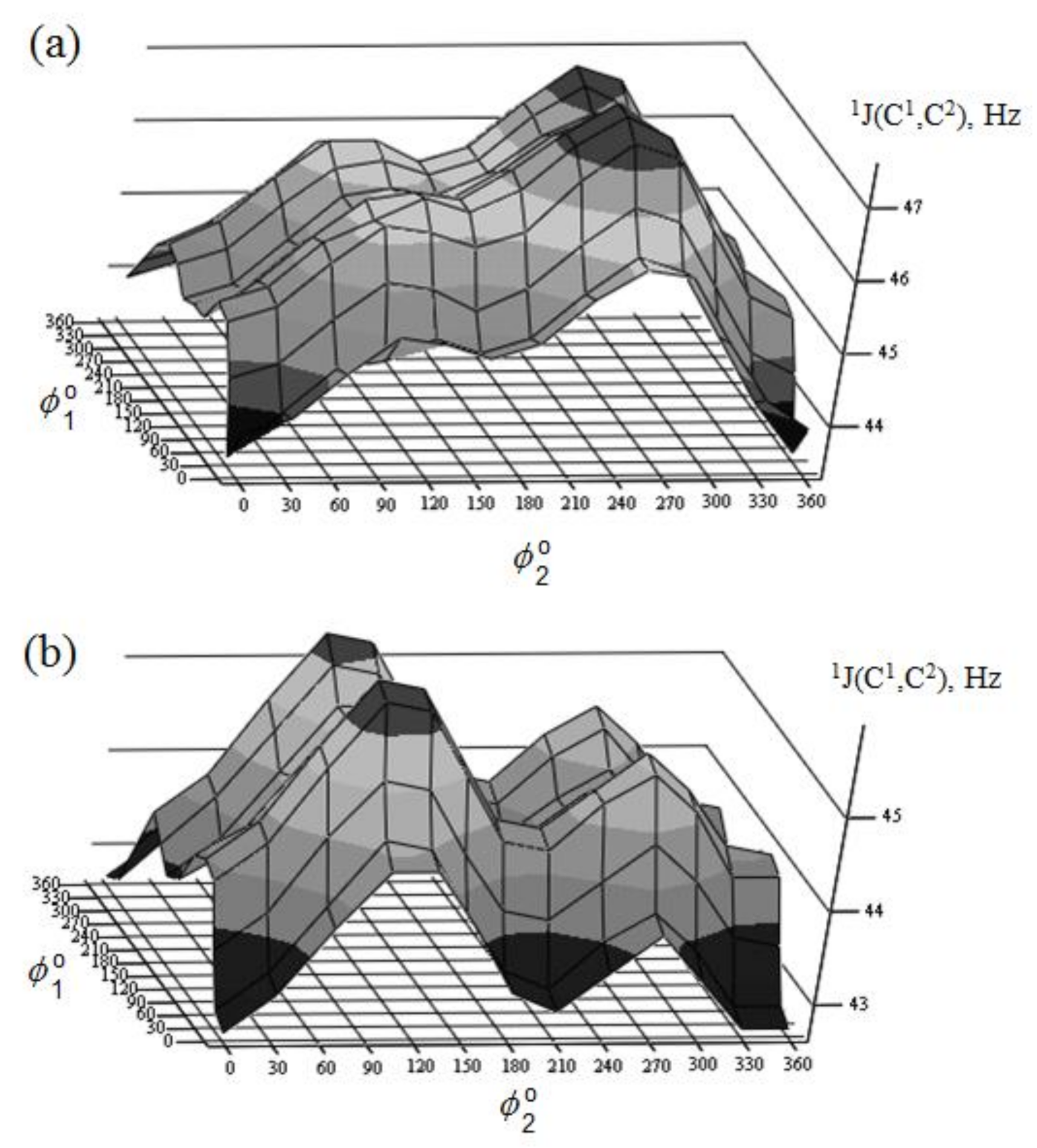
| Cmpd. | Orientation of OH at C1 and C2 | 1J(C-1,C-2) | Cmpd. | Orientation of OH at C1 and C2 | 1J(C-1,C-2) |
|---|---|---|---|---|---|
| α-D-allo-4C1 | ae | 44.8 (45.4) | α-D-gulo-4C1 | ae | 47.7 (45.9) |
| α-D-allo-1C4 | ea | 43.4 | α-D-gulo-1C4 | ea | 43.8 |
| β-D-allo-4C1 | ee | 47.9 (47.3) | β-D-gulo-4C1 | ee | 47.6 (47.7) |
| β-D-allo-1C4 | aa | 46.2 | β-D-gulo-1C4 | aa | 46.6 |
| α-D-altro-4C1 | ae | 45.2 (46.2) | α-D-ido-4C1 | ae | 48.7 (46.2) |
| α-D-altro-1C4 | ea | 45.9 (46.2) | α-D-ido-1C4 | ea | 45.8 (46.2) |
| β-D-altro-4C1 | ee | 45.3 (43.9) | β-D-ido-4C1 | ee | 45.9 (43.8) |
| β-D-altro-1C4 | aa | 45.8 | β-D-ido-1C4 | aa | 45.6 |
| α-D-gluco-4C1 | ae | 45.8 (46.2) | α-D-galacto-4C1 | ae | 46.0 (46.0) |
| α-D-gluco-1C4 | ea | 44.4 | α-D-galacto-1C4 | ea | 44.0 |
| β-D-gluco-4C1 | ee | 46.2 (46.0) | β-D-galacto-4C1 | ee | 46.1 (45.9) |
| β-D-gluco-1C4 | aa | 47.5 | β-D-galacto-1C4 | aa | 48.2 |
| α-D-manno-4C1 | ae | 46.9 (46.7) | α-D-talo-4C1 | ae | 47.5 (46.5) |
| α-D-manno-1C4 | ea | 47.2 | α-D-talo-1C4 | ea | 47.5 |
| β-D-manno-4C1 | ee | 44.2 (42.7) | β-D-talo-4C1 | ee | 44.8 (42.3) |
| β-D-manno-1C4 | aa | 46.6 | β-D-talo-1C4 | aa | 44.7 |
| Residue (a) | Coupled Nuclei | Calculated 3JHH (Conformationally Averaged) | Exp. |
|---|---|---|---|
| GlcNS,6SNR | H-1,H-2 | 3.9 | 3.5 |
| H-2,H-3 | 10.0 | 10.3 | |
| H-3,H-4 | 9.1 | 9.7 | |
| H-4,H-5 | 9.9 | 9.7 | |
| IdoA2SNR | H-1,H-2 | 2.1 | 2.9 |
| H-2,H-3 | 3.2 | 5.4 | |
| H-3,H-4 | 3.0 | 3.8 | |
| H-4,H-5 | 2.8 | 2.7 | |
| GlcNS,6SR | H-1,H-2 | 3.1 | 3.5 |
| H-2,H-3 | 10.9 | 10.3 | |
| H-3,H-4 | 9.9 | 9.2 | |
| H-4,H-5 | 9.5 | 9.2 | |
| IdoA2SR | H-1,H-2 | 3.0 | 2.9 |
| H-2,H-3 | 5.3 | 5.3 | |
| H-3,H-4 | 3.5 | 3.9 | |
| H-4,H-5 | 3.0 | 2.7 |
| Residue (a) | Conformation | Coupled Nuclei | Calculated 3JHH (Conformationally Averaged) | Exp. |
|---|---|---|---|---|
| GlcN,6SNR | 4C1 | H-1,H-2 | 3.2 | 3.8 |
| H-2,H-3 | 10.0 | 10.3 | ||
| H-3,H-4 | 8.3 | 9.6 | ||
| H-4,H-5 | 9.7 | 10.1 | ||
| GlcA | 4C1 | H-1,H-2 | 8.0 | 7.99.5 |
| H-2,H-3 | 10.9 | |||
| H-3,H-4 | 8.1 | |||
| H-4,H-5 | 9.3 | |||
| GlcN,3,6S | 4C1 | H-1,H-2 | 4.6 | 3.5 |
| H-2,H-3 | 11.5 | 10.7 | ||
| H-3,H-4 | 10.4 | 9.3 | ||
| H-4,H-5 | 9.9 | 9.9 | ||
| IdoA2S | 1C4/2S0 | H-1,H-2 | 3.2 | 3.8 |
| H-2,H-3 | 7.1 | 7.2 | ||
| H-3,H-4 | 1.3 | 2.4 | ||
| H-4,H-5 | 4.7 | 3.1 | ||
| GlcN,6SR | 4C1 | H-1,H-2 | 4.6 | 3.6 |
| H-2,H-3 | 10.7 | 10.4 | ||
| H-3,H-4 | 9.6 | 8.5 | ||
| H-4,H-5 | 9.5 | 10.0 |
| Method | Basis Set | Slope | Intercept | RMSD |
|---|---|---|---|---|
| RHF | cc-pVDZ | −0.956 | 205.2 | 4.14 |
| cc-pVTZ | −0.966 | 196.0 | 3.73 | |
| HF+Becke | cc-pVDZ | −1.091 | 192.5 | 5.02 |
| cc-pVTZ | −1.150 | 183.7 | 5.08 | |
| HF+Slater | cc-pVDZ | −1.144 | 200.1 | 5.38 |
| cc-pVTZ | −1.203 | 189.7 | 5.49 | |
| BLYP | cc-pVDZ | −1.108 | 194.0 | 5.05 |
| cc-pVTZ | −1.171 | 185.0 | 5.03 | |
| B3LYP | cc-pVDZ | −1.085 | 197.6 | 4.70 |
| cc-pVTZ | −1.133 | 188.2 | 4.60 | |
| B3P86 | cc-pVDZ | −1.091 | 201.1 | 4.51 |
| cc-pVTZ | −1.130 | 192.0 | 4.31 | |
| BVWn | cc-pVDZ | −1.099 | 193.0 | 4.81 |
| cc-pVTZ | −1.156 | 184.0 | 4.76 | |
| SVWN | cc-pVDZ | −1.155 | 201.1 | 4.98 |
| cc-pVTZ | −1.211 | 190.4 | 4.99 | |
| mPW1PW91 | cc-pVDZ | −1.081 | 201.8 | 4.42 |
| cc-pVTZ | −1.112 | 193.8 | 5.58 |
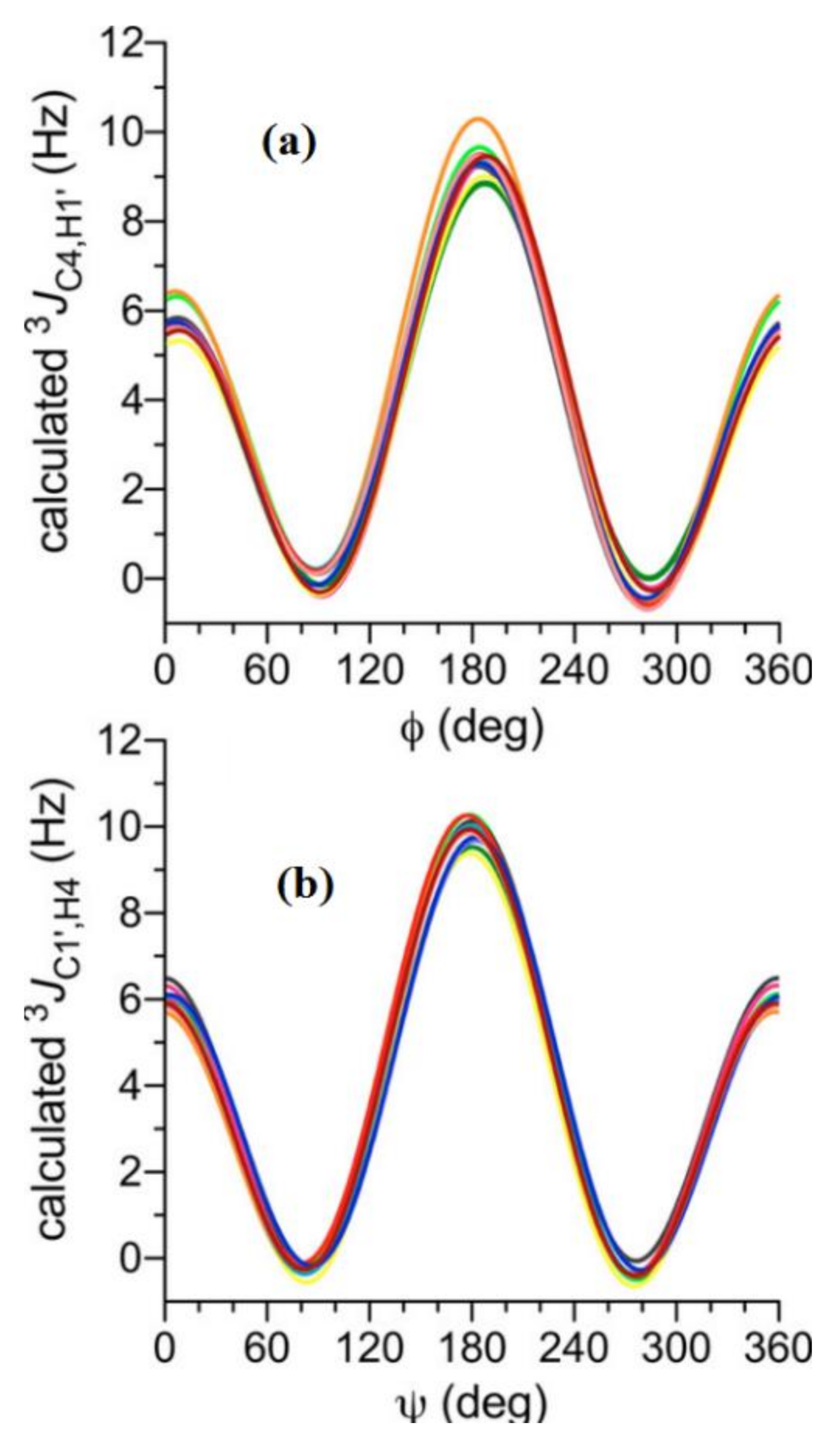
| Oligosaccharide | φ | ψ | C-1 | C-1′ (C-4′) |
|---|---|---|---|---|
| Trehalose | −49.0 (−51.9) | −49.0 (−51.9) | 93.4 (93.0) | 93.4 (93.0) |
| Cellobiose | 40.6 (41.2) | −16.4 (−12.9) | 104.8 (104.6) | 85.3 (85.0) |
| Cellotetraose | 25.8 (27.3) | −28.9 (−25.5) | 107.2 (107.4) | 88.7 (89.7) |
| Cellohexaose | 31.3 | −35.0 | 106.2 (107.1) | 87.9 (89.3) |
| Cellulose II | 31.3 (21.9) | −35.0 (−29.0) | 106.2 (107.1) | 87.9 (88.9) |
| Amilose V6 | −7.4 (−9.6) | −22.2 (−9.0) | 102.3 (103.8) | 82.0 (82.4) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krivdin, L.B. Computational NMR of Carbohydrates: Theoretical Background, Applications, and Perspectives. Molecules 2021, 26, 2450. https://doi.org/10.3390/molecules26092450
Krivdin LB. Computational NMR of Carbohydrates: Theoretical Background, Applications, and Perspectives. Molecules. 2021; 26(9):2450. https://doi.org/10.3390/molecules26092450
Chicago/Turabian StyleKrivdin, Leonid B. 2021. "Computational NMR of Carbohydrates: Theoretical Background, Applications, and Perspectives" Molecules 26, no. 9: 2450. https://doi.org/10.3390/molecules26092450
APA StyleKrivdin, L. B. (2021). Computational NMR of Carbohydrates: Theoretical Background, Applications, and Perspectives. Molecules, 26(9), 2450. https://doi.org/10.3390/molecules26092450






