Free Radical Isomerizations in Acetylene Bromoboration Reaction
Abstract
:1. Introduction
2. Results and Discussion
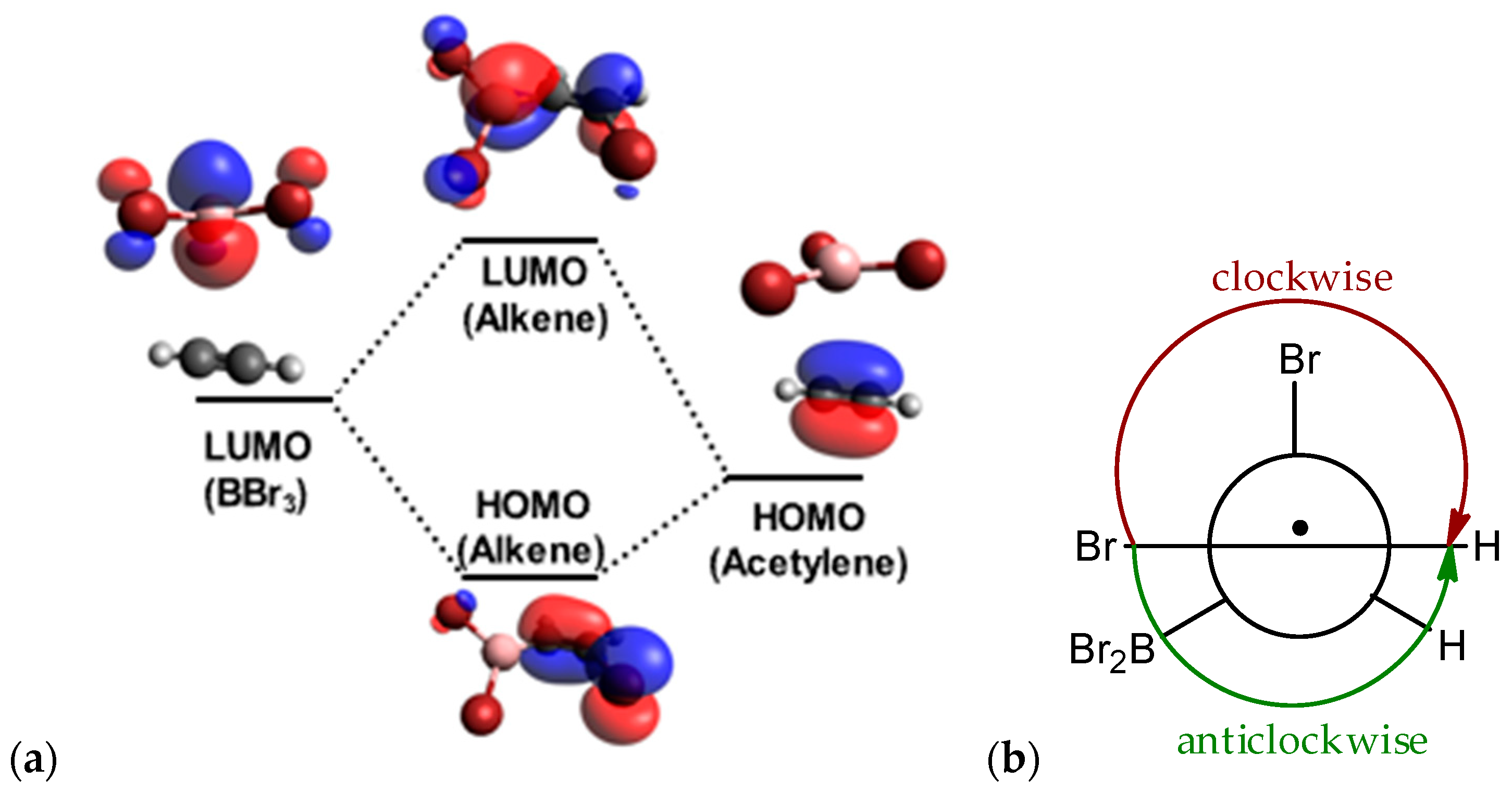
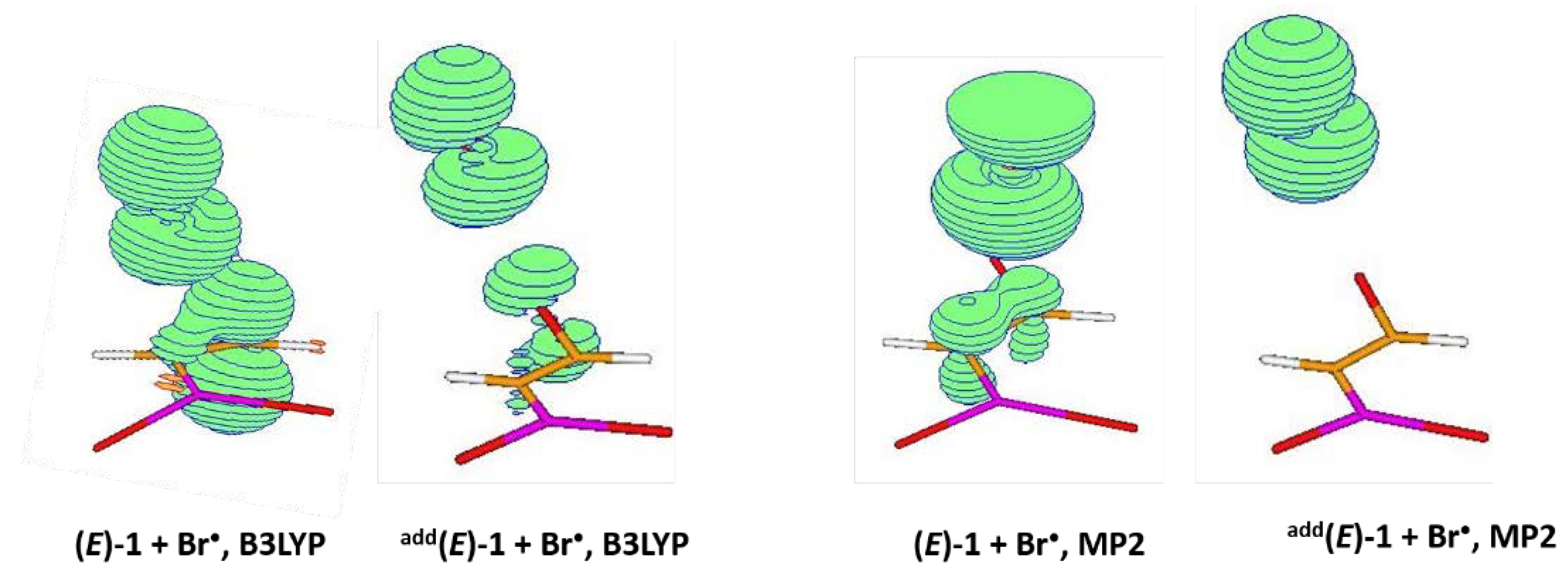
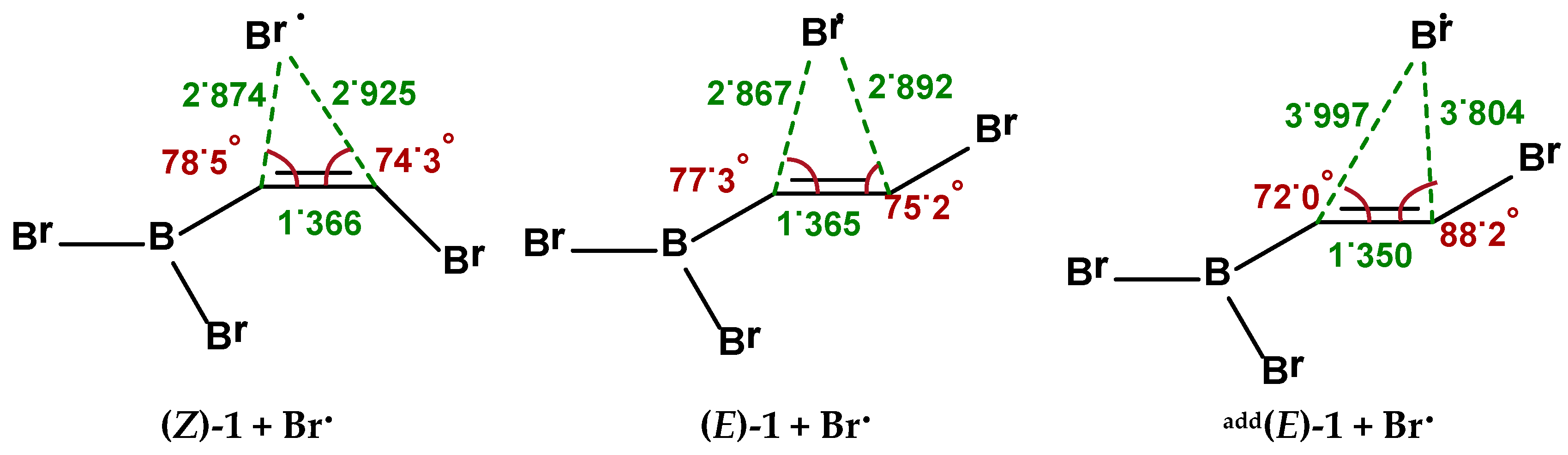
2.1. Addition Step of the Bromoboration Reaction
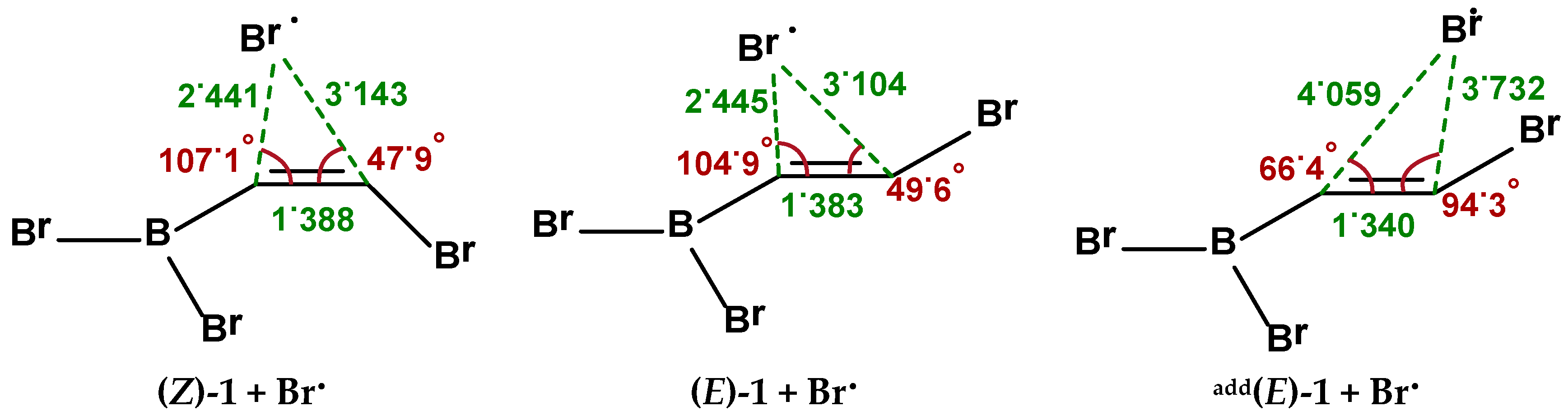
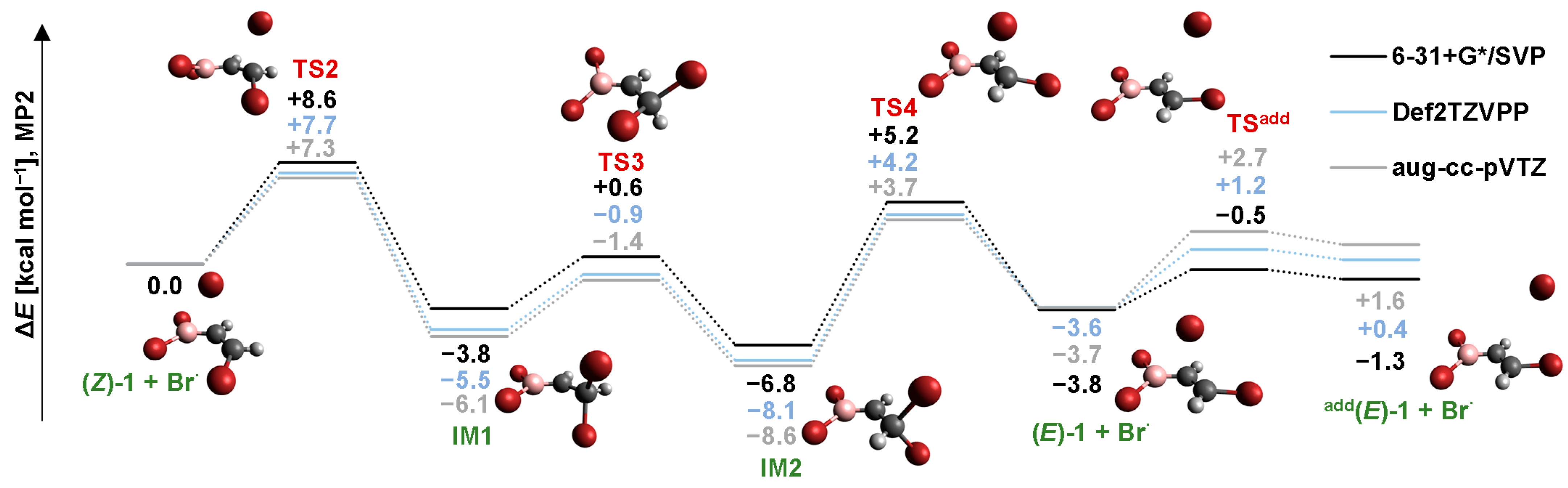
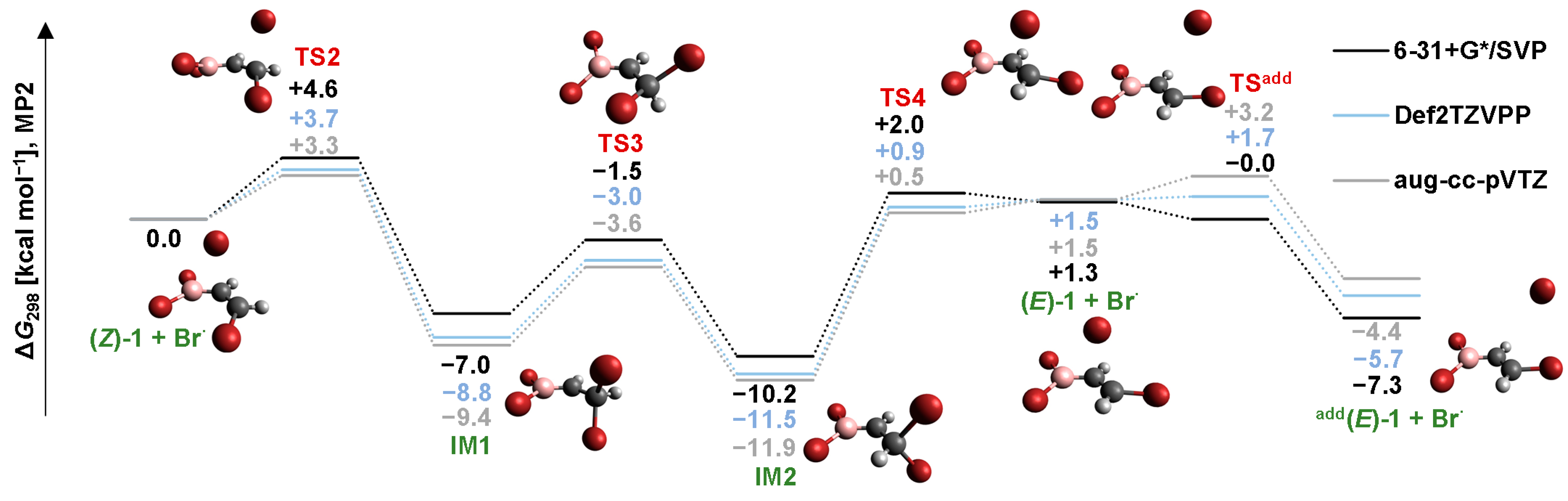
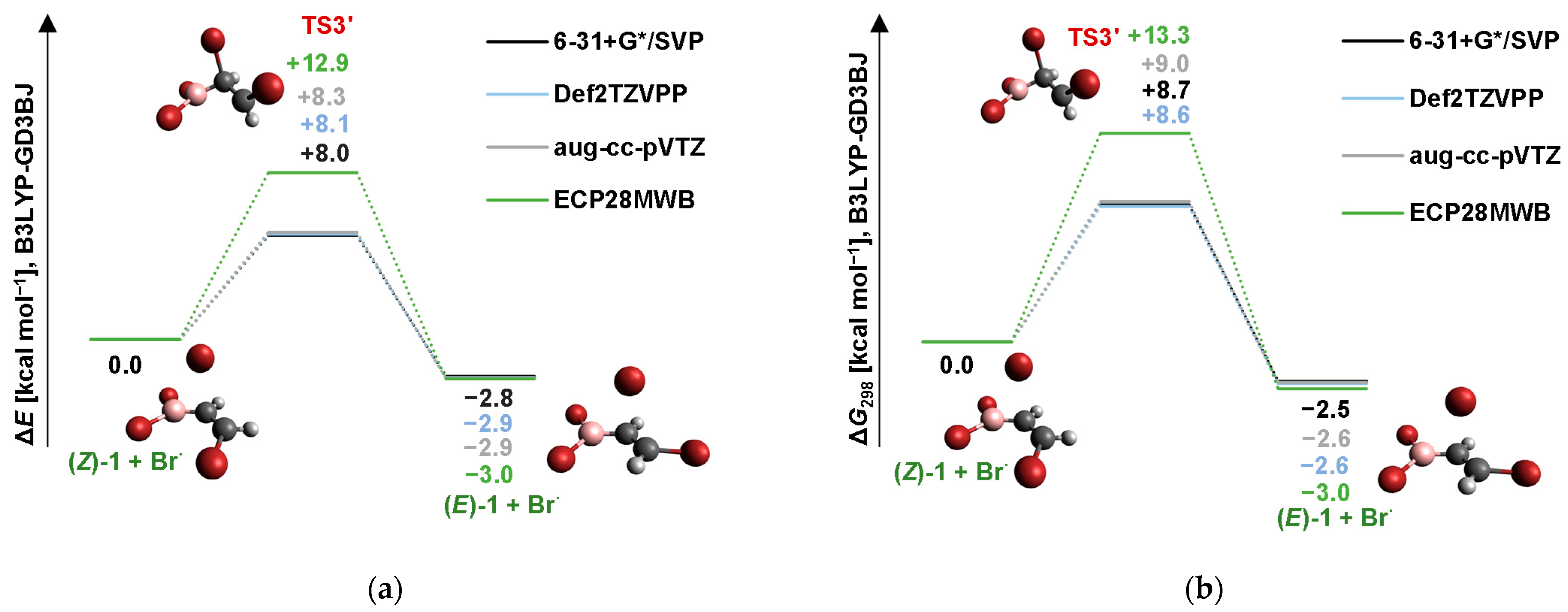
2.2. Isomerization through “Bromine End” Attack
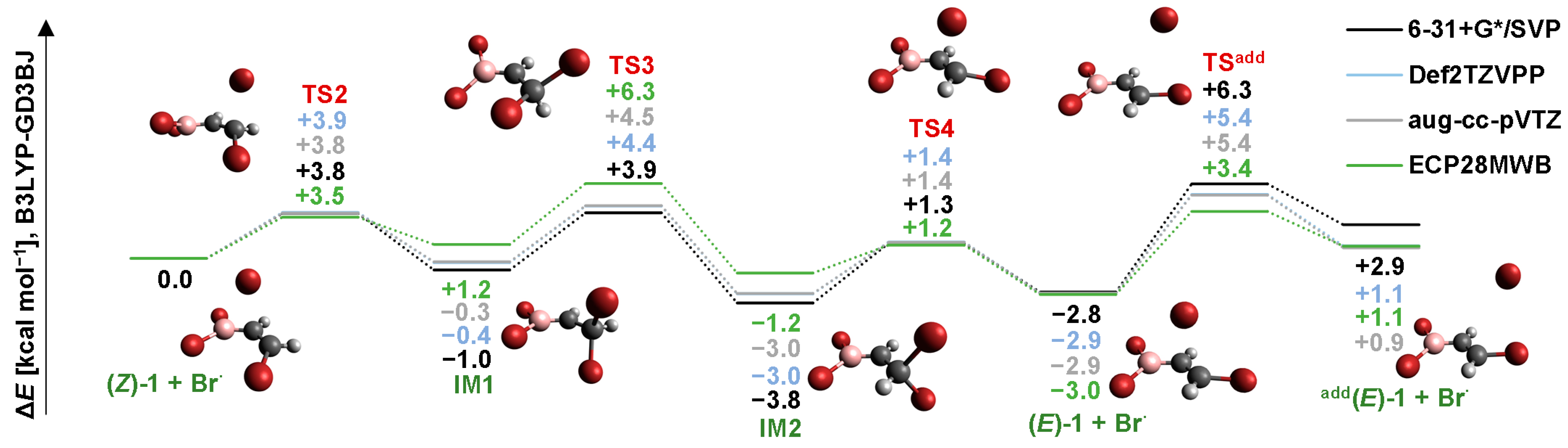
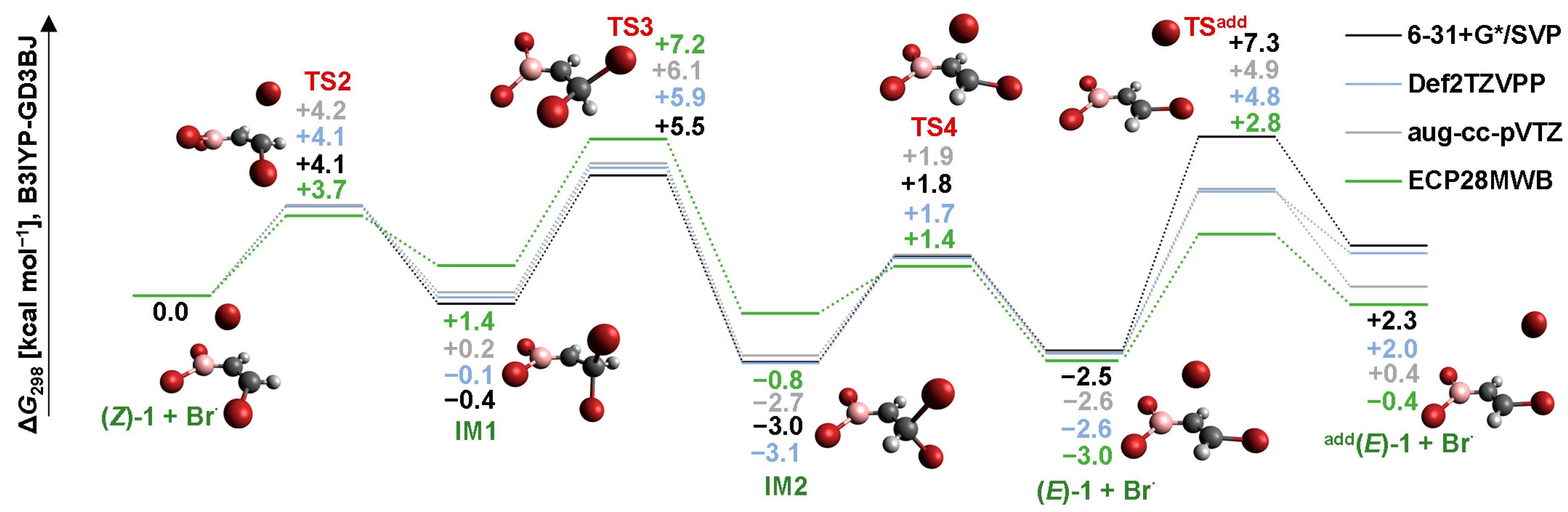
2.2.1. B3LYP Results
2.2.2. MP2 Results
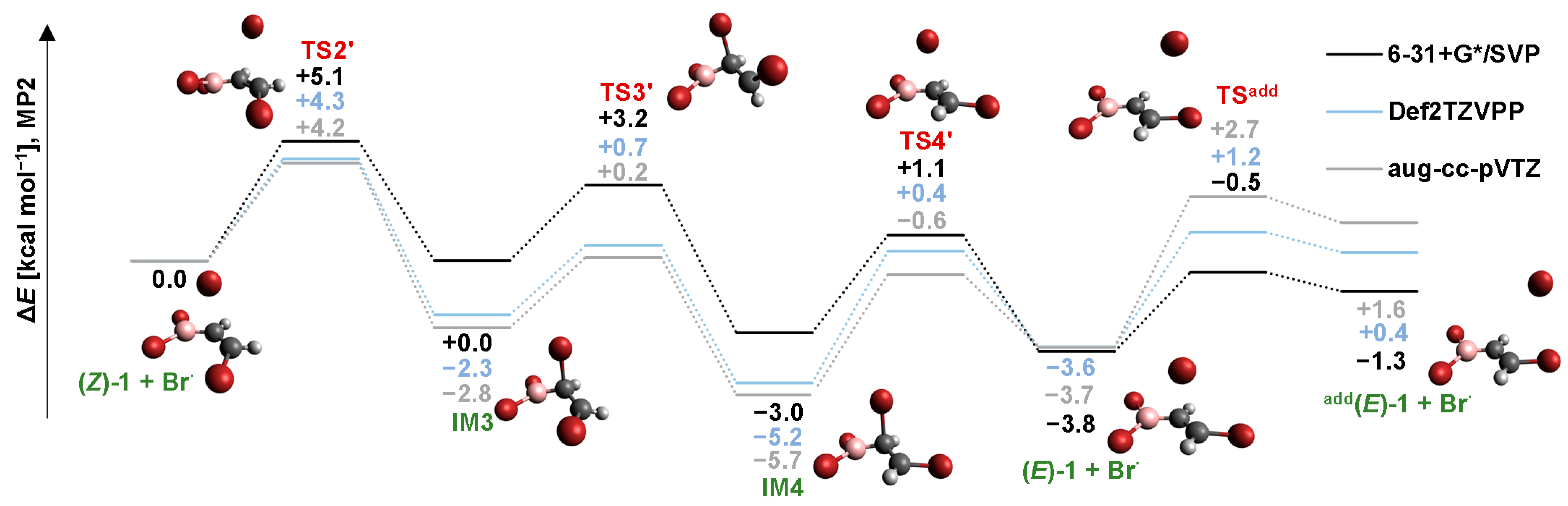
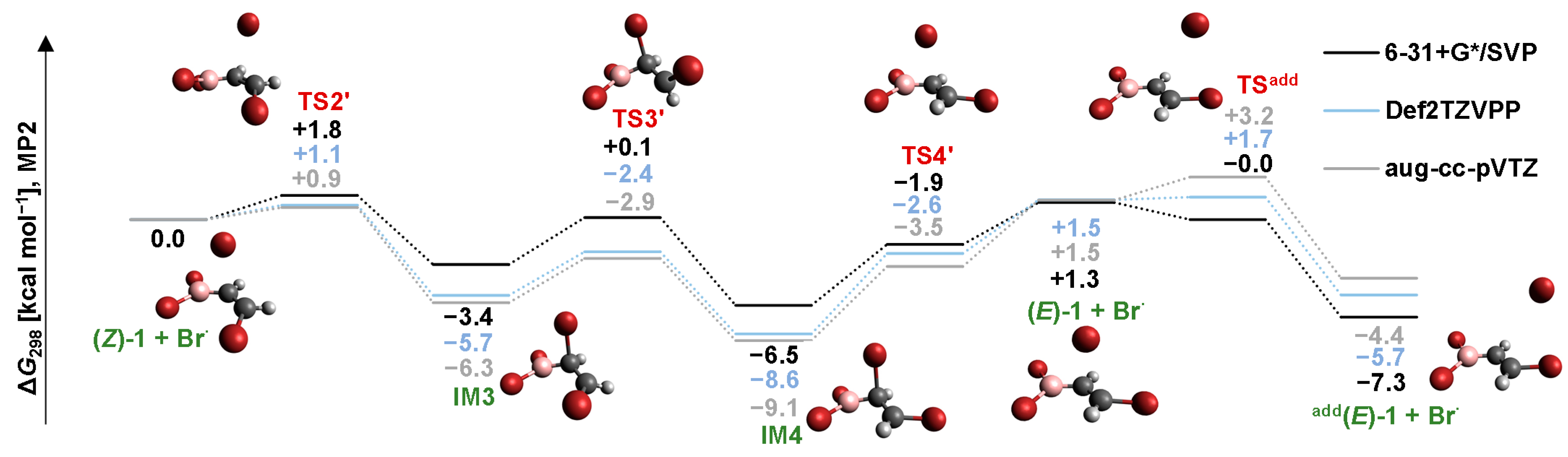
2.3. Isomerization through the “Boron End” Attack with Clockwise Rotation
2.3.1. MP2 Results
2.3.2. B3LYP Results
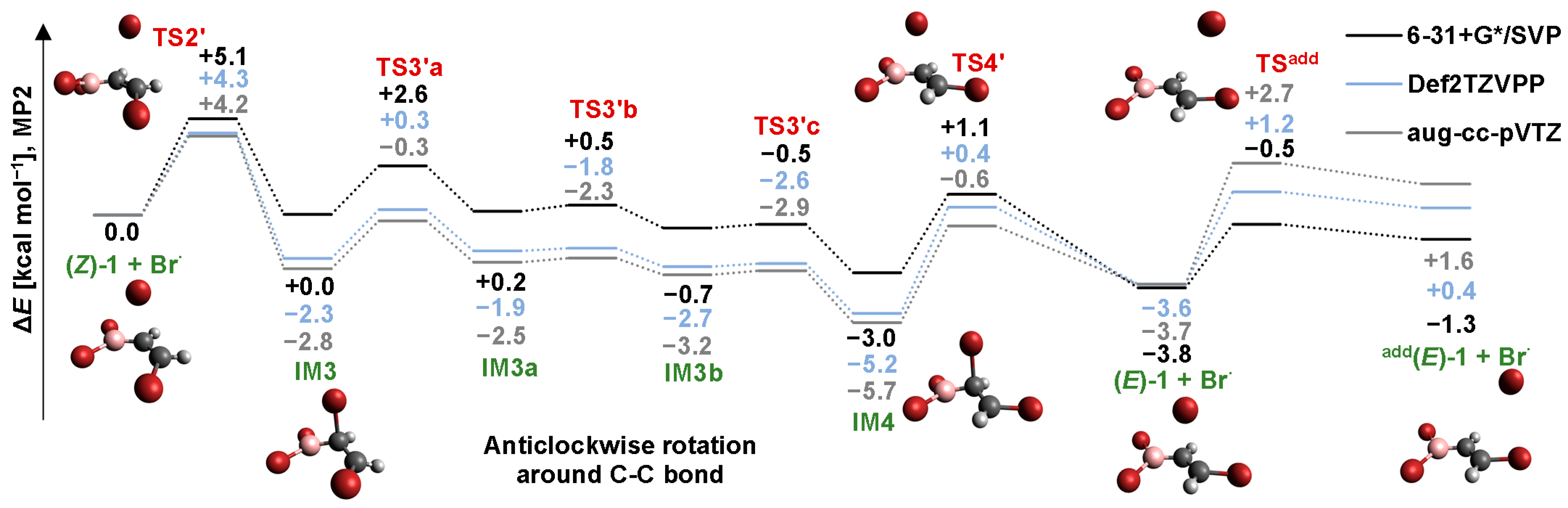
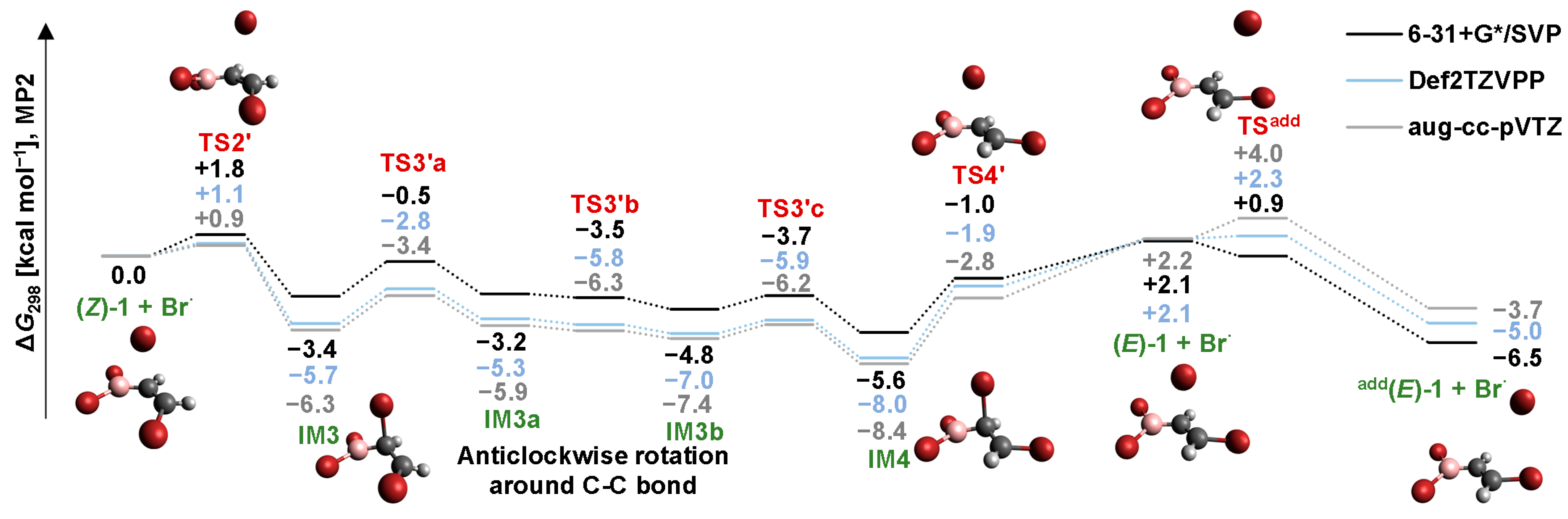
2.4. Isomerization through the “Boron End” Attack with Anticlockwise Rotation
2.4.1. MP2 Results
2.4.2. B3LYP Results
3. Computational Details
3.1. Starting Structures, PES Stationary Point Determination, and Their Verification
3.2. Ab Initio Methods, Basis Sets, Pseudopotentials, and Solvent Model
3.3. Implementation, Energy Contribution Representations, and Structure Visualizations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Lappert, M.F.; Prokai, B. Chloroboration and allied reactions of unsaturated compounds. II. Haloboration and phenylboration of Acetylenes; and the preparation of some alkynylboranes. J. Organometal. Chem. 1964, 1, 384–400. [Google Scholar] [CrossRef]
- Blackborow, J.R. Stereoselectivity of Halogenoboration of Phenylacetylene. J. Chem. Soc. Perkin Trans. 1973, 2, 1989–1993. [Google Scholar] [CrossRef]
- Wrackmeyer, B. Long-range nuclear spin-spin coupling between 11B and 13C, 29Si or 119Sn: A promising tool for structural assignment. Polyhedron 1986, 5, 1709–1721. [Google Scholar] [CrossRef]
- Mazal, C.; Vaultier, M. A simple, general and stereoselective synthesis of 1-(dialkoxyboryl)-1,3-dienes. Tetrahedron Lett. 1994, 35, 3089–3090. [Google Scholar] [CrossRef]
- Suzuki, A. Organoboranes in Organic Syntheses Including Suzuki Coupling Reaction. Heterocycles 2010, 80, 15–43. [Google Scholar] [CrossRef] [Green Version]
- Kirschner, A.; Yuan, K.; Ingleson, M.J. Haloboration: Scope, mechanism and utility. New J. Chem. 2021. [Google Scholar] [CrossRef]
- Wang, C.; Uchyiama, M. Mechanistic Understanding of Alkyne Haloboration: An Ab Initio Study. Eur. J. Org. Chem. 2012, 2012, 6548–6554. [Google Scholar] [CrossRef]
- Lawson, J.R.; Clark, E.R.; Cade, I.A.; Solomon, S.A.; Ingleson, M.J. Haloboration of Internal Alkynes with Boronium and Borenium Cations as a Route to Tetrasubstituted Alkenes. Angew. Chem. Int. Ed. 2013, 52, 7518–7522. [Google Scholar] [CrossRef] [Green Version]
- Polášek, J.; Paciorek, J.; Stošek, J.; Semrád, H.; Munzarová, M.; Mazal, C. Stereoselective Bromoboration of Acetylene with Boron Tribromide: Preparation and Cross-Coupling Reactions of (Z)-Bromovinylboronates. J. Org. Chem. 2020, 85, 6992–7000. [Google Scholar] [CrossRef]
- Hyuga, S.; Chiba, Y.; Yamashina, N.; Hara, S.; Suzuki, A. (E)-(2-Bromoethenyl)dibromoborane. A New Precursor for (E)-1,2-Disubstituted Ethenes. Chem. Lett. 1987, 16, 1757–1760. [Google Scholar] [CrossRef]
- Hyuga, S.; Yamashina, N.; Hara, S.; Suzuki, A. (E)-(2-Bromoethenyl)diisopropoxyborane. A New Building Block for (E)-Olefins. Chem. Lett. 1988, 17, 809–812. [Google Scholar] [CrossRef]
- Grabowski, S. Triel Bonds, π-Hole-π-Electrons Interactions in Complexes of Boron and Aluminium Trihalides and Trihydrides with Acetylene and Ethylene. Molecules 2015, 20, 11297–11316. [Google Scholar] [CrossRef]
- Grabowski, S. Triel bond and coordination of triel centres—Comparison with hydrogen bond interaction. Coord. Chem. Rev. 2020, 407, 213171. [Google Scholar] [CrossRef]
- Alves, M.; Méreau, R.; Grignard, B.; Detrembleur, C.; Jérôme, C.; Tassaing, T. DFT investigation of the reaction mechanism for the guanidine catalyzed ring-opening of cyclic carbonates by aromatic and alkyl-amines. RSC Adv. 2017, 7, 18993–19001. [Google Scholar] [CrossRef] [Green Version]
- Merrick, J.P.; Moran, D.; Radom, L. An Evaluation of Harmonic Vibrational Frequency Scale Factors. J. Phys. Chem. A 2007, 111, 11683–11700. [Google Scholar] [CrossRef] [PubMed]
- Kesharwani, M.K.; Brauer, B.; Martin, J.M.L. Frequency and Zero-Point Vibrational Energy Scale Factors for Double-Hybrid Density Functionals (and Other Selected Methods): Can Anharmonic Fields Be Avoided? J. Phys. Chem. A 2015, 119, 1701–1714. [Google Scholar] [CrossRef]
- Joo, H.; Kraka, E.; Quapp, W.; Cremer, D. The mechanism of a Barrierless Reaction: Hidden Transition State and Hidden Intermediates in the Reaction of Methylene with Ethene. Mol. Phys. 2007, 105, 2697–2717. [Google Scholar] [CrossRef]
- Lu, Y.-J.; Lee, L.; Pan, J.-W.; Xie, T.; Witek, H.A.; Lin, J.J. Barrierless reaction between two closed-shell molecules. I. Dynamics of F2 + CH3SCH3 reaction. J. Chem. Phys. 2008, 128, 104317. [Google Scholar] [CrossRef]
- Sandhyia, L.; Zipse, H. Initiation Chemistries in Hydrocarbon (Aut)Oxidation. Chem. Eur. J. 2015, 21, 14060–14067. [Google Scholar] [CrossRef]
- Piletic, I.R.; Edney, E.O.; Bartolotti, L.J. Barrierless Reactions with Loose Transition States Govern the Yields and Lifetimes of Organic Nitrates Derived from Isoprene. J. Phys. Chem. A 2017, 121, 8306–8321. [Google Scholar] [CrossRef]
- Zhao, L.; Kaiser, R.I.; Lu, W.; Ahmed, M.; Evseev, M.M.; Bashkirov, E.K.; Azyazov, V.N.; Tönshoff, C.; Reicherter, F.; Bettinger, H.F.; et al. A Free-Radical Prompted Barrierless Gas-Phase Synthesis of Pentacene. Angew. Chem. Int. Ed. 2020, 59, 11334–11338. [Google Scholar] [CrossRef]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminformatics 2012, 4, 17. [Google Scholar] [CrossRef] [Green Version]
- Avogadro: An Open-Source Molecular Builder and Visualization Tool. Version 1.1.1. Available online: http://avogadro.cc/ (accessed on 26 March 2014).
- Henkelman, G.; Jóhannesson, G.; Jónsson, H. Methods for Finding Saddle Points and Minimum Energy Paths. Prog. Theor. Chem. Phys. 2000, 5, 269–302. [Google Scholar]
- Schlegel, H.B. Exploring Potential Energy Surfaces for Chemical Reactions: An Overview of Some Practical Methods. J. Comp. Chem. 2003, 24, 1514–1527. [Google Scholar] [CrossRef] [PubMed]
- Fukui, K. The path of chemical-reactions—The IRC approach. Acc. Chem. Res. 1981, 14, 363–368. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 31, 785–789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Austin, A.; Petersson, G.A.; Frisch, M.J.; Dobek, F.J.; Scalmani, G.; Throssel, K. A density functional with spherical atom dispersion terms. J. Chem. Theory Comput. 2012, 8, 4989–5007. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comp. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Frisch, M.J.; Head-Gordon, M.; Pople, J.A. Direct MP2 gradient method. Chem. Phys. Lett. 1990, 166, 275–280. [Google Scholar] [CrossRef]
- Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self-Consistent Molecular Orbital Methods XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar]
- Hariharan, P.C.; Pople, J.A. The influence of polarization functions on molecular orbital hydrogenation energies. Theor. Chim. Acta 1973, 28, 213–222. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li-F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Schaefer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian-basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Uchimaru, T.; Mikami, M.; Tanabe, K. New Medium-Size Basis Sets To Evaluate the Dispersion Interaction of Hydrocarbon Molecules. J. Phys. Chem. A 1998, 102, 2091–2094. [Google Scholar] [CrossRef]
- Bergner, A.; Dolg, M.; Kuechle, W.; Stoll, H.; Preuss, H. Ab-initio energy-adjusted pseudopotentials for elements of groups 13–17. Mol. Phys. 1993, 80, 1431–1441. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B. 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision, D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Schaftenaar, G.; Noordik, J.H. Molden: A pre-and post-processing program for molecular and electronic structures. J. Comput. Aided Mol. Des. 2000, 14, 123–134. [Google Scholar] [CrossRef]
- Sandhiya, L.; Zipse, H. Radical-Pair Formation in Hydrocarbon (Aut)Oxidation. Chem. Eur. J. 2019, 25, 8604–8611. [Google Scholar] [CrossRef] [PubMed]


| ZPE Corrections/ kcal mol−1 | MP2 | B3LYP-GD3BJ | |||||
|---|---|---|---|---|---|---|---|
| 6-31+G*/ SVP a | Def2-TZVPP b | aug-cc-pVTZ c | 6-31+G*/ SVP d | Def2-TZVPP e | aug-cc-pVTZ f | 6-31+G*/ ECP28MWB d | |
| (Z)-1 + Br• | 29.1/28.1 | 52.9/51.6 | 39.6/38.8 | 24.1/23.8 | 24.0/23.7 | 24.0/23.8 | 24.3/24.0 |
| TS2 | 24.7/23.9 | 24.7/24.1 | 24.6/24.1 | 24.1/23.8 | 23.9/23.6 | 23.9/23.7 | 23.9/23.6 |
| IM1 | 25.1/24.2 | 24.9/24.3 | 24.9/24.4 | 24.4/24.1 | 24.3/24.0 | 24.2/23.9 | 24.3/24.0 |
| TS3 | 25.0/24.1 | 24.8/24.2 | 24.7/24.2 | 24.2/23.9 | 24.0/23.7 | 24.0/23.8 | 23.9/23.6 |
| IM2 | 25.4/24.5 | 25.2/24.6 | 25.2/24.7 | 24.8/24.4 | 24.6/24.3 | 24.6/24.3 | 24.7/24.3 |
| TS4 | 24.8/23.9 | 24.7/24.1 | 24.6/24.1 | 24.1/23.8 | 23.9/23.6 | 23.9/23.7 | 23.9/23.6 |
| (E)-1 + Br• | 33.8/32.6 | 32.8/32.0 | 30.8/3 0.2 | 24.2/23.9 | 24.2/23.9 | 24.1/23.8 | 24.3/24.0 |
| TSadd | 29.6/28.6 | 28.0/27.3 | 27.5/26.9 | 24.1/23.8 | 24.0/23.7 | 24.0/23.8 | 23.9/23.6 |
| add(E)-1 + Br• | 24.6/23.8 | 24.7/24.1 | 24.7/24.2 | 24.5/24.1 | 24.3/24.0 | 24.4/24.1 | 24.3/24.0 |
| ZPE Corrections/ kcal mol−1 | MP2 | B3LYP-GD3BJ | |||||
|---|---|---|---|---|---|---|---|
| 6-31+G*/ SVP a | Def2-TZVPP b | aug-cc-pVTZ c | 6-31+G*/ SVP d | Def2-TZVPP e | aug-cc-pVTZ f | 6-31+G*/ ECP28MWB d | |
| Clockwise rotation around C–C bond | |||||||
| (Z)-1 + Br• | 29.1/28.1 | 52.9/51.6 | 39.6/38.8 | 24.1/23.8 | 24.0/23.7 | 24.0/23.8 | 24.3/24.0 |
| TS2′ | 25.0/24.1 | 25.1/24.5 | 25.1/24.6 | ||||
| IM3 | 24.8/23.9 | 24.4/23.8 | 24.4/23.9 | ||||
| TS3′ | 24.3/23.5 | 24.1/23.5 | 24.0/23.5 | 23.5/23.2 | 23.4/23.1 | 23.3/23.1 | 24.3/24.0 |
| IM4 | 24.9/24.0 | 24.6/24.0 | 24.6/24.1 | ||||
| TS4′ | 25.0/24.1 | 25.0/24.4 | 24.7/24.2 | ||||
| (E)-1 + Br• | 33.8/32.6 | 32.8/32.0 | 30.8/30.2 | 24.2/23.9 | 24.2/23.9 | 24.1/23.8 | 24.3/24.0 |
| TSadd | 29.6/28.6 | 28.0/27.3 | 27.5/26.9 | 24.1/23.8 | 24.0/23.7 | 24.0/23.8 | 23.9/23.6 |
| add(E)-1 + Br• | 24.6/23.8 | 24.7/24.1 | 24.7/24.2 | 24.5/24.1 | 24.3/24.0 | 24.4/24.1 | 24.3/24.0 |
| Anticlockwise rotation around C–C bond | |||||||
| (Z)-1 + Br• | 29.1/28.1 | 52.9/51.6 | 39.6/38.8 | 24.1/23.8 | 24.0/23.7 | 24.0/23.8 | 24.3/24.0 |
| TS2′ | 25.0/24.1 | 25.1/24.5 | 25.1/24.6 | ||||
| IM3 | 24.8/23.9 | 24.4/23.8 | 24.4/23.9 | ||||
| TS3′a | 24.5/23.7 | 24.3/23.7 | 24.2/23.7 | 23.8/23.5 | 23.7/23.4 | 23.6/23.4 | - |
| IM3a | 24.7/23.9 | 24.423.8 | 24.4/23.9 | 23.9/23.6 | 23.7/23.4 | 23.6/23.4 | - |
| TS3′b | 24.1/23.3 | 23.8/23.2 | 23.8/23.3 | 23.5/23.2 | 23.4/23.1 | 23.4/23.2 | - |
| IM3b | 24.8/23.9 | 24.5/23.9 | 24.4/23.9 | ||||
| TS3′c | 24.6/23.8 | 24.4/23.8 | 24.3/23.8 | ||||
| IM4 | 24.9/24.0 | 24.6/24.0 | 26.6/24.1 | ||||
| TS4′ | 25.0/24.1 | 25.0/24.4 | 24.7/24.2 | ||||
| (E)-1 + Br• | 33.8/32.6 | 32.8/32.0 | 30.8/30.2 | 24.2/23.9 | 24.2/23.9 | 24.1/23.8 | 24.3/24.0 |
| TSadd | 29.6/28.6 | 28.0/27.3 | 27.5/26.9 | 24.1/23.8 | 24.0/23.7 | 24.0/23.8 | 23.9/23.6 |
| add(E)-1 + Br• | 24.6/23.8 | 24.7/24.1 | 24.7/24.2 | 24.5/24.1 | 24.3/24.0 | 24.4/24.1 | 24.3/24.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Semrád, H.; Mazal, C.; Munzarová, M. Free Radical Isomerizations in Acetylene Bromoboration Reaction. Molecules 2021, 26, 2501. https://doi.org/10.3390/molecules26092501
Semrád H, Mazal C, Munzarová M. Free Radical Isomerizations in Acetylene Bromoboration Reaction. Molecules. 2021; 26(9):2501. https://doi.org/10.3390/molecules26092501
Chicago/Turabian StyleSemrád, Hugo, Ctibor Mazal, and Markéta Munzarová. 2021. "Free Radical Isomerizations in Acetylene Bromoboration Reaction" Molecules 26, no. 9: 2501. https://doi.org/10.3390/molecules26092501
APA StyleSemrád, H., Mazal, C., & Munzarová, M. (2021). Free Radical Isomerizations in Acetylene Bromoboration Reaction. Molecules, 26(9), 2501. https://doi.org/10.3390/molecules26092501





